Relationship between degree of obstruction and airflow limitation in subglottic stenosis

Abstract

Objectives

Subglottic stenosis (SGS) is one of the most common airway disorders in pediatric patients. Currently, treatment decisions rely primarily on the Cotton-Myer scale, which classifies SGS severity based on percentage reduction in airspace cross-sectional area (CSA). However, the precise relationship between upper airway resistance and subglottic CSA is unknown. We hypothesize that airway resistance can be described by the Bernoulli Obstruction Theory, which predicts that airway resistance is inversely proportional to airspace CSA (R ∝ A⁻¹) in cases of severe constriction.

Methods

Computed tomography scans of 6 healthy subjects and 5 SGS patients were used to create three-dimensional models of the respiratory tract from nostrils to carina. Cylindrical segments of varying lengths and varying diameters were digitally inserted in the subglottis of the healthy subjects to create simulated SGS models. Computational fluid dynamics (CFD) simulations were run and airway resistance was computed in the simulated SGS models and actual SGS models.

Results

Constriction diameter had a greater impact in airway resistance than constriction length. In agreement with the Bernoulli Obstruction Theory, airway resistance in the simulated SGS models was well represented by the power law R = aA^b, where a is a constant and the exponent b ranged from −0.85 to −1.07. The percentage reduction in airflow $\left(\frac{Q_{\mathit{OBSTRUCTION}}}{Q_{\mathit{HEALTHY}}}\right)$ at a constant pressure drop was found to be directly proportional to the percentage reduction in CSA $\left(\frac{A_{\mathit{OBSTRUCTION}}}{A_{\mathit{HEALTHY}}}\right)$ in the limit of severe constrictions, namely $\frac{Q_{\mathit{OBSTRUCTION}}}{Q_{\mathit{HEALTHY}}}=k\frac{A_{\mathit{OBSTRUCTION}}}{A_{\mathit{HEALTHY}}}$, where k = 2.25 ± 0.15. Airway resistances in the simulated SGS models were similar to resistances in models based on CT scans of actual SGS patients, suggesting that our simulated SGS models were representative of airway resistance in actual SGS patients.

Conclusions

Our computer simulations suggest that the degree of airflow limitation in SGS patients may be estimated based on anatomic measurements alone. Future studies are recommended to tests these predictions in larger cohorts.

Introduction

Subglottic stenosis (SGS) remains one of the most common airway problems in neonates and children younger than 1 year old.¹ Traditionally, intervention relies on clinical observations alone without objective measures of respiratory airflow. One common criterion to guide SGS treatment is the Cotton-Myer classification system, which is based on endoscopic estimates of the airspace cross-sectional area (CSA) at the subglottis and classifies obstruction severity as follows: grade I stenosis, less than 50% obstruction; grade II stenosis, 51% to 70% obstruction; grade III stenosis, 71% to 99% obstruction; and grade IV stenosis, no detectable lumen or complete stenosis.² This grading system serves as a simple method of relating lesion severity to prognosis for decannulation and can help to predict success of pediatric laryngotracheal reconstruction (LTR).^3–5 However, the precise relationship between airspace CSA and airway resistance to airflow is still not fully understood. Specifically, the Cotton-Myer grading system does not provide an exact measurement of the degree of airflow reduction that corresponds to a percent reduction in cross-sectional area. Consequently, patient selection for surgeries is challenging and is currently performed without objective measures of airflow and anatomy, thus possibly limiting the effectiveness of treatment plans.⁶

The goal of this study is to investigate the relationship between airflow resistance and constriction geometry (length and cross-sectional area) in the context of subglottic stenosis. It has been previously assumed that the pressure-flow relationship of the human upper airway in the context of subglottic stenosis obeys the Hagen-Poiseuille equation,⁷ which predicts that airflow resistance (R) is inversely proportional to the fourth power of the tube diameter $R=\frac{128\mu L}{\pi d^4}$, where μ is fluid viscosity and L is the tube length), which is equivalent to the resistance being inversely proportional to the second power of the airspace cross-sectional area (R ∝ A⁻²). However, the Hagen-Poiseuille equation is valid only for fully-developed, laminar flow in straight circular tubes.^8,9 Airflow in the human upper respiratory tract is near the transition from laminar to turbulent flow,^10,11 and the airflow patterns are affected by entrance effects and bends, which invalidate the assumptions of the Hagen-Poiseuille equation. Our hypothesis is that upper airway resistance is better described by the Bernoulli Obstruction Theory^8,9,12 which predicts that airway resistance is inversely proportional to airspace cross-sectional area (R ∝ A⁻¹). The Bernoulli Obstruction Theory predicts that a 4-fold reduction in cross-sectional area would result in a 4-fold increase in upper airway resistance, while the Hagen-Poiseuille equation predicts that the same change in cross-sectional area would result in a 16-fold increase in resistance. Our underlying hypothesis is that a better understanding of the relationship between degree of stenosis and airway resistance will help clinicians identify the optimal treatment plan for each SGS patient.

Materials and Methods

Study Design

This study was designed as a systematic investigation of the relationship between upper airway resistance (R) and airspace cross-sectional area (CSA) at the subglottis using computational techniques. Two patient cohorts were investigated, namely a cohort of healthy subjects and a cohort of SGS patients. The healthy cohort provided the baseline upper airway resistance and the baseline geometries used to create simulated SGS models by digitally inserting constrictions of different sizes in the subglottis to quantify the relationship between R and subglottic CSA. The SGS cohort was used only as a qualitative validation to demonstrate that airway resistances in simulated SGS models were similar to airway resistances in actual SGS patients.

Patient Selection

IRB approval was not required for this study since de-identified 3D reconstructions of the upper airway were available from previous studies.¹³ Five pediatric patients with SGS and five children with radiographically normal airways (as determined by a pediatric otolaryngologist) were obtained from UNC’s Pediatric Airway Atlas.¹³ Healthy and SGS pediatric subjects were matched for age and weight, but not gender (Table S1 in the online-only Supporting Information). In addition to the pediatric models, a model representing a healthy adult was also included. The subjects were selected to represent a wide range of body sizes and ages (Table S1), thus allowing us to investigate whether body size and inter-individual variability in airway anatomy affect the relationship between R and subglottic CSA. The 6-month-old SGS model was created from a pre-intervention CT scan, while all other SGS models represent post-intervention scans (Table S1).

Construction of Original Models

The airway reconstructions of the pediatric patients were created from high resolution computed tomography (CT) scans with slice increment between 0.3 mm and 0.6 mm in all patients, except for one patient who had a slice increment of 1.0 mm. Magnetic Resonance Imaging (MRI) of the healthy adult subject had a pixel size of 0.59 mm and a distance of 0.50 mm between slices. Airway geometries of the pediatric models were reconstructed using the Virtual Pediatric Airway Workbench,¹⁴ while the adult model was built in Mimics^™ (Materialise, Leuven, Belgium). All models included the geometry from nostrils to carina (Figure 1). The airway geometries were exported in STL format and imported into ICEM-CFD (Ansys, Inc., Canonsburg, PA), where tetrahedral meshes were created with at least 4 million cells. All tetrahedral elements were checked to have an aspect ratio larger than 0.3 to avoid distorted elements. For greater accuracy, the meshes were refined around the stenosis region with tetrahedral sizes ¼ smaller at the stenosis than elsewhere in the model.

Figure 1.

Three-dimensional models of the respiratory tract representing 5 healthy children, 1 healthy adult, and 5 SGS patients. The 6-month-old SGS model was based on a pre-intervention CT scan while all other SGS models were based on post-intervention CT scans.

Construction of Models with Varying Levels of Obstruction

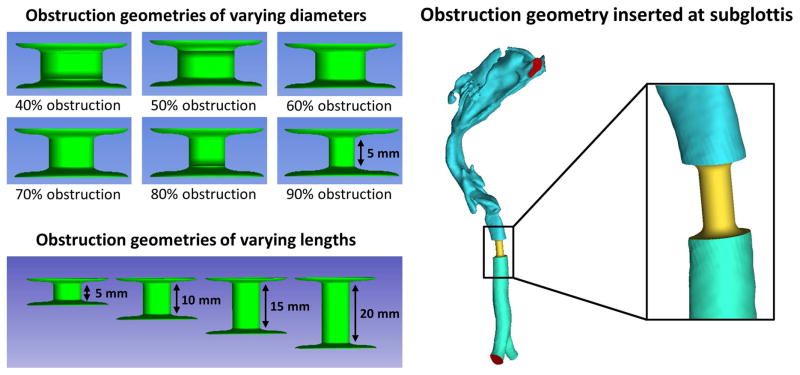
To simulate airway constrictions, a standard 5-mm long cylindrical segment was created and digitally rescaled in ICEM-CFD to represent cross-sectional areas corresponding to 40%, 50%, 60%, 70%, 80%, and 90% obstruction (Figure 2). Each cylinder was then re-scaled to fit inside the airway of each healthy model at the level of the subglottis as identified by an otolaryngologist (Figure 2). To study the effect of obstruction length, cylindrical geometries with lengths of 10 mm, 15 mm, and 20 mm were also created for the healthy adult model and re-scaled to correspond to 50%, 70%, and 90% obstruction (Figure 2).

Figure 2.

Method to create simulated obstructions at the subglottis. Cylindrical segments 5-mm in length and with diameters corresponding to 40% to 90% obstruction were inserted at the subglottis of all healthy models. In the obstruction length study, cylindrical segments with lengths of 5 mm, 10 mm, 15 mm, and 20 mm were inserted into the subglottics of the healthy adult model.

Computational Fluid Dynamics (CFD) Simulations

Steady-state airflow simulations were conducted in Fluent 14.0 (ANSYS, Inc) for airflow rates corresponding to a patient breathing at rest. The following boundary conditions were used: (1) inlet pressure at the nostrils with gauge pressure 0 Pa, (2) no-slip conditions (zero velocity) at the wall, and (3) a constant negative outlet pressure was imposed to achieve the desired inhalation rate for each patient (Table S1). The k-omega turbulence model was used with a turbulent scale of 1 mm and 5% turbulence intensity at the nostrils. Previous studies have demonstrated that the standard k-omega turbulence model accurately reproduces experimental measurements of air pressure in patient-specific replicas of the human upper airway.¹¹ Since breathing rates were not measured in vivo, the inhalation rates were estimated using each child’s body mass using the following equation:¹⁵

$${\mathrm{V}}_{\mathrm{E}}=(1.36\pm 0.10){\mathrm{M}}^{0.44\pm 0.22},\mathrm{r}=0.995$$ (1)

where V_E is the minute volume (i.e., volume of air expired per minute). The steady-state inhalation rate was computed as 2 times the minute volume under the assumption that inspiration and expiration have the same duration (Table S1). For the adult model, a steady-state inhalation rate of 15 L/min was used, which is the most common inhalation rate used for adults in the CFD literature.¹⁶ Airway resistance was defined as R = ΔP/Q, where ΔP is the pressure drop from nostrils to carina and Q is the inhalation rate. The same outlet pressure was used in all simulated SGS models (40% to 90% obstruction) of each patient, so that the desired inhalation rate (Table S1) was obtained only in the original healthy model (0% obstruction), but the pressure drop ΔP was the same in all simulated SGS models of a given subject.

Bernoulli Obstruction Theory

We propose that the relationship between airway resistance and airspace cross-sectional area at the subglottis can be described by the Bernoulli Obstruction Theory.^8,9 The continuity equation and the Bernoulli equation for steady frictionless incompressible flow imply that

$$Q=A_1{V}_1=A_2{V}_2$$ (2)

$$P_1+\frac{1}{2}\rho V_1^2=P_2+\frac{1}{2}\rho V_2^2$$ (3)

where A is cross-sectional area, V is air velocity, P is air pressure, ρ = 1.204 kg/m³ is air density, and the indices 1 and 2 refer to two positions along a streamline, one upstream from the constricted region and one at the center of the constriction (Figure S1). The Bernoulli Obstruction Theory is derived by solving for V₂ and substituting the result back into the continuity equation:⁹

$$Q=C_{D}A\sqrt{\frac{2\mathrm{\Delta }P}{\rho \mid 1-{\beta }^4\mid }}$$ (4)

where A is the airspace CSA at the constriction, ΔP = P₁ − P₂ is the pressure drop, and β = d₂/d₁ is the ratio of the airway diameters at cross-sections 1 and 2. The discharge coefficient C_D serves as a correction for the following approximations: (a) the Bernoulli equation is exact only for an ideal fluid (zero viscosity), and (b) the diameter determining the pressure drop is not the constriction diameter d₂ itself, but the diameter of the fluid jet exiting the constriction.⁹ C_D is a function of the Reynolds number Re and the geometry (ratio β); its value is obtained via experimental measurements, and it typically ranges from 0.6 to 1.0 for flowmeter designs with 0.25 < β < 0.75 and 10⁴ < Re < 10^7.8,9

The total pressure drop from nostrils to carina, (ΔP)_TOTAL = P_nostrils − P_carina, can be written as

$${(\mathrm{\Delta }P)}_{\mathit{TOTAL}}={(\mathrm{\Delta }P)}_{\mathit{UPSTREAM}}+{(\mathrm{\Delta }P)}_{\mathit{STENOSIS}}$$ (5)

where (ΔP)_UPSTREAM = P_nostrils − P_oropharynx is the pressure drop upstream from the stenosis and (ΔP)_STENOSIS = P_oropharynx − P_carina is the pressure drop due to the stenosis. Dividing by the airflow rate Q and using the definition of resistance (R = ΔP/Q), we have that

$$R_{\mathit{TOTAL}}=R_{\mathit{UPSTREAM}}+R_{\mathit{STENOSIS}}$$ (6)

In the limit of very small constrictions (A → 0), the resistance of the stenosis is much greater than the upstream resistance (R_STENOSIS ≫ R_UPSTREAM). Thus, using Equation (4) in the limit of severe constrictions (β → 0), we find that the Bernoulli Obstruction Theory predicts an inverse relationship between upper airway resistance and the minimal CSA at the constriction, namely

$$R_{\mathit{TOTAL}}=R_{\mathit{STENOSIS}}=\frac{1}{C_D}\sqrt{\frac{\rho \mathrm{\Delta }P}{2}}\frac{1}{A}(\text{severe}\text{constrictions})$$ (7)

In addition, using Equation (4) in the limit of severe constrictions (β → 0) and assuming a constant pressure drop ΔP, we find that the Bernoulli Obstruction Theory predicts that the relative reduction in airflow (Q_OBSTRUCTED/Q_HEALTHY) is directly proportional to the relative reduction in airspace cross-sectional area (A_OBSTRUCTED/A_HEALTHY), namely

$$\frac{Q_{\mathit{OBSTRUCTION}}}{Q_{\mathit{HEALTHY}}}=k\frac{A_{\mathit{OBSTRUCTION}}}{A_{\mathit{HEALTHY}}}$$ (8)

where $k=C_D^{\mathit{OBSTRUCTION}}/C_D^{\mathit{HEALTHY}}$ is a constant.

Results

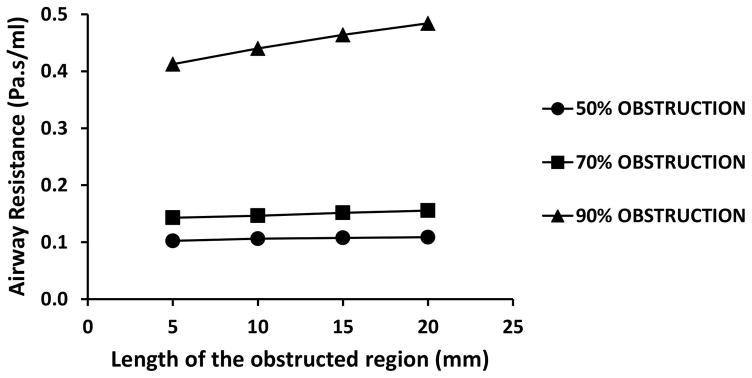
Airway resistance from nostrils to carina was plotted as a function of obstruction length in the adult model with simulated subglottic stenoses corresponding to 50%, 70%, and 90% obstruction (Figure 3). Obstruction length had a greater effect in models with more severe constrictions than in models with less severe constrictions. More specifically, when obstruction length increased from 5 mm to 20 mm, airway resistance increased by 6.4% (0.102 to 0.109 Pa.s/ml), 8.8% (0.143 to 0.156 Pa.s/ml), and 17.3% (0.413 to 0.484 Pa.s/ml) in models with 50% obstruction, 70% obstruction, and 90% obstruction, respectively (Figure 3). Importantly, obstruction diameter had a greater effect on airway resistance than obstruction length. For example, airway resistance increased more than 400% (from 0.106 to 0.440 Pa.s/ml) when obstruction severity increased from 50% to 90% obstruction in models with 10-mm obstructions (Figure 3).

Figure 3.

Airway resistance as a function of obstruction length for simulated subglottic stenosis corresponding to 50%, 70%, and 90% obstruction in the healthy adult model.

Airway resistance was plotted as a function of airspace CSA at the subglottis in the simulated stenosis models created by inserting 5-mm long obstructions in the six healthy models (Figure 4). To test the hypothesis that airway resistance is inversely proportional to cross-sectional area at the subglottis (R_TOTAL ∝ A⁻¹) as predicted by the Bernoulli Obstruction Theory (Equation 7), we fitted the CFD results with a power law curve

Figure 4.

Airway resistance as a function of airspace cross-sectional area in simulated stenosis models with obstruction lengths of 5mm.

$$R_{\mathit{TOTAL}}=a{A}^b$$ (9)

where a and b are constants. The exponent b was found to range from −0.85 to −1.07 among the six subjects in good agreement with the Bernoulli Obstruction Theory (Table S2 in the online-only Supporting Information).

The resistance of the subglottis (R_STENOSIS) contributed to an increasingly higher proportion of the total airway resistance as the stenosis became more severe. More specifically, the ratio of the stenosis resistance to the total airway resistance R_STENOSIS/R_TOTAL increased on average (± standard deviation) from 0.68 ± 0.18 in models with 50% obstruction, to 0.83 ± 0.09 in models with 70% obstruction, to 0.97 ± 0.02 in models with 90% obstruction. Thus, as the obstruction became more severe, the pressure drop became increasingly more confined to the stenotic region at the subglottis (Figure 5), thus confirming our expectation that the resistance of the stenosis is much greater than the upstream resistance (R_STENOSIS ≫ R_UPSTREAM) in the limit of very small constrictions.

Figure 5.

Air pressure field in the 10-month-old model with varying levels of simulated subglottic stenosis. Note that the pressure drop becomes increasingly confined to the subglottis as the severity of obstruction increases.

When the ratio of airflow in the simulated stenosis models to airflow in the original healthy model (Q_OBSTRUCTED/Q_HEALTHY) was plotted as a function of the relative reduction in subglottic airspace cross-sectional area (A_OBSTRUCTED/A_HEALTHY), the data points of all subjects fell approximately on the same curve (Figure 6). As predicted by the Bernoulli Obstruction Theory, the relationship was linear in the limit of severe constrictions with the constant in Equation (8) estimated to be k = 2.25 ± 0.15 (r²=0.93) based on a fit to all six simulated stenosis models with 70%, 80%, and 90% obstruction. The average percent reduction in airflow associated with a percentage reduction in subglottic CSA is listed in Table 1.

Figure 6.

Percent reduction in airflow as a function of percent reduction in airspace cross-sectional area in all six simulated SGS models compared to the Bernoulli obstruction theory.

Table 1.

Average percent airflow for each level of obstruction estimated with CFD simulations by inserting simulated stenoses that are 5 mm long at the subglottis of 6 healthy subjects, while keeping the pressure drop from nostrils to carina constant in each subject.

Area at subglottis (% of original)	Airflow (% of original)
100 %	100 %
60 %	97 ± 4 %
50 %	91 ± 5 %
40 %	81 ± 6 %
30 %	67 ± 7 %
20 %	48 ± 6 %
10 %	24 ± 4 %
0 %	0 %

Airway resistance in healthy subjects (simulated SGS models) with 0% obstruction, 50% obstruction, and 90% obstruction were compared to airway resistances in actual SGS patients (Figure 7). Simulated SGS models with 50% obstruction had resistances slightly higher than the healthy models, while simulated SGS models with 90% obstruction had substantially higher resistances. Actual SGS patients with Cotton-Myer grades I and II had resistances comparable to the simulated SGS models with 50% obstruction. Meanwhile, the two actual SGS patients with Cotton-Myer grade III had resistances comparable to simulated SGS models with 90% obstruction (Table S1 and Figure 7). These results confirm that the simulated SGS models have resistances comparable to actual SGS patients.

Figure 7.

Effects of age and body mass on airway resistance for healthy subjects (simulated SGS models) with 0% obstruction, 50% obstruction, and 90% obstruction, and actual SGS patients with Cotton-Myer grades I, II, and III.

Discussion

Due to the rapid onset and progression of symptoms in many SGS patients, a simple and reliable method to estimate the severity of airflow limitation would be valuable to inform treatment decisions. Our CFD simulations suggest that airspace cross-sectional area has a much greater effect on airway resistance than the constriction length for rigid, mature stenoses (Figure 3). Our study also suggests that the flow-pressure relationship of the upper airway in SGS patients can be described by the Bernoulli Obstruction Theory, which predicts an inverse relationship between airway resistance and subglottic cross-sectional area (R ∝ A⁻¹). This relationship was observed for subjects of different ages and body sizes, irrespective of inter-individual variability in upper airway anatomy. This suggests that a 2-fold reduction in cross-sectional area is associated with a 2-fold reduction in airflow, rather than the 4-fold reduction in airflow that would be expected if airflow limitation in SGS patients were consistent with Poiseuille flow.

One limitation of this study is that the cohort studied was relatively small, and only two actual SGS patients with severe stenosis were investigated. Another limitation is that we focused solely on airway resistance in relation to static parameters such as CSA and length of obstruction. Many forms of airway obstruction that are dynamic in nature were not taken into consideration, and it remains to be seen what methodology will best characterize the compliant airway. In addition, other geometric parameters that may impact airflow resistance such as the shape of the constriction should also be tested in future studies. Furthermore, our steady-state simulations represent the average flowrate during inspiration. Future studies are needed to investigate time-dependent effects. The upper airway resistance experienced by a subject during the breathing cycle may not be perfectly represented by the steady-state resistance at the average inhalation rate. Finally, this study was purely computational in nature and in vivo measurements were not available for validation. Future in vivo and in vitro measurements should be performed to confirm or refute our hypothesis that the relationship between airflow reduction and airspace cross-sectional area in SGS can be described by the Bernoulli Obstruction Theory.

The search for objective methods to assess SGS severity and predict treatment outcomes remains active. Pressure-flow relationships can be measured with a pneumotachograph and a pressure catheter,¹⁷ or less invasively with spirometry.¹⁸ Pulmonary function variables, such as the expiratory disproportion index [ratio of the forced expiratory volume in 1 second (FEV₁) to the peak expiratory flowrate (PEFR)], that are commonly used to diagnose lung pathologies, including COPD and asthma, have been shown to reliably diagnose adult laryngotracheal stenosis.^19,20 Nouraei and colleagues reported a strong correlation of pulmonary compliance (defined as the change in lung volume in response to unit change in driving pressure) with both anatomical stenosis severity and perceptual dyspnea severity.²¹ Pulmonary function tests such as these could provide a non-invasive objective method to evaluate subglottic stenosis lesions. However, using pulmonary function tests in infants and children can be difficult to perform and may require anesthesia or sedation, and thus are mostly used in adults. Further studies of spirometry as an objective measure of SGS severity and treatment outcomes in young children are needed.

The use of computational fluid dynamics to investigate obstructive airway diseases has gained much traction in the research field. However, to date, few studies have used CFD methodology to examine subglottic stenosis.^22–24 Zdanski and colleagues demonstrated that geometric and CFD measures were effective in discriminating between pediatric SGS patients who received intervention versus those who did not, thus validating non-invasive imaging and derived CFD metrics as useful diagnostic and treatment planning tools in subglottic stenosis.²³ Brouns and colleagues performed CFD simulations in one idealized model generated from a CT scan of a healthy adult in which simulated stenoses of varying sizes were created.²⁴ The authors observed that the pressure drop was increasingly confined to the stenotic region with increasing stenosis severity, in agreement with our simulations (Figure 5).

Our findings may have implications for clinical care of SGS patients. Physicians most often employ the Cotton-Myer grading system,² in conjunction with the patient’s presenting symptoms and medical history, to determine the best course of treatment.^7,25–27 However, the exact guidelines stratifying severity of disease and how best to treat is largely subjective and practitioner-dependent. There is no widely accepted standardized system on how best to manage children with SGS that is based on objective measures, which can detract from our ability to determine the best treatment for each patient. This study suggests that the degree of airflow limitation may be estimated based on anatomical measurements alone, which can be obtained using endotracheal tubes,² MRI, CT scans, or stereovision endoscopy.²⁸ By estimating the relative reduction in airspace cross-sectional area (A_OBSTRUCTED/A_HEALTHY), providers may be able to estimate the relative reduction in airflow (Q_OBSTRUCTED/Q_HEALTHY) from tables. Future studies in larger cohorts can test the validity of the relationship between relative reduction in subglottic CSA and relative reduction in airflow reported in this study (Table 1).

Conclusion

This study suggests that the relationship between the severity of airflow limitation and the degree of anatomical obstruction in subglottic stenosis can be described with the Bernoulli Obstruction Theory. As predicted by the theory, our CFD simulations revealed that the upper airway resistance is inversely proportional to subglottic cross-sectional area (R ∝ A⁻¹ ) in the limit of severe obstructions. Thus, a 2-fold reduction in cross-sectional area is expected to be associated with a 2-fold reduction in airflow (as opposed to the 4-fold reduction that would be observed in Poiseuille flow) for a constant pressure drop. Future in vivo and in vitro studies should be performed to confirm these findings.

Supplementary Material

Supp info

Table S1. Demographics and estimated minute volumes at rest for the healthy subjects and SGS patients included in the study. The Cotton-Myer grades of the healthy subjects were defined as I by default, while the Cotton-Myer grades of the SGS patients were defined by measuring in the 3D models the ratio of the CSA at the stenosis to the CSA downstream of the stenosis.

Table S2. Coefficients in the power law R_TOTAL = aA^b obtained by fitting the relationship between total airway resistance (R_TOTAL) and airspace cross-sectional area at the subglottis (A) for simulated stenosis ranging from 60% obstruction to 90% obstruction. r² is the goodness of fit.

Figure S1 – Diagram illustrating a cylindrical tube of diameter D with a constricted region with diameter d. Air pressure and velocity on the cylinder axis are P₁ and V₁ at a location upstream from the constricted region and P₂ and V₂ at the constriction, respectively.