Skip to main content
NCBI home page
Heliyon logoLink to Heliyon
. 2018 Mar 27;4(3):e00586. doi: 10.1016/j.heliyon.2018.e00586

Analysis and modeling of the inverted bioconvection in Chlamydomonas reinhardtii: emergence of plumes from the layer of accumulated cells

Naoki Sato a,∗, Kaoru Sato a,b, Masakazu Toyoshima a,1
PMCID: PMC5968142  PMID: 29862349

Abstract

Bioconvection is a convective flow found in a suspension of motile cells that swim against gravity, and is a primitive form of order formation of cells, which has been studied both experimentally and theoretically. We formulate here an inverted bioconvection occurring in a suspension of phototactic cells in a high-density medium, which is illuminated from the bottom. We used a highly phototactic strain 137c of Chlamydomonas reinhardtii in the experiments. Using a custom-made lateral microscope, we observed a close view of cellular dynamics in the initiation of inverted bioconvection. In conventional bioconvection, convective flows of cells are formed spontaneously with or without formation of the surface cell layer. In inverted convection, a crowded cell layer was initially formed at the bottom, which was a prerequisite for the subsequent emergence of plumes, namely, floating populations of cells. The plume formation was a result of neither uneven initial cell density nor unequal light intensity. Based on detailed analysis of individual cells, we constructed a model of inverted bioconvection, in which each cell experiences a transition between two modes of movement: phototactically swimming cell and non-motile cell aggregate. A simulation using the CompuCell3D software reproduced basic behaviors of the plume formation. The modal transition has not been a subject of basic studies, but provides an interesting target of study of cell-to-cell interactions.

Keywords: Biophysics, Cell biology, Mathematical biosciences, Systems biology

1. Introduction

Bioconvection is a convective flow (of cells and medium) found in a suspension of motile cells that are tactic to some directional stimuli, such as oxygen, nutrient, chemicals or light (for reviews, see Pedley and Kessler, 1992; Hill and Pedley, 2005). The term “bioconvection” was coined by Platt (1961), but the observation had been reported in early twentieth century (Wager, 1910–1911) or earlier. Experimental description of bioconvection was reported in bacteria such as Bacillus subtilis (Metcalfe and Pedley, 1998; Mendelson and Lega, 1998; Mendelson, 1999), ciliates such as Tetrahymena pyriformis (Plesset and Winet, 1974; Pedley and Kessler, 1992; Mogami et al., 2004), T. thermophila (Mogami et al., 2004) and Paramecium tetraurelia (Kitsunezaki et al., 2007), and phototactic algae such as Chlamydomonas nivalis (Pedley et al., 1988; Pedley and Kessler, 1990), C. reinhardtii (Brokaw et al., 1982; Yamamoto et al., 1992), Dunaliella tertiolecta (Pedley and Kessler, 1992) and Karenia mikimotoi (Gentien et al., 2007). All these reports described bioconvection as regular patterns of cell density. The actual movement of individual cells was not observed directly. Many fluid mechanics studies also reported results of simulations with varying parameters. However, experimental verification of the simulation results has been limited to the comparison of pattern wavelength in many cases. In other words, bioconvection has been studied in physics and biology quite separately. Bioconvection is supposed to be favorable for the cells, namely, for better supply of oxygen (in non-photosynthetic cells), better supply of nutrients (in all cases), or equal opportunity of light reception (in photosynthetic cells). However, various reports did not support significantly favorable effects of bioconvection (Jánosi et al., 2002).

Another possible significance of bioconvection is that this may be a form of structure formation by cell association. Traditional theoretical treatment of bioconvection used the continuum fluid model, which approximated the medium containing a high-density population of cells as a single fluid having an average density dependent on the concentration of cells (Plesset and Winet, 1974; Hill and Pedley, 2005). In this model, each cell moved along a straight trajectory at a constant speed. A contact of cells, a cell-to-cell interaction, or an increase in viscosity of the fluid due to the presence of cells was not considered explicitly. Therefore, the system was supposed to consist of two phases with different concentrations of cells. An overlay of a lighter fluid by a heavier fluid was a source of turbulent flow of the fluids (Plesset and Winet, 1974; Plesset et al., 1976), similar to the Rayleigh-Taylor instability studied extensively in physics (see for example, George et al., 2002). In many actual experiments, the cells within the plumes were swimming individually, in accordance with the continuum model.

We might suspect, however, a possible importance of intercellular interaction. If such interaction is involved in the formation of a particular type of bioconvection, we might be able to envisage bioconvection as the most primitive form of structure formation by cell association. Multicellularity is based on the interaction of differentiated cells. Establishment of cellular differentiation from a uniform population of cells is well documented in the cellular slime-mold Dictyostelium discoideum (Du et al., 2015). This phenomenon is different from the differentiation occurring in the early development of mammalian embryo, which is dependent on the pre-formed gradient of maternal factors in the unfertilized egg. The formation of moving aggregates of cells or slugs is the critical step of forming fruiting body in slime-mold. The flow of cells in dense population as found in slugs is reminiscent of the flow of cells in bioconvection, although the mechanisms of cell movement and cell attraction are different. In this respect, bioconvection may be regarded as a preparatory step before the establishment of cell differentiation system.

Bioconvection in phototactic algae drew special attention of researchers, because light may be positively or negatively phototactic depending on the intensity or wavelength. Vincent and Hill (1996) formulated the layer formation of phototactic algal cells that are positively phototactic to weak light and negatively phototactic (“photophobic” was used in the paper) to high light. They considered explicitly the effect of shading in a dense population of algae. However, they ignored that the light receptor for phototaxis (absorbing blue-green light) is different from the photosynthetic pigments (absorbing red light). Two rhodopsins, CSRA and CSRB (now called channelrhodopsins 1 and 2), were found to be responsible for the perception of phototactic light and to mediate the signal, in the form of excitation of membrane potential, to the regulatory machinery of flagellar motion (Sineshchekov et al., 2002; Govorunova et al., 2004). This indicates that the effect of shading by cell population could be considerably smaller than that evaluated previously, and must be experimentally measured.

Another point to be reconsidered is that the trajectory of a swimming algal cell is not a straight line, and that the speed of swimming is not uniform. The movement of a C. reinhardtii (hereafter called Chlamydomonas) cell has been well characterized by high-speed movies (Rüffer and Nultsch, 1985). The two flagella beat in an asymmetric breast-stroke to make the cell proceed in the forward direction. The cell rotates (counterclockwise, when viewed from behind) while swimming in a helical path. In addition, in the recovery stroke, the cell rolls back, in a way “three steps ahead and two steps behind”. It is not evident if this complex motion of the cell can be approximated by a uniform straight motion in the classical models of bioconvection even if the cells are separated from one another. The actual motion of the cells must be important when the cells contact with one another.

Bioconvection has been believed as a result of gravitational imbalance of the layer of “denser” (or “heavier”) cells and the “less dense” fluid medium. However, experimental evidence for the importance of gravitation was not given except in Mogami et al. (2004). If the density of the fluid medium is increased, then the difference of density between the cells and the fluid decreases, so that bioconvection will be hard to occur. However, if the density of the fluid exceeds that of the cells, then we might expect that another type of bioconvection occurs, namely, inverted bioconvection. To realize inverted bioconvection, the cells must accumulate at the bottom of the vessel by some kind of stimulus. In this respect, phototaxis is the best to satisfy such conditions. The density of the medium may be increased by an addition of any solute, but high concentration of solutes affects the osmotic homeostasis, hence, the motility and viability of the cells. In this respect, the density media such as hydrophilic silica sol (available as Percoll) are suitable, because they are inert for living cells such as sperms, and the osmotic pressure of such media is negligible. Viscosity increase of such media is also kept to a minimum: for example, 10 cP in 100% Percoll vs 1 cP in water (cP = centipoise). This does not have significant effects on the swimming of cells except swimming speed. The slower motion of cells is convenient for recording cell dynamics.

Another significance of inverted bioconvection is that the border of the accumulated cell population is flat, which is always the pre-requisite for the fluid mechanic simulation. In the real bioconvection of aerobic bacteria or ciliates, the surface of the fluid medium is concave, and the walls are wetted by the fluid. The cells can travel along the walls unexpectedly high above the concave surface. The concave surface facilitates the cells to slip down on the hill formed near the walls. These effects possibly add additional border conditions, and complicates the analysis of bioconvection. In this respect, inverted bioconvection is an ideal system to analyze because the border (the bottom) is flat. The phototaxis-driven inverted convection is different from “reversed convection” reported by Hosoya et al. (2010), which also occurs in a dense medium (45% Percoll), but the convection occurs spontaneously without external light, driven by positive gravitaxis explained by the drag-gravity model.

In the present study, we will describe cellular dynamics of the inverted bioconvection driven by phototaxis in Chlamydomonas. We will show how the cells are densely accumulated, and how cell-to-cell interaction is important for the initiation of inverted bioconvection. Based on detailed observations, we constructed a model of plume initiation, in which modal change is explicitly considered. The model was evaluated by a computer simulation. We noted a possible phase transition in the parameter space. We will discuss possible implications of the present model of the inverted bioconvection.

2. Results

2.1. Experimental setup

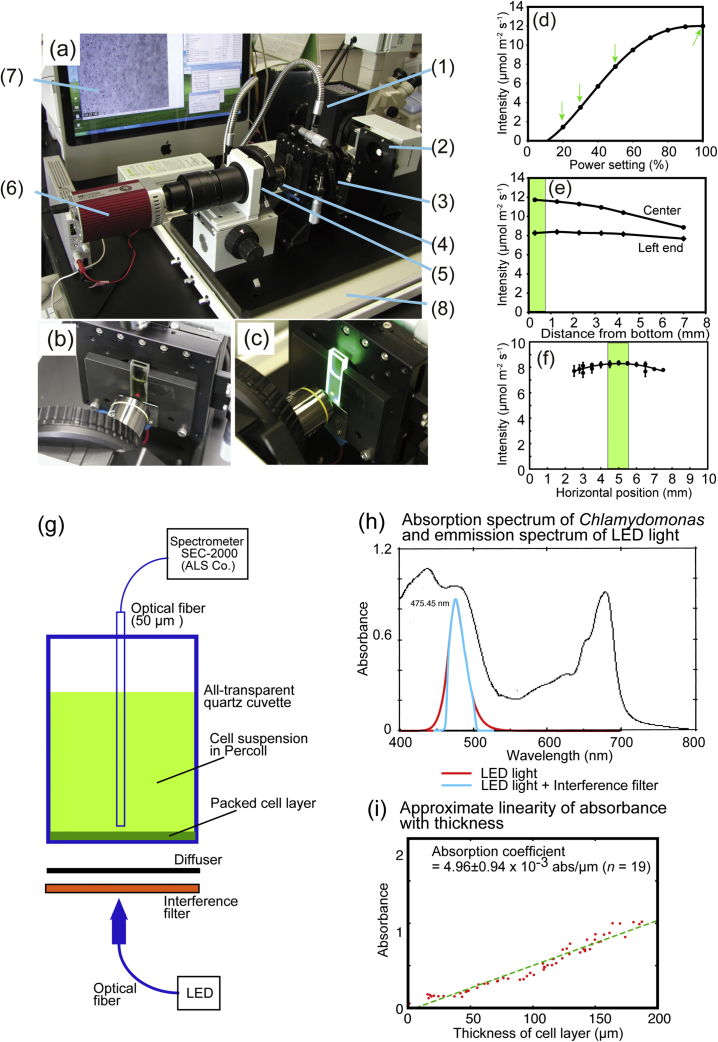
Fig. 1a shows the custom-made lateral microscope that was used for the observation of bioconvection. Bright field images were obtained with a red light, which was inactive in phototaxis. Time-lapse images were recorded with the CCD camera at 15–40 fps (frames per second). Phototaxis was induced by a blue LED (light-emitting diode) light introduced under the quartz cuvette (2 mm thick: panels b and c) through an optical fiber (panel g). The light intensity was varied with the power setting (panel d). It was rather homogeneous within the cuvette (panels e and f). The variation in light intensity was small within the view area (colored part) of the CCD camera.

Fig. 1.

Fig. 1

Open in a new tab

Experimental setup with lateral microscope and light measuring system. (a) Overview of the system. (1) Phototactic light provided from above (white light), used to disperse the cells after an experiment, (2) Light source for observation with a cut-off filter (Kenko SR64), (3) Long working distance condenser, (4) Long working distance objective lens, (5) Band-pass filter, (6) CCD camera, (7) PC, (8) Vibration isolator (damper). LED and its power supply are not shown. (b) A 2 mm-thick quartz cuvette containing algal suspension viewed with red light; (c) A cuvette illuminated by a green LED at 507 nm. (d) Light intensity vs power setting curve with a blue LED at 475 nm, used for all of the quantitative studies. At 100% power, the photon flux density was 12 μmol photons m−2 s−1. (e) Light intensity vs height curve. The bottom of the cuvette was located at 42 mm from the light source. The green part shows the region used for the observation (height of a single image). (f) Light intensity at different positions within a cuvette (10-mm wide). The green part shows the region used for the observation (width of a single image). (g) Measurement of light intensity within the cuvette. (h) Absorption spectrum of the cells and the emission spectrum of the LED light (i) Relationship between the absorbance and the thickness of cell layer formed at the bottom of the cuvette.

Fig. 2 shows behaviors of various strains of Chlamydomonas within a culture flask. Among the various strains tested, the strain 137c showed the most prominent bioconvection patterns. We therefore used this strain throughout the experiments.

Fig. 2.

Fig. 2

Open in a new tab

Macroscopic view of bioconvection in various wild-type strains of Chlamydomonas. (a)–(c) 137c. (d) CC-125. (e) CC-1010 (Modified Bristol Medium). (f) CC-1009 (Modified Bristol Medium). (g) CC-1328 (agg1). (h) CC-124 (agg1). (i) CC-124 illuminated from the bottom. Except in (i), light was illuminated from the top. In (i), negatively phototactic cells accumulated at the surface by the bottom light, and plumes appeared occasionally. The cells of the strain 137c (panels a, b, and c) were accumulated at the surface of culture medium, and formed stripes near the wall of the flask (panel a). In a more dense suspension of the cells (panel b), a two-dimensional pattern was observed on the surface. The stripe pattern on the wall was quite regular, having an identical spacing between the stripes (panel c). These are representative patterns of bioconvection that have been reported in the literature. Other strains, such as CC-125 (panel d), CC-1010 (panel e) and CC-1009 (panel f), also showed similar patterns, although the pattern was less marked. The strains having the agg1 mutation, such as CC-1328 (panel g) and CC-124 (panel h), presented a negative phototaxis, and aggregated at the bottom of the flasks. Nevertheless, when illuminated from the bottom, the CC-124 cells accumulated at the surface, and showed a bioconvection pattern (panel i). All these results show that the swimming cells accumulated at the surface of the medium, irrespective of the reason of accumulation, tend to form patterns characteristic of bioconvection.

2.2. Inverted bioconvection

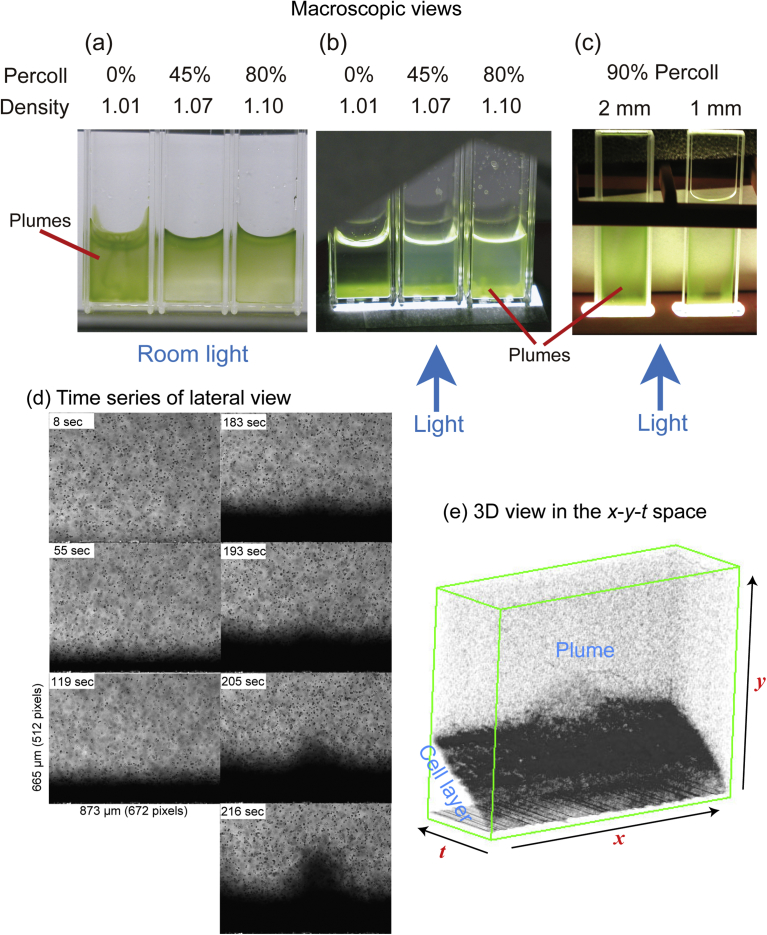
When a dense suspension of Chlamydomonas cells (strain 137c) was placed in an optical cuvette (10 × 10 × 40 mm, w/d/h), and illuminated from the top, the cells accumulated at the surface and formed plumes (Fig. 3a). If Percoll (specific gravity of 1.13 g mL−1) was added to the medium to a final concentration of 45% or 80%, the cells accumulated at the surface, but there were no plumes. On the contrary, if the cells were illuminated from the bottom, they accumulated at the bottom of the cuvette. In this case, plumes were found in the medium containing 80% Percoll (Fig. 3b). These results demonstrated that the difference in density of the cells and the medium was the principal cause that determined the behavior of bioconvection. We were not able to detect “reverse bioconvection” in these media (see Introduction). To examine if a thinner cuvette (with shorter light path) can be used for inverted bioconvection, two optical cuvettes, one with a 2-mm light path and another with a 1-mm light path, were tested (Fig. 3c). 2-mm light-path cuvettes showed a clear plume, and were used in the following experiments. As explained in Materials and Methods, we finally found that pure Percoll could be used without seriously affecting the motility of the cells. The cells were suspended in pure Percoll at about 3 × 107 cells mL−1.

Fig. 3.

Fig. 3

Open in a new tab

Plume formation of Chlamydomonas 137c cells. (a) Plume formation under room light (from the top). (b) Plume formation with the illumination from the bottom. (c) Plume formation in flat cuvettes. Plume formation is a sign of bioconvection. In (b) and (c), inverted bioconvection is shown. (d) Time series of selected views of inverted bioconvection observed by lateral microscope. This is the central part of the cuvette. This is taken from the experiment #42 in Fig. 6, in which cell density was 1.0 × 107 cells mL−1 and the light intensity was 1.4 μmol photons m−2 s−1. (e) 3D view of the plume formation in (d) obtained with the VCAT5 software.

2.3. Close view of bioconvection observed with a lateral microscope

Dynamics of motile cells was observed with the lateral microscope (Fig. 3d). To initiate phototaxis, the cells were illuminated from the bottom by a high irradiance blue LED. The cells moved downwards to the bottom of the cuvette and formed a thick cell layer, which became thicker with time, and suddenly turned uneven. Finally, a thick part began to move upward, and inverted convection started (Supplementary Video S1). The dense, crowded cell layer was different from the supposed “concentrated cell suspension” as approximated as a dense fluid in the continuum model, because the cells contacted with one another in the crowded cell layer.

Inverted bioconvection was not exactly similar to the normal or traditionally studied bioconvection, in which the flow of cells began spontaneously within the fluid, and the formation of the layer of accumulated cells was not a prerequisite. In the theory of algal bioconvection (Vincent and Hill, 1996), formation of a crowded cell layer was not assumed. We confirmed this in Chlamydomonas (without addition of Percoll) as well as in two other algae of larger sizes: Chattonella antiqua and Euglena gracilis. In fact, it is very difficult to prepare a homogeneous suspension of flagellated cells. Even after mixing, streams of water remain in the medium, which caused uneven distribution and flow of cells that was self-enhanced to become a convective flow. The situation is quite different in the case of inverted bioconvection, in which a homogeneous suspension was formed in the dark (without phototactic light) after the flow of water caused by mixing was settled. The spontaneous formation of non-homogeneous distribution of cells in an algal suspension is partly explained by gyrotaxis, a phenomenon in which swimming cells are attracted to a downward flow of the surrounding fluid (Kessler, 1985). Gyrotaxis acts in concert with the downward flow of accumulated cells in the normal bioconvection. In the case of inverted bioconvection, gyrotaxis acts against the upward flow of cells, while the effect of gyrotaxis on the surrounding downward flow was not evident. Therefore, the cells in the upward flow of plume tend to dissipate into the surrounding medium (Fig. 3d, 216 sec), and this is likely an explanation of homogeneity of cell suspension in Percoll.

Fig. 3d shows that a thick layer of crowded cells that accumulated by phototaxis was formed before the plume formation. The thickening of the cell layer continued without being inhibited by shading, which was due to light absorption by the chloroplast pigments (Fig. 1h) or light scattering. The thickness of cell layer increased linearly with time, until the accumulation of cells attained 200 μm or more (Fig. 3e). Fig. 1i shows the result of simultaneous measurement of the light intensity within the cuvette (Fig. 1g). A linear relationship between the thickness and the absorbance, analogous to the Lambert-Beer law, was obtained. The absorption coefficient per unit light path was calculated to be 4.96 ± 0.94 × 10−3 absorbance unit μm−1. Considering that the dimension of a cell was about 8 μm in the long axis, this means that the light intensity becomes 1/10 (OD = 1.0) after passing through about 25 cells.

The linear increase in the thickness of cell layer with time (Fig. 3e) suggests that the phototactic movement of the swimming cells was not dependent on the light intensity, at least in this range of light intensity. This is in contrast with the previous hypothesis (Vincent and Hill, 1996) that formulated the cell velocity as a function of light intensity (see Introduction). A recent report also assumed a similar light dependence (Dervaux et al., 2017). We never observed light dependence of swimming speed in either mass movement as shown in Fig. 3e or individual motion in the 137c cells (see below).

2.4. Analysis of cell movements in the fluid and the crowded cell layer

To track the movements of the cells and to analyze the distribution of cells within the fluid, we used a 3D visualization software VCAT5, which has been developed in the RIKEN Institute. With this software, we can visualize the cells within a 3D space, namely, x, y, and t. By tilting the y-t axis about 2°, the movement of an individual cell can be traced easily (Fig. 4a). All the cells moved in the same direction.

Fig. 4.

Fig. 4

Open in a new tab

Measurement of various parameters of cell movement. Each Chlamydomonas cell swims in a helical path. We selected clearly identifiable trajectories, and calculated the speed along the spiral axis, the amplitude of the spiral, and the pitch. (a) Lateral (upper panel) and projection views of phototactic swimming. Some trajectories are traced in red in the lateral view. In the projection view, the trace of cell movement was a short segment (pointed by an arrow). (b) Micrographs of wild-type (137c) and GFP-expressing cells (line 2-1). DIC, differential interference image; DAPI, fluorescence of DNA-staining; GFP, fluorescence of GFP. (c) Movement of individual fluorescent cells within the crowded cell layer. This is an inverted (light <--> dark) image. Trajectories of selected fluorescent cells are shown. The start of each trajectory is marked by the trajectory number. The image at the start of recording is presented as a background image to locate the trajectories within the cell layer. (d) x – t plot of the movement of fluorescent cells within the crowded cell layer. Not all cells gave clear traces. We selected some traces that were better recognized. Sinusoidal traces were visible for oscillating cells as indicated by arrows. Non-motile cells gave linear traces.

We first analyzed the distribution of cells, which would become non-homogeneous spontaneously in the case of conventional bioconvection without Percoll. If the distribution of cells became non-homogeneous with time, this could be the explanation of non-homogeneous thickening of the accumulated cell layer and plume formation. Fig. 5a shows that the distribution of the cells was not completely uniform, but varied only smoothly (note that the vertical scale is expanded), and was not related to the position of the plume to be formed (Fig. 5b). The measurement of cell density might be less accurate with a lateral view than with a cross-section view (Fig. 5c). The cell density obtained with a cross-section view was very flat. We obtained similar results with several other experiments. These results suggest that the cell density in the fluid (in the region sufficiently distant from the bottom) was kept homogeneous until the beginning of plume formation.

Fig. 5.

Fig. 5

Open in a new tab

Analysis of cell density in the fluid. (a) Cell density along the x-axis (cells per unit volume as measured by the average darkness of a unit area) in the fluid sufficiently distant from the bottom. Note that the density scale is enlarged. (b) Final view of the movie showing the formation of a plume. (c) Cell density along the x-axis measured in the cross-section, vertical to the axis of cell swimming.

2.5. Measurement of basic properties of individual cell movement

The 3D viewing was used to obtain basic properties of cell movement (Table 1). We can calculate the speed from the tilting angle y-t, and the amplitude (of helical path) from the projection on the cross-section plane (Fig. 4a). In general, swimming was slower in Percoll than in the TAP medium, but light and dark did not affect the swimming speed. The amplitude of spiral motion was rather stable, and was not affected by the presence/absence of Percoll or light/dark (about 11 μm). Curiously, the pitch of the spiral motion was also stable in the light, but it was smaller in the dark. According to this situation, each cell spent a longer time in Percoll for a single pitch due to decreased speed, keeping the amplitude identical.

Table 1.

Metrics of cell movement.

TAP medium Fluid phase of Percoll Cell layer in Percoll
Swimming speed (light) [μm s−1] 103.4 ± 9.6 μm (7) 39.9 ± 8.1 (28) 33.3 ± 13.5 (42)
Swimming speed (dark) [μm s−1] 104.0 ± 25.2 (13) 35.7 ± 15.8 (6) N/A
Amplitude of spiral motion (light) [μm] 12.2 ± 4.6 11.2 ± 3.4 34.4 ± 14.6
Amplitude of spiral motion (dark) [μm] 10.3 ± 6.1 11.4 ± 2.1 N/A
Pitch of spiral motion (light) [μm] 65.4 ± 9.8 66.8 ± 10.9 N/A
Pitch of spiral motion (dark) [μm] 56.0 ± 10.3 39.4 ± 16.0 N/A
Time for a pitch (light) [s] 0.64 ± 0.12 1.76 ± 0.47 1.03 ± 1.08
Time for a pitch (dark) [s] 0.55 ± 0.11 1.14 ± 0.23 N/A
Open in a new tab

Number in parenthesis shows number of cells analyzed. N/A, not applicable.

Note that only straight trajectories were used for the measurement of swimming.

To obtain similar measures for the cells within the crowded cell layer, we used fluorescently labeled cells. Fig. 4b shows micrographs of the wild-type cells and the cells transiently expressing GFP. GFP was excited by the same actinic light for phototaxis (475 nm), and the GFP fluorescence was detected by the same CCD at a higher sensitivity. Although the fluorescence was weak (about 2.5 times the intrinsic fluorescence of wild-type cells), we tried to use it to selectively detect fluorescing cells within the population of crowded cells consisting of 5% GFP-expressing cells in wild-type cells (Fig. 4c). In the background of wild-type cells, we were able to detect the movement of some GFP-expressing cells (Supplementary Video S2). In this way, individual cells at the bottom of the cuvette near the wall were identified. Fig. 4d shows oscillatory movement in the x-position over time, and the metrics are shown in Table 1. The cells were oscillating within the crowded cell layer with a larger amplitude. This active movement of the cells within the crowded cell layer was unexpected, because the crowded cell layer was quite stable until the first plume emerged (Fig. 3d and e). The stability of the crowded cell layer was, therefore, a dynamic structure maintained by the cells moving in mass.

2.6. Global behavior of the cells in the fluid and the crowded cell layer

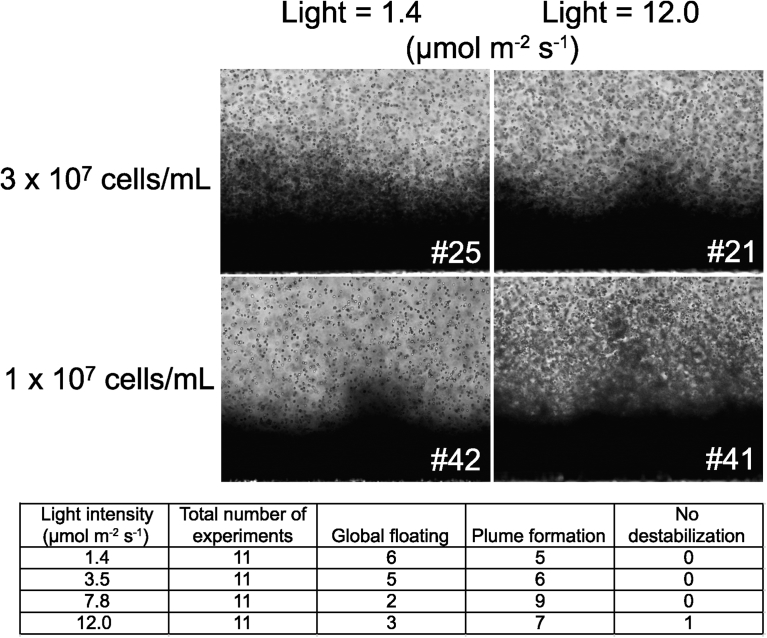
We observed the global behavior of the cells by changing the cell density and the intensity of the actinic light. We tested cell densities from 1.0 × 107 to 3.0 × 107 cells mL−1, and the light intensities were varied from 12% to the full power (power settings are indicated by arrows in Fig. 1d). We performed many measurements with varying these parameters, and Fig. 6 shows representative patterns of plumes in the four conditions (high light or low light, and high density or low density). The lower part summarizes the occurrence of respective incidences. As a general rule, high light stabilized the cell layer, whereas low light favored global floating of cells. Clear plumes were observed in the low light with low-density cell suspension, or in the high light with high-density cell suspension. Apparently, cell density and light intensity for plume formation were correlated. Fig. 7 shows effects of light intensity and cell density on the time needed for the start of plume formation. At low cell densities, the onset of plume formation was retarded, but within 1.5–3.0 × 107 cells/mL, the time was rather constant at about 80 sec. This could be an invariable that characterizes this system. In addition, we found that cell aggregates were floating in the plumes. This was clearly observed in the experiment #41, but in other experiments, smaller aggregates were always seen. Aggregates were also seen in Fig. 5b. The aggregates did not swim, but apparently passively floated according to the difference in density between the cells and the fluid medium.

Fig. 6.

Fig. 6

Open in a new tab

Effects of light intensity and cell density on the pattern of plume formation. The image #21 and Fig. 5b show different frames of an identical time series.

Fig. 7.

Fig. 7

Open in a new tab

Effects of light intensity and cell density on the onset of plume formation.

How could these cell aggregates emerged? As we described above, many cells were actively moving within the crowded cell layer. It seemed that the motile cells changed into non-motile cell aggregates within the crowded cell layer.

We then analyzed the global characteristics of cell movement by plotting the vertical speed component (dy/dt) against the distance y from the bottom in the four representative conditions (Fig. 8). Before the start of illumination (0–8 sec), cell movement was isotropic, as shown by the blue areas above and below the zero line. We confirmed that the horizontal speed component (dx/dt) was always isotropic (not shown). Soon after the illumination, a large population of cells (as shown by magenta or white area) began to swim downwards with an average speed of about −3 pixels per frame (−60 μm sec−1), although exact values depended on experiments. The speed was approximately identical over the whole range of y, the distance from the bottom, and over the whole time range. This is consistent with the observation that swimming speed was not affected by light and dark in individual cells (Table 1).

Fig. 8.

Fig. 8

Open in a new tab

Histograms of swimming speed (dy/dt) vs distance (y) during the selected time intervals (from the start of experiment until the emergence of plumes). Plotting intervals are 10 in the distance (y) axis, and 0.1 in the speed (dy/dt) axis. Note that the direction of y is upward, and the cell movement (shown by the dense area with clearer coloration) was downward in the fluid. A population of cells having positive speed values appeared at the end of each experiment. The dark area in the left end of each panel represents the crowded cell layer, in which individual cells could not be tracked. Immobilized cells sticking to the cuvette surface appeared as a middle line (speed = 0).

The dark area on the left of each panel of Fig. 8 corresponded to the formation of crowded cell layer, which grew linearly with time (Fig. 3e). Close examination of the profile indicated that a small population of cells began to have positive speed values about 40–60 seconds from the beginning of experiment. They were found within 50 pixels from the bottom, and represented a small population of cells that floated above the cell layer (blue protruding area at the left), but soon re-oriented to enter the cell layer. At the end of the experiments #25 and #41, a significant population having positive speed values appeared (blue area above the zero line). This corresponds to the global floating as found in Fig. 6. In experiments #21 (high light, high density) and #42 (low light, low density), a distinct plume appeared, but this was not clearly shown in the profile in Fig. 8.

These results showed that the phototactic cells in the fluid continued to swim at a fairly constant speed, which was not changed significantly even after the formation of accumulated cell layer at the bottom. A minor population of floating cells exists all through the experiment after the initial formation of the cell layer. They were moving individually, but did not form aggregates. In contrast, the floating cells in the plumes and the global floating seemed to be aggregated, and depended on cell-to-cell interactions. In this respect, the cells within a plume of conventional bioconvection (Chlamydomonas without Percoll, Chattonella or Euglena) move individually, but are not aggregated. In inverted bioconvection, aggregated cells floated within the plumes. This is a fundamental difference of the two types of bioconvection.

2.7. Model of inverted bioconvection and examination by simulation

Based on the observations described above, we constructed a model of inverted bioconvection (Fig. 9a). After the onset of illumination from the bottom, the cells swim downwards, and accumulate at the bottom of the cuvette. The thickness of the cell layer increases with time. The cells move around at the bottom, according to oscillatory trajectories. A minor population of cells within the crowded cell layer form non-motile aggregates, and move to the surface of cell layer, and occasionally float into the fluid phase. The non-motile cells float at a speed determined by the density difference, which is different from the swimming speed. We call this modal transition from Mode 1 (motile) to Mode 2 (non-motile aggregate). After a while, these cells regain swimming activity by an inverse modal change, and swim towards the light. Despite these occasional floating, the cell layer remains apparently stable. Plume formation is likely driven by massive aggregates that float as a mass. After floating for some time, large aggregates split into smaller aggregates, which then become dissociated.

Fig. 9.

Fig. 9

Open in a new tab

Model and simulation results of inverted bioconvection. (a) Model of modal change in massively accumulated cells. (b) Phase diagram of the behavior of the system in the n – p space. (c) Comparison of similar plumes obtained in the simulations and the experiments.

Can this simple model involving modal changes account for the plume formation? We used a simulator of cell movement, CompuCell3D, to simulate the inverted bioconvection using a rectangular lattice. This simulation was not intended to faithfully reproduce the actual cell-to-cell interactions within the cell layer, but to test if plume formation can occur by such simple assumptions. In Mode 1, the cell swims and attracted by light towards the bottom. In Mode 2, the cell become non-motile and passively floats. The modal conversion from Mode 1 to Mode 2 occurs stochastically (probability p) when a cell contacts a defined number n of Mode 1 cells within a defined distance (neighbor order = 4: about two layers of cells), which are also converted to Mode 2 cells stochastically (for simplicity, the probability was set to 0.5). Mode 2 cells are not explicitly connected in the model setting, but the following condition imposes that many Mode 2 cells move as an aggregate, namely, conversion of Mode 2 to Mode 1 occurs only when the cell loses all neighbors. This simple model incorporates most of the experimental observations as described above. Details of this simulation are provided in Supplementary document S1 containing a short explanation and the actual script for CC3D. All the simulation was performed in 2D, but not 3D, because we were not able to run the program in the 3D mode, most probably due to the limitation of computational resource. An example is shown in Supplementary Video S3.

We tested the simulation by changing the two parameters, n and p. The results were classified into three cases, namely, explosion (or global floating), plumes, and stable cell layer. The plume formation seen in a limited region within the n – p space (Fig. 9b) demonstrated that our simple model involving modal changes did work. We still do not know if this region corresponds to the actual experimental conditions, but we found many cases of plumes that were similar to the plumes detected in the real experiments (see examples in Fig. 9c). These results suggest that the simulation based on our model can reproduce some essential characteristics of the inverted bioconvection involving cell-to-cell interaction.

3. Discussion

In the present study, we formulated a new type of bioconvection, "inverted bioconvection". In contrast with various forms of normal bioconvection, the inverted bioconvection occurs at the bottom of a container containing phototactic flagellates (such as Chlamydomonas) illuminated from the bottom. It is difficult to imagine a similar situation in the natural habitats of Chlamydomonas or other algae. In this sense, this is an artificial experimental setting. Nevertheless, the inverted bioconvection sheds new light on the dynamics of flagellates, namely, the dynamics within the crowded cell layer. It is hard to understand how Chlamydomonas cells move towards the light within a crowded population. The cells cannot beat their flagella freely, and the flagellar beat attacks neighboring cells. The cells keep their trials to move towards the light, and this tendency maintains the stability of the cell layer, although individual cells move laterally, or oscillate within the cell layer.

At first sight, we considered the inverted bioconvection a two-phase system obeying the Rayleigh-Taylor instability of two immiscible fluids with different densities: a denser fluid is layered over a lighter fluid. In a common two-phase system, the two layers are rapidly reversed by forming turbulent flows. The cell layer of Chlamydomonas, on the other hand, was growing continuously and maintained evenly for a minute or two before the plume was formed. In the explanation in fluid dynamics, we must assume a high viscosity and surface tension of the lighter phase (i.e., cell layer), which is quite unlikely in this biological system, because the cells are motile within the cell layer. Rather, the stability of the cell layer is assured by the mobility of the cells. Therefore, this is a dynamic stability.

The model of two-phase system can be applied, however, to the plume formation. Many cells cease to move and form a large aggregate. Detailed microscopic observation showed that the individual cells within such aggregates did not beat their flagella. This is the reason why we assume a modal transition. The cells in the aggregates must be in a different state than the swimming cells in the fluid or agitating cells within the crowded cell layer. We observed an instantaneous stop response (2.55 ± 1.25 and 1.49 ± 0.48 sec in TAP and Percoll, respectively) in 137c cells after a dark-to-light transition. The photophobic response (or photoshock, see Witman, 1993), a transitory reaction, is certainly different from the loss of motility in the aggregates, which are formed in the light (more than 10% of incident light was available within the cell layer) and stably maintained for tens of seconds, and which requires encounter of several cells. We call the non-motile state Mode 2 in contrast with Mode 1 in which the cells move or try to move by beating actively their flagella. The aggregate of non-motile cells can be considered similar to the viscous fluid (lower layer) in the two-phase system. Once formed, the aggregate of the non-motile cells float easily by the density difference, but this is also supported by the fact that the motile cells surrounding the aggregate try to invade into the space under the aggregate. Therefore, the situation is not exactly the same as the inanimate two-phase system.

The plausibility of our model including the modal changes was tested by computer simulation. We were able to find a region within the plane of variables, in which plume formation occurs. The variables, n and p, were introduced to describe the formation of cell aggregates, and are not directly related to measurable values of the actual system. However, the fact that plume formation was reproduced within a certain range of these variables suggests that the aggregate formation can initiate plume formation. Three global behaviors were detected in the system: explosion, plume formation, and stable cell layer. This difference can be qualitatively explained by the differences in the probability of modal change. If the cells remain in Mode 1, the cell layer is stable and continues to grow. If the transition to Mode 2 occurs easily and massively in most cells, the entire cell layer float in a number of blocks of cell aggregates like an explosion. Between the two extremes, plume formation takes place.

We still do not know exactly how the transition from Mode 1 to Mode 2 occurs, or vice versa. We already know that a swimming Chlamydomonas cell stops abruptly and stay non-motile for a while, when they are suddenly illuminated as described above. This occurs in individual, freely swimming cells, and might not exactly the same as the Mode 2 cells, which form aggregate and become non-motile. This comparison, however, suggests that the Chlamydomonas cell experiences at least two states, namely, the swimming and non-motile states. The non-motile state could be triggered not only by light stimulus, but also by cell-to-cell contact. The agg1 mutant cells such as CC-124 (Fig. 2) escape from the light and become aggregated and non-motile at the bottom of a flask. The CC-124 cells form a bioconvection at the surface of the liquid medium, if illuminated from the bottom. This situation might be similar to the inverted bioconvection of wild-type cells, and supports the modal change hypothesis.

4. Materials and methods

4.1. Strains and growth of organisms

Wild type strain of Chlamydomonas reinhardtii 137c (mating type minus, offspring of C8 mt+ × NO mt−), originally maintained in Kamiya Laboratory, University of Tokyo, was obtained from Dr. T. Minoura, University of Tokyo (now in Chuo University), and used throughout the present study as a standard strain. Other strains, CC-124, CC-125, CC-1009, CC-1010, and CC-1328, were obtained from Chlamydomonas Stock Center, Duke University. All strains were grown in the TAP medium (Gorman and Levine, 1965) under moderate illumination by fluorescent lamps (about 30 μE m-2 s−1) at room temperature (22–25 °C). CC-1009 and CC-1010 (nit1+) were also grown in the Modified Bristol Medium (Watanabe, 1960). The GFP (green fluorescent protein)-expressing line was constructed by transforming 137c cells (treated with GeneArt MAX Efficiency Transformation Reagent for Algae, Thermofisher) with the pMF59 plasmid (Fuhrmann, 2001) using the NEPA-21 electroporator (NEPA GENE Co. Ltd., Ichikawa, Japan: two times of 8 ms pulses at 250 V with an interval of 50 ms. The damping rate was 40%). Transformants were selected with 5 μg mL−1 zeocin.

Experiments of bioconvection require high-density population of actively swimming cells. Actively swimming cells were collected manually, two or three days after inoculation, from the surface of the culture medium with a Pasteur pipette. The cells were then placed in a small test tube, which was illuminated from the bottom using a photographic viewer (Light Viewer 5700, Hakuba, Tokyo). After several minutes, all cells accumulated at the bottom of the tube. The supernatant was removed, and the cells were gently suspended in a small volume of remaining medium. For inverted bioconvection, Percoll was gently added under the suspension, and then the cells were allowed to accumulate at the bottom by phototaxis. This step was repeated to prepare a cell suspension in 100% Percoll. It was not necessary to add nutrients to Percoll, because the cell motility was maintained for an hour or two, during the time necessary for the experiments. The cells were finally suspended in a small volume of Percoll.

4.2. Lateral microscope

A custom-made lateral microscope was constructed based on the Olympus industrial microscope parts (BXFM-S) as shown in Fig. 1a. For bright field observation, the light from a halogen lamp, which was filtered through a red cut-off filter (Kenko, SR-64), was illuminated on a 2-mm light-path all-transparent quartz cuvette for spectrophotometry (panels b and c). Images were obtained through a long-working-distance objective (10×, 20× or 40×) and appropriate band-pass filters (Fuji, BPB60 plus SC62) to remove the actinic light for phototaxis (see below), and then captured by a CCD camera (model Rolera-XR, QImaging, Surrey, BC, Canada, or model ORCA R2, Hamamatsu Photonics, Hamamatsu, Japan), which was connected to a computer (Apple iMac with a Core 2 Duo processor, 2.4 GHz, and 2 GB memory, operated on Windows XP) through IEEE 1394b interface. The time-lapse images were recorded directly on the hard disk of the computer at 15–40 fps (frames per second) using the StreamPix software (version 3.45.0, NorPix Inc., Montreal, Quebec, Canada) or the HC Image software (version 1.1.3.1, Hamamatsu Corporation, Bridgewater, NJ). Phototaxis was induced by an LED (light-emitting diode), which was located below the quartz cuvette or a light of LED introduced by an optical fiber. A blue LED peaking at 475 nm with a band-pass filter (460–500 nm) connected with a fiber-optics (Optoline Co. Ltd, Osaka) was used in most experiments, but during the initial experiments, a green LED peaking at 507 nm and a blue LED peaking at 456 nm were also used.

4.3. Image processing

Image processing was performed in two ways. In the first analysis, each image sequence was written to a file in the AVI format, and then it was split and converted to a Quick-Time movie by Quick Time software (version 7.6, Apple). Image processing was performed by Image J software (version 1.41 for Mac OS X, http://rsb.info.nih.gov/ij/index.html) with the plug-ins, SpotTracker plus Spot Enhancing Filter 2D (Sage et al., 2005) (http://bigwww.epfl.ch/sage/soft/spottracker/) and ParticleTracker version 1.5 (Sbalzarini and Koumoutsakos, 2005) (http://weeman.inf.ethz.ch/particletracker/). The dimension of a frame was 692 × 520 for Rolera-XR, or 672 × 512, 672 × 256 or 336 × 256 pixels (or even smaller to increase the frame rate) for ORCA R2. Each cell was enhanced by the Spot Enhancing Filter 2D using the radius setting of 2.5, and then, the trajectories were estimated by the ParticleTracker plug-in, using typically the following settings: Kernel radius = 3 or 4, percentile = 5.0, displacement = 12. The coordinates of the trajectories were saved as a text file. Statistics of cellular trajectories was calculated by perl scripts. Short trajectories of individual cells (over 6 frames) were selected from the trajectory lists, and then the average speed components in the x and y directions were calculated. The data were mapped as a histogram with an interval of 10 in the y-axis and 0.1 in the speed axis (either dx/dt or dy/dt) by the GNU Plot software version 5.

In a 3D analysis with x, y and t axes, each image sequence was converted to the sequential TIF format by the Image J software, and then visualized and manipulated by the VCAT5 software which was developed by the RIKEN Institute (http://logistics.riken.jp/vcat/vcat/en), run on a 64-bit Windows 10 workstation with a GPU (nVidia Geforce GTX) and 64 GB memory.

4.4. Measurement of light intensity

The light intensity within the optical cuvette was measured by the spectrometer model SEC2000 UV/VIS (ALS Co. Ltd., Tokyo), which was equipped with a microprobe (50 μm in diameter) connected with an optical fiber (Fig. 1g). The light intensity within the cuvette is shown in Fig. 1d–f. As far as we used the central region (the colored part corresponded to the image field), variation in light intensity could be ignored.

4.5. Simulation

The behavior of Chlamydomonas cells in the inverted bioconvection was simulated with the CompuCell3D software version 3.7.4 (Swat et al., 2012) on the Windows workstation as described in Section 4.3. Details of the model setting is provided in Supplementary document S1.

Declarations

Author contribution statement

Naoki Sato: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Wrote the paper.

Kaoru Sato: Analyzed and interpreted the data.

Masakazu Toyoshima: Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data.

Funding statement

This work was supported in part by KAKENHI from the Japan Society for Promotion of Science (JSPS) (nos. 24570043 and 15K12433 to NS) and from the Ministry of Education, Culture, Sports, Science and Technology (MEXT), Japan (no. 25111706 to NS).

Competing interest statement

The authors declare no conflict of interest.

Additional information

No additional information is available for this paper.

Appendix A. Supplementary data

The following are the supplementary data related to this article:

SupplementaryDataS1final

Documentation on the simulation of plume formation.

mmc1.docx (50.2KB, docx)
Supplementary Video S1

Movie of plume formation for Fig. 3d.

Download video file (9.7MB, mp4)
Supplementary Video S2

Movement of cells within the dense cell layer.

Download video file (1.6MB, mp4)
Supplementary Video S3

Simulation of plume formation.

Download video file (848.2KB, mp4)

References

  1. Brokaw C.J., Luck D.J.L., Huang B. Analysis of the movement of Chlamydomonas flagella: the function of the radial-spoke system is revealed by comparison of wild-type and mutant flagella. J. Cell Biol. 1982;92:722–732. doi: 10.1083/jcb.92.3.722. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Dervaux J., Resta M.C., Brunet P. Light-controlled flows in active fluids. Nat. Phys. 2017;13:306–312. [Google Scholar]
  3. Du Q., Kawabe Y., Schilde C., Chen Z.H., Schaap P. The evolution of aggregative multicellularity and cell-cell communication in the Dictyostelia. J. Mol. Biol. 2015;427:3722–3733. doi: 10.1016/j.jmb.2015.08.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Fuhrmann M. Universität Regensburg; Regensburg, Germany: 2001. Grün fluoreszierendes Protein und gezielte Genstilllegung in Chlamydomonas reinhardtii. Dissertation. [Google Scholar]
  5. Gentien P., Lunven M., Lazure P., Youenou A., Crassous M.P. Motility and autotoxicity in Karenia mikimotoi (Dinophyceae) Phil. Trans. Roy. Soc. Lond. B. 2007;362:1937–1946. doi: 10.1098/rstb.2007.2079. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. George E., Glimm J., Li X.L., Marchese A., Xu Z.L. A comparison of experimental, theoretical, and numerical simulation Rayleigh-Taylor mixing rates. Proc. Natl. Acad. Sci. U. S. A. 2002;99:2587–2592. doi: 10.1073/pnas.032568799. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Gorman D.S., Levine R.P. Cytochrome f and plastocyanin: their sequence in the photosynthetic electron transport chain of Chlamydomonas reinhardi. Proc. Natl. Acad. Sci. U. S. A. 1965;54:1665–1669. doi: 10.1073/pnas.54.6.1665. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Govorunova E.G., Jung K.-H., Sineshchekov O.A., Spudich J.L. Chlamydomonas sensory rhodopsins A and B: cellular content and role in photophobic responses. Biophys. J. 2004;86:2342–2349. doi: 10.1016/S0006-3495(04)74291-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Hill N.A., Pedley T.J. Bioconvection. Fluid Dynam. Res. 2005;37:1–20. [Google Scholar]
  10. Hosoya C., Akiyama A., Kage A., Baba S.A., Mogami Y. Reverse bioconvection of Chlamydomonas in the hyper-density medium. Biol. Sci. Space. 2010;24:145–152. [Google Scholar]
  11. Jánosi I.M., Czirók A., Silhavy D., Holczinger A. Is bioconvection enhancing bacterial growth in quiescent environments? Environ. Microbiol. 2002;4:525–531. doi: 10.1046/j.1462-2920.2002.00328.x. [DOI] [PubMed] [Google Scholar]
  12. Kessler J.O. Hydrodynamic focusing of motile algal cells. Nature. 1985;313:218–220. [Google Scholar]
  13. Kitsunezaki S., Komori R., Harumoto T. Bioconvection and front formation of Paramecium tetraurelia. Phys. Rev. E. 2007;76 doi: 10.1103/PhysRevE.76.046301. 046301. [DOI] [PubMed] [Google Scholar]
  14. Mendelson N.H. Bacillus subtilis macrofibres, colonies and bioconvection patterns use different strategies to achieve multicellular organization. Environ. Microbiol. 1999;1:471–477. doi: 10.1046/j.1462-2920.1999.00066.x. [DOI] [PubMed] [Google Scholar]
  15. Mendelson N.H., Lega J. A complex pattern of traveling stripes is produced by swimming cells of Bacillus subtilis. J. Bacteriol. 1998;180:3285–3294. doi: 10.1128/jb.180.13.3285-3294.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Metcalfe A.M., Pedley T.J. Bacterial bioconvection: weakly nonlinear theory for pattern selection. J. Fluid Mech. 1998;370:249–270. [Google Scholar]
  17. Mogami Y., Yamane A., Gino A., Baba S.A. Bioconvective pattern formation of Tetrahymena under altered gravity. J. Exp. Biol. 2004;207:3349–3359. doi: 10.1242/jeb.01167. [DOI] [PubMed] [Google Scholar]
  18. Pedley T.J., Kessler J.O. A new continuum model for suspensions of gyrotactic micro-organisms. J. Fluid Mech. 1990;212:155–182. doi: 10.1017/s0022112090001914. [DOI] [PubMed] [Google Scholar]
  19. Pedley T.J., Kessler J.O. Hydrodynamic phenomena in suspensions of swimming microorganisms. Annu. Rev. Fluid Mech. 1992;24:313–358. [Google Scholar]
  20. Pedley T.J., Hill N.A., Kessler J.O. The growth of bioconvection patterns in a uniform suspension of gyrotactic micro-organisms. J. Fluid Mech. 1988;195:223–237. doi: 10.1017/s0022112088002393. [DOI] [PubMed] [Google Scholar]
  21. Platt J.R. “Bioconvection patterns” in cultures of free-swimming organisms. Science. 1961;133:1766–1777. doi: 10.1126/science.133.3466.1766. [DOI] [PubMed] [Google Scholar]
  22. Plesset M.S., Winet H. Bioconvection patterns in swimming microorganism cultures as an example of Rayleigh-Taylor instability. Nature. 1974;248:441–443. doi: 10.1038/248441a0. [DOI] [PubMed] [Google Scholar]
  23. Plesset M.S., Whipple C.G., Winet H. Rayleigh-Taylor instability of surface layers as the mechanism for bioconvection in cell cultures. J. Theor. Biol. 1976;59:331–351. doi: 10.1016/0022-5193(76)90174-0. [DOI] [PubMed] [Google Scholar]
  24. Rüffer U., Nultsch W. High-speed cinematographic analysis of the movement of Chlamydomonas. Cell Motil. 1985;5:251–263. [Google Scholar]
  25. Sage D., Neumann F.R., Hediger F., Gasser S.M., Unser M. Automatic tracking of individual fluorescence particles: application to the study of chromosome dynamics. IEEE Trans. Image Process. 2005;14:1372–1383. doi: 10.1109/tip.2005.852787. [DOI] [PubMed] [Google Scholar]
  26. Sbalzarini I.F., Koumoutsakos P. Feature point tracking and trajectory analysis for video imaging in cell biology. J. Struct. Biol. 2005;151:182–195. doi: 10.1016/j.jsb.2005.06.002. [DOI] [PubMed] [Google Scholar]
  27. Sineshchekov O.A., Jung K.-H., Spudich J.L. Two rhodopsins mediate phototaxis to low- and high-intensity light in Chlamydomonas reinhardtii. Proc. Natl. Acad. Sci. U. S. A. 2002;99:8689–8694. doi: 10.1073/pnas.122243399. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Swat M.H., Thomas G.L., Belmonte J.M., Shirinifard A., Hmeljak D., Glazier J.A. Multi-scale modeling of tissues using CompuCell3D. Meth. Cell Biol. 2012;110:325–366. doi: 10.1016/B978-0-12-388403-9.00013-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Vincent R.V., Hill N.A. Bioconvection in a suspension of phototactic algae. J. Fluid Mech. 1996;327:343–371. [Google Scholar]
  30. Wager H. On the effect of gravity upon the movements and aggregation of Euglena viridis, Ehrb., and other micro-organisms. Phil. Trans. Roy. Soc. Lond. B. 1910–1911;201:339–390. [Google Scholar]
  31. Watanabe A. List of algal strains in collection at the Institute of applied microbiology, University of Tokyo. J. Gen. Appl. Microbiol. 1960;6:283–292. [Google Scholar]
  32. Witman G.B. Chlamydomonas phototaxis. Trends Cell Biol. 1993;3:403–408. doi: 10.1016/0962-8924(93)90091-e. [DOI] [PubMed] [Google Scholar]
  33. Yamamoto Y., Okayama T., Sato K., Takaoki T. Relation of pattern formation to external conditions in the flagellate, Chlamydomonas reinhardtii. Eur. J. Pristol. 1992;28:415–420. doi: 10.1016/S0932-4739(11)80005-2. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

SupplementaryDataS1final

Documentation on the simulation of plume formation.

mmc1.docx (50.2KB, docx)
Supplementary Video S1

Movie of plume formation for Fig. 3d.

Download video file (9.7MB, mp4)
Supplementary Video S2

Movement of cells within the dense cell layer.

Download video file (1.6MB, mp4)
Supplementary Video S3

Simulation of plume formation.

Download video file (848.2KB, mp4)

Articles from Heliyon are provided here courtesy of Elsevier

RESOURCES