Abstract
Climate policy making is challenging primarily in that it involves the assessment of data and methods across a multitude of scientific fields and disciplines. In this respect, integrated assessment models are being used, the level of detail in which allows for modelling all relations between climate and human activity. As a result, their structure is usually significantly complex and their use often excludes stakeholders and their valuable knowledge. The aim of this paper is to assess how multiple criteria decision analysis can bridge the gap between climate policy studies and experts, by delving into the literature and reaching a methodological framework appropriate for solving complex problems of this particular problem domain, featuring multiple alternatives, criteria and decision makers. Based on the findings, the Multiple Alternatives—Criteria—Experts Decision Support System is developed and presented. Finally, the capacity of this spreadsheet-based tool is demonstrated by means of a two-stage case study, which includes assessing the importance of a number of exogenous policy risks, as well as evaluating different short-term policy instruments against these risks.
Keywords: Industrial engineering, Energy, Computer science
1. Introduction
Promoting transition pathways towards low carbon societies can only be achieved through robust climate policy making processes that take into account the various types of risk and uncertainty, which are intertwined with climate change and respective policy design, implementation and acceptance. Climate policy support almost exclusively comes in the form of climate-economy modelling activities, by means of Integrated Assessment Models (IAMs), which have largely contributed to understanding the complex interactions between energy, climate, economy and all dimensions of human activity as well as the impacts of potential policy strategies on each one of these modules.
In order to capture these interactions, the structure of these models has grown inevitably and significantly complex, and data unavailability is compensated for by using a number of assumptions as a means of dealing with uncertainty. As a result of this hard-to-follow, exclusively data-driven procedure that is climate-economy quantitative modelling, there is little room for policy makers as well as other key stakeholder groups to provide their insights and experience in order to bridge knowledge gaps. In turn, this exclusion of the human factor from the equation, in combination with said complexity, makes policy makers reluctant to trust and use their results. It is evident that there is significant need for appropriate decision support frameworks towards bridging the gap between experts and modellers.
In this direction, stakeholder engagement and participation has been gaining growing attention in environmental and climate policy studies (van Vliet et al., 2010) and so has the implementation of different expert-driven decision support approaches (Nikas et al., 2017). One such approach can be found in Multiple Criteria Decision Analysis (MCDA), which is a sub-discipline of Operational Research focusing on supporting policy and decision making in multi-dimensional problem domains, where different alternatives must be assessed against different evaluation criteria, across different dimensions of said domains. Despite the notably late start, due to lack of appropriate guidelines (Borges and Villavicencio, 2004), MCDA has been gaining increasing attention in the climate policy domain, primarily due to the need for determining parts of scenario inputs (e.g. technological preferences, distinct values for uncertain parameters, possible future socioeconomic developments, climate- and economy-related requirements, etc.) as well as the ever-growing popularity of MCDA frameworks in studies on energy policy (Doukas, 2013), which expectedly constitutes the core aspect of climate policy: the energy system is the most responsible driver of greenhouse gas emissions (Bruckner et al., 2014) as well as lies at the heart of all economic activities.
Of course, MCDA encompasses a diverse range of different methodologies, with varying features and based on substantially different approaches, as well as can be implemented across a large number of applications and problem domains. A preliminary objective of this study, therefore, is to critically review climate policy related studies in the multicriteria decision making literature, in order to assess their scope and explore the applicability of different methodological MCDA frameworks in the climate policy domain. Additionally, given the need for integration with other modelling frameworks and tools, the assessment of their capacity to integrate with different approaches is also pursued.
Drawing from the findings of this review, an appropriate MCDA approach is selected. It should be noted, however, that a significant aspect of MCDA, on which the selected framework largely depends, lies in the available capacity to support a number of stakeholders; given that the participation of different stakeholder groups with different types and levels of knowledge of different aspects of the problem domain is desired (Xu et al., 2015), it is of vital importance that the group decision making aspect of MCDA be highlighted. The core aim of this paper, therefore, is to develop a decision support tool that can both support climate policy making by means of an appropriate MCDA methodology and emphasise the desired group decision making aspect. In this context, a Behavioural TOPSIS-oriented methodological framework is introduced and a dedicated spreadsheet-based tool that can support this process, with the capacity of enabling disagreement-driven consensus control and building, is developed and presented. The analytical framework is finally applied in a case study aiming to assess different climate policy instruments against implementation risks in the Greek building, energy and transport sectors towards the desired low carbon transformation.
In this respect, Section 2 presents the findings of the thorough literature review of MCDA applications in the climate policy literature. Section 3 describes the stages of the developed methodological framework and introduces MACE-DSS (Multiple Alternatives-Criteria-Experts Decision Support System), a dedicated spreadsheet-based tool that can support this framework. An implementation of said framework and application of the tool is carried out in Section 4, while Section 5 concludes the analysis, by evaluating the tool's capacity to deal with the problem at hand as well as its limitations, and presents future prospects.
2. Study area
In this section, we seek to review all studies in the MCDA literature with climate policy implications. The primary objective of this task is to assess the applicability of multiple-criteria decision analysis in the climate policy domain. This is done by looking at the different application areas and economic sectors in which it has been used; exploring the scope and geographic level it can support; evaluating the exhaustiveness and non-redundancy of the evaluation criteria against which the alternative actions have been analysed; appreciating the extent to which risks and uncertainties are adequately included in the analyses; and assessing the featured capacity to integrate with other methodological approaches towards providing more robust results. At a subsequent level and drawing from this analysis, we aim to lay the groundwork for selecting the appropriate methodological frameworks based on the requirements of our analysis. For the purposes of this research, we used the search engines of Scopus, ScienceDirect and Google Scholar and carried out queries for alternative key phrases referring to multiple criteria decision making (such as “multiple criteria”, “multicriteria”, “MCDA”, “MCDM”, “decision support”) followed by the AND operator and key phrases referring to climate policy (“mitigation”, “adaptation”, “energy policy”, “climate policy”, “climate”). Additionally, instead of looking at keywords and phrases revolving around climate policy, we also focused on the sectors of human activity. The “title”, “abstract” and “keyword” sections of all retrieved studies were, then, manually reviewed in order to carefully select the pieces of literature that were of interest to our purposes, before thoroughly going through the manuscripts and extract the information in detail, in a structured manner.
The most significant difficulty in effectively supervising the respective literature lies in the growing proliferation of multicriteria analysis approaches and methodological frameworks during the past two decades, both in general and in the context of our problem domain. This is one of the main reasons why individual MCDA frameworks were not queried with regard to their application in climate policy studies, since this would significantly delay the manual selection process. Furthermore, since climate policy has so far been mostly supported by means of Integrated Assessment Models that have the capacity to study very complex sets of economy-, climate-, society-, and energy-associated parameters in detail, MCDA is used as a stakeholder engagement-facilitating framework for complementing integrated climate policy simulation and evaluation approaches or in applications of limited scope. The latter may not explicitly address climate policy selection problems but may very well have implications for climate mitigation and adaptation policies.
Indeed, only nine studies were found to be explicitly carried out in the context of climate mitigation and/or adaptation. Among these studies and with the exception of an evaluation of all EU member states with regard to their greenhouse gas emissions in the agricultural sector (Dace and Blumberga, 2016), all focused on evaluating climate policy instruments or strategies: de Bruin et al. (2009) assessed a mix of cross-sectoral climate adaptation options in the Netherlands, Michailidou et al. (2016) delved into the interactions between tourism and climate change by assessing both mitigation and adaptation options in this industry sector, while the remaining studies revolved around primarily mitigation-oriented policy instruments in the energy sector (e.g. Blechinger and Shah, 2011; Georgopoulou et al., 2003; and Streimikiene and Baležentis, 2013b), the transport sector (AlSabbagh et al., 2016), or in cross-sectoral domains at either a national (Borges and Villavicencio, 2004) or regional (Konidari and Mavrakis, 2007) level. A significantly larger number of studies were found to be carried out in a diverse number of applications (such as evaluating policies, selecting green projects, assessing decarbonisation technologies, analysing possible future developments, assessing climate change- or policy-related risks, etc.) with obvious implications for climate policy—either by examining policy-related alternatives or by assessing alternative courses of action against strictly-defined environment- and climate-related evaluation criteria. Apart from the latter, the studied multicriteria analyses appear to almost always include economic and societal criteria, as opposed to regulatory criteria that are less frequently used.
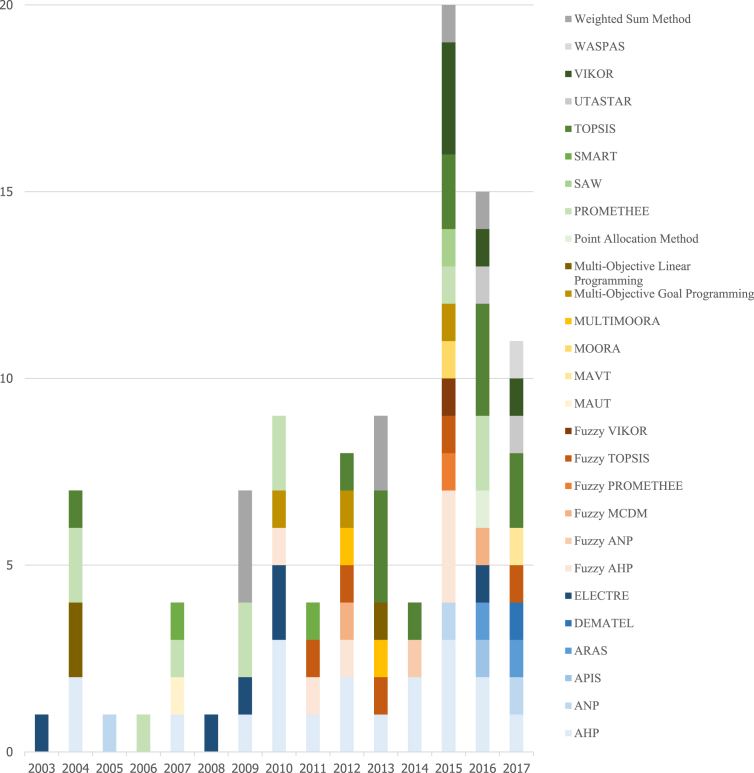
From a methodological point of view, said proliferation is reflected on the twenty seven different MCDA frameworks that were found in the reviewed literature. A very interesting outcome of this analysis can be found in the observation of the MCDA evolution trends in the problem domain, by identifying the frequency of adoption of each methodological framework during the past fifteen years (Fig. 1). Among these frameworks, the most popular ones appear to be two pairwise comparison approaches, namely the Analytic Hierarchy Process (AHP) and PROMETHEE, and the distance-based TOPSIS methodology. Another straightforward observation concerns some newer methodological frameworks, which have been enjoying increasing attention in the reviewed literature, such as the compromise-oriented VIKOR approach or the disaggregation-aggregation paradigm (like UTASTAR). Among the “traditional” multicriteria analysis techniques, there appear to be some that have remained popular in the wider climate policy domain, like PROMETHEE and the ELECTRE family of methods, while others like AHP or TOPSIS have been gaining more ground of late.
Fig. 1.
Evolution trends of the MCDA methodological frameworks in the studied problem domain, 2003–2017.
Fig. 1 also reflects the growing attention that MCDA, as a sub-discipline of Operational Research, has been gaining lately; it should be noted that this analysis was concluded in May 2017, i.e. there is significant potential for more MCDA studies to be carried out, completed and published later in 2017.
As mentioned in the first section, a key aspect of multiple-criteria decision making can be found in its capacity not only to assess numerous alternatives against multiple criteria in a structured manner but also to support the elicitation of knowledge from a large number of stakeholders, also referred to as group decision making. Table 1 presents the reviewed pieces of literature that feature group decision making, classified by methodological framework, with a focus on the different types of evaluation criteria employed in the respective analyses.
Table 1.
Overview of group decision making MCDA frameworks used in climate policy-related studies. Italic formatting indicates studies with multiple frameworks, either in different stages of the analysis or in a comparative manner. Asterisk (*) indicates sensitivity analysis.
| Methodological Approach | Study | Type of Evaluation Criteria |
Sector of human activity | |||||
|---|---|---|---|---|---|---|---|---|
| Financial | Energy | Env/mental | Regulatory | Societal | Tech/cal | |||
| AHP | (AlSabbagh et al., 2016) | ✓ | ✓ | ✓ | ✓ | Transport | ||
| (Biloslavo and Dolinšek, 2010) | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | Power | |
| (Biloslavo and Grebenc, 2012) | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | Power | |
| (Blechinger and Shah, 2011)* | ✓ | ✓ | ✓ | ✓ | ✓ | Power | ||
| (Borges and Villavicencio, 2004) | ✓ | ✓ | ✓ | ✓ | Agriculture; Power; Transport | |||
| (Büyüközkana and Karabulutb, 2017) | ✓ | ✓ | ✓ | Power | ||||
| (Cowan et al., 2010)* | ✓ | ✓ | ✓ | ✓ | Power | |||
| (Javid et al., 2014) | ✓ | ✓ | Transport | |||||
| (Konidari and Mavrakis, 2007) | ✓ | ✓ | ✓ | All sectors | ||||
| (Montanari, 2004) | ✓ | ✓ | ✓ | Power | ||||
| (Paul et al., 2015) | ✓ | ✓ | Transport | |||||
| (Rojas-Zerpa and Yusta, 2015) | ✓ | ✓ | ✓ | ✓ | ✓ | Power | ||
| (Shiau and Liu, 2013) | ✓ | ✓ | ✓ | ✓ | Transport | |||
| (Streimikiene et al., 2016)* | ✓ | ✓ | ✓ | ✓ | ✓ | Power | ||
| (Talaei et al., 2014)* | ✓ | ✓ | ✓ | ✓ | Power | |||
| (Yap and Nixon, 2015)* | ✓ | ✓ | ✓ | ✓ | ✓ | Power | ||
| ANP | (Büyüközkan and Güleryüz, 2017)* | ✓ | ✓ | ✓ | ✓ | ✓ | Power | |
| (Sakthivel et al., 2015) | ✓ | ✓ | Transport | |||||
| (Ulutaş, 2005) | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | Power | |
| ARAS | (Streimikiene et al., 2016)* | ✓ | ✓ | ✓ | ✓ | ✓ | Power | |
| DEMATEL | (Büyüközkan and Güleryüz, 2017)* | ✓ | ✓ | ✓ | ✓ | ✓ | Power | |
| ELECTRE | (Georgopoulou et al., 2003) | ✓ | ✓ | ✓ | Power | |||
| (Karakosta et al., 2009) | ✓ | ✓ | ✓ | ✓ | ✓ | Power | ||
| (Michailidou et al., 2016)* | ✓ | ✓ | ✓ | Industry | ||||
| Fuzzy AHP | (Heo et al., 2010) | ✓ | ✓ | ✓ | ✓ | Power | ||
| (Kaya and Kahraman, 2011)* | ✓ | ✓ | ✓ | ✓ | Power | |||
| (Luthra et al., 2015)* | ✓ | ✓ | ✓ | ✓ | Power | |||
| (Ren and Lützen, 2015)* | ✓ | ✓ | ✓ | ✓ | Industry; Transport | |||
| Fuzzy ANP | (Promentilla et al., 2014) | ✓ | ✓ | ✓ | ✓ | Power | ||
| Fuzzy MCDM | (Chang et al., 2012) | ✓ | ✓ | ✓ | ✓ | Buildings; Power; Transport | ||
| (Cutz et al., 2016) | ✓ | ✓ | ✓ | ✓ | Power | |||
| Fuzzy PROMETHEE | (Chen and Pan, 2015) | ✓ | ✓ | ✓ | Buildings | |||
| Fuzzy TOPSIS | (Jun et al., 2013) | ✓ | ✓ | ✓ | Buildings | |||
| (Kaya and Kahraman, 2011)* | ✓ | ✓ | ✓ | ✓ | Power | |||
| (Onu et al., 2017) | ✓ | ✓ | ✓ | ✓ | ✓ | Environment; Power | ||
| Fuzzy VIKOR | (Vahabzadeh et al., 2015) | ✓ | Industry | |||||
| MAUT | (Konidari and Mavrakis, 2007) | ✓ | ✓ | ✓ | All sectors | |||
| MOORA | (Paul et al., 2015) | ✓ | ✓ | Transport | ||||
| Multi-Objective Goal Programming | (Cowan et al., 2010) | ✓ | ✓ | ✓ | ✓ | Power | ||
| Multi-Objective Linear Programming | (Ribeiro et al., 2013)* | ✓ | ✓ | ✓ | ✓ | ✓ | Power | |
| Point Allocation Method | (Xu et al., 2016) | ✓ | ✓ | ✓ | ✓ | Power | ||
| PROMETHEE | (Borges and Villavicencio, 2004) | ✓ | ✓ | ✓ | ✓ | Agriculture; Power; Transport | ||
| (Doukas et al., 2006) | ✓ | ✓ | ✓ | ✓ | ||||
| (Ghafghazi et al., 2010) | ✓ | ✓ | ✓ | ✓ | Buildings | |||
| (Paul et al., 2015) | ✓ | ✓ | Transport | |||||
| (Tsoutsos et al., 2009)* | ✓ | ✓ | ✓ | ✓ | ✓ | Power | ||
| (Vaillancourt and Waaub, 2004)* | ✓ | ✓ | ✓ | ✓ | Industry | |||
| (Xu et al., 2016) | ✓ | ✓ | ✓ | ✓ | ||||
| SMART | (Blechinger and Shah, 2011)* | ✓ | ✓ | ✓ | ✓ | ✓ | Power | |
| (Konidari and Mavrakis, 2007)* | ✓ | ✓ | ✓ | All sectors | ||||
| TOPSIS | (Brand and Missaoui, 2014)* | ✓ | ✓ | ✓ | ✓ | Power | ||
| (Büyüközkan and Güleryüz, 2017)* | ✓ | ✓ | ✓ | ✓ | ✓ | Power | ||
| (Jun et al., 2013) | ✓ | ✓ | ✓ | Buildings | ||||
| (Montanari, 2004) | ✓ | ✓ | ✓ | Power | ||||
| (Mourhir et al., 2016) | ✓ | ✓ | ✓ | ✓ | ✓ | Environment | ||
| (Sakthivel et al., 2015) | ✓ | ✓ | Transport | |||||
| UTASTAR | (Papapostolou et al., 2016) | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | Power |
| (Papapostolou et al., 2017) | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | Power | |
| VIKOR | (Büyüközkan and Karabulut, 2017)* | ✓ | ✓ | ✓ | Power | |||
| (Ren and Lützen, 2015)* | ✓ | ✓ | ✓ | ✓ | Industry; Transport | |||
| (Rojas-Zerpa and Yusta, 2015) | ✓ | ✓ | ✓ | ✓ | ✓ | Power | ||
| (Sakthivel et al., 2015) | ✓ | ✓ | Transport | |||||
| Weighted Sum Method | (de Bruin et al., 2009) | ✓ | ✓ | All sectors | ||||
| (Jun et al., 2013) | ✓ | ✓ | ✓ | Buildings | ||||
| (Ribeiro et al., 2013)* | ✓ | ✓ | ✓ | ✓ | ✓ | Power | ||
| (Roth et al., 2009)* | ✓ | ✓ | ✓ | Power | ||||
As mentioned earlier, multiple-criteria decision making cannot replace integrated assessment modelling activities but, given the need to bridge the gap between modellers and stakeholders, it can significantly enhance climate policy support processes. In order to do so, MCDA studies are usually carried out in a focused manner, in one or multiple greenhouse gas emitting sectors of economic activity and in application areas that are not limited to evaluating climate policy instruments. Table 1 also records the sector of human activity in which group MCDA has been applied, including agriculture, buildings, environment, industry, power and transport.
Although risk assessment appeared to be carried out in very few of the reviewed pieces of literature (e.g. Branco et al., 2012), other researchers pursued to analyse risks in respective frameworks, such as the Benefits – Opportunities – Costs – Risks framework (Ulutaş, 2005; and Yap and Nixon, 2015), as well as assess uncertainties in various approaches, with the most prominent one being Monte Carlo Analysis (Baležentis and Streimikiene, 2017; and Shmelev and van den Bergh, 2016).
MCDA is claimed to be a process that can bring stakeholders, i.e. decision makers, closer to the decision and policy support process. Sometimes, however, the employed MCDA framework is far too complex for stakeholders to understand or analysts to elicit and process the experts' input, or the large number of alternatives or criteria make the engagement process significantly harder. These conditions usually dictate the utilisation of a stakeholder-friendly yet simpler approach, such as the AHP, or the employment of appropriate communication techniques, like Delphi (e.g. Xu et al., 2016) or Input-Output Analysis (e.g. Jayaraman et al., 2015).
As far as its capacity to be used as part of an integrated assessment approach is concerned, MCDA appears to have successfully complemented both quasi-quantitative modelling frameworks, like fuzzy cognitive mapping (e.g. Biloslavo and Grebenc, 2012), and purely quantitative modelling activities, such as IAMs (Baležentis and Streimikiene, 2017), energy system models (e.g. Shmelev and van den Bergh, 2016), climate analysis models (Jun et al., 2013), and portfolio analysis (Almaraz et al., 2013).
Finally, with regard to their geographic scope, most climate policy-related MCDA studies appear to have been carried out in Europe on a national level, with only a few on an EU- (Baležentis and Streimikiene, 2017; and Branco et al., 2012) or regional level (Konidari and Mavrakis, 2007; and Xu et al., 2016) and one study focusing on two countries across different regions (Yap and Nixon, 2015). Table 2 summarises the geographic scope of the reviewed studies.
Table 2.
Geographic scope of MCDA studies with climate policy implications.
From both Tables 1 and 2, it is evident that almost all MCDA studies focus on one specific sector, with the exception of three studies that assess cross-sectoral climate policy instruments, as well as two technology assessment analyses (Chang et al., 2012; and Ren and Lützen, 2015). We can also see that policy evaluation MCDA studies appear fairly distributed across the numerous sectors, whereas the scope of all other multicriteria analyses appears to be dominated by the power sector, which is followed by transportation. As far as application areas are concerned, technology assessment seems to be the primary objective the most, followed by policy evaluation.
3. Methodology
Drawing from the results of our analysis, the Technique for Order of Preference by Similarity to Ideal Solution or TOPSIS (Hwang and Yoon, 1981) multicriteria analysis method was selected to be used as the principal component of our methodological framework. TOPSIS was developed as an alternative to the ELECTRE family of methods and is a compensatory aggregation method, which is based on the principle that the selected action must feature the shortest geometric distance from the positive ideal solution and the largest from the negative ideal solution. The TOPSIS approach includes the formulation and normalisation of the decision (alternatives against criteria) table, the calculation of the weighted decision table, the determination of the positive (for benefit-associated criteria) and negative (for cost-associated criteria) ideal solutions, and the calculation of the distance of each alternative from these solutions, towards reaching a final ranking. TOPSIS was later extended by Chen (2000), by introducing a vertex method for calculating the distance between two triangular fuzzy numbers, thus developing Fuzzy TOPSIS, which was further extended to handle different types of input data (Chen and Tsao, 2008; Chen and Lee, 2010).
As can be seen in Tables 1 and 2, there have been a large number of TOPSIS and Fuzzy TOPSIS applications in the climate policy literature, showing a diverse set of application areas as well as economic sectors and evaluating alternative actions against criteria of a diverse set of evaluation axes. Part of the reasons behind selecting TOPSIS is summarised in Table 3. One of these reasons is that TOPSIS appears to feature the most balanced distribution of individual and group decision making applications, a fact that indicates its capacity to support any MCDA problem, regardless of the number of stakeholders that must participate in the decision making process. Furthermore, sensitivity analysis has been carried out in many of these studies, leading to enhanced robustness of their results. But, most importantly, and in line with the core objective of this study, TOPSIS features the largest number of applications in which the multiple-criteria decision making method is integrated with a quantitative modelling framework. In fact, with the exception of two studies that used two different MCDA frameworks, namely APIS (Shmelev and van den Bergh, 2016) and PROMETHEE (Vaillancourt and Waaub, 2004), only TOPSIS has been integrated with purely quantitative modelling frameworks. More specifically, Almaraz et al. (2013) design a hydrogen supply chain through mixed integer linear programming and assess a number of solutions based on their cost, climate mitigation potential and safety risk, by integrating an ε-constraint portfolio analysis approach with TOPSIS as well as a modified version of TOPSIS (M-TOPSIS). Baležentisa and Streimikiene (2017) ranked a number of energy policy scenarios in the European Union, by means of two integrated assessment models (WITCH and TIAM-WORLD) and three different multicriteria analysis methodologies (WASPAS, ARAS and TOPSIS), while also applying Monte Carlo simulations for analysing the sensitivity of their results against changes to criterion weights. Brand and Missaoui (2014) referred to TOPSIS as featuring a logic closely representing the rationale of human choice and a simple computation process, and linked it with an electricity system model presented in (Brand et al., 2012), a bottom-up linear optimisation model, in order to assess different electricity generation mixes in Tunisia. In a more climate-change-oriented approach, Jun et al. (2013) used two climate change models of the National Center for Atmosphere Research, namely the Community Climate System Model 3 and the MM5 mesoscale model, in order to develop 19 different climate change scenarios, which they ranked with Fuzzy TOPSIS. Last but not least, and outside the strictly quantitative climate and energy modelling framework, Mourhir et al. (2016) used the Driving Forces-Pressures-State-Impact-Response (DPSIR) Integrated Environmental Assessment framework to enable their stakeholders to select appropriate indicators, which were later used by their experts to qualitatively design and describe Fuzzy Cognitive Maps; the latter were then quasi-quantitatively simulated and the most optimal scenarios were then ranked in a TOPSIS-oriented MCDA framework.
Table 3.
An overview of modelling-integrated TOPSIS applications used in the climate policy literature. Bold formatting indicates Fuzzy TOPSIS. Italic formatting indicates that other MCDA methods were used in addition to TOPSIS.
| Study | Stakeholders | Sensitivity Analysis | Integration with modelling frameworks |
|---|---|---|---|
| (Almaraz et al., 2013) | Individual | Portfolio Analysis (ε-constraint) | |
| (Baležentis and Streimikiene, 2017) | Individual | ✓ | Integrated Assessment Modelling (TIAM, WITCH); Monte Carlo Analysis |
| (Brand and Missaoui, 2014) | Group | ✓ | Electricity System Modelling |
| (Büyüközkan and Güleryüz, 2017) | Group | ✓ | |
| (Dace and Blumberga, 2016) | Individual | ||
| (Jun et al., 2013) | Group | Climate System Modelling (CCSM3; MM5) | |
| (Kaya and Kahraman, 2011) | Group | ✓ | |
| (Maimoun et al., 2016) | Individual | ✓ | |
| (Montanari, 2004) | Group | ||
| (Mourhir et al., 2016) | Group | Fuzzy Cognitive Mapping; Integrated Environmental Assessment (Driving Forces–Pressures–State–Impact–Response) | |
| (Onu et al., 2017) | Group | ||
| (Ramazankhani et al., 2016) | Individual | ✓ | |
| (Sadeghi et al., 2012) | Individual | ||
| (Sakthivel et al., 2015) | Group | ||
| (Şengül et al., 2015) | Individual | ✓ | |
| (Streimikiene et al., 2012) | Individual | ||
| (Streimikiene and Baležentis, 2013a) | Individual |
Despite the fact that there exist a plethora of MCDA approaches (e.g. PROMETHEE, ELECTRE, AHP, UTA, etc.) (Greco et al., 2016), the outcomes of the literature analysis summarise part of the logic behind selecting the TOPSIS multicriteria method as the heart of our methodological framework. Furthermore, as Kim et al. (1997) and Shih et al. (2007) note, TOPSIS features a sound logic that represents the rationale of individual choice; simultaneously considers both the ideal and the anti-ideal solutions; and employs a systematic, explicit and easily programmable computation procedure. Unlike pairwise comparison methods, it also allows for a large number of both criteria and alternatives. Aside from the recorded advantages and the domain popularity of the method, as indicated by the results of the literature review, the selection of TOPSIS was also motivated by the availability of its methodological extensions in the fuzzy environment, facilitating the prospective enhancement of the tool, as well as its capacity to effectively tackle the problematic of interest, which is ranking the alternatives. Finally, despite its 36-year presence in the MCDA discipline and driven by the need to include the notion of loss aversion behaviour, the TOPSIS framework was recently further enhanced by part of the research team that originally introduced it, producing Behavioural TOPSIS (Yoon and Kim, 2017). In fact, it is this specific variation of TOPSIS that was included in the presented methodological framework, since it additionally incorporates the decision makers' behavioural tendency to avoid loss and enables easy sensitivity analysis of results against changes in the attribute weights and loss aversion ratios.
The proposed approach comprises three stages: (a) unification of input data, (b) multi-criteria analysis, and (c) consensus control. In this respect, a spreadsheet-based tool, MACE-DSS, has been developed, featuring the capacity to deal with problems of up to 12 alternatives, against up to 12 criteria, evaluated by up to 12 decision makers; to assess either of two different linguistic term scales; to assign criteria and expert weights; as well as to specify the consensus control thresholds. The user is only required to fill in the input data in the first sheet, including expert judgment for each alternative against each criterion, as well as the number of alternatives, criteria and experts, the thresholds, the selected scale, and the criteria and expert weights.
These three stages are described in detail in the sub-sections below.
3.1. Data unification
Since the original TOPSIS and Behavioural TOPSIS frameworks work with numerical data and given that certain stakeholders may either be reluctant to provide their insights in a purely numerical scale or find it hard to express them in such a scale because of the qualitative nature of such opinions (Agell et al., 2012; Estrella et al., 2017), the option of providing input into linguistic variables has been commonly used in the literature and in our case must be provided for. However, before proceeding to a multicriteria analysis, there must be consistency among the input data.
As a result, all data is initially transformed into a uniform numerical scale. The analyst may choose a specific numerical scale and an appropriate linguistic term scale, so that every decision maker is free to provide their input into whichever scale they feel more comfortable with. The terms of the linguistic scale are matched with discrete numbers of the numerical scale and the final input is numerical.
Given that numerical input can be continuous whereas linguistic variables are discrete, MACE-DSS also allows for assessing a hybrid input model, aimed at decision makers who wish to provide their input into the form of a linguistic term “and then some”, in order to compensate for the precision gap between the two types of input.
3.2. Multi-criteria analysis
The multi-criteria analysis is largely based on the Behavioural TOPSIS methodological framework. The TOPSIS model (Hwang and Yoon, 1981) includes the following steps:
-
1.
Designing the decision matrix (Equation 1), which comprises alternatives and evaluation criteria
| (1) |
where are the alternatives, are the criteria and is the score of alternative against criterion .
-
2.
Calculating the normalised decision matrix (Equation 2), where each element can be calculated as follows:
| (2) |
where represents the normalised score of against criterion .
-
3.
Calculating the weighted normalised matrix , by multiplying the normalised matrix with the relevant weights. The weight vector consists of individual weights for each criterion that satisfy the constraint shown in Equation 3.
| (3) |
The weighted normalised value can then be calculated (Equation 4).
| (4) |
-
4.
Determining the positive ideal (positive impact criteria) and negative ideal (negative impact criteria) solution vectors (Equations 5 and 6, respectively), by calculating the positive and negative ideal solutions for each criterion (Equations 7 and 8), respectively).
| (5) |
| (6) |
| (7) |
| (8) |
where represents positive impact criteria and represents negative impact criteria.
-
5.
Calculating the distance of each alternative from the positive ideal solution (Equation 9) and the negative ideal solution (Equation 10).
| (9) |
| (10) |
-
6.
Finally, calculating the relative closeness to the ideal solution for each , as shown in Equation 11.
| (11) |
Straying from the original TOPSIS model, Behavioural TOPSIS acknowledges the relationship between the distance from the ideal (or positive ideal) solution and the distance from the anti-ideal (or negative ideal) solution , by considering the former as the opportunity loss and the latter as the gain earned from taking solution instead of the anti-ideal solution. A loss aversion rate is thus defined in Equation 12.
| (12) |
where the behaviour is risk-seeking for , neutral for , and risk-averse for . The risk aversion behaviour can be configured in MACE-DSS. Finally, the value function for each alternative is given by Equation 13, based on which the alternatives are ranked.
| (13) |
In group decision making processes, aggregating input is one of the most critical aspects (Lan et al., 2013). For the purposes of developing a group decision making decision support tool, the proposed approach involves utilising the Behavioural TOPSIS methodological framework twice, one for aggregating the individual preference models of the stakeholders into a global model, and another one for assessing the global model towards reaching a final ranking. This approach is presented in (Krohling and Campanharo, 2011), although that particular study used the Fuzzy TOPSIS approach based on triangular fuzzy numbers.
In this approach, after eliciting all decision makers' knowledge and unifying it into a consistent numerical scale, the Behavioural TOPSIS model is used for each one of the decision makers and a relative closeness matrix (Global Closeness, or ) is formulated so as to incorporate all individual preference models (Equation 14).
| (14) |
Furthermore, if there have been determined weights for each of the stakeholders and based on the respective weight vector , one can then calculate the weighted global model matrix (Equation 15).
| (15) |
Alternatively, the user may select a different Behavioural TOPSIS-oriented approach, in which the weighted sum method (WSM) is implemented towards reaching one single score for each alternative against each criterion, thereby aggregating the scores of all decision makers, and then the Behavioural TOPSIS framework is implemented once towards reaching the final ranking. This approach has been suggested by (Chen, 2000), for the original TOPSIS method.
For the sake of enhancing diversity and robustness of results, a substantially different approach based on an aggregation and translation model presented in (Herrera et al., 2005) is also modelled in the tool, which considers that the final evaluation of alternative actions must be expressed in comprehensible, easy-to-digest linguistic terms. This approach essentially uses the weighted sum method and the 2-tuple linguistic computational model (Martínez and Herrera, 2012), a symbolic model that improves other linguistic modelling approaches in several ways (Rodríguez and Martínez, 2013), by translating aggregated data into comprehensible information while ensuring that no loss of data occurs in the process:
-
•
The linguistic computational model based on linguistic 2-tuples carries out linguistic computational processes easily and without loss of information.
-
•
The linguistic domain can be treated as continuous, whilst in the classical linguistic models it is treated as discrete.
-
•
The results of the computational processes are always expressed in the initial linguistic domain extended to a pair of values that include the linguistic label and additional information.
To represent the linguistic information, this model uses a pair of values called linguistic 2-tuple (s, α), where s is a linguistic term and α is a numeric value representing a symbolic translation.
Definition 1
Let be a linguistic term set and β be the result of an aggregation of the indexes of a set of labels assessed in a linguistic term set S, i.e., the result of a symbolic aggregation operation. β in [0,g], being g + 1 the cardinality of S. Let i = round(β) and α = β - i be two values, such that i in [−0.5,0.5), then α is called a symbolic translation.
The symbolic translation of a linguistic term si is a numerical value within [−0.5, 0.5) indicating the difference of the information between the calculated value , and its closest element within indicating the content of the closest linguistic term.
This 2-tuple linguistic representation model extends the use of indexes modifying the fuzzy linguistic approach adding a new parameter, the so-called symbolic translation, and representing the linguistic information by means of a linguistic 2-tuple (si,α) ∈ S × [−0.5,0.5), being s ∈ S a linguistic term and α ∈ [−0.5,0.5) a numerical value representing the symbolic translation (Equation 16).
| (16) |
The 2-tuple linguistic model defines a set of functions between linguistic 2-tuples and numerical values that facilitates the accurate computations with linguistic information.
Definition 2
Let be a linguistic term set and a value supporting the result of a symbolic aggregation operation. Then the 2-tuple that expresses the equivalent information to is obtained with the function of Equation (17).
| (17) |
where round is the usual round operation, has the closest index label to and is the value of the symbolic translation.
For example, for a 5-term scale and , the 2-tuple representation of this information would be .
Proposition 1
Let be a linguistic term set and be a linguistic 2-tuple. There is always a function, such that, from a 2-tuple it returns its equivalent numerical value in the interval of granularity of S (Equation 18).
Proof. It is trivial, we consider the following function:
| (18) |
Remark 1. From Definitions 1 and 2 and Proposition 1, it is obvious that the conversion of a linguistic term into a linguistic 2-tuple consists of adding a value 0 as symbolic translation:
This model has a computational technique based on the 2-tuple linguistic representation model that has been widely described in (Martínez and Herrera, 2012).
3.3. Consensus control
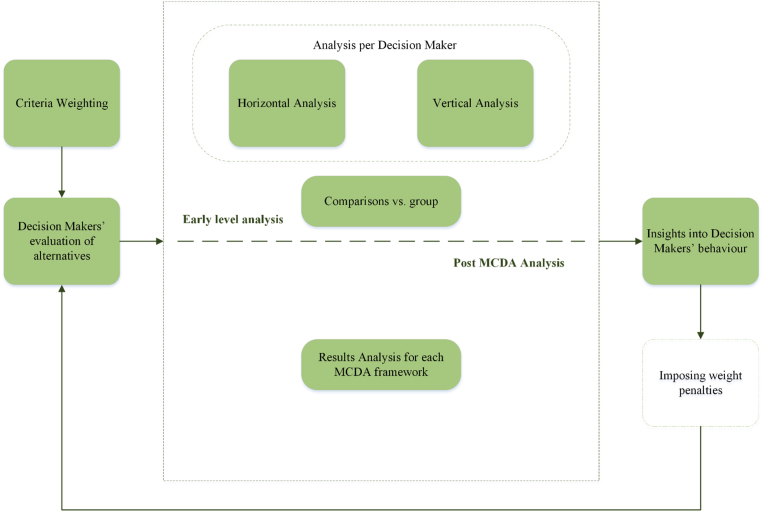
Although group decision making is an iterative process in which selection and consensus are intertwined (Choudhury et al., 2006), consensus control in MCDA is in principal a separate process (Dong et al., 2010). MACE-DSS allows for consensus control, an outlier detection process based on a classical statistical approach, which enables the analyst to easily detect potential disagreements among stakeholders across different stages of the process, in order to polish these disagreements and increase consensus. As a result, the input of the participating decision makers can be evaluated towards reaching valuable insights into their behaviour and, optionally, easily modifying their weights accordingly, in order to balance the perceived bias.
At a very early stage and regardless of the chosen MCDA framework, an analysis per decision maker is carried out based on their input. A horizontal analysis calculates the mean value and standard deviation for each alternative and against all criteria; the standard score is calculated and compared against a set of user-defined thresholds, one for slight and one for large deviation, in which cases the corresponding cell turns yellow and red respectively. The standard score expresses the number of standard deviations by which a value is above or below the mean value. In this respect, the user may select thresholds of their own preference; for example, a threshold of 1.0 reflects value deviation from the mean value by one standard deviation. A standard score above the user-defined upper threshold indicates large deviation, while a standard score between the two thresholds indicates slight deviation. This type of analysis helps to identify whether the expert has provided extreme scores for specific criteria, for each alternative. A vertical analysis calculates the mean value and standard deviation of all alternatives for each criterion; again, by comparing the standard score to the user-defined thresholds, the user can determine whether extreme scores have been elicited for specific alternatives, in each criterion. Additionally, a vertical analysis is also carried out per alternative, in which for every alternative the input of all stakeholders is compared against the mean value and standard deviation of the group for each criterion; this constitutes the most significant early level analysis that MACE-DSS features, since it allows for identifying whether the overall behaviour of a decision maker is in line with the other stakeholders. Such an approach can lead to penalising a stakeholder, by modifying the weight of their input. Stakeholder penalisation is used for cases where stakeholders appear less knowledgeable in a subject than others or where stakeholders employ strategies towards optimising their individual payoff resulting from the process (Yager, 2001), and is not uncommon in the MCDA literature (e.g. Yager, 2002; Quesada et al., 2015).
Finally, for each methodological framework, a post-MCDA analysis is carried out. In this type of analysis, the scores for each criterion have been aggregated—as per respective MCDA framework; as a result, two analyses take place at the table, similar to the horizontal and vertical early-level analyses but instead comparing each stakeholder against the others.
The aforementioned consensus control options are displayed in Fig. 2.
Fig. 2.
Consensus control in MACE-DSS.
4. Example
In order to implement and stress-test the proposed framework, MACE-DSS is applied in a case study aiming to assess twelve climate policy instruments, from the Greek national energy efficiency action plan (NEEAP, 2014), against ten implementation risks in the Greek building, energy and transport sectors towards a low carbon transformation. Six stakeholders participated in the process, the initial weighting of each was determined based on their expertise and position in their organisation: .
Since the weights of the criteria (implementation risks) were not known a priori as well as difficult to directly elicit from the stakeholders, the case study is broken down into two stages: one for determining a ranking of the implementation risks; and another one for assessing the policy instruments against these risks and based on the weights extracted from the ranking of the first stage. In other words, risks initially constitute the set of alternatives and, during the second stage, the set of evaluation criteria. It should be noted that, in the first stage, the loss aversion ratio that Behavioural TOPSIS introduces is not meaningful, since the aim of this stage is to rank risks, and λ is set to 1 implying a loss-indifferent behaviour; in the second stage, the goal is to assess policy instruments and a loss-averse behaviour is introduced, as discussed in Section 4.2.
4.1. Calculating the importance of implementation risks
The risks include political inertia and instability, lack of institutional and financial capacity, bureaucracy, lack of trust and societal acceptance, insufficient technical skills, market instability, and inadequate infrastructure. These are evaluated against their likelihood to manifest, the stakeholders' level of concern over them, the level of their perceived impact on a climate mitigation policy framework, the capacity to mitigate them, and the number of socio-economic pathways (SSPs) they can affect based on the story factors for each SSP (see O'Neill et al., 2017). Risks were evaluated by stakeholders against all criteria but one: the number of SSPs a risk can influence, which was assessed by the authors and therefore featured no deviation across the stakeholders. The weights for the five evaluation criteria were also determined by the authors (Table 4).
Table 4.
Stage 1: Implementation risks (alternatives), risk evaluation factors (criteria) and weights.
| Alternatives (Risks) | Evaluation Criteria | Weights |
|---|---|---|
| R1. Political inertia | C1. Likelihood to manifest | 9 |
| R2. Political instability | C2. Level of concern | 3 |
| R3. Lack of institutional capacity | C3. Number of pathways | 4 |
| R4. Lack of financial capacity | C4. Impact on policy | 9 |
| R5. Bureaucracy | C5. Lack of mitigation capacity | 5 |
| R6. Lack of trust | ||
| R7. Lack of societal acceptance | ||
| R8. Insufficient technical skills | ||
| R9. Market instability | ||
| R10. Inadequate infrastructure |
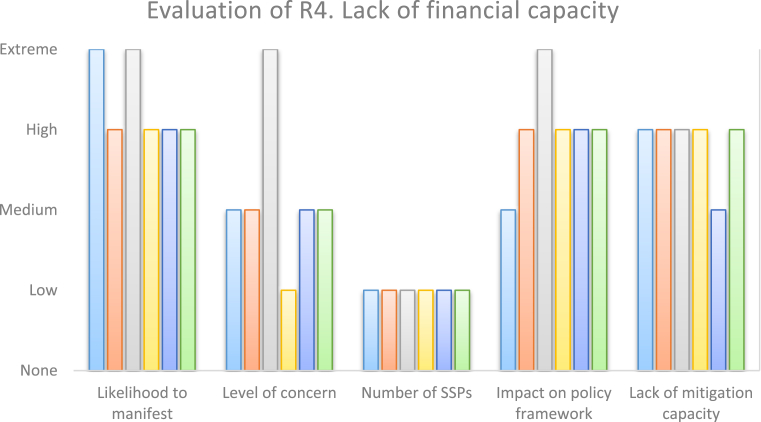
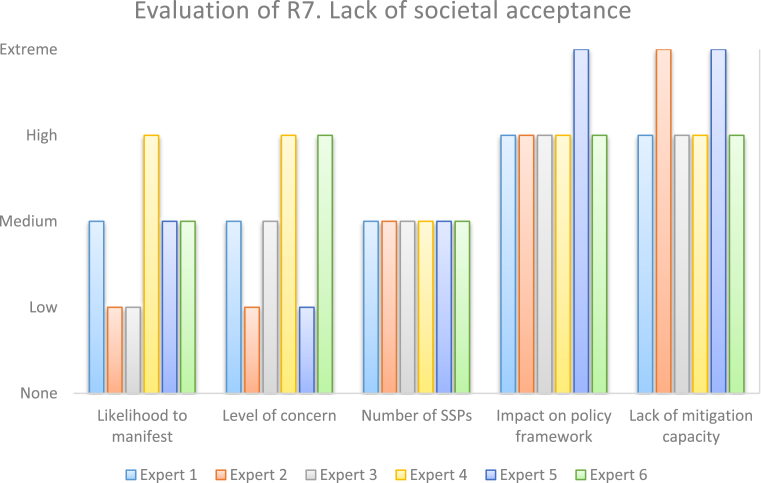
In order for the stakeholders to evaluate the alternative risks against the five evaluation criteria, a 5-term linguistic scale was used: . Given that the objective of this process is to reach a meaningful ranking from worst (most significant) to best (least significant) risk, as well as that all evaluation criteria have a negative impact on the risks, we consider that the problem features benefit criteria. After eliciting the information from the decision makers (for example, see Figs. 3 and 4), we use MACE-DSS to calculate the rankings for each implementation risk (Table 5).
Fig. 3.
Stakeholders' input regarding the evaluation of risk R4.
Fig. 4.
Stakeholders' input regarding the evaluation of risk R7.
Table 5.
Stage 1: Final collective assessment of implementation risks, according to all three supported methodologies.
| Alternatives | 2-tuple WSM x WSM (Herrera et al., 2005) |
TOPSIS x TOPSIS (Krohling and Campanharo, 2011) |
WSM x TOPSIS (Chen, 2000) |
||
|---|---|---|---|---|---|
| Collective assessment |
Closeness to ideal solution | Closeness to ideal solution | |||
| Δ−1(sn, α) | sn | α | |||
| R1 | 3.2962 | H | 0.2962 | 0.0487 | 0.0822 |
| R2 | 2.7894 | H | −0.2106 | −0.0169 | −0.0194 |
| R3 | 2.5712 | H | −0.4288 | −0.0185 | −0.0038 |
| R4 | 2.7568 | H | −0.2432 | −0.0063 | −0.0075 |
| R5 | 2.9614 | H | −0.0386 | 0.0096 | 0.0257 |
| R6 | 3.2045 | H | 0.2045 | 0.0183 | 0.0349 |
| R7 | 2.4894 | M | 0.4894 | −0.0337 | −0.0259 |
| R8 | 2.2939 | M | 0.2939 | −0.0357 | −0.0299 |
| R9 | 3.1394 | H | 0.1394 | 0.0159 | 0.0324 |
| R10 | 2.7326 | H | −0.2674 | −0.0064 | 0.0034 |
As can be concluded by Table 5, the three methodological frameworks show large convergence regarding the final ranking of the ten implementation risks; the only slight differences can be observed in ranks 5–8, among all methodologies. The observed convergence enhances the robustness of our ranking. Another useful observation regards the numerical differences among risks for each methodological framework. For example, some deviations in the 2-tuple WSM method might seem insignificant, whereas in Behavioural TOPSIS these are exaggerated; this observation can have significant implications for the sensitivity of the rankings in case different stakeholder preferences are inserted in the tool, as well as the weights derived for the second stage of the case study.
Weights for the implementation risks, as evaluation criteria, in the second stage of the case study are extracted from the results of the principal component of the proposed approach, i.e. the TOPSIS-oriented methodological framework (Krohling and Campanharo, 2011), as discussed in Section 3. Before, extracting these weights, however, it is interesting to look at potentially extreme values provided by the six decision makers for specific alternatives (Table 6), for slight and strong deviation from thresholds set at 1.2 (indicated with “†”) and 2 (indicated with “‡”) respectively.
Table 6.
Stage 1: Post-MCDA Analysis for Behavioural TOPSIS (based on Krohling and Campanharo, 2011) results.
| Alternatives | Expert 1 | Expert 2 | Expert 3 | Expert 4 | Expert 5 | Expert 6 |
|---|---|---|---|---|---|---|
| R1 | 0.56543 | 0.05605 | 0.83832 | 1.51452† | 1.13003 | 1.18475 |
| R2 | 0.75971 | 0.64562 | 1.12878 | 1.83305† | 0.27327 | 0.54510 |
| R3 | 0.53237 | 1.14515 | 0.08486 | 0.01671 | 1.20505† | 1.71627† |
| R4 | 0.00368 | 0.19227 | 1.91835† | 1.10469 | 0.96909 | 0.35139 |
| R5 | 0.68393 | 0.29723 | 1.81436† | 1.38426† | 0.48043 | 0.07064 |
| R6 | 0.60050 | 0.37440 | 0.96889 | 0.88868 | 1.74551† | 0.85083 |
| R7 | 0.16292 | 1.41566† | 1.32047† | 0.74634 | 0.91288 | 0.91398 |
| R8 | 0.31309 | 2.08144‡ | 1.02228 | 0.40265 | 0.21781 | 0.56122 |
| R9 | 0.48635 | 1.39744† | 0.62921 | 0.84823 | 1.34613† | 0.93978 |
| R10 | 1.58987† | 0.42496 | 1.04092 | 0.59303 | 0.53576 | 1.25279† |
This post-MCDA analysis suggests that many experts appear to potentially have provided extreme values for specific alternatives. By delving into the stakeholders' original input and drawing comparisons between each expert and the group, as part of the consensus control capacity featured by MACE-DSS, we notice that Expert 3 shows the widest disagreement with the group of decision makers (Table 7). As expected, no divergence can be observed with regard to the third evaluation criterion, since it concerns the number of SSPs each risk can affect, a piece of information that is filled in by the authors and is common among all stakeholders.
Table 7.
Stage 1: Comparisons between Expert 3's input and the group's collective input.
| Alternatives | C1 | C2 | C3 | C4 | C5 |
|---|---|---|---|---|---|
| R1 | 1.414213562† | 1.732050808† | 0 | 0.707106781 | 0.707106781 |
| R2 | 1 | 0.707106781 | 0 | 0.447213595 | 1 |
| R3 | 0.447213595 | 1.788854382† | 0 | 1.414213562† | 0 |
| R4 | 1.414213562† | 2.04264872‡ | 0 | 1.732050808† | 0.447213595 |
| R5 | 1 | 0.447213595 | 0 | 0 | 1.788854382† |
| R6 | 1 | 2.236067977‡ | 0 | 0.707106781 | 1.212678125† |
| R7 | 1.212678125† | 0 | 0 | 0.447213595 | 0.707106781 |
| R8 | 1.224744871† | 1.212678125† | 0 | 0.707106781 | 0.707106781 |
| R9 | 1 | 0.707106781 | 0 | 0.707106781 | 0 |
| R10 | 0.447213595 | 1.212678125† | 0 | 0 | 0 |
Drawing from the above tables, we tried penalising Expert 3, by reducing their weight from 9 to 6 (Table 8). The new multicriteria analysis results showed no difference in respect to the final ranking for the two Behavioural TOPSIS-oriented frameworks and little difference to the 2-tuple WSM-oriented framework. However, numerical results appeared to differ across all three frameworks, to the extent that this might have significant implications for the weights of the risks, when used as evaluation criteria in Stage 2 of the case study. For the purposes of our case study and despite having experimented on expert penalties in this first stage, we extract our risk weights from the original ranking of the main Behavioural TOPSIS-oriented methodology.
Table 8.
Stage 1: Changes in the MCDA results in respect to weight penalty on Expert 3. Bold formatting indicates the methodology and respective results chosen for the second part of the analysis in Section 4.2.
| 2-tuple WSM x WSM (Herrera et al., 2005) |
TOPSIS x TOPSIS (Krohling and Campanharo, 2011) |
WSM x TOPSIS (Chen, 2000) |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Without penalty |
With Penalty |
Without penalty |
With Penalty |
Without penalty |
With Penalty |
||||||
| Ranking | Score | Ranking | Score | Ranking | Score | Ranking | Score | Ranking | Score | Ranking | Score |
| R1 | 3.2962 | R1 | 3.2789 | R1 | 0.0487 | R1 | 0.0466 | R1 | 0.0822 | R1 | 0.0822 |
| R6 | 3.2045 | R6 | 3.2171 | R6 | 0.0183 | R6 | 0.0210 | R6 | 0.0349 | R6 | 0.0349 |
| R9 | 3.1394 | R9 | 3.1593 | R9 | 0.0159 | R9 | 0.0186 | R9 | 0.0324 | R9 | 0.0324 |
| R5 | 2.9614 | R5 | 2.9341 | R5 | 0.0096 | R5 | 0.0059 | R5 | 0.0257 | R5 | 0.0257 |
| R2 | 2.7894 | R2 | 2.7740 | R4 | −0.0063 | R10 | −0.0079 | R10 | 0.0034 | R10 | 0.0034 |
| R4 | 2.7568 | R10 | 2.7228 | R10 | −0.0064 | R4 | −0.0128 | R4 | −0.0038 | R3 | −0.0038 |
| R10 | 2.7326 | R4 | 2.7073 | R2 | −0.0169 | R3 | −0.0180 | R3 | −0.0075 | R4 | −0.0075 |
| R3 | 2.5712 | R3 | 2.5715 | R3 | −0.0185 | R2 | −0.0193 | R2 | −0.0194 | R2 | −0.0194 |
| R7 | 2.4894 | R7 | 2.5130 | R7 | −0.0337 | R7 | −0.0299 | R7 | −0.0259 | R7 | −0.0259 |
| R8 | 2.2939 | R8 | 2.3106 | R8 | −0.0357 | R8 | −0.0322 | R8 | −0.0299 | R8 | −0.0299 |
4.2. Evaluating policy instruments
In the second stage of the case study, implementation risks are no longer the alternatives of the problem, but rather the evaluation criteria, weighted based on the results of the first stage. The selected policy instruments (NEEAP, 2014), as well as the evaluation criteria and respective weights (as calculated in Stage 1 and following normalisation in MACE-DSS) are displayed in Table 9.
Table 9.
Stage 2: Policy instruments (alternatives), implementation risks (criteria) and weights.
| Alternatives (Policy instruments) | Evaluation Criteria (Risks) | Weights (%) |
|---|---|---|
| P1. "Saving at Home" Programmes | R1. Political inertia | 19.80% |
| P2. "Saving at Local Authority I and II″ Programmes | R2. Political instability | 6.90% |
| P3. "Energy upgrade of residential buildings" Programme | R3. Lack of institutional capacity | 7.00% |
| P4. "Energy upgrade of public buildings" Programme | R4. Lack of financial capacity | 8.50% |
| P5. "Energy upgrade of commercial buildings" Programme | R5. Bureaucracy | 12.00% |
| P6. Training actions for service sector personnel | R6. Lack of trust | 14.30% |
| P7. Diffusion of smart metering systems | R7. Lack of societal acceptance | 4.70% |
| P8. Energy managers in public buildings | R8. Insufficient technical skills | 3.90% |
| P9. Replacement of old public and private light-duty trucks | R9. Market instability | 13.80% |
| P10. Replacement of old private vehicles | R10. Inadequate infrastructure | 9.00% |
| P11. Development of the Metro transport network in Thessaloniki | ||
| P12. Extension of the Metro transport network in Athens |
In a slightly different setting, the alternatives are now evaluated by means of a 7-term linguistic scale: . Additionally, a loss-averse behaviour is configured and, as suggested by Yoon and Kim, 2017, λ is set to 2. Following the same procedure, the results for each methodological framework can be seen in Table 10. Note that the 2-tuple WSM x WSM approach assumes that the larger the final score, the riskier the policy, contrary to the two cost-driven Behavioural TOPSIS-based frameworks.
Table 10.
Stage 2: Final collective assessment of policy instruments, according to all three supported methodologies.
| Alternatives | 2-tuple WSM x WSM (Herrera et al., 2005) |
TOPSIS x TOPSIS (Krohling and Campanharo, 2011) |
WSM x TOPSIS (Chen, 2000) |
||
|---|---|---|---|---|---|
| Collective assessment |
Closeness to ideal solution | Closeness to ideal solution | |||
| Δ−1(sn, α) | sn | α | |||
| P1 | 3.5962 | H | −0,4038 | −0.10101 | −0.0990 |
| P2 | 3.4466 | M | 0,4466 | −0.09801 | −0.0892 |
| P3 | 3.6235 | H | −0,3765 | −0.10227 | −0.1084 |
| P4 | 3.1786 | M | 0,1786 | −0.06011 | −0.0623 |
| P5 | 3.6886 | H | −0,3114 | −0.11409 | −0.1044 |
| P6 | 2.9473 | M | −0,0527 | −0.06239 | −0.0622 |
| P7 | 3.5885 | H | −0,4115 | −0.15240 | −0.1466 |
| P8 | 3.4718 | M | 0,4718 | −0.12128 | −0.1173 |
| P9 | 3.6836 | H | −0,3164 | −0.14396 | −0.1341 |
| P10 | 3.4851 | M | 0,4851 | −0.10756 | −0.1087 |
| P11 | 1.8952 | L | −0,1048 | 0.09079 | 0.0733 |
| P12 | 1.7993 | L | −0,2007 | 0.06521 | 0.0525 |
Again, by looking at comparisons between each expert and the group's collective input, we identify that Experts 1 and 6 appear to show the largest differences. Table 11 displays this comparison analysis for Expert 6.
Table 11.
Stage 2: Comparisons between Expert 6's input and the group's collective input.
| Alternatives | R1 | R2 | R3 | R4 | R5 | R6 | R7 | R8 | R9 | R10 |
|---|---|---|---|---|---|---|---|---|---|---|
| P1 | 1.7179† | 1.2127† | 2.1106‡ | 1.0000 | 0.4472 | 0.4472 | 0.3974 | 1.7179† | 0.5222 | 0.4472 |
| P2 | 1.0000 | 1.2999† | 2.0426‡ | 0.7071 | 0.0000 | 0.8944 | 0.8660 | 1.4142† | 0.6030 | 1.0000 |
| P3 | 1.2060† | 0.9285 | 2.1106‡ | 0.6547 | 0.3974 | 1.2247† | 1.5652† | 1.5667† | 0.4472 | 0.7071 |
| P4 | 0.4472 | 1.2247† | 1.7179† | 1.0000 | 0.4472 | 0.0000 | 0.2425 | 1.0000 | 0.2673 | 1.0000 |
| P5 | 0.7809 | 0.7071 | 1.3644† | 0.7071 | 0.6030 | 1.2247† | 1.0000 | 1.2127† | 0.4472 | 1.2999† |
| P6 | 1.2127† | 1.2127† | 0.7071 | 0.7071 | 1.4142† | 1.2247† | 1.6125† | 1.2247† | 1.0000 | 0.0000 |
| P7 | 1.9373† | 1.6977† | 0.8660 | 0.9285 | 1.7179† | 1.9868† | 0.8341 | 1.2127† | 0.2425 | 0.1857 |
| P8 | 1.6977† | 1.6977† | 1.0000 | 0.6547 | 0.7071 | 0.6547 | 1.0932 | 0.0000 | 0.9285 | 0.5222 |
| P9 | 0.2673 | 0.6868 | 0.0000 | 1.0000 | 0.6547 | 0.2425 | 1.0000 | 0.2425 | 1.7321† | 1.0000 |
| P10 | 0.0000 | 0.4472 | 1.0000 | 1.0000 | 0.4472 | 0.8944 | 0.6547 | 0.8944 | 0.7071 | 0.8944 |
| P11 | 0.4472 | 1.2999† | 1.1921 | 1.0000 | 0.7809 | 0.6547 | 0.7071 | 1.7678† | 0.4472 | 0.0000 |
| P12 | 0.9285 | 1.2127† | 0.5698 | 0.7071 | 0.8944 | 1.7678† | 0.9285 | 1.2247† | 0.0000 | 0.2425 |
By lowering the weights for both experts (1 and 6), the new results can be seen in Table 12.
Table 12.
Stage 2: Changes in the MCDA results in respect to weight penalties on Experts 1 and 6.
| 2-tuple WSM x WSM (Herrera et al., 2005) |
TOPSIS x TOPSIS (Krohling and Campanharo, 2011) |
WSM x TOPSIS (Chen, 2000) |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Without penalty |
With Penalty |
Without penalty |
With Penalty |
Without penalty |
With Penalty |
||||||
| Ranking | Score | Ranking | Score | Ranking | Score | Ranking | Score | Ranking | Score | Ranking | Score |
| P12 | 1.7993 | P12 | 1.7756 | P11 | 0.09079 | P11 | 0.09216 | P11 | 0.0733 | P11 | 0.0750 |
| P11 | 1.8952 | P11 | 1.8860 | P12 | 0.06521 | P12 | 0.06979 | P12 | 0.0525 | P12 | 0.0553 |
| P6 | 2.9473 | P6 | 2.9496 | P4 | −0.06011 | P6 | −0.06391 | P6 | −0.0622 | P6 | −0.0603 |
| P4 | 3.1786 | P4 | 3.1911 | P6 | −0.06239 | P4 | −0.06420 | P4 | −0.0623 | P4 | −0.0620 |
| P2 | 3.4466 | P2 | 3.4503 | P2 | −0.09801 | P1 | −0.09761 | P2 | −0.0892 | P2 | −0.0874 |
| P8 | 3.4718 | P10 | 3.4650 | P1 | −0.10101 | P3 | −0.09896 | P1 | −0.0990 | P1 | −0.0951 |
| P10 | 3.4851 | P8 | 3.5036 | P3 | −0.10227 | P2 | −0.09965 | P5 | −0.1044 | P5 | −0.1028 |
| P7 | 3.5885 | P1 | 3.5896 | P10 | −0.10756 | P10 | −0.10146 | P3 | −0.1084 | P10 | −0.1030 |
| P1 | 3.5962 | P3 | 3.6263 | P5 | −0.11409 | P5 | −0.11778 | P10 | −0.1087 | P3 | −0.1037 |
| P3 | 3.6235 | P7 | 3.6422 | P8 | −0.12128 | P8 | −0.13256 | P8 | −0.1173 | P8 | −0.1212 |
| P9 | 3.6836 | P9 | 3.6737 | P9 | −0.14396 | P9 | −0.14356 | P9 | −0.1341 | P9 | −0.1311 |
| P5 | 3.6886 | P5 | 3.6990 | P7 | −0.15240 | P7 | −0.16883 | P7 | −0.1466 | P7 | −0.1527 |
As far as 2-tuple WSM is concerned, it is evident that penalising both experts significantly impacts the final ranking of the policy instruments, between positions 6–10. Regarding the first Behavioural TOPSIS-oriented framework, a similar impact can be observed between positions 3–7. However, enforcing weight penalties on the first and sixth experts has little impact on the second Behavioural TOPSIS-based method, by inverting policies in ranks #8 and #9. Of course, the penalty affected the final results of all MCDA frameworks, but without further implications for the ranking of the alternative policy instruments.
It is noteworthy, however, that 2-tuple WSM largely differs from the other two frameworks, which can be attributed to the methodological differences among the respective approaches as well as the large sensitivity of the 2-tuple WSM results across positions #5– #12. Despite these differences in the results of the three frameworks, all analyses agree on the four optimal policy instruments, P11, P12, P6 and P4. As a result, it is safe to conclude that, according to the six stakeholders involved in the case study, investments in the Metro transport network of Athens and Thessaloniki, as well as upgrades in the public building sector and technical training in the service sector, appear to comprise the optimal and most robust policy mix, when taking into account the identified implementation risks.
5. Conclusions
In this paper, we have thoroughly reviewed the contribution of multiple criteria decision analysis frameworks in the climate policy support domain, especially focusing on their group decision making capacity, drawing from the trending necessity to include multiple stakeholders in the climate policy making process. Based on our analysis, we have concluded that TOPSIS appears to be a popular and fitting framework in this problem domain. In this respect, we have proceeded to develop a Behavioural TOPSIS-oriented approach to carrying out multicriteria analyses as well as supervising the consensus of involved stakeholders, and a respective user-friendly spreadsheet-based tool, MACE-DSS.
The proposed approach and tool consist of three key components. First of all, the use of linguistic variables enables the stakeholders to easily and meaningfully provide their knowledge, when evaluating the alternative options, and the capacity to include hybrid information can provide a sense of precision regarding stakeholder input. Secondly, the analysis component allows for dealing with real-world problems by supporting the assessment of up to twelve alternative options against up to twelve evaluation criteria, while involving up to twelve decision makers and comprises three different group decision making multicriteria analysis methodologies; as a result, the analyst can automatically address problems with a diverse set of methods, thereby enhancing the robustness of their results. Finally, MACE-DSS features the capacity to overview and gain insights into the decision makers' preference models, by means of a number of consensus control analyses, as well as impose weight penalties based on these insights towards balancing the identified collective bias or even re-engaging stakeholders in the aim of eliciting a feedback-driven round of input.
The development of the presented methodological framework and tool was motivated by the need to enhance climate policy making processes and the selection of the supported MCDA methodologies was driven by the need to effectively tackle the challenges associated with this domain. However, exploitation of MACE-DSS should not be limited to supporting climate policy. In fact, the software does not impose domain-related restrictions or limitations and can be applied in close areas—such as energy policy, environmental policy, sustainable development, etc.—as well as other problem domains with similar nature and type of input data, problematic and outcome requirements as well as necessity to include multiple stakeholders.
There currently exist a number of limitations regarding MACE-DSS and, therefore, as many aspects in which the tool can be further improved. These primarily consist of restrictions in the number of alternatives, criteria and stakeholders; and limitations concerning the number of linguistic variables, two scales of which are currently supported. Furthermore, MACE-DSS can be enhanced by incorporating the capacity to handle input in different formats, such as uncertainty-driven intervals (e.g. Martinez et al., 2007) or fuzzy preference relations (e.g. Herrera-Viedma et al., 2007); and integrating a more diverse set of consensus control and robustness indices.
Most importantly, MACE-DSS can be significantly improved by using a Fuzzy TOPSIS framework in order to effectively assess fuzzy linguistic information while overcoming the existing precision gap between linguistic and numerical data, which is described in the Methodology Section. In this direction, the 2-tuple representation model can again be used throughout the process, towards ensuring the elimination of any loss of information caused by the approximation procedures, as presented in (Doukas and Psarras, 2009) and (Doukas et al., 2010).
Finally, MACE-DSS features only a short collection of currently supported MCDA methodological frameworks, mostly oriented on the distance-based TOPSIS method. As the literature review indicates, other equally domain-popular methodologies (e.g. AHP, PROMETHEE, etc.) can address climate policy-related issues; incorporating them into the tool, can provide methodological diversity with the capacity to address problems of different nature, complexity or problematic.
Declarations
Author contribution statement
Alexandros Nikas: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.
Haris Doukas: Conceived and designed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.
Luis Martínez López: Conceived and designed the experiments; Contributed reagents, materials, analysis tools or data.
Funding statement
This work was supported by the H2020 European Commission Project “Transitions pathways and risk analysis for climate change mitigation and adaptation strategies—TRANSrisk” under grant agreement No. 642260. The sole responsibility for the content of this paper lies with the authors; the paper does not necessarily reflect the opinion of the European Commission.
Competing interest statement
The authors declare no conflict of interest.
Additional information
No additional information is available for this paper.
References
- Agell N., SáNchez M., Prats F., Roselló L. Ranking multi-attribute alternatives on the basis of linguistic labels in group decisions. Inf. Sci. 2012;209:49–60. [Google Scholar]
- Almaraz S.D.L., Azzaro-Pantel C., Montastruc L., Pibouleau L., Senties O.B. Assessment of mono and multi-objective optimization to design a hydrogen supply chain. Int. J. Hydrogen Energy. 2013;38(33):14121–14145. [Google Scholar]
- AlSabbagh M., Siu Y.L., Guehnemann A., Barrett J. Integrated approach to the assessment of CO 2 e-mitigation measures for the road passenger transport sector in Bahrain. Renew. Sustain. Energy Rev. 2016 [Google Scholar]
- Antunes C.H., Martins A.G., Brito I.S. A multiple objective mixed integer linear programming model for power generation expansion planning. Energy. 2004;29(4):613–627. [Google Scholar]
- Baležentis T., Streimikiene D. Multi-criteria ranking of energy generation scenarios with Monte Carlo simulation. Appl. Energy. 2017;185:862–871. [Google Scholar]
- Batubara M., Purwanto W.W., Fauzi A. Proposing a decision-making process for the development of sustainable oil and gas resources using the petroleum fund: a case study of the East Natuna gas field. Resour. Pol. 2016;49:372–384. [Google Scholar]
- Biloslavo R., Dolinšek S. Scenario planning for climate strategies development by integrating group Delphi, AHP and dynamic fuzzy cognitive maps. Foresight. 2010;12(2):38–48. [Google Scholar]
- Biloslavo R., Grebenc A. Integrating group Delphi, analytic hierarchy process and dynamic fuzzy cognitive maps for a climate warning scenario. Kybernetes. 2012;41(3/4):414–428. [Google Scholar]
- Blechinger P.F.H., Shah K.U. A multi-criteria evaluation of policy instruments for climate change mitigation in the power generation sector of Trinidad and Tobago. Energy Pol. 2011;39(10):6331–6343. [Google Scholar]
- Borges P.C., Villavicencio A. Avoiding academic and decorative planning in GHG emissions abatement studies with MCDA: the Peruvian case. Eur. J. Oper. Res. 2004;152(3):641–654. [Google Scholar]
- Branco D.A.C., Rathmann R., Borba B.S.M., de Lucena A.F.P., Szklo A., Schaeffer R. A multicriteria approach for measuring the carbon-risk of oil companies. Energy Strat. Rev. 2012;1(2):122–129. [Google Scholar]
- Brand B., Missaoui R. Multi-criteria analysis of electricity generation mix scenarios in Tunisia. Renew. Sustain. Energy Rev. 2014;39:251–261. [Google Scholar]
- Brand B., Stambouli A.B., Zejli D. The value of dispatchability of CSP plants in the electricity systems of Morocco and Algeria. Energy Pol. 2012;47:321–331. [Google Scholar]
- Bruckner T., Bashmakov I.A., Mulugetta Y., Chum H., de la Vega Navarro A., Edmonds J., Faaij A., Fungtammasan B., Garg A., Hertwich E., Honnery D., Infield D., Kainuma M., Khennas S., Kim S., Nimir H.B., Riahi K., Strachan N., Wiser R., Zhang X. Energy systems. In: Edenhofer O., Pichs-Madruga R., Sokona Y., Farahani E., Kadner S., Seyboth K., Adler A., Baum I., Brunner S., Eickemeier P., Kriemann B., Savolainen J., Schlömer S., von Stechow C., Zwickel T., Minx J.C., editors. Climate Change 2014: Mitigation of Climate Change. Contribution of Working Group III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge University Press; Cambridge, United Kingdom and New York, NY, USA: 2014. [Google Scholar]
- Büyüközkan G., Güleryüz S. Evaluation of Renewable Energy Resources in Turkey using an integrated MCDM approach with linguistic interval fuzzy preference relations. Energy. 2017;123:149–163. [Google Scholar]
- Büyüközkan G., Karabulut Y. Energy project performance evaluation with sustainability perspective. Energy. 2017;119:549–560. [Google Scholar]
- Chang P.L., Hsu C.W., Lin C.Y. Assessment of hydrogen fuel cell applications using fuzzy multiple-criteria decision making method. Appl. Energy. 2012;100:93–99. [Google Scholar]
- Chen C.T. Extensions of the TOPSIS for group decision-making under fuzzy environment. Fuzzy Set Syst. 2000;114(1):1–9. [Google Scholar]
- Chen S.M., Lee L.W. Fuzzy multiple attributes group decision-making based on the interval type-2 TOPSIS method. Expert Syst. Appl. 2010;37(4):2790–2798. [Google Scholar]
- Chen L., Pan W. A BIM-integrated fuzzy multi-criteria decision making model for selecting low-carbon building measures. Proc. Eng. 2015;118:606–613. [Google Scholar]
- Chen T.Y., Tsao C.Y. The interval-valued fuzzy TOPSIS method and experimental analysis. Fuzzy Set Syst. 2008;159(11):1410–1428. [Google Scholar]
- Choudhury A.K., Shankar R., Tiwari M.K. Consensus-based intelligent group decision-making model for the selection of advanced technology. Decis. Support Syst. 2006;42(3):1776–1799. [Google Scholar]
- Cowan K., Daim T., Anderson T. Exploring the impact of technology development and adoption for sustainable hydroelectric power and storage technologies in the Pacific Northwest United States. Energy. 2010;35(12):4771–4779. [Google Scholar]
- Cutz L., Haro P., Santana D., Johnsson F. Assessment of biomass energy sources and technologies: the case of Central America. Renew. Sustain. Energy Rev. 2016;58:1411–1431. [Google Scholar]
- Dace E., Blumberga D. How do 28 European Union Member States perform in agricultural greenhouse gas emissions? It depends on what we look at: application of the multi-criteria analysis. Ecol. Indicat. 2016;71:352–358. [Google Scholar]
- de Bruin K., Dellink R.B., Ruijs A., Bolwidt L., van Buuren A., Graveland J. Adapting to climate change in The Netherlands: an inventory of climate adaptation options and ranking of alternatives. Climatic Change. 2009;95(1):23–45. [Google Scholar]
- Diakoulaki D., Georgiou P., Tourkolias C., Georgopoulou E., Lalas D., Mirasgedis S., Sarafidis Y. A multicriteria approach to identify investment opportunities for the exploitation of the clean development mechanism. Energy Pol. 2007;35(2):1088–1099. [Google Scholar]
- Dong Y., Zhang G., Hong W.C., Xu Y. Consensus models for AHP group decision making under row geometric mean prioritization method. Decis. Support Syst. 2010;49(3):281–289. [Google Scholar]
- Doukas H. Modelling of linguistic variables in multicriteria energy policy support. Eur. J. Oper. Res. 2013;227(2):227–238. [Google Scholar]
- Doukas H., Psarras J. A linguistic decision support model towards the promotion of renewable energy. Energy Sources, Part B. 2009;4(2):166–178. [Google Scholar]
- Doukas H., Patlitzianas K.D., Psarras J. Supporting sustainable electricity technologies in Greece using MCDM. Resour. Pol. 2006;31(2):129–136. [Google Scholar]
- Doukas H., Karakosta C., Psarras J. Computing with words to assess the sustainability of renewable energy options. Expert Syst. Appl. 2010;37(7):5491–5497. [Google Scholar]
- Estrella F.J., Cevik Onar S., Rodríguez R.M., Oztaysi B., Martínez L., Kahraman C. Selecting firms in University technoparks: a hesitant linguistic fuzzy TOPSIS model for heterogeneous contexts. J. Intell. Fuzzy Syst. 2017;33(2):1155–1172. [Google Scholar]
- Fozer D., Sziraky F.Z., Racz L., Nagy T., Tarjani A.J., Toth A.J., Haaz E., Benko T., Mizsey P. Life cycle, PESTLE and multi-criteria decision analysis of CCS process alternatives. J. Clean. Prod. 2017 [Google Scholar]
- Georgopoulou E., Sarafidis Y., Mirasgedis S., Zaimi S., Lalas D.P. A multiple criteria decision-aid approach in defining national priorities for greenhouse gases emissions reduction in the energy sector. Eur. J. Oper. Res. 2003;146(1):199–215. [Google Scholar]
- Ghafghazi S., Sowlati T., Sokhansanj S., Melin S. A multicriteria approach to evaluate district heating system options. Appl. Energy. 2010;87(4):1134–1140. [Google Scholar]
- Greco S., Ehrgott M., Figueira J.R. Multiple Criteria Decision Analysis: State of the Art Surveys. Second Edition. Vols. 1 & 2. Springer; 2016. (International Series in Operations Research & Management Science). [Google Scholar]
- Heo E., Kim J., Boo K.J. Analysis of the assessment factors for renewable energy dissemination program evaluation using fuzzy AHP. Renew. Sustain. Energy Rev. 2010;14(8):2214–2220. [Google Scholar]
- Herrera F., Martınez L., Sánchez P.J. Managing non-homogeneous information in group decision making. Eur. J. Oper. Res. 2005;166(1):115–132. [Google Scholar]
- Herrera-Viedma E., Alonso S., Chiclana F., Herrera F. A consensus model for group decision making with incomplete fuzzy preference relations. IEEE Trans. Fuzzy Syst. 2007;15(5):863–877. doi: 10.1109/tsmcb.2006.875872. [DOI] [PubMed] [Google Scholar]
- Hwang C.L., Yoon K.P. Springer; Berlin: 1981. Multiple Attribute Decision Making: Methods and Applications. [Google Scholar]
- Javid R.J., Nejat A., Hayhoe K. Selection of CO 2 mitigation strategies for road transportation in the United States using a multi-criteria approach. Renew. Sustain. Energy Rev. 2014;38:960–972. [Google Scholar]
- Jayaraman R., Colapinto C., La Torre D., Malik T. Multi-criteria model for sustainable development using goal programming applied to the United Arab Emirates. Energy Pol. 2015;87:447–454. [Google Scholar]
- Jun K.S., Chung E.S., Kim Y.G., Kim Y. A fuzzy multi-criteria approach to flood risk vulnerability in South Korea by considering climate change impacts. Expert Syst. Appl. 2013;40(4):1003–1013. [Google Scholar]
- Karakosta C., Doukas H., Psarras J. Directing clean development mechanism towards developing countries' sustainable development priorities. Energy Sustain. Dev. 2009;13(2):77–84. [Google Scholar]
- Kaya T., Kahraman C. Multicriteria decision making in energy planning using a modified fuzzy TOPSIS methodology. Expert Syst. Appl. 2011;38(6):6577–6585. [Google Scholar]
- Kim G., Park C.S., Yoon K.P. Identifying investment opportunities for advanced manufacturing systems with comparative-integrated performance measurement. Int. J. Prod. Econ. 1997;50(1):23–33. [Google Scholar]
- Klein S.J., Whalley S. Comparing the sustainability of US electricity options through multi-criteria decision analysis. Energy Pol. 2015;79:127–149. [Google Scholar]
- Konidari P., Mavrakis D. A multi-criteria evaluation method for climate change mitigation policy instruments. Energy Pol. 2007;35(12):6235–6257. [Google Scholar]
- Krohling R.A., Campanharo V.C. Fuzzy TOPSIS for group decision making: a case study for accidents with oil spill in the sea. Expert Syst. Appl. 2011;38(4):4190–4197. [Google Scholar]
- Lan J., Sun Q., Chen Q., Wang Z. Group decision making based on induced uncertain linguistic OWA operators. Decis. Support Syst. 2013;55(1):296–303. [Google Scholar]
- Luthra S., Mangla S.K., Kharb R.K. Sustainable assessment in energy planning and management in Indian perspective. Renew. Sustain. Energy Rev. 2015;47:58–73. [Google Scholar]
- Maimoun M., Madani K., Reinhart D. Multi-level multi-criteria analysis of alternative fuels for waste collection vehicles in the United States. Sci. Total Environ. 2016;550:349–361. doi: 10.1016/j.scitotenv.2015.12.154. [DOI] [PubMed] [Google Scholar]
- Martínez L., Herrera F. An overview on the 2-tuple linguistic model for computing with words in decision making: extensions, applications and challenges. Inf. Sci. 2012;207:1–18. [Google Scholar]
- Martínez L., Liu J., Ruan D., Yang J.B. Dealing with heterogeneous information in engineering evaluation processes. Inf. Sci. 2007;177(7):1533–1542. [Google Scholar]
- Michailidou A.V., Vlachokostas C., Moussiopoulos Ν. Interactions between climate change and the tourism sector: multiple-criteria decision analysis to assess mitigation and adaptation options in tourism areas. Tourism Manag. 2016;55:1–12. [Google Scholar]
- Mohamadabadi H.S., Tichkowsky G., Kumar A. Development of a multi-criteria assessment model for ranking of renewable and non-renewable transportation fuel vehicles. Energy. 2009;34(1):112–125. [Google Scholar]
- Montanari R. Environmental efficiency analysis for enel thermo-power plants. J. Clean. Prod. 2004;12(4):403–414. [Google Scholar]
- Mourhir A., Rachidi T., Papageorgiou E.I., Karim M., Alaoui F.S. A cognitive map framework to support integrated environmental assessment. Environ. Model. Software. 2016;77:81–94. [Google Scholar]
- NEEAP . Centre for Renewable Energy Sources (CRES); Athens: 2014. National Energy Efficiency Action Plan. Pursuant to Article 24(2) of Directive 2012/27/EU. [Google Scholar]
- Nikas A., Doukas H., Lieu J., Alvarez-Tinoco R., Charisopoulos V., van der Gaast W. Managing stakeholder knowledge for the evaluation of innovation systems in the face of climate change. J. Knowl. Manag. 2017;21(5):1013–1034. [Google Scholar]
- Oliveira C., Antunes C.H. A multiple objective model to deal with economy–energy–environment interactions. Eur. J. Oper. Res. 2004;153(2):370–385. [Google Scholar]
- Onar S.C., Oztaysi B., Otay İ., Kahraman C. Multi-expert wind energy technology selection using interval-valued intuitionistic fuzzy sets. Energy. 2015;90:274–285. [Google Scholar]
- Onu P.U., Quan X., Xu L., Orji J., Onu E. Evaluation of sustainable acid rain control options utilizing a fuzzy TOPSIS multi-criteria decision analysis model frame work. J. Clean. Prod. 2017;141:612–625. [Google Scholar]
- O’Neill B.C., Kriegler E., Ebi K.L., Kemp-Benedict E., Riahi K., Rothman D.S., van Ruijven B.J., van Vuuren D.P., Birkmann J., Kok K., Levy M. The roads ahead: narratives for shared socioeconomic pathways describing world futures in the 21st century. Global Environ. Change. 2017;42:169–180. [Google Scholar]
- Papadopoulos A., Karagiannidis A. Application of the multi-criteria analysis method Electre III for the optimisation of decentralised energy systems. Omega. 2008;36(5):766–776. [Google Scholar]
- Papapostolou A., Karakosta C., Marinakis V., Flamos A. Assessment of RES cooperation framework between the EU and North Africa: a multicriteria approach based on UTASTAR. Int. J. Energy Sect. Manag. 2016;10(3):402–426. [Google Scholar]
- Papapostolou A., Karakosta C., Nikas A., Psarras J. Exploring opportunities and risks for RES-E deployment under Cooperation Mechanisms between EU and Western Balkans: a multi-criteria assessment. Renew. Sustain. Energy Rev. 2017;80:519–530. [Google Scholar]
- Paul S., Sarkar B., Bose P.K. Eclectic decision for the selection of tree borne oil (TBO) as alternative fuel for internal combustion engine. Renew. Sustain. Energy Rev. 2015;48:256–263. [Google Scholar]
- Perkoulidis G., Papageorgiou A., Karagiannidis A., Kalogirou S. Integrated assessment of a new Waste-to-Energy facility in Central Greece in the context of regional perspectives. Waste Manag. 2010;30(7):1395–1406. doi: 10.1016/j.wasman.2009.11.021. [DOI] [PubMed] [Google Scholar]
- Promentilla M.A.B., Aviso K.B., Tan R.R. A group fuzzy analytic network process to prioritize low carbon energy systems in the Philippines. Energy Proc. 2014;61:808–811. [Google Scholar]
- Quesada F.J., Palomares I., Martínez L. Managing experts behavior in large-scale consensus reaching processes with uninorm aggregation operators. Appl. Soft Comput. 2015;35:873–887. [Google Scholar]
- Ramazankhani M.E., Mostafaeipour A., Hosseininasab H., Fakhrzad M.B. Feasibility of geothermal power assisted hydrogen production in Iran. Int. J. Hydrogen Energy. 2016;41(41):18351–18369. [Google Scholar]
- Ren J., Lützen M. Fuzzy multi-criteria decision-making method for technology selection for emissions reduction from shipping under uncertainties. Transport. Res. Transport Environ. 2015;40:43–60. [Google Scholar]
- Ribeiro F., Ferreira P., Araújo M. Evaluating future scenarios for the power generation sector using a Multi-Criteria Decision Analysis (MCDA) tool: the Portuguese case. Energy. 2013;52:126–136. [Google Scholar]
- Rodríguez R.M., Martínez L. An analysis of symbolic linguistic computing models in decision making. Int. J. Gen. Syst. 2013;42(1):121–136. [Google Scholar]
- Rojas-Zerpa J.C., Yusta J.M. Application of multicriteria decision methods for electric supply planning in rural and remote areas. Renew. Sustain. Energy Rev. 2015;52:557–571. [Google Scholar]
- Roth S., Hirschberg S., Bauer C., Burgherr P., Dones R., Heck T., Schenler W. Sustainability of electricity supply technology portfolio. Ann. Nucl. Energy. 2009;36(3):409–416. [Google Scholar]
- Sadeghi A., Larimian T., Molabashi A. Evaluation of renewable energy sources for generating electricity in province of Yazd: a fuzzy MCDM approach. Proc. Soc. Behav. Sci. 2012;62:1095–1099. [Google Scholar]
- Sakthivel G., Ilangkumaran M., Gaikwad A. A hybrid multi-criteria decision modeling approach for the best biodiesel blend selection based on ANP-TOPSIS analysis. Ain Shams Eng. J. 2015;6(1):239–256. [Google Scholar]
- San Cristóbal J.R. A goal programming model for environmental policy analysis: application to Spain. Energy Pol. 2012;43:303–307. [Google Scholar]
- Şengül Ü., Eren M., Shiraz S.E., Gezder V., Şengül A.B. Fuzzy TOPSIS method for ranking renewable energy supply systems in Turkey. Renew. Energy. 2015;75:617–625. [Google Scholar]
- Shiau T.A., Liu J.S. Developing an indicator system for local governments to evaluate transport sustainability strategies. Ecol. Indicat. 2013;34:361–371. [Google Scholar]
- Shih H.S., Shyur H.J., Lee E.S. An extension of TOPSIS for group decision making. Math. Comput. Model. 2007;45(7):801–813. [Google Scholar]
- Shmelev S.E., van den Bergh J.C. Optimal diversity of renewable energy alternatives under multiple criteria: an application to the UK. Renew. Sustain. Energy Rev. 2016;60:679–691. [Google Scholar]
- Streimikiene D., Baležentis T. Multi-criteria assessment of small scale CHP technologies in buildings. Renew. Sustain. Energy Rev. 2013;26:183–189. [Google Scholar]
- Streimikiene D., Balezentis T. Multi-objective ranking of climate change mitigation policies and measures in Lithuania. Renew. Sustain. Energy Rev. 2013;18:144–153. [Google Scholar]
- Streimikiene D., Balezentis T., Krisciukaitienė I., Balezentis A. Prioritizing sustainable electricity production technologies: MCDM approach. Renew. Sustain. Energy Rev. 2012;16(5):3302–3311. [Google Scholar]
- Štreimikienė D., Šliogerienė J., Turskis Z. Multi-criteria analysis of electricity generation technologies in Lithuania. Renew. Energy. 2016;85:148–156. [Google Scholar]
- Talaei A., Ahadi M.S., Maghsoudy S. Climate friendly technology transfer in the energy sector: a case study of Iran. Energy Pol. 2014;64:349–363. [Google Scholar]
- Theodorou S., Florides G., Tassou S. The use of multiple criteria decision making methodologies for the promotion of RES through funding schemes in Cyprus, A review. Energy Pol. 2010;38(12):7783–7792. [Google Scholar]
- Tsoutsos T., Drandaki M., Frantzeskaki N., Iosifidis E., Kiosses I. Sustainable energy planning by using multi-criteria analysis application in the island of Crete. Energy Pol. 2009;37(5):1587–1600. [Google Scholar]
- Ulutaş B.H. Determination of the appropriate energy policy for Turkey. Energy. 2005;30(7):1146–1161. [Google Scholar]
- Vahabzadeh A.H., Asiaei A., Zailani S. Green decision-making model in reverse logistics using FUZZY-VIKOR method. Resour. Conserv. Recycl. 2015;103:125–138. [Google Scholar]
- Vaillancourt K., Waaub J.P. Equity in international greenhouse gases abatement scenarios: a multicriteria approach. Eur. J. Oper. Res. 2004;153(2):489–505. [Google Scholar]
- van Vliet M., Kok K., Veldkamp T. Linking stakeholders and modellers in scenario studies: the use of Fuzzy Cognitive Maps as a communication and learning tool. Futures. 2010;42(1):1–14. [Google Scholar]
- Volkart K., Bauer C., Burgherr P., Hirschberg S., Schenler W., Spada M. Interdisciplinary assessment of renewable, nuclear and fossil power generation with and without carbon capture and storage in view of the new Swiss energy policy. Int. J. Greenh. Gas Contr. 2016;54:1–14. [Google Scholar]
- Xu X.H., Du Z.J., Chen X.H. Consensus model for multi-criteria large-group emergency decision making considering non-cooperative behaviors and minority opinions. Decis. Support Syst. 2015;79:150–160. [Google Scholar]
- Xu B., Nayak A., Gray D., Ouenniche J. Assessing energy business cases implemented in the North Sea region and strategy recommendations. Appl. Energy. 2016;172:360–371. [Google Scholar]
- Yager R.R. Penalizing strategic preference manipulation in multi-agent decision making. IEEE Trans. Fuzzy Syst. 2001;9(3):393–403. [Google Scholar]
- Yager R.R. Defending against strategic manipulation in uninorm-based multi-agent decision making. Eur. J. Oper. Res. 2002;141(1):217–232. [Google Scholar]
- Yap H.Y., Nixon J.D. A multi-criteria analysis of options for energy recovery from municipal solid waste in India and the UK. Waste Manag. 2015;46:265–277. doi: 10.1016/j.wasman.2015.08.002. [DOI] [PubMed] [Google Scholar]
- Yoon K.P., Kim W.K. The behavioral TOPSIS. Expert Syst. Appl. 2017;89:266–272. [Google Scholar]