Variable selection – A review and recommendations for the practicing statistician

Abstract

Statistical models support medical research by facilitating individualized outcome prognostication conditional on independent variables or by estimating effects of risk factors adjusted for covariates. Theory of statistical models is well‐established if the set of independent variables to consider is fixed and small. Hence, we can assume that effect estimates are unbiased and the usual methods for confidence interval estimation are valid. In routine work, however, it is not known a priori which covariates should be included in a model, and often we are confronted with the number of candidate variables in the range 10–30. This number is often too large to be considered in a statistical model. We provide an overview of various available variable selection methods that are based on significance or information criteria, penalized likelihood, the change‐in‐estimate criterion, background knowledge, or combinations thereof. These methods were usually developed in the context of a linear regression model and then transferred to more generalized linear models or models for censored survival data. Variable selection, in particular if used in explanatory modeling where effect estimates are of central interest, can compromise stability of a final model, unbiasedness of regression coefficients, and validity of p‐values or confidence intervals. Therefore, we give pragmatic recommendations for the practicing statistician on application of variable selection methods in general (low‐dimensional) modeling problems and on performing stability investigations and inference. We also propose some quantities based on resampling the entire variable selection process to be routinely reported by software packages offering automated variable selection algorithms.

1. INTRODUCTION

Statistical models are useful tools applied in many research fields dealing with empirical data. They connect an outcome variable to one or several so‐called independent variables (IVs; a list of abbreviations can be found in the Supporting Information Table S1) and quantify the strength of association between IVs and outcome variable. By expressing these associations in simple, interpretable quantities, statistical models can provide insight to the way how multiple drivers cooperate to cause a specific outcome. In life sciences, many such mechanisms are still not well understood but it is often plausible to assume that they are multifactorial. Therefore, empirical data collection and multivariable analysis are important contributors to knowledge generation.

Statistical models have been defined and described in various ways, ranging from pure mathematical notation over philosophical aspects to emphasis on their usefulness. While many scientists agree that the formal definition of a statistical model is “A set of probability distributions on the sample space $\mathcal{S}$” (Cox & Hinkley, 1979), this does not satisfactorily describe its relevance in science. More self‐explanatory descriptions are “Statistical models summarize patterns of the data available for analysis” (Steyerberg, 2009), “A powerful tool for developing and testing theories by way of causal explanation, prediction, and description” (Shmueli, 2010), “A simplification or approximation of reality” (Burnham & Anderson, 2002) or “A statistical model represents, often in considerably idealized form, the data‐generating process” (Wikipedia, 2017).

The question whether empirical observations are realizations of an ascertainable data‐generating mechanism, which possibly can be broken down to simple, comprehensible rules, is as old as science itself. For example, ancient Greek philosopher Aristotle has often been quoted with “Nature operates in the shortest ways possible” (AZquotes.com, 2017a), or physicist Isaac Newton with “We are to admit no more causes of natural things than such as are both true and sufficient to explain their appearance” (Newton, Motte, & Machin, 1729). By contrast, many modern life scientists cast doubts on the existence of a single “true model” that could be detected by empirical data collection. Examples are Burnham and Anderson (2002) (“We do not accept the notion that there is a simple “true model” in the biological sciences.”), Steyerberg (2009) (“We recognize that true models do not exist. … A model will only reflect underlying patterns, and hence should not be confused with reality.”), Box and Draper (1987) (Essentially, “all models are wrong, but some are useful”), or Breiman (2001a) (“I started reading Annals of Statistics, and was bemused: Every article started with “Assume that the data are generated by the following model: … “ followed by mathematics exploring inference, hypothesis testing and asymptotics.”).

Following this skepticism, in our view “Statistical models are simple mathematical rules derived from empirical data describing the association between an outcome and several explanatory variables” (Dunkler, Plischke, Leffondré, & Heinze, 2014). In order to be of use, statistical models should be valid, that is providing predictions with acceptable accuracy, and practically useful, that is allowing for conclusions such as “how large is the expected change in the outcome if one of the explanatory variables changes by one unit”. If interpretability of a statistical model is of relevance, simplicity must also be kept in mind. Seconders of this proposal include universal scientist and artist Leonardo da Vinci (to whom the quote “Simplicity is the ultimate sophistication” has often been attributed), possibly physicist Albert Einstein (“Make everything as simple as possible, but not simpler”), and businessman Sir Richard Branson, founder of the Virgin Group (“Complexity is our enemy. Any fool can make something complicated”). (AZquotes.com, 2017b–d) Practical usefulness, for example concerning the costs of collecting variables needed to apply a model, is a further important aspect of statistical modeling, otherwise a model is likely to be "quickly forgotten" (Wyatt and Altman, 1995). Finally, as we recognize that no statistical model comes without any assumptions, we conclude that robustness to mild or moderate violations of those assumptions is also a key requirement.

The quote by Sir Richard Branson ends with the apodosis “It is hard to keep things simple”. In the context of data‐driven variable selection, many statisticians agree with Branson, as variable selection can induce problems such as biased regression coefficients and p‐values and invalidity of nominal confidence levels. According to the famous problem‐solving principle “Occam's razor,” simpler solutions are preferable to more complex ones as they are easier to validate. This principle is often used to justify ”simpler models”. However, in search of simpler models, statistical analysis gets actually more complex, as then additional problems such as model instability, the possibility of several equally likely competing models, the problem of postselection inference, etc. has to be tackled. Therefore, various authors of textbooks on statistical modeling have raised differentially graded concerns about the use of variable selection methods in practice, depending on their personal experience and research areas where weak or strong theories may dominate (Burnham & Anderson, 2002; Harrell Jr., 2015; Royston & Sauerbrei, 2008; Steyerberg, 2009), while in other fields of empirical research, for example in machine learning, variable (or feature) selection seems to be the standard. Therefore, there is an urgent need for guidance through these partly controversial positions on the relevance of variable selection methods in real‐life data analysis in life sciences.

The types of statistical models that we will consider here are those that use a linear combination of IVs as their core ingredient. Furthermore, we require that regression coefficients β or simple transformations thereof, for example exp(β), have a practical interpretation for scientists. However, we do not impose any restrictions on the type of outcome variable, whether continuous, binary, count, or time‐to‐event, or on its distribution. This is because most of the methods that are described and discussed here were developed for the linear model with Gaussian errors, but were then transferred to other models for noncontinuous outcome variables.

This paper is based on a lecture held in the series “Education for Statistics in Practice” by Georg Heinze and Daniela Dunkler at the conference of the “Deutsche Arbeitsgemeinschaft Statistik” in Göttingen, Germany, March 2016. The slides used in the lecture are available at http://www.biometrische-gesellschaft.de/arbeitsgruppen/weiterbildung/education-for-statistics-in-practice.html. The paper is intended for the practicing statistician, whose routine work includes the development, estimation, and interpretation of statistical models for observational data to help answering research questions in life sciences. Based on our own experience, we assume that the statistician is responsible for statistical study design and analysis, but is working in an interdisciplinary environment with the possibility to discuss questions on the meaning of variables with applied life scientists, who often act as the principal investigators (PI). We will first review various statistical prerequisites for variable selection, and will subsequently use this toolbox to describe the most important variable selection methods that are applied in life sciences. We will discuss the impact of variable selection methods on properties of regression coefficients, confidence intervals, and p‐values. Recommendations for practitioners and software developers are then given, and their application exemplified in analysis of a real study.

2. VARIABLE SELECTION TOOLBOX

2.1. Statistical prerequisites

2.1.1. Main purposes of models

Shmueli (2010) identified three main purposes of statistical models. Within predictive research questions, predictive (or prognostic) models have the aim to accurately predict an outcome value from a set of predictors. Explanatory models are used in etiological research and should explain differences in outcome values by differences in explanatory variables. Finally, descriptive models should “capture the association between dependent and independent variables” (Shmueli, 2010). In the life sciences, models of all three types are needed. Still, they differ in the way they are used and interpreted. While prognostic models focus on predictions, explanatory models are used to estimate (causal) effects of risk factors or exposures by means of adjusted effect estimation, and descriptive models can have elements of both.

The purpose of statistical modeling in a particular analysis will have impact on the selection of IVs for a model. This becomes apparent when considering (Hastie, Tibshirani, & Friedman, 2009, p. 223)

$$\mathrm{expected}\mathrm{prediction}\mathrm{error}=\mathrm{irreducible}\mathrm{error}+\mathrm{bia}{\mathrm{s}}^2+\mathrm{variance}.$$

While the expected prediction error is the quantity of main concern in predictive modeling, explanatory modeling primarily aims at minimizing bias, in particular in the regression coefficients. Descriptive models also focus on the regression coefficients, but do not consider causality in a formal manner. Here, we mainly deal with the latter type of models, which are probably the most often used in life sciences, but we always keep in mind interpretability of effect estimates and accuracy of predictions.

2.1.2. Linear predictor models and interpretation of regression coefficients

Depending on the type of outcome variable, models that are often used in the life sciences are the linear model, the logistic model and the semiparametric Cox (1972) model. The linear model is defined by $Y={\beta }_0+{\beta }_1{X}_1+\dots +{\beta }_k{X}_k+\epsilon$, with Y a continuous outcome variable and $\epsilon \sim N(0,{\sigma }^2)$ a normally distributed error. The logistic model is expressed by $Pr(Y=1)=\mathrm{expit}({\beta }_0+{\beta }_1{X}_1+\dots +{\beta }_K{X}_k$), with $\mathrm{expit}(z)=exp(z)/[1+exp(z)]$, and Y a binary outcome variable. For time‐to‐event data, the semiparametric Cox proportional hazards regression model is often used and has the form $h(X,t)=h_0(t)exp({\beta }_1{X}_1+\dots +{\beta }_k{X}_k)$, where $h(x,t)$ denotes the hazard of an individual with covariate row vector x at time t, and $h_0(t)$ is an unspecified baseline hazard. All three models became popular in life sciences because regression coefficients (or transforms thereof such as exp( · )) are readily interpretable. The IVs $X_1,\dots ,X_k$ have the role of “explanatory variables” in explanatory models and of “predictors” in predictive models.

Common assumptions of these models are linearity, that is the expected outcome value is thought to be modeled by a linear combination of IVs, and additivity, that is the effects of the IVs can be added. Various extensions of the basic “linear predictor” models exist that can relax the linearity assumption, such as polynomial models, splines, fractional polynomials, or generalized additive models, but will not be considered here. Still, all these modifications assume additivity of effects, even if a particular IV is no longer included in the model as a single, untransformed model term. Relaxation of the additivity assumption would require consideration of interaction (product) terms between IVs, or the use of more complex functional relationship such as power functions. In the following, we will not consider these modifications, and will denote the linear, logistic, and Cox model as “linear predictor models”.

In a setting with several IVs, the fundamental interpretation of a regression coefficient ${\beta }_j$ in a linear predictor model is that of the expected change in outcome (or log odds or log hazard) if $X_j$ changes by one unit and all other variables $X_1,\dots X_{j-1},X_{j+1},\dots ,X_k$ are held constant. Consequently, ${\beta }_j$ measures the conditional effect of $X_j$. However, as outlined above, the existence of a single true model and hence of correct model specification can rarely be assumed. This implies that the interpretation of ${\beta }_j$ changes if the set of IVs in the model changes and $X_j$ is correlated with other IVs. (In logistic and Cox regression models, this may even happen for uncorrelated variables (Robinson & Jewell, 1991).) As an example, consider a model explaining percentage of body fat by weight, height, and abdomen circumference, three highly correlated IVs. The study is explained in more detail in Section 3. Table 1 shows regression coefficients resulting from four potential models. We see that the coefficient of weight changes considerably in magnitude and even in its sign if different IVs are used for adjustment; this is because the meaning of the weight coefficient is fundamentally different in the four models. Also the effect of height can be deemed irrelevant or highly predictive, depending on whether abdomen circumference was adjusted for or not. Comparison of adjusted R ² of the models underlines the dominance of abdomen circumference. Therefore, any variable selection applied in a linear predictor model with correlated IVs will always change the interpretation of effects. This is of high relevance in explanatory or descriptive models, where there is an interest in interpretability of regression coefficients.

Table 1.

Four potential models to estimate body fat in %

Regression coefficients
Model	Intercept		Weight in kg		Height in cm		Abdomen circumference		$R_{\mathrm{adj}}^2$
	Estimate	SE	Estimate	SE	Estimate	SE	Estimate	SE
1	−14.892	2.762	0.420	0.034					0.381
2	76.651	9.976	0.582	0.034	−0.586	0.062			0.543
3	−47.659	2.634	−0.292	0.047			0.979	0.056	0.722
4	−30.364	11.432	−0.215	0.068	−0.096	0.062	0.910	0.071	0.723

$R_{\mathrm{adj}}^2$, adjusted R ²; SE, standard error

2.1.3. Events‐per‐variable

The ratio between sample size (or the number of events in Cox models or the number of the less frequent outcome in logistic regression) and the number of IVs is often expressed in a simple ratio, termed “events‐per‐variable” (EPV). EPV quantifies the balance between the amount of information provided by the data and the number of unknown parameters that should be estimated. It is intuitive to assume that with limited sample size it cannot be possible to accurately estimate many regression coefficients. Therefore, simple rules like “EPV should at least be greater than ten” became popular in the literature (Harrell, Lee, Califf, Pryor, & Rosati, 1984). Recently, Harrell (2015, p. 72) recommended a more stringent rule of 1:15. However, expressing a possible disparity between sample size and number of parameters to be estimated in a simple ratio is often oversimplifying the problem because beyond the number of IVs, many other quantities such as the strength of effects or the correlation structure of IVs may influence accuracy (Courvoisier, Combescure, Agoritsas, Gayet‐Ageron, & Perneger, 2011). Nevertheless, EPV is easy to assess and can roughly inform about the maximum size of a model that could in principle be fitted to a data set. Some further discussion can be found in Schumacher, Holländer, Schwarzer, Binder, and Sauerbrei (2012).

If a model may also include extensions such as non‐linear transformations of IVs or interaction (product) terms requiring additional degrees of freedom (DF), then this must be accounted for in the denominator of EPV. When considering variable selection, it is the total number of candidate IVs (and of their considered transformations) that counts; this has often been misconceived (Heinze & Dunkler, 2017).

2.2. Criteria for selecting variables

2.2.1. Significance criteria

Hypothesis tests are the most popular criteria used for selecting variables in practical modeling problems. Without loss of generality, consider that we compare two models $M_1:{\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2$ and $M_2:{\gamma }_0+{\gamma }_1{X}_1$. The null hypothesis that ${\beta }_2=0$ implies that ${\beta }_0={\gamma }_0$ as well as ${\beta }_1={\gamma }_1$. Such a hypothesis could be tested by comparing the log likelihoods of M ₁and M ₂ (using a likelihood ratio test), requiring fitting of the two models. Logistic and Cox models need iterative fitting, such that this test is often approximated by step‐up (score test) or step‐down (Wald test) tests. The score test only needs the fitted M ₂ model, assumes ${\beta }_0={\gamma }_0$ and ${\beta }_1={\gamma }_1$ and evaluates the derivative of the log likelihood at ${\beta }_2=0$. It is typically used in forward steps to screen IVs currently not included in a model for their ability to improve model fit. By contrast, the Wald test starts at M ₁ and evaluates the significance of β₂ by comparing the ratio of its estimate and its standard error with an appropriate t distribution (for linear models) or standard normal distribution (for logistic or Cox regression). It is routinely contained in the standard output of many software packages, and lends itself for a step‐down procedure. Likelihood ratio tests provide the best control over nuisance parameters by maximizing the likelihood over them both in M ₁ and M ₂. In particular, if several coefficients are being tested simultaneously, likelihood ratio tests for model comparison are preferred over Wald or score tests.

Iterated testing between models yields the forward selection (FS) or backward elimination (BE) variable selection algorithms, depending on whether one starts with an empty model or with a model with all IVs that were considered upfront. Iterative FS or BE is done, using prespecified significance levels ${\alpha }_F$ or ${\alpha }_B,$ until no further variables are included or excluded. A FS procedure that includes BE steps is often denoted as a stepwise (forward) selection procedure, and correspondingly, a BE procedure with FS steps is denoted as stepwise backward selection. Most statisticians prefer BE over FS, especially when collinearity is present (Mantel, 1970). However, when models can become complex, for example in the context of high‐dimensional data, then FS is still possible.

As it is always required in statistical inference, tests between models are reliable only if these comparisons are prespecified, that is if a small number of prespecified models are compared. However, tests performed during the procedure of model‐building are not pre‐specified, as the models to be compared are often already the result from (several) previous variable inclusion or exclusion steps. This causes two problems in the interpretability of p‐values for coefficient tests from a model derived by variable selection. First, unaccounted multiple testing will generally lead to underestimated p‐values. Second, p‐values for coefficient tests from a model do not test whether a variable is relevant per se, but rather whether it is relevant given the particular set of adjustment variables in that specific model.

2.2.2. Information criteria

While significance criteria are usually applied to include or exclude IVs from a model, the focus of information criteria is on selecting a model from a set of plausible models. Since including more IVs in a model will slightly increase the apparent model fit (as expressed by means of model likelihood), information criteria were developed to penalize the apparent model fit for model complexity. In his seminal work, Akaike (1973) proposed to approximate the expectation of the cross‐validated log likelihood, $E_{test}{E}_{train}[logL(x_{test}|{\widehat{\beta }}_{train})]$, by $logL(x_{train}|{\widehat{\beta }}_{train})-k$, where $logL(x_{test}|{\widehat{\beta }}_{train})$ and $logL(x_{train}|{\widehat{\beta }}_{train})$ are the apparent log likelihood from applying a model to an independent test data set, and the log likelihood from applying it to the data with which it was developed, respectively. The Akaike information criterion (AIC) is formulated equivalently as $-2logL(x_{train}|{\widehat{\beta }}_{train})+2k$ (“smaller is better” formulation).

AIC can be used to compare two models even if they are not hierarchically nested. It can also be employed to select one out of several models. For example, it is often used as selection criterion in a “best subset” selection procedure evaluating all (2^k for k variables) models resulting from all possible combinations of IVs.

If several models were fitted to a data set, let denote ${\mathrm{\Delta }}_i=AI{C}_i-AI{C}_{min}$ the AIC of model $M_i$ minus the minimum AIC across all models. Burnham and Anderson (2002, p. 70) denoted models with ${\mathrm{\Delta }}_i\le 2$as having “substantial empirical support,” models with $4\le {\mathrm{\Delta }}_i\le 7$ as having “considerably less empirical support,” and models with ${\mathrm{\Delta }}_i>10$ as having essentially no support. Akaike weights can be derived from the ${\mathrm{\Delta }}_i$’s computed for a set of R competing models as

$${\displaystyle w_i=exp\left(-\frac{1}{2}{\mathrm{\Delta }}_i\right)/\sum _{r=1}^{R}exp\left(-\frac{1}{2}{\mathrm{\Delta }}_r\right)}$$

These weights transform the AIC values back to scale of relative likelihood of a model. They describe the probability that a model $M_i$ is the actual best model in terms of Kullback–Leibler information conditional on the assumption that one of the R models must be the Kullback–Leibler best model.

While at first sight selection based on information criteria seems different to significance‐based selection, there is a connection between these two concepts. Consider two competing hierarchically nested models differing by one DF. Here, AIC optimization corresponds to significance‐based selection at a significance level of 0.157. More generally, the significance level corresponding to AIC selection in hierarchical model comparisons is ${\alpha }_{AIC}(DF)=1-F_{{\chi }^2,DF}(2·DF)$, with $F_{{\chi }^2,DF}(x)$ denoting the cumulative distribution function of the ${\chi }_{\mathit{DF}}^2$ distribution evaluated at x. Therefore, AIC‐selected models will generally contain effects with p‐values (in the final model) lower than approximately 0.157. Moreover, as sample size gets larger, they will include a larger number of irrelevant IVs, in line with the belief that there exists no true data generating model. The Bayesian information criterion (BIC) was developed for situations where one assumes existence of a true model that is in the scope of all models that are considered in model selection. With selection guided by BIC, the selected model converges to the “true” data generating model (in a pointwise manner) (Schwarz, 1978). BIC is defined as $BIC=-2logL+log(n)·k$, where n is the sample size (or, in Cox or logistic models, the number of events or number of less frequent outcomes, respectively). It also has a significance correspondence, ${\alpha }_{BIC}(DF,n)=1-F_{{\chi }^2,DF}(log(n)·DF)$; for example ${\alpha }_{BIC}(DF=1,n=100)=0.032$. Consequently, for any suitable sample size the penalty factor of BIC is larger than that of AIC and BIC will select smaller models.

2.2.3. Penalized likelihood

Model selection can also be achieved by applying least angle selection and shrinkage operator (LASSO) penalties, which are based on subtracting a multiple (λ) of the absolute sum of regression coefficients from the log likelihood and thus setting some regression coefficients to zero (Tibshirani, 1996). Availability of efficient software (e.g. PROC GLMSELECT in SAS software or the R package glmnet) (Friedman, Hastie, & Tibshirani, 2010; SAS Institute Inc., 2016) allows to fit linear, logistic, and Cox models with such penalties, and to optimize the tuning parameter λ, which controls the penalization strength via cross‐validation or information criteria.

LASSO models have been used extensively in high‐dimensional model selection problems, that is when the number of IVs k by far exceeds the sample size n. In low‐dimensional problems ($k<n)$ researchers are usually interested in interpretable regression coefficients, and for that purpose LASSO models are far less understood than for their predictive performance. Regression coefficients estimated by the LASSO are biased by intention, but can have smaller mean squared error (MSE) than conventional estimates. Because of the bias, their interpretation in explanatory or descriptive models is difficult, and confidence intervals based on resampling procedures such as the percentile bootstrap do not reach their claimed nominal level. Recently the problem of performing valid inference on the regression coefficients after model selection by the LASSO was investigated (Taylor & Tibshirani, 2015) and a solution was proposed. However, there is still not enough evidence on the performance of this method. Valid inference requires that both the bias and the variance components in the sampling distribution of the regression coefficients are adequately captured. However, to determine the bias component, one needs an estimate of the bias, essentially requiring comparison with an unbiased regression coefficient, which in turn cannot be obtained within the variance‐reducing penalization framework. Therefore, postselection confidence intervals can be even wider than their maximum likelihood counterparts computed from a model that includes all considered IVs, which is also demonstrated in one of the examples of Taylor and Tibshirani (2015).

Another problem with LASSO estimation is its dependence on the scale of the covariates. Therefore, LASSO implementations in standard software perform an internal standardization to unit variance which in some of its software implementations is invisible to the user as regression coefficients are transformed back and reported on the original scale. Still, it is not clear if this type of “one size fits all” standardization is optimal for all modeling purposes; consider, for example the typical case of a mixture of continuous and binary covariates, where continuous covariates can have different skewness and binary covariates can have substantially different degrees of balance. This case has also been addressed, for example by Porzelius, Schumacher, and Binder (2010).

2.2.4. Change‐in‐estimate criterion

In particular in epidemiologic research the change‐in‐estimate criterion is often applied to select adjustment variables for explanatory models (Bursac, Gauss, Williams, & Hosmer, 2008; Lee, 2014; Maldonado & Greenland, 1993; Mickey & Greenland, 1989; Vansteelandt, Bekaert, & Claeskens, 2012). Reconsidering models M ₁ and M ₂ of Section 2.2 Significance Criteria, the change‐in‐estimate ${\delta }_{X_1}^{(-X_2)}={\gamma }_1-{\beta }_1$ is the change in the regression coefficient of X ₁ (a “passive” IV, $M_1:{\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2$) by removing X ₂ (an “active” IV; $M_2:{\gamma }_0+{\gamma }_1{X}_1$) from a model. The change‐in‐estimate criterion is often also expressed as a “relative” change ${\delta }_{X_1}^{(-X_2)}/{\beta }_1\times 100\%$. These criteria were also incorporated in the “purposeful selection algorithm” proposed by Hosmer, Lemeshow et al. (2011; 2013). Recently, the criterion was investigated by Dunkler et al. (2014). These authors approximated the change‐in‐estimate by ${\widehat{\delta }}_{X_1}^{(-X_2)}=-{\widehat{\beta }}_2{\widehat{\sigma }}_{12}/{\widehat{\sigma }}_2^2$, where ${\widehat{\sigma }}_2^2$ and ${\widehat{\sigma }}_{12}$ are the variance of ${\widehat{\beta }}_2$ and the covariance of ${\widehat{\beta }}_1$ and ${\widehat{\beta }}_2$, respectively. Using this approximation, it could be shown that eliminating a “significant” IV from a model will lead to a “significant” change‐in‐estimate, and eliminating a “nonsignificant” IV to a “nonsignificant” change‐in‐estimate. Moreover, the authors standardized the change‐in‐estimate criterion for use in linear, logistic, and Cox regression models, such that the change‐in‐estimate can be compared to a single, common threshold value τ in order to decide whether an IV $X_j$ should be dropped from a model or not. Dunkler et al. (2014) suggested to combine the standardized change‐in‐estimate criterion with significance‐based BE, yielding the “augmented backward elimination” (ABE) procedure. Simulation results showed that in general, ABE leads to larger models and less biased regression coefficients than BE, and to MSE of regression coefficients that often fall between those achieved by BE and by models including all considered IVs. Therefore, ABE may be useful to eliminate IVs from a model that are irrelevant both for model fit and for interpretation of βs of other IVs, for example for confounder selection. However, experience with this approach is still limited.

2.2.5. Background knowledge

Many authors have repeatedly highlighted the importance of using background knowledge to guide variable selection. Background knowledge can be incorporated at least at two stages, and it requires an intensive interplay between the PI of the research project (usually a nonstatistician) and the statistician in charge of designing and performing statistical analysis. At the first stage, the PI will use subject‐specific knowledge to derive a list of IVs which in principle are relevant as predictors or adjustment variables for the study in question. This list will mostly be based on the availability of variables, and must not take into account the empirical association of IVs with the outcome variable in the data set. The number of IVs to include in the list may also be guided by the EPV (see our discussion in Section 2.1 Events‐per‐variable).

Together with the PI, the statistician will go through the list and critically question the role and further properties of each of the variables, such as chronology of measurement collection, costs of collection, quality of measurement, or availability also to the “user” of the model. Having appropriately pruned this working set of IVs, a first multivariable model could be estimated (the “global model”).

It is often helpful to draft a sketch of a graph visualizing assumed causal dependencies between the IVs, where the level of formalization of those dependencies may sometimes reach that of a directed acyclic graph (DAG) (Greenland, Pearl, & Robins, 1999). In developing explanatory models, such a DAG is a necessary prerequisite to identify the sets of variables necessary to adjust for in order to avoid bias (Evans, Chaix, Lobbedez, Verger, & Flahault, 2012; Greenland et al., 1999; VanderWeele & Shpitser, 2011). Developing DAGs can also be of help in predictive model building, for example to identify redundant or alternative predictors.

Given that one of the IVs is of primary interest, for example expressing an exposure the effect of which should be inferred by a study, DAGs allow to classify the other IVs into confounders, mediators, and colliders (Andersen & Skovgaard, 2010). (A short explanation of differences between confounders, mediators, and colliders can be found in the Supporting Information Figure S1). This is important because in order to obtain an unbiased estimate of the causal effect of the exposure on the outcome, all confounders should be adjusted for, but colliders or mediators must not be included in a model. Simple and more involved DAGs are exemplified by Greenland et al. (1999). These authors point out that counter to intuition, adjusting for an IV in a multivariable model may not only eliminate association between marginally associated IVs, but may also induce an association between marginally unassociated IVs. They provide extended rules to be applied to DAGs in order to determine the set of IVs necessary for adjustment. DAGs always heavily rely on prior belief of the investigators on the roles of the explanatory variables, which will not be always available in research projects. Therefore, robust confounder selection procedures based on DAGs were proposed such as the disjunctive cause criterion (VanderWeele & Shpitser, 2011).

Often one is willing to trade in a little bias in return for considerably reduced variance. This means, that even in explanatory models where the set of adjustment variables necessary to control confounding is assumed to be known, some of the confounders’ association with the outcome may be so weak that adjustment may increase variance in the effect estimate of main interest more than reducing its bias. Consequently, depending on whether the true association of a potential confounder with the outcome is weak or strong, variable selection may be beneficial or harmful, even if performed with the same significance criterion. This is exemplified by means of a simple simulation study in Figure 1. From this simplified simulation study we conclude, that (i) if background knowledge on the strength of a confounder exists, it should be used to decide whether variable selection should be applied or not, and (ii) one cannot recommend a universally applicable significance criterion for variable selection that fits all needs.

Figure 1.

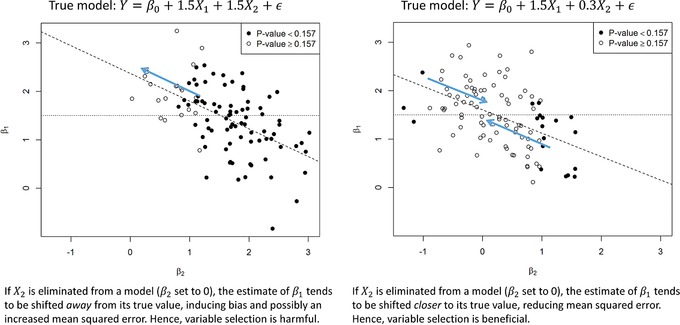
Simulation study to illustrate possible differential effects of variable selection. Graphs show scatterplots of estimated regression coefficients ${\widehat{\beta }}_1$ and ${\widehat{\beta }}_2$ in 50 simulated datasets of size $N=50$ with two standard normal IVs with correlation $\rho =0.5$. Circles and dots indicate simulated datasets where a test of the null hypothesis ${\beta }_2=0$ yields p‐values greater or lower than 0.157, respectively. The dashed lines are regression lines of β₁ on β₂; thus they indicate how β₁ would change if β₂ is set to 0

2.3. Variable selection algorithms

Table 2 lists some of the most popular variable selection methods for explanatory or descriptive models. Each variable selection algorithm has one or several tuning parameters that can be fixed to a prespecified value or estimated, for example by cross‐validation or AIC optimization. Note that tenfold cross‐validation and selection by AIC are asymptotically equivalent (Stone, 1977). Moreover, comparison of two hierarchically nested models with a difference of one DF by AIC is equivalent to performing a likelihood ratio test at a significance level of 0.157.

Table 2.

Some popular variable selection algorithms

Algorithm	Description	Stopping rule
Backward elimination (BE)	Start with the global model. Repeat: Remove the most insignificant independent variable (IV) and reestimate the model. Stop if no insignificant IV is left.	All (Wald) p‐values in multivariable model < ${\alpha }_B$
Forward selection (FS)	Start with the most significant univariable model. Repeat: Evaluate the added value of each IV that is currently not in the model. Include the most significant IV and reestimate the model. Stop if no significant IV is left to include.	All (score) p‐values of variables currently not in the multivariable model > ${\alpha }_F$
Stepwise forward	Start with the null model. Repeat: Perform an FS step. After each inclusion of an IV, perform a BE step. In subsequent FS steps, reconsider IVs that were removed in former steps. Stop if no IV can be removed or added.	All p‐values of variables in the model < ${\alpha }_B$, and all p‐values of variables not in the model > ${\alpha }_F$
Stepwise backward	Stepwise approach (see above) starting with the global model, cycling between BE and FS steps until convergence.	All p‐values of variables in the model < ${\alpha }_B$, and all p‐values of variables not in the model > ${\alpha }_F$
Augmented backward elimination	Combines BE with a standardized change‐in‐estimate criterion. IVs are not excluded even if $p>{\alpha }_B$ if their exclusion causes a standardized change‐in‐estimate > τ in any other variable.	No further variable to exclude by significance and change‐in‐estimate criteria
Best subset selection	Estimate all 2k possible models. Choose the best model according to an information criterion, for example AIC, BIC.	No subset of variables attains a better information criterion.
Univariable selection	Estimate all univariable models. Let the multivariable model include all IVs with $p<{\alpha }_U$.
LASSO	Imposes a penalty on the sum of squares or log likelihood that is equal to the absolute sum of regression coefficients.	Relative weight of penalty is optimized by cross‐validated sum of squares or deviance.

2.4. Consequences of variable selection and possible remedies

2.4.1. Consequences of variable selection

The basis of unbiased and accurate regression coefficients and predictions is the identification of the true data generating mechanism. In Section 1, we already engaged in a philosophical discussion on whether the existence of such a mechanism can be assumed at all, and if such a mechanism would be “simple enough” to be detectable by regression models with linear predictors. These important aspects held aside, falsely including or excluding IVs will have direct consequences on the variance and the bias of the regression coefficients (Figure 2). However, as Figure 2 shows, these dependencies can be complex and their direction and magnitude depend on the correlation of IVs and are hard to predict in a particular data set.

Figure 2.

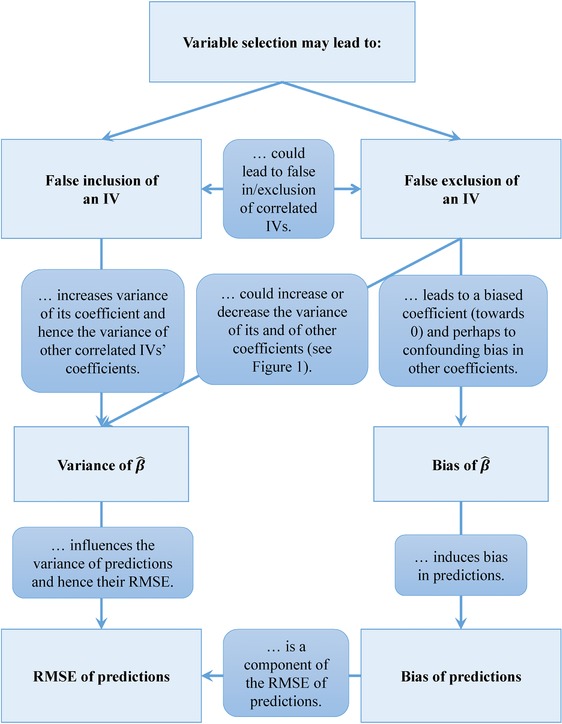
A schematic network of dependencies arising from variable selection. β, regression coefficient; IV, independent variable; RMSE, root mean squared error

In general, while variable selection has often been described as inducing a bias away from zero, nonselection of a variable could also be interpreted as shrinkage toward zero. Consequently, variable selection methods often reduce the RMSE of regression coefficients, in particular for weak or noise predictors. From our experience, this shrinkage effect is quite extreme for LASSO at small sample sizes (EPV < 10), which can result in considerably reduced RMSEs of true regression coefficients. This comes at the cost of predictions that are considerably biased toward the mean and may even have larger RMSEs than competing methods. In particular, this may be observed at the tails of the distribution of the true outcome variable.

While univariable variable selection, that is including those IVs in a multivariable model that show significant association with the outcome in univariable models, is one of the most popular approaches in many fields of research, it should be generally avoided (Heinze & Dunkler, 2017; Sun, Shook, & Kay, 1996). Among the significance‐based selection methods, we prefer BE over FS (Mantel, 1970). From our experience, use of the AIC, which corresponds to ${\alpha }_B\approx 0.157$, but no smaller ${\alpha }_B$ is recommendable if less than 25 EPV are available. For samples with more EPV, researchers believing that a true simple model exists and is identifiable may prefer a more stringent threshold (${\alpha }_B=0.05$). They may also prefer BIC as it has the potential to identify the correct model asymptotically.

LASSO selection tends to select more IVs than BE, underestimating the effects of IVs with an effect while assigning nonzero values to the regression coefficients of some IVs without an effect. Generally, it results in more homogenous shrinkage of all regression coefficients, while BE shrinks effects of IVs without an effect more heavily than effects of IVs with an effect.

2.4.2. Model stability

A very important, but often ignored problem of data‐driven variable selection is model stability, that is the robustness of the selected model to small perturbations of the data set (Sauerbrei, Buchholz, Boulesteix, & Binder, 2015). Bootstrap resampling with replacement or subsampling without replacement are valuable tools to investigate and quantify model stability of selected models (De Bin, Janitza, Sauerbrei, & Boulesteix, 2016; Sauerbrei & Schumacher, 1992). The basic idea is to draw $B$resamples from the original data set and to repeat variable selection in each of the resamples. Important types of quantities that this approach can provide are (i) bootstrap inclusion frequencies to quantify how likely an IV is selected, (ii) sampling distributions of regression coefficients, (iii) model selection frequencies to quantify how likely a particular set of IVs is selected, and (iv) pairwise inclusion frequencies, evaluating whether pairs of (correlated) IVs are competing for selection.

Inclusion frequencies of any type will always depend on the chosen selection criteria, for example the significance level ${\alpha }_B$ for including effects in a model, or the criterion τ for evaluating changes‐in‐estimate. The dependence of these quantities on the selection criterion can be visualized by model stability paths, as exemplified by Dunkler et al. (2014), Sauerbrei et al. (2015), or Meinshausen and Bühlmann (2010). The use of such resampling methods often leads to simpler final models (Sauerbrei, 1999).

Moreover, if setting a resampled regression coefficient of an IV not selected in a particular resample to 0, the resampled distribution of regression coefficients can give insight in the sampling distribution caused by variable selection. For example, the median regression coefficient for each IV computed over the resamples can yield a sparse model that is less prone to overestimation than if variable selection is applied only to the original data set. The 2.5th and 97.5th percentiles of the resampled regression coefficients can serve as resampling‐based confidence intervals, taking into account model uncertainty without making assumptions on the shape of the sampling distribution. However, they may severely underestimate the true variability if bootstrap inclusion frequencies are low, for example below 50%.

To derive a predictor that incorporates model uncertainty, Augustin, Sauerbrei, and Schumacher (2005) and Buchholz, Holländer, and Sauerbrei (2008), proposed a two‐stage bootstrap procedure. In the first step, IVs are screened based on their inclusion frequencies, and IVs with negligible effects eliminated. In the second step, bootstrap model averaging is used to obtain an aggregated model. The regression coefficients are simply averaged over the bootstrap resamples. Variances for the regression coefficients can be obtained by making use of Buckland, Burnham, and Augustin (1997)’s variance formula taking into account both within‐model variance and model selection uncertainty. This approach has two control parameters, the significance level in the variable selection procedure and the minimum bootstrap inclusion frequency required to include an IV in the second step.

Pairwise inclusion frequencies can be easily compared against their expected values given independent selection of the pair of IVs. Values below the expectation would give rise for assuming selection competition between the two IVs, while values above the expectation indicate joint selection of a “rope team” of IVs; an IV's effect is then amplified by adjustment for a particular other IV.

2.4.3. Shrinkage and bias‐variance trade‐off

Shrinkage has two meanings in statistics: as a phenomenon, shrinkage describes the situation where predictions from a model are too optimistic, that is if observed outcomes are closer to the overall mean outcome than the predictions. As a technique it prepares estimates such that the phenomenon of shrinkage should not occur, that is a shrinkage estimator anticipates shrinkage and adjusts estimators accordingly. Even unbiased estimators can yield shrinkage (see Harrell Jr. (2015, p. 75) for an intuitive explanation). Shrinkage estimators are generally biased, usually toward zero. Shrinkage estimators can be obtained by postestimation procedures (Dunkler, Sauerbrei, & Heinze, 2016) or by penalized likelihood; for example the LASSO is a shrinkage estimator.

Shrinking estimates, that is taking a certain amount of bias toward zero into account, can have desirable effects on the variance of those estimates. Intuitively, this decrease in variance results naturally from restricting the sampling space of regression coefficients when applying shrinkage methods (Greenland, 2000; Hastie et al., 2009, p. 225). Therefore, shrinkage methods are useful in prediction modeling tasks where the focus is on obtaining accurate predictions, that is predictions with a low MSE.

Shrinkage methods were also proposed to reduce overestimation bias of regression coefficients and MSE in models obtained by variable selection (Dunkler et al., 2016; Sauerbrei, 1999; van Houwelingen & Sauerbrei, 2013). In particular, parameterwise shrinkage assigns different shrinkage factors to each regression coefficient depending on the strength of association that it expresses (Sauerbrei, 1999). Regression coefficients for which selection is less stable are shrunken more strongly than coefficients for which selection is stable. The shrinkage factors are obtained by leave‐one‐out resampling. Dunkler et al. (2016) suggest an extension of these shrinkage factors for semantically related regression coefficients (e.g. dummy variables coding a categorical IV), propose a computational approximation to their estimation and provide an R package shrink to facilitate their application in practice.

3. TOWARD RECOMMENDATIONS

3.1. Recommendations for practicing statisticians

Many researchers seek advice for the typical situation where there are many IVs to be potentially considered in a model but where sample size is limited (EPV ≈10 or lower). In applied research, variable selection methods have too often been misused, giving such data‐driven methods the exclusive control over model building. This has often resulted from common misconceptions about the capabilities of variable selection methods (Heinze & Dunkler, 2017).

3.1.1. Generate an initial working set of variables

Modeling should start with defendable assumptions on the roles of IVs that can be based on background knowledge (that a computer program typically does not possess), that is from previous studies in the same field of research, from expert knowledge or from common sense. Following this golden rule, an initial working set of IVs, the “global model,” can often be compiled without yet using the data set at hand to uncover the relationships of IVs with the outcome (Harrell Jr., 2015). The assumed relationships between the variables of this working set may be summarized, for example by drafting a DAG (Andersen & Skovgaard, 2010). Often it may be only possible to draw a rudimentary DAG or apply a simple criterion like the disjunctive cause criterion (VanderWeele & Shpitser, 2011). It may then well turn out that some IVs are not needed in a multivariable model because of redundancy or because their effects, adjusted for others, are not of much interest per se.

Using background knowledge only it should be aimed to determine whether the association of each variable with the outcome, given the other IVs, is assumed to be relatively strong, or rather unclear. The EPV ratio should be computed for the global model ($EP{V}_{global}$).

3.1.2. Decide whether variable selection should be applied, which IVs are considered and which variable selection method is employed

We advise not to consider variable selection on “strong” IVs, and to subject IVs with unclear role to variable selection only with a sufficient sample size. If variable selection is applied, it should be accompanied by stability investigations. Some further rules based on the $EP{V}_{global}$ can be found in Table 3. Of course, these limits are subject to the aforementioned limitations of $EPV$. They are rough rules of thumb based on our experience, the assumption that there exist some nonpredictive IVs, our simulations done for this and our previous paper (Dunkler et al., 2014), and on recommendations of other authors. The recommended $EP{V}_{global}$ limits should be adapted to the situation, for example raised if correlations between candidate IVs are particularly strong, or lowered if the candidate variables are all independent of each other. As we have mentioned above, some authors even suggest an $EP{V}_{global}$ of at least 15 as a meaningful number needed for interpretability of a global model (Harrell, 2015). Among the variable selection procedures BE is preferred as it starts with the assumed unbiased global model. AIC (${\alpha }_B=0.157)$ could be used as a default stopping criterion, but in some situations larger values of ${\alpha }_B$ may be needed to increase stability. Only in very large data sets, $EP{V}_{global}>100$, one could consider the BIC or ${\alpha }_B\le 0.05$. If it should be guaranteed that important predictors or confounders should not be missed, then ABE may be a useful extension to BE.

Table 3.

Some recommendations on variable selection, shrinkage, and stability investigations based on events‐per‐variable ratios

Situation	Recommendation
For some IVs it is known from previous studies that their effects are strong, for example age in cardiovascular risk studies or tumor stage at diagnosis in cancer studies.	Do not perform variable selection on IVs with known strong effects.
$EP{V}_{global}>25$	Variable selection (on IVs with unclear effect size) should be accompanied by stability investigation.
$10<EP{V}_{global}\le 25$	Variable selection on IVs with unclear effect size should be accompanied by postestimation shrinkage methods (e.g. Dunkler et al., 2016), or penalized estimation (LASSO selection) should be performed. In any case, a stability investigation is recommended.
$EP{V}_{global}\le 10$	Variable selection not recommended. Estimate the global model with shrinkage factor, or penalized likelihood (ridge regression). Interpretation of effects may become difficult because of biased effect estimation.

3.1.3. Perform stability investigations and sensitivity analyses

Variable selection generally introduces additional uncertainty. In the following subsection, we propose a list of quantities useful to assess selection stability and model uncertainty, which should be routinely reported whenever variable selection is employed. In some software such as SAS/PROC GLMSELECT, most of those quantities are already available. In other packages such as Stata or R, they can be easily obtained using few lines of additional code, following our example R codes provided as Supporting Information on the journal's web page. Unfortunately, this possibility is missing in some popular software packages, for example in IBM SPSS Statistics.

Stability investigations should at least comprise the assessment of the impact of variable selection on bias and variance of regression coefficient and the computation of bootstrap inclusion frequencies. Optionally, model selection frequencies, and pairwise inclusion frequencies could be added. An extended stability investigation as that performed by Royston and Sauerbrei (2003), who performed a re‐analysis of the bootstrap inclusion fractions of each IV using log‐linear analysis, can be very informative but may go beyond the usual requirements.

Overestimation bias results if a variable has been selected only because its regression coefficient appeared to be extreme in the particular sample. This conditional bias can be expressed relative to the (assumed unbiased) regression coefficient in the global model estimated on the original data, and computed as the difference of the mean of resampled regression coefficients computed from those resamples where the variable was selected and the global model regression coefficient, divided by the global model regression coefficient.

For assessing variance, we propose to compute the root mean squared difference (RMSD) of the bootstrap estimates of a regression coefficient and its corresponding (assumed unbiased) value in the global model estimated on the original data. The “RMSD ratio,” that is RMSD divided by the standard error of that coefficient in the global model, intuitively expresses the variance inflation or deflation caused by variable selection.

Furthermore, we advise to perform sensitivity analyses by changing decisions made in the various analysis steps. For example, there may be competing sets of assumptions on the roles and assumed strengths of variables in the first step that might lead to different working sets. Or, selection or nonselection of IVs and estimated regression coefficients are sensitive to the p‐value thresholds used. This sensitivity can be visualized using stability paths as exemplified in Dunkler et al. (2014). Sensitivity analyses should be prespecified in the analysis protocol.

The most unpleasant side effect of variable selection is its impact on inference about true values of regression coefficients by means of tests and confidence intervals. Only with large sample sizes, corresponding to EPV greater than 50 or 100, we can trust in the asymptotic ability of some variable selection methods to identify the true model, thus making inference conditional on the selected model approximately valid. With more unfavorable EPVs, model instability adds a nonnegligible source of uncertainty, which would be simply ignored by performing inference only conditional on the selected model. It has been pointed out that valid postselection inference cannot be achieved (Leeb & Pötscher, 2005).

Depending on a specific situation, we propose some pragmatic solutions:

1. Situation: The effect of an IV should be formally tested, but no theory exists on which subset of variables should be included in the model.

   Solution: Perform inference in the global model.

   In Section 3.1, we discuss how to use background knowledge to build a global model without uncovering the relationship of the IVs with the outcome variable. Thus, this model can be used to provide a valid p‐value for an IV that is adjusted for all other IVs that were in principle considered in model‐building. The purpose of variable selection would then be restricted to reducing this global model to a prediction model of higher practical usability, but not to draw conclusions about effects.

2. Situation: There exists a strong theory supporting only a small number of competing models.

   Solution: Perform multimodel inference with AIC.

   Burnham and Anderson (2002) have proposed to use a few prespecified, approximately equally plausible models for drawing inference about regression coefficients. In order to compute total variances, the average within‐model variance and the between‐model variance should be added, where within‐model variances are weighted by model importance measured, for example by Akaike weights or by bootstrap model frequencies (Buckland et al., 1997). This type of inference may be indicated for example for explanatory models, where there are often strong arguments against the plausibility of a global model, and if there are only a few competing models.

3. Situation: There is no strong theory that can be used for model‐building, but the global model is implausible. Although in this case effects of IVs can no longer be formally tested, still some evidence on the variability of estimates is needed.

   Solution: Perform multi‐model inference with the resampled distribution of regression coefficients.

   In absence of a strong theory model selection is often purely based on the evidence provided by the data, for example by applying a variable selection algorithm. The sampling distribution of a regression coefficient can be obtained by bootstrap resampling, repeating variable selection in each bootstrap resample. If this sampling distribution is approximately centered at the estimate from the global model, then there is no indication of bias induced by variable selection, and multimodel inference can be performed by evaluating quantiles of the sampling distribution to define confidence intervals or to derive p‐values. In other cases such intervals may give at least a realistic impression of variability. The median of the bootstrap distribution could be used as multimodel point estimate, having the advantage to be zero in case a variable was selected in less than 50% of the resamples. Alternative proposals to yield a parsimonious aggregated model were made by Augustin et al. (2005) and Buchholz et al. (2008). Finally, we would like to point at the shrinkage methods that were developed to reduce the MSE of estimates and predictions, and which can also serve to reduce a possible overestimation bias induced by variable selection (Dunkler et al., 2016; Sauerbrei, 1999; van Houwelingen, 2001; van Houwelingen & Sauerbrei, 2013).

3.2. Recommendations for developers of standard software packages

BE, FS, or stepwise selection algorithms are available in many statistical software packages, see Table 4 for an overview. However, in many cases these implementations leave the user alone with an uncritically reported “finally selected model” with coefficients, standard errors, confidence intervals, and p‐values that do not differ from those that would be computed for a predefined model. Usually, implementations do not make any account of the modeling decisions made to arrive at that final model. The reported quantities often overstate the true relationship of the selected variables with the outcome, which often results in conditional bias away from zero, and underestimated standard errors, widths of confidence intervals, and p‐values. Reporting a single final model generates the impression that selection or nonselection of an IV is a safe bet. This impression arises partly because no variance is reported for the nonselected variables, and partly because the reported standard errors of selected variables do not account for the selection uncertainty.

Table 4.

Implementations of variable selection methods and resampling‐based stability analysis in selected statistical softwares

	SAS procedures				SPSS	R packages and functions
Modeling techniques	PROC GLMSELECT	PROC REG	PROC LOGISTIC PROC PHREG	%ABE macro		lm(), glm(), survival	step()	mfp	glmulti	glmnet, penalized	rms
Backward	Yes	Yes	Yes	Yes	Yes	No	Yes	No	No	No	Yes
Forward	Yes	Yes	Yes	No	Yes	No	Yes	No	No	No	No
Stepwise forward	Yes	Yes	Yes	No	Yes	No	Yes	No	No	No	No
Stepwise backward	No	No	No	No	No	No	No	Yes	No	No	No
Best subset/other	Yes	Yes	Yes	No	—	No	No	No	Yes	No	No
Augmented backward	No	No	No	Yes	No	abe	—	—	—	—	—
LASSO	Yes	No	No	No	No	No	No	No	No	Yes	No
Multi‐model inference	(Yes)	No	No	No	No	No	No	No	Yes	No	(Yes)
Bootstrap stability investigation	Yes	No	No	(No)	No(!)	No	No	No	No	No	(Yes)
Linear	Yes	Yes	No	Yes	Yes	lm()	Yes	Yes	Yes	Yes	Yes
Logistic	No	No	Yes (LOGISTIC)	Yes	Yes	glm()	Yes	Yes	Yes	Yes	Yes
Cox	No	No	Yes (PHREG)	Yes	Yes	coxph()	Yes	Yes	?	Yes	Yes

With the recent advances in computing speed, there is no excuse for still refraining from including stability investigations using resampling methods in the default output of standard software implementations of variable selection algorithms. As a minimum, we would call for reporting the following quantities, cf. also Altman, McShane, Sauerbrei, & Taube (2012):

1. The EPV ratio, computed from the number of candidate variables, accompanied by a warning note if a user attempts to invoke variable selection if EPV is lower than 25.

2. The global model including all candidate variables with regression coefficients and standard errors. (See also REMARK guidelines, item 17, Altman et al., 2012).

3. Bootstrap inclusion frequencies for each candidate variable (not only the selected ones).

4. The RMSD of the bootstrapped regression coefficients compared to the regression coefficients of the global model is given by $RMSD({\beta }_j)=\sqrt{{\displaystyle \sum _b{({\widehat{\beta }}_{boot,j}^{(b)}-{\widehat{\beta }}_{global,j})}^2/n_{boot}}},j=1,\dots ,k$. We propose that software output should at least contain an “RMSD ratio,” which is the RMSD divided by the standard error of ${\widehat{\beta }}_{global,j}$.

5. Relative bias conditional on selection, computed as $[({\overline{\widehat{\beta }}}_{boot})/({\widehat{\beta }}_{global}·BIF)-1]\times 100\%$ with ${\overline{\widehat{\beta }}}_{boot}$, ${\widehat{\beta }}_{global}$ and BIF denoting the mean bootstrapped estimate, the global model estimate, and the bootstrap inclusion frequency of an IV, respectively.

6. The bootstrap model selection frequencies for the finally selected model and the most often selected models, for example the list of models with cumulative frequency of at least 80%, or the list of 20 top‐ranked models, whichever list is shorter.

7. A matrix with pairwise inclusion frequencies, which are suitably summarized, for example as odds ratios obtained by log‐linear analysis (see Royston & Sauerbrei, 2003) or as “significant” pairwise over‐ or underselection.

In the next section, we exemplify how these quantities may help the analyst in getting more insight in the variable selection mechanism and in interpreting the results of variable selection.

3.3. Application: Approximation of proportion body fat by simple anthropometry

Research question: “We would like to approximate the proportion of body fat by simple anthropometric measures”

Johnson's (1996) body fat study was intended as an educational data set to teach multivariable linear regression in the classroom. Nevertheless, the example has a relevant scientific question, namely the approximation of a costly measurement of body density (from which proportion of body fat can be derived with Siri's (1956) formula) by a combination of age, height, weight, and ten simple anthropometric circumference measures through multivariable linear regression. The data set, consisting of measurements on 252 men, appears at several places in the statistical model‐building literature, for example also in the books of Burnham and Anderson (2002) and of Royston and Sauerbrei (2008), and in several journal articles. The data set is available at https://ww2.amstat.org/publications/jse/v4n1/datasets.johnson.html. (In line with literature we removed one observation with implausible values, thus, the analysis set consists of 251 subjects). The interesting feature of the data set is that many of the anthropometric measures are intrinsically correlated: out of 13 IVs, there are two pairs of IVs (hip with weight, abdomen with chest) having Pearson correlation coefficients greater than 0.9, and a group of ten IVs with all pairwise correlation coefficients greater than 0.5 (forearm, biceps, wrist, neck, knee, hip, weight, thigh, abdomen, chest). These high correlations impose some challenges in model development and interpretation. In particular, interpretation of regression coefficients as adjusted effects in the global model, or, if variable selection is applied, interpretation of non‐selected variables as “nonpredictive” seems problematic.

We have analyzed this data set following the recommendations given above. $EP{V}_{global}$ amounts to 251 / 13 = 19.3. We consider abdomen and height as two central IVs for estimating body fat proportion, and will not subject these two to variable selection. In our prior assessment, we further believe that all other IVs may be strongly interrelated and exchangeable when used for body fat estimation. Therefore, we will subject them to BE with AIC as stopping criterion. This gives a model consisting of the IVs abdomen, height, wrist, age, neck, forearm, and chest (Table 5). The adjusted R ² only slightly increases from 73.99% in the global model to 74.16% in the selected model. The estimated shrinkage factor of the latter model is 0.983 and therefore additional post‐estimation shrinkage is not necessary. (We do not recommend parameterwise shrinkage factors for this data set because of the high correlations between the variables, see Dunkler et al., 2016). Bootstrap resampling indicates the instability of this model, as it was selected in only 1.9% of the resamples, and if models are ranked by their selection frequencies, it ranks only fourth (Table 6). However, a low bootstrap model frequency like this is not untypical in a biomedical data set. Variable selection adds to uncertainty about the regression coefficients, which is evidenced by RMSD ratios all above 1, except for knee (0.78) and for weight (0.95). By contrast, the model‐based standard errors in the selected model, which ignore the selection uncertainty, would wrongly suggest more precise estimates. Relative conditional bias quantifies how much variable‐selection‐induced bias one would have to expect if an IV is selected. This bias is negligible for height, abdomen, wrist, or age, all of which with bootstrap inclusion frequencies greater than 80%, but becomes more relevant in IVs for which selection is less sure. A sparse aggregate over the different models estimated in the bootstrap procedure could be obtained by the bootstrap medians, in this analysis it resembles the selected model. The coefficients of the selected IVs are very similar to the global model estimates, indicating no selection bias in the aggregated model. The 2.5th and 97.5th percentiles can be interpreted as limits of 95% confidence intervals obtained by resampling‐based multi‐model inference.

Table 5.

Body fat study: global model, model selected by backward elimination with a significance level of 0.157 (AIC selection), and some bootstrap‐derived quantities useful for assessing model uncertainty

	Global model			Selected model
Predictors	Estimate	Standard error	Bootstrap inclusion frequency (%)	Estimate	Standard error	RMSD ratio	Relative conditional bias (%)	Bootstrap median	Bootstrap 2.5th percentile	Bootstrap 97.5th percentile
(Intercept)	4.143	23.266	100 (fixed)	5.945	8.150	0.97		5.741	–49.064	50.429
height	–0.108	0.074	100 (fixed)	–0.130	0.047	1.02	+4.9	–0.116	–0.253	0.043
abdomen	0.897	0.091	100 (fixed)	0.875	0.065	1.05	–2.1	0.883	0.687	1.050
wrist	–1.838	0.529	97.6	–1.729	0.483	1.07	–1.6	–1.793	–2.789	–0.624
age	0.074	0.032	84.6	0.060	0.025	1.14	+4.2	0.069	0	0.130
neck	–0.398	0.234	62.9	–0.330	0.219	1.24	+30.3	–0.387	–0.825	0
forearm	0.276	0.206	54.0	0.365	0.192	1.14	+46.6	0.264	0	0.641
chest	–0.127	0.108	50.9	–0.135	0.088	1.14	+68.0	–0.055	–0.342	0
thigh	0.173	0.146	47.9			1.13	+64.4	0	0	0.471
biceps	0.175	0.170	43.1			1.15	+101.4	0	0	0.541
hip	–0.149	0.143	41.4			1.08	+85.3	0	–0.415	0
ankle	0.190	0.220	33.5			1.11	+82.2	0	–0.370	0.605
weight	–0.025	0.147	28.3			0.95	+272.3	0	–0.355	0.295
knee	–0.038	0.244	17.8			0.78	+113.0	0	–0.505	0.436

RMSD, root mean squared difference, see Section 3.2(iv).

Table 6.

Body fat study: model selection frequencies. Selected model is model 4

Model	Included predictors	Count	Percent	Cumulative percent
1	Height abdomen wrist age chest biceps	32	3.2	3.2
2	Height abdomen wrist age neck forearm thigh hip	29	2.9	6.1
3	Height abdomen wrist age forearm chest	19	1.9	8.0
4	Height abdomen wrist age neck forearm chest	19	1.9	9.9
5	Height abdomen wrist age neck forearm chest thigh hip	19	1.9	11.8
6	Height abdomen wrist age neck chest biceps	18	1.8	13.6
7	Height abdomen wrist age neck thigh biceps hip	16	1.6	15.2
8	Height abdomen wrist age neck forearm	15	1.5	16.7
9	Height abdomen wrist age neck biceps	15	1.5	18.2
10	Height abdomen wrist age neck forearm chest biceps	14	1.4	19.6
11	Height abdomen wrist age neck forearm chest ankle	12	1.2	20.8
12	Height abdomen wrist age neck forearm chest thigh hip ankle	12	1.2	22.0
13	Height abdomen wrist age neck forearm thigh	10	1.0	23.0
14	Height abdomen wrist age neck forearm biceps	10	1.0	24.0
15	Height abdomen wrist age forearm chest ankle	10	1.0	25.0
16	Height abdomen wrist age neck forearm thigh hip knee	10	1.0	26.0
17	Height abdomen wrist age neck thigh hip	9	0.9	26.9
18	Height abdomen wrist age chest biceps ankle	9	0.9	27.8
19	Height abdomen wrist age neck thigh hip ankle	9	0.9	28.7
20	Height abdomen wrist age chest	8	0.8	29.5

Table 6 shows model selection frequencies. The highest selection frequency is only 3.2% and is obtained for the model including height, abdomen, wrist, age, chest, and biceps. Notably, this is not the final model from the original data set and there are many competing models with similar selection frequencies. The model suggested by the bootstrap medians is the same as the selected model; however, for neck and forearm the bootstrap medians are clearly closer to zero than in the selected model.

Pairwise inclusion frequencies inform about “rope teams” and “competitors” among the IVs (Supporting Information Table S2). For example, thigh and biceps were both selected in only 14.3% of the resamples, while one would expect a frequency of 19.8% ( = 47.9% × 43.1%) given independent selection. Therefore, the pair is flagged with “‐” in the lower triangle of Supporting Information Table S1. Thigh and hip are flagged with “+” because they are simultaneously selected in 28.7% of the resamples, while the expectation under independency is only 19.8%. In this table, we used significance of a χ² test at the 0.01 level as the formal criterion for the flags. Interestingly, age forms a “rope team” with neck, forearm, chest, and thigh, but weight is a competitor to age.

Analyses of two further case studies can be found in the Supporting Information on the journal's web page.

4. OUTLOOK

We have explained underlying concepts and important consequences of variable selection methods that may still not be clear to many practitioners and software developers. Variable selection algorithms are available in any statistical software package, but stability investigations are still not part of those implementations (Table 4). Therefore, we have proposed some quantities to be routinely computed in standard software packages whenever a user requests to apply a variable selection algorithm. We have also exemplified how these quantities may help the analyst. We strongly believe that the practice of conducting and reporting variable selection will improve greatly if this request finds its way into routine.

We have focused on models in which effect estimates should be interpretable (in addition to pure prediction models where this is not the case), but we did not consider methods that were exclusively designed for confounder selection. Our “augmented backward elimination” algorithm that we introduced in Dunkler et al. (2014) may be particularly interesting for studies with that purpose. It gives the researcher more control on the role of the IVs in model building and often results in models that include more IVs than by BE, increasing the stability of those models. Augmented backward elimination is implemented in a SAS macro (Dunkler et al., 2014) and an R package (Blagus, 2017). We refer the interested reader to the former paper for further details on that method. De Luna, Waernbaum, and Richardson (2011), VanderWeele and Shpitser (2011) and Greenland and colleagues (Greenland et al., 1999; Greenland, 2008; Greenland and Pearce, 2015) suggested some other approaches for confounder selection.

Our review was written under the assumption that nonlinear relationships of continuous IVs with the outcome and interactions between IVs do not play a role. Both are important but also difficult topics requiring separate papers.

We have not covered more refined versions of penalized estimation such as the adaptive LASSO (Zou, 2006) or smoothly clipped absolute deviation (SCAD) (Fan & Li, 2001). Those methods were intended to reduce the false inclusion rates that were observed for the LASSO and improve its performances in situations where existence of a true data generating mechanism can be assumed. We have also not considered boosting (Bühlmann & Yu, 2003), random forests (Breiman, 2001b) or other machine learning techniques that may provide variable selection, mainly in the context of high‐dimensional data, that is when the number of IVs exceeds the effective sample size. In such cases these methods may still find a sparse set of IVs, for example genetic markers, predicting the outcome accurately, but the resulting models will hardly serve an explanatory purpose in the sense of Shmueli (2010). Incorporating biological background knowledge about genetic networks and pathways (Binder & Schumacher, 2009) and dimension reduction techniques may often greatly reduce the number of IVs to an order of magnitude comparable to the sample size (cf. Sokolov, Carlin, Paull, Baertsch, & Stuart, 2016, pp. 2–4). Regularization methods may then still be needed because of the failure of classical methods to deal with the high dimensionality, but resulting models will be more stable and better interpretable than those purely developed by data mining.

Variable selection methods have always been seen controversially. Users of statistical modeling software appreciate the built‐in automation to select the “relevant” effects, and often apply a reverse argument to conclude that nonselection of effects means that they are not relevant. By contrast, many experienced statisticians have warned for the instability issues and invalidated inference implied by datadependent model building. Obviously, evidence supported guidance is urgently needed. Topic group 2 “Selection of variables and functional forms in multivariable analysis” of the recently launched initiative “Strengthening Analytical Thinking for Observational Studies (STRATOS)” has started to work on it (Sauerbrei, Abrahamowicz, Altman, le Cessie, and Carpenter (2014); https://www.stratos-initiative.org, assessed November 10, 2017).

We have compiled the above recommendations believing that it needs both, a basic understanding of the possible model instabilities incurred by variable selection methods and the availability of software tools for routine use to assess and eventually correct this instability. If samples are not too small and if applied with care, variable selection methods may reduce the MSE of regression coefficients and predictions by separating irrelevant information from a model. As we have outlined above, statistical models can serve different purposes. In explanatory research, where effect estimation for one or a few IVs plays a central role, the starting point will usually be a set of IVs with assumed relationship with the outcome and those IVs of main interest. Variable selection methods may then be used to sort out irrelevant IVs in order to improve accuracy of the effect estimates of main interest (VanderWeele & Shpitser, 2011). In predictive research, variable selection may improve the accuracy of the predictions, but background knowledge can also be incorporated, going as far as updating the coefficients of an existing model with new data, and employing variable selection methods to assess that coefficients to update (Moons et al., 2012; Su, Jaki, Hickey, Buchan, & Sperrin, 2016). Descriptive models are perhaps the most frequent type of models estimated in life sciences, and here variable selection may help to obtain interpretable and practically applicable models. In all three cases, the exemplified stability investigations, readily available in the R package abe (Blagus, 2017), can be used to assess possible additional uncertainties induced.

CONFLICT OF INTEREST

The authors have declared no conflict of interest.

Supporting information

Supporting Material

Supporting Material

Heinze G, Wallisch C, Dunkler D. Variable selection – A review and recommendations for the practicing statistician. Biometrical Journal. 2018;60:431–449. https://doi.org/10.1002/bimj.201700067