Abstract
Deficiencies in the parameterizations of convection used in global climate models often lead to a distorted representation of the simulated rainfall intensity distribution (i.e., too much rainfall from weak rain rates). While encouraging improvements in high percentile rainfall intensity have been found as the horizontal resolution of the Community Atmosphere Model is increased to ∼25 km, we demonstrate no corresponding improvement in the moderate rain rates that generate the majority of accumulated rainfall. Using a statistical framework designed to emphasize links between precipitation intensity and accumulated rainfall beyond just the frequency distribution, we show that CAM cannot realistically simulate moderate rain rates, and cannot capture their intensification with climate change, even as resolution is increased. However, by separating the parameterized convective and large‐scale resolved contributions to total rainfall, we find that the intensity, geographic pattern, and climate change response of CAM's large‐scale rain rates are more consistent with observations (TRMM 3B42), superparameterization, and theoretical expectations, despite issues with parameterized convection. Increasing CAM's horizontal resolution does improve the representation of total rainfall intensity, but not due to changes in the intensity of large‐scale rain rates, which are surprisingly insensitive to horizontal resolution. Rather, improvements occur through an increase in the relative contribution of the large‐scale component to the total amount of accumulated rainfall. Analysis of sensitivities to convective timescale and entrainment rate confirm the importance of these parameters in the possible development of scale‐aware parameterizations, but also reveal unrecognized trade‐offs from the entanglement of precipitation frequency and total amount.
Keywords: climate change, extreme precipitation, rainfall intensity, large‐scale precipitation, convective precipitation, community atmosphere model, superparameterization
Key Points
The total amount of large‐scale rain is sensitive to horizontal resolution but the intensity is not
The distribution of large‐scale rain is more realistic than the weak parameterized rain in CAM
The large‐scale rain in CAM captures the climate change intensification simulated by SPCAM
1. Introduction
Many important characteristics of precipitation are expected to change in response to climate forcing, including the mean, frequency, intensity, and spatial pattern. Current global climate models (GCMs) are able to capture expected global mean changes with some confidence (Allen & Ingram, 2002; Pendergrass & Hartmann, 2014a), and there is evidence that the multimodel mean follows the expected Clausius‐Clapeyron scaling (∼7% °C−1) of extremes on global scales (O'Gorman, 2015; Pendergrass & Hartmann, 2014c). However, regional intensity changes are much less certain, especially over the tropics where the 99.9th percentile changes range from almost 0 to over 30% °C−1 across CMIP5 models, while observational constraints suggest the value should be close to 11% °C−1 (O'Gorman, 2015). Recent work has shown that not only are extreme rates uncertain in the tropics, but frequent moderate rates that produce the majority of accumulated surface rainfall also have major biases. In conventionally parameterized versions of the Community Atmosphere Model (CAM), moderate rates represented by the mode (i.e., the rain rate range associated with the most accumulated rainfall) and median (i.e., the rain rate where half the accumulated rainfall comes from more/less intense rates) of the rainfall amount distribution are significantly weaker than observed, particularly in regions of organized convection associated with the Madden Julian Oscillation (MJO), tropical waves, and monsoons (Kooperman et al., 2016a). Likewise, conventional versions of CAM simulate a much weaker response of moderate rates to climate forcing relative to superparameterized versions that represent convection with embedded cloud resolving models (Kooperman et al., 2016b).
Some recent studies have found an improvement in the representation of rainfall intensity, particularly high percentile rates, when the horizontal resolution is increased (e.g., approximately 0.25°, Kopparla et al., 2013; O'Brien et al., 2016). However, these improvements are limited to middle and high‐latitude regions where the fractional contribution of resolved large‐scale processes to total rainfall increases most with resolution. At higher latitudes, the synoptic‐scale frontal systems that generate the majority of rainfall are better resolved at 0.25° resolution, but in the tropics the organized mesoscale systems that generate the majority of rainfall are not resolved until grids reach kilometer scales. Dai (2006) compared the fractional contribution of simulated large‐scale and convective rain to observational estimates, and found that models underestimate both the large‐scale fraction and rainfall intensity in the tropics. On the other hand, increases in the contribution of large‐scale rain have also been shown to distort the representation of extreme events. Wehner et al. (2014) found that an over simulation of extreme rainfall in warm wet regions is associated with large‐scale processes, which they hypothesize results from the use of a fixed 1 h convective timescale in high‐resolution simulations with shorter model time steps (e.g., 15 min) that over‐stabilize the atmosphere and allow the development of saturated large‐scale instabilities. These events, sometimes referred to as grid‐point storms (Held et al., 2007), result from resolved‐scale overturning of entire grid cells, and are associated with an extreme mode climate change response in some models (Pendergrass & Hartmann, 2014c).
Several recent studies have assessed the impacts of parameter settings, including the convective timescale, on mean‐state climate biases, and precipitation statistics (Gustafson et al., 2014; Ma et al., 2014; Qian et al., 2015; Williamson, 2013). Qian et al. (2015) and Williamson (2013) both found that increasing the convective timescale leads to more intense precipitation associated with large‐scale resolved processes due to a suppression of the deep convective parameterization leaving the model dynamics to remove moist instability at the grid‐scale. Qian et al. (2015) also found that increasing the magnitude of the entrainment rate similarly suppresses the convective parameterization and increases the variance of extreme precipitation. Gustafson et al. (2014) tested a range of convective timescale values and found tradeoffs for different precipitation statistics, with longer timescales improving the intensity and diurnal cycle rainfall over the Central United States at the expense of worsening the mean‐state precipitation biases.
Both resolution (e.g., O'Brien et al., 2016) and perturbed parameter (e.g., Williamson 2013) sensitivity experiments have previously demonstrated that the partitioning of convective and large‐scale precipitation influences the representation of total precipitation intensity. However, analysis of the convective and large‐scale precipitation rates in these studies has been presented in a way that convolves changes in the intensity and mean amount of precipitation. By only examining changes in the frequency distribution, these studies were limited by an inability to discriminate changes in the intensity of precipitation rates from changes in relative contributions of large‐scale versus convective components to the total amount of precipitation. For example, if large‐scale precipitation tends to be associated with more extreme rain rates, then total rain rates can become more intense by either shifting the intensity of large‐scale rates or by increasing the relative contribution of large‐scale rain to the total amount. In this study, we will present a new methodology for decomposing precipitation distributions in a way that clearly discriminates these two effects and thus, adds to what has previously been highlighted in perturbed parameter sensitivities of deep convection.
Our analysis is also complementary in its focus on moderate rain rates. The influence of large‐scale versus convective processes on precipitation intensity has primarily focused on mean contributions and extreme rates, but the impact of resolved‐scale processes on moderate rain rates (i.e., amount mode and median rates) is also important because these rates generate the majority of accumulated precipitation. In this study, we explore the contribution of parameterized and resolved‐scale processes to total rainfall rates, their sensitivity to horizontal resolution and parameter settings, and their response to climate change across the entire distribution in the Community Atmosphere Model (CAM). We focus on the representation of moderate rain rates that generate the majority of accumulated rainfall and evaluate CAM results against observations and superparameterized CAM (SPCAM). We demonstrate several interesting properties of the isolated large‐scale component of CAM's rainfall that emerge when it is analyzed statistically in a way that clarifies contributions to total accumulated rainfall by moderate rates. The models, observations, and methods used are described in section 2, followed by an overview of the results in section 3, and conclusions in section 4.
2. Background
2.1. Models and Simulations
Our primary analysis focuses on results from the Community Climate System Model version 4 (CCSM4), a coupled GCM with interactive atmospheric (i.e., Community Atmosphere Model 4; Neale et al., 2010), land (i.e., Community Land Model 4; Lawrence et al., 2011), ocean (i.e., Parallel Ocean Program 2; Smith et al., 2010), and sea‐ice (i.e., Community Ice CodE 4; Hunke & Lipscomb, 2008) components. The atmospheric component was run with both conventional convective parameterization (CAM) and superparameterization (SPCAM), which are described in more detail below. For a general description of conventional and superparameterized versions of the fully coupled CCSM4, see Gent et al. (2011) and Stan and Xu (2014), respectively.
In the conventional version of CAM, subgrid deep convection is represented by an ensemble of convective updraft plumes that deplete convective available potential energy at a fixed timescale (Zhang & McFarlane, 1995). In version 4, this scheme includes entrainment mixing (Raymond & Blyth, 1992) and vertical transport of horizontal momentum (Richter & Rasch, 2008). The shallow convective scheme solves vertical mass flux iteratively from the bottom to top layers of the model to remove thermal instabilities and adjust the energy and moisture budget equations (Hack, 1994; Neale et al., 2010). In CAM, rainfall is generated by both the convective parameterizations and prognostic cloud processes, which control the conversion of cloud condensate to precipitation as a function of resolved large‐scale forcing (Rasch & Kristjansson, 1998; Zhang et al., 2003). For more details see Neale et al. (2010).
In the superparameterized version (i.e., SPCAM), parameterizations of convection and boundary layer processes are replaced with simplified (two‐dimensional and laterally periodic) cloud resolving models (CRMs) using kilometer‐scale horizontal resolution, which are embedded within each grid column of the conventional CAM (Randall et al., 2003). The CRMs are forced by large‐scale conditions resolved on the GCM grid and return convective (i.e., energy and moisture) tendencies as a CRM mean response (Benedict & Randall, 2009). The approach is at least an order of magnitude more computationally expensive than CAM but readily affordable today. In SPCAM, all rainfall is generated by CRM resolved processes, which treat deep, shallow, and nonconvecting conditions in a unified framework. For more details, see Khairoutdinov and Randall (2001).
In this study, we analyze results from three sets of complementary simulations: (1) the present‐day and future climates represented by the Representative Concentration Pathway 8.5 (RCP8.5) emissions scenario, (2) the present‐day climate simulated at conventional (∼1° or 110 km) and high (∼0.25° or 28 km) resolutions, and (3) the present‐day climate represented across a range of perturbed physics parameter settings. Since these simulations are computationally intensive, particularly high‐resolution and superparameterization members, we have based our analysis on a synthesis of preexisting simulations that were originally run for independent experiments and are available through public archives. As a result, there is some variation in the exact model version and configuration of CAM. While this in some ways limits their direct intercomparison, the simulations within each experiment sensitivity suite are internally consistent with each other, and we limit our focus to results that are robust across all of the experiments despite differences in configuration and model version. Each experiment subset is described in more detail below.
2.1.1. Present‐Day and Climate Change Experiment Analysis
For the primary analysis in this study, both CAM and SPCAM were configured with a finite volume dynamical core at 0.9° × 1.25° horizontal resolution with 30 vertical levels, and the CRM in SPCAM was configured with 32 3 km resolution columns oriented in the zonal direction. The simulations were run for the 21st century forced by the RCP8.5 emissions scenario (Taylor et al., 2012). An overview of results from these simulations is given by Meehl et al. (2012) and Stan and Xu (2014) for CAM and SPCAM, respectively. For the results presented below, present‐day conditions are represented by the first 10 years (2006–2015) and future (end of century) conditions are represented by the last 10 years (2091–2100) of the simulations.
2.1.2. Horizontal Resolution Sensitivity Experiment Analysis
To explore the sensitivity to horizontal resolution, we evaluate two additional sets of simulations using CAM version 5 with the spectral element atmospheric dynamical core run at both 110 km (i.e., approximate resolution of CAM and SPCAM simulations described above) and 28 km horizontal resolutions. These simulations were run with the Community Earth System Model (CESM1, successor of CCSM4) as atmosphere‐only (i.e., prescribed sea‐surface temperature and sea‐ice configuration) for 5 day hindcasts of present‐day conditions (2005–2009) initialized from Climate Forecast System v2 (Saha et al., 2010). Both resolutions used a model physics time step of 15 min and a deep convective timescale of 60 min. Here, we evaluate only day five of the hindcasts, interpolated to a common 2° horizontal grid for both resolutions. For more details on model configuration and interpolation, see O'Brien et al. (2016).
2.1.3. Perturbed Parameter Sensitivity Experiment Analysis
To explore the impact of perturbed physics parameter changes (Table 1) on amount distributions of convective and large‐scale precipitation, we also evaluate output from a wide ensemble of simulations generated from CESM1 run with a finite volume dynamical core at 0.9° × 1.25° horizontal resolution (i.e., as in CCSM4/SPCCSM4). This experiment was originally designed to explore the sensitivity of changes in extremes to parameter perturbations, to be described more thoroughly in a forthcoming manuscript. Briefly, the experiment consists of a control set of simulations containing ∼50 groups, each of which adopts a set of parameter values drawn from a Latin hypercube design methodology described by Williamson (2015). Each group therefore represents a point in parameter space, and itself consists of 28 or more initial condition simulations spanning the years 2011–2013; composites across all ensemble members are used in our analysis. All control simulations use observed, time‐varying sea surface temperatures (SSTs), sea ice, greenhouse gas concentrations, aerosol concentrations, insolation, and landcover, following the Climate of the 20th Century + protocol described by Stone et al. (2018). The experiment varies a set of seven parameters that have been identified in the literature to have a large influence on mean climate, precipitation, and extremes (e.g., Qian et al., 2015).
Table 1.
Parameters, Default Values, and Ranges Perturbed Used in the Perturbed Parameter Ensemble Simulation Design
| Parameter | Description | Lower bound | Default value | Upper bound | Physics scheme |
|---|---|---|---|---|---|
| tau | Timescale for consumption rate of deep CAPE | 1,800 s | 3,600 s | 9,000 s | ZM deep convection |
| dmpdz | Parcel fractional mass entrainment rate | −2.0 × 10−3 | −1.0 × 10−3 | −0.2 × 10−3 | ZM deep convection |
| c0_lnd | Deep convection precipitation efficiency over land | 0 | 5.9 × 10−3 | 0.01 | ZM deep convection |
| ke | Evaporation efficiency of precipitation | 0.1 × 10−6 | 1.0 × 10−6 | 10.0 × 10−6 | ZM deep convection |
| rhminl | Minimum relative humidity for low stable clouds | 0.8 | 0.8875 | 0.99 | Cloud fraction |
| criqc | Maximum updraft condensate | 0.50 | 0.70 | 1.5 | UW shallow convection |
| kevp | Evaporation efficiency | 1.0 × 10−6 | 2.0 × 10−6 | 20.0 × 10−6 | UW shallow convection |
2.2. Observations
To evaluate the present‐day representation of rainfall intensity, we include observations from two products that have been used extensively in previous model evaluation, the Global Precipitation Climatology Project One‐Degree Daily (GPCP 1DD) (Huffman et al., 2001, 2012a) and the Tropical Rainfall Measuring Mission 3B42 version 7 (TRMM 3B42; Huffman et al., 2007, 2012b). GPCP 1DD is a daily estimate of accumulated precipitation on a 1° global grid, based on infrared (IR) measurements calibrated to monthly Special Sensor Microwave Imager and GPCP version 2 satellite‐gauge precipitation data (Huffman et al., 2001). TRMM 3B42 is a 3 hourly estimate of instantaneous precipitation on a 0.25° grid from 50°S to 50°N, which combines visible, IR, and microwave radiometer measurements from the TRMM satellite calibrated to monthly Global Precipitation Climatology Center rain gauge data (Huffman et al., 2007); 3 hourly estimates have been averaged to form a daily mean time series for this study. For many high‐order statistics, including the intensity of moderate rain rates evaluated here, these two data products differ significantly. Many studies evaluating rainfall intensity statistics have found the TRMM 3B42 daily rate estimates to be more reliable than GPCP 1DD (Behrangi et al., 2012; Dinku et al., 2011; Liu & Allan, 2012; Tan et al., 2015), but we include both products here to provide a range of observational estimates and global coverage outside the TRMM region. These data products are used in the present‐day comparison in section 3.1 and have been regridded to the horizontal resolution of the model (0.9° × 1.25°) using an area‐conserving interpolation scheme.
2.3. Methods
In this study, we focus on an important characteristic of the daily rainfall amount distribution, its peak or “amount mode”—the rain rate associated with the most accumulated rainfall. The amount distribution calculated here is based on discrete histograms formed using logarithmically spaced rainfall rate bins, as described in Pendergrass and Hartmann (2014b) and Kooperman et al. (2016a). The bin structure covers 4 orders of magnitude (i.e., 0.1 to 1,000 mm d−1) with bin center values 10 times larger than their widths (i.e., ΔR/R = 0.1, where R is rain rate bin center value) and a dry day threshold of 0.1 mm d−1. The amount distribution graphically depicts how much accumulated surface rainfall is generated by different rain rates, where the area under the distribution is the total mean rainfall in units of mm d−1, when multiplied by ΔlnR (or ΔR/R). Including this scaling term in equation (1) (i.e., ΔlnR −1), which has units of mm d−1/mm d−1 (i.e., unitless), produces a distribution that is independent of arbitrary bin spacing. The amount distribution ( ) is calculated at the grid‐point level before area‐weighted averaging over regions of interest and is given by:
| (1) |
where is the daily rainfall rate, is the bin index, is the bin center with edges and , I is a binary operator (i.e., zero or one depending on whether the precipitation rate falls within a given bin or not), is the total number of days, and bin width . It is useful to note that this is approximately proportional to the integrand for the first moment of the probability distribution fi of rainfall: .
The rainfall amount mode is the peak in the amount distribution, and is thus, associated with the rate that produces the most accumulated surface rainfall. A rightward shift of the amount mode in response to climate change suggests that not only will infrequent extreme events become more intense, but frequent moderate events will also become more intense (Kooperman et al., 2016b). Evaluating the mode geographically shows that the regions associated with organized convection (e.g., the MJO, monsoons, and tropical waves) have the heaviest rates (Kooperman et al., 2016a). However, assessing the mode spatially, as well as changes in response to climate forcing, can be difficult because it is based on discrete logarithmic bins that can be under sampled in regions with little rainfall and is undefined for negative changes. Therefore, for geographic assessment, we focus on the “amount median” (i.e., the rate associated with 50% of accumulated rainfall), a complementary statistic of moderate rain that is calculated independently of the bin structure.
We further deconstruct the total amount distribution simulated by CAM into contributions from parameterized convective and resolved large‐scale processes in order to unfold their influence on rain rates across the distribution. The amount distributions for total (pT), convective (pC), and large‐scale (pL) precipitation contributions, respectively, are given by:
| (2) |
| (3) |
| (4) |
where rT is the total precipitation rate, rC is the convective precipitation rate, and rL is the large‐scale precipitation rate. Here, we are interested in the contribution of convective and large‐scale processes to the total rainfall rates, not simply the rates produced by these processes alone. Therefore, the total rain rates are used to determine histogram bin assignment for each day and grid‐point (i.e., rT is used within the binary operator I for equations (2)–(4)), and the associated convective (rC) and large‐scale (rL) rates are summed to calculate their accumulated contribution for each bin. Thus, for each bin, the convective (pC) plus large‐scale (pL) contribution is equal to the total (pT) accumulated amount, the fractional contribution of convective and large‐scale precipitation is equal to pC/pT and pL/pT, respectively, and each component has an independent calculation of the amount mode. The amount median is calculated in a similar way, where the median rate for convective and large‐scale rainfall is the rain rate from total precipitation that is associated with 50% of the convective and large‐scale rainfall, respectively.
For horizontal resolution analysis (section 3.2), partitioning of the amount distribution is calculated in the same way, but additional steps are applied to evaluate partitioning of the frequency distribution and extreme percentile rates. Previous studies have calculated frequency distributions from independent time series of convective and large‐scale rain (e.g. O'Brien et al., 2016), which naturally yields distributions that are weaker than that of total rain, since the total precipitation rate is equal to the convective plus large‐scale rate. Thus, these distributions do not accurately reflect their contribution to the intensity of total rainfall rates but, are more a function of the relative amount of rain they contribute. Partitioned frequency distributions conditioned on total rainfall rates cannot be calculated directly from independent time series because an event either occurs (1) or does not occur (0). However, the relationship between frequency and amount distributions (i.e., the amount distribution is equal to the frequency distribution multiplied by the bin center values RC) can be exploited to calculate an effective frequency distribution (f), the cumulative inverse of which is an effective percentile rate distribution (F):
| (5) |
| (6) |
where the 99th percentile rain rate is the value of R interpolated to F = 0.99. We call these effective distributions because they are based indirectly on the amount distribution rather than a direct independent calculation of the frequency histogram. In the case of partitioning, the convective and large‐scale amount distributions are first scaled to equal the amount of rain in the total amount distribution (see Section 3.2. for more details), then the frequency distribution is calculated using equation (5). This scaling is achieved by simply multiplying the convective and large‐scale distributions by the total mean precipitation divided by the convective and large‐scale mean precipitation, respectively. To calculate the percentile rates, the dry day frequency bin (i.e., rates less than 0.1 mm d−1) is first increased so that the integral of the distribution equals one, then the cumulative distribution is calculated using equation (6). For more details on the relationship between these distributions, see Kooperman et al. (2016a).
3. Results and Discussion
3.1. Present‐Day Comparison
Distributions of total rainfall as a function of rain rate and latitude are shown in Figure 1 for TRMM 3B42 (grey), GPCP 1DD (black), SPCAM (green), and CAM (purple). For CAM, the convective (red) and large‐scale (blue) distributions are also shown along with their relative fractional contribution to total rainfall (i.e., bottom subplots). The majority of global rain in CAM is produced by parameterized convection (1.7 mm d−1) relative to large‐scale processes (1.3 mm d−1), with the largest differences in the tropics (3.8 versus 1.1 mm d−1). Globally, SPCAM and CAM have similar mean rainfall values that are slightly higher than observational estimates (i.e., 2.7, 3.0, and 2.9 mm d−1 in GPCP 1DD, CAM, and SPCAM, respectively).
Figure 1.
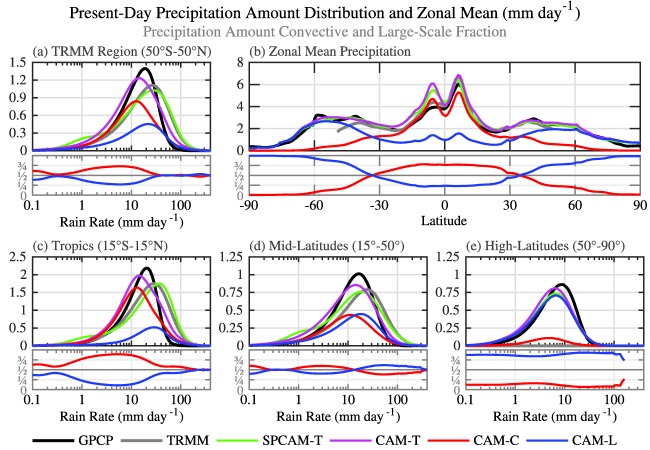
Annual precipitation amount distributions from (a) 50°S to 50°N (c) 15°S to 15°N, (d) 15° to 50°, (e) 50° to 90°, and (b) zonal mean precipitation of present‐day daily rates for GPCP 1DD (black), TRMM 3B42 (grey), SPCAM total (T, green), CAM total (T, purple), CAM convective (C, red), and CAM large‐scale (L, blue) contributions; lower subplots show fractional contributions of convective and large‐scale precipitation to total precipitation. The units for all plots are mm d−1 (as given in the figure title), however the amount distributions are scaled by ΔlnR−1, where ΔlnR = ΔR/R, which has units of mm d−1/mm d−1 and is thus a unitless scaling term.
As discussed above and in detail in Kooperman et al. (2016a), distributions from the two observational products are very different from each other. In general, GPCP 1DD is considerably weaker than TRMM 3B42 and SPCAM, especially for the peak in the amount distribution. For most of the discussion here, we focus on TRMM 3B42 results, which span 50°S–50°N, since GPCP 1DD likely misses the intensity of rain rates on daily timescales.
Over the TRMM region, the amount distribution in CAM is significantly weaker than observed and simulated by SPCAM, primarily due to the convective contribution, which controls the peak (i.e., amount mode) of the total distribution (Figure 1a). However, the large‐scale rainfall distribution in CAM contributes to more intense rates and its mode is a good match to TRMM 3B42 and SPCAM. For rates above ∼30 mm d−1, large‐scale and convective processes contribute nearly the same fraction of accumulated rainfall. This threshold is also seen in lower resolution (i.e., 1.9° × 2.5°) versions of CAM (not shown), and found in other studies (Li et al., 2011). Geographically, resolved processes produce the most rain poleward of 30° (Figure 1b, blue line), where large‐scale frontal systems drive the majority of precipitation. Convective parameterization produces the most rainfall at low‐latitudes, where local forcing in CAM drives precipitation processes. This pattern of increasing large‐scale contribution with higher latitudes can be seen in the regional distributions as well, which separate Figure 1a into contributions from the (c) tropics, (d) subtropics and midlatitudes, and (e) high‐latitudes (note that the y axis range is twice as large for the tropics). From the fractional plots in the bottom subplots, it is clear that large‐scale processes (blue lines) dominate high‐latitudes and parameterized convection (red lines) plays a larger role transitioning to the tropics across all rates.
Analysis of the large‐scale component of the amount distribution in CAM (Figure 1, blue lines) reveals a surprising fact—despite issues with its parameterized rainfall, the location, and peak of CAM's large‐scale rainfall distribution realistically tracks the TRMM 3B42 and SPCAM distributions. This can be seen in each region but is most significant in the tropics, where the total rainfall amount mode in CAM is biased 2–3 times low relative to TRMM 3B42 and SPCAM, but the large‐scale mode is amazingly unbiased (∼29 mm d−1 for both CAM large‐scale and TRMM 3B42).
To evaluate if the geographic pattern of large‐scale moderate rainfall rates in CAM is likewise realistic, Figure 2 shows the simulated median rain rate pattern. Equatorward of 30°, the median of total rainfall is biased low in CAM (Figure 2d) and fails to highlight key maximum activity centers that are associated with tropical waves (e.g., West Africa), monsoons (e.g., South Asia), the Madden Julian Oscillation (MJO; e.g., northwestern tropical Pacific and Indian Ocean), and the Inter‐Tropical Convergence Zone. Total rainfall in CAM also has a stronger land‐sea contrast in some regions (e.g., east coast of the United States versus West Atlantic Ocean), resulting from too little continental rainfall. These features tend to dominate rain amount median maps in SPCAM and TRMM 3B42 (Figures 2a and 2c). Kooperman et al. (2016a) pointed out that the mismatch between plots 2c and 2d emphasizes a deficiency of rainfall intensity in standard CAM that is especially clear in analyses of the rain amount mode/median.
Figure 2.
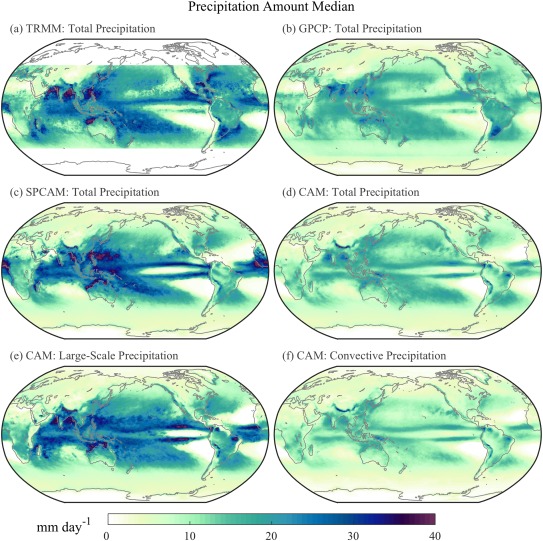
Present‐day annual precipitation amount median for (a) TRMM 3B42 total, (b) GPCP 1DD total, (c) SPCAM total, (d) CAM total, (e) CAM large‐scale, and (f) CAM convective contributions; Plots (a)–(d) were previously published in Kooperman et al. (2016a).
Surprisingly, the large‐scale component of tropical precipitation does not suffer from many of the above issues when it is isolated in CAM (Figure 2e). The amount median low bias is remedied, and missing regional activity centers emerge, suggesting the essence of an appropriate modulation of moderate rainfall intensity is captured, if hidden, in CAM. This is especially true off‐equatorially and in monsoon regions; activity centers along the equator in the Western Tropical Pacific and in the SPCZ are still missing. However, the median pattern from parameterized convection is much weaker everywhere, and since it dominates total rainfall production in the tropics, median rates from total rainfall are also much weaker than SPCAM and TRMM 3B42.
Overall, large‐scale processes contribute the most rainfall at high‐latitudes and to heavier rates. Despite the fact that the total accumulated rainfall in the tropics is primarily produced by parameterized convection in CAM, large‐scale rain makes a significant contribution to events that produce the heavier rates. Interestingly, the rain rates that deliver the most accumulated large‐scale tropical rain in CAM are an excellent match to observations and superparameterized simulations, suggesting that the underlying mechanisms linking resolved convection to rainfall intensity may be present in CAM. In the next section, we investigate whether these features of the amount distribution that we have identified with low resolution are also found with higher resolution.
3.2. Horizontal Resolution Sensitivity
Figure 3 depicts the same set of distributions shown in Figure 1, but here comparing the 110 and 28 km configurations in hindcast simulations. The most striking result of this analysis is the stationarity of the amount mode rate, which is almost identical in both resolutions for total, convective, and large‐scale precipitation. The difference between resolutions is not so much due to the intensity of rates produced by large‐scale processes, but rather the relative contribution to the total amount of rain (area under the curve), which increases as a function of resolution. Although many previous studies have suggested that large‐scale precipitation becomes more intense and realistic with higher resolution (e.g., Kopparla et al., 2013; O'Brien et al., 2016), this analysis demonstrates that the intensity actually remains mostly unchanged (i.e., location and shape of large‐scale distributions in all regions are the same in both resolutions), and the amplitude of the distribution simply increases with resolution. When combined in the total precipitation distribution, the larger contribution from resolved processes enhances the right tail, which leads to more realistic extremes. This effect is seen over a large area between 50°S and 50°N and for rain rates greater than ∼1 mm d−1 (Figure 3a). In the tropics, the total amount of large‐scale rain is still smaller than parameterized convection, even at high resolution, so the total amount mode remains weak. Also, the separation of large‐scale and convection processes produces a right shoulder at 30–50 mm d−1 in the total distribution that is not seen in the observations or SPCAM.
Figure 3.
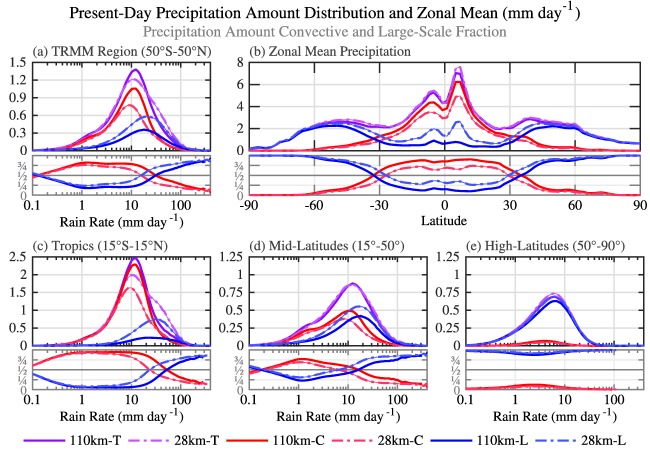
Annual precipitation amount distributions from (a) 50°S to 50°N (c) 15°S to 15°N, (d) 15° to 50°, (e) 50° to 90°, and (b) zonal mean precipitation of present‐day daily rates for CAM at 110 km (dark‐solid) and 28 km (light‐dashed) horizontal resolutions of total (T, purple), convective (C, red), and large‐scale (L, blue) contributions; lower subplots show fractional contributions of convective and large‐scale precipitation to total precipitation. The units for all plots are mm d−1 (as given in the figure title), however the amount distributions are scaled by ΔlnR−1, where ΔlnR = ΔR/R, which has units of mm d−1/mm d−1 and is thus a unitless scaling term.
As discussed in the methods section above, our “effective” percentile rain rate distributions are formed from a series of steps: (1) scaling the convective and large‐scale distributions to match the amount of total rainfall (i.e., multiplying by the ratio of total mean precipitation to convective and large‐scale mean precipitation, Figures 4c and 4d), (2) dividing by the central rain rate of each bin (Figure 4b), and (3) forming a cumulative sum (Figure 4f). This demonstrates that the effective extreme rates associated with convective and large‐scale rainfall are mostly insensitive to changes in resolution. That is, large‐scale resolved processes contribute to more extreme rates regardless of resolution, but with higher resolution they produce enough rain to have a larger impact on the total rainfall rates. The rainfall rates that both convective and large‐scale processes produce seems to be mostly fixed and do not change much with resolution. This resolution‐independent behavior also extends to the geographic distribution of the amount median shown in Figure 5. The median from convective precipitation is weak in both resolutions relative to the large‐scale median, particularly in the tropics over monsoon regions and the ITCZ. This implies that aspects of the processes generating rainfall in these regions may be partially resolved even at low resolution. To investigate what controls this fixed behavior in the model, we next explore the sensitivities to parameter settings in perturbed parameter ensembles of simulations varying seven parameters that have been shown previously to impact the representation of precipitation in CAM.
Figure 4.
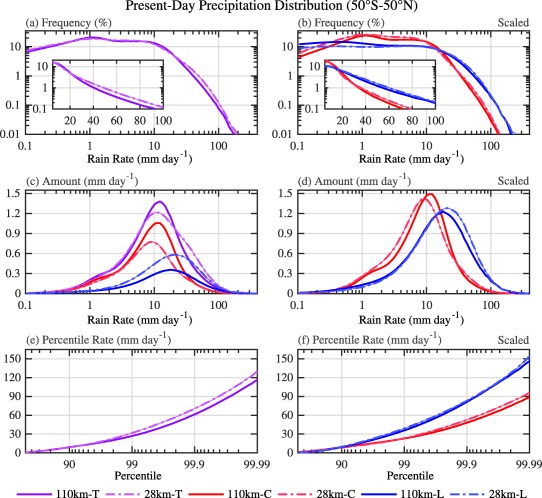
Annual precipitation (a, b) frequency, (c, d) amount, and (e, f) percentile distributions from 50°S to 50°N of present‐day daily rates for CAM at 110 km (dark‐solid) and 28 km (light‐dashed) horizontal resolutions of total (T, purple), convective (C, red), and large‐scale (L, blue) contributions; Figures 4b, 4d, 4f are distributions based on scaling the convective and large‐scale contributions to match the total precipitation amount as described in the text; small plots in Figures 4a, 4b are frequency distributions shown on a linear x axis. The units of the amount distributions Figures 4c, 4d are shown as mm d−1 (as given in the figure title), however they are scaled by ΔlnR−1, where ΔlnR = ΔR/R, which has units of mm d−1/mm d−1 and is thus a unitless scaling term.
Figure 5.
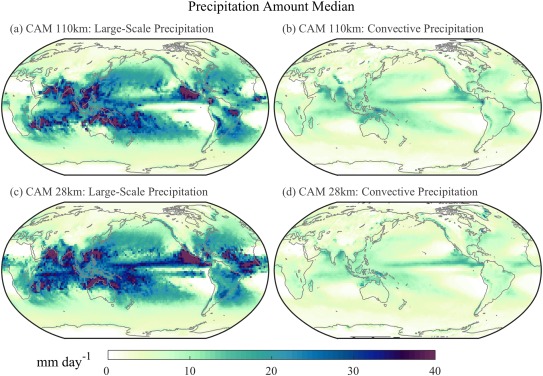
Present‐day annual precipitation amount median for CAM at (a, b) 110 km and (c, d) 28 km horizontal resolutions of (a, c) large‐scale and (b, d) convective contributions.
3.3. Perturbed Parameter Sensitivity
Since we have argued that the partitioning of total rainfall between convective and large‐scale components is important to the representation of precipitation intensity, we begin our analysis of the perturbed parameter experiment by regressing each parameter in Table 1 against the annual mean large‐scale precipitation fraction averaged over 50°S–50°N. This simple analysis turns out to be quite revealing and identifies two correlations that stand out in the seven parameters that have been varied for this experiment (Figures 6a and 6b), though it is worth noting that future assessments based on more sophisticated multiple regression methods may be useful for identifying additional sensitivities. Similar to Qian et al. (2015), we find that the convective timescale (tau, R = 0.57) and parcel mass entrainment rate (dmpdz, R = −0.55) are the most highly correlated parameters. The next highest correlation is for the evaporation efficiency of precipitation (ke, R = 0.35), followed by correlations of less than 0.1. Regressions of these parameters (i.e., tau and dmpdz) against the large‐scale mean precipitation fraction, shown in Figures 6a, 6b, 7a, and 7b, demonstrate the variability associated with perturbing the values across all seven parameters (blue stars). When the range of entrainment rate values are constrained (red dots), most of the variability in the regression against the convective timescale is removed (Figure 6a) and the correlation in the subset of simulations increases to R = 0.91. Likewise, when the convective timescales are constrained, most of the variability in the regression against the entrainment rate is removed (Figure 7b) and the correlation in the subset of simulations increases to R = −0.94, confirming that these two parameters play an important role in governing the representation of precipitation intensity.
Figure 6.
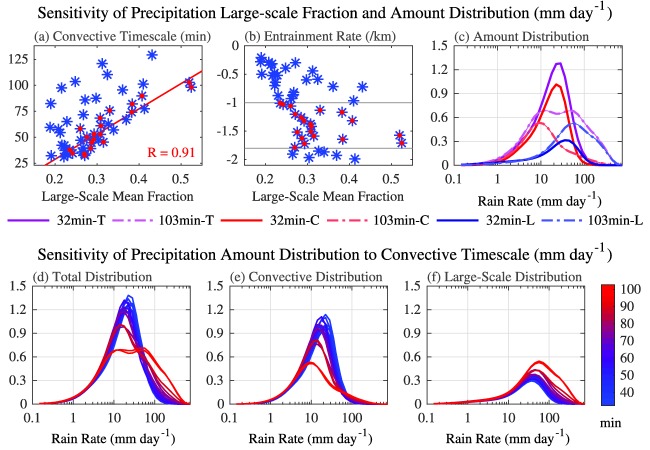
Large‐scale fraction of annual mean precipitation from 50°S to 50°N regressed against the (a) convective timescale and (b) entrainment rate for the CAM perturbed parameter ensemble of simulations; blue stars are all simulations and red dots are a subset within a range of entrainment rate values from −1.8 to −1 km−1; (c) annual precipitation amount distributions for simulations with 32 min (dark‐solid) and 103 min (light‐dashed) convective timescales (i.e., the end members of the subset simulations) of total (T, purple), convective (C, red), and large‐scale (L, blue) contributions; and annual precipitation amount distributions of (d) total, (e) convective, (f) and large‐scale contributions from the subset simulations. The units of the amount distributions are shown as mm d−1 (as given in the figure title), however they are scaled by ΔlnR−1, where ΔlnR = ΔR/R, which has units of mm d−1/mm d−1 and is thus a unitless scaling term.
Figure 7.
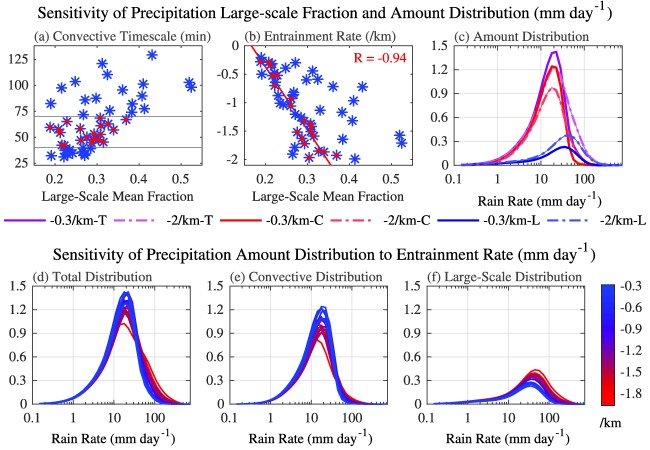
Large‐scale fraction of annual mean precipitation from 50°S to 50°N regressed against the (a) convective timescale and (b) entrainment rate for the CAM perturbed parameter ensemble of simulations; blue stars are all simulations and red dots are a subset within a range of convective timescale values from 40 to 70 min; (c) annual precipitation amount distributions for simulations with −0.3 km−1 (dark‐solid) and −2.0 km−1 (light‐dashed) entrainment rates (i.e., the end members of the subset simulations) of total (T, purple), convective (C, red), and large‐scale (L, blue) contributions; and annual precipitation amount distributions of (d) total, (e) convective, (f) and large‐scale contributions from the subset simulations. The units of the amount distributions are shown as mm d−1 (as given in the figure title), however they are scaled by ΔlnR−1, where ΔlnR = ΔR/R, which has units of mm d−1/mm d−1 and is thus a unitless scaling term.
Sorting the total, convective, and large‐scale precipitation amount distributions by the convective timescale in Figures 6d–6f reveals a clear increase in the amount of large‐scale rain and decrease in convective rain with longer timescales. Because large‐scale processes are associated with more intense total precipitation rates in CAM, this increase in large‐scale rain contributes to more intense total precipitation rates, which is consistent with the analysis of frequency distributions in Williamson (2013). Similarly, sorting the distributions by the entrainment rate in Figures 7d–7f reveals an increase in the amount of large‐scale rain with higher magnitude entrainment rates, which also increases the intensity of total precipitation rates. Additionally, partitioning of the convective and large‐scale contributions to the amount distribution, as shown here, distinguishes changes in the amount from changes in the intensity for each component. This demonstrates that the intensity of the convective amount mode (i.e., peak in the distribution) decreases with longer convective timescales but is less sensitive to changes in the entrainment rate. Furthermore, since the large‐scale amount mode intensity increases with longer convective timescales, sufficiently large timescale increases (greater than 90 min) can lead to a bifurcated amount distribution for total precipitation (Figure 6c).
The different sensitivities related to amount and intensity thus control the ways in which these two parameters can influence total precipitation intensity, a feature that would be obscured by analysis of the frequency distribution alone. Unlike changes in the entrainment rate, the convective timescale has the ability to exert controls on both the amount and intensity of convective and large‐scale rain. It is natural to wonder if the convective timescale could be tuned to produce a more realistic total rainfall distribution (as in Gustafson et al., 2014). Within the conventional‐resolution (∼1°) configuration this seems unlikely, since increasing the convective timescale to capture the more intense rates on the right tail of the distribution will shift the convective distribution toward weaker rates. This again leads to a right shouldered (or at the extreme even bimodal) amount distribution that does not resemble the observations (Figure 1).
It has also been suggested that changing the convective timescale in concert with horizontal resolution could remove unrealistic “grid‐point storms” and lead to a more scale‐insensitive precipitation distribution (Gustafson et al., 2014; Ma et al., 2014; Williamson, 2013). Consistent with this view, our results imply that decreasing the convective timescale could reduce the amount of rain from large‐scale processes, and that, this somewhat offsets the changes associated with high‐resolution (∼0.25°). However, since lower‐resolution configurations do not capture the intensity of the observations, this gain of precipitation scale‐insensitive may be won at the cost of realism and loss of the improvements in total precipitation extremes noted in previous studies (Kopparla et al., 2013, O'Brien et al., 2016). Again, decomposing the relative contributions to the amount distribution helps to illuminate these trade‐offs and their influence on total precipitation.
In summary, unsurprisingly, the artificial separation of processes into convective and large‐scale components that contribute to the production of total rainfall in CAM limits its ability to capture a realistic precipitation distribution. Similar to Gustafson et al. (2014), we find that the distribution can be improved in some ways by changing parameter settings, but improvements to some features may come at the expense of others; the amount distribution offers a complementary viewpoint from which to assess such trade‐offs. Ultimately, this artificial separation may also play a role in limiting the response of simulated precipitation to climate change, which is investigated in the next section.
3.4. Climate Change Response
Changes in the character of rainfall in response to climate forcing are assessed as differences between the beginning and end of the 21st century under the RCP8.5 emissions scenario. Under these conditions, the global mean temperature in CAM increases by 3.4°C (from 14.7 to 18.2°C) and in SPCAM increases by 3.8°C (from 13.9 to 17.7°C). The geographic pattern of this change is very similar in both models, with the largest changes over land and at high‐latitudes. For a full overview and visualization of these temperature changes, see Kooperman et al. (2016b). Here, the global mean temperature changes are used to normalize the precipitation change in units of mm d−1 °C−1 in order to consistently compare the two models. Globally, both CAM and SPCAM increase mean precipitation by a similar percentage (1.6 and 1.5% °C−1, respectively), with a slightly larger relative increase from convective than large‐scale rain in CAM (1.8 versus 1.4% °C−1). Equatorward of 50° the relative large‐scale change in mean rainfall is even smaller (1.7 versus 0.1% °C−1). The largest percentage changes occur at high‐latitudes in both models (percentage changes are not shown), but the largest absolute changes are seen in the tropics (Figure 8). The smallest percentage and absolute changes in both models occur in the subtropics and midlatitudes.
Figure 8.
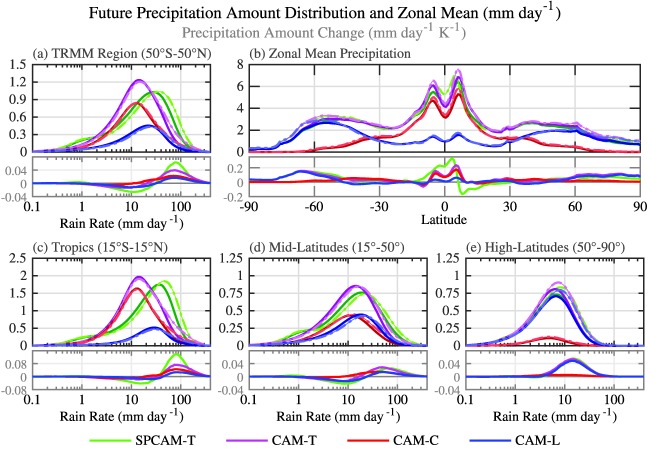
Annual precipitation amount distributions from (a) 50°S to 50°N (c) 15°S to 15°N, (d) 15° to 50°, (e) 50° to 90°, and (b) zonal mean precipitation of present‐day (dark‐solid) and future climate (light‐dashed) daily rates for SPCAM total (T, green), CAM total (T, purple), CAM convective (C, red), and CAM large‐scale (L, blue) contributions; lower subplots show the difference between future and present‐day climates (RCP8.5: 2091–2100 minus 2006–2015). The units for all plots are mm d−1 (as given in the figure title), however the amount distributions are scaled by ΔlnR−1, where ΔlnR = ΔR/R, which has units of mm d−1/mm d−1 and is thus a unitless scaling term.
As in Figure 1, rainfall distributions as a function of rain rate and latitude are shown in Figure 8, but for future climate conditions (light‐dashed lines) as well as present‐day (dark‐solid lines). The bottom plots in Figure 8 also show the change in distributions (future minus present‐day) per degree of global mean temperature change. Over the TRMM region, the total rainfall response, especially for the amount mode, is very different in the two models. SPCAM simulates a smooth rightward shift across all rain rates, while CAM increases the amount of rain from heavier rates without shifting the moderate rate peak as much. The difference between the models is primarily in the tropics; transitioning to higher latitudes the total and large‐scale responses in CAM are similar to SPCAM. The large‐scale response in CAM captures a reduction in part of the midlatitudes associated with rain rates below 20 mm d−1, which resembles the shift mode response seen in SPCAM rather than an increase alone. In the tropics, CAM's total rainfall shows almost no amount mode shift, while SPCAM has a significant 8.7% °C−1 shift response. However, the isolated large‐scale component of rain in CAM exhibits a shift in all regions, including a 2.9% °C−1 increase in the tropics.
The geographic pattern of the median rain rate response to climate change is shown in Figure 9. Like the baseline signal, the changes associated with total and convective rainfall in CAM are much weaker than SPCAM. SPCAM again highlights regions of organized convection in the tropics including the MJO (i.e., equatorial Pacific and Indian Oceans), ITCZ, and monsoons. The large‐scale response in CAM captures several aspects of this change associated with the ITCZ (double‐ITCZ pattern in CAM) and monsoon regions; though some of the Indian and West Pacific response is missing. However, the magnitude of CAM's large‐scale median rainfall change is also surprisingly similar to SPCAM. The large‐scale distribution responds in a way that suggests important underlying mechanisms may be embedded within resolved processes in CAM, but that these do not produce enough accumulated rainfall at 0.9° × 1.25° horizontal resolution to be visible in the total precipitation response.
Figure 9.
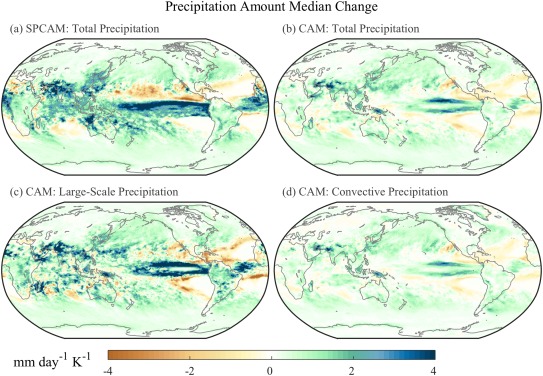
Annual precipitation amount median change (RCP8.5: 2091–2100 minus 2006–2015) for (a) SPCAM total, (b) CAM total, (c) CAM large‐scale, and (d) CAM convective contributions; Figures 9a, 9b were previously published in Kooperman et al. (2016b).
Overall, the large‐scale rainfall distribution in CAM better captures the intensification response to climate change that is simulated by SPCAM than its total rainfall distribution (i.e., Figure 9a is a much better match to Figure 9c than Figure 9b). This includes increases in rainfall at the tail of the distribution and a broad reduction in light rates that shifts the peak amount mode toward heavier rates. The geographic pattern of median rates also highlights monsoon and ITCZ regions.
4. Conclusions
In this study, we evaluated rainfall intensity simulated by conventional and superparameterized versions of CAM, as well as a perturbed‐physics ensemble of CAM, focusing on the moderate rates as represented by the rainfall amount mode and median. In general, total rainfall in CAM is unable to capture the intensity of moderate rates in present‐day climate or their response to climate change simulated by SPCAM, most notably in the tropics. Separating the parameterized convective and resolved large‐scale contributions to total rainfall in CAM reveals that this deficiency is primarily due to limitations associated with parameterized convection, which produces most of the rainfall in the tropics and controls the peak in the amount distribution. Large‐scale rainfall contributes most at high‐latitudes, to the heaviest rainfall rates, and simulates an amount mode that better matches TRMM 3B42 observations and SPCAM simulations. The geographic pattern of median large‐scale rates also highlights similar regions as SPCAM (e.g., monsoons, ITCZ, etc.), but still under‐simulates the intensity along the equator in the Indian and West Pacific Oceans (MJO region).
The preferred rain rate that delivers the most accumulated large‐scale rainfall (i.e., amount mode) is largely insensitive to the horizontal resolution, but the amount increases with higher resolution. The amount of large‐scale rain also increases with longer convective timescales and higher magnitude entrainment rates. The intensity of large‐scale rain is somewhat sensitive to convective timescale and increases with longer timescales, while the intensity of convective rain decreases. Adjusting these parameters in concert with the horizontal resolution may be useful for improving the representation of intensity or achieving a more scale‐insensitive behavior, but this requires consideration of their influences on both amount and intensity contributions to the total rainfall distribution. We have demonstrated the amount distribution as a promising diagnostic for assessing such trade‐offs.
In response to climate change, CAM's large‐scale precipitation captures a rightward shift in the amount distribution that resembles the change in SPCAM, but the total amount mode does not shift because the intensity of the mode from convective processes remains fixed. This leads to an increase in extreme rates (the right tail of the distribution), but not moderate rates, which has implications for impacts assessment. Similarly, the geographic pattern of median rain rates only shows relatively small changes in the total and convective precipitation maps. However, CAM's large‐scale precipitation response to warming enhances the median in regions that are similar to SPCAM, suggesting that resolved processes in CAM are better able to capture important underlying mechanisms controlling rainfall intensity changes.
The results of this study have implications for future model development and build on a chain of work that has pointed toward improvements in the representation of precipitation intensity requiring better links between resolved large‐scale and convective processes. This work also outlines a new methodology for assessing the influence of different model components on the representation of precipitation intensity, which may be useful for evaluating new stochastic (e.g., Wang et al., 2016; Watson et al., 2017) and unified (e.g., Park, 2014; Thayer‐Calder et al., 2015) convective schemes or methods that turn off the deep convection parameterization altogether (e.g., Webb et al., 2015; Zhao et al., 2009), and for investigating the roles of precipitation processes for cloud feedbacks (e.g., Webb et al., 2015) and convective self‐aggregation (e.g., Becker et al., 2017). This methodology effectively reveals how different components of the model contribute to both the amount of mean precipitation and the intensity of precipitation, which have typically been conflated in previous studies. Here, we have applied this method to better understand the relative contributions of large‐scale and convective rainfall in a series of simulations with varied resolution, perturbed physics parameter settings, and climate forcing. In the future, it could be worth applying a similar method to discriminate subprocesses in the model, such as separating the influences of shallow versus deep convection or cloud‐water sedimentation versus cloud microphysics in the convective and large‐scale distributions, respectively.
Since organized convective systems in the tropics are not statistically resolved until grid‐scales approach the order of 1–4 km, parameterized convection of some kind is likely to be in use for years to come, and improving the realism of the rainfall it produces is critical. The methods we have outlined here provide an efficient means to evaluate the intensity distribution of simulated rainfall, test whether the next generation of climate models with updated parameterizations and higher resolution continue to suffer similar deficiencies, and discriminate the individual components that contribute to the deficiency. Our results suggest modeling schemes that more directly link large‐scale resolved processes to mechanisms controlling total rainfall production will likely produce the most realistic moderate rainfall rates. Furthermore, identifying the most realistic components of rainfall may provide an opportunity for better downscaling of GCM projections; e.g., downscaling rates based on large‐scale distributions alone in CAM may provide more consistent results than total precipitation, which includes biased convective contributions.
Acknowledgments
Kooperman acknowledges funding from an NSF Postdoctoral Research Fellowship grant (AGS‐1349579). Pritchard acknowledges funding from the NSF grant (AGS‐1419518) and DOE Early Career and SciDac programs grants (DE‐SC0012152 and DE‐SC0012548). Part of this material is based upon work supported by the U.S. DOE Office of Science, Office of Biological and Environmental Research, Climate and Environmental Sciences Division, Regional and Global Climate Modeling Program under award DE‐AC02–05CH11231. CAM development is led by NCAR and supported by the NSF and DOE. SPCAM development was led by CMMAP (http://www.cmmap.org) and funded by the NSF (ATM‐0425247). Current versions of CAM and SPCAM are available for download through the NCAR subversion code repository (https://www2.cesm.ucar.edu). The horizontal resolution and perturbed parameter ensemble experiments are based on CAM5 in CESM version 1.2.2. The CCSM4 and SPCCSM4 experiments are based on CCSM version 4.0 (repo tag ccsm4_0_beta45); for access to this earlier version of SPCCSM4 contact Cristiana Stan (cstan@gmu.edu). CCSM4 was run at the DOE NCCS/ORNL (DE‐AC05‐00OR22725); SPCCSM4 was run at the DOE NERSC (DE‐AC02–05CH11231), and supported by the DOE RGCM (SC0006722); and CAM5 was run at the DOE NERSC (DE‐AC02–05CH11231). The CCSM4 output (variables: pr and prc, time frequency: daily, experiment: RCP8.5) is available through the CMIP5 archives on the ESG (https://cmip.llnl.gov/cmip5/availability.html). The daily SPCCSM4 output is available upon request from Cristiana Stan (monthly SPCCSM4 output is available on the ESG). The CAM5 output (variables PRECT, PRECC, and PRECL, time frequency: daily) from the horizontal‐resolution experiments is available on the NERSC Portal (http://portal.nersc.gov/project/m1949/iliad/); and the CAM5 output from the perturbed parameter ensemble experiments will also be made available on the NERSC Portal when the full set of simulations are complete and are currently available upon request from Ben Timmermans (bwtimmermans@lbl.gov). The GPCP 1DD and TRMM 3B42 data are provided by the NASA GSFC, which develops 1DD as a contribution to GEWEX GPCP and 3B42 as a contribution to TRMM. The GPCP 1DD and TRMM 3B42 data are available from NASA GSFC RSD (ftp://rsd.gsfc.nasa.gov/pub/1dd-v1.2/) and Mirador (http://mirador.gsfc.nasa.gov), respectively. The authors thank Cristiana Stan and Li Xu for additional SPCCSM4 output. The authors also thank two anonymous reviewers and the editors of helpful feedback and suggestions.
Kooperman, G. J. , Pritchard, M. S. , O'Brien, T. A. , & Timmermans, B. W. (2018). Rainfall from resolved rather than parameterized processes better represents the present‐day and climate change response of moderate rates in the community atmosphere model. Journal of Advances in Modeling Earth Systems, 10, 971–988. https://doi.org/10.1002/2017MS001188
References
- Allen, M. R. , & Ingram, W. J. (2002). Constraints on future changes in climate and the hydrologic cycle. Nature, 419, 224–232. [DOI] [PubMed] [Google Scholar]
- Becker, T. , Stevens, B. , & Hohenegger, C. (2017). Imprint of the convective parameterization and sea‐surface temperature on large‐scale convective self‐aggregation. Journal of Advances in Modeling Earth Systems, 9, 1488–1505. https://doi.org/10.1002/2016MS000865 [Google Scholar]
- Behrangi, A. , Lebsock, M. , Wong, S. , & Lambrigtsen, B. (2012). On the quantification of oceanic rainfall using spaceborne sensors. Journal of Geophysical Research, 117, D20105. https://doi.org/10.1029/2012JD017979 [Google Scholar]
- Benedict, J. J. , & Randall, D. A. (2009). Structure of the Madden‐Julian oscillation in the superparameterized CAM. Journal of the Atmospheric Sciences, 66(11), 3277–3296. [Google Scholar]
- Dai, A. (2006). Precipitation characteristics in eighteen coupled climate models. Journal of Climate, 19, 4605–4630. [Google Scholar]
- Dinku, T. , Ceccato, P. , & Connor, S. J. (2011). Challenges of satellite rainfall estimating over mountainous and arid parts of east Africa. International Journal of Remote Sensing, 32, 5965–5979. [Google Scholar]
- Gent, P. R. , Danabasoglu, G. , Donner, L. J. , Holland, M. M. , Hunke, E. C. , Jayne, S. R. , et al. (2011). The community climate system model version 4. Journal of Climate, 24, 4973–4991. [Google Scholar]
- Gustafson, W. I. , Ma, P.‐L. , & Singh, B. (2014). Precipitation characteristics of CAM5 physics at mesoscale resolution during MC3E and the impact of convective timescale choice. Journal of Advances in Modeling Earth Systems, 6, 1271–1287. https://doi.org/10.1002/2014MS000334 [Google Scholar]
- Hack, J. J. (1994). Parameterization of moist convection in the National Center for Atmospheric Research Community Climate Model (CCM2). Journal of Geophysical Research, 99(D3), 5551–5568. https://doi.org/10.1029/93JD03478 [Google Scholar]
- Held, I. M. , Zhao, M. , & Wyman, B. (2007). Dynamic radiative‐convective equilibria using GCM column physics. Journal of the Atmospheric Sciences, 64(1), 228–238. [Google Scholar]
- Huffman, G. J. , Adler, R. F. , Morrissey, M. M. , Curtis, S. , Joyce, R. , McGavock, B. , et al. (2001). Global precipitation at one‐degree daily resolution from multi‐satellite observations. Journal of Hydrometeorology, 2, 36–50. [Google Scholar]
- Huffman, G. J. , Bolvin, D. T. , & Adler, R. F. (2012a). GPCP version 1.2 1‐degree daily (1DD) precipitation data set Asheville, NC: WDC‐A, NCDC. Data set accessed November 2014 at ftp://rsd.gsfc.nasa.gov/pub/1dd-v1.2/
- Huffman, G. J. , Bolvin, D. T. , Nelkin, E. J. , Wolff, D. B. , Adler, R. F. , Gu, G. , et al. (2007). The TRMM multisatellite precipitation analysis (TMPA): Quasi‐global, multiyear, combined‐sensor precipitation estimates at fine scales. Journal of Hydrometeorology, 8, 38–55. [Google Scholar]
- Huffman, G. J. , Stocker, E. F. , Bolvin, D. T. , Nelkin, E. J. , & Adler, R. F. (2012b). TRMM version 7 3B42 and 3B43 data sets Greenbelt, MD: NASA/GSFC. Data set accessed November 2014 at http://mirador.gsfc.nasa.gov
- Hunke, E. C. , & Lipscomb, W. H. (2008). CICE: The Los Alamos sea ice model user's manual, version 4 (Tech. Rep. LA‐CC‐06–012, p. 76). Los Alamos, NM: Los Alamos National Laboratory.
- Khairoutdinov, M. F. , & Randall, D. A. (2001). A cloud resolving model as a cloud parameterization in the NCAR community climate system model: Preliminary results. Geophysical Research Letters, 28(18), 3617–3620. https://doi.org/10.1029/2001GL013552 [Google Scholar]
- Kooperman, G. J. , Pritchard, M. S. , Burt, M. A. , Branson, M. D. , & Randall, D. A. (2016a). Robust effects of cloud superparameterization on simulated daily rainfall intensity statistics across multiple versions of the Community Earth System Model. Journal of Advances in Modeling Earth Systems, 8, 140–165. https://doi.org/10.1002/2015MS000574 [Google Scholar]
- Kooperman, G. J. , Pritchard, M. S. , Burt, M. A. , Branson, M. D. , & Randall, D. A. (2016b). Impacts of cloud superparameterization on projected daily rainfall intensity climate changes in multiple versions of the Community Earth System Model. Journal of Advances in Modeling Earth Systems, 8, 1727–1750. https://doi.org/10.1002/2016MS000715 [Google Scholar]
- Kopparla, P. , Fischer, E. M. , Hannay, C. , & Knutti, R. (2013). Improved simulation of extreme precipitation in a high‐resolution atmosphere model. Geophysical Research Letters, 40, 5803–5808. https://doi.org/10.1002/2013GL057866 [Google Scholar]
- Lawrence, D. M. , Oleson, K. W. , Flanner, M. G. , Thornton, P. E. , Swenson, S. C. , Lawrence, P. J. , et al. (2011). Parameterization improvements and functional and structural advances in version 4 of the Community Land Model. Journal of Advances in Modeling Earth Systems, 3, M03001. https://doi.org/10.1029/2011MS00045 [Google Scholar]
- Li, F. , Collins, W. D. , Wehner, M. F. , Williamson, D. , Olson, J. , & Algieri, C. (2011). Impact of horizontal resolution on simulation of precipitation extremes in an aqua‐planet version of Community Atmospheric Model (CAM3). Tellus Series A, 63, 884–823. [Google Scholar]
- Liu, C. , & Allan, R. P. (2012). Multi‐satellite observed responses of precipitation and its extremes to interannual climate variability. Journal of Geophysical Research, 117, D03101. https://doi.org/10.1029/2011JD016568 [Google Scholar]
- Ma, P.‐L. , Rasch, P. J. , Fast, J. D. , Easter, R. C. , Gustafson, W. I. Jr. , Liu, X. , et al. (2014). Assessing the CAM5 physics suite in the WRF‐Chem model: Implementation, resolution sensitivity, and a first evaluation for a regional case study. Geoscientific Model Development, 7, 755–778. [Google Scholar]
- Meehl, G. A. , Washington, W. M. , Arblaster, J. M. , Hu, A. , Teng, H. , Tebaldi, C. , et al. (2012). Climate system response to external forcings and climate change projections in CCSM4. Journal of Climate, 25, 3661–3683. [Google Scholar]
- Neale, R. B. , Richter, J. H. , Conley, A. J. , Park, S. , Lauritzen, P. H. , Gettelman, A. , et al. (2010). Description of the NCAR community atmosphere model (CAM 4.0) (NCAR Tech. note NCAR/TN‐485+STR). Boulder, CO: National Center for Atmospheric Research.
- O'Brien, T. A. , Collins, W. D. , Kashinath, K. , Rubel, O. , Byna, S. , Gu, J. , et al. (2016). Resolution dependence of precipitation statistical fidelity in hindcast simulations. Journal of Advances in Modeling Earth Systems, 8, 976–990. https://doi.org/10.1002/2016MS000671 [Google Scholar]
- O'Gorman, P. A. (2015). Precipitation extremes under climate change. Current Climate Change Reports, 1, 49–59. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park, S. (2014). A unified convection scheme (UNICON). Part I: Formulation. Journal of the Atmospheric Sciences, 71, 3902–3930. [Google Scholar]
- Pendergrass, A. G. , & Hartmann, D. L. (2014a). The atmospheric energy constraint on global‐mean precipitation change. Journal of Climate, 27, 757–768. [Google Scholar]
- Pendergrass, A. G. , & Hartmann, D. L. (2014b). Two modes of change of the distribution of rain. Journal of Climate, 27, 8357–8371. [Google Scholar]
- Pendergrass, A. G. , & Hartmann, D. L. (2014c). Changes in the distribution of rain frequency and intensity in response to global warming. Journal of Climate, 27, 8372–8383. [Google Scholar]
- Qian, Y. , Yan, H. , Hou, Z. , Johannesson, G. , Klein, S. , Lucas, D. , et al. (2015). Parametric sensitivity analysis of precipitation at global and local scales in the Community Atmosphere Model CAM5. Journal of Advances in Modeling Earth Systems, 7, 382–411. https://doi.org/10.1002/2014MS000354 [Google Scholar]
- Randall, D. , Khairoutdinov, M. , Arakawa, A. , & Grabowski, W. (2003). Breaking the cloud parameterization deadlock. Bulletin of the American Meteorological Society, 84(11), 1547. [Google Scholar]
- Rasch, P. J. , & Kristjansson, J. E. (1998). A comparison of the CCM3 model climate using diagnosed and predicted condensate parameterizations. Journal of Climate, 11, 1587–1614. [Google Scholar]
- Raymond, D. J. , & Blyth, A. M. (1992). Extension of the stochastic mixing model to cumulonimbus clouds. Journal of the Atmospheric Sciences, 49(21), 1968–1983. [Google Scholar]
- Richter, J. H. , & Rasch, P. J. (2008). Effects of convective momentum transport on the atmospheric circulation in the Community Atmosphere Model, version 3. Journal of Climate, 21, 1487–1499. [Google Scholar]
- Saha, S. , Moorthi, S. , Pan, H.‐L. , Wu, X. , Wang, J. , Nadiga, S. , et al. (2010). The NCEP climate forecast system reanalysis. Bulletin of the American Meteorological Society, 91(8), 1015–1057. [Google Scholar]
- Smith, R. D. , Jones, P. , Briegleb, B. , Bryan, F. , Danabasoglu, G. , Dennis, J. , et al. (2010). The parallel ocean program (POP) reference manual (LANL Tech. Rep. LAUR‐10–01853, p. 140). Los Alamos, NM: Los Alamos National Laboratory.
- Stan, C. , & Xu, L. (2014). Climate simulations and projections with a super‐parameterized climate model. Environmental Modelling and Software, 60, 134–152. [Google Scholar]
- Stone, D. , Risser, M. D. , Angélil, O. M. , Wehner, M. F. , Cholia, S. , Keen, N. , et al. (2018). A basis set for exploration of sensitivity to prescribed ocean conditions for estimating human contributions to extreme weather in CAM5.1‐1degree. Weather and Climate Extremes, https://doi.org/10.1016/j.wace.2017.12.003, in press. [Google Scholar]
- Tan, J. , Jakob, C. , Rossow, W. B. , & Tselioudis, G. (2015). Increases in tropical rainfall driven by changes in frequency of organized deep convection. Nature, 519, 451–454. [DOI] [PubMed] [Google Scholar]
- Taylor, K. E. , Stouffer, R. J. , & Meehl, G. A. (2012). An overview of CMIP5 and the experiment design. Bulletin of the American Meteorological Society, 93, 485–498. [Google Scholar]
- Thayer‐Calder, K. , Gettelman, A. , Craig, C. , Goldhaber, S. , Bogenschutz, P. A. , Chen, C.‐C. , et al. (2015). A unified parameterization of clouds and turbulence using CLUBB and subcolumns in the Community Atmosphere Model. Geoscientific Model Development, 8, 3801–3821. [Google Scholar]
- Wang, Y. , Zhang, G. J. , & Craig, G. C. (2016). Stochastic convective parameterization improving the simulation of tropical precipitation variability in the NCAR CAM5. Geophysical Research Letters, 43, 6612–6619. https://doi.org/10.1002/2016GL069818 [Google Scholar]
- Watson, P. A. G. , Berner, J. , Corti, S. , Davini, P. , von Hardenberg, J. , Sanchez, C. , et al. (2017). The impact of stochastic physics on tropical rainfall variability in global climate models on daily to weekly time scales. Journal of Geophysical Research: Atmospheres, 122, 5738–5762. https://doi.org/10.1002/2016JD026386 [Google Scholar]
- Webb, M. J. , Lock, A. P. , Bretherton, C. S. , Bony, S. , Cole, J. N. , Idelkadi, A. , et al. (2015). The impact of parametrized convection on cloud feedback. Philosophical Transactions. Series A, Mathematical, Physical, and Engineering Sciences, 373, 20140414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wehner, M. F. , Reed, K. A. , Li, F. , Bacmeister, P. J. , Chen, C.‐T. , Paciorek, C. , et al. (2014). The effect of horizontal resolution on simulation quality in the Community Atmospheric Model, CAM5.1. Journal of Advances in Modeling Earth Systems, 6, 980–997. https://doi.org/10.1002/2013MS000276 [Google Scholar]
- Williamson, D. L. (2013). The effect of time steps and time‐scales on parametrization suites. Quarterly Journal of the Royal Meteorological Society, 139, 548–560. https://doi.org/10.1002/qj.1992 [Google Scholar]
- Williamson, D. (2015). Exploratory ensemble designs for environmental models using k‐extended Latin hypercubes. Environmetrics, 26, 268–283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang, G. J. , & McFarlane, N. A. (1995). Sensitivity of climate simulations to the parameterization of cumulus convection in the Canadian climate center general‐circulation model. Atmosphere‐Ocean, 33(3), 407–446. [Google Scholar]
- Zhang, M. , Lin, W. , Bretherton, C. S. , Hack, J. J. , & Rasch, P. J. (2003). A modified formulation of fractional stratiform condensation rate in the NCAR Community Atmospheric Model (CAM2). Journal of Geophysical Research, 108(D1), 4035. https://doi.org/10.1029/2002JD002523 [Google Scholar]
- Zhao, M. , Held, I. M. , Lin, S. J. , & Vecchi, G. A. (2009). Simulations of global hurricane climatology, interannual variability, and response to global warming using a 50‐km resolution GCM. Journal of Climate, 22, 6653–6678. [Google Scholar]


