Summary
Terrestrial primary productivity and carbon cycle impacts of droughts are commonly quantified using vapour pressure deficit (VPD) data and remotely sensed greenness, without accounting for soil moisture. However, soil moisture limitation is known to strongly affect plant physiology.
Here, we investigate light use efficiency, the ratio of gross primary productivity (GPP) to absorbed light. We derive its fractional reduction due to soil moisture (fLUE), separated from VPD and greenness changes, using artificial neural networks trained on eddy covariance data, multiple soil moisture datasets and remotely sensed greenness.
This reveals substantial impacts of soil moisture alone that reduce GPP by up to 40% at sites located in sub‐humid, semi‐arid or arid regions. For sites in relatively moist climates, we find, paradoxically, a muted fLUE response to drying soil, but reduced fLUE under wet conditions.
fLUE identifies substantial drought impacts that are not captured when relying solely on VPD and greenness changes and, when seasonally recurring, are missed by traditional, anomaly‐based drought indices. Counter to common assumptions, fLUE reductions are largest in drought‐deciduous vegetation, including grasslands. Our results highlight the necessity to account for soil moisture limitation in terrestrial primary productivity data products, especially for drought‐related assessments.
Keywords: drought impacts, eddy covariance, gross primary productivity (GPP), light use efficiency, photosynthesis, soil moisture, standardized precipitation index, vapour pressure deficit (VPD)
Short abstract
See also the Commentary on this article by https://doi.org/10.1111/nph.15176.
Introduction
Water availability limits ecosystem productivity across much of the Earth's surface (Beer et al., 2010; Schwalm et al., 2010; Seneviratne et al., 2010; Ahlström et al., 2015). In arid, semi‐arid and Mediterranean ecosystems, limiting water availability is a recurrent phenomenon and governs plant growth and phenology (Reichstein et al., 2002). In addition, in temperate, boreal and tropical ecosystems, sporadic prolonged dry periods can lead to water‐limited conditions and can have far‐reaching impacts on ecosystem carbon (C) balance (Ciais et al., 2005; Granier et al., 2007; Doughty et al., 2015) and structure (Orth et al., 2016). Here, we investigate ‘droughts’, identified by their impact on vegetation productivity. This corresponds most closely to the definition of ‘agricultural droughts’ (Trenberth et al., 2007) and also includes seasonally recurring dry conditions.
Most plants tightly co‐regulate water loss and CO2 assimilation with the effect that, under conditions of low soil moisture and high atmospheric water vapour pressure deficit (VPD), stomatal conductance and hence assimilation and transpiration rates are reduced in order to prevent exceedingly low leaf water potentials and resulting plant tissue damage from cavitation (Cowan & Farquhar, 1977; McDowell et al., 2008; Sperry & Love, 2015). The CO2 assimilation rate at the leaf level, or gross primary productivity (GPP) – its integral at the ecosystem level – is the ‘engine’ of C cycling in terrestrial ecosystems. GPP emerges as the dominant driver of year‐to‐year variations in the global land C balance (Poulter et al., 2014; Ahlström et al., 2015), and is closely controlled by water availability in the rooting zone across much of the Earth's surface (Beer et al., 2010; Ahlström et al., 2015).
The effects of dryness on CO2 assimilation and light use efficiency (LUE, GPP normalized by absorbed light) are represented in global vegetation models and satellite data‐driven products by accounting for VPD only (Running et al., 2004; Beer et al., 2010; Best et al., 2011; Clark et al., 2011), soil moisture only (Knorr & Heimann, 2001; Sitch et al., 2003; Stocker et al., 2013) or both (Medvigy et al., 2009; Zaehle & Friend, 2010; Bonan et al., 2014). However, model parametrizations are divergent (Medlyn et al., 2016; Rogers et al., 2017), and there is a lack of empirical data covering diverse ecosystems (Sulman et al., 2016). Furthermore, quantifications of impacts by low soil moisture and high VPD have commonly relied on a priori specified functional relationships (Reichstein, 2003; Leuning et al., 2005; Pan et al., 2006; Verstraeten et al., 2006; Granier et al., 2007; Yuan et al., 2007; Novick et al., 2016). These aspects limit the power of global vegetation models and our ability to monitor terrestrial primary productivity from space.
GPP can generally be formulated as the product of the incident photosynthetically active radiation (PAR), the fraction of absorbed PAR (fAPAR) and LUE (Monteith, 1972):
| (Eqn 1) |
fAPAR is commonly derived from remotely sensed greenness indices and captures first‐order effects on GPP by vegetation cover (Wang et al., 2014) and – when reflected in ecosystem structural change – its variation during droughts. Data on fAPAR alone have served as the basis for the identification and quantification of C cycle extreme events (Reichstein et al., 2013; Zscheischler et al., 2013). However, high VPD and dry soil conditions can lead to severely reduced LUE before becoming manifest in vegetation structure (Garbulsky et al., 2010). It is commonly held that this affects mostly evergreen ecosystems (Gamon et al., 2016; Walther et al., 2016), whereas seasonal GPP variations are well captured by remotely sensed greenness in regions dominated by drought‐deciduous vegetation, in particular grasslands (Rossini et al., 2012; Verma et al., 2014; Ali et al., 2016; Konings et al., 2017). Hence, the accurate prediction of variations in LUE and its sensitivity to VPD and soil moisture is essential for the simulation of GPP and C cycle variations in response to interannually varying climate.
Satellite data‐based GPP products are widely used in assessments of global C cycle changes, their interannual variability in recent decades and impacts of droughts (Zhao & Running, 2010; Ballantyne et al., 2017; Jung et al., 2017; Schwalm et al., 2017). These commonly rely on the assumption that VPD and vegetation greenness are correlated with soil moisture and other limitations on vegetation productivity, and should thus suffice for model predictions across a wide range of environmental conditions without accounting for direct information on soil moisture (Field et al., 1995; Veroustraete et al., 2002; Running et al., 2004; Heinsch et al., 2006; Fisher et al., 2008; Biederman et al., 2017). The correlation between soil moisture and VPD arises as a result of the feedback between soil moisture, stomatal conductance and transpiration under dry conditions (Seneviratne et al., 2010). However, mechanistic considerations suggest that this coupling deteriorates under very dry conditions (Ruddell & Kumar, 2009). Therefore, it has been argued that the combination of dry soil (low soil moisture) and dry air (high VPD) should be considered for the appropriate modelling of plant responses to drought (Egea et al., 2011; Sulman et al., 2016; Rogers et al., 2017). Although needed for the benchmarking of competing representations in models and to improve data‐based estimates of global GPP and C cycle changes, independent observational constraints for soil moisture effects, additional to VPD, are missing.
Recently, global‐scale, satellite‐based observations of soil moisture based on microwave measurements have become available. However, their representativeness is limited to moisture in upper soil layers, complicating their usability for the estimation of productivity of deeper rooting vegetation (Hirschi et al., 2014; Dorigo et al., 2017). Other information based on surface reflectance (Xiao et al., 2004), the Earth's gravitational field and information from the Gravity Recovery and Climate Experiment (GRACE) mission (Tapley et al., 2004; Rodell et al., 2009; Humphrey et al., 2016), or from alternative remotely sensed vegetation indices (PRI (photochemical reflectance index) (Gamon et al., 1992, 2016; Peñuelas et al., 1995; Goerner et al., 2009; He et al., 2016), SiF (sun‐induced fluorescence) (Porcar‐Castell et al., 2014) or NIRV (near‐infrared reflectance of terrestrial vegetation) (Badgley et al., 2017)), has the potential to provide complementary information relevant for the capture of drought impacts on LUE and GPP. However, the spatial resolution of GRACE is very low (c. 102 km) and is affected by other surface water storage, and the complementarity of PRI, SiF and NIRV to greenness indices (normalized difference vegetation index (NDVI) and Enhanced Vegetation Index (EVI)) and how their information is to be used to capture drought impacts remain challenging (He et al., 2016; Vicca et al., 2016).
Eddy covariance measurements provide data on CO2 gas exchange at a high temporal resolution (Baldocchi et al., 2001). These data can be used to estimate GPP and to reveal, at scales ranging from hours to years, how ecosystem functioning is affected by the combination of multiple, simultaneously changing drivers. The recently published FLUXNET 2015 dataset provides an unprecedented wealth of flux data, complemented by meteorological variables and soil moisture, measured in parallel. However, these data cannot provide direct information on partial effects by soil moisture. Such effects would ideally be quantified in an experimental setup with and without limiting soil water availability around the flux measurement towers (Beier et al., 2012). However, this is generally not feasible because of the relatively large spatial extent of tower footprints and the required resources for controlled conditions at this scale. Furthermore, feedbacks between soil moisture and VPD would confound a separation (Beier et al., 2012). Hence, analyses of VPD and soil moisture controls commonly rely on a priori specified functional relationships and model‐based analyses of observational data from unmanipulated sites alone (Granier et al., 2007; Novick et al., 2016).
Here, we identify soil moisture‐related reductions in LUE and derive their empirical functional relationship from data alone, across sites in the FLUXNET 2015 dataset, covering a wide range of biomes and vegetation types. We make use of c. 250 000 site days to empirically estimate the potential light use efficiency (LUEpot) under hypothetical, non‐soil moisture‐limited conditions. The ratio of actual over potential LUE (fLUE) reveals the timing and quantifies the magnitude of soil moisture effects, separated from VPD effects and additional to changes in vegetation greenness (fAPAR). This analysis thereby provides an impact‐oriented quantification of droughts.
Materials and Methods
An extended methods description is available as Supporting Information Methods S1 and as reproducible code (rmarkdown) through https://github.com/stineb/nn_fluxnet2015 (doi: https://doi.org/10.5281/zenodo.1158575). fLUE data are available through doi: https://doi.org/10.5281/zenodo.1158524.
Approach
We quantify the fractional reduction in LUE due to soil moisture, separated from VPD and greenness effects, as the ratio of actual over potential LUE:
| (Eqn 2) |
‘Potential’ light use efficiency (LUEpot) is predicted using artificial neural networks (NNs, see later), trained on the empirical relationship between observed LUE (LUEobs) and its predictors (temperature, VPD and PAR) during days in which soil moisture is relatively high (‘moist days’). All NN training is performed for each site specifically. ‘Actual’ LUE (LUEact) is derived from NNs using all data and, in contrast with the NN for LUEpot, with soil moisture as an additional predictor (Fig. 1). LUEobs is calculated on the basis of daily total observed GPPobs (GPP_NT_VUT_REF in the FLUXNET 2015 dataset), PAR (based on incoming shortwave radiation, SW_IN_F in FLUXNET 2015) and fAPAR (fraction of absorbed PAR, based on MODIS EVI, extracted for site location) (see Eqn (Eqn 1)). The use of NN‐derived LUEact instead of LUEobs in Eqn (Eqn 2) reduces noise in fLUE as LUEact and LUEobs are affected by similar errors. fLUE distills the effect of accounting for information on soil moisture.
Figure 1.
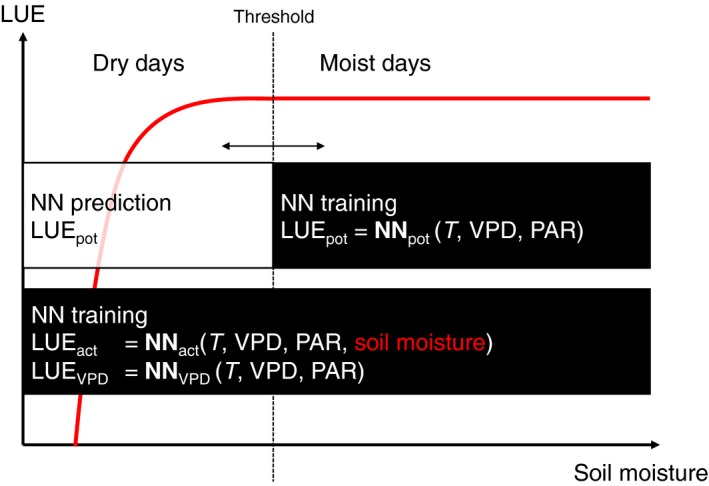
Illustration of the methods for neural network (NN) training. ‘Potential’ light use efficiency (LUE pot) is predicted using NN models, trained on the empirical relationship between observed LUE (LUE obs) and its predictors, temperature (T), vapour pressure deficit (VPD) and photosynthetically active radiation (PAR), during days in which soil moisture is relatively high (‘moist days’). The threshold between moist and dry days is optimized with respect to NN model performance (see the Materials and Methods section). ‘Actual’ LUE (LUE act) is derived from NNs using all data and with soil moisture as an additional predictor. LUEVPD is derived from NNs, trained at all data, but without soil moisture as a predictor.
We limit the NN training to a small number of predictors that are reflective of process understanding regarding the controls on LUE (Prentice et al., 2014) and to avoid over‐fitting. Data are split into ‘moist’ and ‘dry’ days, where ‘moist days’ data are used to train NNpot and all data are used to train NNact (Fig. 1). The threshold for splitting is determined by optimal model performance in the face of the trade‐off between the number of data points and including data in which low soil moisture affects fluxes. The criterion applied is the smallest variance in fLUE during moist days of a subset of thresholds in which the difference between LUEact and LUEpot during dry days is highest. The agreement between potential and actual LUE, using the two NN models’ prediction, should be good during ‘moist days’ (high soil moisture). By contrast, LUEpot, trained at ‘moist days’ data, is expected to overestimate LUE during days in which soil moisture is low (see Figs 2, 3). With the only difference between NN models being soil moisture as an additional predictor, the ratio fLUE thus indicates the separated effect of soil moisture on LUE. ‘fLUE droughts’ are identified when fLUE falls below a site‐specific threshold. To test the power of VPD as a predictor for LUE, we used an alternative NN setup in which temperature, VPD and PAR are used as predictors (but not soil moisture) and all days (moist and dry) are used for training (LUEVPD = NNVPD(T, VPD, PAR)). The only difference compared with NNpot is that dry day data are also used for training.
Figure 2.
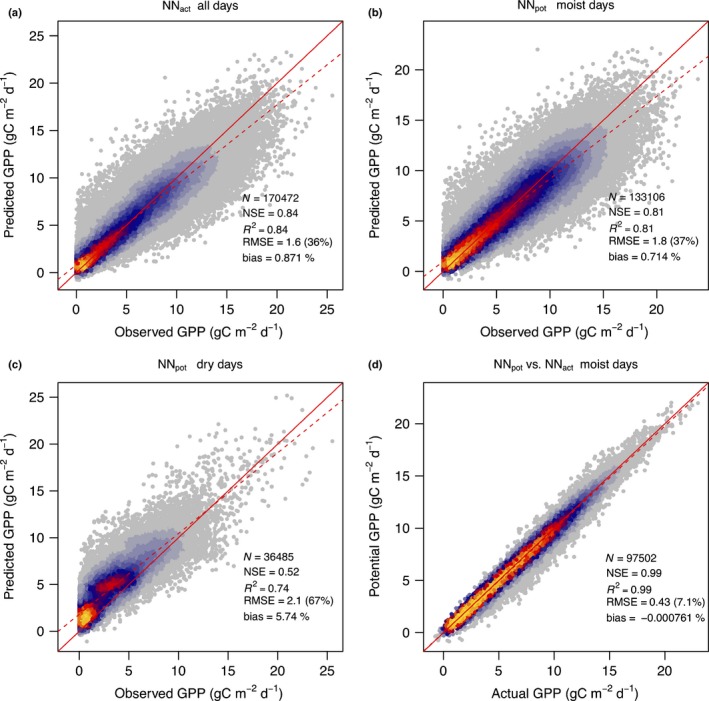
Neural network (NN)‐based predicted vs observed gross primary productivity (GPP). (a) Predicted values are based on the NN model estimating actual light use efficiency, NN act, using all input variables (temperature, vapour pressure deficit (VPD), photosynthetically active radiation (PAR), soil moisture) and ‘all days’ data. (b) Predicted values are based on the NN model estimating potential light use efficiency, NN pot, trained at data from days above the soil moisture threshold (‘moist days’), using temperature, VPD and PAR as input and evaluated only on ‘moist days’ data. (c) Same as (b) but evaluated on ‘dry days’ data. (d) Predicted values based on NN pot vs predicted values based on NN act, evaluated only on ‘moist days’ data. NSE, Nash‐Sutcliffe model efficiency; RMSE, root‐mean‐square error.
Figure 3.
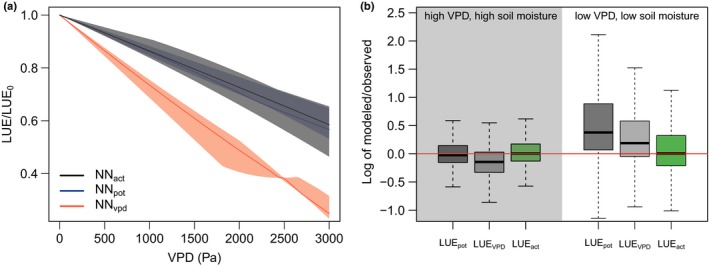
(a) Sensitivity of light use efficiency (LUE) to vapour pressure deficit (VPD), derived from different neural network (NN) setups. The evaluation of sensitivity is performed by holding all predictors, except VPD, at their pre‐drought median (across 20 d preceding drought, identified by fLUE deviation from 1). Shown is the median and the 40–60% quantile range of LUE values, normalized relative to LUE(VPD = 0), pooled across sites for models NN act, NN pot and NNVPD (see text and Fig. 1). (b) Distribution of the bias of predicted LUE, based on different NN setups. Biases are evaluated for days with low VPD (below 10% quantile) and low soil moisture (below 0.25 relative soil water content, left) and high VPD (above 90% quantile) and high soil moisture (above 0.75 relative soil water content, right). Boxes represent the interquartile range of values (Q 25, Q 75, logarithm of modelled over observed LUE), whiskers cover Q 25 − 1.5 × (Q 75 − Q 25) to Q 75 + 1.5 × (Q 75 − Q 25). Data are for NN predictions using soil moisture from the SWBM model and represent pooled sites from clusters ‘cDD’ and ‘cGR’ (see ‘Materials and Methods’, ‘Site clustering’).
NN training
Feed‐forward artificial NNs (one hidden layer) are trained (R packages ‘nnet’ (Venables & Ripley, 2002) and ‘caret’ (Kuhn, 2016)) using repeated (five times) five‐fold cross‐validation, where 75% of the data are used for training in each iteration. The learning rate decay rate is set to 0.1 and the number of nodes in the hidden layer is sampled from 4 to 20 (step size 2). The best‐performing NN (by root‐mean‐square error (RMSE)) is selected and the same procedure is repeated five times. In order to reduce scatter in time series, we used the mean across repetitions for further analyses. All predictors are scaled by range to within 0 and 1. NN training is performed for multiple soil moisture datasets (see subsection ‘Soil moisture’) separately. In order to enhance the robustness of NN models under uncertain soil moisture data, we use the mean across the resulting set of fLUE realizations for further analyses.
Soil moisture
Soil moisture data are based on direct measurements, provided through the FLUXNET 2015 dataset, and five alternative bucket‐type models. Measured soil moisture is provided in units of volume water per volume soil. Where separate data for multiple depths were available, we used them as individual predictors for NN training. As a result of the limited observational soil moisture data availability and mostly unavailable soil moisture data for deep soil layers, we also used simulated soil moisture, provided by alternative, bucket‐type soil water balance models, described later.
SPLASH
SPLASH (Davis et al., 2017) is based on a Priestley–Taylor formulation for the simulation of evapotranspiration (ET). Two alternative water‐holding capacities (‘bucket depth’) are used: 150 mm (as in Davis et al., 2017) and 220 mm (as for the SWBM model, see Orth et al., 2013).
SWBM
SWBM (Orth et al., 2013 ) uses measured net radiation from local measurements (FLUXNET 2015 data) and generates runoff before the bucket water‐holding capacity (220 mm) is reached (see Eqn 3 in Orth et al. (2013), α = 6.4 used here). Similarly, an empirical function down‐scales the fraction of ET to net radiation as a function of soil water content (Eqn 2 in Orth et al. (2013), γ = 0.06 used here).
ET‐driven bucket
The soil water balance is simulated using precipitation and latent heat flux, measured at the FLUXNET sites. The latent heat flux is converted to mass H2O using a constant conversion factor of 2.26476 × 106 J mm−1. Latent heat flux data from FLUXNET 2015 (variable LE_F_MDS) are cleaned first if > 80% of the underlying half‐hourly data are gap‐filled, and then gap‐filled using NNs (temperature, PAR, VPD and ET simulated by the SPLASH model as predictors, using R package ‘nnet’ (Venables & Ripley, 2002) and ‘caret’ (Kuhn, 2016), single hidden layer, 20 nodes, 10‐fold cross‐validated). The water‐holding capacity of the ET‐driven buckets is set to 220 mm. Two bucket versions are used. One in which no runoff is generated before the soil water‐holding capacity is reached, and one in which runoff is generated before as in the SWBM model.
All models are driven by observed precipitation, measured at the FLUXNET sites.
GPP data
Daily data are used from the FLUXNET 2015 Tier 1 dataset, downloaded on 13 November 2016. We use GPP based on the night‐time partitioning method, and the variable u‐star threshold method, named GPP_NT_VUT_REF. In the FLUXNET 2015 dataset, daily values are sums over half‐hourly data. We use only daily values in which < 50% of the respective half‐hourly data are gap‐filled. We further remove data points in which the daytime and night time methods (GPP_DT_VUT_REF and GPP_NT_VUT_REF, resp.) are inconsistent, that is, the upper and lower 2.5% quantiles of the difference between each method's GPP quantification. Finally, we remove all negative daily GPP values.
Greenness (fAPAR) data
We use MODIS EVI (MOD13Q1, 16 d, 250 m, Collection 5) and tested MODIS fraction of PAR (FPAR) (MOD15A2, 8 d, 1 km) data to quantify fAPAR. As a result of its higher spatial resolution, smaller scatter and smaller tendency to saturate at high values (Fig. S1), EVI is preferred here and all results below are based on analyses with EVI data. Data were downloaded for the pixel surrounding each flux tower location using the ‘MODIStools’ R package. Data were cleaned, eliminating contamination associated with clouds, shadows and snow/ice, and were interpolated to daily values using a Savitzky–Golay smoothing filter (‘signal’ R package) of order 3 and length 31 d. This generally maintains the full seasonal amplitude, crucial for analyses performed here, but does not fully remove noise.
Site selection
We evaluated fLUE for 135 sites of the total of 166 sites in the FLUXNET Tier 1 dataset, where modelled soil moisture gave consistent results across different models and was consistent with observed soil moisture where available. For 63 sites, the available cleaned data were either too small (< 500 d, 24 sites) or NN results failed performance criteria. Primary criteria, excluding 14 sites, were as follows: mean LUEact during fLUE drought days had to be smaller than LUEpot; RMSE of LUEact or LUEpot had to be smaller than 2.8 g C mol−1; R 2 of LUEact and LUEobs had to be > 0.5; R 2 of LUEpot and LUEobs had to be > 0.3. Additional performance criteria, excluding 19 sites, plus six sites excluded by visual inspection, are described in Methods S1. The remaining 71 sites provide 233 369 d of data and were used for subsequent analyses. These are listed in Table 1.
Table 1.
FLUXNET Tier 1 sites in clusters cDD, cGR, cLS and cNA
| Site | Longitude | Latitude | Start | End | IGBP class | Cluster | Reference |
|---|---|---|---|---|---|---|---|
| AU‐ASM | 133.25 | −22.28 | 2010 | 2013 | ENF | cDD | Cleverly (2011) |
| AU‐DaP | 131.32 | −14.06 | 2007 | 2013 | GRA | cDD | Beringer (2013b) |
| AU‐Fog | 131.31 | −12.55 | 2006 | 2008 | WET | cDD | Beringer (2013e) |
| AU‐Stp | 133.35 | −17.15 | 2008 | 2014 | GRA | cDD | NA |
| SD‐Dem | 30.48 | 13.28 | 2005 | 2009 | SAV | cDD | Sjöström et al. (2008) |
| SN‐Dhr | −15.43 | 15.4 | 2010 | 2013 | SAV | cDD | NA |
| US‐SRG | −110.83 | 31.79 | 2008 | 2014 | GRA | cDD | Biederman et al. (2016) |
| US‐SRM | −110.87 | 31.82 | 2004 | 2014 | WSA | cDD | Scott (2016) |
| US‐Ton | −120.97 | 38.43 | 2001 | 2014 | WSA | cDD | Baldocchi (2016a) |
| US‐Var | −120.95 | 38.41 | 2000 | 2014 | GRA | cDD | Baldocchi (2016b) |
| ZM‐Mon | 23.25 | −15.44 | 2000 | 2009 | DBF | cDD | Merbold et al. (2011) |
| AR‐Vir | −56.19 | −28.24 | 2009 | 2012 | ENF | cGR | Posse et al. (2016) |
| AU‐Ade | 131.12 | −13.08 | 2007 | 2009 | WSA | cGR | Beringer (2013a) |
| AU‐DaS | 131.39 | −14.16 | 2008 | 2014 | SAV | cGR | Beringer (2013c) |
| AU‐Dry | 132.37 | −15.26 | 2008 | 2014 | SAV | cGR | Beringer (2013d) |
| AU‐Gin | 115.71 | −31.38 | 2011 | 2014 | WSA | cGR | NA |
| AU‐How | 131.15 | −12.49 | 2001 | 2014 | WSA | cGR | Eamus et al. (2001) |
| AU‐Whr | 145.03 | −36.67 | 2011 | 2014 | EBF | cGR | Beringer (2013f) |
| CN‐Qia | 115.06 | 26.74 | 2003 | 2005 | ENF | cGR | Yu et al. (2006) |
| FR‐LBr | −0.77 | 44.72 | 1996 | 2008 | ENF | cGR | Berbigier et al. (2001) |
| FR‐Pue | 3.6 | 43.74 | 2000 | 2014 | EBF | cGR | Rambal et al. (2004) |
| IT‐Cp2 | 12.36 | 41.7 | 2012 | 2014 | EBF | cGR | Fares & Loreto (2014) |
| IT‐Cpz | 12.38 | 41.71 | 1997 | 2009 | EBF | cGR | Garbulsky et al. (2008) |
| IT‐Noe | 8.15 | 40.61 | 2004 | 2014 | CSH | cGR | Spano et al. (2006) |
| IT‐Ro1 | 11.93 | 42.41 | 2000 | 2008 | DBF | cGR | Rey et al. (2002) |
| IT‐SRo | 10.28 | 43.73 | 1999 | 2012 | ENF | cGR | Matteucci et al. (2015) |
| AU‐Wom | 144.09 | −37.42 | 2010 | 2012 | EBF | cLS | NA |
| CH‐Oe1 | 7.73 | 47.29 | 2002 | 2008 | GRA | cLS | Ammann et al. (2007) |
| CN‐Cng | 123.51 | 44.59 | 2007 | 2010 | GRA | cLS | Dong et al. (2011) |
| CZ‐wet | 14.77 | 49.02 | 2006 | 2014 | WET | cLS | NA |
| DE‐Akm | 13.68 | 53.87 | 2009 | 2014 | WET | cLS | NA |
| DE‐Geb | 10.91 | 51.1 | 2001 | 2014 | CRO | cLS | Anthoni et al. (2004) |
| DE‐Hai | 10.45 | 51.08 | 2000 | 2012 | DBF | cLS | Knohl et al. (2003) |
| DK‐Sor | 11.64 | 55.49 | 1996 | 2014 | DBF | cLS | Pilegaard et al. (2001) |
| FR‐Fon | 2.78 | 48.48 | 2005 | 2014 | DBF | cLS | Migliavacca et al. (2010) |
| IT‐Col | 13.59 | 41.85 | 1996 | 2014 | DBF | cLS | Van Dijk & Dolman (2004) |
| IT‐PT1 | 9.06 | 45.2 | 2002 | 2004 | DBF | cLS | Migliavacca et al. (2009b) |
| IT‐Ren | 11.43 | 46.59 | 1998 | 2013 | ENF | cLS | Marcolla et al. (2005) |
| IT‐SR2 | 10.29 | 43.73 | 2013 | 2014 | ENF | cLS | Matteucci et al. (2015) |
| IT‐Tor | 7.58 | 45.84 | 2008 | 2014 | GRA | cLS | Galvagno et al. (2013) |
| NL‐Hor | 5.07 | 52.24 | 2004 | 2011 | GRA | cLS | Vandermolen et al. (2004) |
| NL‐Loo | 5.74 | 52.17 | 1996 | 2013 | ENF | cLS | Dolman et al. (2002) |
| RU‐Fyo | 32.92 | 56.46 | 1998 | 2014 | ENF | cLS | Kurbatova et al. (2008) |
| US‐GLE | −106.24 | 41.37 | 2004 | 2014 | ENF | cLS | NA |
| US‐Me2 | −121.56 | 44.45 | 2002 | 2014 | ENF | cLS | Sun et al. (2004) |
| US‐MMS | −86.41 | 39.32 | 1999 | 2014 | DBF | cLS | Philip (2016) |
| US‐UMB | −84.71 | 45.56 | 2000 | 2014 | DBF | cLS | Gough et al. (2008) |
| US‐UMd | −84.7 | 45.56 | 2007 | 2014 | DBF | cLS | Curtis (2016) |
| US‐WCr | −90.08 | 45.81 | 1999 | 2014 | DBF | cLS | Desai (2016a) |
| BE‐Bra | 4.52 | 51.31 | 1996 | 2014 | MF | cNA | Carrara et al. (2003) |
| BE‐Vie | 6 | 50.31 | 1996 | 2014 | MF | cNA | Aubinet et al. (2001) |
| CH‐Fru | 8.54 | 47.12 | 2005 | 2014 | GRA | cNA | Eugster & Zeeman (2006) |
| CH‐Lae | 8.37 | 47.48 | 2004 | 2014 | MF | cNA | Göckede et al. (2008) |
| DE‐Gri | 13.51 | 50.95 | 2004 | 2014 | GRA | cNA | Gilmanov et al. (2007) |
| DE‐Kli | 13.52 | 50.89 | 2004 | 2014 | CRO | cNA | Ceschia et al. (2010) |
| DE‐Obe | 13.72 | 50.78 | 2008 | 2014 | ENF | cNA | Zimmermann et al. (2006) |
| DE‐RuR | 6.3 | 50.62 | 2011 | 2014 | GRA | cNA | Borchard et al. (2015) |
| DE‐Spw | 14.03 | 51.89 | 2010 | 2014 | WET | cNA | NA |
| DE‐Tha | 13.57 | 50.96 | 1996 | 2014 | ENF | cNA | Grünwald & Bernhofer (2007) |
| DK‐NuF | −51.39 | 64.13 | 2008 | 2014 | WET | cNA | Westergaard‐Nielsen et al. (2013) |
| FI‐Hyy | 24.3 | 61.85 | 1996 | 2014 | ENF | cNA | Vesala et al. (2005) |
| FI‐Sod | 26.64 | 67.36 | 2001 | 2014 | ENF | cNA | Suni et al. (2003) |
| IT‐Isp | 8.63 | 45.81 | 2013 | 2014 | DBF | cNA | Ferréa et al. (2012) |
| IT‐Lav | 11.28 | 45.96 | 2003 | 2014 | ENF | cNA | Cescatti & Zorer (2003) |
| IT‐MBo | 11.05 | 46.01 | 2003 | 2013 | GRA | cNA | Migliavacca et al. (2009a) |
| JP‐SMF | 137.08 | 35.26 | 2002 | 2006 | MF | cNA | Yamazaki et al. (2013) |
| US‐Ha1 | −72.17 | 42.54 | 1991 | 2012 | DBF | cNA | Urbanski et al. (2007) |
| US‐Los | −89.98 | 46.08 | 2000 | 2014 | WET | cNA | Desai (2016b) |
| US‐Syv | −89.35 | 46.24 | 2001 | 2014 | MF | cNA | Desai (2016b,2016c) |
| US‐Wi4 | −91.17 | 46.74 | 2002 | 2005 | ENF | cNA | Noormets et al. (2008) |
Cluster refers to the clustering of sites according to their greenness response and sensitivity to soil moisture (cDD: drought‐deciduous, 11 sites; cGR: evergreen, 15 sites; cLS: low sensitivity to soil moisture, 23 sites; and cNA: not affected by low soil moisture, 21 sites). Longitude and latitude in decimal degrees. Start and End are the first and last years in which data are available for the respective site. IGBP class is the vegetation class (GRA, grasslands; SAV, savannah; WSA, woody savannah; ENF, evergreen needleleaved forest; EBF, evergreen broadleaved forest; DBF, deciduous broadleaved forest; CSH, closed shrubland; WET, wetland; CRO, cropland; MF, mixed forest). NA, not available.
Site clustering
First, we identified 21 sites that were not affected by low soil moisture during the period in which measurements were available, that is where available values of relative soil moisture (as a fraction of water‐holding capacity) did not fall below 0.25. This cluster is referred to as cNA (not affected) in the figures below. Second, we identified 23 sites that exhibited a particularly small reduction in fLUE at low soil moisture (cLS, low sensitivity). After removing cNA sites from the 71 sites investigated, cLS sites were identified based on the magnitude of the fLUE reduction with soil moisture approaching zero (termed fLUE0, see Fig. S2), and contained sites with fLUE0 > 0.8. Third, we used the remaining sites (26) to distinguish between clusters of sites with similar responses in greenness and LUE during droughts. We used a k‐means algorithm (R package ‘cluster’ (Maechler et al., 2016)) with predefined k = 2 (two clusters). Each site formed one observation, with data points given by a vector of length six, containing the median relative reduction of greenness and of fLUE, aggregated across drought events within the respective site and averaged across days −20 − (−1), 0–19 and 20–39 after fLUE drought onset (day 0 is the fLUE drought onset). This separates sites into a cluster with no reduction in greenness and an intermediate reduction in fLUE (cGR, evergreen) and a cluster with a clear greenness reduction, accompanied by a strong reduction in fLUE (cDD, drought‐deciduous).
Results
NN performance
Across all sites and days (pooled), the NN‐based GPP predictions following Eqn (Eqn 1) and using LUEact achieve an R 2 of 0.84 against observed GPP, an RMSE of 1.6 g C m−2 d−1 and a negligible bias (Fig. 2). A similar performance is achieved by NNpot for the subset of data above the soil moisture threshold (‘moist days’). It should be noted that NNpot refers to the ‘model’, whereas LUEpot refers to its prediction of LUE. By contrast, the NNpot‐based prediction of GPP is consistently biased high during days below the soil moisture threshold (‘dry days’). This is a direct consequence of the method and performance criteria (LUEpot > LUEact). When comparing LUEact directly with LUEobs = GPPobs/(fAPAREVI × PAR), R 2 is reduced to 0.7 (Fig. S3). During moist days, the two NN‐based predictions, in which LUEact includes soil moisture as a predictor and LUEpot does not, agree closely (R 2 = 0.99), indicating that NNpot and NNact capture very similar sensitivities to VPD, temperature and PAR during moist days. This is confirmed by the evaluation of sensitivities of different NN setups to VPD (Fig. 3a).
The sensitivity to VPD warrants particular attention. The NN‐based separation between soil moisture and VPD effects is subject to the accuracy of their sensitivities to partly covarying VPD and soil moisture. We tested this using an additional setup, NNVPD, trained at all data, but without soil moisture as a predictor, and evaluated its performance under conditions in which soil moisture and VPD are decoupled, that is, under simultaneously high (low) soil moisture and VPD. In general, NNVPD exhibits a higher sensitivity than NNact and NNpot to VPD (Fig. 3a). Under conditions in which soil moisture is high (non‐limiting) and VPD is high (limiting), the strong sensitivity of NNVPD to VPD leads to an underestimation of LUEVPD compared with LUEobs (Fig. 3b). By contrast, LUEact and LUEpot are both unbiased with respect to LUEobs and hence accurately capture effects of VPD alone. Under conditions of low soil moisture (limiting) and low VPD (non‐limiting), the NNpot model strongly overestimates LUE. Also, LUEVPD is biased high compared with LUEobs under dry soil and moist air conditions. This indicates that information contained in VPD is insufficient to fully capture dryness effects – even with a model that features a relatively high sensitivity to VPD. By contrast, NNact yields unbiased LUE estimates also under these conditions, indicating that its sensitivity to soil moisture alone is accurate.
Time series
The evaluation of fLUE reveals substantial soil moisture impacts across a wide range of climatic zones and ecosystem types. Periods of significant fLUE reductions below 1.0 (referred to as ‘fLUE droughts’) are seasonally recurring in dry grasslands (e.g. US‐Var), savannahs (e.g. US‐Ton, AU‐How, AU‐DaS), shrublands (e.g. IT‐Noe), broadleaf evergreen (e.g. FR‐Pue, FR‐LBr) and deciduous (e.g. IT‐Ro1) forests, and occur sporadically in needleleaf evergreen ecosystems in the temperate (e.g. DE‐Tha) and boreal (e.g. FI‐Hyy) zones (Figs 4, S4).
Figure 4.
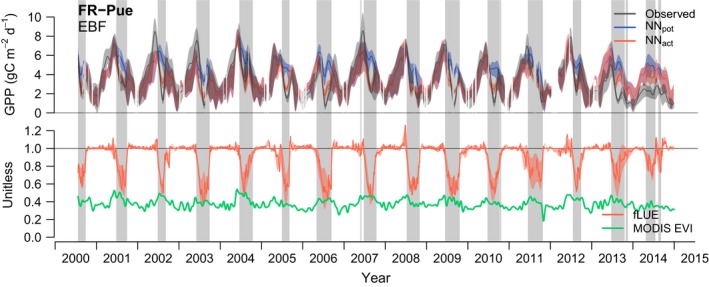
Time series for site ‘FR‐Pue’ (more sites are shown in Supporting Information Fig. S4). Upper panel: time series of observed values and neural network (NN)‐based estimates of gross primary productivity (GPP). Curves are splined daily values with shaded ranges representing splines of minimum and maximum values within 7‐d sliding windows. Lower panel: fractional reduction in light use efficiency due to soil moisture (fLUE) and the fraction of absorbed photosynthetically active radiation (fAPAR) based on MODIS Enhanced Vegetation Index (EVI) data. The shaded range around fLUE represents the splined minimum and maximum fLUE across its quantifications based on different soil moisture datasets, and the solid line is its mean. The site name is given in the upper left corner, together with the vegetation type (EBF, evergreen broadleaved forest). Grey vertical bars illustrate periods identified as ‘droughts’, that is, where fLUE falls below a site‐specific threshold (see the Materials and Methods section).
fLUE droughts cover from a few days per year at mesic sites to over 90% of days in desert sites (see also Fig. S5). Impacts of known droughts, for example summer 2003 in Europe, are reflected by particularly strong fLUE reductions, clearly visible at sites with sporadically occurring fLUE droughts (e.g. FR‐LBr and DE‐Tha, Fig. S4). Anomalously high GPP deficits, that is cumulative fLUE deviations from 1, may trigger legacy effects on ecosystem structure via mortality and aboveground primary productivity (Zhang et al., 2013; Anderegg et al., 2015). We investigated whether high cumulative fLUE deficits are reflected in greenness anomalies, but found no clear relationship between the two (not shown).
Aligned and aggregated by drought events
To distill regularities in the co‐evolution of multiple variables during the course of recurring fLUE droughts, all events (grey bands in Fig. 4) per site are aligned by their fLUE drought onset and data are aggregated across drought events. Examples from clusters cGR (FR‐Pue and AU‐DaS) and cDD (US‐Var) are shown in Fig. 5 (further examples in Fig. S7). At all sites, fLUE shows an abrupt transition, whereas soil moisture starts its gradual decline well before the onset of fLUE droughts. This reveals a sharp delineation between a soil moisture‐controlled regime below a given threshold and a regime in which changes in soil moisture do not affect LUE. Although soil moisture follows a very narrow typical course during progressive droughts, VPD exhibits more day‐to‐day variability and does not follow the same pattern of a continued decline during drought events at all sites (Fig. 5). The fLUE reductions during drought periods range from c. 10% at mesic sites (DE‐Tha, FI‐Hyy, Fig. S7) to over 90% at the US‐Var grassland site. The course of vegetation greenness during drought periods varies substantially between sites and gives rise to a distinction between ecosystems with similar structural responses to drought (see later).
Figure 5.
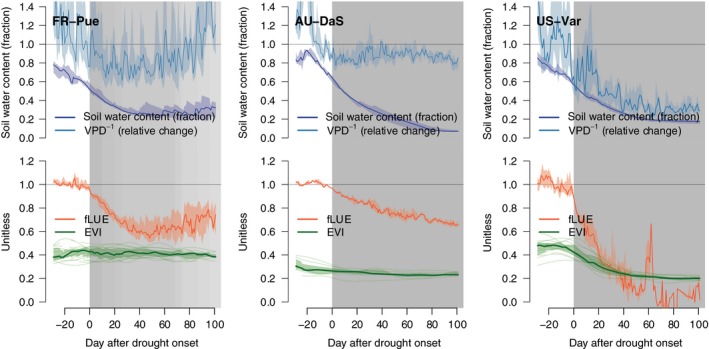
Evolution of soil moisture and vapour pressure deficit (VPD, given in the top panel of each sub‐plot) and fractional reduction in light use efficiency (fLUE, red) and MODIS Enhanced Vegetation Index (EVI) data (second panel, green) throughout drought events. Values shown by VPD −1 (light blue) are calculated by first normalizing values relative to the median of VPD values during 20 d before drought onset and then taking the inverse. Soil moisture values are not normalized, but represent a fraction of water‐holding capacity. Coloured shaded ranges represent the upper and lower quartiles across drought events. The vertical grey shading illustrates the length of individual fLUE drought events. Darker grey shades indicate multiple aligned drought events.
Site clustering
After grouping sites not affected by low soil moisture into cluster cNA (‘not affected’, 21 sites) and sites exhibiting a particularly low sensitivity to soil moisture into cluster cLS (‘low sensitivity’, 23 sites, see Materials and Methods), we clustered the remaining 26 sites according to the co‐evolution of fLUE and EVI during droughts. An overview of all sites by clusters is given in Fig. S5. The stark difference in greenness changes is the dominant factor that separates sites into clusters cDD (‘drought‐deciduous’, 11 sites) and cGR (‘evergreen’, 15 sites) (see Fig. 6).
Figure 6.
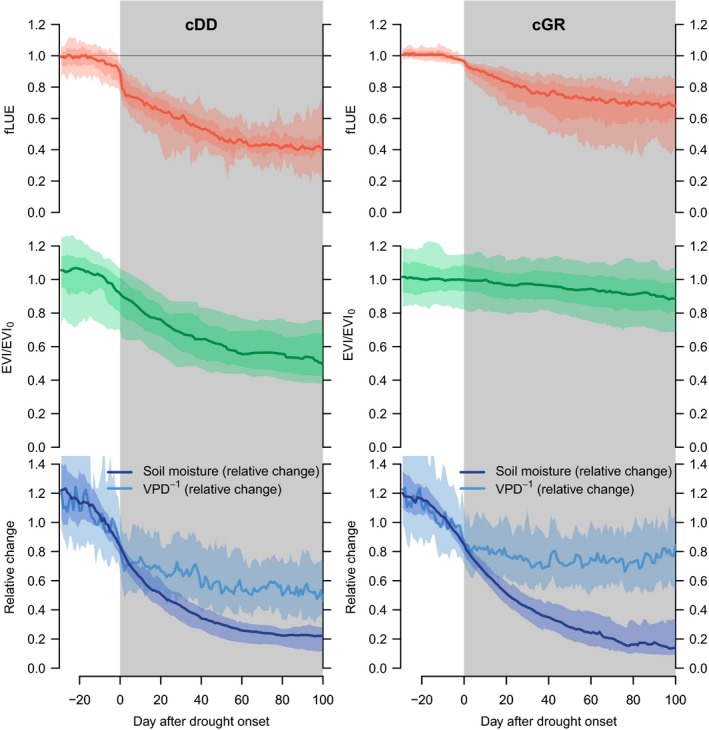
Evolution of variables throughout drought periods, aggregated by clusters cDD (left, drought‐deciduous cluster) and cGR (right, evergreen cluster). Top: fractional reduction in light use efficiency (fLUE). Middle: changes in Enhanced Vegetation Index (EVI), relative to its value before the onset of droughts (median across preceding 20 d). Bottom: changes in soil moisture and vapour pressure deficit (VPD), relative to values before the onset of droughts (median across preceding 20 d). VPD −1 is shown here for a better comparison with soil moisture variations and is calculated as the inverse of the relative VPD change. Data are aligned by the drought onset and aggregated across each event and site in the respective cluster. Bold lines represent the median, and shaded areas represent the upper and lower 10% and 25% quantiles across all events and all sites pooled within a cluster.
fLUE is reduced most strongly in cDD with values reaching 0.4. This is a 60% reduction in LUE from pre‐drought values due to soil moisture alone. In cluster cGR, fLUE declines to typical values of c. 0.7 (30% reduction). In cGR, EVI shows no general response to drought, whereas, in cDD, greenness starts to decline before soil moisture effects on LUE become apparent. Similarly, soil moisture and VPD−1 (the inverse of the relative VPD change is shown in Fig. 6) gradually decline well before the onset of fLUE droughts, but start to diverge directly thereafter.
Functional relationship
The functional relationship between fLUE and soil moisture is analysed by plotting pooled fLUE values against soil moisture (mean across multiple datasets) (Fig. 7). Its general form is similar across clusters, but shows substantial differences in the magnitude of the fLUE reduction with soil moisture approaching zero (fLUE0). The distribution of fLUE values at soil moisture below 0.1 from pooled data exhibits three peaks (Fig. 7a). These are associated with distinct fLUE0 values within clusters. Reflecting the temporal course shown in Figs 5 and 6, the strongest reduction in fLUE as a function of soil moisture is recorded for cDD, for which most common fLUE0 values are c. 0.4, but can reach values below 0.1 at sites at which GPP approaches zero, whereas EVI (and FPAR) remain substantially higher (e.g. site US‐Var). The most common magnitude of fLUE0 in cGR is c. 0.7, but individual sites (e.g. IT‐Noe) show a stronger reduction. By definition, sites in cNA are not affected by very low soil moisture.
Figure 7.
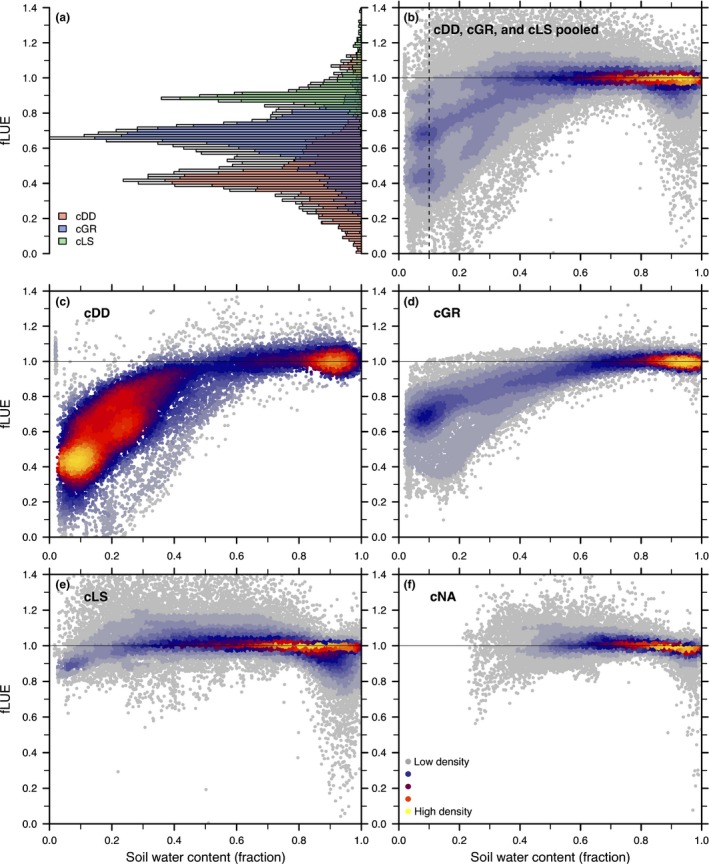
Functional relationship of the fractional reduction in light use efficiency due to soil moisture (fLUE) vs soil moisture by cluster. (a) Distribution of fLUE values at a fractional soil water content below 0.1. Grey bars represent pooled data from drought‐deciduous (cDD), evergreen (cGR) and low sensitivity (cLS) clusters. Coloured bars represent data by clusters. (b) Functional relationship of fLUE vs soil moisture for pooled data from clusters cDD, cGR and cLS. (c–f) Functional relationship by cluster. Colours in the point cloud represent a Kernel Density Estimation (R package ‘lsd’; Schwalb et al., 2015) and visualize overlapping points.
Above a relative soil water content of 0.5, effects on LUE are negligible. This is true for all clusters and is consistent with previous studies (Reichstein, 2003; Granier et al., 2007). An exception is the reduction in fLUE with soil moisture approaching saturation, as apparent at some sites, mostly in cLS (see also fLUE1 column in Fig. S5). This indicates negative effects of very wet soil conditions on GPP. Sites in clusters cDD and cGR show no fLUE reductions at the high end of the soil moisture range. Cluster cLS is, by definition, characterized by small fLUE reductions.
GPP loss
Clusters identified by drought responses exhibit a clear relationship to climate (Fig. 8). Aridity, quantified by precipitation/potential evapotranspiration (P/PET) (ratio of annual totals) or the mean of daily actual evapotranspiration (AET)/PET, is systematically related to the association of sites and clusters. This ranges from cDD at the arid end of the spectrum to cGR, cLS and cNA at the moist end.
Figure 8.
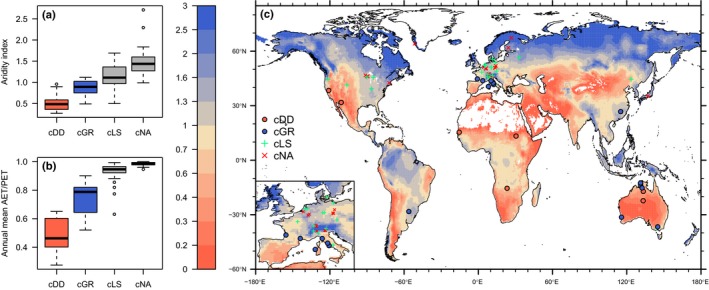
(a) Aridity index by cluster, defined as the ratio of annual precipitation (P) over potential evapotranspiration (PET), here calculated for all years in which data were available for the respective sites. Precipitation data are from the FLUXNET 2015 Tier 1 dataset; PET is calculated following the Priestly–Taylor equation, as implemented in the SPLASH model (Davis et al., 2017). Clusters are defined based on vegetation responses to drought, with cDD referring to drought‐deciduous, cGR to evergreen, and cLS to vegetation with low sensitivity to low soil moisture. Sites in cNA are not affected by low soil moisture. (b) Annual mean actual evapotranspiration (AET) over PET by cluster. AET and PET are calculated using the SPLASH model (Davis et al., 2017). (c) Distribution of sites and clusters across the globe. Colours of land areas represent the aridity index (P/PET) with data from (Greve et al., 2014). In (a,b), boxes represent the interquartile range of values (Q 25, Q 75,), whiskers cover Q 25 − 1.5 × (Q 75 − Q 25) to Q 75 + 1.5 × (Q 75 − Q 25).
The magnitude of additional, soil moisture‐related reductions in annual GPP follows the same pattern (Fig. 9). We find that separate effects of soil moisture reduce annual GPP by up to c. 40% each year, and that the magnitude of annual GPP reductions scales linearly with the annual mean ratio of AET/PET (Fig. 9a). Annual GPP loss due to low soil moisture is 15–45% at sites in cluster cDD, located in arid and semi‐arid regions (AET/PET < 0.6), and 5–35% at sites in cGR, located in regions of intermediate aridity (0.6 < AET/PET < 0.9, Fig. 9a). At relatively humid sites (AET/PET > 0.9), soil moisture‐limited conditions are sporadic and average annual GPP loss due to soil moisture is relatively small, but highly variable between years (Fig. S4).
Figure 9.
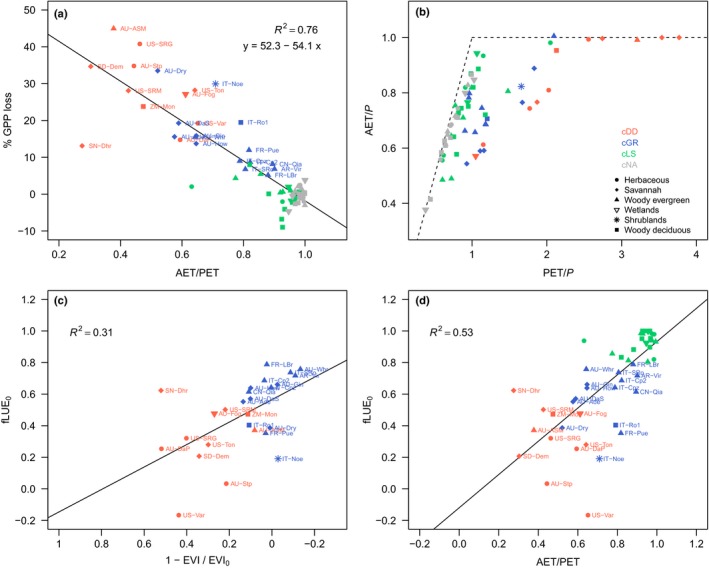
(a) Average annual gross primary productivity (GPP) loss due to soil moisture effects vs the annual average ratio of actual over potential evapotranspiration (AET/PET). (b) Sites in Budyko space (P is annual total precipitation). (c) Maximum reduction in the fractional reduction in light use efficiency (fLUE) with soil moisture approaching zero (fLUE 0) vs greenness change. 1 − EVI/EVI 0 quantifies the degree of drought‐deciduousness of the vegetation (EVI (Enhanced Vegetation Index) quantifies vegetation greenness, MODIS data), quantified as the relative reduction in greenness during fLUE droughts. Values of 1 − EVI/EVI 0 = 0 represent no response in greenness during fLUE drought events. The black line represents a linear fit to values from sites in clusters cDD and cGR. (d) fLUE 0 vs AET/PET. The black line represents a linear fit to values from sites in clusters cDD, cGR and cLS. Clusters are defined based on vegetation responses to drought, with cDD referring to drought‐deciduous, cGR to evergreen, and cLS to vegetation with low sensitivity to low soil moisture. Sites in cNA are not affected by low soil moisture. Symbols represent vegetation types, colours represent clusters (see legend in b).
Relationships to water table depth (WTD) and soil properties
To test whether the low fLUE sensitivity to soil moisture in cLS is related to hydrological settings, we extracted WTD values for each site from a global dataset provided at a resolution of 1 km (Fan et al., 2013) and an alternative dataset provided at a 0.1° (c. 10 km) resolution (de Graaf et al., 2015). However, WTD from neither dataset showed any predictive power in explaining the variations in the maximum reduction in fLUE (fLUE0, adjusted R 2 = −0.02 using data by Fan et al. (2013) and adjusted R 2 = −0.01 using data by de Graaf et al. (2015)). Similarly, information on soil drainage conditions and available water content, extracted from the Harmonized World Soil Database (Shangguan et al., 2014) showed no power in explaining the patterns in the functional relationship between soil moisture and fLUE between clusters.
Discussion
The quantification of fLUE reveals the threshold, duration and magnitude of soil moisture limitation on GPP and is independent of the use of modelling assumptions or other a priori‐specified functional relationships. Instead, it relies on empirical patterns identified by machine learning and benefits from an unprecedented wealth of data, accessible through the FLUXNET 2015 data release.
NNs, as applied here, cannot account for lagged relationships between predictors and target variables. By targeting LUE, we eliminate effects of ecosystem structural change, which responds more slowly than leaf‐level parameters that determine LUE (stomatal and mesophyll conductance, maximum assimilation rate). Nevertheless, a remaining fraction of variability (see Fig. 2) may not be explainable by the daily environmental forcing data used here, but instead relates to measurement imprecision and biotic responses (Richardson et al., 2007). The latter may also be induced by a shift in vegetation composition during the period of flux measurements, if not captured by greenness data (Ahmed et al., 2017).
Relationships to drought indices
The quantification of fLUE provides an impact‐oriented identification of droughts, related to ‘agricultural droughts’ (Trenberth et al., 2007). In climates with seasonally recurring water‐limited conditions, traditional statistical approaches based on anomalies relative to a mean seasonal cycle do not necessarily capture limiting conditions during the dry season (Zscheischler et al., 2014). This affects drought assessments based on widely used drought indices (Palmer drought severity index (PDSI), standardized precipitation index (SPI) and standardized precipitation–evapotranspiration index (SPEI)) (Schwalm et al., 2017), and other anomaly‐based approaches (Schwalm et al., 2010). The approach followed here does not rely on anomaly statistics, but is based on how the relationship between absorbed light and GPP changes, and thereby captures drought effects that operate through physiological mechanisms of water stress. It also identifies regularly recurring water‐stressed conditions (fLUE droughts) which are not captured by SPI or SPEI (Fig. 10). This highlights that climate anomaly‐based drought indices are not directly indicative of plant water stress and thus have limited power for the identification of drought impacts. By contrast, average daily AET/PET is more directly reflective of drought impacts on vegetation productivity.
Figure 10.
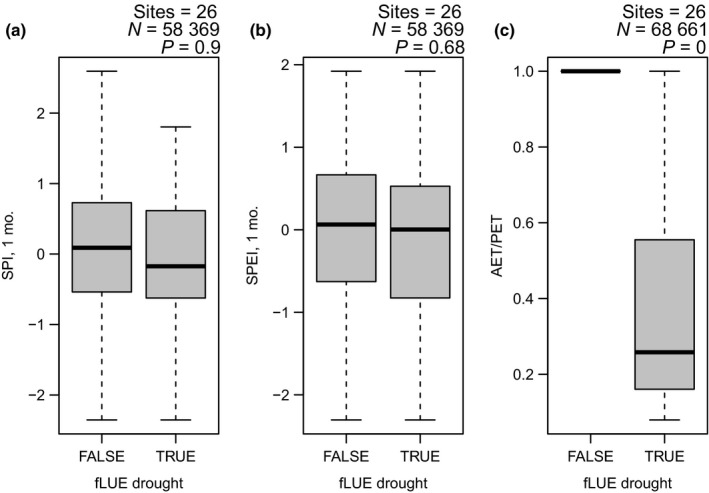
(a) Standardized precipitation–evapotranspiration index (SPEI, 1 month timescale), (b) standardized precipitation index (SPI, 1 month timescale) and (c) the ratio of actual over potential evapotranspiration (AET/PET) during droughts and non‐drought periods, as identified by the fractional reduction in light use efficiency (fLUE). SPI and SPEI were calculated using the R package ‘spei’ based on monthly total precipitation data from WATCH‐WFDEI (0.5°) (Weedon et al., 2014) extracted at site locations, covering the years 1990–2013, and (for SPEI) potential evapotranspiration based on Thornthwaite (1948). AET/PET was calculated using precipitation measured at FLUXNET and potential and actual evapotranspiration from the SPLASH model (Davis et al., 2017). The box for fLUE = FALSE is collapsed as all AET/PET values in respective days are 1.0. N is the total number of daily data points and P is the P value from an unpaired t‐test. Boxes represent the interquartile range of values (Q 25, Q 75) and whiskers cover Q 25 − 1.5 × (Q 75 − Q 25) to Q 75 + 1.5 × (Q 75 − Q 25).
Additional GPP loss
We identified soil moisture‐related losses in annual GPP of up to 40% (Fig. 9a). These are additional to effects by dry air (VPD) and drought‐induced loss of photosynthetically active tissue, reflected by reduced greenness. Multiple studies have indicated that remote sensing‐based GPP estimates tend to be biased high under dry conditions (Leuning et al., 2005; Turner et al., 2005; Pan et al., 2006; Verstraeten et al., 2006; Mu et al., 2007; Maselli et al., 2009). The results shown here suggest that soil moisture data will be crucial to resolve this bias. Semi‐arid regions exert a dominant control on the interannual terrestrial C balance and atmospheric CO2 growth rate (Poulter et al., 2014; Ahlström et al., 2015). The substantial and annually recurring soil moisture‐related GPP reductions found at almost all sites in the intermediate to dry part of a global aridity spectrum indicate that the resolution of drought‐related biases in global datasets is important for the accurate monitoring of vegetation activity and C cycle variability. It remains to be shown whether the accurate accounting for drought effects improves the weak performance of remote sensing‐based GPP models in the simulation of interannual variability in semi‐arid regions (Biederman et al., 2017).
Functional relationship for global predictions
The relationship between LUE, VPD and soil moisture, and its generality across different biomes and vegetation types, is needed to inform remote sensing‐based GPP products and as a benchmark for Earth System Models. The evaluation of the data from all pooled sites suggests three distinct groups of sites with values of the maximum fLUE reduction at very low soil moisture (fLUE0) clustering at c. 0.4, 0.7 and 0.9 (Fig. 7a). The prediction of this functional relationship and fLUE0 is key for the accurate modelling of soil moisture effects.
Independent of the clustering of fLUE0 values, we found stark differences in phenological responses (greenness change) to drought across sites. This greenness response‐based separation of sites coincides largely with the clusters of fLUE0 values in Fig. 7(a). We found that the degree of drought‐deciduousness of the vegetation explains c. 30% of the variation in maximum fLUE reductions (fLUE0) within clusters cDD and cGR (Fig. 9c). Aridity (annual average AET/PET) also emerges as a good predictor of fLUE0 variations and explains c. 50% of its variation within clusters cDD, cGR and cLS (Fig. 9d). Greenness changes and aridity may be extracted from global datasets for the prediction of fLUE0 and the modelling of soil moisture effects on GPP.
cDD and fAPAR data
We found that sites with the strongest fLUE reduction are simultaneously characterized by a clear drought phenology (cluster cDD). These sites are located in the driest climates (Fig. 8), are characterized by particularly low ratios of AET/P (Fig. 9b) and consist predominantly of grasslands and savannas (Fig. S5). This is consistent with the particularly strong soil moisture control found in arid and semi‐arid regions (Seneviratne et al., 2010; He et al., 2016; Nicolai‐Shaw et al., 2017).
Remotely sensed greenness is often used to estimate vegetation productivity, and relationships are commonly assumed to be strongest in drought‐deciduous vegetation, particularly in grasslands (Gamon et al., 1995; Goerner et al., 2009; Rossini et al., 2012; Verma et al., 2014; Ali et al., 2016; Konings et al., 2017). The parallel reduction in fLUE and EVI recorded at sites in cluster cDD highlights that the information contained in remotely sensed optical greenness indices does not capture the full extent of drought impacts on GPP. Consistent with previous studies that noted limited information in greenness data for the prediction of GPP (Goerner et al., 2009; He et al., 2016; Biederman et al., 2017), we found here that the relative reduction in EVI is smaller than the relative reduction in GPP. In parallel with phenological changes, LUE is strongly reduced, reflecting a correlation between LUE and greenness noted earlier (Sims et al., 2006). Hence, the often assumed direct relationship between relative changes in vegetation greenness and productivity in grasslands and other drought‐deciduous ecosystems (Gamon et al., 1995; Goerner et al., 2009) implies an underestimation of drought impacts on GPP. fLUE shows an even stronger decline during droughts in drought‐deciduous vegetation than in evergreen forest ecosystems.
The analysis presented here is centred around the prediction of LUE, whereby observational LUE, used as a target for NN training, is derived from GPP and remotely sensed fAPAR using Eqn (Eqn 1). This implies a linear relationship between fAPAR data and GPP, and the magnitude of the derived LUE variations during droughts is sensitive to the magnitude of simultaneous relative fAPAR variations. We used MODIS EVI data here to represent fAPAR for its high spatial resolution and relatively low scatter compared with MODIS FPAR, and note that absolute EVI values are generally lower than FPAR, implying higher absolute LUE values. However, our finding of strong LUE reductions in drought‐deciduous ecosystems is robust against the use of different greenness data products. We tested this by alternatively using MODIS FPAR data (not shown). The robustness of the derived relative LUE changes is a result of the linear relationship between EVI and MODIS FPAR across a wide range of values (Fig. S1). However, EVI tends to saturate less than FPAR and NDVI at high values (Huete et al., 2010), and should thus imply even smaller relative LUE variations and soil moisture impacts. Whether EVI is affected by significant PAR absorption by non‐photosynthetically active tissue, and thereby underestimates fAPAR reductions in seasonally ‘brown’ vegetation, remains to be addressed.
cGR and plant strategies
We found that sites with intermediate fLUE reductions are simultaneously characterized by evergreen, mostly woody, vegetation. The respective sites are located at intermediate aridity (Fig. 8). The separation of clusters along the aridity spectrum and in Budyko space (Budyko, 1974; Williams et al., 2012) (Fig. 9b) suggests alternative successful plant strategies, governed by water availability and its seasonality. Drought adaptation to maintain intact structure (e.g. deep rooting, adaptation to low leaf water potentials) and protection against LUE reductions and drought damage of green tissue are costly (van der Molen et al., 2011), and appear to be a successful plant strategy only at intermediate aridity, accessible mostly to woody vegetation. The dominance of short‐lived, drought‐deciduous vegetation indicates that the prevention of tissue damage under conditions with extensive soil moisture‐limited periods outweighs the costs of rebuilding senesced tissue. In particular, a low ratio of annual average AET/P (Fig. 9b) is indicative of a strong seasonality with asynchronicity of precipitation and radiation and limited surface water storage capacity (Milly, 1994; Potter et al., 2005; Williams et al., 2012), and appears to favour drought‐deciduous vegetation, for example grasslands. This is in contrast with the results of Williams et al. (2012), who found high AET/P values in grasslands. It should be noted, however, that both AET and PET used here are model‐derived and do not capture additional factors that may influence AET over different vegetation types (different surface–atmosphere coupling or drought sensitivity of stomatal conductance).
cLS, soil moisture data and WTD
Sites in cLS are generally located in intermediate to wet climates (Fig. 8), maintain a relatively high LUE during dry conditions and we derived only slight reductions related to soil moisture. At the same time, fLUE appears to be negatively affected by very wet conditions (Fig. 7). Together, this may indicate particular local hydrological conditions that enable plants to access water during prolonged periods without precipitation and that inhibit effective soil drainage and promote water‐logged, anaerobic soil conditions after high rainfall. GPP and stomatal conductance have been reported previously to respond negatively within a few days after the onset of water‐logging in laboratory experiments (Terazawa et al., 1992; Terazawa & Kikuzawa, 1994). In addition, at the ecosystem scale, persistent water‐logging in a boreal forest has been found to reduce surface conductance, ET and GPP over years (Ohta et al., 2014). Reduced LUE under very wet conditions across multiple sites, as found here, suggests that this phenomenon may be common in wet climates.
The soil moisture data used here are representative of the topsoil. Information on WTD across FLUXNET sites is not generally accessible, and whether plants access the saturated zone and are thus capable of withstanding dry conditions in the topsoil without effects on LUE is not generally known, and respective information is mostly lacking in published site descriptions. The possibility of important effects by access to groundwater on ecosystem fluxes and drought responses has been discussed previously (Reichstein et al., 2002). We could not find any relationship between fLUE sensitivity and WTD (Fan et al., 2013; Shangguan et al., 2014; de Graaf et al., 2015). In view of the scale and nature of the WTD data used here (1 and 10 km, model‐based), it may be worthwhile to revisit these relationships using actual, site‐specific data.
Soil moisture vs VPD
VPD and soil moisture are correlated at weekly to monthly timescales (Sulman et al., 2016). Also, at daily timescales, a correlation emerges, at least under dry soil conditions (Fig. S6). This underlies the use of only VPD data as surrogate for dryness in global GPP data products, and makes it difficult to unambiguously attribute respective predictive power in a machine‐learning context. We addressed this by assessing whether the sensitivities of different NN setups are accurate and lead to unbiased predictions under conditions in which only one of the two is expected to limit plant productivity. Our analysis confirms that NNact and NNpot pick up the same and appropriate sensitivity to VPD, and that NNact accurately captures the effects of low soil moisture, also when VPD is not limiting.
This separation of effects is enabled by the fact that training data include days in which only one of the two factors limits LUE. This reflects the high day‐to‐day variability in VPD and the known decoupling of VPD and soil moisture at short timescales (Seneviratne et al., 2010; Sulman et al., 2016). Mechanistically, this arises because VPD is not only affected by soil moisture, but also by the prevailing atmospheric advection and entrainment from the boundary layer (Raupach, 1991; Betts & Ball, 1995). Under wet conditions, soil moisture is not limiting for ET (Seneviratne et al., 2010) and thus does not control VPD. A correlation of VPD and soil moisture emerges under intermediately dry conditions. However, VPD and soil moisture become decoupled under very dry conditions and progressive fLUE droughts (Fig. 6). At this stage, soil moisture is depleted, and so its variations have a declining impact on changes in ET and no longer control VPD. Again, atmospheric advection dominates VPD. This is summarized in Fig. S8 and explains why information contained in VPD is not sufficient to fully capture drought effects and to explain the variability in LUE across the full dryness spectrum. These findings are consistent with Ruddell & Kumar (2009).
In conclusion, we show that accounting for soil moisture effects, in addition to VPD, is critical for the estimation of vegetation productivity across the globe and to quantify drought impacts. The general form of the functional relationship between LUE and soil moisture is uniform across contrasting ecosystems and climates, but the magnitude of the maximum LUE reductions is variable and related to shifting plant phenological strategies across the aridity gradient. Evergreen vegetation achieves higher LUE than drought‐deciduous vegetation during dry conditions, but is restricted to zones of intermediate aridity. Newly available global remote sensing‐based soil moisture datasets (Al Bitar et al., 2016; Dorigo et al., 2017) or alternative vegetation indices (PRI, chlorophyll‐carotenoid index (CCI), SiF) will be useful to provide critical additional information for global GPP estimates. Our results indicate that local hydrological conditions are important for understanding drought impacts on vegetation productivity. The provision of information on WTD should thus be made a high priority for future FLUXNET data distributions.
Author contributions
B.D.S., J.Z., T.F.K., S.I.S., I.C.P. and J.P. designed the research. B.D.S. performed the research and analysed the data. B.D.S. wrote the manuscript in collaboration with all co‐authors.
Supporting information
Please note: Wiley Blackwell are not responsible for the content or functionality of any Supporting Information supplied by the authors. Any queries (other than missing material) should be directed to the New Phytologist Central Office.
Fig. S1 MODIS FPAR vs MODIS EVI data.
Fig. S2 Functional relationship of the fractional reduction in light use efficiency (fLUE) and soil moisture.
Fig. S3 Neural network‐based predicted vs observed light use efficiency (LUE).
Fig. S4 Overview of sites by cluster.
Fig. S5 Coevolution of ecosystem state variables throughout droughts.
Fig. S6 Time series for different sites.
Fig. S7 Relationship between vapour pressure deficit (VPD) and soil moisture.
Fig. S8 Conceptual relationship between vapour pressure deficit (VPD) and soil moisture (SM).
Methods S1 Extended methods description.
Acknowledgements
We thank R. Orth for sharing code (SWBM model) and P. Greve for sharing data (global PET/P). B.D.S. was funded by an ERC Marie Sklodowska‐Curie fellowship H2020‐MSCA‐IF‐2015, project FIBER, grant no. 701329. J.P. was funded by ERC Synergy grant ERC‐SyG‐2013‐610028 IMBALANCE‐P, the Spanish Government grant CGL2016‐79835‐P and the Catalan Government grant SGR 2014‐274. T.F.K. was supported by the NASA Terrestrial Ecology Program IDS Award NNH17AE86I. This work is a contribution to the AXA Chair Programme in Biosphere and Climate Impacts and the Imperial College Initiative on Grand Challenges in Ecosystems and the Environment (I.C.P.). S.I.S. acknowledges support from the EU FP7 programme, through the ERC DROUGHT‐HEAT project (contract no. 617518). This work used eddy covariance data acquired and shared by the FLUXNET community, including these networks: AmeriFlux, AfriFlux, AsiaFlux, CarboAfrica, CarboEuropeIP, CarboItaly, CarboMont, ChinaFlux, Fluxnet‐Canada, GreenGrass, ICOS, KoFlux, LBA, NECC, OzFlux‐TERN, TCOS‐Siberia and USCCC. The FLUXNET eddy covariance data processing and harmonization were carried out by the European Fluxes Database Cluster, AmeriFlux Management Project and Fluxdata project of FLUXNET, with the support of CDIAC and ICOS Ecosystem Thematic Center, and the OzFlux, ChinaFlux and AsiaFlux offices.
See also the Commentary on this article by https://doi.org/10.1111/nph.15176.
References
- Ahlström A, Raupach MR, Schurgers G, Smith B, Arneth A, Jung M, Reichstein M, Canadell JG, Friedlingstein P, Jain AK et al 2015. Carbon cycle. The dominant role of semi‐arid ecosystems in the trend and variability of the land CO₂ sink. Science 348: 895–899. [DOI] [PubMed] [Google Scholar]
- Ahmed M, Else B, Eklundh L, Ardö J, Seaquist J. 2017. Dynamic response of NDVI to soil moisture variations during different hydrological regimes in the Sahel region. International Journal of Remote Sensing 38: 5408–5429. [Google Scholar]
- Al Bitar A, Mialon A, Kerr Y, Jacquette E, Cabot F, Richaume P, Quesney A, Tarrot S, Parrens M, Tomer S et al 2016. The SMOS level 3 daily soil moisture maps using multi‐orbit retrieval algorithm. Remote Sensing of Environment 9: 293–315. [Google Scholar]
- Ali I, Cawkwell F, Dwyer E, Barrett B, Green S. 2016. Satellite remote sensing of grasslands: from observation to management. Journal of Plant Ecology 9: 649–671. [Google Scholar]
- Ammann C, Flechard CR, Leifeld J, Neftel A, Fuhrer J. 2007. The carbon budget of newly established temperate grassland depends on management intensity. Agriculture, Ecosystems & Environment 121: 5–20. [Google Scholar]
- Anderegg WRL, Schwalm C, Biondi F, Camarero JJ, Koch G, Litvak M, Ogle K, Shaw JD, Shevliakova E, Williams AP et al 2015. FOREST ECOLOGY. Pervasive drought legacies in forest ecosystems and their implications for carbon cycle models. Science 349: 528–532. [DOI] [PubMed] [Google Scholar]
- Anthoni PM, Knohl A, Rebmann C, Freibauer A, Mund M, Ziegler W, Kolle O, Schulze E‐D. 2004. Forest and agricultural land‐use‐dependent CO2 exchange in Thuringia, Germany. Global Change Biology 10: 2005–2019. [Google Scholar]
- Aubinet M, Chermanne B, Vandenhaute M, Longdoz B, Yernaux M, Laitat E. 2001. Long term carbon dioxide exchange above a mixed forest in the Belgian Ardennes. Agricultural and Forest Meteorology 108: 293–315. [Google Scholar]
- Badgley G, Field CB, Berry JA. 2017. Canopy near‐infrared reflectance and terrestrial photosynthesis. Science Advances 3: e1602244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baldocchi D. 2016a. AmeriFlux US‐Ton Tonzi Ranch. doi: 10.17190/AMF/1245971.
- Baldocchi D. 2016b. AmeriFlux US‐Var Vaira Ranch‐Ione. doi: 10.17190/AMF/1245984.
- Baldocchi D, Falge E, Gu L, Olson R, Hollinger D, Running S, Anthoni P, Bernhofer C, Davis K, Evans R et al 2001. FLUXNET: a new tool to study the temporal and spatial variability of ecosystem‐scale carbon dioxide, water vapor, and energy flux densities. Bulletin of the American Meteorological Society 82: 2415–2434. [Google Scholar]
- Ballantyne A, Smith W, Anderegg W, Kauppi P, Sarmiento J, Tans P, Shevliakova E, Pan Y, Poulter B, Anav A et al 2017. Accelerating net terrestrial carbon uptake during the warming hiatus due to reduced respiration. Nature Climate Change 7: 148–152. [Google Scholar]
- Beer C, Reichstein M, Tomelleri E, Ciais P, Jung M, Carvalhais N, Rödenbeck C, Arain MA, Baldocchi D, Bonan GB et al 2010. Terrestrial gross carbon dioxide uptake: global distribution and covariation with climate. Science 329: 834–838. [DOI] [PubMed] [Google Scholar]
- Beier C, Beierkuhnlein C, Wohlgemuth T, Penuelas J, Emmett B, Körner C, de Boeck H, Christensen JH, Leuzinger S, Janssens IA et al 2012. Precipitation manipulation experiments – challenges and recommendations for the future. Ecology Letters 15: 899–911. [DOI] [PubMed] [Google Scholar]
- Berbigier P, Bonnefond J‐M, Mellmann P. 2001. CO2 and water vapour fluxes for 2 years above Euroflux forest site. Agricultural and Forest Meteorology 108: 183–197. [Google Scholar]
- Beringer J. 2013a. Adelaide River OzFlux tower site. OzFlux: Australian and New Zealand Flux Research and Monitoring; [WWW document] URL https://researchdata.ands.org.au/adelaide-river-ozflux-tower-site/449264. [Google Scholar]
- Beringer J. 2013b. Daly Pasture OzFlux tower site. OzFlux: Australian and New Zealand Flux Research and Monitoring; [WWW document] URL https://researchdata.ands.org.au/daly-pasture-ozflux-tower-site/449263. [Google Scholar]
- Beringer J. 2013c. Daly Uncleared OzFlux tower site. OzFlux: Australian and New Zealand Flux Research and Monitoring; [WWW document] URL https://researchdata.ands.org.au/daly-uncleared-ozflux-tower-site/449258. [Google Scholar]
- Beringer J. 2013d. Dry River OzFlux tower site. OzFlux: Australian and New Zealand Flux Research and Monitoring; [WWW document] URL https://researchdata.ands.org.au/dry-river-ozflux-tower-site/449267. [Google Scholar]
- Beringer J. 2013e. Fogg Dam OzFlux tower site. OzFlux: Australian and New Zealand Flux Research and Monitoring; [WWW document] URL https://researchdata.ands.org.au/fogg-dam-ozflux-tower-site/618994. [Google Scholar]
- Beringer J. 2013f. Whroo OzFlux tower site. OzFlux: Australian and New Zealand Flux Research and Monitoring; [WWW document] URL https://researchdata.ands.org.au/whroo-ozflux-tower-site/449276. [Google Scholar]
- Best MJ, Pryor M, Clark DB, Rooney GG, Essery RLH, Ménard CB, Edwards JM, Hendry MA, Porson A, Gedney N et al 2011. The Joint UK Land Environment Simulator (JULES), model description – Part 1: Energy and water fluxes. Geoscientific Model Development Discussions 4: 595–640. [Google Scholar]
- Betts AK, Ball JH. 1995. The FIFE surface diurnal cycle climate. Journal of Geophysical Research 100: 25679. [Google Scholar]
- Biederman JA, Scott RL, Bell TW, Bowling DR, Dore S, Garatuza‐Payan J, Kolb TE, Krishnan P, Krofcheck DJ, Litvak ME et al 2017. CO2 exchange and evapotranspiration across dryland ecosystems of southwestern North America. Global Change Biology 23: 4204–4221. [DOI] [PubMed] [Google Scholar]
- Biederman JA, Scott RL, Goulden ML, Vargas R, Litvak ME, Kolb TE, Yepez EA, Oechel WC, Blanken PD, Bell TW et al 2016. Terrestrial carbon balance in a drier world: the effects of water availability in southwestern North America. Global Change Biology 22: 1867–1879. [DOI] [PubMed] [Google Scholar]
- Bonan GB, Williams M, Fisher RA, Oleson KW. 2014. Modeling stomatal conductance in the earth system: linking leaf water‐use efficiency and water transport along the soil–plant–atmosphere continuum. Geoscientific Model Development 7: 2193–2222. [Google Scholar]
- Borchard N, Schirrmann M, von Hebel C, Schmidt M, Baatz R, Firbank L, Vereecken H, Herbst M. 2015. Spatio‐temporal drivers of soil and ecosystem carbon fluxes at field scale in an upland grassland in Germany. Agriculture, Ecosystems & Environment 211: 84–93. [Google Scholar]
- Budyko MI. 1974. Climate and life. New York, NY, USA: Academic Press. [Google Scholar]
- Carrara A, Kowalski AS, Neirynck J, Janssens IA, Yuste JC, Ceulemans R. 2003. Net ecosystem CO2 exchange of mixed forest in Belgium over 5 years. Agricultural and Forest Meteorology 119: 209–227. [Google Scholar]
- Cescatti A, Zorer R. 2003. Structural acclimation and radiation regime of silver fir (Abies alba Mill.) shoots along a light gradient. Plant, Cell & Environment 26: 429–442. [Google Scholar]
- Ceschia E, Béziat P, Dejoux JF, Aubinet M, Bernhofer C, Bodson B, Buchmann N, Carrara A, Cellier P, Tommasi PD et al 2010. Management effects on net ecosystem carbon and GHG budgets at European crop sites. Agriculture, Ecosystems & Environment 139: 363–383. [Google Scholar]
- Ciais P, Reichstein M, Viovy N, Granier A, Ogée J, Allard V, Aubinet M, Buchmann N, Bernhofer C, Carrara A et al 2005. Europe‐wide reduction in primary productivity caused by the heat and drought in 2003. Nature 437: 529–533. [DOI] [PubMed] [Google Scholar]
- Clark DB, Mercado LM, Sitch S, Jones CD, Gedney N, Best MJ, Pryor M, Rooney GG, Essery RLH, Blyth E et al 2011. The Joint UK Land Environment Simulator (JULES), model description – Part 2: Carbon fluxes and vegetation dynamics. Geoscientific Model Development 4: 701–722. [Google Scholar]
- Cleverly J. 2011. Alice Springs Mulga OzFlux site. OzFlux: Australian and New Zealand Flux Research and Monitoring. [Google Scholar]
- Cowan IR, Farquhar GD. 1977. Stomatal function in relation to leaf metabolism and environment. Symposia of the Society for Experimental Biology 31: 471–505. [PubMed] [Google Scholar]
- Curtis P. 2016. AmeriFlux US‐UMd UMBS Disturbance. doi: 10.17190/AMF/1246134
- Davis TW, Prentice IC, Stocker BD, Thomas RT, Whitley RJ, Wang H, Evans BJ, Gallego‐Sala AV, Sykes MT, Cramer W. 2017. Simple process‐led algorithms for simulating habitats (SPLASH v.1.0): robust indices of radiation, evapotranspiration and plant‐available moisture. Geoscientific Model Development 10: 689–708. [Google Scholar]
- Desai A. 2016a. AmeriFlux US‐WCr Willow Creek. doi: 10.17190/AMF/1246111
- Desai A. 2016b. AmeriFlux US‐Los Lost Creek. doi: 10.17190/AMF/1246071
- Desai A. 2016c. AmeriFlux US‐Syv Sylvania Wilderness Area. doi: 10.17190/AMF/1246106
- Dolman AJ, Moors EJ, Elbers JA. 2002. The carbon uptake of a mid latitude pine forest growing on sandy soil. Agricultural and Forest Meteorology 111: 157–170. [Google Scholar]
- Dong G, Guo J, Chen J, Sun G, Gao S, Hu L, Wang Y. 2011. Effects of spring drought on carbon sequestration, evapotranspiration and water use efficiency in the Songnen meadow steppe in northeast China. Ecohydrology 4: 211–224. [Google Scholar]
- Dorigo W, Wagner W, Albergel C, Albrecht F, Balsamo G, Brocca L, Chung D, Ertl M, Forkel M, Gruber A et al 2017. ESA CCI Soil Moisture for improved Earth system understanding: state‐of‐the art and future directions. Remote Sensing of Environment 203: 185–215. [Google Scholar]
- Doughty CE, Metcalfe DB, Girardin CAJ, Amézquita FF, Cabrera DG, Huasco WH, Silva‐Espejo JE, Araujo‐Murakami A, da Costa MC, Rocha W et al 2015. Drought impact on forest carbon dynamics and fluxes in Amazonia. Nature 519: 78–82. [DOI] [PubMed] [Google Scholar]
- Eamus D, Hutley LB, O'Grady AP. 2001. Daily and seasonal patterns of carbon and water fluxes above a north Australian savanna. Tree Physiology 21: 977–988. [DOI] [PubMed] [Google Scholar]
- Egea G, Verhoef A, Vidale PL. 2011. Towards an improved and more flexible representation of water stress in coupled photosynthesis–stomatal conductance models. Agricultural and Forest Meteorology 151: 1370–1384. [Google Scholar]
- Eugster W, Zeeman MJ. 2006. Micrometeorological techniques to measure ecosystem‐scale greenhouse gas fluxes for model validation and improvement. International Congress Series/Excerpta Medica 1293: 66–75. [Google Scholar]
- Fan Y, Li H, Miguez‐Macho G. 2013. Global patterns of groundwater table depth. Science 339: 940–943. [DOI] [PubMed] [Google Scholar]
- Fares S, Loreto F. 2014. Isoprenoid emissions by the Mediterranean vegetation in Castelporziano. Rendiconti Lincei. Scienze Fisiche e Naturali 26: 493–498. [Google Scholar]
- Ferréa C, Zenone T, Comolli R, Seufert G. 2012. Estimating heterotrophic and autotrophic soil respiration in a semi‐natural forest of Lombardy, Italy. Pedobiologia 55: 285–294. [Google Scholar]
- Field CB, Randerson JT, Malmström CM. 1995. Global net primary production: combining ecology and remote sensing. Remote Sensing of Environment 51: 74–88. [Google Scholar]
- Fisher JB, Tu KP, Baldocchi DD. 2008. Global estimates of the land–atmosphere water flux based on monthly AVHRR and ISLSCP‐II data, validated at 16 FLUXNET sites. Remote Sensing of Environment 112: 901–919. [Google Scholar]
- Galvagno M, Wohlfahrt G, Cremonese E, Rossini M, Colombo R, Filippa G, Julitta T, Manca G, Siniscalco C, di Cella UM et al 2013. Phenology and carbon dioxide source/sink strength of a subalpine grassland in response to an exceptionally short snow season. Environmental Research Letters 8: 025008. [Google Scholar]
- Gamon JA, Field CB, Goulden ML, Griffin KL, Hartley AE, Joel G, Penuelas J, Valentini R. 1995. Relationships between NDVI, canopy structure, and photosynthesis in three Californian vegetation types. Ecological Applications 5: 28–41. [Google Scholar]
- Gamon JA, Huemmrich KF, Wong CYS, Ensminger I, Garrity S, Hollinger DY, Noormets A, Peñuelas J. 2016. A remotely sensed pigment index reveals photosynthetic phenology in evergreen conifers. Proceedings of the National Academy of Sciences, USA 113: 13087–13092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gamon JA, Peñuelas J, Field CB. 1992. A narrow‐waveband spectral index that tracks diurnal changes in photosynthetic efficiency. Remote Sensing of Environment 41: 35–44. [Google Scholar]
- Garbulsky MF, Peñuelas J, Papale D, Ardö J, Goulden ML, Kiely G, Richardson AD, Rotenberg E, Veenendaal EM, Filella I. 2010. Patterns and controls of the variability of radiation use efficiency and primary productivity across terrestrial ecosystems. Global Ecology and Biogeography 19: 253–267. [Google Scholar]
- Garbulsky MF, Peñuelas J, Papale D, Filella I. 2008. Remote estimation of carbon dioxide uptake by a Mediterranean forest. Global Change Biology 14: 2860–2867. [Google Scholar]
- Gilmanov TG, Soussana JF, Aires L, Allard V, Ammann C, Balzarolo M, Barcza Z, Bernhofer C, Campbell CL, Cernusca A et al 2007. Partitioning European grassland net ecosystem CO2 exchange into gross primary productivity and ecosystem respiration using light response function analysis. Agriculture, Ecosystems & Environment 121: 93–120. [Google Scholar]
- Göckede M, Foken T, Aubinet M, Aurela M, Banza J, Bernhofer C, Bonnefond JM, Brunet Y, Carrara A, Clement R et al 2008. Quality control of CarboEurope flux data – Part 1: Coupling footprint analyses with flux data quality assessment to evaluate sites in forest ecosystems. Biogeosciences 5: 433–450. [Google Scholar]
- Goerner A, Reichstein M, Rambal S. 2009. Tracking seasonal drought effects on ecosystem light use efficiency with satellite‐based PRI in a Mediterranean forest. Remote Sensing of Environment 113: 1101–1111. [Google Scholar]
- Gough CM, Vogel CS, Schmid HP, Su H‐B, Curtis PS. 2008. Multi‐year convergence of biometric and meteorological estimates of forest carbon storage. Agricultural and Forest Meteorology 148: 158–170. [Google Scholar]
- de Graaf IEM, Sutanudjaja EH, van Beek LPH, Bierkens MFP. 2015. A high‐resolution global‐scale groundwater model. Hydrology and Earth System Sciences 19: 823–837. [Google Scholar]
- Granier A, Reichstein M, Bréda N, Janssens IA, Falge E, Ciais P, Grünwald T, Aubinet M, Berbigier P, Bernhofer C et al 2007. Evidence for soil water control on carbon and water dynamics in European forests during the extremely dry year: 2003. Agricultural and Forest Meteorology 143: 123–145. [Google Scholar]
- Greve P, Orlowsky B, Mueller B, Sheffield J, Reichstein M, Seneviratne SI. 2014. Global assessment of trends in wetting and drying over land. Nature Geoscience 7: 716–721. [Google Scholar]
- Grünwald T, Bernhofer C. 2007. A decade of carbon, water and energy flux measurements of an old spruce forest at the Anchor Station Tharandt. Tellus. Series B, Chemical and Physical Meteorology 59: 387–396. [Google Scholar]
- He M, Kimball JS, Running S, Ballantyne A, Guan K, Huemmrich F. 2016. Satellite detection of soil moisture related water stress impacts on ecosystem productivity using the MODIS‐based photochemical reflectance index. Remote Sensing of Environment 186: 173–183. [Google Scholar]
- Heinsch FA, Zhao M, Running SW, Kimball JS, Nemani RR, Davis KJ, Bolstad PV, Cook BD, Desai AR, Ricciuto DM et al 2006. Evaluation of remote sensing based terrestrial productivity from MODIS using regional tower eddy flux network observations. IEEE Transactions on Geoscience and Remote Sensing 44: 1908–1925. [Google Scholar]
- Hirschi M, Mueller B, Dorigo W, Seneviratne SI. 2014. Using remotely sensed soil moisture for land–atmosphere coupling diagnostics: the role of surface vs. root‐zone soil moisture variability. Remote Sensing of Environment 154: 246–252. [Google Scholar]
- Huete A, Didan K, van Leeuwen W, Miura T, Glenn E. 2010. MODIS Vegetation Indices In: Ramachandran B, Justice C, Abrams M, eds. Remote sensing and digital image processing. New York, NY, USA: Springer, 579–602. [Google Scholar]
- Humphrey V, Gudmundsson L, Seneviratne SI. 2016. Assessing global water storage variability from GRACE: trends, seasonal cycle, subseasonal anomalies and extremes. Surveys in Geophysics 37: 357–395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jung M, Reichstein M, Schwalm CR, Huntingford C, Sitch S, Ahlström A, Arneth A, Camps‐Valls G, Ciais P, Friedlingstein P et al 2017. Compensatory water effects link yearly global land CO2 sink changes to temperature. Nature 541: 516–520. [DOI] [PubMed] [Google Scholar]
- Knohl A, Schulze E‐D, Kolle O, Buchmann N. 2003. Large carbon uptake by an unmanaged 250‐year‐old deciduous forest in Central Germany. Agricultural and Forest Meteorology 118: 151–167. [Google Scholar]
- Knorr W, Heimann M. 2001. Uncertainties in global terrestrial biosphere modeling, Part II: Global constraints for a process‐based vegetation model. Global Biogeochemical Cycles 15: 227–246. [Google Scholar]
- Konings AG, Williams AP, Gentine P. 2017. Sensitivity of grassland productivity to aridity controlled by stomatal and xylem regulation. Nature Geoscience 10: 284–288. [Google Scholar]
- Kuhn M. 2016. caret: Classification and Regression Training. R package version 6.0‐73. https://CRAN.R-project.org/package=caret
- Kurbatova J, Li C, Varlagin A, Xiao X, Vygodskaya N. 2008. Modeling carbon dynamics in two adjacent spruce forests with different soil conditions in Russia. Biogeosciences 5: 969–980. [Google Scholar]
- Leuning R, Cleugh HA, Zegelin SJ, Hughes D. 2005. Carbon and water fluxes over a temperate Eucalyptus forest and a tropical wet/dry savanna in Australia: measurements and comparison with MODIS remote sensing estimates. Agricultural and Forest Meteorology 129: 151–173. [Google Scholar]
- Maechler M, Rousseeuw P, Struyf A, Hubert M, Hornik K. 2016. cluster: Cluster Analysis Basics and Extensions. R package version 2.0.5. https://CRAN.R-project.org/package=cluster
- Marcolla B, Cescatti A, Montagnani L, Manca G, Kerschbaumer G, Minerbi S. 2005. Importance of advection in the atmospheric CO2 exchanges of an alpine forest. Agricultural and Forest Meteorology 130: 193–206. [Google Scholar]
- Maselli F, Papale D, Puletti N, Chirici G, Corona P. 2009. Combining remote sensing and ancillary data to monitor the gross productivity of water‐limited forest ecosystems. Remote Sensing of Environment 113: 657–667. [Google Scholar]
- Matteucci M, Gruening C, Ballarin IG, Seufert G, Cescatti A. 2015. Components, drivers and temporal dynamics of ecosystem respiration in a Mediterranean pine forest. Soil Biology & Biochemistry 88: 224–235. [Google Scholar]
- McDowell N, Pockman WT, Allen CD, Breshears DD, Cobb N, Kolb T, Plaut J, Sperry J, West A, Williams DG et al 2008. Mechanisms of plant survival and mortality during drought: why do some plants survive while others succumb to drought? New Phytologist 178: 719–739. [DOI] [PubMed] [Google Scholar]
- Medlyn BE, De Kauwe MG, Duursma RA. 2016. New developments in the effort to model ecosystems under water stress. New Phytologist 212: 5–7. [DOI] [PubMed] [Google Scholar]
- Medvigy D, Wofsy SC, Munger JW, Hollinger DY, Moorcroft PR. 2009. Mechanistic scaling of ecosystem function and dynamics in space and time: Ecosystem Demography model version 2. Journal of Geophysical Research 114: doi: 10.1029/2008jg000812 [Google Scholar]
- Merbold L, Ziegler W, Mukelabai MM, Kutsch WL. 2011. Spatial and temporal variation of CO2 efflux along a disturbance gradient in a miombo woodland in Western Zambia. Biogeosciences 8: 147–164. [Google Scholar]
- Migliavacca M, Meroni M, Busetto L, Colombo R, Zenone T, Matteucci G, Manca G, Seufert G. 2009a. Modeling gross primary production of agro‐forestry ecosystems by assimilation of satellite‐derived information in a process‐based model. Sensors 9: 922–942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Migliavacca M, Meroni M, Manca G, Matteucci G, Montagnani L, Grassi G, Zenone T, Teobaldelli M, Goded I, Colombo R et al 2009b. Seasonal and interannual patterns of carbon and water fluxes of a poplar plantation under peculiar eco‐climatic conditions. Agricultural and Forest Meteorology 149: 1460–1476. [Google Scholar]
- Migliavacca M, Reichstein M, Richardson AD, Colombo R, Sutton MA, Lasslop G, Tomelleri E, Wohlfahrt G, Carvalhais N, Cescatti A et al 2010. Semiempirical modeling of abiotic and biotic factors controlling ecosystem respiration across eddy covariance sites. Global Change Biology 17: 390–409. [Google Scholar]
- Milly PCD. 1994. Climate, soil water storage, and the average annual water balance. Water Resources Research 30: 2143–2156. [Google Scholar]
- van der Molen MK, Dolman AJ, Ciais P, Eglin T, Gobron N, Law BE, Meir P, Peters W, Phillips OL, Reichstein M et al 2011. Drought and ecosystem carbon cycling. Agricultural and Forest Meteorology 151: 765–773. [Google Scholar]
- Monteith JL. 1972. Solar radiation and productivity in tropical ecosystems. Journal of Applied Ecology 9: 747–766. [Google Scholar]
- Mu Q, Zhao M, Heinsch FA, Liu M, Tian H, Running SW. 2007. Evaluating water stress controls on primary production in biogeochemical and remote sensing based models. Journal of Geophysical Research: Biogeosciences 112: doi: 10.1029/2006JG000179 [Google Scholar]
- Nicolai‐Shaw N, Zscheischler J, Hirschi M, Gudmundsson L, Seneviratne SI. 2017. A drought event composite analysis using satellite remote‐sensing based soil moisture. Remote Sensing of Environment 203: 216–225. [Google Scholar]
- Noormets A, Desai AR, Cook BD, Euskirchen ES, Ricciuto DM, Davis KJ, Bolstad PV, Schmid HP, Vogel CV, Carey EV et al 2008. Moisture sensitivity of ecosystem respiration: comparison of 14 forest ecosystems in the Upper Great Lakes Region, USA. Agricultural and Forest Meteorology 148: 216–230. [Google Scholar]
- Novick KA, Ficklin DL, Stoy PC, Williams CA, Bohrer G, Christopher Oishi A, Papuga SA, Blanken PD, Noormets A, Sulman BN et al 2016. The increasing importance of atmospheric demand for ecosystem water and carbon fluxes. Nature Climate Change 6: 1023–1027. [Google Scholar]
- Ohta T, Kotani A, Iijima Y, Maximov TC, Ito S, Hanamura M, Kononov AV, Maximov AP. 2014. Effects of waterlogging on water and carbon dioxide fluxes and environmental variables in a Siberian larch forest, 1998–2011. Agricultural and Forest Meteorology 188: 64–75. [Google Scholar]
- Orth R, Koster RD, Seneviratne SI. 2013. Inferring soil moisture memory from streamflow observations using a simple water balance model. Journal of Hydrometeorology 14: 1773–1790. [Google Scholar]
- Orth R, Zscheischler J, Seneviratne SI. 2016. Record dry summer in 2015 challenges precipitation projections in Central Europe. Scientific Reports 6: 28334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pan Y, Birdsey R, Hom J, McCullough K, Clark K. 2006. Improved estimates of net primary productivity from MODIS satellite data at regional and local scales. Ecological Applications 16: 125–132. [DOI] [PubMed] [Google Scholar]
- Peñuelas J, Filella I, Gamon JA. 1995. Assessment of photosynthetic radiation‐use efficiency with spectral reflectance. New Phytologist 131: 291–296. [Google Scholar]
- Philip R. 2016. AmeriFlux US‐MMS Morgan Monroe State Forest. doi: 10.17190/AMF/1246080
- Pilegaard K, Hummelshøj P, Jensen NO, Chen Z. 2001. Two years of continuous CO2 eddy‐flux measurements over a Danish beech forest. Agricultural and Forest Meteorology 107: 29–41. [Google Scholar]
- Porcar‐Castell A, Tyystjärvi E, Atherton J, van der Tol C, Flexas J, Pfündel EE, Moreno J, Frankenberg C, Berry JA. 2014. Linking chlorophyll a fluorescence to photosynthesis for remote sensing applications: mechanisms and challenges. Journal of Experimental Botany 65: 4065. [DOI] [PubMed] [Google Scholar]
- Posse G, Lewczuk N, Richter K, Cristiano P. 2016. Carbon and water vapor balance in a subtropical pine plantation. IForest – Biogeosciences and Forestry 9: 736–742. [Google Scholar]
- Potter NJ, Zhang L, Milly PCD, McMahon TA, Jakeman AJ. 2005. Effects of rainfall seasonality and soil moisture capacity on mean annual water balance for Australian catchments. Water Resources Research 41: 1–11. [Google Scholar]
- Poulter B, Frank D, Ciais P, Myneni RB, Andela N, Bi J, Broquet G, Canadell JG, Chevallier F, Liu YY et al 2014. Contribution of semi‐arid ecosystems to interannual variability of the global carbon cycle. Nature 509: 600–603. [DOI] [PubMed] [Google Scholar]
- Prentice IC, Dong N, Gleason SM, Maire V, Wright IJ. 2014. Balancing the costs of carbon gain and water transport: testing a new theoretical framework for plant functional ecology. Ecology Letters 17: 82–91. [DOI] [PubMed] [Google Scholar]
- Rambal S, Joffre R, Ourcival JM, Cavender‐Bares J, Rocheteau A. 2004. The growth respiration component in eddy CO2 flux from a Quercus ilex Mediterranean forest. Global Change Biology 10: 1460–1469. [Google Scholar]
- Raupach MR. 1991. Vegetation–atmosphere interaction in homogeneous and heterogeneous terrain: some implications of mixed‐layer dynamics. Vegetatio 91: 105–120. [Google Scholar]
- Reichstein M. 2003. Inverse modeling of seasonal drought effects on canopy CO2/H2O exchange in three Mediterranean ecosystems. Journal of Geophysical Research 108: doi: 10.1029/2003jd003430 [Google Scholar]
- Reichstein M, Bahn M, Ciais P, Frank D, Mahecha MD, Seneviratne SI, Zscheischler J, Beer C, Buchmann N, Frank DC et al 2013. Climate extremes and the carbon cycle. Nature 500: 287–295. [DOI] [PubMed] [Google Scholar]
- Reichstein M, Tenhunen JD, Roupsard O, Ourcival J‐M, Rambal S, Miglietta F, Peressotti A, Pecchiari M, Tirone G, Valentini R. 2002. Severe drought effects on ecosystem CO2 and H2O fluxes at three Mediterranean evergreen sites: revision of current hypotheses? Global Change Biology 8: 999–1017. [Google Scholar]
- Rey A, Pegoraro E, Tedeschi V, Parri ID, Jarvis PG, Valentini R. 2002. Annual variation in soil respiration and its components in a coppice oak forest in Central Italy. Global Change Biology 8: 851–866. [Google Scholar]
- Richardson AD, Hollinger DY, Aber JD, Ollinger SV, Braswell BH. 2007. Environmental variation is directly responsible for short‐ but not long‐term variation in forest–atmosphere carbon exchange. Global Change Biology 13: 788–803. [Google Scholar]
- Rodell M, Velicogna I, Famiglietti JS. 2009. Satellite‐based estimates of groundwater depletion in India. Nature 460: 999–1002. [DOI] [PubMed] [Google Scholar]
- Rogers A, Medlyn BE, Dukes JS, Bonan G, von Caemmerer S, Dietze MC, Kattge J, Leakey ADB, Mercado LM, Niinemets Ü et al 2017. A roadmap for improving the representation of photosynthesis in Earth system models. New Phytologist 213: 22–42. [DOI] [PubMed] [Google Scholar]
- Rossini M, Cogliati S, Meroni M, Migliavacca M, Galvagno M, Busetto L, Cremonese E, Julitta T, Siniscalco C, di Cella UM et al 2012. Remote sensing‐based estimation of gross primary production in a subalpine grassland. Biogeosciences 9: 2565–2584. [Google Scholar]
- Ruddell BL, Kumar P. 2009. Ecohydrologic process networks: 1. Identification. Water Resources Research 45: doi:10.1029/2008wr007279 [Google Scholar]
- Running SW, Nemani RR, Heinsch FA, Zhao M, Reeves M, Hashimoto H. 2004. A continuous satellite‐derived measure of global terrestrial primary production. BioScience 54: 547–560. [Google Scholar]
- Schwalb B, Tresch A, Torkler P, Duemcke S, Demel C. 2015. LSD: Lots of Superior Depictions. https://CRAN.R-project.org/package=LSD
- Schwalm CR, Anderegg WRL, Michalak AM, Fisher JB, Biondi F, Koch G, Litvak M, Ogle K, Shaw JD, Wolf A et al 2017. Global patterns of drought recovery. Nature 548: 202–205. [DOI] [PubMed] [Google Scholar]
- Schwalm CR, Williams CA, Schaefer K, Arneth A, Bonal D, Buchmann N, Chen J, Law BE, Lindroth A, Luyssaert S et al 2010. Assimilation exceeds respiration sensitivity to drought: a FLUXNET synthesis. Global Change Biology 16: 657–670. [Google Scholar]
- Scott R. 2016. AmeriFlux US‐SRM Santa Rita Mesquite. doi:10.17190/AMF/1246104
- Seneviratne SI, Corti T, Davin EL, Hirschi M, Jaeger EB, Lehner I, Orlowsky B, Teuling AJ. 2010. Investigating soil moisture–climate interactions in a changing climate: a review. Earth‐Science Reviews 99: 125–161. [Google Scholar]
- Shangguan W, Dai Y, Duan Q, Liu B, Yuan H. 2014. A global soil data set for earth system modeling. Journal of Advances in Modeling Earth Systems 6: 249–263. [Google Scholar]
- Sims D, Luo H, Hastings S, Oechel W, Rahman A, Gamon J. 2006. Parallel adjustments in vegetation greenness and ecosystem CO2 exchange in response to drought in a Southern California chaparral ecosystem. Remote Sensing of Environment 103: 289–303. [Google Scholar]
- Sitch S, Smith B, Prentice IC, Arneth A, Bondeau A, Cramer W, Kaplan JO, Levis S, Lucht W, Sykes MT et al 2003. Evaluation of ecosystem dynamics, plant geography and terrestrial carbon cycling in the LPJ dynamic global vegetation model. Global Change Biology 9: 161–185. [Google Scholar]
- Sjöström M, Ardö J, Eklundh L, El‐Tahir BA, El‐Khidir HAM, Pilesjö P, Seaquist J. 2008. Evaluation of satellite based indices for primary production estimates in a sparse savanna in the Sudan. Biogeosciences Discussions 5: 2985–3011. [Google Scholar]
- Spano D, Duce P, Zara P, Snyder RL, U KTP. 2006. Micrometeorogical measurements to assess fire fuel dryness. Forest Ecology and Management 234: S65. [Google Scholar]
- Sperry JS, Love DM. 2015. What plant hydraulics can tell us about responses to climate‐change droughts. New Phytologist 207: 14–27. [DOI] [PubMed] [Google Scholar]
- Stocker BD, Roth R, Joos F, Spahni R, Steinacher M, Zaehle S, Bouwman L, Xu‐Ri X‐R, Prentice IC. 2013. Multiple greenhouse‐gas feedbacks from the land biosphere under future climate change scenarios. Nature Climate Change 3: 666–672. [Google Scholar]
- Sulman BN, Roman DT, Yi K, Wang L, Phillips RP, Novick KA. 2016. High atmospheric demand for water can limit forest carbon uptake and transpiration as severely as dry soil. Geophysical Research Letters 43: 9686–9695. [Google Scholar]
- Sun OJ, Campbell J, Law BE, Wolf V. 2004. Dynamics of carbon stocks in soils and detritus across chronosequences of different forest types in the Pacific Northwest, USA. Global Change Biology 10: 1470–1481. [Google Scholar]
- Suni T, Rinne J, Reissell A, Altimir N, Keronen P, Rannik Ü, Maso MD, Kulmala M, Vesala T. 2003. Long‐term measurements of surface fluxes above a Scots pine forest in Hyytiälä, southern Finland, 1996–2001. Boreal Environment Research 8: 287–301. [Google Scholar]
- Tapley BD, Bettadpur S, Ries JC, Thompson PF, Watkins MM. 2004. GRACE measurements of mass variability in the Earth system. Science 305: 503–505. [DOI] [PubMed] [Google Scholar]
- Terazawa K, Kikuzawa K. 1994. Effects of flooding on leaf dynamics and other seedling responses in flood‐tolerant Alnus japonica and flood‐intolerant Betula platyphylla var. japonica . Tree Physiology 14: 251–261. [DOI] [PubMed] [Google Scholar]
- Terazawa K, Maruyama Y, Morikawa Y. 1992. Photosynthetic and stomatal responses of Larix kaempferi seedlings to short‐term waterlogging. Ecological Research 7: 193–197. [Google Scholar]
- Thornthwaite CW. 1948. An approach toward a rational classification of climate. Geographical Review 38: 55. [Google Scholar]
- Trenberth KE, Jones PD, Ambenje P, Bojariu R, Easterling D, Klein Tank A, Parker D, Rahimzadeh F, Renwick JA, Rusticucci M et al 2007. Observations: surface and atmospheric climate change In: Solomon S, Qin D, Manning M, Chen Z, Marquis M, Averyt KB, Tignor M, Miller HL, eds. Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge, UK and New York, NY, USA: Cambridge University Press. [Google Scholar]
- Turner DP, Ritts WD, Cohen WB, Maeirsperger TK, Gower ST, Kirschbaum AA, Running SW, Zhao M, Wofsy SC, Dunn AL et al 2005. Site‐level evaluation of satellite‐based global terrestrial gross primary production and net primary production monitoring. Global Change Biology 11: 666–684. [Google Scholar]
- Urbanski S, Barford C, Wofsy S, Kucharik C, Pyle E, Budney J, McKain K, Fitzjarrald D, Czikowsky M, Munger JW. 2007. Factors controlling CO2 exchange on timescales from hourly to decadal at Harvard Forest. Journal of Geophysical Research 112: doi: 10.1029/2006jg000293 [Google Scholar]
- Van Dijk AIJM, Dolman AJ. 2004. Estimates of CO2 uptake and release among European forests based on eddy covariance data. Global Change Biology 10: 1445–1459. [Google Scholar]
- Vandermolen M, Gash J, Elbers J. 2004. Sonic anemometer (co)sine response and flux measurement II. The effect of introducing an angle of attack dependent calibration. Agricultural and Forest Meteorology 122: 95–109. [Google Scholar]
- Venables WN, Ripley BD. 2002. Modern applied statistics with S. New York, NY, USA: Springer. [Google Scholar]
- Verma M, Friedl MA, Richardson AD, Kiely G, Cescatti A, Law BE, Wohlfahrt G, Gielen B, Roupsard O, Moors EJ et al 2014. Remote sensing of annual terrestrial gross primary productivity from MODIS: an assessment using the FLUXNET La Thuile data set. Biogeosciences 11: 2185–2200. [Google Scholar]
- Veroustraete F, Sabbe H, Eerens H. 2002. Estimation of carbon mass fluxes over Europe using the C‐Fix model and Euroflux data. Remote Sensing of Environment 83: 376–399. [Google Scholar]
- Verstraeten WW, Veroustraete F, Feyen J. 2006. On temperature and water limitation of net ecosystem productivity: implementation in the C‐Fix model. Ecological Modelling 199: 4–22. [Google Scholar]
- Vesala T, Suni T, Rannik Ü, Keronen P, Markkanen T, Sevanto S, Grönholm T, Smolander S, Kulmala M, Ilvesniemi H et al 2005. Effect of thinning on surface fluxes in a boreal forest. Global Biogeochemical Cycles 19: doi: 10.1029/2004gb002316 [Google Scholar]
- Vicca S, Balzarolo M, Filella I, Granier A, Herbst M, Knohl A, Longdoz B, Mund M, Nagy Z, Pintér K et al 2016. Remotely‐sensed detection of effects of extreme droughts on gross primary production. Scientific Reports 6: 28269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walther S, Voigt M, Thum T, Gonsamo A, Zhang Y, Köhler P, Jung M, Varlagin A, Guanter L. 2016. Satellite chlorophyll fluorescence measurements reveal large‐scale decoupling of photosynthesis and greenness dynamics in boreal evergreen forests. Global Change Biology 22: 2979–2996. [DOI] [PubMed] [Google Scholar]
- Wang H, Prentice IC, Davis TW. 2014. Biophysical constraints on gross primary production by the terrestrial biosphere. Biogeosciences 11: 5987–6001. [Google Scholar]
- Weedon GP, Balsamo G, Bellouin N, Gomes S, Best MJ, Viterbo P. 2014. The WFDEI meteorological forcing data set: WATCH Forcing Data methodology applied to ERA‐Interim reanalysis data. Water Resources Research 50: 7505–7514. [Google Scholar]
- Westergaard‐Nielsen A, Lund M, Hansen BU, Tamstorf MP. 2013. Camera derived vegetation greenness index as proxy for gross primary production in a low Arctic wetland area. ISPRS Journal of Photogrammetry and Remote Sensing 86: 89–99. [Google Scholar]
- Williams CA, Reichstein M, Buchmann N, Baldocchi D, Beer C, Schwalm C, Wohlfahrt G, Hasler N, Bernhofer C, Foken T et al 2012. Climate and vegetation controls on the surface water balance: synthesis of evapotranspiration measured across a global network of flux towers. Water Resources Research 48: doi: 10.1029/2011wr011586 [Google Scholar]
- Xiao X, Hollinger D, Aber J, Goltz M, Davidson EA, Zhang Q, Moore B. 2004. Satellite‐based modeling of gross primary production in an evergreen needleleaf forest. Remote Sensing of Environment 89: 519–534. [Google Scholar]
- Yamazaki T, Kato K, Ito T, Nakai T, Matsumoto K, Miki N, Park H, Ohta T. 2013. A common stomatal parameter set used to simulate the energy and water balance over boreal and temperate forests. Journal of the Meteorological Society of Japan. Ser. II 91: 273–285. [Google Scholar]
- Yu G‐R, Wen X‐F, Sun X‐M, Tanner BD, Lee X, Chen J‐Y. 2006. Overview of ChinaFLUX and evaluation of its eddy covariance measurement. Agricultural and Forest Meteorology 137: 125–137. [Google Scholar]
- Yuan W, Liu S, Zhou G, Zhou G, Tieszen LL, Baldocchi D, Bernhofer C, Gholz H, Goldstein AH, Goulden ML et al 2007. Deriving a light use efficiency model from eddy covariance flux data for predicting daily gross primary production across biomes. Agricultural and Forest Meteorology 143: 189–207. [Google Scholar]
- Zaehle S, Friend AD. 2010. Carbon and nitrogen cycle dynamics in the O‐CN land surface model: 1. Model description, site‐scale evaluation, and sensitivity to parameter estimates. Global Biogeochemical Cycles 24: doi: 10.1029/2009gb003521 [Google Scholar]
- Zhang Y, Susan Moran M, Nearing MA, Ponce Campos GE, Huete AR, Buda AR, Bosch DD, Gunter SA, Kitchen SG, Henry McNab W et al 2013. Extreme precipitation patterns and reductions of terrestrial ecosystem production across biomes. Journal of Geophysical Research: Biogeosciences 118: 148–157. [Google Scholar]
- Zhao M, Running SW. 2010. Drought‐induced reduction in global terrestrial net primary production from 2000 through 2009. Science 329: 940–943. [DOI] [PubMed] [Google Scholar]
- Zimmermann F, Plessow K, Queck R, Bernhofer C, Matschullat J. 2006. Atmospheric N‐ and S‐fluxes to a spruce forest – comparison of inferential modelling and the throughfall method. Atmospheric Environment 40: 4782–4796. [Google Scholar]
- Zscheischler J, Mahecha MD, Harmeling S, Reichstein M. 2013. Detection and attribution of large spatiotemporal extreme events in Earth observation data. Ecological Informatics 15: 66–73. [Google Scholar]
- Zscheischler J, Michalak AM, Schwalm C, Mahecha MD, Huntzinger DN, Reichstein M, Berthier G, Ciais P, Cook RB, El‐Masri B et al 2014. Impact of large‐scale climate extremes on biospheric carbon fluxes: an intercomparison based on MsTMIP data. Global Biogeochemical Cycles 28: 585–600. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Please note: Wiley Blackwell are not responsible for the content or functionality of any Supporting Information supplied by the authors. Any queries (other than missing material) should be directed to the New Phytologist Central Office.
Fig. S1 MODIS FPAR vs MODIS EVI data.
Fig. S2 Functional relationship of the fractional reduction in light use efficiency (fLUE) and soil moisture.
Fig. S3 Neural network‐based predicted vs observed light use efficiency (LUE).
Fig. S4 Overview of sites by cluster.
Fig. S5 Coevolution of ecosystem state variables throughout droughts.
Fig. S6 Time series for different sites.
Fig. S7 Relationship between vapour pressure deficit (VPD) and soil moisture.
Fig. S8 Conceptual relationship between vapour pressure deficit (VPD) and soil moisture (SM).
Methods S1 Extended methods description.


