High-performance organic light-emitting diodes comprising ultrastable glass layers

Organic light-emitting diodes with ultrastable glass emission layers show increased efficiency and device stability.

Abstract

Organic light-emitting diodes (OLEDs) are one of the key solid-state light sources for various applications including small and large displays, automotive lighting, solid-state lighting, and signage. For any given commercial application, OLEDs need to perform at their best, which is judged by their device efficiency and operational stability. We present OLEDs that comprise functional layers fabricated as ultrastable glasses, which represent the thermodynamically most favorable and, thus, stable molecular conformation achievable nowadays in disordered solids. For both external quantum efficiencies and LT₇₀ lifetimes, OLEDs with four different phosphorescent emitters show >15% enhancements over their respective reference devices. The only difference to the latter is the growth condition used for ultrastable glass layers that is optimal at about 85% of the materials’ glass transition temperature. These improvements are achieved through neither material refinements nor device architecture optimization, suggesting a general applicability of this concept to maximize the OLED performance, no matter which specific materials are used.

INTRODUCTION

Organic light-emitting diodes (OLEDs) are no longer a laboratory curiosity but rather represent a mature technology that allows high-performance displays and extremely customizable area light sources to be used in signaling and solid-state lighting. The long-term stability of state-of-the-art OLEDs constantly defines the range of possible applications. Currently, the specifications for mobile displays and televisions are reached. In general, the longevity of OLEDs correlates inversely to the operating brightness. High-brightness applications (greater than a few thousands of candelas per square meter) still cannot be realized with LEDs made of organic materials because they lack sufficient stability (1–3). Efficiency optimization of OLEDs has been and is still approached from various angles, which can be grouped into two: material development of emitters and other functional materials and the exploration of advanced optics concepts for improved light outcoupling efficiency. The former is currently led by the investigation of thermally activated delayed fluorescence (TADF) as a novel excitonic concept to realize 100% exciton harvesting (4, 5). Although it is hoped that TADF will allow superior device lifetimes compared to phosphorescence especially in the blue range of the electromagnetic spectrum, this benchmark has still to be overcome. The latter research facet to realize higher light outcoupling makes use of stack layer optimization to minimize the coupling of emission to loss modes (3, 6–8), random and Bragg scattering (9–12), functionalized substrates to redirect light (13–15), advanced optical elements as outermost interfaces to air (7, 16, 17), and orientation of the emitters’ transition dipole moment (18–21). To date, a global solution for a successful optical concept has not been found, as it heavily depends on the given OLED architecture, its potential to be scaled up, and the added cost it brings to the systematic production.

When it comes to improvement, the growth of the organic layers used in OLEDs has been widely unaddressed (22), which is in stark contrast to the attention given to performance optimization of organic photovoltaics. There, an optimized substrate temperature during film growth involving the transition to crystalline order is thought to allow best nano- and macroscopic blend morphologies, which are needed to maximize charge separation and extraction (23). From a different and more fundamental approach, in recent years, there has been an increasing interest in using physical vapor deposition as a powerful strategy to define the properties of amorphous layers of organic molecules (24). By properly setting the deposition conditions, essentially the growth rate and the substrate temperature during deposition, it is possible to achieve glasses with properties that outperform both conventional glasses prepared by quenching the liquid and traditional vapor-deposited molecular glasses grown at temperatures far below the glass transition temperature T_g. The specific properties of the glass are highly dependent on the deposition temperature. Glasses evaporated at substrate temperatures (T_sub) around 85% of T_g (K) and low growth rates, generally below 5 Å/s (25), show higher thermal and kinetic stabilities, lower enthalpies (26–28), higher densities (28, 29), higher elastic moduli (30), lower water uptake (31), and lower expansion coefficient and can also exhibit a certain degree of anisotropy (29, 32). Glasses obtained under these conditions were dubbed highly stable glasses or ultrastable glasses because their equivalent stability would only be attained after an extended aging (thousands or even millions of years) of a conventional glass. The enhanced surface diffusion at the outer surface of the glass during the deposition process is believed to be at the origin of the observed stability and density enhancement (24, 33). Understanding of vapor-deposited glasses, allowing the outstanding properties mentioned, has recently been addressed by computational methods (34, 35).

Although the impact of the deposition temperature of the layers on the performance of OLED stacks has generally gone unnoticed in the OLED community, some recent studies have analyzed how it affects molecular alignment in single layers of organic semiconductors. Recent works from Yokoyama et al. (32) and Dalal et al. (29) report how the molecular orientation of linear-shaped molecules can be effectively tuned from horizontal orientation when deposited at lower temperatures to a complete randomization when increasing the deposition temperature close to T_g. The former work also reports how a higher horizontal orientation increases charge mobility due to a higher π-π orbital overlap. A more recent study by Mu et al. (36) addressed the effect of the deposition temperature on the performance of a highly simplified OLED based on a CBP:Ir(ppy)₃ [CBP = 4′-bis(carbazol-9-yl)biphenyl] emission layer (EML). However, in this study, the best performance devices were grown at temperatures above the glass transition temperature of the electron and hole transport layers (ETL and HTL, respectively), that is, in their supercooled liquid state, precluding a proper correlation between the properties of the organic layers and the variation of the external quantum efficiency (EQE). On the other hand, it should be pointed out that a common practice for solution-processed OLEDs is to perform a post-deposition thermal annealing after the preparation of the emissive layers, a procedure that has been previously shown to be effective in enhancing the performance of polymer OLEDs (37). However, vapor deposition at around 0.85 T_g has been shown to be much more efficient than annealing in accessing low-energy positions in the potential energy landscape and, consequently, glasses with enhanced stability and higher density (24). Here, we focus on the influence of ultrastable glass formation on two key OLED performance indicators: the EQE and the operational stability. We approach this by using a suitable OLED architecture comprising materials that allow such a temperature treatment having suitable glass transition temperatures (see Fig. 1A). Our results demonstrate a significant enhancement of the OLED efficiency that correlates with the increased stability and better packing of the EML and ETL when deposited at temperatures close to 85% of T_g.

Fig. 1. Schematic device structure and performance of the studied device at different substrate temperatures.

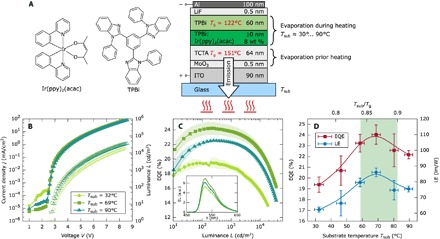
(A) As a first study, a single OLED sample set is prepared using the green emitter Ir(ppy)₂(acac) [8 weight % (wt %)] (G0) while evaporating the EML and ETL layers at six different substrate temperatures. The rest of the layers were deposited at RT. (B) j-V and L-V characteristics of the G0 devices deposited at three different substrate temperatures: 32°C (RT), 69°C, and 90°C. Each curve is the mean of two to six devices. (C) EQE versus luminance characteristics for the same three temperatures for the G0 devices. The shadowed area represents the error bars, which are the SD with 95% confidence interval weighted with the Student’s t factor for small amount of samples. The inset shows the corresponding integrated electroluminescence (EL) spectra of the devices obtained at j = 15.4 mA/cm² in arbitrary units (a.u.). (D) EQE (red, left axis) and LE (blue, right axis) at 100 cd/m² in dependence of the deposition temperature. Lines are guides to the eyes. The green highlighted region corresponds to the range from 0.84 to 0.9 T_g, where T_g is the glass transition temperature of TPBi expressed in kelvin.

RESULTS

For our study, we have chosen a simple but highly efficient OLED design by Meyer et al. (38) (see Fig. 1A and Materials and Methods for details). This stack matches several requirements, which are crucial for our investigations. First, it consists merely of two organic layers, which reduces the complexity of the OLED. The HTL is based on TCTA [4,4′,4″-tris(carbazol-9-yl)triphenylamine], whereas TPBi [2,2′,2″-(1,3,5-benzinetriyl)-tris(1-phenyl-1-H-benzimidazole)] serves as an emitter matrix for the EML and as ETL. Both materials have their 0.85 T_g value above room temperature (RT) in a technically feasible range with T_g = 151°C (39) and T_g = 122°C, for TCTA and TPBi, respectively. Furthermore, the T_g of the first evaporated material (TCTA) is higher than that of the material under investigation (TPBi), which is important to minimize any influence caused by possible TCTA morphology changes. Here, the deposition temperature is set by the substrate temperature T_sub, which is varied through controlled heating. The fabricated OLEDs can be divided into two groups: First, a full deposition temperature variation in the range from 30° to 90°C is performed with the green (G) phosphorescent emitter Ir(ppy)₂(acac). These OLED devices will be referred to as G0 from now on. Second, two distinct deposition temperatures (31° and 66°C) are compared for devices with additional commonly used emitters, Ir(MDQ)₂(acac) for red (R), Ir(ppy)₃ for green, and FIrpic for blue (B), where the higher temperature, 66°C, is selected on the basis of the optimal deposition temperature for TPBi. These devices will be referred to as R1, G1, and B1, respectively, from now on. Furthermore, we prepared photoluminescence (PL) samples with Ir(ppy)₂(acac) as the emitter embedded in TPBi at nominal deposition temperatures in the range of 30° to 100°C. With these samples, the transition dipole moment orientation is determined to analyze how any configurational changes affect the outcoupling efficiency. Finally, a detailed thermal characterization by means of the in situ nanocalorimetry technique of the matrix TPBi is performed for deposition temperatures ranging from −20° to 120°C.

Figure 1B shows the j-V-L characteristics of the G0 devices for three (of six) explored deposition temperatures. Although the j-V data are very similar for all deposition temperatures, the device fabricated at 69°C shows the highest luminance. Figure 1C shows the EQE for the same three devices as a function of the luminance (integrated electroluminescence spectra; inset of Fig. 1C). The complete device efficiency characteristics in dependence of the deposition temperature are summarized in Fig. 1D, showing the EQE (red, left axis) and the luminous efficacy (LE) (blue, right axis) at a luminance of 100 cd/m². At this brightness, an EQE of 24.0% and an LE of 85.6 lm/W are achieved for the device deposited at 69°C. This gives significant relative improvements with respect to the RT device of +24 and +37% for the EQE and LE, respectively. The tendency is similar for both quantities showing an increase over substrate temperature up to a maximum around 69°C, which is followed by an efficiency decrease. The highest studied temperature of 90°C still gives a better performance than the reference sample at RT.

The results concerning the performance of the devices R1, G1, and B1 hosting additional phosphorescent emitters are summarized in Fig. 2 (A to C), showing the EQE curves versus luminance comparing two deposition temperatures: the reference at RT (31°C) and at an elevated temperature of 66°C, close to the temperature with the best performance for the G0 device series and matching the 0.85 T_g criteria. The electroluminescence spectra obtained in an integrating sphere are shown for a current density of j = 15.4 mA/cm² in Fig. 2 (D to F). In all three devices, there is a significant enhancement between the RT device and the device with the ETL and EML deposited at 0.85 T_g (66°C). The EQE enhancements at 100 cd/m² are 15% for the red R1 devices, 22% for the green G1 devices, and 163% for the blue B1 devices. All devices fabricated at 66°C show an increased effective phosphorescence PL lifetime, that is, the decay of the excited molecules within an optical cavity, τ_eff (18, 40): 1.16 to 1.36 μs (+17% increase) for R1, 0.87 to 1.00 μs (+15%) for G1, and 1.07 to 1.38 μs (+29%) for B1, as obtained from PL transient spectroscopy of the complete OLEDs (see Fig. 2, G to I). An enhanced lifetime τ_eff could also be observed for G0: 0.74 to 0.80 μs (+8%) from T_sub = 46° to 69°C (see fig. S1). Note that the emitted spectra obtained at RT and 0.85 T_g for each emitter do not show any sign of peak shift or broadening (see Figs. 1C, inset, and 2, D to F, and fig. S2) so that effects due to different emitter aggregation can be excluded (41). The j-V-L curves of all devices R1, G1, and B1 can be found in the Supplementary Materials (see fig. S3).

Fig. 2. Performance characteristics of the devices R1, G1, and B1 with three different phosphorescent emitters comparing two deposition temperatures.

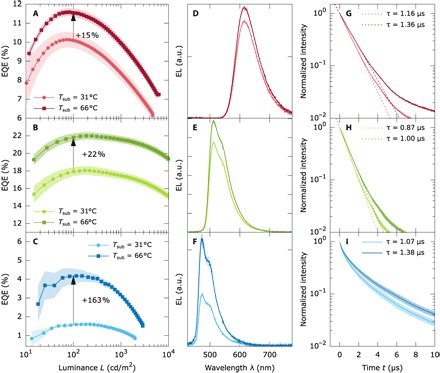
EQE (A to C), integrated electroluminescence spectra obtained at j = 15.4 mA/cm² (D to F), and PL transients of the complete OLEDs (G to I) for the devices R1, G1, and B1, which only differ in the emitter with respect to the G0 stack. (A, D, and G) OLED with the red emitter [Ir(MDQ)₂(acac)], (B, E, and H) OLED with a second green emitter Ir(ppy)₃, and (C, F, and I) OLED with the blue emitter (FIrpic). For each emitter, two deposition temperatures are studied: RT (31°C) and 66°C. The arrows in (A) to (C) with the label indicate the EQE improvement at a luminance of 100 cd/m².

Figure 3 (A and B) summarizes the device lifetimes LT₇₀, that is, the time to reach 70% of initial luminance (see also fig. S4), for the green devices G0 and G1 as well as for the red device R1 at various luminance values, although measured at constant current densities of j = 5, 10, 20, and 30 mA/cm². Typically, the initial luminance and the device lifetimes, for example, LT₇₀, are inversely proportional to each other (42), as indicated by solid lines in Fig. 3. For G0, we find the highest LT₇₀ for a deposition temperature of 46°C at both 1000 and 10,000 cd/m² (see Fig. 3A, inset). Compared to RT, this is an enhancement of a factor of 5 (74.2 versus 14.8 hours) and a factor of 2.4 (0.85 versus 0.35 hours), respectively. Similarly, for G1 and R1, the LT₇₀ peaks for all luminance values at 66°C. At 1000 cd/m², the enhancement is +86% for G1 (110 versus 59 hours) and +119% for R1 (22.3 versus 10.2 hours). It is important to note that for G1 and R1 at a constant current density j, samples evaporated close to T_sub = 0.85 T_g show not only enhanced luminance but also higher LT₇₀. For a comparison at a constant luminance, the enhancement is now twofold because the current can be even further reduced. Just like for the correlation of the device efficiency values, the different maxima in device lifetimes coincide with the substrate temperature range for the formation of ultrastable glasses. For a list of all LT₇₀ values, the reader is referred to the Supplementary Materials (table S1). The lifetime of the blue device series B1 was not evaluated, because the emitter FIrpic shows insufficient intrinsic stability not allowing a sound analysis (3). A summary of the devices’ performance (EQE and LT₇₀) is given in Table 1.

Fig. 3. Device lifetimes for G0, R1, and G1 at different luminance levels in dependence of the deposition temperature.

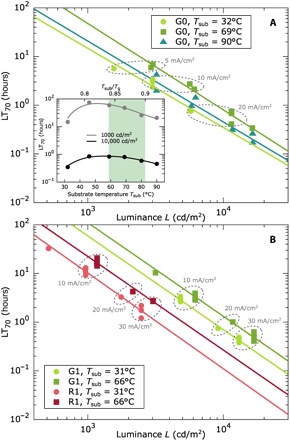
The lifetime LT₇₀ is defined as the time it takes for the initial luminance to drop to 70%. Lower luminance values L lead to higher lifetimes. Samples measured at equal current densities are grouped by dashed ellipses. (A) For G0, we find enhanced LT₇₀ at the temperature close to 0.85 T_g at a luminance L = 10,000 cd/m² (inset). (B) Devices R1 and G1 show highest lifetimes over the full luminance range for the substrate temperature of T_sub = 66°C. Device B1 could not be measured because of the unstable blue emitter FIrpic.

Table 1. Summary of EQEs and lifetimes (LT₇₀).

The EQEs are obtained at 100 cd/m², and the lifetime values are obtained at 1000 cd/m². RT refers to the tool’s standard temperature, which is close to 30°C. The 0.85 T_g criteria refer to the temperature closest to the optimal growth condition of the TPBi layers.

	Deposition temperature	G0	R1	G1	B1
EQE (%)	RT	19.4	10.1	17.9	1.6
	0.85 Tg	24.0	11.6	21.8	4.2
LT70 (hours)	RT	14.8	10.2	59.0	—
	0.80–0.85 Tg	74.2	22.3	110.0	—

DISCUSSION

As seen in Fig. 1 (B to D), the deposition temperature at which the ETL and EML layers are evaporated has a clear impact on the device’s performance (for both efficiency and lifetime). For instance, looking at the EQE as a benchmark efficiency, it can be enhanced from 19.4 to 24.0% between the RT and the 69°C G0 devices. When trying to understand the origin of this improvement, we have to consider all possible sources of influence on the device efficiency. The EQE of an OLED can be factorized into four main influencing parameters (18, 40)

$$\text{EQE}\equiv {\mathrm{\eta }}_{\text{EQE}}=\mathrm{\gamma }·{\mathrm{\eta }}_{\mathrm{S}/\mathrm{T}}·{\mathrm{\eta }}_{\text{rad},\text{eff}}·{\mathrm{\eta }}_{\text{out}}$$ (1)

The first factor γ is the electrical efficiency, which accounts for injected charge carriers that do not contribute to exciton formation. The second factor, η_S/T, quantifies the fraction of excitons that are allowed to decay radiatively due to the quantum mechanics spin selection rules and is one for phosphorescent emitters (43–45). η_rad,eff expresses the effective radiative quantum efficiency of the emitter material that describes the efficiency of the emitter to recombine radiatively from the emitting state (here, triplet state). It accounts for possible enhancements of the radiative transition rate induced by the optical cavity (18). Ultimately, η_out denotes the outcoupling factor, which depends mainly on the optical environment and the orientation of the emitter. In the following, these parameters are discussed step by step with respect to the observed EQE enhancement. Only the spin formation factor η_S/T does not need discussion, because it can be considered unity for all phosphorescent emitters used (43–45).

Beginning with η_out, it is known that the thickness of an OLED has direct and significant influence on the EQE (40, 46). In the present configuration, the thickness of the ETL sets the crucial distance between the EML and the opaque reflective electrode, thus determining the amount of light that can be outcoupled because of the cavity resonances inside the device (40, 47). Here, multiple samples are created on one common wafer without breaking the vacuum to assure comparability between different samples that could be scrutinized in a sequential fabrication scheme. A minor thickness gradient might be the result of devices being located at different positions on the 15 cm by 15 cm glass wafer. The comparison of different OLEDs with nominally identical stack sequences on this wafer did not yield any noticeable difference. Still, on the basis of tool calibration tests, thickness deviations of ±10% at most can occur across the substrate. In addition, the mentioned density changes in the range of 1 to 2% (29) of the evaporated materials can alter the layer thickness, although the optical thickness is expected to be constant. To evaluate the impact of any thickness changes, we performed optical simulations with ETL thicknesses of 60 nm with generous deviations of ±20%. These variations yield relative EQE changes smaller than +5%, which are much lower than the experimental EQE enhancements obtained. Therefore, it can be assumed that possible differences in the ETL layer thickness, if any, play a minimal role in the EQE improvement. It should be pointed out that these arguments cannot be generalized to all OLED concepts. Although they are reasonable for bottom-emitting OLEDs that form a weak optical cavity, top-emitting or cavity-enhanced designs will be much more sensitive to thickness changes (48, 49).

Another major parameter that strongly affects the light outcoupling is the transition dipole moment orientation of the emissive molecules within an OLED stack (19). Most of the light gets trapped in substrate, waveguided, and plasmonic modes when the emissive dipoles are oriented vertically to the substrate plane. On the contrary, horizontally oriented dipoles can couple most of the emitted light to the outside of the device. Yokoyama et al. (32) and Dalal et al. (29) showed how the molecular orientation of different organic semiconductor molecules can be tuned solely by changing the deposition temperature. In all cases, and as a general trend, the lower the deposition temperature, the more horizontally oriented are the molecules (32, 50, 51). Although the deposition temperature might influence the orientation of both the matrix and the emitter, only the orientation of the emitter affects η_out. The anisotropy coefficient a, which corresponds to the ratio between the number of vertically oriented dipoles to the total number of dipoles (21), is commonly used to quantify the effect of emitter orientation. For our G0 device, with the matrix-emitter system TPBi:Ir(ppy)₂(acac), a value of a = 0.27 is found in the literature when deposited at RT (52). Other deposition temperatures have not been reported.

To better evaluate this possible effect in our devices, we measured the transition dipole moment orientation of 50-nm-thick TPBi:Ir(ppy)₂(acac) layers evaporated at substrate temperatures T_sub ranging from 30° to 100°C according to the method of Frischeisen et al. (53). In agreement with the literature (52), Fig. 4 shows a preferentially horizontal alignment of the emitting dipoles from RT up to 60°C, with a = 0.30 (blue points). However, surpassing 60°C, the dipole orientation becomes less horizontal and finally even reaches a slightly vertical alignment at 100°C with a = 0.35 (one-third corresponds to isotropic orientation), which is an expected result when considering the similar behavior seen in other organic molecules (29). The inset of Fig. 4 shows the angular-dependent p-polarized PL intensity at the peak wavelength of 526 nm, indicating increasing contributions of the vertical dipoles with increasing temperature. Optical simulations reveal that this leads to an absolute drop of the outcoupling efficiency of 2% (red points) for the transition from RT to 100°C, which is well above the 0.85 T_g criteria. This anticipated fact should produce the contrary effect seen in our devices; the higher temperature OLED should give, if any, less outcoupled light if only the orientation was considered. Thus, there must be some other property producing the enhancement of the OLED performance and even further compensating the decreased outcoupling factor due to the dipole orientation.

Fig. 4. Anisotropy coefficient and outcoupling efficiency for different deposition temperatures.

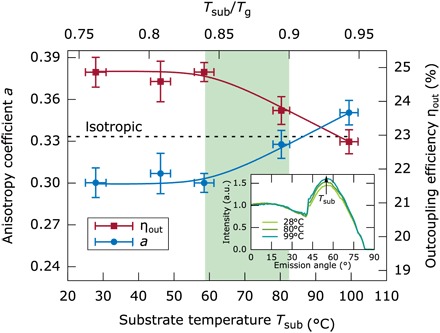
The anisotropy coefficient was determined by angular-resolved PL measurements (inset) of the p-polarized light from 50-nm-thick layers of TPBi:Ir(ppy)₂(acac) 8 wt %. On the basis of optical thin-film simulations of dipole emitters in stratified layers, the outcoupling efficiency is calculated. Both quantities stay constant until 0.84 T_g. Reaching the substrate temperature of 100°C, the anisotropy coefficient is increased from 0.30 to 0.35, changing from preferentially horizontal aligned transition dipole moments to a more vertical arrangement. This leads to an absolute drop in outcoupling efficiency of approximately 2%.

Having ruled out the outcoupling factor in Eq. 1 as the cause of the performance enhancement, γ and η_rad,eff remain as possible origins. The materials, as well as the layer and heating sequence chosen, allow the exclusive study of the effects that the variation of the deposition temperature has on the host and ETL material TPBi. Besides possible changes in the molecular orientation, it has been shown that more stable and dense amorphous layers can be obtained if the substrate temperature is set around 85% of the corresponding material’s T_g (26–32). Using fast scanning quasi-adiabatic nanocalorimetry, it is possible to measure the specific heat of TPBi layers deposited at different temperatures. Looking at the devitrification peak in the specific heat curves (see fig. S5), it is possible to extract the glass stability of a given material. Figure 5 shows the limiting fictive temperature and the onset temperature as a function of the deposition temperature of TPBi. The onset temperature at which the glassy layer devitrificates is indicative of the kinetic stability nature of the glass; the higher the onset, the later the glass transforms into the liquid and, thus, the higher the thermal stability is. The fictive temperature is used to quantify the thermodynamic stability of the glass (27); in that case, the lower the fictive temperature, the higher the thermodynamic stability. These quantities indicate a maximum in both stabilities around the highlighted region of 0.84 to 0.9 T_g. Although the fictive temperature shows a minimum plateau over a wide range between 20° and 70°C, the kinetic stability shows a clear maximum around 60° to 70°C, which coincides with the typical highly stable glass formation range. These results prove that TPBi is part of the extensive family of organic molecular glass formers that can be prepared into their ultrastable glass form when deposited at the optimal T_sub. Although we do not have a direct measure of density changes for TPBi, increased densities have been observed for similar OLED materials before (29).

Fig. 5. Thermal characterization as a function of the deposition temperature of TPBi single layers.

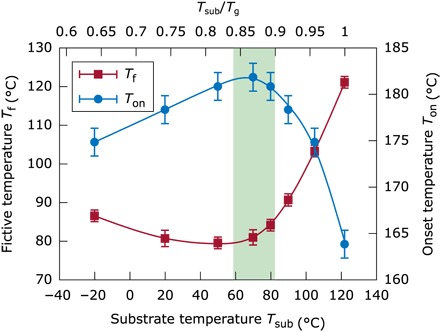
The fictive temperature (red, left axis) as a thermal stability parameter and the onset of the glass transition (blue, right axis) as a kinetic stability parameter of 60- to 80-nm films of TPBi as a function of the substrate temperature. These parameters are extracted from the heat capacity curves performed using quasi-adiabatic fast scanning calorimetry, as described in Materials and Methods and fig. S5.

Although the relative changes of the layer density are typically in the range of 1 to 2% (29), this subtle difference will likely influence the excitonic properties significantly because all couplings and transfer processes come with nanoscale sensitivity (54, 55). The TPBi layer is the host for the green emitter in the G0 devices, in which the 8 wt % doping of Ir(ppy)₂(acac) is assumed to not influence the glassy matrix properties decisively. To test the hypothesis that the changes in stability and molecular packing of TPBi cause the enhanced efficiencies, we used the same device architecture with three additional phosphorescent emitters [Ir(MDQ)₂(acac), Ir(ppy)₃, and FIrpic]. Figure 2 shows how the EQE is enhanced when the temperature is set to 66°C for the devices R1, G1, and B1, using the red, green, and blue emitter, respectively. These results further support the idea that the host (TPBi) properties are the ones affecting the device performance. Looking at the increase of the PL decay times τ_eff of +8% (G0), +17% (R1), +15% (G1), and +29% (B1) in fig. S1 and Fig. 2 (G to I), with the assumption that the cavity influence, due to constant device thickness, and the radiative rate stay constant (40, 55, 56), one can relate the transient time enhancement directly to an improved radiative efficiency due to reduced nonradiative rates. The origin of this reduction can be manifold: Either it is related to reduced excitonic trap states in the bulk of the EML or it could be rationalized in terms of a possible suppression of the β-relaxation—molecule vibrations within a cage formed by its neighbors—in the ultrastable glass of TPBi, which could slow down the nonradiative phonon-mediated monomolecular thermal relaxation processes (54, 55). Similar observations of reduced nonradiative recombination rates have been observed in polymer-based systems that were prepared in a very rigid form that led to a higher packing density compared to a conventionally fabricated reference sample (56). Currently, this suppression has only been reported for ultrastable glasses of toluene and other molecular glass formers (57); although caution must be applied at the limited data available, it may be a general feature of ultrastable glasses. The enhancements of EQE, that is, η_↑EQE = [η_EQE(0.85 T_g)/η_EQE(RT)] − 1, and radiative efficiency, that is, η_↑rad,eff = [τ_eff(0.85 T_g)/τ_eff(RT)] − 1, are η_{↑ EQE} = +(22–28)% and η_↑rad,eff = +15% for G1 and η_↑EQE = +(14–23)% and η_↑rad,eff = +17% for R1, respectively. Here, η_↑EQE is determined for all luminance values obtained >100 cd/m², which leads to the range given (see Fig. 2, A to C). Within this range, the EQE increase can be fully correlated to the changes observed for the excited state lifetime τ_eff, resulting in improved radiative efficiency. For the device series G0, the improvements are η_↑EQE = +(11–16)% and η_↑rad,eff = +8%, with the difference that the values are determined between 46°C and 0.85 T_g (RT samples degraded). Although the increase of radiative efficiency for the device B1 is significantly larger with η_↑rad,eff = +39%, it fails to explain the massive enhancement of the device efficiency [η_↑EQE = +(150–165)%]. In this particular case, host and emitter are energetically in resonance at about 2.6 eV with respect to their triplet (T₁) levels, where a delayed emitter population has been shown (3). Increased packing would greatly enhance triplet migration in the film and by that/therefore, the efficiency. Unfortunately, the transient measurements do not allow the investigation of this delayed effect in more detail.

The remaining parameter of Eq. 1 determining the OLED EQE is γ. Referring to the heating sequence during device processing, a change in transport properties can only be expected for the TPBi-based layers because the TCTA HTLs undergo identical treatment for all devices. Although both j-V characteristics (Fig. 1B and fig. S3) and EQE versus luminance data (Figs. 1C and 2, A to C) for the different devices look very similar, changes in the mobility may induce subtle changes in the electron and hole concentration and distribution, which could be a cause for efficiency modulations. These carrier transport–related changes, however, do not influence the radiative efficiency η_rad,eff, especially at low brightness levels, where a possible influence by nonlinear quenching (carrier-exciton collisions) can be excluded. Hence, with the good agreement of η_↑EQE and η_↑rad,eff for devices G0, G1, and R1, an altered electrical efficiency can be considered a minor effect. On the contrary, transport changes seem to cause most of the EQE enhancement for the FIrpic-based device B1. Here, it is possible that the resonant triplet energy character of the TPBi:FIrpic EML as mentioned above is more sensitive to a redistribution of the charge carrier and recombination profiles (58).

As mentioned in the Introduction, Mu et al. (36) addressed the electroluminescent dependence of a simplified OLED on in situ thermal treatment. In their work, they use the simplified stack CBP/CBP:Ir(ppy)₃/TPBi prepared under different deposition temperatures. Although they report a significant EQE improvement, it is worth noting that their RT reference device only reached 10.6% EQE and the best thermally treated OLED reached 17.9%, where the latter is about as efficient as the reference in this study (see Table 1, device G1). The HTL and EML host material CBP has a much lower T_g of 62°C so that CBP would be a supercooled liquid, where more drastic morphological and performance changes can be expected.

Besides EQE enhancements, the operational lifetime of the devices prepared at ~0.80 to 0.85 T_g is also improved (see Fig. 3, Table 1, table S1, and fig. S4). In general, it is a tough and laborious task to investigate the degradation of OLEDs and correlate these findings to the nanoscopic level of the molecular building blocks (42, 59). Here, if only a change of the deposition parameters for EML and ETL (composed mostly of TPBi) leads to a similar correlation with the 0.85 T_g criteria to form an ultrastable glass, that is, LT₇₀ peaks at these deposition temperatures, then it can be deduced that the molecular conformation at the nanoscale favors a more durable device operation. A clear correlation between the glass density and the photostability—which measures the resistance of the material to light irradiation—has been recently established by Qiu et al. (60). They prepare samples of DO37 (3-[[4-(2,6-dichloro-4-nitrophenyl)azo]-N-ethylanilino]-pro-pionitrile or Dispersive Orange 37) glass by physical vapor deposition at different substrate temperatures and find that glasses prepared at 0.88 T_g have, besides higher kinetic stability and higher density, higher photostability. A qualitative argument for the enhanced stability is similar to the one used above for increased radiative efficiency. The rigidity of the films formed as ultrastable glasses is likely to suppress coupling to generally accessible decomposition routes present in OLEDs.

In summary, this study shows that the performance of state-of-the-art OLEDs can be significantly enhanced by optimizing the growth condition of the organic layers. The results show that the enhancement in device EQE can be correlated very well to an increased radiative efficiency of the EML, particularly for the exothermic host-emitter systems (T_1,host > T_1,emitter). A detailed investigation of the transition dipole moment of the emitter Ir(ppy)₂(acac) does not give any hint that a change of orientation is the cause for the enhancement. A modification of the electrical efficiency upon the deposition temperature variation can never be excluded easily. However, this effect only has a minimal impact on the results. Here, the resonant triplet energy TPBi:FIrpic-based OLED must be seen as an exception, where more than one influencing parameter seems to be at work.

CONCLUSIONS

We anticipate that our finding will allow the increase of the OLED performance (efficiency and device lifetime), especially because it can directly be correlated to a very fundamental material property, that is, the glass transition temperature. Although the enhancements presented here may seem incremental, it is important to highlight that they can be anticipated to be on top of material development efforts, which are the current driver for progress. Improvements in energy efficiency and durability are of ultimate importance to the further success of the OLED technology in applications such as high brightness displays and solid-state lighting. The concept of incorporating ultrastable glass layers is independent of the emitter technology used so that OLEDs based on either high-performance emitter types, that is, phosphorescence as discussed here and TADF (61), can equally benefit, if the emitter orientation is not hampered at the respective substrate temperature. Future research needs to investigate material and device properties, which could possibly counteract the observed effects. The influence of the material deposition conditions on the charge carrier transport of organic small molecules must be correlated to solely excitonic effects to achieve a complete understanding. Beyond the OLED technology platform, the formation of organic ultrastable glasses has a high potential to further increase the performance of various organic electronic devices and systems.

MATERIALS AND METHODS

OLED devices

Glass substrates (Corning Eagle XG, Thin Film Devices Inc.) with 90 nm of predeposited indium tin oxide (ITO) as a transparent bottom electrode were treated by a standard cleaning procedure (including rinsing with N-methyl-2-pyrrolidone, ethanol, and deionized water as well as treatment with ultraviolet ozone). All the subsequent layers were deposited in a single ultrahigh vacuum (UHV) chamber evaporation tool (Kurt J. Lesker Co.) at a base pressure of 10⁻⁷ mbar. The thickness and deposition rates were monitored using a quartz crystal microbalance. First, a 0.5-nm-thin layer of MoO₃ was evaporated on top of the ITO to facilitate the injection of holes from the anode ITO. The electrode was followed by the two organic layers TCTA and TPBi, where TCTA and TPBi were used as HTLs and ETLs, respectively. The EML was formed by doping the first part (10 nm) of the ETL with the respective phosphorescent dopant. Four different phosphorescent emitters were tested, with the remaining stack architecture kept identical. The deposition rates for the EML were 0.4 and 1.0 Å/s for both HTL and ETL, respectively, well below the criteria for realizing ultrastable glasses (25). For all emitters, the layer thicknesses of HTL and ETL were optimized using a thin-film optics simulation tool (40), including transition dipole moment orientation. To study the effect of the TPBi layer’s properties on the device performance, different samples were prepared by changing solely the substrate temperature during the evaporation of the EML and ETL layers for each of the mentioned devices. Finally, a bilayer cathode consisting of 0.5-nm LiF followed by 100-nm aluminum was deposited on top of the organic layers. Immediately after fabrication, all OLEDs were encapsulated with glass lids under nitrogen atmosphere along with a getter material.

In the first studied device (device G0), the structure was as follows: ITO (90 nm)/MoO₃ (0.5 nm)/TCTA (64 nm)/TPBi:Ir(ppy)₂(acac) 8 wt % (10 nm)/TPBi (60 nm)/LiF (0.5 nm)/Al (100 nm), where Ir(ppy)₂(acac) (bis(2-phenylpyridine) (acetylacetonate)iridium(III)) is a green phosphorescent emitter dopant. After depositing the HTL layer, the temperature of the whole substrate was set to the highest temperature studied, 90°C, where the EML and ETL were evaporated to a limited area using a wedge tool. After reaching the next temperature by passively cooling the whole substrate, the EML and ETL were evaporated again into another predefined region. This procedure was repeated six times at the nominal temperatures of 90°C, 80°C, 70°C, 60°C, 50°C, and RT (ca. 30°C—set by the evaporation tool environment). The actual substrate temperature was determined by a previously performed calibration. Once RT was reached, the cathode layers were evaporated at once for all the samples.

Another set of three different devices was prepared using the same structure and changing only the emitter—that is, using the same electrode scheme but with the HTL and ETL thicknesses optimized for each emitter spectrum. All three devices were prepared in a single process by using shadow masks and a wedge tool. The structure of these three devices is as follows: a red OLED (device R1) with TCTA (90 nm)/TPBi:Ir(MDQ)₂(acac) 10 wt % (10 nm)/TPBi (70 nm), another green OLED (device G1) with TCTA (64 nm)/TPBi:Ir(ppy)₃ 10 wt % (10 nm)/TPBi (60 nm), and a blue OLED (device B1) with TCTA (40 nm)/TPBi:FIrpic 10 wt % (10 nm)/TPBi (35 nm). Ir(MDQ)₂(acac) stands for bis(2-methyldibenzo[f,h]quinoxaline)(acetylacetonate)iridium(III), Ir(ppy)₃ stands for tris[2-phenylpyridine]iridium(III), and FIrpic stands for bis[2-(4,6-difluorophenyl)pyridinato-C2,N](picolinato)iridium(III). On the basis of the results obtained from the G0 device, for each one of the three devices, R1, G1, and B1, two deposition temperatures for the EML and ETL layers were explored: RT and 66°C using the aforementioned procedure.

Current-voltage characteristics (j-V) were measured using a Keithley 2400 SourceMeter unit, whereas the luminance was recorded simultaneously with a fast Si photodiode. The active area of the devices is 6.49 mm². For luminance calibration, the spectral radiance in the forward direction was taken by a calibrated Instrument Systems GmbH CAS 140 CT spectrometer at approximately 1000 cd/m². EQE and LE were obtained in an integrating sphere (LMS-100, Labsphere Inc.) with a calibrated spectrometer (CDS-600, Labsphere Inc.). For each deposition temperature, the data of two to four identically prepared devices having four distinct pixels each were averaged. The error bars correspond to the SD with 95% confidence interval corrected by the Student’s t factor for low numbers of samples. Device lifetimes were measured for all devices at multiple current densities and are reported as LT₇₀ lifetimes, which are defined as the times at which the brightness of the OLEDs drops to 70% of the initial value. The anisotropy coefficient as a measure of the averaged orientation of the emitter molecules’ transition dipole moments is extracted from angular-resolved PL spectra following the method of Frischeisen et al. (53). A 50-nm-thick encapsulated single layer of TPBi:Ir(ppy)₂(acac), evaporated on the aforementioned substrate type, was attached to a 4-cm diameter glass half-cylinder prism using index matching oil. The organic film was excited optically by a 405-nm laser diode (STAR405F10, Roithner Lasertechnik). The emitted light was detected by a USB4000 spectrometer from Ocean Optics. To balance the vertical and horizontal contributions of the transition dipole emission, only the p-polarized light was measured by inserting a Glan-Taylor polarizer (PGT-5010, Casix) in front of the spectrometer. Furthermore, the excitation light was filtered out using a 435-nm edge filter. The sample and the excitation source were placed on a rotary stage that allows an automated angle by angle emission measurement, resulting in the so-called spectral radiant intensity (SRI). Finally, a fitting algorithm based on the optical model described by Furno et al. (40) was used to approximate the experimental SRI numerically and to obtain the anisotropy coefficient as a fitting parameter. In this optical simulation, the EML was represented by six infinitely thin active layers that are homogeneously distributed over the total EML thickness and separated by five passive layers with the same optical constants. The overall thickness served as a second fitting parameter to regard for production caused thickness variations between the samples.

Time-resolved PL

For measuring the time-resolved PL, the OLEDs G0, R1, G1, and B1 were excited with a pulsed nitrogen laser (MNL 202-C/ATM 200, Lasertechnik Berlin) with an operational wavelength of 337 nm. A mask was used to ensure excitation to be only in the active area of the devices. The emitted light was focused and recorded with a Si-amplified photodetector (PDA100A-EC, Thorlabs). Various long-pass filters were used to exclude the laser light and the fluorescence from the signal. The effective PL lifetimes τ_eff were derived using a single exponential decay after rejecting residual fluorescence of adjacent layers from the data and not considering the weak delayed components. The latter are emission artifacts that result from the complex excitation of the complete OLED layers. For the OLEDs G0 and B1, τ_eff was approximated as the time where the intensity dropped to 1/e, due to the multiexponential decay.

Thermal measurements of single TPBi layers

The glass transition temperature of TPBi was determined using differential scanning calorimetry. Single TPBi layers were thermally characterized by means of quasi-adiabatic nanocalorimetry in differential mode. This technique used membrane-based microcalorimeters and high heating rates (ca. 3 × 10⁴ K/s, for this work) achieving high sensitivities (62). A current short pulse (~35 mA during few milliseconds) using a Keithley 2400 SourceMeter unit raises the temperature of the calorimeters, whereas the voltage drop was acquired during the pulse with a 16-bit and 2.5 MS/s DAQ from National Instruments. The raw voltage and current data were converted into heat capacity curves following a procedure explained elsewhere (62). Films from 60 to 80 nm of TPBi were deposited in an UHV chamber at 1 Å/s at substrate temperatures between −20° and 122°C (the glass transition of TPBi). The deposition temperature was set by feeding the microcalorimeter with a specific constant intensity. The mass was inferred from the heat capacity in the supercooled liquid range and knowing the specific heat capacity by previously calibrating the deposition rate with thickness values obtained by a profilometer. From the heat capacity scans, the onset temperature of the glass transition and the limiting fictive temperature were obtained as indicators of the kinetic and thermodynamic stability of the glasses, respectively. The fictive temperature is the temperature at which the enthalpy of the glass intersects the extrapolated supercooled liquid “equilibrium” line, which can be obtained by integrating the heat capacity data.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/5/eaar8332/DC1

table S1. Overview of the device lifetimes at different substrate temperatures and luminance values.

fig. S1. PL transients of G0.

fig. S2. Normalized forward emission spectra of G0, R1, G1, and B1.

fig. S3. Optoelectronic characterization of devices R1, G1, and B1.

fig. S4. Exemplary lifetime and voltage characteristics over aging time for two OLEDs of the R1 series.

fig. S5. Calorimetric trace of TPBi layers deposited at different temperatures.