Gold nanocrystal labels provide a sequence–to–3D structure map in SAXS reconstructions

Gold labels provide a sequence–to–low-resolution structure map in SAXS measurements of biological macromolecules.

Abstract

Small-angle x-ray scattering (SAXS) is a powerful technique to probe the structure of biological macromolecules and their complexes under virtually arbitrary solution conditions, without the need for crystallization. While it is possible to reconstruct molecular shapes from SAXS data ab initio, the resulting electron density maps have a resolution of ~1 nm and are often insufficient to reliably assign secondary structure elements or domains. We show that SAXS data of gold-labeled samples significantly enhance the information content of SAXS measurements, allowing the unambiguous assignment of macromolecular sequence motifs to specific locations within a SAXS structure. We first demonstrate our approach for site-specifically internally and end-labeled DNA and an RNA motif. In addition, we present a protocol for highly uniform and site-specific labeling of proteins with small (~1.4 nm diameter) gold particles and apply our method to the signaling protein calmodulin. In all cases, the position of the small gold probes can be reliably identified in low-resolution electron density maps. Enhancing low-resolution measurements by site-selective gold labeling provides an attractive approach to aid modeling of a large range of macromolecular systems.

INTRODUCTION

Small-angle x-ray scattering (SAXS) is a powerful technique to probe the structure, dynamics, and conformational transitions of biological macromolecules and their complexes in free solution (1–3). In a typical SAXS experiment, macromolecules in solution are exposed to an x-ray beam, and the scattered photons are detected and analyzed (Fig. 1A). An important advantage of SAXS is that it does not require crystallization of the sample. It can probe macromolecules under a range of solution conditions, from (near) physiological to highly denaturing. This enables, for example, the detection of conformational changes as a function of pH, temperature, salt, or ligand concentration. The fact that SAXS is a solution technique is a disadvantage; however, that information is lost due to rotational averaging, and it does not provide the atomic resolution achieved by crystallography, nuclear magnetic resonance spectroscopy, and cryo–electron microscopy (cryo-EM).

Fig. 1. Schematic of SAXS measurements and workflow to determine gold label positions in macromolecular reconstructions.

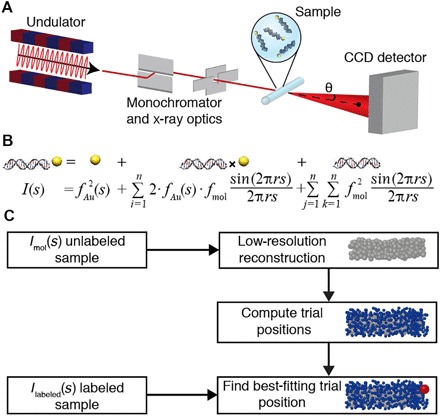
(A) Schematic of SAXS measurements. The incident synchrotron-generated x-ray beam (red line) is shown with x-ray optics. Single gold-labeled macromolecules are placed into the x-ray beam in a sample cell. The direct beam is blocked by a beam stop, and scattered photons are detected using a charge-coupled device (CCD) detector. (B) Scattering intensity equation for a single labeled molecule. The scattering signal can be decomposed into a sum of the individual scattering contributions: the gold label scattering, the gold-macromolecule cross-term, and the scattering from the macromolecule only. (C) Schematic of the workflow to determine the positions of gold labels relative to low-resolution three-dimensional (3D) reconstructions of unlabeled macromolecules. The SAXS profile of the unlabeled sample is used in ab initio reconstruction of a low-resolution model consisting of dummy residues or beads. Sterically allowed gold label trial positions are computed in the bead model. Experimental data from the gold-labeled sample are compared to the computed scattering profile for each of the trial positions, and the best-fitting positions are identified.

Despite the comparatively limited information content, it is possible to reconstruct low-resolution 3D electron density maps from SAXS data. Algorithms for ab initio reconstruction of low-resolution 3D structures from 1D SAXS data (4–6) have sparked an explosive growth of the use of SAXS to probe and model the structure of biological macromolecules and their complexes. The underlying principle of the reconstruction algorithms is to represent the molecule of interest as a collection of beads or “dummy residues” and to optimize the bead positions to best fit the experimental scattering profiles. The results are low-resolution (~1 nm) 3D electron density maps of the samples (5–8). Unfortunately, assignment of particular domains in high-resolution protein and RNA structures to positions in a low-resolution SAXS map is often difficult and typically requires additional information (9–15). Fundamentally, a SAXS measurement provides information about the distribution of pairwise distances within a structure but, taken in isolation, does not reveal the specific identities of the atoms or residues that contributed to the distribution.

Recently, SAXS and anomalous SAXS (ASAXS) measurements on molecules modified by two gold nanocrystal probes have been used to measure highly accurate distance distributions between the probes (16–23). While these approaches were able to determine the spacing of the two gold labels very precisely, a general method to relate the label position or distances to ab initio–generated low-resolution maps is currently lacking. Here, we demonstrate that single gold nanocrystal labels attached to specific residues of biological macromolecules can serve as fiducial markers to provide a map from the primary sequence (and therefore, domain structure) to the low-resolution 3D electron density map computed from SAXS data. We show that our approach is broadly applicable by evaluating its performance on gold-labeled DNA and RNA constructs with known structures, using a range of previously described labeling strategies (16, 21, 22). In addition, we extend its application to gold-labeled proteins using a novel labeling approach. Our results suggest that the positions of the gold labels can be assigned in the low-resolution map with near–base pair (bp) resolution (down to ~2 Å) and enable the assignment of protein or nucleic acid subdomains.

RESULTS

According to the Debye formula (1), the scattering intensity from a collection of N scatterers is given by

$$\mathit{I}(\mathit{s})={\displaystyle \sum _{\mathit{i}=1}^{\mathit{N}}}{\displaystyle \sum _{\mathit{j}=1}^{\mathit{N}}}{\mathit{f}}_{\mathit{i}}(\mathit{s})\cdot {\mathit{f}}_{\mathit{j}}(\mathit{s})\frac{\text{sin}(2\cdot \mathrm{\pi }\cdot \mathit{s}\cdot {\mathit{r}}_{\mathit{i}\mathit{j}})}{2\cdot \mathrm{\pi }\cdot \mathit{s}\cdot {\mathit{r}}_{\mathit{i}\mathit{j}}}$$ (1)

where f_i and f_j denote the individual scattering factors of scatterers i and j, s is the magnitude of the momentum transfer [with s = 2⋅sin(θ)/λ, where 2⋅θ is the total scattering angle and λ is the x-ray wavelength], and r_ij is the distance between the ith and jth scatterer. For a gold-labeled macromolecule, the scattering profile I(s) contains contributions from the gold nanocrystal label, from pairs of scatterers in the macromolecule, and from pairs consisting of one macromolecular scatterer and the gold label (Fig. 1B). Therefore, the overall scattering profile depends on the position of the gold probes relative to the macromolecule (Fig. 1B).

An overview of our approach is as follows: We directly measure the scattering profiles of the bare gold probes I_Au(s), the unlabeled macromolecule I_mol(s), and the macromolecule with a single attached gold probe I_L(s). We compute the profile for cross-scattering between the gold probe and the macromolecule, I_Au-mol(s), by subtracting the gold probe profile and the unlabeled macromolecule profile from the profile of the singly labeled macromolecule, after normalization. The scattering profile of the unlabeled macromolecule was used to generate an ab initio low-resolution 3D electron density map. The low-resolution bead model was then used to generate a set of sterically allowed trial gold positions. The experimentally measured cross-scattering term I_Au-mol(s) was then compared to the predicted cross-scattering terms for each of the trial gold label positions. The trial position that gives the best fit was identified as the most likely gold label placement. A schematic of our workflow is presented in Fig. 1C.

We used 7 Å–radius thioglucose-passivated gold nanocrystals synthesized by the Brust method (see Materials and Methods) as fiducial markers attached to a range of different biological macromolecules. As test samples, we used (i) double-stranded DNA (dsDNA) molecules ranging from 10- to 35-bp length labeled at their ends; (ii) dsDNA molecules of a fixed length of 26 bp internally labeled at various positions; (iii) kinked-turn RNA constructs labeled at two respective ends of the RNA motif; and (iv) the signaling protein calmodulin labeled at two different positions, corresponding to the two lobes of its known structure (see Materials and Methods for details of the sample preparation and labeling procedures). SAXS data were recorded at beamline 12-ID of the Advanced Photon Source (APS) and at beamline 4-2 of the Stanford Synchrotron Radiation Lightsource (SSRL) (Fig. 1A and Materials and Methods). Because matched sample concentrations are needed in the analysis but challenging to achieve experimentally (16), we corrected intensity profiles computationally (see Materials and Methods). In the first step, I_L(s) was normalized by matching its tail to the tail of I_Au(s) at s ≥ 0.04 Å⁻¹ (see Materials and Methods for details), where the scattering is dominated by the gold probe (compare Fig. 2, A and B, yellow lines and red lines). In the second step, Guinier analysis was applied to estimate the forward scattering intensity for all scattering profiles (Fig. 2, A and B) and used to normalize the molecule-only scattering profile I_mol(s).

Fig. 2. SAXS shape reconstruction, trial gold label positions, and computed scattering intensity profiles.

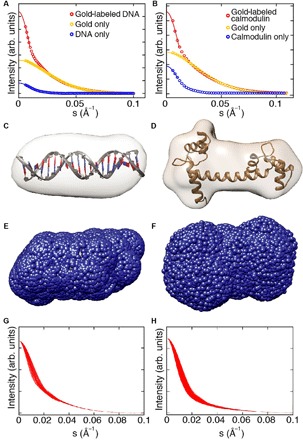
(A and B) SAXS profiles and Guinier fits for representative samples [20-bp end-labeled DNA in (A) and calmodulin labeled at position N111C in (B)]. Experimental SAXS profiles are shown as circles and the number of s-bins is reduced for clarity. Guinier fits to determine I(0) are shown as solid lines. (C and D) 3D reconstructions of 20-bp DNA in (C) and calmodulin in (D). The known high-resolution structures are superimposed (27). (E and F) Trial gold label positions (blue spheres) calculated around the envelope of the 3D reconstruction for the 20-bp DNA (E) and calmodulin (F). (G and H) Calculated total intensity profiles for a reduced set of trial gold label positions for 20-bp DNA (G) and calmodulin (H). All trial profiles were ordered from the best to the worst fitting, and every 20th curve is shown for clarity, resulting in 91 traces for 20-bp DNA (G) and 1200 traces for calmodulin (H).

Next, we analyzed the gold-only scattering I_Au by decomposing the experimental scattering signal into a linear combination of basis profiles for spherical scatterers (fig. S1) (16). Non-negative least square fits showed agreement with the experimental data (fig. S2) and suggested a narrow size distribution of the gold nanocrystals used. The fitted representation of the gold scattering was used subsequently as the form factor f_Au(s) for the gold particles in evaluation of the Debye formula (Eq. 1).

We built ab initio low-resolution models of the macromolecules under study using the scattering data from the unlabeled macromolecules using established procedures (see Materials and Methods). The low-resolution reconstructed electron density maps show agreement with the high-resolution structures for all measured DNA constructs assuming standard B-form DNA helix geometries (Figs. 2C, 3, and 4B) (24), the RNA kink-turn motif (Fig. 5B) (22, 25, 26), and the calcium-bound holo conformation of calmodulin (Fig. 2D) (27, 28).

Fig. 3. Determination of gold label positions for end-labeled DNA.

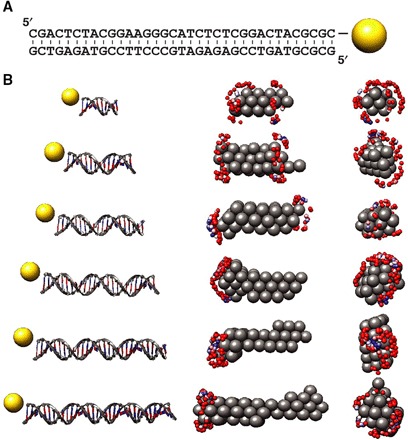
(A) Secondary structure of the 35-bp DNA duplex and the gold label position indicated on the 3′ end of the upper strand. (B) Mapping gold label positions to 3D reconstructions using SAXS data for end-labeled DNA. Left column: Schematic representations of the 10-, 15-, 20-, 25-, 30-, and 35-bp DNA constructs end-labeled with gold nanocrystals used in the study. Middle and right columns: Side (middle) and front (right) views of the 3D reconstructions of the unlabeled samples (shown as gray spheres) and mapped positions of the gold labels (blue to red spheres; blue spheres correspond to the best fit). The placement of the gold labels at the end and off-center is reproduced well.

Fig. 4. Determination of gold label positions for internally labeled DNA.

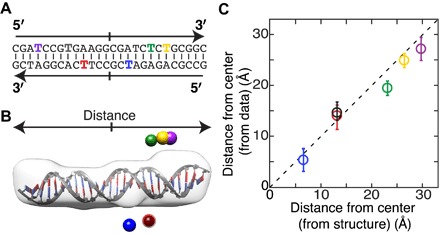
(A) Secondary structure of the 26-bp DNA duplex. Colored letters indicate bases used for internal labeling. The same color code is used in (B) and (C). (B) Low-resolution shape reconstructions of the unlabeled DNA (gray) superimposed on a high-resolution structure. The best-fitting label positions for the six different internal gold label positions are shown as colored spheres. (C) Distance to the center of the DNA computed as the mean and SD of the best 50 reconstructed and filtered label positions for each attachment point as a function of the distance of the labeled base from the center of the helix [converted using a helical rise per base of 3.3 Å (16, 17)]. The dashed line indicates 45°. The RMSD between computed and expected positions is 2.1 Å.

Fig. 5. Gold label positions for an RNA kink-turn motif.

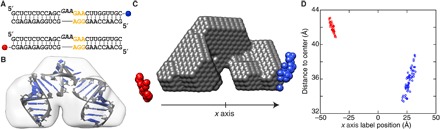
(A) Secondary structure of the RNA kink-turn and the two labeling positions at the 3′ ends for the individual constructs. The 3-nt kink-turn bulge is displayed with a small vertical offset, and the three-base mismatch region is shown in orange. (B) Shape reconstruction of the unlabeled RNA kink-turn (light gray shape) superimposed with the high-resolution structure (22). (C) Low-resolution model (gray spheres) and best-fitting gold nanocrystal positions (blue and red spheres) after filtering. (D) Scatter plot of filtered gold label positions. The x axis value of the fitted label positions is plotted versus the overall distance to the geometrical center of the low-resolution shape reconstruction.

To determine the gold label position, we created gold marker trial positions by randomly generating ~100 positions on an 11 Å–radius sphere (corresponding to the extension of the 7 Å–radius gold particle and the ~4 Å linker) around each bead in the low-resolution reconstruction (see Materials and Methods). Subsequently, positions that result in steric clashes were eliminated. The sterically allowed trial positions (typically ~1000 to 25,000 for the structures investigated here) enveloped the entire reconstructed low-resolution maps (Fig. 2, E and F). We then computed the total scattering intensity for every gold label trial position by adding the gold-labeled and unlabeled macromolecule scattering terms to the calculated scattering cross-term between the gold marker and the macromolecule. We found that different trial positions resulted in significantly different calculated scattering intensities I_total(s), with the resulting profiles depending on the relative label-molecule placement (Fig. 2, G and H), suggesting that the scattering profiles of the gold-labeled macromolecules contain the desired information about the relative gold probe–macromolecule arrangement. To determine the best trial position, we evaluated the normalized square difference between the computed profiles and the experimental scattering profile of the labeled macromolecules (Eq. 13). The trial positions were ordered from the best to worst fitting. We associated the best-fitting trial position with the most likely gold marker placement.

End-labeled dsDNA constructs

We first applied our procedure to determine the gold label positions to end-labeled dsDNA molecules ranging from 10 to 35 bp (table S1). The low-resolution reconstructed structures exhibited cylindrical shapes with a width and length as expected for our different DNA constructs (Fig. 3B). The calculated profiles for the gold form factor model, the 3D bead reconstruction, and the best-fitting trial position showed excellent agreement with the experimental data for the gold nanocrystals, the unlabeled DNA molecules, and the labeled molecules, respectively (fig. S2).

All trial gold label positions were ordered from best to worst fitting for each DNA length. For visualization, the best 100 positions (out of a total of 1055 to 2521) are shown, with the top 10 positions colored from blue to white and the next 90 positions colored from white to red. The best-fitting positions were located at the ends of the reconstructed cylindrical density maps for all investigated DNA lengths and off the cylindrical axis (Fig. 3B), as expected for the end-labeled constructs with a linker that positions the gold nanocrystal label off-axis (17, 23). The DNA constructs are almost symmetric under both rotation along the helix axis and exchange of the ends. These symmetries are visible in the reconstructed label positions: At each end, the best-fitting positions resulted in a doughnut-like shape (Fig. 3B, right). In addition, we observed well-fitting gold label positions at both ends of the reconstructed cylindrical shapes.

Because the scattering contribution (in particular, the forward scattering) increases approximately quadratically with molecular mass (1, 2), the contribution of the DNA relative to the (fixed-size) gold label increases with increasing DNA length for the gold-labeled DNA constructs (fig. S2, compare the square and circle data points). The larger relative signal from the DNA appears to enhance the positioning accuracy in our gold label assignment procedure, as evidenced by a reduced scatter and stronger clustering of the best-fitting trial positions for the longer DNA constructs (Fig. 3B). In summary, the data for end-labeled DNA constructs demonstrate that it is possible to reliably assign the label positions to the end of the helix and off-axis for all investigated DNA lengths.

Internally labeled dsDNA

To test our method for labels attached in the interior of a nucleic acid sequence, we used dsDNA gold constructs with a fixed length of 26 bp and varying internal label positions (Fig. 4A and table S2). Again, the different calculated profiles gave excellent fits to the experimental scattering profiles of the single-labeled DNA, the unlabeled DNA, and the gold nanocrystals (fig. S3). The data indicate that distinct label positions yield different cross-scattering terms (fig. S3, red lines) and, thus, can be distinguished. All trial label positions were again ordered from best to worst fitting, and the best-fitting positions for each of the internal label placements are shown in Fig. 4B. The nomenclature for the internal label positions is based on the distance of the labeled base position (in bases) and the DNA strand (strand A or B; table S2), counting from the 5′ ends. For example, A4 (Fig. 4B, purple sphere) carries a label on the fourth base from the 5′ end of DNA strand A, and B11 (Fig. 4B, blue sphere) carries a label on the 11th base of DNA strand B. For example, as expected, the A4 (Fig. 4B, purple sphere) label position is located near the end of the reconstructed DNA molecule (Fig. 4B, gray envelope), whereas the B11 (Fig. 4B, blue sphere) position was determined to be almost at the midpoint of the duplex. We computed the mean and SD of the distance from the center of the reconstructed shape along the helical axis (indicated by the arrows in Fig. 4B) for the 50 best-fitting positions for all six internally labeled constructs. We note that, similar to the end-labeled DNA constructs discussed in the previous section, the very high degree of symmetry of the bare DNA duplex does not allow us to uniquely assign the ends. However, we can determine the distance from the center of the duplex with high accuracy for each of the label positions: The reconstructed label positions are compared to the distance from the center that is expected from the DNA structure, taking into account that the label position is shifted by slightly less than one base in the 3′ direction because of the orientation of the attachment to the DNA (Fig. 4B) (21). Overall, we find agreement between the computed and expected label positions [the root mean square deviation (RMSD) is 2.1 Å and the reduced χ² = 1.7; Fig. 4C]. We expected label positions A8 and B17 to have almost identical distances to the center, which is reproduced well by the best-fitting trial positions (Fig. 4). We can reliably distinguish the position of labels separated by only 1 to 2 bp (Fig. 4C), corresponding to a distance of ~3 to 5 Å. The average deviation between measured and expected positions is 0.6 bp or 1.9 Å. Together, our results suggest that our procedure to assign the position of gold labels can achieve a few Ångström resolution, close to the resolution achieved in x-ray scattering interferometry measurements with two gold labels (16, 20–23, 29, 30) and better than the ~10 Å resolution for standard SAXS measurements.

RNA kink-turn motif

Having demonstrated the applicability of our method to DNA, we next tested it on gold-labeled RNA constructs. We used an RNA kink-turn motif (table S3) that was modified with gold nanoparticles at the 3′ end positions (Fig. 5A) (22, 29). RNA kink-turn motifs are commonly found in functional RNAs, including the ribosome. They consist of a 3–nucleotide (nt) bulge flanked by a GA/AG tandem base pair, which stabilizes a kink of more than 90° in the flanking helices (22, 25, 26). Again, ab initio shape reconstruction was used first to compute a low-resolution electron density map, which showed agreement with a high-resolution model (Fig. 5B) (22). The experimentally recorded and reconstructed profiles were again in agreement for the best-fitting trial positions at both probe locations (fig. S4). The trial positions were filtered (see Materials and Methods), and the final calculated probe positions for the two gold labels were located on opposite sides of the RNA kink-turn motif (Fig. 5, B and C). The computed gold label positions (Fig. 5B, blue and red spheres) show agreement with the positions of the probe-modified bases in the high-resolution model. For further analysis and quantification, the low-resolution density map and the calculated trial points were aligned (Fig. 5B). The positions of the trial points along the x axis were defined as in Fig. 5C, and their distances from the geometrical center of the reconstructed shape were calculated (Fig. 5, B and C, gray shape). We note that the RNA kink-turn motif in our study is almost symmetric, having 12-nt pairs in the “arms” on either side of the 3-nt central kink-turn bulge. The only difference between the two arms is that one side is fully base-paired, whereas the other side has a three-base mismatch next to the central bulge (Fig. 5D and table S3). The clear separation of the fitted label position for the labels at the two distinct termini demonstrates that specific nucleotide sequences can be unambiguously located in low-resolution reconstructed density maps, even for relatively minor differences in the structures.

Gold-labeled calmodulin constructs

Having demonstrated our method for a range of DNA and RNA constructs that relied on proven labeling chemistries, we next developed a protocol to attach the same gold nanocrystal labels to proteins. The ability to label proteins extends our approach to the third major class of biological macromolecules. We used two different mutants of the calcium-binding messenger protein calmodulin that carry single-cysteine mutations at selected positions (R37C and N111C; see Materials and Methods) as a model system. We took advantage of the thiol side chain of cysteine to couple gold nanocrystals directly to the selected positions of the protein (31–33). We focused on the calcium-bound state, that is, the holo conformation of calmodulin, which features two roughly globular and distinct lobes (27).

While calmodulin is well known to undergo large conformational changes upon Ca²⁺ binding or interactions with other binding partners, under the conditions of our experiment (≥5 mM Ca²⁺; measurement with 5 and 10 mM Ca²⁺ gave identical results, within error; fig. S5A), calmodulin has two rigid globular Ca²⁺-binding domains connected by an α-helical linker region that provides interdomain flexibility (34–40). The assumption of an overall folded protein with two lobes that are connected by a linker region with some flexibility is supported by several lines of evidence: (i) the Kratky representation [s²⋅I(s) versus s] of the scattering data is indicative of a folded protein (fig. S5B); (ii) the histogram of pairwise distance P(r) is consistent with the typical bend dumbbell shape of calmodulin in the presence of Ca²⁺ (fig. S6F) (36, 41, 42); (iii) our experimental SAXS profiles are reasonably close to the predicted profile (43) from an available crystal structure (Fig. 2D) of Ca²⁺-bound calmodulin (fig. S5C), in line with previous SAXS work (42), but the shoulder at s ≈ 0.025 Å⁻¹ is less pronounced in the experimental data, indicating a smaller separation between the two domains than in the crystal structure; and (iv) multiple ab initio reconstruction runs converged on a single structure, as indicated by pairwise normalized spatial discrepancy (44) values of ≈0.5, in agreement with previous SAXS work that has modeled calmodulin with a single conformation under similar experimental conditions (42).

The two mutants were chosen such that the cysteines are positioned at the surface of the two different lobes and placed to avoid steric clashes of the gold labels with the protein. Labeling of similar calmodulin constructs with cyanine dyes (45) or large gold nanoparticles (~40 to 60 nm in diameter via a biotin-streptavidin linkage) (46) left them fully functional. In addition, attachment of ~1.5-nm gold nanoparticles coated with uncharged ligands, similar to the particles used in this work, directly to cysteine residues of cytochrome c did not perturb the structure of the folded protein (32).

For data analysis and gold marker position reconstruction of the labeled calmodulin data, we used the same procedure as for the labeled nucleic acid constructs. For each construct, the best-fitting trial positions were calculated and sorted according to the quality of fit. The best trial positions were filtered as described in Materials and Methods. The reconstructed intensity profiles show very close similarity to the experimentally measured profiles (fig. S7). The best-fitting trial positions after filtering for the R37C (Fig. 6A, green spheres) and N111C constructs (Fig. 6A, red spheres) match the positions of these amino acids in the high-resolution structures (Fig. 6, A and B). The Ca²⁺-bound calmodulin has two approximately symmetric helix-loop-helix domains separated by a linker (27); the clear separation of the reconstructed gold label positions suggests that our method can assign the accurate positions of both labels despite the flexibility of the central linker and therefore distinguish domains with even relatively small differences in structure.

Fig. 6. Gold label position reconstructions for labeled calmodulin constructs.

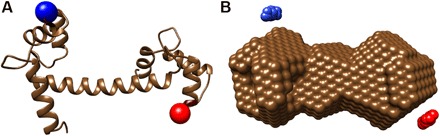
(A) Crystal structure of Ca²⁺-bound calmodulin (27) with mutated amino acid positions indicated by colored spheres (R37, blue; N111, red). (B) View of the 3D reconstructions of the unlabeled protein (shown as brown spheres) and mapped positions of the gold labels at R37C (blue) and N111C (red) as colored spheres for the filtered final label positions. The placement of the gold labels at the designated positions is well reproduced.

DISCUSSION

We used SAXS measurements to determine gold nanocrystal label positions relative to low-resolution electron density maps computed from SAXS data for a range of biological macromolecules, including 10- to 35-bp-long end-labeled dsDNA, internally labeled dsDNA, an RNA kink-turn motif, and calmodulin as a protein model system. Combined, our results show that our method is broadly applicable to all major classes of biological macromolecules and that, by using small (~7 Å in radius; ~80 gold atoms) gold nanocrystals as fiducial markers, the position of gold probes and the corresponding labeled residues can be accurately located in low-resolution reconstructions. Determining the 3D position of specific labeled residues allows the sequence of the macromolecule to be placed within the macromolecular shape. The gold-labeling approach distinguishes different domains and secondary structure elements.

Our work opens up several possibilities and future directions. The demonstrated ability to site-specifically label proteins with small gold nanocrystals creates the possibility of extending x-ray scattering interferometry gold-gold distance measurements by SAXS (16, 17, 29) or ASAXS (23) to proteins and analysis of the structural arrangement of protein–nucleic acid complexes. Application of our reconstruction method to doubly gold-labeled macromolecules could provide additional information, in particular, to resolve ambiguities in the relative placements of residues, for example, in reconstructions that have internal symmetry. Our current protocol assumes that the macromolecule of interest adopts a well-defined structure or at least one dominant conformation in solution. It might be possible to relax this assumption in the future, since SAXS is capable, in principle, of probing conformational ensembles (47–49). While labeling small gold nanoparticles with uncharged ligands tends to maintain the structure of proteins and nucleic acids, for macromolecules or complexes of unknown structure, in general, testing the functionality and structural integrity of the labeled constructs will be important.

While this proof-of-concept study uses gold nanoparticles as labels, we expect our method to be equally applicable to other labels, such as silver and platinum nanoparticles, which could provide equally attractive and orthogonal labeling options and might permit simultaneous measurements of several marker positions using ASAXS. Finally, we envision that our general approach will not be limited to SAXS. Zhang and coworkers (50) recently demonstrated that gold labels can be used to obtain structural and dynamical information for labeled DNA duplexes in cryo-EM measurements. In conclusion, nanometer-sized metal probes provide a powerful new approach to determining precise residue positions in a biological macromolecule. We anticipate that this approach will provide new and quantitative insights into macromolecular structure, dynamics, and interactions.

MATERIALS AND METHODS

Gold nanoparticle preparation

Water-soluble gold nanocrystals were synthesized and purified as described previously (16, 17, 29). The resulting gold nanocrystals were passivated with a 1-thio-β-d-glucose ligand shell to stabilize the gold nanoparticles and to achieve a highly monodisperse size distribution (fig. S1) (51).

Preparation of gold-labeled DNA and RNA samples

All DNA/RNA sequences used in this study are given in tables S1 to S3. The DNA and RNA oligonucleotides for gold labeling at the ends were prepared on an automated ABI 394 DNA synthesizer (Applied Biosystems), and thiols were incorporated using a C3-thiol-modifier (part #20-2933-41, Glen Research) on the 3′ end of the single-stranded DNA or RNA. Oligonucleotides were purified using ion-exchange high-performance liquid chromatography (HPLC), followed by reversed-phase HPLC. The coupling of the gold nanoparticles to the 3′ ends of DNA was as described by Mathew-Fenn et al. (16, 17), and the protocol for gold-labeling RNA constructs was carried out as described by Shi et al. (22). Briefly, a fivefold excess of gold nanocrystals was mixed with the thiol-modified single-stranded DNA or RNA molecules in a buffer solution at a pH of 9.0. After 2 hours, uncoupled gold nanoparticles or gold nanocrystals conjugated with multiple single-stranded DNA strands were removed by ion-exchange HPLC, and the product was stored at −20°C. A NanoDrop ND-1000 (NanoDrop Technologies) was used to determine final sample concentrations by quantifying the absorbance at 260 and 360 nm. The single-stranded DNA oligonucleotides were annealed with their complementary strands at room temperature for 30 min, whereas RNA oligonucleotides were annealed at 40°C for 30 min.

The procedure for preparing the internally labeled DNA constructs was as described (21). The oligonucleotides (table S2) with internal amino-modified thymine (Amino-Modifier, C2 dT) were prepared on an ABI 394 DNA synthesizer (part #20-2933-41, Glen Research) and reacted with a solution containing 1 mg of succinimidyl 3-(2-pyridyldithio)propionate per 10 μl of dimethyl sulfoxide, and the disulfide bridge was cleaved afterward using a solution composed of 200 mM dithiothreitol (DTT) and 50 mM tris-HCl (pH 9.0). Finally, complementary DNA strands were hybridized and purified by anion exchange HPLC to obtain pure single-labeled samples.

Preparation of gold-labeled protein samples

We used calmodulin as a protein model system. Calmodulin is a well characterized and stable protein with a known crystal structure; in addition, it has the advantage that the wild type is naturally cysteine-free. Calmodulin was expressed and labeled with gold nanocrystals as follows: A single cysteine was introduced in sea urchin calmodulin by means of the mutation R37C or N111C. This calmodulin was expressed in Escherichia coli and purified as described by Gopalakrishna and Anderson (52). The calmodulin [800 μM in 50 mM tris-HCl (pH 7.4) and 1 mM DTT] was incubated in 150 μl of 10 mM DTT and 50 mM tris-HCl (pH 9.0). Excess DTT was removed by a fast-flow G25-sepharose spin filtration column (GE Healthcare), and immediately after purification, a 5:1 ratio of purified and desalted gold nanocrystals to protein and 20 μl of 1 M tris-HCl (pH 9.0) were added to the solution and incubated for 2 hours at room temperature. The reaction was stopped by adding 15 μl of 2 M ammonium acetate solution (pH 5.6). Finally, unreacted gold nanocrystals and unlabeled proteins were removed using the Superdex 75 gel filtration column.

SAXS measurements

SAXS experiments were performed at the BESSRC-CAT beamline (53) 12-ID of the APS (for end-labeled DNA and calmodulin) and at beamline 4-2 of the SSRL (for end-labeled and internally labeled DNA and the RNA kink-turn). At beamline 12-ID, we used an x-ray energy of 12 keV, a sample detector distance of 1 m, and a custom-made sample cell (54). For calibration, a silver behenate standard was used to locate the beam center and calibrate the scattering angle. An exposure time of 10 × 1 s and a CCD detector were used for data collection. Data were reduced using the Goldcontrol software package. At SSRL, an x-ray energy of 9 keV and a sample-detector distance of 1.5 m or an x-ray energy of 11 keV and a sample-detector distance of 1.1 m were chosen. Data were collected using a linear position–sensitive proportional counter (LPSPC) in 10 1-min exposures and a Mar CCD165 (MAR) in 20 15-s exposures. Data collected using the LPSPC detector were reduced with the OTOKO and SAPOKO software packages, and data collected using the MAR detector were reduced with the BlueIce software package and additional scripts provided at the beamline.

All SAXS measurements for DNA samples were performed in 70 mM tris-HCl buffer (pH 8.0) with 100 mM NaCl and 10 mM sodium ascorbate added. SAXS measurements for RNA kink-turn samples were obtained in 70 mM tris-HCl buffer (pH 7.4) with 60 mM NaCl, 10 mM MgCl₂, and 10 mM sodium ascorbate added, and measurement for calmodulin samples used 60 mM tris-HCl buffer (pH 8.0) with 100 mM NaCl, 10 mM sodium ascorbate, and 5 mM CaCl₂, unless otherwise indicated. Samples were measured at room temperature in sample cells with a 2-mm path length and 25-μm mica windows (54). Buffer profiles were measured before and after each sample using identical procedures and subtracted for background correction. Scattering curves containing dsDNA were recorded at 50 μM and dsRNA at 30 μM sample concentration, whereas calmodulin data were obtained at 250 μM.

SAXS data analysis

We used SAXS3D (6) and DAMMIN (5, 55) to reconstruct the low-resolution bead models from the scattering profiles of the unlabeled samples. In all cases, repeated DAMMIN runs converged and yielded structures with pairwise normalized spatial discrepancy (44) values of <1.0. Custom-written MATLAB scripts were used to fit the intensity profile of the unlabeled sample using the reconstructed bead model and the gold-only scattering profile, and to reconstruct the macromolecule–gold label interference term. These intensity patterns were used to reconstruct position-dependent scattering profiles of gold label–molecule constructs, as described below. In addition, radii of gyration and P(r) functions were computed for all samples using PRIMUS (56) and are presented in table S4 and fig. S6.

Shape reconstruction of the unlabeled sample

Ab initio shape reconstructions are based on representing the structure in solution by a collection of beads or dummy residues using the Debye formula (6) or approximations to it (5, 55). The shape reconstruction algorithms used either simulated annealing (in the case of DAMMIN) or a “give-and-take” protocol (SAXS3D) to obtain the best fit to experimental data. In the reconstructions, the beads were treated as point scatterers such that all f_i are identical and independent of s. Therefore, the scattering profile from a particular bead model is given by

$${\mathit{I}}_{\text{mol}}^{\text{model}}(\mathit{s})={\mathit{c}}_1\cdot {\displaystyle \sum _{\mathit{i}=1}^{\mathit{N}}}{\displaystyle \sum _{\mathit{j}=1}^{\mathit{N}}}\frac{\text{sin}(2\cdot \mathrm{\pi }\cdot \mathit{s}\cdot {\mathit{r}}_{\mathit{i}\mathit{j}})}{2\cdot \mathrm{\pi }\cdot \mathit{s}\cdot {\mathit{r}}_{\mathit{i}\mathit{j}}}+{\mathit{c}}_2$$ (2)

The scattering pattern computed from the Debye formula was adjusted using a multiplicative constant c₁ and an additive constant c₂ to achieve the best fit to the experimental data I_mol(s). Shape reconstructions for the 10- to 35-bp DNA constructs were performed using SAXS3D; control calculations with DAMMIN gave similar results. The experimental scattering profiles of the unlabeled samples were given as an input. Reconstructions calculated on a 10 Å lattice achieved the most robust results for all six DNA lengths compared to smaller lattice spacing without losing too much resolution, and were finally exported as Protein Data Bank coordinate files. For the 26-bp DNA, the RNA kink-turn, and calmodulin, DAMMIN was used for reconstructions, with typical dummy atom radii between 1.5 and 2 Å.

Representation of the gold nanocrystal scattering

The gold nanocrystal labels used in this study exhibited small polydispersity, and their scattering contribution was previously shown to be well described as superposition of spheres with different radii (16, 17). The gold nanocrystal profile I_Au was fitted using a set of basis functions and coefficients determined by a non-negative least square fit using custom routines in MATLAB. The basis profiles I(s, R) were generated assuming spherical scatterers with radii R ranging from 2 to 100 Å

$$\mathit{I}(\mathit{s}\mathit{,}\mathit{R})=3\cdot \frac{\text{sin}(2\cdot \mathrm{\pi }\cdot \mathit{s}\cdot \mathit{R})-2\cdot \mathrm{\pi }\cdot \mathit{s}\cdot \mathit{R}\cdot \text{cos}(2\cdot \mathrm{\pi }\cdot \mathit{s}\cdot \mathit{R})}{{(2\cdot \mathrm{\pi }\cdot \mathit{s}\cdot \mathit{R})}^3}$$ (3)

A typical radius distribution is shown in fig. S1. We note that the atomic substructure of the particles only affects scattering at much higher s values than used in this study (57).

Normalization of scattering profiles

Our analysis of the labeled samples requires appropriate normalization of the scattering intensities for the labeled, unlabeled, and gold-only samples. In principle, this normalization is not necessary if all three samples are measured at identical (molar) concentrations. However, in practice, it is difficult to prepare different samples at precisely matched concentrations, and therefore, the following normalization procedure was implemented. First, the intensity profile of the gold nanocrystal–labeled sample I_L(s) was matched to the intensity profile of the gold nanoclusters I_Au(s) in such a way that the best overlap of both scattering profiles was achieved for intensities at s > 0.04 Å⁻¹ where the scattering of the labeled sample is dominated by the gold nanocrystal (Fig. 2, A and B) (16, 17). Second, Guinier analysis was carried out for all three profiles to determine the forward scattering intensities I_Au(0), I_L,N(0), and I_mol(0) using PRIMUS (56), where I_L,N(s) denotes the gold-labeled profile after the initial normalization to the gold-only profile. For the forward scattering intensity, that is, for the limit s → 0, the Debye formula simplifies to

$$\mathit{I}(0)={\mathit{N}}^2{\mathit{f}}_{\mathit{i}}(0)\cdot {\mathit{f}}_{\mathit{j}}(0)={\mathit{N}}^2{\mathit{f}}_{\mathit{i}}^2={\mathit{A}}^2(0)$$ (4)

where we have assumed identical f_i and defined the scattering amplitude A in the last step. The scattering intensity of the labeled sample is the sum of the normalized scattering intensity of the gold crystal, normalized unlabeled molecule, and the scattering cross-term of gold crystal and unlabeled molecule.

$$\begin{array}{cc}{\mathit{I}}_{\mathit{L},\mathit{N}}(0)& ={\mathit{I}}_{\text{Au}}(0)+{\mathit{I}}_{\text{mol}}(0)+{\mathit{I}}_{\text{Au-mol}}(0)\\ & ={\mathit{A}}_{\text{Au}}^2(0)+{\mathit{A}}_{\text{mol},1}^2(0)+{\mathit{A}}_{\text{Au-mol}}^2(0)\\ & ={\mathit{A}}_{\text{Au}}^2(0)+{\mathit{A}}_{\text{mol},1}^2(0)+2{\mathit{A}}_{\text{Au}}(0)\cdot {\mathit{A}}_{\text{mol},1}(0)\end{array}$$ (5)

$${\mathit{A}}_{\text{mol},1}^2(0)+2{\mathit{A}}_{\text{Au}}(0)\cdot {\mathit{A}}_{\text{mol},1}(0)+{\mathit{A}}_{\text{Au}}^2(0)-{\mathit{A}}_{\mathit{L},\mathit{N}}^2(0)=0$$ (6)

Using the Guinier extrapolated I_Au(0) as A²_Au(0) and I_L,N(0) as A²_L,N(0), this quadratic equation can be solved for A_mol(0); the solution with the negative root for A_mol(0) value was neglected as negative values for A_mol(0) were nonphysical in this context. Using the computed value A_mol from Eq. 6, the scaling value c_unlabeled was calculated as the ratio between the computed A²_mol and the Guinier extrapolated I_mol(0) of the experimental data for the unlabeled sample to scale the experimental profile of the unlabeled sample for the further analysis described below.

$${\mathit{c}}_{\text{unlabeled}}=\frac{{\mathit{A}}_{\text{mol},1}^2(0)}{{\mathit{I}}_{\text{mol}}(0)}$$ (7)

$$\mathit{I}{(\mathit{s})}_{\text{mol},\mathit{N}}={\mathit{c}}_{\text{unlabeled}}\cdot {\mathit{I}}_{\text{mol}}(\mathit{s})$$ (8)

Determination of the gold label position in the low-resolution structure

Our method requires a set of trial gold label positions enveloping the low-resolution electron density map and compares the scattering profile for placing the gold label at each individual trial point to the experimental data for the gold-labeled macromolecule. To obtain a set of possible gold label positions, 100 random coordinates on a sphere of 11 Å radius [corresponding to the 7 Å gold nanocrystal radius and the approximately 4 Å linker length (16, 17, 21, 58)] were generated around each dummy atom or bead in the reconstruction. Next, sterically forbidden positions were eliminated from this set of trial gold positions by discarding all trial positions that were located within 7 Å (the nanocrystal size) of any bead of the reconstructed model. Control calculations with fewer or more trial positions per bead (fig. S8) suggest that 100 trial positions provide sufficient accuracy for the assignment of best label positions while being computationally efficient.

Next, theoretical scattering profiles for the labeled molecule with the gold label in each of the trial gold positions were calculated. This computation can be carried out efficiently, since the scattering cross-term caused by interference between the gold nanocrystal and the macromolecule is the only term affected by the label position relative to the molecule. The intensity of the cross-term was calculated using the Debye formula (Eq. 1), including only gold-molecule terms, that is, the index i runs over all beads or point scatterers in the representation of the macromolecule (see Eq. 2), and r_i is the distance from bead i to the center of the gold label

$${\mathit{I}}_{\text{Au-mol}}(\mathit{s})={\displaystyle \sum _{\mathit{i}=1}^{\mathit{N}}}2\cdot {\mathit{A}}_{\text{Au}}(\mathit{s})\cdot {\mathit{A}}_{\text{mol}}\frac{\text{sin}({2\cdot \mathrm{\pi }\cdot \mathit{s}\cdot \mathit{r}}_{\mathit{i}})}{({2\cdot \mathrm{\pi }\cdot \mathit{s}\cdot \mathit{r}}_{\mathit{i}})}$$ (9)

The scattering amplitude A_Au(s) was determined by taking the square root of the non-negative least square fit to the experimental measure data of the gold nanocrystals.

$${\mathit{A}}_{\text{Au}}(\mathit{s})=\sqrt{{\mathit{I}}_{\text{Au}}(\mathit{s})}$$ (10)

This procedure takes into account the angle dependency of the gold particle scattering. We note that Eq. 10 neglects the imaginary part of the atomic form factors, that is, of the anomalous dispersion. However, contributions from the imaginary part of the dispersion are negligible for our measurements, since we are sufficiently far (≥80 eV) from the absorption edges of all atomic species involved. Moreover, the molecular scattering amplitude A_mol, approximated as s-independent, was calculated via the following expression

$${\mathit{A}}_{\text{mol}}={\left(\frac{{\mathit{c}}_1\cdot {\mathit{I}}_{\text{mol}}^{\text{model}}({\mathit{s}}_1)+{\mathit{c}}_2}{{\mathit{N}}^2}\right)}^{\frac{1}{2}}$$ (11)

The scaling values c₁ and c₂ were obtained from fitting the Debye formula (Eq. 2). N is given by the number of dummy atoms in the shape reconstruction and s₁ by the smallest scattering angle s appearing in the interpolated experimental data. After computing the cross-scattering term I_Au-mol for every trial gold label position using Eqs. 9 to 11, the cross-scattering intensity profiles were summed with the reconstructed gold label I_Au and unlabeled molecule I_mol scattering term to get a reconstructed scattering profile of the labeled sample I_total (Fig. 1B)

$${\mathit{I}}_{\text{total}}={\mathit{I}}_{\text{Au}}(\mathit{s})+{\mathit{I}}_{\text{mol}}(\mathit{s})+{\mathit{I}}_{\text{Au-mol}}(\mathit{s})$$ (12)

To determine the most likely label position, we compared the computed scattering profiles for the labeled molecule I_total to the experimentally measured scattering profiles of the labeled samples using the following criterion

$$\mathit{T}=\frac{{\displaystyle {\sum }_{\mathit{S}}}{[{\mathit{c}}_{\text{min},1}\cdot {\mathit{I}}_{\text{total}}(\mathit{s})+{\mathit{c}}_{\text{min},2}-{\mathit{I}}_{\mathit{L},\mathit{N}}(\mathit{s})]}^2}{{\sum }_{\mathit{S}}{\mathit{I}}_{\mathit{L},\mathit{N}}^2(\mathit{s})}$$ (13)

where I_L,N is the experimental measured (normalized) scattering profile of the gold-labeled sample; and I_Au, I_mol, and I_Au-mol are the reconstructed scattering intensity profiles of the gold nanocrystals, the unlabeled macromolecule, and the cross-scattering term, respectively. The scaling parameters c_min,1 and c_min,2 were determined for every trial position using the fminsearch function in MATLAB to minimize T. Finally, all trial label positions were sorted by their T scores from best to worst fitting.

Filtering of gold label positions

For some of the samples, the best-fitting gold label positions were further processed using the following clustering approach. First, we computed the mean (x,y,z) position for the 10 best-fitting trial positions. Next, we evaluated the distance from the mean (x,y,z) position and the SD in each Cartesian coordinate for the 100 best-fitting trial positions. Points were eliminated if their distance from the mean (x,y,z) position was greater than 1 SD in any of the three coordinates. The remaining points were used for further analysis.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/5/eaar4418/DC1

fig. S1. Radius distribution of gold nanocrystals.

fig. S2. SAXS scattering profiles of end-labeled DNA samples for label position reconstruction.

fig. S3. SAXS scattering profiles of the full set of DNA samples for internal label position reconstruction.

fig. S4. SAXS scattering profiles of two end-labeled RNA kink-turn motif samples.

fig. S5. SAXS data for unlabeled calmodulin.

fig. S6. Pair-distance distributions for all unlabeled and labeled samples.

fig. S7. SAXS scattering profiles of two different labeled calmodulin samples.

fig. S8. Spread of the best-fitting position depending on the initial trial point density.

table S1. DNA sequences used in the experiments on end-labeled DNA.

table S2. DNA sequences used in the experiments with internally labeled DNA.

table S3. RNA kink-turn sequence.

table S4. Radii of gyration R_g values for all unlabeled and labeled samples.