Abstract
Because in PET imaging cervical tumors are close to the bladder with high capacity for the secreted 18FDG tracer, conventional intensity-based segmentation methods often misclassify the bladder as a tumor. Based on the observation that tumor position and area do not change dramatically from slice to slice, we propose a two-stage scheme that facilitates segmentation. In the first stage, we used a graph-cut based algorithm to obtain initial contouring of the tumor based on local similarity information between voxels; this was achieved through manual contouring of the cervical tumor on one slice. In the second stage, initial tumor contours were fine-tuned to more accurate segmentation by incorporating similarity information on tumor shape and position among adjacent slices, according to an intensity-spatial-distance map. Experimental results illustrate that the proposed two-stage algorithm provides a more effective approach to segmenting cervical tumors in 3D 18FDG PET images than the benchmarks used for comparison.
Keywords: cervical PET, tumor segmentation, graph-cut, similarity-based variational model
1 Introduction
In 2015, cervical cancer was the second leading cause of death due to cancer in women aged 20 to 39 years. Moreover, 13,240 new cases of cervical cancer are predicted for 2018 resulting in an estimated 4,170 deaths [1]. Positron emission tomography (PET) employing radiopharmaceutical 18fludeoxyglucose (18FDG) is one of the most valuable imaging modalities for the staging and follow-up of cervical cancer [2], offering accurate identification of primary tumors and metastases [3–7] [8] and providing important information to delineate treatment targets. In addition, quantitative information extracted from PET also allows health care providers to evaluate treatment response [9]. All these potential applications can only be achieved upon accurate segmentation of tumors in 18FDG PET images. Although manual segmentation/delineation is routinely used in the clinic, this process is time-consuming and observer-dependent, indicating the need for automatic or semi-automatic segmentation of tumors from PET.
However, one particular challenge in the automatic segmentation of cervical tumors is their proximity to normal organs with high capacity of the secreted 18FDG tracer (e.g., bladder). The intensity values of the normal organs may be similar or even higher than those of avid tumors (Fig. 1), confounding the definition of simple standardized uptake value (SUV)-based region-of-interest (ROI) according to a certain threshold value. Over the past few years, various methods have been proposed to segment tumors in 18FDG PET. As 18FDG PET images are usually characterized by low spatial resolution and high contrast [10], most of the developed segmentation methods are based on thresholding techniques [11–15]. However, because these techniques define target/ROI volumes from thresholding value(s) based on image intensity, any fixed or iterative thresholding method may fail to segment cervical tumors if their SUV intensity values are similar to those of normal organs. The same situation is expected for region-growing [16, 17], gradient-based [18], and active-contour [17] methods because they primarily rely on variations in intensity values. In contrast, affinity propagation clustering [19, 20] and graph-based segmentation [21–23] methods have also been applied to PET imaging. These methods rely on similarities computed among the voxels by comparing their extracted local features that may contain more information beyond voxel intensity. However, global and geometrical features of the tumors are not included, which may bias the final results, especially in cervical tumor segmentation on PET images where local features of tumor and bladder may be close to each other. In addition to the unsupervised methods mentioned earlier, deep convolutional neural network-based methods [24–27] have also demonstrated to be promising in medical image segmentation. However, these learning-based models require a large training dataset, and their performance strongly depends on the hyper-parameters used for network construction and training.
Fig. 1.
Representative 18FDG PET image slices from a patient with cervical cancer: red outline indicates tumor contour; the 18FDG signal is contiguous with nearby normal organs (bladder), and is indicated by the arrow.
We developed a novel segmentation algorithm for cervical tumors on PET by explicitly considering the similarity between two adjacent slices. Our study is based on the observation that tumor shape and area are relatively “continuous” in adjacent slices. In other words, accurate segmentation on one of the slices can help regularize the contours on the rest of the slices. We propose a two-stage scheme that combines graph-cut algorithm and a similarity based variational model (GCSV). In the first stage, we perform a rough segmentation by incorporating local intensity and texture information for the rest of the slices based on graph-cut. The segmentation is conducted on a manually contoured tumor on one of the slices as reference. In the second stage, a novel similarity-based variational model is formulated to propagate the manual contour and adjust the initial segmentation. The similarity information is extracted by integrating the total variation among adjacent slices with segmentation accuracy probability (SAP). The proposed SAP aims to estimate the probability of correct segmentation for each voxel based on its positional similarity to the tumor contour on the reference slice, while the total variation among adjacent slices is used to regularize the shape similarity. Hence, a larger penalty will be assigned to the variations corresponding to the voxels with lower SAP to enforce higher consistency along the different slices. By combining the two stages of the proposed scheme, the problem of segmenting the bladder out as a tumor would be resolved as the information of tumor shape and position would help exclude the bladder from the segmentation results.
2. Methods and Materials
2.1. Overview
The development of our algorithm was motivated by the fact that tumor shape and position are relatively “continuous” in adjacent slices among PET images. The miss-segmented voxels on contoured adjacent slices are shown compared with the tumor contour ground truth (Fig. 2). The top region (indicated by the arrow in Fig. 2 (b)) segmented out on one slice by the conventional thresholding-based method is likely incorrect according to the ground truth tumor contour of its adjacent slice (Fig. 2 (a)).
Fig. 2.
(a) Tumor delineated in one slice; (b) Tumor roughly segmented in the adjacent slice of (a); (c) SAP map of (b) using equation (8).
Such observation can be quantified by a probability map of the segmentation accuracy computed from the ground truth tumor contour (Fig. 2 (c)), as the intensity of each voxel indicates the relative probability of each voxel that is classified correctly. The detailed calculation of the probability map will be introduced in Section 2.2.2.1. By propagating the shape and position information of the ground truth slice, we may obtain more accurate segmentation results by correcting the voxels that have low probability of being segmented correctly.
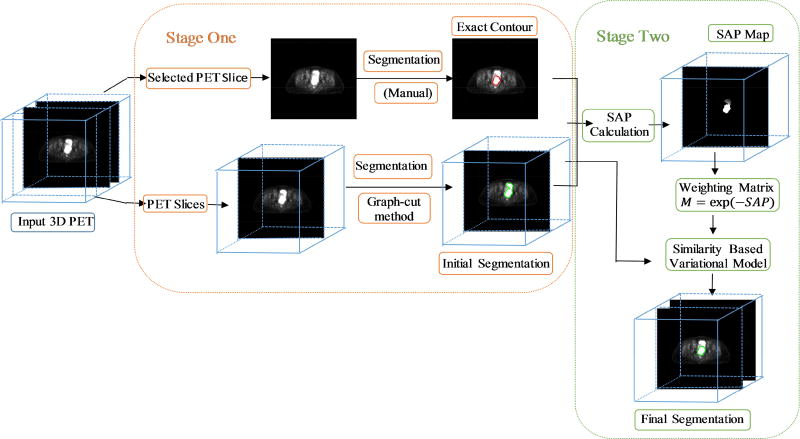
We propose a two-stage method for segmenting cervical tumors on PET images. In stage one, we roughly segment the initial contours in all the slices using a graph-cut method. In stage two, we fine-tune the segmentation results under the guidance of the ground truth tumor contour on a given slice by employing the proposed similarity-based variational model. The pipeline of the proposed two-stage segmentation method is shown in Fig. 3.
Fig. 3.
Pipeline of the proposed two-stage segmentation method (GCSV).
2.2. Detailed Methods
A summary of the operator notations used throughout the paper is provided in Table 1.
Table 1.
Main mathematical operator notations
| Variable | Meaning |
|---|---|
| Dl,2 = [Dl;D2] | Discrete gradient operator on 2D image |
| D3 | Gradient operator along slice number direction |
| ‖ ‖F | Frobenius norm of matrix |
| <,> | Inner product |
| · | Pointwise multiplication operator |
| ∧ | Fourier transform |
2.2.1. Stage One: Initial contours obtained by the graph-cut method
Graph-cut based methods have shown to be robust and reliable [10, 28] as they complete global PET segmentation by measuring local similarities. For the first stage of our proposed scheme, we developed a graph-cut based algorithm that generates the initial contours of all the slices under the guidance of the reference slice. As the construction of the similarity graph is the most time-consuming procedure for graph cut-based algorithms, we only chose voxels with relatively high intensity values as graph nodes to boost computational efficiency. Since the voxels in cervical tumors always contain high uptakes of the image tracer, excluding low intensity voxels does not affect the tumor segmentation results.
Unlike the conventional generation of the graph Laplacian matrix [10, 28] in which the similarity graphs are computed based on node intensities only, we built similarity graph S by incorporating the extended structure tensor (EST) features [29]. This similarity graph incorporates intensities and structural tensors to represent local features. The nodes in the graph are connected by measuring the Gaussian similarity between their corresponding EST features. Since the k-nearest neighbor graph is more sensitive to the local structure, we set the similarity scores in S to 0 except for nodes within the k-nearest neighbor. Finally, the corresponding Laplacian matrix L was calculated based on the similarity graph:
| (1) |
where D is a diagonal matrix with .
Then, the proposed graph-cut method can be formulated as a convex optimization problem:
| (2) |
where L indicates the graph Laplacian matrix. Ω is a subset of nodes selected from the slice contoured manually, and z is their corresponding label. u indicates the desired clustering result.
The proposed model requires the reference label to remain true in the resulting u, while broadcasting the clustering label via local similarity information embedded in the graph Laplacian matrix. The solution of the model in Eq. (2) can be explicitly written as:
| (3) |
where
| (4) |
Then, the k-means algorithm is applied to the resulting u to obtain the initial segmentation for all the selected voxels. The implementation of the k-means algorithm is introduced in the Appendix.
2.2.2. Stage Two: Fine-tuning on initial segmentation
Motivated by the fact that tumor shape and position do not dramatically change from slice to slice, we propose to fine-tune the initial segmentation by constraining the weighted total variation [30, 31] along different slices, enforcing the similarity across neighboring slices. The weight of total variation is derived based on the probability of correct segmentation guided by the reference contoured slice. Specifically, a large penalty is assigned to the slice variation of the voxel with a low probability of being correct, so that the final label of this voxel is forced to be similar to the adjacent slices. In addition, if we require the segmentation results to be smooth within each slice, the fine tuning strategy in the second stage can be formulated into the following model,
| (5) |
where w indicates the desired segmentation, and λ1 and λ2 are regularization parameters. The first term in the optimization problem of Eq. (5) prevents solution w from being too different from the initial contour. The second term imposes the smoothness within each slice to complete the tumor shape. The third term restricts the similar tumor position and shape in the adjacent slices. M is a weighting matrix derived from a SAP map of the segmentation results. M aims to further penalize the discrepancy among adjacent slices based on the SAP map.
We denoted w = (w1, …, wn) and M = (M1, …, Mn), where wj and Mj indicate the segmentation result and corresponding weighting factor for the j slice. Assuming that slice k is the one with the manual contour, we obtain wk =z, which is already known. We can rewrite equation (5) as a sum of a series of sub-problems as follows:
| (6) |
This optimization problem can be solved by iteratively updating w and M, in a column- wise fashion: we start calculating the k−1-th column until the first column is solved; then, we start from the k+1-th column until completing the last column.
2.2.2.1 Step 1: Updating Mj
In the proposed iterative algorithm, Mj would be updated according to the latest segmentation result wj. More specifically, at each iteration l, is computed by
| (7) |
The formulation of SAP is essential to the success of the second stage of the scheme. SAP is derived from each updated segmentation result w under the guidance of the manual contour in the reference slice. Most incorrect segmentations in cervical cancer are caused by mislabeling the voxels in the bladder as those of tumors. Therefore, the desired SAP should be able to evaluate the position similarity compared to the baseline of ground truth segmentation in the reference slice. The proposed SAP for each voxel of wj is formulated as
| (8) |
with a maximum value equal to 1. p is the voxel in wj, and p0 is the central voxel of the segmented tumor in its adjacent slice (wj∓1); is the squared intensity difference between p and p0, and is the squared Euclidean distance between p and p0, divided by slice area (e.g. slice size is m × m, then the slice area is m2); a, b are parameters that balance the effect of the intensity difference and spatial distance. Such formulated SAP considers both positioning and intensity information. In principle, a voxel receiving low SAP value implies a low probability of correct segmentation. Hence, large smoothness regularization penalty M should be assigned to encourage the similarity across the neighboring slices so that the mislabeled voxels can be corrected according to the correct labels on their neighboring slices.
2.2.2..2 Step 2: Updating wj
For each iteration l, with fixed, we can update as follows:
| (9) |
where π1 is a binary projector defined as π1(p) = 1{p>threshold}. The threshold is set through the k-means algorithm [32, 33] (its implementation is introduced in the Appendix). The Fourier transform was used to solve the minimization problem in Eq. (9) and the solution is
| (10) |
Overall, the algorithm that iteratively solves the optimization problem in Eq. (6) is summarized as follows:
Algorithm 1.
for solving the optimization problem in Eq. (6)
| 1. | Fix the regularization parameters λ1 > 0 and λ2 > 0 and choose the initial estimate w ∈ ℝm2×n, M ∈ ℝm2×n; |
| 2. | Update each column of weighting matrix M by Eq. (7) and desired solution w by Eq. (10) |
| 3. | Stop; or go to step 2 until converge |
The initial estimate of the w used in Algorithm 1 was generated by one direction propagation algorithm.
2.3. Comparison methods
We compared our proposed two-stage GCSV method with three commonly used segmentation techniques in 18FDG PET: automatic thresholding (AT), 3D region-growing (RG), and affinity propagation (AP). In addition, we evaluated the performance of the proposed graph-cut (GC) method in the first stage to demonstrate the effect of fine-tuning in the second stage. The AT method used in this study was based on the work by Ridler and Calvard [34], in which an iterative technique was used to select a threshold based on the image histogram. As described [35], the RG method is a robust and efficient algorithm for tumor segmentation in 18FDG PET [16]. The AP method used in this study was proposed previously [19, 20] and was shown to be effective to segment non-convex tumors [36].
In principle, the proposed fine-tuning strategy in the second stage can be applied to the initial segmentation obtained by any segmentation algorithm. As such, the fine-tuning scheme has also been adopted for the contours generated by the AT, RG, and AP algorithms. We denote these three combined approaches in the following sections as ATSV, RGSV, and APSV to indicate AT, RG, and AP, respectively.
2.4. Datasets and evaluation criteria
We used 18FDG PET images from 86 cervical cancer patients and divided them into two categories to further illustrate the algorithm performance under different situations: (1) tumor intensities similar to or higher than those of the bladder (57 patients); (2) bladder intensities higher than those of tumors (29 patients). While both categories are challenging for conventional segmentation methods, the second category can be even more difficult than the first. The ground truth tumor contours used for quantitative evaluation were delineated by a radiation oncologist with four years of experience and reviewed by another radiation oncologist with 19 years of experience.
We considered four commonly used criteria including Matthews correlation coefficient (MCC) [37], Dice similarity coefficient (DSC) (which is equivalent to the F1 score) [38], classification error (CE) [39], and volume error (VE) [39, 40] to quantitatively evaluate the segmentation accuracy of different algorithms. The formulation of each criterion is summarized in Table 2. Based on their definitions, higher MCC and DSC as well as lower VE and CE scores imply better segmentation.
Table 2.
Four criteria for quantitatively evaluating the segmentation accuracy
| Formula | ||
|---|---|---|
|
|
||
| MCC |
|
|
| DSC(F1) |
|
|
| VE |
|
|
| CE |
|
Abbreviations: TP (true positive) indicates the number of correctly classified tumor voxels; FN (false negative) indicates the number of tumor voxels labeled as normal voxels; TN (true negative) indicates the number of correctly classified normal voxels; FP (false positive) indicates the number of normal voxels labeled as tumor voxels; F0 represents the ground truth tumor; FT represents the segmented tumor; B0 represents the ground truth normal part; BT represents the segmented normal part.
2.5. Implementation details
All experiments were executed on an ACPI×64-based PC with 2.27GHz and 2.26 GHz CPU and Matlab R2016a. For each comparison method, we tuned the parameters to achieve the best average Dice similarity coefficient. In particular, size N of the nearest neighbor was set to 20. In the RG algorithm, we located the central point of the tumor in the given slice as the initial seed position. For the AP method, the histogram with 256 bins was considered in our implementation.
3. Results
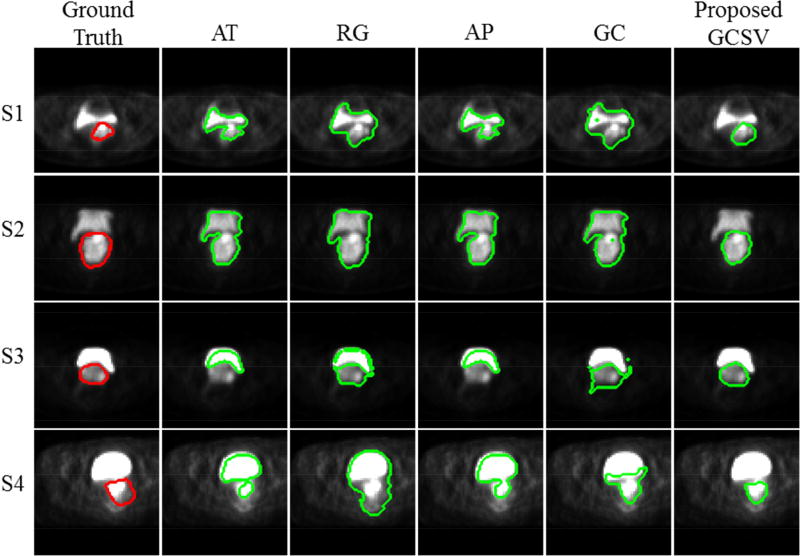
To illustrate the performance of different algorithms in segmenting cervical tumors on PET images, first we depicted the segmentation results on four slices taken from four different patients (Fig. 4). Rows one and two depict segmentation results from category one patients where the tumor exhibits the same intensity level as the bladder. Rows three and four display another two cases from category two where the bladder presents higher uptake than that of the tumor (Fig. 4). In all four slices, the tumor and bladder are connected to each other. The GC method performs similarly to AT, RG, and AP when intensities of the tumor and bladder are on the same level, but its advantage can be easily observed when bladder intensities are much higher than those of the tumor. More importantly, the proposed GCSV method fine-tunes the contours obtained by GC and yields the most accurate segmentations in terms of shape, location, and tumor area. The GCSV method clearly eliminates miss-segmented voxels especially in the first two cases where large bladder regions segmented by GC are excluded in the final results. Furthermore, the fine-tune effect of the second stage is demonstrated in both S3 and S4, in which tumor shape and position are regularized toward the ground truth.
Fig. 4.
Segmentation results of four slices from four different patients obtained by different segmentation methods.
The average performance (mean ± std) on two categories of patient data is reported in Table 3 and Table 4. Overall, results from the GC method are better than those from AT, RG, and AP for most of evaluation metrics. By further incorporating the fine-tuning stage, the proposed GCSV method substantially outperforms all the other methods for both data categories. In addition, the proposed GCSV is more stable, with a standard deviation at least 2 times smaller than that of the other methods.
Table 3.
DSC, MCC, CE and VE values obtained by different methods for Category 1 patients.
| Category 1 | DSC | MCC | CE | VE |
|---|---|---|---|---|
| AT | 0.59 ± 0.26 | 0.63 ± 0.17 | 0.70 ± 0.29 | 0.34 ± 0.27 |
| RG | 0.52 ± 0.21 | 0.57 ± 0.21 | 1.18 ± 1.12 | 1.09 ± 1.27 |
| AP | 0.57 ± 0.14 | 0.59 ± 0.14 | 0.73 ± 0.27 | 0.31 ± 0.23 |
| GC | 0.64 ± 0.16 | 0.67 ± 0.13 | 0.52 ± 0.17 | 0.47 ± 0.20 |
| GCSV | 0.83 ± 0.04 | 0.84 ± 0.04 | 0.30 ± 0.09 | 0.14 ± 0.09 |
Abbreviations: AT: automatic-thresholding; RG: region-growing; AP: affinity propagation clustering; GC: graph-cut; ATSV, RGSV, APSV and GCSV represent AT, RG, AP and GC method combined with similarity based variational model, respectively. Here, GCSV is the proposed two-stage segmentation method.
Table 4.
DSC, MCC, CE and VE values obtained by different methods for Category 2 patients.
| Category 2 | DSC | MCC | CE | VE |
|---|---|---|---|---|
| AT | 0.35 ± 0.30 | 0.37 ± 0.30 | 1.45 ± 1.44 | 0.75 ± 1.00 |
| RG | 0.48 ± 0.24 | 0.54 ± 0.22 | 3.08 ± 6.99 | 3.09 ± 7.52 |
| AP | 0.42 ± 0.24 | 0.43 ± 0.25 | 1.10 ± 0.89 | 0.46 ± 0.61 |
| GC | 0.56 ± 0.11 | 0.59 ± 0.10 | 0.62 ± 0.13 | 0.56 ± 0.16 |
| GCSV | 0.76 ± 0.09 | 0.77 ± 0.09 | 0.45 ± 0.26 | 0.24 ± 0.25 |
Abbreviations: AT: automatic-thresholding; RG: region-growing; AP: affinity propagation clustering; GC: graph-cut; ATSV, RGSV, APSV and GCSV represent AT, RG, AP and GC method combined with similarity based variational model, respectively. Here, GCSV is the proposed two-stage segmentation method.
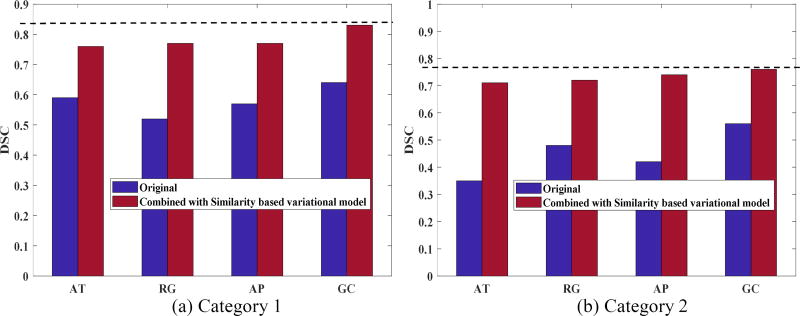
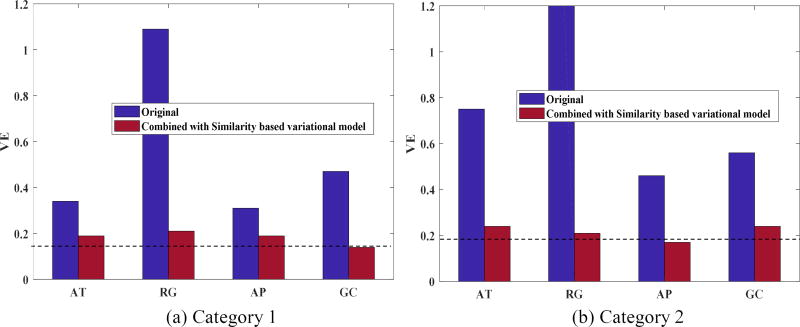
As the proposed second stage can be applied to the first stage segmentation results obtained by any algorithm, we further compared the performance of AT, RG, and AP before and after incorporating the fine-tuning scheme. The average DSC and VE values are shown in Figure 5 and Figure 6, respectively. Segmentation accuracy consistently improved for all methods. On average, the DSC value was increased by 20.25% while the VE value was reduced by 37%. The GCSV algorithm performed better than the other methods, demonstrating the effectiveness of the proposed two-stage scheme.
Fig. 5.
Comparison of average DSC value between AT, RG, AP, GC and ATSV, RGSV, APSV, GCSV for a) Category 1 patients and b) Category 2 patients, respectively.
Fig. 6.
Comparison of average VE value between AT, RG, AP, GC and ATSV, RGSV, APSV, GCSV for a) Category 1 patients and b) Category 2 patients respectively.
4. Discussion and Conclusion
We developed a two-stage segmentation method for cervical tumors that cannot be segmented automatically on 18FDG PET because they exhibit a signal contiguous with nearby normal tissues. Based on the assumption that tumor area and position do not change dramatically between two adjacent slices, an accurate segmentation result of one slice can be applied to assisting the segmentation of adjacent slices. In the proposed method, based on the known tumor contour in this given slice, a rough estimate on segmentation can be obtained from the GC approach, which provides better local information by incorporating EST features and reduces processing time substantially by selecting only those voxels with large intensities as graph nodes of interest. In addition, a novel similarity-based variational model is adopted in the second stage to fine-tune the initial tumor contour based on shape and position similarity between adjacent slices guided by the known contour in the given slice.
As observed in the experimental results reported in Section 6, the proposed GCSV approach outperformed the other conventional segmentation methods (e.g. automatic thresholding and 3D region-growing methods) in resolving a tumor’s partial connection to normal organs and tissues. In general, any existing segmentation method could be used to obtain the initial segmentation. The proposed GC-based method was shown to be more effective than the other methods.
Despite the promising performance of the two-stage scheme in cervical tumor segmentation, our study presents several limitations. First, the construction of a similarity graph is still time-consuming although computational effort was reduced significantly by selecting the nodes of interest. This limitation could be overcome by employing parallel computing techniques, such as GPU programming, as the calculation of the similarities among different nodes can be carried out independently on multiple threads. Second, a few parameters need to be tuned into both stages of the proposed method. For optimal performance, the parameters should either be determined empirically or selected from candidate sets. To handle more practical situations, the proposed method should be tested further on a wide range of patient cases so that a robust parameter setup can be implemented to achieve consistently acceptable performance in routine clinical practice. Finally, we considered the slice nearest to the tumor center as reference, with a known tumor contour. Although this setup is beneficial to fully exploit the shape and position information for segmentation, it is not required since the principal manual tumor contour of any slice can be employed as reference. In future studies we plan on evaluating the effect of different reference slices on final segmentation results.
Highlights.
Proximity between cervix and bladder makes PET segmentation challenging
Similarity among adjacent slices in tumor shape and position improves segmentation
Proposed two-stage method improves dice coefficient from one-stage methods
Proposed two-stage method outperforms other commonly used segmentation methods
Acknowledgments
This work was supported in part by the Cancer Prevention and Research Institute of Texas (RP160661) and US National Institutes of Health (R01 EB020366). The authors would like to thank Dr. Damiana Chiavolini for editing the manuscript.
Appendix
K-means clustering
Given image I (such as: the resulting u of Eq. (3) or optimal solution wj to the minimization problem of Eq. (9)), we first vectorize I and denote it as Iv = (Iv1,…, Ivn), where n is the number of pixels in I. K indicates the number of phases of I. Then, the k-means algorithm minimizes the following objective function:
| (11) |
where S(i) indicates the label of the ith pixel, mk indicates the mean value of the kth cluster, and Nk indicates the number of pixels in the kth cluster.
The k-means++ algorithm proposed by Arthur et al. [32] was used to find the minimal solution S to Eq. (11). Hence, when I is assigned with the resulting u of Eq. (3), the S is the initial segmentation result obtained from the first stage; when I is assigned with the optimal solution wj to the minimization problem of Eq. (9), the threshold needed in the binary projector is defined as the average value of m1 and m2.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Disclosures
All the authors have no relevant financial interests in the manuscript and no other potential conflicts of interest.
References
- 1.Siegel Rebecca L, Kimberly DM, Ahmedin Jemal. Cancer Statistics, 2018. CA Cancer J CLIN, 2018. 2018;68:7–30. doi: 10.3322/caac.21442. [DOI] [PubMed] [Google Scholar]
- 2.Miller TR, Grigsby PW. Measurement of tumor volume by PET to evaluate prognosis in patients with advanced cervical cancer treated by radiation therapy. International Journal of Radiation Oncology* Biology* Physics. 2002;53:353–359. doi: 10.1016/s0360-3016(02)02705-0. [DOI] [PubMed] [Google Scholar]
- 3.Grigsby PW, Dehdashti F, Siegel BA. FDG-PET evaluation of carcinoma of the cervix. Clinical Positron Imaging. 1999;2:105–109. doi: 10.1016/s1095-0397(99)00008-4. [DOI] [PubMed] [Google Scholar]
- 4.Reinhardt MJ, Ehritt-Braun C, Vogelgesang D, Ihling C, Högerle S, Mix M, Moser E, Krause TM. Metastatic Lymph Nodes in Patients with Cervical Cancer: Detection with MR Imaging and FDG PET 1. Radiology. 2001;218:776–782. doi: 10.1148/radiology.218.3.r01mr19776. [DOI] [PubMed] [Google Scholar]
- 5.Sugawara Y, Kosuda AES, Recker BE. Evaluation of FDG PET in patients with cervical cancer. The Journal of Nuclear Medicine. 1999;40:1125. [PubMed] [Google Scholar]
- 6.Grigsby PW, Siegel BA, Dehdashti F. Lymph node staging by positron emission tomography in patients with carcinoma of the cervix. Journal of Clinical Oncology. 2001;19:3745–3749. doi: 10.1200/JCO.2001.19.17.3745. [DOI] [PubMed] [Google Scholar]
- 7.Rose PG, Adler LP, Rodriguez M, Faulhaber PF, Abdul-Karim FW, Miraldi F. Positron emission tomography for evaluating para-aortic nodal metastasis in locally advanced cervical cancer before surgical staging: a surgicopathologic study. Journal of Clinical Oncology. 1999;17:41–41. doi: 10.1200/JCO.1999.17.1.41. [DOI] [PubMed] [Google Scholar]
- 8.Miller TR, Pinkus E, Dehdashti F, Grigsby PW. Improved prognostic value of 18F-FDG PET using a simple visual analysis of tumor characteristics in patients with cervical cancer. Journal of Nuclear Medicine. 2003;44:192–197. [PubMed] [Google Scholar]
- 9.Lu W, Wang J, Zhang H. Computerized PET/CT image analysis in the evaluation of tumour response to therapy. The British journal of radiology. 2015;88:20140625. doi: 10.1259/bjr.20140625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Bagci U, Udupa JK, Mendhiratta N, Foster B, Xu Z, Yao J, Chen X, Mollura DJ. Joint segmentation of anatomical and functional images: Applications in quantification of lesions from PET, PET-CT, MRI-PET, and MRI-PET-CT images. Medical image analysis. 2013;17:929–945. doi: 10.1016/j.media.2013.05.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Erdi YE, Mawlawi O, Larson SM, Imbriaco M, Yeung H, Finn R, Humm JL. Segmentation of lung lesion volume by adaptive positron emission tomography image thresholding. Cancer. 1997;80:2505–2509. doi: 10.1002/(sici)1097-0142(19971215)80:12+<2505::aid-cncr24>3.3.co;2-b. [DOI] [PubMed] [Google Scholar]
- 12.Jentzen W, Freudenberg L, Eising EG, Heinze M, Brandau W, Bockisch A. Segmentation of PET volumes by iterative image thresholding. Journal of Nuclear Medicine. 2007;48:108–114. [PubMed] [Google Scholar]
- 13.Zaidi H, El Naqa I. PET-guided delineation of radiation therapy treatment volumes: a survey of image segmentation techniques. European journal of nuclear medicine and molecular imaging. 2010;37:2165–2187. doi: 10.1007/s00259-010-1423-3. [DOI] [PubMed] [Google Scholar]
- 14.Drever L, Robinson DM, McEwan A, Roa W. A local contrast based approach to threshold segmentation for PET target volume delineation. Medical physics. 2006;33:1583–1594. doi: 10.1118/1.2198308. [DOI] [PubMed] [Google Scholar]
- 15.Drever L, Roa W, McEwan A, Robinson D. Iterative threshold segmentation for PET target volume delineation. Medical physics. 2007;34:1253–1265. doi: 10.1118/1.2712043. [DOI] [PubMed] [Google Scholar]
- 16.Day E, Betler J, Parda D, Reitz B, Kirichenko A, Mohammadi S, Miften M. A region growing method for tumor volume segmentation on PET images for rectal and anal cancer patients. Medical physics. 2009;36:4349–4358. doi: 10.1118/1.3213099. [DOI] [PubMed] [Google Scholar]
- 17.Li H, Thorstad WL, Biehl KJ, Laforest R, Su Y, Shoghi KI, Donnelly ED, Low DA, Lu W. A novel PET tumor delineation method based on adaptive region-growing and dual-front active contours. Medical physics. 2008;35:3711–3721. doi: 10.1118/1.2956713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Geets X, Lee JA, Bol A, Lonneux M, Grégoire V. A gradient-based method for segmenting FDG-PET images: methodology and validation. European journal of nuclear medicine and molecular imaging. 2007;34:1427–1438. doi: 10.1007/s00259-006-0363-4. [DOI] [PubMed] [Google Scholar]
- 19.Foster B, Bagci U, Luna B, Dey B, Bishai W, Jain S, Xu Z, Mollura DJ. Robust segmentation and accurate target definition for positron emission tomography images using affinity propagation. Biomedical Imaging (ISBI); 2013 IEEE 10th International Symposium on, IEEE; 2013. pp. 1461–1464. [Google Scholar]
- 20.Foster B, Bagci U, Xu Z, Dey B, Luna B, Bishai W, Jain S, Mollura DJ. Segmentation of PET images for computer-aided functional quantification of tuberculosis in small animal models. IEEE Transactions on Biomedical Engineering. 2014;61:711–724. doi: 10.1109/TBME.2013.2288258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Han D, Bayouth J, Song Q, Taurani A, Sonka M, Buatti J, Wu X. Information Processing in Medical Imaging. Springer; 2011. Globally optimal tumor segmentation in PET-CT images: a graph-based co-segmentation method; pp. 245–256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Bağc U, Yao J, Caban J, Turkbey E, Aras O, Mollura DJ. A graph-theoretic approach for segmentation of PET images, Engineering in Medicine and Biology Society, EMBC. Annual International Conference of the IEEE; IEEE; 2011; 2011. pp. 8479–8482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Yang F, Grigsby PW. Delineation of FDG-PET tumors from heterogeneous background using spectral clustering. European journal of radiology. 2012;81:3535–3541. doi: 10.1016/j.ejrad.2012.01.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Zhu Q, Du B, Turkbey B, Choyke PL, Yan P. Deeply-Supervised CNN for Prostate Segmentation. arXiv preprint arXiv:1703.07523. 2017 [Google Scholar]
- 25.Havaei M, Davy A, Warde-Farley D, Biard A, Courville A, Bengio Y, Pal C, Jodoin P-M, Larochelle H. Brain tumor segmentation with deep neural networks. Medical image analysis. 2017;35:18–31. doi: 10.1016/j.media.2016.05.004. [DOI] [PubMed] [Google Scholar]
- 26.Çiçek Ö, Abdulkadir A, Lienkamp SS, Brox T, Ronneberger O. International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer; 2016. 3D U-Net: learning dense volumetric segmentation from sparse annotation; pp. 424–432. [Google Scholar]
- 27.Shen YGC, Chen L, Jiang SB, Jia X. Intelligent Parameter Tuning in Optimization-based Iterative CT Reconstruction via Deep Reinforcement Learning. arXiv:1711.00414 [physics.med-ph] 2017 doi: 10.1109/TMI.2018.2823679. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Bağci U, Yao J, Caban J, Turkbey E, Aras O, Mollura DJ. A graph-theoretic approach for segmentation of PET images, Engineering in Medicine and Biology Society, EMBC. Annual International Conference of the IEEE; IEEE; 2011; 2011. pp. 8479–8482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Wang X-F, Huang D-S, Xu H. An efficient local Chan–Vese model for image segmentation. Pattern Recognition. 2010;43:603–618. [Google Scholar]
- 30.Niu S, Gao Y, Bian Z, Huang J, Chen W, Yu G, Liang Z, Ma J. Sparse-view x-ray CT reconstruction via total generalized variation regularization. Physics in Medicine & Biology. 2014;59:2997. doi: 10.1088/0031-9155/59/12/2997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Niu S, Zhang S, Huang J, Bian Z, Chen W, Yu G, Liang Z, Ma J. Low-dose cerebral perfusion computed tomography image restoration via low-rank and total variation regularizations. Neurocomputing. 2016;197:143–160. doi: 10.1016/j.neucom.2016.01.090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Arthur D, Vassilvitskii S. k-means++: The advantages of careful seeding; Proceedings of the eighteenth annual ACM-SIAM symposium on Discrete algorithms, Society for Industrial and Applied Mathematics; 2007. pp. 1027–1035. [Google Scholar]
- 33.Lloyd S. Least squares quantization in PCM. IEEE transactions on information theory. 1982;28:129–137. [Google Scholar]
- 34.Ridler T, Calvard S. Picture thresholding using an iterative selection method. IEEE trans syst Man Cybern. 1978;8:630–632. [Google Scholar]
- 35.Adams R, Bischof L. Seeded region growing. Pattern Analysis and Machine Intelligence, IEEE Transactions on. 1994;16:641–647. [Google Scholar]
- 36.Foster B, Bagci U, Mansoor A, Xu Z, Mollura DJ. A review on segmentation of positron emission tomography images. Computers in biology and medicine. 2014;50:76–96. doi: 10.1016/j.compbiomed.2014.04.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Matthews BW. Comparison of the predicted and observed secondary structure of T4 phage lysozyme. Biochimica et Biophysica Acta (BBA)-Protein Structure. 1975;405:442–451. doi: 10.1016/0005-2795(75)90109-9. [DOI] [PubMed] [Google Scholar]
- 38.Powers DM. Evaluation: from precision, recall and F-measure to ROC, informedness, markedness and correlation. 2011 [Google Scholar]
- 39.Prieto E, Lecumberri P, Pagola M, Gómez M, Bilbao I, Ecay M, Penuelas I, Marti-Climent JM. Twelve automated thresholding methods for segmentation of PET images: a phantom study. Physics in medicine and biology. 2012;57:3963. doi: 10.1088/0031-9155/57/12/3963. [DOI] [PubMed] [Google Scholar]
- 40.Zhou Z-G, Liu F, Jiao L-C, Li L-L, Wang X-D, Gou S-P, Wang S. Object information based interactive segmentation for fatty tissue extraction. Computers in biology and medicine. 2013;43:1462–1470. doi: 10.1016/j.compbiomed.2013.07.023. [DOI] [PubMed] [Google Scholar]