Stochastic gating and drug-ribosome interactions

Abstract

Gentamicin is a potent antibiotic used in combination therapy for inhalation Anthrax disease. The drug is also often used in therapy for Methicillin-Resistant Staphylococcus Aureus (MRSA). Gentamicin works by flipping a conformational switch on the ribosome, disrupting the reading head (i.e. 16S ribosomal decoding bases 1492–1493) used for decoding the messenger RNA. We use explicit solvent all-atom molecular simulation to study the thermodynamics of the ribosomal decoding site and its interaction with gentamicin. The replica exchange molecular dynamics simulations used an aggregate sampling of 15-microseconds, when summed over all replicas, allowing us to explicitly calculate the free energy landscape, including a rigorous treatment of enthalpic and entropic effects. Here, we show that the decoding bases flip on a time scale faster than that of gentamicin binding, supporting a stochastic gating mechanism for antibiotic binding, rather than an induced-fit model where the bases only flip in the presence of a ligand. The study also allows us to explore the non-specific binding landscape near the binding site and reveals that, rather than a two-state bound/unbound scenario, drug dissociation entails a shuttling between many metastable local minima in the free energy landscape. Special care is dedicated to validation of the obtained results, both by direct comparison to experiment and by estimating simulation convergence.

More than 50% of antibiotic compounds used today target bacterial ribosomes, interfering with protein synthesis¹. Anthrax and plague diseases are often treated with a combination of antibiotics that includes gentamicin, an aminoglycoside antibiotic that induces aberrant protein synthesis in bacteria by altering the decoding process. Gentamicin is also used to treat GS-MRSA (gentamicin-susceptible methicillin-resistant Staphylococcus aureus), the deadly superbugs that infect or colonize nearly 5% of all US hospital patients. Drug resistant mutations in bacteria and the severe side effects induced by prolonged aminoglycoside treatments in humans call for development of novel antibiotic compounds that can effectively target the ribosomal decoding center (i.e. the aminoacyl site of the small ribosomal subunit). Understanding the detailed mechanism of the binding and dissociation of gentamicin from the ribosome will aid in the rational design of new aminoglycosides.

Aminoglycoside antibiotics act to lock the reading head of the ribosome (i.e., 16S rRNA nucleotides A1492 and A1493) in place², resulting in widespread misreading errors, malfunctioning proteins, and subsequent death of the bacteria. These two critical universally conserved nucleotides appear to constitute a molecular switch. When a tRNA is not bound to the aminoacyl site (A site) of the ribosome, the decoding bases (A1492 and A1493) are found to reside inside their helix (small subunit helix 44)³, or in a disordered state^4,5.When a tRNA is bound to the A site, however, the decoding bases are flipped out of their helix, able to form hydrogen bonds with both the codon and anticodon. This network of interactions is used by the ribosome to discriminate between cognate and near-cognate tRNAs^6–13. Aminoglycosides bind inside helix 44, locking the decoding bases into their flipped-out state^2,9,14–19 (Fig. 1a). This configuration mimics the presence of a cognate tRNA, causing the ribosome to accept near-cognate tRNAs and to incorporate incorrect amino acids into the nascent protein.

Figure 1.

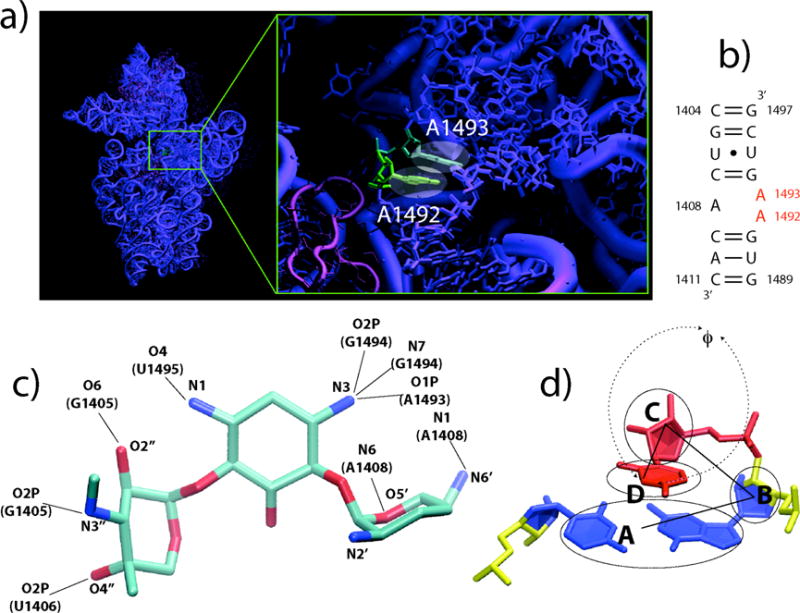
The ribosomal A site and gentamicin. a) The A site in the context of the 30S ribosomal subunit. b) Secondary structure of the simulated A site. c) Gentamicin structure from reference 17, the nine crystal contacts to the A site are evidenced. d) Definition of the flipping angle F used here to characterize the flipped in/out states of A1492 and A1493, taken from reference 49. For a given base, F is defined as the pseudo-dihedral angle determined by points A, B, C and D, where A is the center of mass of the neighboring base pair, B is that of the neighboring sugar, C is that of the sugar of the base itself and D that of the base.

While the mechanism of decoding has been extensively studied,^20,21 the detailed molecular and dynamical aspects remain unclear. In particular, although the mechanism of tRNA recognition has been described as an induced-fit, it is not clear that the ligands binding to the ribosome (tRNAs or antibiotics) actually induce a change in the conformation of A1492 and A1493. Instead, a stochastic gating mechanism might operate, where the decoding bases may be continuously flipping in and out of helix 44,²² as evidenced by the low density and high B-factors often observed in x-ray crystallography structures for these two bases in absence of ligands. In this case, ligand binding would trap the system in the flipped out state rather than inducing a conformational change.²³

The distinction between induced-fit and stochastic gating is a subtle, but important one that can lead to significant changes in drug-design strategy. Induced-fit involves the creation of a new minimum in the free energy by a ligand-target interaction. The new minimum is rarely, if ever, sampled in ligand-free state. Consistent with previous definitions of induced-fit, the binding of the ligand causes a change in the shape of the binding site.{Koshland, 1958 #4471} Stochastic gating entails the continual fluctuation of the binding site between bound and free conformations in the absence of the ligand. Here, the bound state of the binding site is sampled frequently without the ligand.

Because these characterizations of induced-fit and stochastic gating use the words “rarely”, “continual” and “frequently”, a more precise set of definitions can be formulated using time scales. In the case of the decoding center, the binding site has a bound conformation, with decoding bases flipped-out, and a free conformation, with decoding bases flipped-inside helix 44. For the purposes of this discussion, we define stochastic gating as the limit that the binding site switches between these configurations much faster than ligand binding, Likewise, we define induced-fit as the opposite limit, where the time scale of the binding site conformational change is similar to or slower than ligand binding. It is the goal of this study to determine whether base-flipping occurs faster than or slower than ligand binding and to address the question: does gentamicin bind via induced-fit or stochastic gating? In addition, we wish to gain insight into the process of binding and dissociation to address the question: does the ligand move directly from the bound to unbound state, or does the drug gradually migrate to less and less favorable non-specific binding sites?

In a recent experimental study²⁴, the energetics and dynamics of A1492 and A1493 have been characterized using steady-state and time-resolved fluorescence techniques. Here, the Pilch group finds evidence of stacking interactions of A1492 both in the presence and absence of aminoglycosides bound to the ribosomal A site.

MD simulations have previously been used to investigate drug binding^25,26. Until now, no theoretical investigation of RNA-drug complexes has reached sufficient sampling to 1) arrive at a full quantitative representation of the free energy landscape, including transition states, for the flipping of A1492 and A1493 and 2) elucidate binding/unbinding pathways and relative free energy differences along these pathways. The REMD methodology used in our present aggregate ms time scale simulations is a thermodynamically reversible, enhanced sampling method which can achieve significantly more sampling than an equivalent classical MD simulation^27,28. REMD simulations have been used extensively in the study of peptides, RNA and proteins^{27,29–31,32} and have proven to give reliable estimates of folding/unfolding free energies and pathways. We note that a limitation to our method is that it is difficult to obtain kinetic information because the algorithm produces simulation trajectories with time-dependent temperatures. Thus, it is not possible to directly calculate rates by counting events. The method only allows one to accurately gauge the relative probability of finding the system in a given state at a given temperature and thus to obtain a free-energy for that state. In this context, a more meaningful analysis can be obtained from the free energy landscape of the system. By comparing the free energy barriers of base flipping and drug dissociation, we can determine the relative ordering of the time scales, and, in turn, whether we are in the induced-fit or stochastic gating regime.

Results

We present two REMD simulations of the ribosomal A site. Simulation S1 consists of >1 μs (21 ns per replica) total sampling of the empty, or “free” A site. Simulation S2 simulates the gentamicin/A site complex, consisting of > 15 μs (320 ns per replica) total sampling of the gentamicin / A site complex, representing the “bound” state.

Flipping of A1492 and A1493

The question of how the A site switch moves between ON/OFF states and how this is influenced by gentamicin was addressed by calculating one- and two-dimensional free energy landscapes for the flipping of A1492 and A1493 at 300K from two REMD simulations (S1 and S2) of the E. coli A site in the absence and presence of gentamicin (Fig. 1c), respectively. A suite of relevant x-ray structures were used as the basis of initial starting conditions distributed throughout the temperature distribution of replicas^3,4,8,9,19. Although NMR structures of both the bound and unbound states have been solved, x-ray structures were used to determine whether or not the system would spontaneously relax towards the NMR bound state¹⁴. The coordinate f (Fig. 1d) describing the flip state for the two adenines is defined so that values in the vicinity of f=0 correspond to the residue lying inside helix 44 (flipped-in), whereas values of f~±180 correspond to completely flipped-out states. All free energy values reported are relative to the global minimum of the landscape itself and are expressed in kcal/mol.

At a first glance, both landscapes (Fig. 2) appear rugged and with several local minima, connected by higher free energy pathways. The morphologies of the two landscapes appear to be very different, although the free energy values at the minima and heights of the barriers connecting them are comparable.

Figure 2.

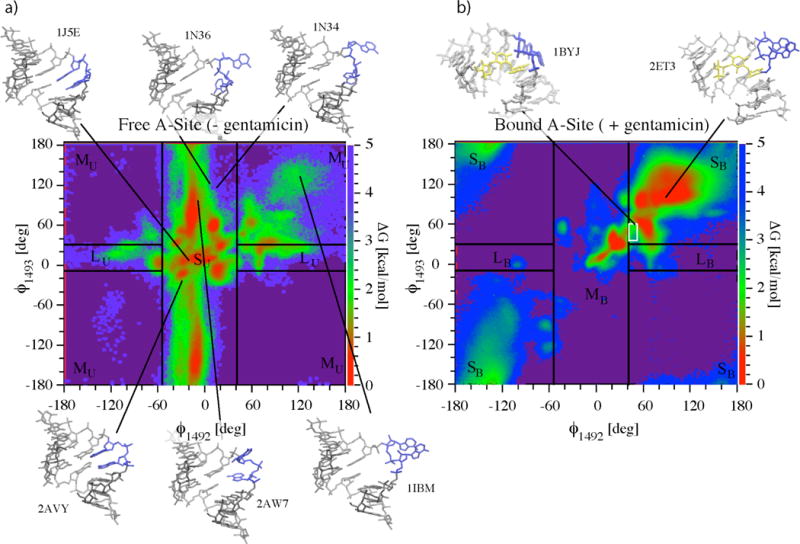
Two-dimensional free energy landscapes as a function of base flipping coordinates F₁₄₉₂ and F₁₄₉₃ resulting from simulations S1 (a) and S2 (b) for the flipping of A₁₄₉₂ and A₁₄₉₃. Starting x-ray structures used for the two simulations and relative PDB accession codes are shown along with one NMR ensemble structure (1BYJ)^{3,4,8,9,14,19}. Arrows evidence the position of the corresponding structures on the (F₁₄₉₂, F₁₄₉₃) plane. The 37 structures from the NMR ensemble for the bound state all lay within the white box in (b). Lines delimiting areas S, M, and L (with subscript U for the unbound state) correspond to values F_1492,min=−41°, F_1493,min, F_1492,max=55° and F_1492,max. These were obtained by matching time-resolved fluorescence amplitudes from reference³⁸ to the probability amplitudes from simulation S1 of finding the system in areas S, M, and L described in text (a). The same experimentally calibrated values of F_1492,min, F_1493,min, F_1492,max and F_1492,max are applied to the free energy landscape of the gentamicin simulation (subscript B for bound state) in (b).

Convergence of simulations S1 and S2 was estimated by calculating the time dependence of the average deviations σ (t) of the two dimensional potential of mean force (PMF) landscapes:

$$\sigma \left(t\right)=\sqrt{\frac{{\displaystyle \sum _{i,j}{\left(\mathrm{\Delta }G{(i,j)}_t-\mathrm{\Delta }G{(i,j)}_{t_0}\right)}^2}}{N}},$$ (1a)

Here, ΔG(i, j)_t denotes the free energy surface over the (f₁₄₉₂, f₁₄₉₃)-plane obtained after time t of the simulation with and $\mathrm{\Delta }G{\left(i,j\right)}_{t_0}$ denotes the free energy surface obtained at a time t₀, where t₀ = 0.05 ms (total sampling) for simulation S1 and t₀ = 2.5 ms (total sampling) for S2. N is the total number of grid-points on the landscape. Similarly, the average statistical fluctuation as a function of time, ς (t), of the PMF landscapes was estimated as follows:

$$\varsigma \left(t\right)=\sqrt{\frac{{\displaystyle \sum _{i,j}{\left(\mathrm{\Delta }G{(i,j)}_t-\mathrm{\Delta }G{(i,j)}_{t-\mathrm{\Delta }t}\right)}^2}}{N}},$$ (1b)

Results are shown in Fig. 3a and Fig. 3b. Values of σ (t) approach a plateau indicating convergence after ~0.5ms in the case of the free A site and after ~12 ms in that of the gentamicin-bound A site complex. In both simulations S1 and S2, ς (t) tends to zero and remains below 0.2 kcal/mol in the plateau region. The landscape for flipping of A1492 and A1493 arising from simulation S1 converges much more rapidly than that of simulation S2. This is not surprising since the presence of the antibiotic bound to the A site drastically changes the average flipping time of the decoding bases.

Figure 3.

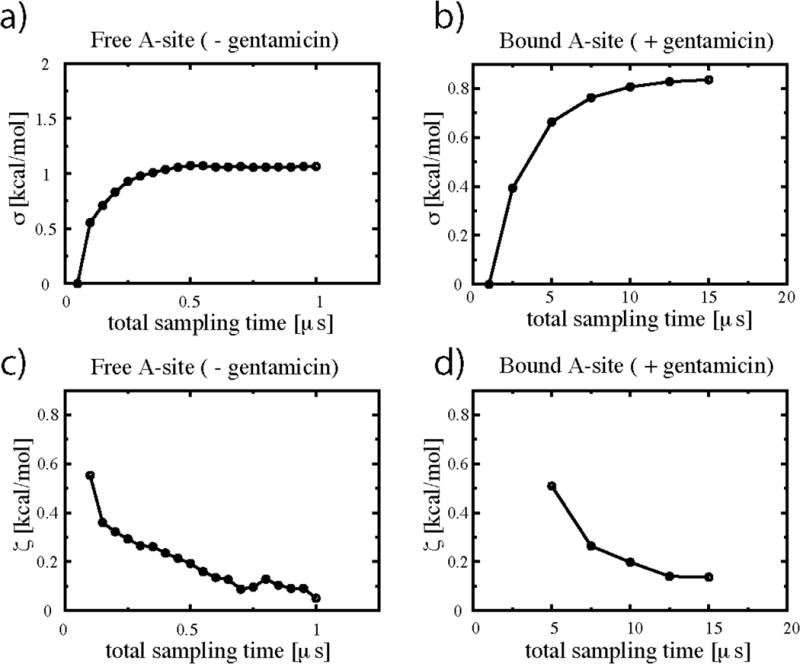
Convergence and fluctuation estimates for the free energy landcapes of Fig. 2. (a) and (c) refer to simulation S1; (b) and (d) to simulation S2. Convergence was estimated by calculating the deviation σ (t) (eq. 1a), of the two dimensional cumulative PMF landscapes DG_flip(F₁₄₉₂, F₁₄₉₃)_t obtained after time t from those obtained at time t₀. Values of σ approach a plateau indicating convergence after ~0.5 ms in the case of the free A site and after ~12ms in that of the gentamicin/A site complex. Fluctuations ς (t) were similarly derived using eq. 1b. Values of ς (t) remain below 0.2 kcal/mol in the plateau region for both simulations.

In absence of gentamicin (Figs. 2a, 4a and 4c), A1492 is essentially confined to the flipped-in states (−50<f<50) whereas A1493 explores the whole spectrum of f-space. The flipped-out states of A1492 are essentially limited to positive f angles. States with both residues flipped-out occur less frequently and are limited to the upper right hand quadrant of the landscape (f₁₄₉₂>100, f₁₄₉₃>100). With the exception of this high free energy region of the plane, flipping motions of A1492 are independent of the state of A1493. Flipping-out of A1492 involves crossing of high free energy barriers (between 3 and 3.5 kcal/mol), while the barriers for A1493 are significantly smaller (~1.3 kcal/mol). This higher mobility of A1493 is in agreement with available structural and biochemical data on the ribosomal A site^9,24. Movie 1 (see supporting information) shows a typical example of flipping events for both A1492 and A1493 in the context of the 30S ribosomal subunit during the S1 simulation (gentamicin-free). We cannot overemphasize that this movie displays a minute fraction of our total simulation data (less than 1/1,000^th). Because of the large amount of data, no single trajectory is representative of the entire dataset. We observe thousands of events such as those displayed in the movie (>10,000 base flipping events). The entire dataset is described by the free energy landscapes discussed above. The movie shows an example of what a flipping event might look like. The movie represents a single replica moving from T~300K to higher temperatures and then back to room temperature. What can be seen a typical illustration of the REMD methodology at work: at lower temperatures, the global free energy minimum (most probable states) corresponds to both A1492 and A1493 flipped-in; at higher temperatures, the barriers for flipping are more easily overcome and both bases can flip freely; as the system returns to lower temperatures it has a higher probability to be in a flipped-in state as seen at the end of the movie.

Figure 4.

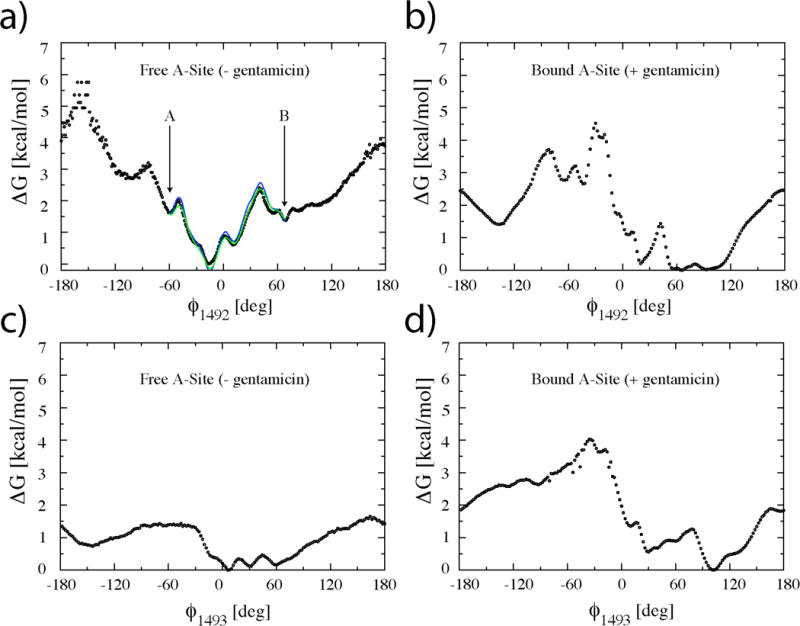
One-dimensional free energy landscapes as a function of base flipping coordinates F₁₄₉₂ and F₁₄₉₃ resulting from simulations S1 (a and c) and S2 (b and d) for the flipping of A1492 and A1493. A1492 is confined to mostly flipped-in states in the absence of gentamicin (a), whereas A1493 is highly mobile (c). Gentamicin binding to the A site shifts the equilibrium from flipped-in states to flipped-out states of both A1492 and A1493. The blue curve in (a) represents the effective free energy as re-derived between points A and B from simulation S1 using the solution of the steady state Fokker-Planck equation³³ and not directly from the simulation data. The green curve in (a) represents the homogeneous diffusion approximation³³, to the effective free energy. Both curves are in good agreement with the free energies derived directly from eq. 3 (black circles).

In order to obtain the relevant time scale for the flipping out of A1492 from the minimum of Fig. 4a, angular diffusion and drift coefficients (D(f₁₄₉₂), v(f₁₄₉₂)) were derived from simulation S1 from the short time scale evolution of the first two moments of the flipping angle f₁₄₉₂ as described in references^33–35. The validity of the obtained diffusion and drift coefficients was verified by re-deriving the one dimensional PMF of Fig. 2a within the global minimum (between points A and B in Fig. 2a). This was done using an equilibrium probability distribution derived substituting D(f₁₄₉₂) and v(f₁₄₉₂) into the solution of the steady state Fokker-Planck equation and not directly from the simulation data. The blue solid curve in Fig. 4a is the effective free energy³³, G_FP, resulting from this calculation; the green line represents the homogeneous diffusion approximation³³, G⁰_FP, to the effective free energy.

In Fig. 4a, both G⁰_FP and G_FP match the G_MD curve closely for values of f₁₄₉₂ inside the minimum confirming the validity of the calculated diffusion/drift constants. An estimate based on the average diffusion constant <D(f₁₄₉₂)>= 7.5 deg²/ps and a free energy barrier in the range of 2.3 to 2.4 kcal/mol yields escape times from the minimum of Fig. 4a between 560 ps and 660 ps.

The presence of gentamicin causes a dramatic shift the equilibrium from flipped-in to flipped-out states for both A1492 and A1493. The highest number of configurations is found in the main flipped-out minimum (upper right hand corner of the landscape in Fig. 2b). As mentioned above, these configurations are among those accessible to the free A site. Interestingly, some partially flipped-in states (for both A1492 and A1493) still occur with relatively high frequency, as evidenced by local free energy minimum that displays f values between 30 and 50 degrees. Upon visual inspection of the trajectories, these states are observed to occur at times in which the gentamicin exits the binding site completely. Unlike the free A site, the pathway connecting flipped-in states with flipped-out states follows the diagonal of the plane indicating a high degree of correlation in the flipping-in/out of the two residues. An example of this concerted flipping can be seen in Movie 2 (supporting information).

Gentamicin Binding and Unbinding Pathways

The >15 ms of aggregate enhanced sampling achieved in simulation S2 makes this the first all atom simulation of a drug/RNA complex to allow detailed statistical analysis of the specific binding process. Indeed, many of the trajectories exhibit multiple complete unbinding as well as partial rebinding events in which the center of mass of the gentamicin molecule drifts as far as 10 Å from the binding site and successively re-enters the binding site, exploring a wide range of available configurations. Movie 2 (supporting information) shows an example of such an unbinding/rebinding sequence. We observe approximately 1000 such events.

In order to obtain a quantitative picture of the binding mechanism, the two dimensional PMF, G(R_CM, R_X, T) at T=300K was calculated from simulation S2 as a function of the two reaction coordinates R_CM and R_X defined in the methods section (Fig. 5a). R_CM gives the center-of-mass distance of gentamicin from the binding site, while R_X characterizes the native contacts found in the x-ray structure. At low values of R_CM, R_X is a measure of how closely the orientation of gentamicin in the binding pocket matches that of the crystallographic structure. This is particularly useful to evaluate the relative probability of finding bound conformations (R_CM ~ 0) where the drug is still in the binding pocket but not in the same orientation as in the experimental structure.

Figure 5.

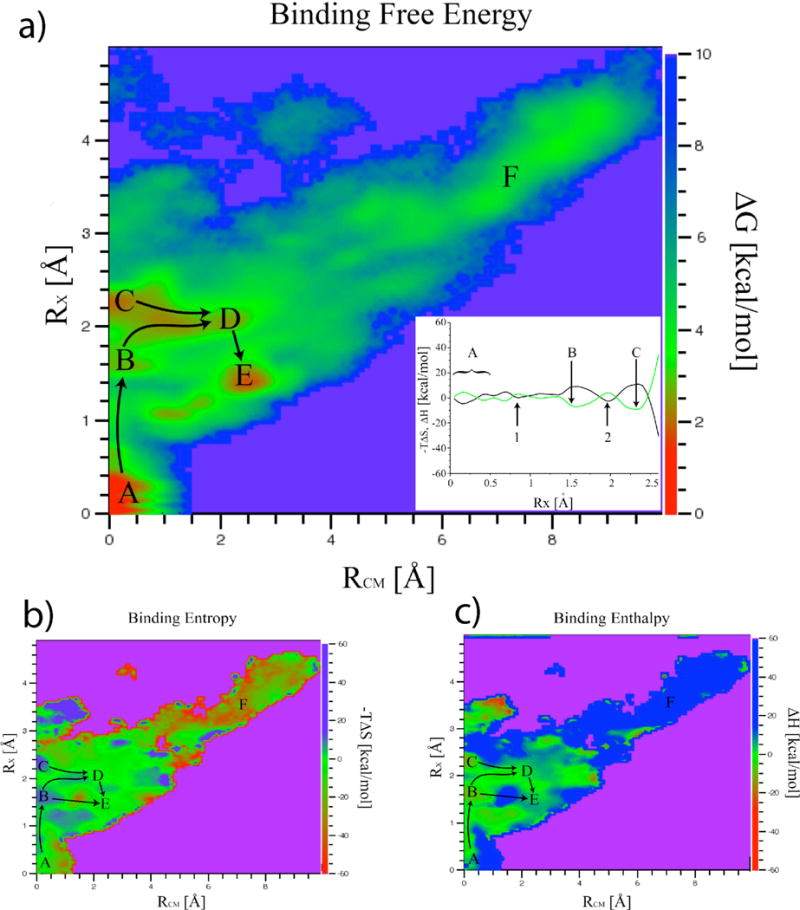
Gentamicin binding and unbinding pathways. Two dimensional binding free energy (a), entropy (b) and enthalpy (c) landscapes obtained at T=300K are shown as a function of coordinates R_CM and R_X. It should be noted that direct entropic contributions to the free energy are plotted here (−TDS). The global minimum of the binding free energy landscape, labeled A, corresponds to the crystallographic structure (R_X ~ R_CM ~ 0 Å). Inside the binding site (R_CM < 3.0 Å) the landscape is very rugged and characterized by the presence of several local minima. Points B through E are kinetic traps within the binding site. Lowest free energy pathways connecting the minima are evidenced. Entropy/enthalpy-dominated regions red to yellow areas of (b)/(c) respectively are scattered across the landscape and not limited to bound states. The inset in a) shows the entropy (black) and enthalpy (green) contributions to the free energy along the path connecting minima A, B and C. Points 1 and 2 along the path are typical examples of entropy shuttling states. States within minima labeled B and C are enthalpy-dominated whereas those labeled D, E and F are entropy-dominated. Escape to the unbound region F involves crossing several barriers where entropy “shuttling” plays a crucial role. It should be noted that the range spanned by the energy scales is very different for the free energy and for its entropic/enthalpic components. This is at the origin of the well known phenomenon of entropy-enthalpy compensation³⁷ clearly visible in the inset of a).

For large values of R_CM, R_X approaches R_CM. The binding free energy landscape (Fig. 5a) has a funneled shape with the global minimum, labeled A in Figure 5, corresponding to the crystallographic structure (R_X ~ R_CM ~ 0 Å). In the vicinity of the binding site region (R_CM < 3.0 Å) the landscape is very rugged and characterized by the presence of several local minima. Two of these minima in particular, points B and C in Fig. 5a, represent kinetic traps within the binding site itself where the center of mass of the gentamicin molecule is very close to the “native” state (R_CM~0 Å), but the orientation of the ligand does not match the crystallographic structure (R_X~1.6 Å and R_X~2.25 Å).

The lowest free energy pathway for the initial stages of gentamicin unbinding initially moves along the R_CM = 0 Å axis and crosses a ~4.5 kcal/mol barrier in the vicinity of R_X = 0.8 Å. Thus, the free energy barrier for gentamicin unbinding (> 4 kcal/mol) is at least twice that of the barrier for base flipping (1–2 kcal/mol) in absence of the gentamicin. Assuming that the rates are proportional to exp(−DG/kT), the unbinding rate is more than an order of magnitude slower than the flipping rate, consistent with the stochastic gating mechanism. We note that the crossing of this barrier involves an initial breaking of the hydrogen bonds between the RNA and the ligand without significant movement of the gentamicin center of mass in the binding site. The most probable (lowest free energy) escape pathways leading away from the two kinetic traps (2 and 3 in Fig. 5a) move along a region of roughly constant R_X and increasing R_CM implying the existence of preferred unbinding orientations. The increase in entropy along this pathway enables gentamicin to tumble within the binding site until it reaches an orientation favorable for it’s center-of-mass to escape from the binding site. This process is analogous to “jiggling” a key until the correct orientation is found to fit into the keyhole. The highest saddle point of the free energy landscape along the escape pathway leading to the region labeled F in Figure 5, positioned at R_CM~4.2, R_X~3.0, is ~5.5 kcal/mol above the global minimum.

In state A of Fig. 5, both bases exist in the flipped-out configuration with the drug in the binding pocket, as in the x-ray structure. State B has A1492 flipped out and A1493 flipped in, interacting with ring 1 of Gentamicin. States C and D are similar. Both states show A1492 and A1493 flipped-out with much weaker Gentamicin-ribosome interactions compared to states A and B. Finally, state E shows both A1492 and A1493 flipped in with few interactions between the antibiotic and the ribosome. It appears that state B may facilitate dissociation by freeing ring 1 from the binding site (Fig. 6).

Figure 6.

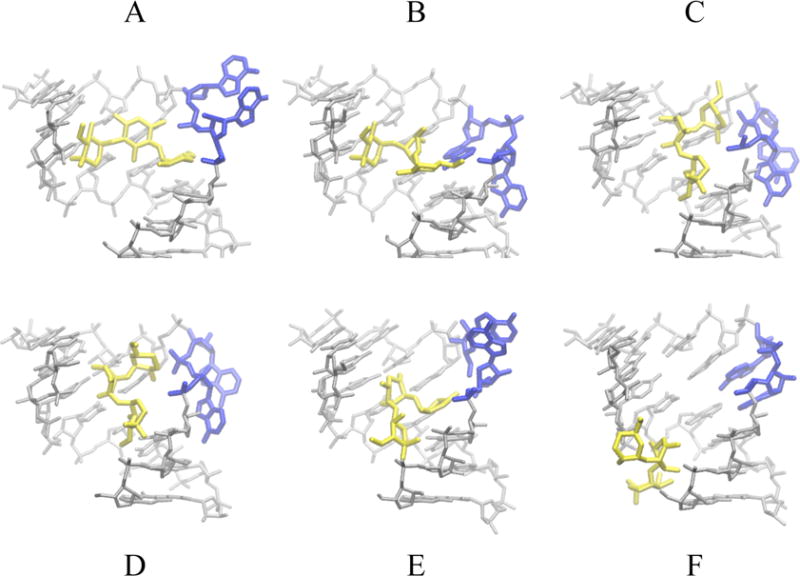
Representative structures of the gentamicin and RNA in states labeled A through F in Figure 5 extracted from simulation S2. Gentamicin is shown in yellow, decoding bases A1492 and A1493 in blue. These adopt a flipped-out conformation in state A with the drug in the binding pocket, as in the x-ray structure. In state B, A1492 is flipped-out and A1493 is flipped-in and interacts with ring 1 of Gentamicin. Both States C and D show A1492 and A1493 flipped-out. Interactions with the RNA are weaker here than those of states A and B. Finally, state E shows both A1492 and A1493 flipped in with few interactions between the antibiotic and the ribosome. In state F Gentamicin has completely left the binding site.

Entropic and enthalpic contributions to the free energy landscape at T = 300 K were obtained from the temperature dependence of the free energy as explained in the methods section. Free energy values were calculated as a function of R_CM, R_X and T for the ten replicas in the vicinity of T = 300 K (T = 283.8 K to T = 315.2 K). Points sampled at more than four of the ten temperatures were used to obtain values of DH(R_CM, R_X, 300 K) and -TDS(R_CM, R_X, 300 K) by fitting eq. (4) as described in³⁶. Enthalpy and entropy contributions to the free energy are shown as a function of R_CM and R_X, in Figs. 5b and 5c respectively. In Fig. 5c the entropic contribution to the free energy is expressed as −TDS, the minus sign assures that this is the direct contribution to the free energy. Thus with this definition of entropy contribution, if at any given point of configurational space, −TDS is lower (in its numerical value) than DH, the entropy is contributing more than the enthalpy in stabilizing (lowering the free energy) the system in that point. The most dominant (stabilizing) effect on the free energy is due to the lower of the two contributions. In this sense we will refer to entropy-dominated regions as opposed to enthalpy-dominated regions of the landscape.

It should be noted that the range spanned by the energy scales in Fig. 5 is very different for the free energy and for its entropic/enthalpic components. This should not be surprising, it is a well known fact equilibrium thermodynamics that, for any given system fluctuations of the free energy are expected to be much smaller than those of the enthalpy/entropy. This leads, as can be seen in Fig. 5, to the well known phenomenon of entropy-enthalpy compensation³⁷.

Enthalpy-dominated regions (yellowish green to red areas of Fig. 5c) are scattered across the landscape and not limited to bound states. The same is true for the entropy-dominated regions (yellowish green to red areas in Fig. 5b). The major free energy local minima basins are not all found in enthalpy-dominated regions. In particular, states within minima labeled D and E are entropy-dominated, with (−TDS)_D ~ −1 kcal/Mol, (−TDS)_E~ −2 kcal/Mol, DH_D ~ 2 kcal/Mol and DH_E ~ 3 kcal/Mol. On the contrary, states within the other two minima in the binding site, B and C, are enthalpy-dominated; however, the barriers between these minima are entropy dominated (Fig. 5a, inset). The completely unbound states in the region marked F of the landscape are highly entropy-dominated ((−TDS)_F~ −23 kcal/Mol, DH_F ~ 28 kcal/Mol)).

Discussion and Conclusions

Gentamicin gradually migrates to less and less favorable non-specific interaction sites

From the decomposition of the free energy into entropic/enthalpic contributions it becomes clear that the above-mentioned “keyhole” effect is much more general in character: along all the minimum free energy pathways connecting the most prominent free energy minima, the system must move through a highly entropy-dominated region (DH > 0 and −TDS < 0) leading to a saddle point before descending into the next minimum. This entropic “shuttling” between free energy minima does not depend on the specific character (entropy- or enthalpy-dominated) of the minima involved and does not imply crossing of purely entropic barriers. The barriers are often mixed in character, with locally entropy-dominated as well as enthalpy-dominated regions. We emphasize that enthalpy plays a key role in drug dissociation, providing a pathway of local minima near the binding site for the entrance and exit of the drug. In our simulations, entropy appears to facillitate movement between these local minima during the dissociation process.

Gentamicin-ribosome interactions occur via stochastic gating rather than induced-fit

Because the free energy barrier for base-flipping in the free state is much lower than than the barrier for drug dissociation, we conclude that the time scale of base flipping is much faster than the time scale of drug dissociation in our simulations. Consistent with this observation, we observe a quite weak correlation between base flipping and drug dissociation for a given replica (correlation coefficient between R_CM and f is approximately −0.1). Some degree of correlation is to be expected due to a steric effect: there is not enough space in the A-site for the two adenines and the antibiotic to be simultaneously within the binding site. So for the states in which the adenines are flipped in, the gentamicin must move out of the binding site.

Comparison with experiment

The higher mobility of A1493 is in general agreement with available crystallographic data: of the six structures used in this study, four have A1493 in a flipped-out state, whereas all but one has A1492 flipped-in. It is this extended mobility of A1493, which makes the ribosomal A site a very atypical adenosine bulge structure. The presence of gentamicin in the binding site drastically reduces the mobility of A1493 as well as shifting the preferred orientation of both adenines to the flipped-out configuration. Interestingly, in the presence of gentamicin, conformations close to that of the x-ray structure correspond to the global free energy minimum, while those corresponding to the 37 NMR structures lie on the pathway connecting the flipped-in and flipped-out minima as is expected from solution structures representing thermodynamic averages over all possible configurations (Fig. 2b)^14,19.

The possibility of stacked (flipped-in) conformations of A1492, even in presence of aminoglycoside drugs bound to the A site, has been experimentally verified by the Pilch group using a fluorescent analog of the ribosomal A site, in which A1492 was substituted by a 2-aminopurine²⁴. In particular, the time-resolved fluorescence experiments described in²⁴ indicate the existence of three distinct fluorescent states (with different lifetimes and amplitudes) both for the empty A site analog and for four aminoglycoside/A site complexes. The three different fluorescent states correspond to different types of stacking interactions of the 2-aminopurine with the surrounding environment. Here we start from the working hypothesis described schematically in Fig.7.

Figure 7.

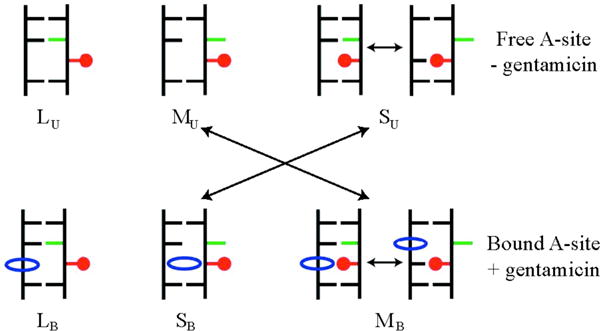
Schematic representation of hypothetical fluorescent states for the A1492/2AP1492 substituted A site (top) and aminoglycoside/A site complexes (bottom) as measured in reference³⁸. The 2AP in position 1492 is represented in red, A1493 in green and the antibiotic in blue. The longest measured lifetime (lowest quenching probability), labeled L_U for the unbound state and L_B for the bound one, corresponds to configurations with 2AP1492 flipped-out and A1493 flipped-in in both the bound and unbound states. In absence of bound antibiotics, the shortest measured lifetime (highest quenching probability), labeled S_U, corresponds to highly populated intra-helical stacked conformations of 2AP1492. Aminoglycoside binding to the A site shifts the highly populated states to extra-helical stacked S_B states of 2AP.

In absence of aminoglycosides to the A site the experimental lifetimes are: i) S_U, τ_S = 0.31ns, this corresponds to an intra-helical stacking of A1492 (highly quenched state); ii) M_U, τ_M=2.85ns, this corresponds to extra-helical stacking between A1492 and A1493; iii) L_U τ_L=9.21ns, this corresponds to configurations in which A1492 is not involved in stacking interactions, i.e. A1492 in an extra-helical state with A1493 inside the helix. The relative fluorescence amplitudes, normalized by the total intensity, give the relative populations of these three states.

The normalized amplitudes for the three distinct fluorescent states in absence of bound antibiotics, a_LU=0.076, and a_MU=0.098, a_SU=0.826 were used to calibrate the free energy landscape of Fig. 2a to the three states as described in methods. The experimentally calibrated values of f_1492,min, f_1493,min, f_1492,max and f_1492,max were then applied to the free energy landscape of the gentamicin simulation (simulation S2, Figure 2.b) and the corresponding amplitudes were calculated from the probability distribution P(f₁₄₉₂, f₁₄₉₃, 300K). Amplitudes in the presence of gentamicin were: a’_LB = 0.0034, a’_MB = 0.160, and a’_SB = 0.837. These values are in the range of those measured for other antibiotics of the same class²⁴, with gentamicin values closer to those of neomycin (a_L = 0.017, a_M = 0.139, and a_S = 0.844). Interestingly, of the four aminoglycosides studied in²⁴, neomycin is the one exhibiting the closest antimicrobial activity to that of gentamicin.

Results from simulation S1 were also compared to fluorescence anisotropy decay measurements²⁴. The anisotropy decay time measured for the free A site is reported to be 540±150 ps. This decay time is linked to the mobility of the 2-aminopurine, specifically to the inter-conversion between flipped in/out states of A1492²⁴. The escape time from the flipped-in states estimated from our simulations was 610±100 ps, in reasonable agreement with the fluorescence anisotropy decay measurements.

Isothermal titration calorimetry (ITC) profiles of paromomycin bound to a ribosomal A site model oligonucleotide performed by the Pilch group³⁸ exhibit a certain amount of non-specificity in the binding of the drug to the RNA. On the other hand, the complex picture emerging from the rugged binding free energy landscape of the simulated gentamicin/A site system also shows significant evidence of unspecific binding. In practice, the simulation data provides a more detailed representation of non-specifically bound states, evidencing the multi-state character of the kinetics within and around the binding site. The simulation, in this sense, complements the ITC data in resolving the complex landscape of the unspecific binding, but cannot access the completely unbound states in which the drug and the RNA are at a distance of much more than 10Å apart.

Enthalpic and entropic contributions to the free energy

The complexity of the free energy landscape itself makes it difficult to describe the enthalpy and entropy of binding in terms of bound and unbound states. The free energy landscape surrounding each local minimum is intermixed with regions where the constant interplay between the entropy and enthalpy allows ligand escape. This interplay cannot be simplified into switching between bound vs. unbound states (or between any other dual classification of states). While the details of the binding free energy landscape are a specific characteristic of this particular gentamicin/RNA complex, the complexity and ruggedness of the landscape itself is not. The same general characteristic complexity exists in systems that range from protein-protein interactions³⁹, small ligand systems to water molecules interacting with biological molecules^26,40.

Implications for high performance computing studies

From our sampling convergence estimates (Fig. 3), the gentamicin bound simulation S2 is near equilibrium after 15 microseconds of total REMD sampling (320 ns per replica); however, it is likely that similar estimates of changes in free energy for tRNA binding, or even tRNA anticodon stem loop binding will require much more sampling than that achieved in this study, due to the large size of the tRNA ligand. Previous estimates of free energies of tRNA binding have been based on simulations of ~ 6 ns, approximately 2500 times less than this study⁴¹. These studies make the intriguing claim that 50 ps (approximately 300,000 times less than the present study) would be sufficient to estimate free energies for tRNA binding.

The simulation produces an aggregate sampling at least 35 times greater than that of earlier drug-binding calculations, which sampled < 400 ns⁴², and 2500 times greater than previous calculations of decoding center / ligand complexes⁴¹. These two studies also used multiple trajectories to achieve aggregate sampling. Furthermore, these estimates, based on the actual simulation time (320 ns per replica), are to be considered as conservative. In fact, the REMD methodology has been estimated to actually enhance sampling by 25–75 fold.^27,28.

The type of statistical analysis performed here (Figure 3) gives only an estimate of the convergence of the landscape and the sampling necessary to obtain such convergence. Our convergence plots (Fig. 3) show that we have reduced sampling artifacts in our free energy estimates to below 0.2 kcal/mol. Fluctuations of the entropy/enthalpy landscapes are higher than those of the free energy landscapes, but relative errors are small in this case given the much larger absolute scales (the relative barriers on these landscapes are generally > 5 kcal/mol). Although our simulations are more precise in estimating thermodynamic properties within the framework of a force-field based model than other simulations which make use of much less sampling, systematic errors due to the force-field itself cannot be excluded. These errors become more apparent as sampling increases because they are no longer “blurred out” by statistical errors arising from insufficient sampling. This type of systematic uncertainty cannot be directly measured from the simulations themselves, it can only be estimated by validation through experiment. The global picture of the flipping of A1492 and A1493, the complexity of the binding free energy landscape and the even higher complexity of entropy/enthalpy decomposition arising from the simulations is confirmed by the consistency of our results with available experiments.

Methods

Simulated Systems

The simulated A site consists of residues 1404 to 1411 and 1489 to 1497 extracted from the E. coli ribosome sequence (Figure 1b). Six different initial structures with different flipping states for residues A1492 and A1493 were used for simulation of the empty A site (system S1)^3,4,8,9. These were derived from two E. coli ribosomal x-ray structures and four T. thermophilus ribosomal structures (Table 1). All nucleotides were unmodified, as in the x-ray structures. We note that while 1407 exists as m5C in E. coli, this modification has previously been shown to have no effect on gentamicin binding nor the associated K_d.{Wong, 1998 #4472} From each of the four thermophilus structures an E. coli A site structure was obtained by modeling the mutation of the G1410 = C1490 base pair to A1410 = U1490 using CHIMERA⁴³. The initial structure for the Gentamicin-bound A site (system S2) was derived from the 2.8 Å x-ray structure¹⁹. System S1 consists of the rRNA A site as defined above, 5324 SPC/E water molecules, 25 K⁺ ions, 12 Cl⁻ ions, and one Mg²⁺ ion to which 6 SPC/E water molecules were bound by a restraining potential forming a hexa-hydrated magnesium ion (MgW₆). System S2 differs from S1 for the presence of one gentamicin molecule and in the number of K⁺ and Cl⁻ ions, respectively 28 and 19. This choice results in a ~0.1 M excess KCl and ~7 mM excess MgCl₂ concentrations for both systems S1 and S2.

Table 1.

Initial structures for simulations S1 and S2

Structure	PDB accession code	Organism	A1492	φ1492 [deg]	A1493	φ1493 [deg]
1	2AVY	EC	In	−39.4	in	−19.3
2	2AW7	EC	In	−0.4	out	−97.4
3	1IBM	TH	Out	125.8	out	130.8
4	1J5E	TH	In	4.7	in	5.6
5	1N34	TH	In	32.9	out	122.0
6	1N36	TH	in/out	22.0	out	126.6
7	2ET3	EC	Out	96.8	out	108.4

Force field parameters

The X-ray structure of gentamicin from¹⁹ was fully protonated (+5) using the LEaP program of the AMBER 8.0 suite⁴⁴. The electrostatic potential was calculated at more than 16,000 points on a molecular surface around the gentamicin molecule from a single point HF/631G* calculation performed on the protonated structure. The set of partial atomic charges for the gentamicin molecule were obtained by fitting the electrostatic potential using the RESP module in the AMBER 8.0 suite⁴⁴. All other parameters for gentamicin were generated using the ANTECHAMBER module in AMBER 8.0 and then converted into GROMACS⁴⁵ format. The MgW₆ ion was treated as a separate residue in GROMACS in which the oxygen atoms of 6 SPC/E water molecules were restrained by bond, angle and dihedral terms to a standard AMBER magnesium ion. This was done to introduce a certain degree of polarizability to the magnesium ion in order to partially compensate for inaccuracies in describing the interactions between solvated magnesium ions and RNA⁴⁶. The full set of parameters for MgW₆ is supplied as supporting information in the form of a GROMACS topology file. Van der Waals parameters for the Cl⁻ and K⁺ ions were extracted from^47,48 and have been extensively tested in combination with the SPC/E water model and AMBER ff99 RNA parameters²⁶. All other simulation parameters were taken from the ffamber99⁴⁹ port of the AMBER 99 force field to GROMACS.

Simulation Protocol

Each of the seven structures (Table 1) was aligned and placed at the center of a cubic box of 55 Å length. Ions were placed in random positions within the box. A minimum distance of 3.0 Å between ions and solute atoms was imposed. The resulting systems were solvated and the MgW₆ residue was placed at one corner of the solvated box, the closest 6 water molecules to this residue were deleted. The seven systems thus obtained were energy minimized and equilibrated in the course of 1.5 ns to a pressure of 1.0 atm and a temperature of 300K using an integration time step of 1.5 fs by a well tested equilibration protocol for molecular dynamics of RNA systems²⁶. In all calculations long-range electrostatic interactions were calculated using the particle mesh Ewald (PME) method^50,51.

In order to mimic the environmental constraints imposed by the rest of the ribosome on the initial structures used for simulation of system S1, the terminal base pairs of the RNA duplex (C1404, C1411, G1489 and G1497) were maintained in their original orientations in all phases of the simulation. Similarly, in the simulation of system S2, the same residues were subject to a 10 kcal/mol Ų harmonic restraint. Imposing such restraints offers the advantage in the replica phase of the simulation of avoiding complete unfolding of the RNA duplex at high temperatures.

For the simulations presented here, 48 replicas with temperatures in the range 276.5 < T < 447.5 K and an exponential temperature distribution⁵² were used. The distribution was calculated using the standard GROMACS recipe (as described on page 32 of the GROMACS manual) to obtain a projected exchange probability of 0.135 in the desired temperature interval.

Simulations were performed using 240/480 processors on the Coyote machine in Los Alamos with the GROMACS package. The 48 replicas for simulation S1 were derived from eight copies of the six systems equilibrated at 300K, these were run without exchanges for an additional 1.5 ns at constant volume each at its respective replica temperature. A similar procedure was followed for the gentamicin simulation (S2). At this point both simulations were set into full replica exchange mode, with exchanges attempted every 125 steps. All replica simulations were conducted at constant volume. An additional 1.5 ns of simulation time was discarded before actual data collection. System S1 was allowed to run in production mode for 21 ns per replica for a total sampling of more than 1 ms. Production time on system S2 was 320 ns per replica for a total of more than 15 ms.

Potential of Mean Force

A pseudo-dihedral angle f (Figure 1d), originally defined by MacKerell⁵³, was used to distinguish flipped-in/out states for A1492 and A1493. For any given base, the angle f is defined as the dihedral angle formed by the centers of mass of: i) the neighboring base pair; ii) the neighboring sugar; iii) the sugar of the base itself; iv) the base. A second pair of coordinates (R_CM, and R_X) was used to describe the binding/unbinding of gentamicin to the A site. The first, R_CM, is defined as the distance between the position of the gentamicin center of mass as derived from the crystallographic structure¹⁹ and its position along the simulation trajectory. The second, R_X, is defined as:

$$R_X=\frac{1}{9}\sqrt{{{\displaystyle {\sum }_{i=1}^9\left(r_i^{\mathit{sim}}-r_i^{\mathit{ref}}\right)}}^2}$$ (2)

where $r_i^{\mathit{ref}}\left\{i=1\dots 9\right\}$ refers to the set of nine closest RNA/gentamicin crystal contact distances described in Figure 1c similarly, $r_i^{\mathit{sim}}$ refers to the same set of distances as they occur in the course of the simulation.

The PMF can be approximated by MD simulations from the probability P(a, b, T) of finding the system in a given state within the subspace of states spanned by the reaction coordinates a and b at a given temperature T⁴⁰:

$$\mathrm{\Delta }G\left(a,b,T\right)=-kT\ln \left[P\left(a,b,T\right)\right]$$ (3)

REMD simulations also provide the temperature dependence of DG(a,b,T), used here to separate enthalpic and entropic contributions to the free energy at T₀ =300K^36,54 for dissociation of gentamicin from the binding site. This is achieved by fitting the thermodynamic formula:

$$\begin{array}{c}\mathrm{\Delta }G=\mathrm{\Delta }H-T\mathrm{\Delta }S\\ \mathrm{\Delta }H=\mathrm{\Delta }{H}_0+{\displaystyle {\int }_{T_0}^T\mathrm{\Delta }{C}_{v}d\mathrm{\Theta }}\\ \mathrm{\Delta }S=\mathrm{\Delta }{S}_0+{\displaystyle {\int }_{T_0}^T\frac{\mathrm{\Delta }{C}_v}{\mathrm{\Theta }}d\mathrm{\Theta }}\\ \mathrm{\Delta }{C}_v=\mathrm{\Delta }{C}_v^0+\left(T-T_0\right){\left[\frac{d\mathrm{\Delta }{C}_v}{dT}\right]}_0\end{array}$$ (4)

Where C_v is the heat capacity at constant volume, H is enthalpy and S is entropy. Calibration by time-resolved fluorescence experiments. The results of experiments by the Pilch group²⁴ performed on a fluorescent analog of the A site were used to calibrate the landscape of Fig. 2a using the working hypothesis described schematically in Fig. 6.

The normalized amplitudes for the three distinct fluorescent states, a_LU=0.076, and a_MU=0.098, a_SU=0.826 were used to assign sections of the free energy landscape to the three states. For the case of simulation S1 (Fig. 2a) these three states correspond to the three different stacking configurations of points i–iii described in Fig. 6 (caption). The landscape was initially divided into three areas characterized by f_1492,min=−60° and f_1492,max=60°, which bound the minimum at f₁₄₉₂=0°. These values were iteratively adjusted in one degree steps in order to obtain exactly a fraction, a_SU, of all configurations of the simulation with f_1492,min<f₁₄₉₂<f_1492,max (area labeled L_U in Fig. 2a). Values obtained for f_1492,min and f_1492,max were −41° and 55° respectively. Similarly, two values of f₁₄₉₃ were used and iteratively refined to distinguish sections M_U and S_U in Fig. 2a. Final values of f_1493,min and f_1493,max were −8° and 31° respectively.