Reversing direction of galvanotaxis by controlled increases in boundary layer viscosity

Abstract

Weak external electric fields (EFs) polarize cellular structure and direct most migrating cells (galvanotaxis) toward the cathode, making it a useful tool during tissue engineering and healing of epidermal wounds. However, the biophysical mechanisms for sensing weak EFs remain elusive. We have reinvestigated the mechanism of cathode-directed water flow (electro-osmosis) in the boundary layer of cells, by reducing it with neutral, viscous polymers. We report that increasing viscosity with low molecular weight polymers decreases cathodal migration and promotes anodal migration in a concentration dependent manner. In contrast, increased viscosity with high molecular weight polymers does not affect directionality. We explain the contradictory results in terms of porosity and hydraulic permeability between the polymers rather than in terms of bulk viscosity. These results provide the first evidence for controlled reversal of galvanotaxis using viscous agents and position the field closer to identifying the putative electric field receptor, a fundamental, outside-in signaling receptor that controls cellular polarity for different cell types.

Introduction

Applied EFs are used in clinical practice to promote healing of chronic, epidermal wounds (1,2). The practice is supported by successful clinical trials spanning decades (3) and nonclinical research showing that endogenous DC EFs are critical components of embryonic development, tissue and organ regeneration, and epidermal wound healing (4–8). Despite its use in the clinic, the mechanism(s) by which non-electrically excitable cells sense weak EFs remains unknown.

In culture, weak DC EFs, in the range of 40-200 mV/mm which have been measured near epidermal wounds (4), polarize cells and direct growth and migration of cells and cell sheets most commonly toward the cathode (9–12). Weak EFs are thought to direct cells to the cathode by causing cell surface signaling receptors to accumulate on the cathode side of the cell (13,14), resulting in cell structure modification in a manner similar to cell polarization during chemotaxis (7). However, there is little understanding of the biophysical mechanism by which negatively charged cell surface macromolecules migrate to the negatively charged cathode.

In aqueous solutions, DC EFs electrophorese mobile charge carriers to the pole of opposite charge (Fig. 1). This forms the basis for macromolecule separation during gel and capillary electrophoresis. However, adjacent to negatively charged surfaces, like glass capillary tubes (15) or plasma membranes (14), the larger number of mobile charge carriers are inorganic cations, like Na⁺, which are electrophoresed to the cathode. Electrophoresed cations drag their shells of hydration toward the cathode, resulting in electrically driven water flow, termed electro-osmosis or electro-osmotic flow (EOF). Hundreds of eukaryotic cell types possess negative surface potentials (16,17), leading to cathodal EOF.

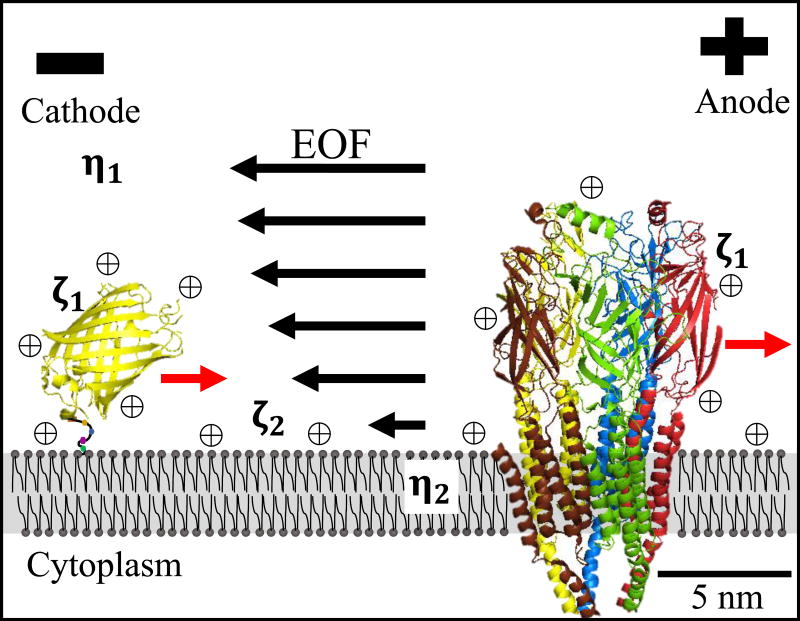
Figure 1.

External DC EFs generate opposing forces on plasma membrane surface proteins. Electrophoretic forces direct net negatively charged proteins, yellow fluorescent protein with a lipid anchor and the transmembrane nicotinic acetylcholine receptor, toward the anode (red arrows). Electrophoresis of mobile cations ⊕ and their shells of hydration, directs water flow to the cathode (EOF) and generates a force on surface exposed proteins toward the cathode.

The electro-osmotic force on surface proteins toward the cathode is proposed to be stronger than the opposing electrophoretic force toward the anode as many surface proteins accumulate on the cathode side of cells (12,14,18–24) and polarize the cytoplasmic cell motility machinery to the cathode (25–27). However, attempts to reduce the electro-osmotic force by increasing media viscosity did not reduce cathodal migration (28,29).

McLaughlin and Poo (1981) modelled the net velocity (u₁) of an electromigrating cell surface macromolecule (Eq. 1) as the difference between electrophoretic and electro-osmotic forces and influenced by drag force exerted by the plasma membrane (eq. 9 from 14). E_θ is the applied DC EF strength and ∈_r∈₀ is the permittivity of the media. The other variables are the physical parameters of the cell membrane and cell surface macromolecule that determine the magnitude of the three forces listed above, where a₁ and a₂ are the equivalent radii of the macromolecule in the extracellular space and embedded in the lipid bilayer, η₁ and η₂ are the viscosity of the extracellular media and the lipid bilayer, and ζ₁ and ζ₂ are the surface zeta potentials of the extracellular domain of the macromolecule and the cell surface, respectively. Fig. 1 includes location for the viscosity and zeta potential terms where ζ₁ could represent any surface protein.

$${\mathrm{u}}_1={\mathrm{E}}_{\mathrm{\theta }}{\in }_{\mathrm{r}}{\in }_0\frac{{\mathrm{a}}_1({\mathrm{\zeta }}_1-{\mathrm{\zeta }}_2)}{{\mathrm{a}}_1{\mathrm{\eta }}_1+{\mathrm{a}}_2{\mathrm{\eta }}_2}$$ Eq. 1

Eq. 1 indicates that macromolecules with larger extracellular domains and smaller lipid bilayer spanning domains will electromigrate at rates closer to the EOF rate which reaches 150 μm/min in normal saline according to Eq. 2, for a 125 mV/mm EF applied to a cell with an average zeta potential of −33.7 mV (16).

$$\mathrm{EOF}\mathrm{rate}={\mathrm{E}}_{\mathrm{\theta }}{\in }_{\mathrm{r}}{\in }_0\frac{{\mathrm{\zeta }}_2}{{\mathrm{\eta }}_1}$$ Eq. 2

Increasing extracellular viscosity (η₁) is hypothesized to decrease electromigration of surface proteins whether ζ₁ (electrophoresis) or ζ₂ (electro-osmosis) dominates (Eq. 1) and will decrease EOF directly (Eq. 2). Therefore, polarized electromigration of cell surface macromolecules will decrease, and cell migration direction will become random in applied DC EFs. Despite these predictions, two attempts to impair galvanotaxis by increasing extracellular viscosity did not affect the direction or speed of cell growth (28) or cell migration (29), leading to the conclusion that EOF is not driving cathode-directed galvanotaxis. Those efforts involved use of only a high molecular weight (HM) polymer (~400 kD) over a wide viscosity range 0.001-300 Pa•s (28) and only a single sized polymer at low viscosity 50 mPa•s (29). Considering that HM polymers give rise to large pores between the polymers with little change to viscosity within those pores (30) we propose that they are less effective than low molecular weight (LM) polymers in altering viscosity within the boundary layer near the cell surface where EOF is generated. To test this hypothesis we have employed a wide range of neutral viscous polymers in attempts to increase viscosity in the boundary layer of cells and influence galvanotaxis.

Methods

Keratocyte culture and EF Application

Adult zebrafish (Danio rerio) were handled and anesthetized before scale removal according to IACUC protocol #15-022A. Keratocyte culture (31) and EF application (12) were performed as described previously, using an enclosed chamber with dimensions of 22 mm × 7.5 mm × 0.3 mm.

Viscosity manipulation

Viscosity of media was manipulated by mixing methyl cellulose (MC) (Methocel A, Sigma-Aldrich, St. Louis MO) into normal fish Ringer’s (FR) media. Centrifugation was used to remove air bubbles and insoluble matter. Viscosity was increased using a range of MC with different molecular weights and a concentration range for the 38 kD MC. The weight average molecular weights of the different MCs are 38 kD, 54 kD, 140 kD, 200 kD, and 400 kD (32). Final viscosity of the media was determined using an AR2000 rotating disk viscometer (TA Instruments, New Castle, DE) calibrated with high and low viscosity standards (Cannon Instrument Company, State College, PA).

Cell motility and particle velocimetry analysis

Time-lapse images of migrating keratocytes were collected each minute for 65 or 125 minutes at ambient temperature, 21°C. The electric field was applied after 5 minutes of random migration. Movement was tracked and quantified using ImageJ image analysis software (33). Single cells chosen for analysis did not contact other cells or debris and remained within the field of view during the entirety of the experiment. The mean cosine ϴ was calculated as described previously (12) and a Student’s t-test was used to compare means.

Small immersed particles of neutral MC were used to measure bulk fluid flow in viscous media during EF application, instead of positively or negatively charged microspheres as the microsphere velocity would have been affected by electrophoresis. ImageJ was used to track and determine particle velocity for high viscosity media made with low and high molecular weight polymers. Shear stress on the cells was determined by multiplying the shear rate by the dynamic viscosity. Shear rate was calculated by dividing particle/fluid speed (μm/s) by 10 μm, assuming that the measured particles were within 10 μm of the plasma membranes, even though the chamber height was 300 μm and the particles could have been much farther away.

Whole cell electrophoresis

Cell surface potentials were determined by monitoring cell velocity during application of an electric field. Chambered dishes, as described above, were coated with polyhydroxyethylmethacrylate (pHEMA) to reduce EOF along the inner surfaces of the chamber. 40 mg of pHEMA was added to a 2 ml Eppendorf tube of EtOH and vortexed for 1 minute before solubilizing at 37°C overnight. Solubilized pHEMA was then pipetted into the trough of chambers and allowed to dry in a humidified 37°C incubator to form a layer of pHEMA hydrogel. This was repeated until pHEMA coated the bottom of the chamber. The top surface of pHEMA was allowed to hydrate in media for a few hours before use. The chamber was capped with a plastic, hydrophobic coverslip. Cells were not allowed to touch down to the pHEMA during measurements as this created measurable resistance to whole cell electrophoresis.

Fish keratocytes and CHO cells were detached from the culture dish bottom with divalent free fish Ringer’s or divalent free Ringer’s to prevent loss of surface proteins and surface charge that occurs during protease treatment. Cells were concentrated with brief centrifugation and resuspended in normal fish Ringer’s or Ringers prior to measurements.

Imaging of Fluorescent Membrane Macromolecules

Electromigration studies of cell surface ConA receptors and yellow fluorescent protein (YFP) bound to an external lipid anchor, glycosylphosphatidylinositol (GPI) with an N-glycosylated site, were performed on spherical CHO cells at room temperature. Newly plated, spherical cells with less formed cytoskeletons help ensure that a large fraction of cell surface macromolecules are freely diffusible in the plasma membrane and not immobilized by the cytoskeleton. Spherical CHO cells also have less tendency to migrate than fully adhered cells. Electromigration of ConA receptors was studied by using confocal fluorescence imaging of tetramethylrhodamine ConA at a low final concentration of 2 μg/mL to minimize capping and crosslinking (34). Also 50 μg/ml ConA inhibits electromigration of surface ConA receptors (35). Plasma membrane TMR-ConA (ex 559 nm, em 625/50 nm) and YFP-GPI (ex 515 em 542/40) distribution were determined at the beginning of experiments and also 20 min after application of a 1000 mV/mm EF using an Olympus FV1200 confocal system with an IX81 inverted microscope. For each treatment, a total of 30-50 cells from at least two different chambers were analyzed before and after EF application. EF magnitude alone does not favor EOF over electrophoretic forces, see Eq. 1 above. A Student’s t-test was used to compare fluorescent intensity ratios.

Fluorescence Correlation Spectroscopy

Single point FCS measurements were performed for fluorescein-labelled dextran (3 kD) and ovalbumin (45 kD) using a Zeiss LSM510 ConfoCor 3 system with Axiovert 200M microscope. The samples were excited with the 488 nm line of an Argon ion laser and the laser power was controlled using an acousto-optic modulator. The samples (final concentration of 20 nM) were placed on a coverslip (No. 1.5) on top a 40X 1.2 NA water immersion objective. The laser was reflected to the objective using a dichroic mirror that reflects the 488 nm laser line but transmits the higher wavelength fluorescence. Fluorescence was collected using the same objective, passed through the dichroic mirror, and focused to the detector after passing through a 505-610 nm band pass filter and a pinhole (2.27 airy units) to reject out of focus light. The signal was collected using an Avalanche Photo Diode. The acquisition of fluorescence intensity traces and the calculation of the correlation functions were performed using the ConfoCor section of LSM-FCS software provided with the microscope. Average FCS decays were calculated from 6 runs of 45 s each. The average correlation functions were then fitted using Origin 9 software (OriginLab, Northampton, MA). The width (w₀) of the point spread function (PSF) was calculated using 30 nM solution of monomeric EGFP in DPBS buffer. The FCS decay from EGFP was fitted to the following FCS equation and the diffusion coefficient (D) was fixed at 90 μm²/s (36).

$$G(\tau )=G(0)\ast {\left(1+\frac{4D\tau }{{w_0}^2}\right)}^{-1}\ast {\left(1+\frac{4D\tau }{{z_0}^2}\right)}^{-1/2}$$ Eq. 3

The value of the axial width of the PSF (z₀) was fixed at 1.5 μm and G(0) represented the amplitude of the correlation function. The calculated w₀ value (0.31 μm) was then used to calculate the diffusion coefficient of the other fluorophores in different MC solutions. The FCS decays from the samples showed a complex behavior and the shape of the single diffusion component FCS decay was unable to describe the shape of these FCS decay curves as reported earlier for diffusion in MC (30). Thus, they were fitted with a dual diffusion component FCS decay equation in a global fit using the following equation.

$$G(\tau )=G_1(0)\ast {\left(1+\frac{4D_1\tau }{{w_0}^2}\right)}^{-1}\ast {\left(1+\frac{4D_1\tau }{{z_0}^2}\right)}^{-1/2}+G_2(0)\ast {\left(1+\frac{4D_2\tau }{{w_0}^2}\right)}^{-1}\ast {\left(1+\frac{4D_2\tau }{{z_0}^2}\right)}^{-1/2}$$ Eq. 4

Here, G₁(0) and G₂(0) are the amplitude of the correlation functions at short lag time (τ) as associated with diffusion coefficients D₁ and D₂. Prior to the fitting and plotting, the FCS decays were normalized to the amplitude of one at the shortest lag time (τ) to determine the shifts in decay times. In these global fits, the faster diffusion component D₁, reflecting diffusion between the MC polymers, was varied, while the slow diffusion coefficient D₂, reflecting fluorescent molecules bound within an MC polymer, was kept constant to obtain the best fit (30).

The PyMOL Molecular Graphics System, Version 2.0 Schrödinger, LLC was used to help generate Figures 1 and 5.

Results

Methyl cellulose (MC) is a neutral, viscous polymer, manufactured at different molecular weights with different molecular radii (37). We measured viscosity of MC solutions to ensure that the predicted viscosity, according to the manufacturer’s instructions, matched the true viscosity. After mixing and removal of insoluble matter in experimental media, we found that MC deviated from predicted viscosity by hundreds of mPa•s at higher concentrations and higher molecular weights. Based on the measured viscosities, the estimated final concentrations (weight/volume) of the polymers are listed in Table 1 to within 0.5% (38).

Table 1.

Experimental Conditions	Estimated MC Concentration (weight/volume)	Applied Field (mV/mm)	Total Experiments	Total Cell Number	Mean Migration Speed (μm/min)	Mean Cosine ϴ
Fish Ringer’s alone	none	none	4	106	3.7	−0.02 ± 0.06
Fish Ringer’s alone	none	125	7	158	4.3	−0.82 ± 0.04
14.9 ± 0.1 mPa•s, 38 kD MC	2.0%	125	5	81	2.4	−0.67 ± 0.10
97.2 ± 0.8 mPa•s, 38 kD MC	3.5%	125	5	152	1.7	−0.22 ± 0.13
200 ± 4 mPa•s, 38 kD MC	4.5%	125	6	160	1.0	+0.61 ± 0.12
473 ± 14 mPa•s, 38 kD MC	5.5%	125	8	255	0.9	+0.35 ± 0.13
226 ± 9 mPa•s, 54 kD MC	3.5%	125	7	152	2.0	−0.23 ± 0.15
307 ± 2 mPa•s, 140 kD MC	2.0%	125	6	100	3.0	−0.44 ± 0.20
508 ± 1 mPa•s, 200 kD MC	1.5%	125	4	56	4.1	−0.83 ± 0.12
334 ± 5 mPa•s, 400 kD MC	1.0%	125	5	85	3.7	−0.88 ± 0.03

Galvanotaxis of zebrafish keratocytes, (illustrated in Fig. 2a), was measured in media with different concentrations of MC polymers with different molecular weights. Directionality was determined by measuring the mean cosine ϴ = (Ʃ_icos ϴ_i)/n, which reflects the mean angle of the path of migration with respect to the cathode-anode axis. A peak cathodal response is −1 and a peak anodal response is +1. In fish Ringer’s (FR) alone (bulk viscosity of 1.2 mPa•s), keratocytes migrate randomly in the absence of an applied EF (Fig. 2b and Table 1), with a mean cosine ϴ value near zero, −0.02 ± 0.06. However, they display robust cathodal migration in response to an EF of 125 mV/mm (Fig. 2c and supplementary video 1). EF exposed cells in FR show a robust cathode-directed migration with a mean cosine ϴ value, of −0.82 which is consistent with an earlier report (12).

Figure 2.

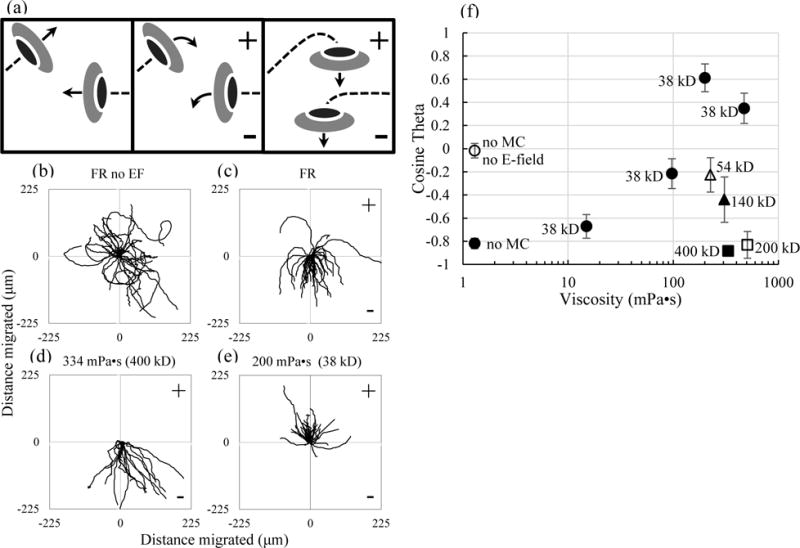
The direction of galvanotaxis is altered by the presence of small viscous polymers. (a) Illustration of the experimental setup where randomly migrating keratocytes (left) turn cathodally in the presence of an EF (middle) and migrate toward the cathode (right) in normal media. (b–e) Trajectory plots acquired over the course of 1 hour (b–d) and 2 hours (e) of keratocyte migration in the absence and presence of an EF of 125 mV/mm. (b) In the absence of applied EFs, cell migration occurs randomly with respect to the point of cellular origin. (c) In FR and in the presence of an applied EF, cells migrate toward the cathode. (d) In high viscosity media, made with HM polymers, cells migrate cathodally. (e) In high viscosity media, made with LM polymers, cells migrate anodally. (f) Small polymers impaired cathodal migration (38 kD, 54 kD and 140 kD) or reversed migration toward the anode at higher concentration (38 kD), while larger polymers (200 and 400 kD) did not alter cathodal migration.

In attempts to reduce boundary layer EOF, we increased external viscosity using a range of high molecular weight (HM) MC polymers. First, bulk viscosity was increased to 334 mPa•s and 508 mPa•s using MC with weight average molecular weights of 400 kD and 200 kD, respectively. Despite the increased viscosity, neither migration speed nor cathodal directionality (Fig. 2d, Table 1, and supplementary video 2) changed significantly compared to FR alone (p>0.1 for both, students t-test), with mean cosine ϴ values of −0.88 and −0.83, respectively. We conclude that these results are highly consistent with previous reports (28,29) which had been used to form the basis for discounting EOF as a mechanism driving cathodal migration.

While HM MC did not affect cathodal migration, we found that LM MC polymers had dose-dependent effects on migration speed (Table 1) and cathodal directionality. Increasing viscosity to 307 mPa•s with 140 kD MC and 226 mPa•s with 54 kD MC caused decreased cathodal migration from −0.82 to −0.44 and −0.23, respectively. Using the lowest molecular weight MC (38 kD) that is commercially available, cathodal migration decreased to −0.67 and −0.22 with viscosities of 14.9 mPa•s and 97.2 mPa•s, respectively. Greater increases in viscosity, to 200 and 473 mPa•s with the 38 kD MC, caused cells to completely reverse direction of migration (Fig. 2e and supplementary video 3) with mean cosine ϴ values of +0.61 and +0.35, respectively. A summary plot of mean cosine ϴ values (Fig. 2f) shows the varying impact of the different polymers on directed migration. Comparison of results from samples with high viscosity, ≥ 200 mPa•s, indicate that the LM polymers reversed migration toward the anode while the HM polymers did not alter cathode directed migration compared to normal FR. The stark difference in response between the LM polymers and the HM polymers should allay concerns of nonspecific chemical effects of MC, considering the polymers are the same except for their size. We conclude that changes to the bulk viscosity alone are not sufficient to account for reversal of migration during galvanotaxis.

In addition to electro-osmosis at the cell surface, there is electro-osmosis against the charged surface of the electrophoretic chamber (tissue culture plastic) and it is obvious in viscous media (supplementary videos 2 and 3). In order to address concerns that bulk flow may direct migration, small insoluble particles of neutral MC that remained in solution were used to estimate fluid flow in the chambers during applied EFs. In LM MC at 200 mPa•s, 4 chambers showed only cathode-directed flow while 2 showed flow in both directions. In LM at 473 mPa•s, 5 chambers showed only cathode-directed fluid flow and 3 showed flow in both directions. In HM at 334 mPa•s, 2 chambers showed cathode-directed flow, 2 showed anode-directed flow and 1 showed both. While cathodal fluid flow is most likely due to electro-osmosis along the culture chamber surfaces, anodal fluid flow may be due to shifting of the height of the agarose bridges leading to subtle pressure changes on either side of the chamber. Regardless of direction, the average flow rate was very slow; 7.5 and 18.1 μm/min in FR with 200 and 473 mPa•s LM, respectively, and 12.7 μm/min for FR with 334 mPa•s HM, producing shear stresses on the cells of 2.5 mPa, 14.3 mPa and 7.1 mPa, respectively. These shear stresses are about 300-1000 times less than those required to direct migration of fish keratocytes in culture (29). We conclude that the bulk fluid flow observed in our experiments is negligible in directing migration. Additionally, anodally migrating keratocytes were more often, migrating against the direction of the bulk fluid flow induced shear stress. Supplementary videos 2 and 3 were chosen to show that cell migration in applied EFs still occurred despite negligible bulk flow in the opposite direction.

Eq. 1, first presented by McLaughlin and Poo (1981), is based on the Stokes-Einstein relation and indicates that an increase in external viscosity will only decrease cathode-directed migration and not reverse migration to the anode. Therefore, we explored the possibility that diffusion in porous media of MC mixtures does not follow the Stokes-Einstein relation. To a limited extent this has already been done. Unlike diffusion in viscous solutions with very small molecular weight viscous agents, diffusion in solutions of polymers of MC does not follow a purely Stokes-Einstein relation (30). To validate this for macromolecules, we measured diffusion coefficients for fluorescein-labelled dextran (3 kD) and ovalbumin (45 kD) in different solutions of MC using fluorescence correlation spectroscopy (FCS). The resulting decay curves from the samples showed a complex behavior, similar to previous measurements in MC (30). Therefore, the curves were fitted with a dual diffusion component (see Eq. 4 in Methods). The fast terms (D₁) for diffusion of fluorescent dextran and ovalbumin between MC polymers are only reduced to about half of their values in FR alone (Fig. 3a and b). According to the Stokes-Einstein relation, a 200 fold increase in viscosity should decrease the diffusion coefficients to 0.5% of their values in FR alone. However, they were only decreased to about 40%, an 80-fold deviation from Stokes-Einstein. We conclude that for the concentrations we used to reverse galvanotaxis, MC reduced diffusion and therefore electrical mobility by only a factor of 2-3, not by a factor of 200 as predicted according to Stokes-Einstein. The best fit models for the fluorescence autocorrelation curves are displayed for the 38 kD MC (Fig. 3c and d) and the HM MC solutions (Fig. 3e and f). It appears than in MC, diffusion is hindered, being constrained to spaces between polymers, a feature common to other porous media like agarose gels or the cytoplasm of cells (39–41). While these results indicate that Eq. 1 does not accurately describe electromigration of surface macromolecules in viscous solutions of MC, it still does not explain reversed galvanotaxis. According to our hypothesis, reversed electromigration of cell surface receptors to the anode would occur if LM MC solutions reduce electro-osmosis or hydraulic permeability to a greater extent than they reduce electrophoresis.

Figure 3.

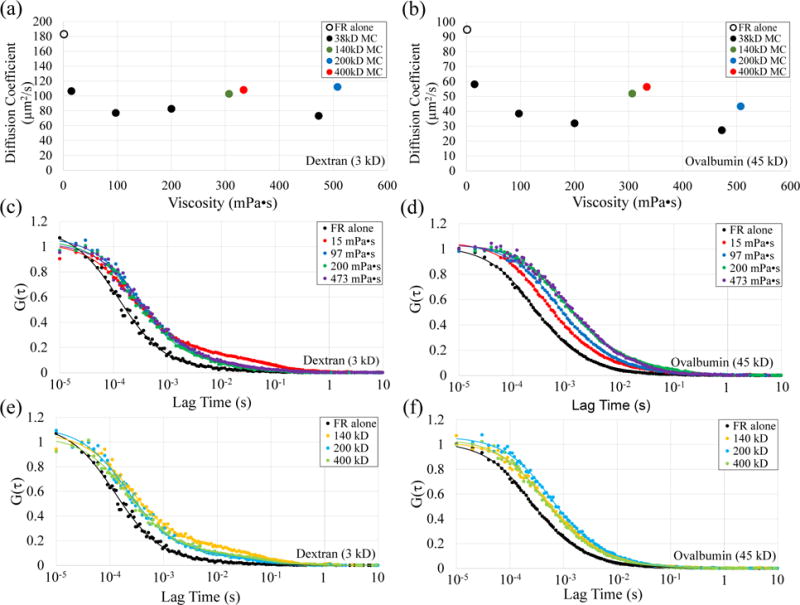
Diffusion of fluorescein-labelled dextran and ovalbumin in MC solutions does not follow a Stokes-Einstein relation. (a,b) Measured diffusion coefficients for dextran (a) and ovalbumin (b) are hindered the most by the smallest MC polymer (38 kD) at 473 mPa•s, but only to values that are 40% and 30%, respectively, compared to their values in FR alone. Standard errors are smaller than the vertical dimensions of the data markers. (c,d) The autocorrelation curves and modelled fit for dextran (c) and ovalbumin (d) over a viscosity range of 1.2 mPa•s to 473 mPa•s for the 38 kD MC. (e,f) The autocorrelation curves and modelled fit for dextran (e) and ovalbumin (f) in FR alone and HM polymers, 307 mPa•s of 140 kD, 508 mPa•s of 200 kD, and 334 mPa•s of 400 kD.

Hydraulic permeability (K) between globular polymers like MC may be similar to solutions of monodisperse spherical particles. In these solutions, hydraulic permeability is proportional to the power of the diameter (d) of the spheres and the power of porosity or void fraction (∈) between the spheres according to the Kozeny-Carman formula (Eq. 5) and the Rumpf and Gupte expression (Eq. 6) (42). Therefore, hydraulic permeability would be 4 fold smaller for a polymer half the diameter of a HM MC. The reduced void fraction is more challenging to compare considering that only the void fraction between the plasma membrane and the first layer of MC polymers is relevant. The void fraction within 15 nm of the membrane is 25% smaller for a polymer half the diameter of the HM MC polymer used in this study. Taken together, a reasonable estimate is that the hydraulic permeability near the membrane would be 10 < K < 100 fold smaller when using LM MC compared to HM MC used in this study.

$$\mathrm{K}=\frac{{\in }^3{\mathrm{d}}^2}{180{(1-\in )}^2}$$ Eq. 5

$$\mathrm{K}=\frac{{\in }^{5.5}{\mathrm{d}}^2}{5.6}$$ Eq. 6

In other porous media like agarose gels, hydraulic permeability has been shown to be reduced to a greater extent than diffusion when void fraction is reduced (43). A step increase in agarose concentration, which reduced pore size and void fraction, decreased hydraulic permeability through an agarose gel by greater than a factor of 10, while diffusivity of macromolecules ranging between 14-105 kD with radii between 2-6 nm, was reduced by only a factor of 2 (43). Therefore, a smaller void fraction between neutral polymers can reduce electro-osmotic force by a significantly greater amount than it reduces electrophoretic force.

In combination, the diffusion measurements we report in MC, along with these earlier results in porous media, support the idea that the closer packing of the smaller LM MC will pose significantly greater reduction in EOF than the HM MC. We conclude that when pore sizes between MC polymers are of similar dimension to the size of diffusing solutes, electro-osmosis of surface macromolecules to the cathode is reduced to a greater extent than electrophoresis of surface macromolecules to the anode. Net negatively charged surface proteins directed toward the cathode by electro-osmosis which promoted cathode migration, now have a greater chance to be electrophoresed to the anode to promote anodal migration.

The most convincing evidence that EOF is strong enough to promote cathodal accumulation of negatively charged surface molecules is obtained by monitoring surface macromolecule redistribution in an applied EF. These experiments have been performed on a range of different eukaryotic cells (14,18–24) as the principles of electrophoresis and electro-osmosis are common. According to our hypothesis, reduction of EOF with LM polymers should reduce cathodal accumulation of surface macromolecules to an extent that is significantly greater than HM polymers. We used Chinese hamster ovary (CHO) cells to follow redistribution of fluorescent TMR-ConA and YFP-GPI on the surface of cells, as zebrafish keratocytes possess rapid membrane turnover making it difficult to distinguish between intracellular or extracellular localization of fluorescent markers. In addition, electromigration of surface markers could not be performed on CHO cells under normal physiological temperatures at which they migrate. Viscosity of MC mixtures is temperature dependent, being one of the few viscous polymers that gels with increasing temperature (32). The higher concentrations of MC, used here, gel below 30°C so experiments were performed at ambient room temperature, 21° C.

Electrical potentials of both zebrafish keratocytes and CHO cells were determined to ensure that they were negative. Cell surface electrical potentials for zebrafish keratocytes −7.4 ± 0.9 mV (n = 34) were slightly weaker than the surface potentials for CHO cells, −16.3 ± 2.7 mV (n = 37). However, these negative values are still within the narrow range common to other eukaryotic cells at neutral pH (16,17) and indicate cathode-directed EOF.

Fluorescently labelled ConA was used to follow rapid redistribution of glycosylated cell surface macromolecules before and after application of a 1000 mV/mm EF. A time course for ConA redistribution (Fig. 4a) is shown with before and after images (inset). In FR immediately before EF exposure (black), CHO cells possessed an average future cathode/future anode (C/A) plasma membrane fluorescence ratio of 1.00 ± 0.02 (n=32) indicating symmetrical distribution of ConA receptors (Fig. 4b). Measurements after 20 min in the EF indicate that the ConA bound receptors redistributed in greater abundance to the cathode, with a C/A fluorescence ratio of 1.60 ± 0.09 (n=32). Similarly, in the highest molecular weight MC (400 kD) at 384 mPa•s, ConA receptors accumulated on the cathodal side of the cells relatively quickly (Fig. 4a). The measured C/A ratio of 2.16 ± 0.30 (n=44) after EF application was twice as great compared to 1.00 ± 0.04 (n=30) measured before EF application. However, conditions that reduced cathodal migration, 38 kD MC at 100 mPa•s, showed decreased electromigration of ConA receptors (Fig. 4b). Moreover, conditions which reversed migration to the anode showed no significant asymmetric redistribution of ConA receptors after 20 min in the EF, 1.11 ± 0.02 (n=88), compared to 1.04 ± 0.03 (n=76) before EF application (p > 0.1, students t-test). These results indicate that LM reduces cathodal accumulation of surface macromolecules in a concentration-dependent manner, corresponding to the concentration-dependent inhibition of cathodal galvanotaxis and ultimate reversal of migration toward the anode.

Figure 4.

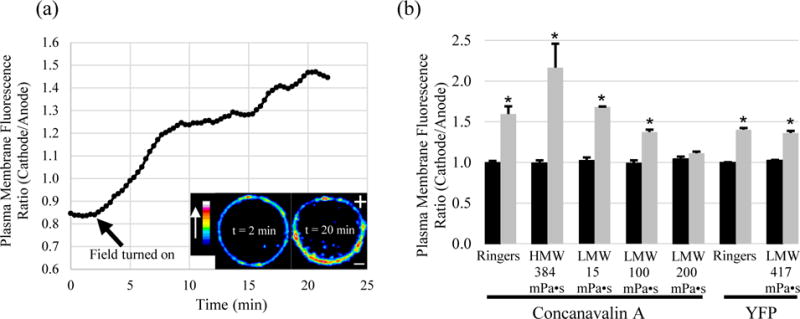
Electric fields direct ConA receptors and YFP-GPI accumulation toward the cathode. (a) Time course of ConA receptor electromigration in 384 mPa•s of 400 kD MC, displayed as a ratio of the plasma membrane ConA fluorescence (cathode facing / anode facing). Color bar indicates relative brightness of TMR-ConA. (b) Summary plot of the plasma membrane fluorescence ratio before EF application (black) and 20 min after EF application (gray). Cathodal accumulation of cell surface ConA receptors occurs in Ringer’s and Ringer’s with HM or low levels of LM (38kD). However, cathodal electromigration of ConA receptors is reduced in 38 kD MC at 100 mPa•s and inhibited at 200 mPa•s. Under similarly viscous conditions with LM, the small YFP-GPI accumulates at the cathode. (* = p < 0.05)

ConA binds to α-D-mannosyl and α-D-glucosyl groups from glycoproteins and glycolipids, so macromolecules over a wide size range are labelled and may be freely diffusing in the plasma membrane or anchored to the cytoskeleton or restricted to a small membrane domain. Therefore, reversed electromigration of a single surface protein to the anode may be hidden, now that bulk electromigration to the cathode (electro-osmosis) has been impaired for many different surface proteins. To determine whether a population of a single type of small, freely diffusing, surface bound protein could still migrate through the smaller pores of the LM and not simply be stuck in place by the MC, yellow fluorescent protein bound to a glycosylphosphatidylinositol anchor (YFP-GPI) was monitored during EF application. In the presence of an EF, the 3 nm by 4 nm YFP (26 kD) with weak negative charge, electromigrated to the cathode with an average C/A fluorescence ratio of 1.40 ± 0.02 (n = 25) compared to 1.00 ± 0.01 (n=14) before EF application (Fig. 4b). In the presence of the 38 kD MC at 417 mPa•s, the YFP-GPI displayed weaker accumulation but still migrated toward the cathode with a C/A fluorescence ratio of 1.36 ± 0.03 (n = 38) compared to 1.03 ± 0.02 (n=15) before EF application. We conclude that despite the high viscosity, EOF is still occurring within nanometers of the plasma membrane between the LM polymers and still directs small proteins with weak surface charge, like YFP-GPI, to the cathode.

Discussion

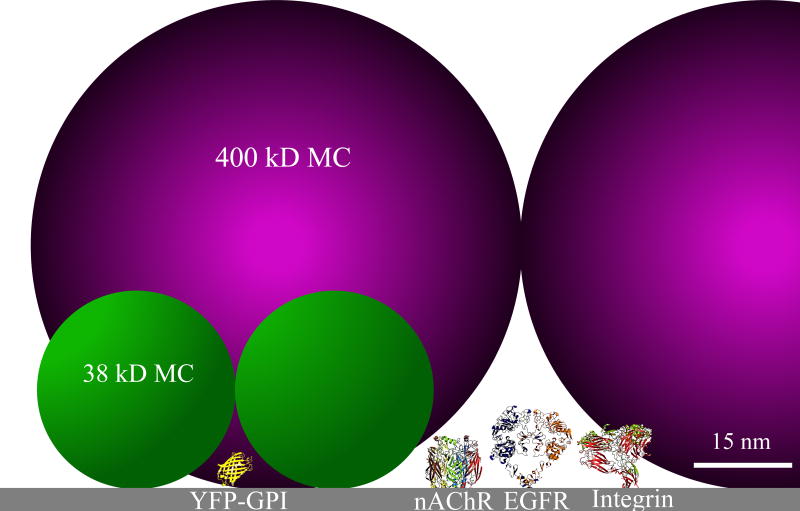
We conclude that MC polymers have high porosity and act more like sieves or porous gels (44,45) than very small viscous agents e.g. glycerol. We also conclude that viscosity alone or changes in osmolality are insufficient to explain our results. High viscosity with large polymers did not alter galvanotaxis and the greatest number of MC polymers altered osmolality of the media by only 0.5% which is relatively insignificant considering keratocytes can withstand a 75% reduction in osmolality without affecting galvanotaxis (29). We propose that in order to impair EOF in the cellular boundary layer, viscosity must be increased in the cellular boundary layer, within nanometers of the plasma membrane, whether the cell surface is closer to being a ‘hard’ surface (46) or a ‘soft’ surface (47). The smaller polymers can more effectively reduce hydraulic permeability next to the membrane. An illustration of the 38 kD and 400 kD MC polymers based on their hydrodynamic radii at 20° C (37,48) is drawn to scale in Fig. 5 along with a number of other surface proteins known to migrate cathodally in weak EFs.

The void fraction against the surface of the plasma membrane is much greater for the larger polymer than the smaller polymer, leading to greater hydraulic permeability through which EOF can continue to drive membrane proteins to the cathode. However, the smaller MC polymers can pack more closely against the plasma membrane, reduce the void fraction and reduce EOF to a greater extent. The smallest MC is still relatively large, giving rise to pores that are larger than the surface proteins shown (Fig 5). The diffusion results (Fig. 3) confirm that the smallest MC does little to impair diffusion and therefore electrophoresis of macromolecules. These conditions would promote electrophoresis over electro-osmosis and negatively charged surface receptors should migrate to the anode like negatively charged proteins in an electrophoretic gel. Anodal accumulation of the cell surface receptors should lead to anodal migration, according to earlier hypotheses (13,14). We conclude that these conditions are met in neutral porous media when the pore sizes are close to the size of the diffusing solutes (30,43).

Figure 5.

Plasma membrane surface in the presence of HM (purple) and LM (green) MC polymers. Surface macromolecules known to electromigrate to the cathode including the nicotinic acetylcholine receptor (nAChR), epidermal growth factor receptor (EGFR), Integrins and YFP-GPI extend from the plasma membrane by less than 15 nm.

Based on the new results presented here and consistent with the original mathematical model for electrophoresis and electro-osmosis near the surface of cells (14), we propose that a small surface macromolecule, with greater net negative surface charge than YFP-GPI, accumulates at the cathode side of the cell when EOF is unimpaired and directs cell migration to the cathode. Conversely, when EOF is significantly attenuated by small viscous polymers, electrophoresis becomes the dominant force. Under these conditions, the small surface macromolecule is able to navigate through the pores of the LM polymers, accumulating on the anode-facing side of the plasma membrane, and directs cell migration to the anode. With further experimentation using LM polymers, the surface EF receptor and its signaling pathway, possibly through cGMP and lipids (25), might be identified, clarifying the fundamental process of symmetry breaking at the cellular level and enabling greater control over cellular polarity during artificial tissue and organ fabrication and epidermal wound healing.