Direct Determination of Absolute Absorption Cross Sections at the L-Edge of Dilute Mn Complexes in Solution using a Transmission Flatjet

Abstract

3d transition metals play a pivotal role in many charge transfer processes in catalysis and biology. X-ray absorption spectroscopy at the L-edge of metal sites probes metal 2p-3d excitations providing key access to their valence electronic structure which is crucial for understanding these processes. We report L-edge absorption spectra of Mn^II(acac)₂ and Mn^III(acac)₃ complexes in solution, utilizing a liquid flatjet for x-ray absorption spectroscopy in transmission mode. With this we derive absolute absorption cross sections for the L-edge transitions with peak magnitudes as large as 12 and 9 Mb for Mn^II(acac)₂ and Mn^III(acac)₃, respectively. We provide insight into the electronic structure with ab-initio restricted active space calculations of these L-edge transitions, reproducing the experimental spectra with excellent agreement in terms of shapes, relative energies and relative intensities for the two complexes. Crystal field multiplet theory is used to assign spectral features in terms of the electronic structure. Comparison to charge transfer multiplet calculations reveals the importance of charge transfer in the core-excited final states. Based on our experimental observations we extrapolate the feasibility of 3d transition metal L-edge absorption spectroscopy using the liquid flatjet approach in probing highly dilute biological solution samples and possible extensions to table-top soft x-ray sources.

Graphical Abstract

We report absolute x-ray absorption cross sections at the L-edges of Mn^II(acac)₂ and Mn^III(acac)₃ complexes in solution, measured in transmission mode with a liquid flatjet. By combining ab-initio restricted active space calculations and charge-transfer multiplet theory we show the connection between electronic structure and x-ray cross sections. We extrapolate the applicability of our approach to studying metal L-edge absorption spectra of highly dilute biological solution samples and possible extensions to table-top soft x-ray sources.

I. Introduction

3d transition metals play an important role as electron donors or acceptors in many catalysts and metalloproteins where they facilitate charge migration and charge transfer reactions.^1–3 For a mechanistic understanding of these reactions, detailed knowledge of the local valence electronic structure at the transition metal sites is essential. X-ray absorption spectroscopy (XAS) at the metal L-edge is an ideal tool for studying this electronic structure. It directly probes the metal 3d-derived orbitals via metal-centered 2p-3d transitions being sensitive to the oxidation state and spin state of the probed metal center, as well as to the ligand environment.^4–13

Studying the important class of solution-phase 3d transition metal complexes and catalysts with L-edge absorption spectroscopy requires special consideration for dedicated in-vacuum sample delivery and adapted soft x-ray detection methods. Soft x-ray absorption spectroscopy of liquid samples has been realized following different conceptual approaches. For example, liquid flow-cells based on soft x-ray transmissive membranes can be used for transmission-detected,^14–18 fluorescence yield-detected¹⁹ and ion yield-detected XAS,²⁰ but their use for studying metal complexes in solution is limited due to the inherent difficulty of avoiding x-ray induced sample damage.^21–22 In a recent approach a highly sensitive photon detector was used for fluorescence-detected XAS of frozen samples, but the applicability of this approach to solution samples of dilute metal complexes at ambient conditions has not yet been proven.²³ Alternatively, Rayleigh-flow liquid jets have been developed²⁴ and have been used for XAS with continuous replenishment of the liquid sample.^25–26 Due to the fast sample flow through the x-ray interaction region, x-ray damage is avoided for most experiments. Since, however, the diameter of such jets is typically on the order of several tens of micrometers and therefore much larger than the typical attenuation length of soft x-rays of most solution samples, these jet systems cannot easily be used for measuring XAS in transmission mode without detrimental distortion effects. Instead, they have been mostly used for XAS in fluorescence-detected mode^{11, 26–27} or for photoelectron spectroscopies.²⁸

Measuring L-edge XAS in transmission mode has several advantages over the more conventional electron- or photon-yield detection methods. First, it allows for determination of absolute absorption cross sections in contrast to determination of relative cross sections with other XAS methods. This is important as it enables inter-system comparison of the metal-ligand covalency in different compounds since the integrated L-edge XAS intensities are proportional to the number of holes in the metal 3d-shell and to the metal 3d-character^{7, 10, 29} (or inversely the degree of covalence bond character) of the probed valence orbitals.³⁰ Second, an advantage compared to detecting the partial fluorescence yield (PFY) for PFY-XAS³¹ is that XAS in transmission mode is unaffected by state-dependent fluorescence yield, which can lead to relative peak intensities deviating from the cross sections due to spectrally variable intensity of the fluorescence signal.^{27, 31–33}

In this paper, we demonstrate L-edge XAS in transmission mode of dilute prototypical Mn complexes in solution using a liquid flatjet system.³⁴ This flatjet provides a stable liquid sheet with thicknesses on the order of 1 μm, which is close to the soft x-ray attenuation length of most solvents, allowing for solution-phase soft x-ray absorption spectroscopy in transmission mode.^35–36 Flow rates on the order of 4 ml/min guarantee a continuously replenished stream of liquid sample resulting in measurements not delimited by sample damage induced by the probing x-rays. This approach offers new capabilities in the study of 3d transition metal complexes in solution.

The herein investigated prototypical high-spin Mn^II(acac)₂ and Mn^III(acac)₃ complexes in solution exhibit variable formal metal oxidation states (Mn^II vs. Mn^III) and spin states (S=5/2 vs. S=2) as well as variable metal-ligand coordination (4 vs. 6 oxygen bonds) and bonding symmetry (T_d vs. O_h/D_4h). With this study we complement previous work by Kubin et al.¹³ on these complexes where L-edge PFY-XAS was used to investigate the origin of the L₃-edge spectral shift between the Mn^II and Mn^III species. Here we focus on the comparison of absolute absorption cross sections of L-edge XAS, on the interpretation of selected spectral features, and on the comparison of spectra from XAS and from PFY-XAS. We compare our experimental spectra to those calculated with the widely used crystal-field multiplet (CFM) and charge-transfer multiplet (CTM) methods,^{7, 37–38} to ab-initio calculations based on the restricted active space (RAS) approach.^39–44 We conclude our study with an assessment of alternative applications of our experimental approach, namely for studying highly dilute biological systems and for using our approach with table-top soft x-ray sources.

II. Materials and Methods

Sample Preparation

Mn^III(acac)₃ (Manganese(3+) tris[(2Z)-4-oxo-2-penten-2-olate]), acetylacetonato ligands are abbreviated as (acac)⁻), and Mn^II(acac)₂ (Manganese(2+) bis[(2Z)-4-oxo-2-penten-2-olate]) were purchased as crystalline powders (technical grade) from Sigma-Aldrich and were used without further purification. They were dissolved in ethanol abs. (≥99.8% purity, Sigma-Aldrich) with concentrations of 100 mM and 15 mM for Mn^III(acac)₃ and of 30 mM for Mn^II(acac)₂. Solutions were filtered with 0.45 μm PTFE Whatman^™ filters before the measurements. Exposure to oxygen and ambient light was minimized during sample preparation and sample injection.

Experimental Setup and Data Analysis

All experiments were performed with the recently reported transmission flatjet setup³⁴ at the undulator beamline UE52-SGM⁴⁵ of the BESSY II synchrotron radiation facility. A schematic side view of the setup is given in Figure 1A. Two sample flasks, one with pure solvent ethanol and one with ethanol solution of the studied Mn complex, were connected to the switching unit (Jasco LG-2080-02S). An HPLC pump (Jasco PU-2085-Plus) injected the selected liquid sample into the x-ray probing region at pressures between 3.0 and 4.0 MPa, keeping the flow rate at a fixed value of 3.4 ml/min. The flatjet was formed by two colliding jets (inner nozzle diameters 48 μm) resulting in a primary liquid sheet formation with typical horizontal and vertical extensions of ~1 mm and ~ 3 mm, respectively. The thickness of the liquid sheet changes between 0.5 and 3.5 μm on a mm length scale within the first sheet,^{34, 36} but is constant in the range of the x-ray spot diameter of approximately 60 μm.⁴⁵ The sheet was placed in the focus of the x-ray beam and horizontally centered with respect to the probing x-ray spot and vertically adjusted for the desired effective thickness. The recycling unit introduced in ref.³⁴ was not used. Instead, we trapped the liquid sample at 77 K below the x-ray probing region, which allowed for working pressures around ~10⁻³ mbar in the experimental chamber. The experimental chamber was separated from the beamline with a differential pumping stage to warrant appropriate vacuum conditions for both the beamline and the experimental chamber. The primary sheet of the liquid flatjet was typically probed here at thicknesses between 2.5 μm and 3.2 μm. The photon flux Φ_L(hν) transmitted through the sample was recorded as a function of the photon energy by a calibrated photodiode (Hamamatsu G1127-04 2K) that was positioned on the x-ray beam axis at ~0.4 m distance from the liquid jet and was read out by a Keithley Electrometer (model 6514B). The noise level of this transmitted flux strongly depends on the stability of the transmission flatjet and was measured around 0.1 % for the most stable jet and around 0.6% for rather unstable jet conditions. The photon flux Φ₀(hν) incident on the sample (I₀) was scanned separately, after removing the liquid jet from the x-ray beam. The noise of this signal was determined around 0.1%. The transmission spectra were eventually obtained from the quotient T_L(hν) = Φ_L(hν)/Φ₀(hν). Further details of the setup can be found in ref.³⁴.

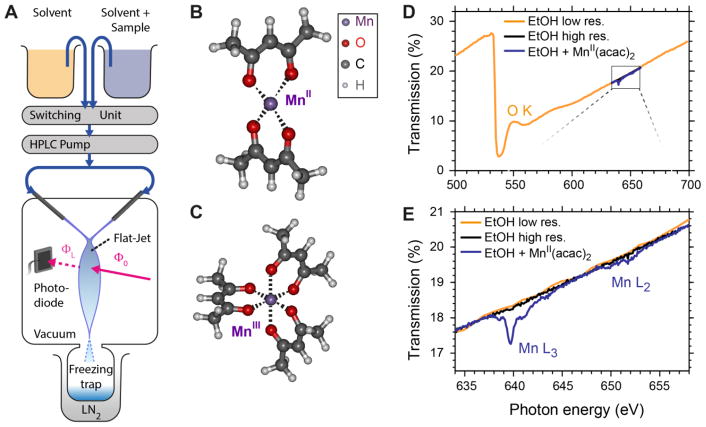
Figure 1.

(A) Schematic of the setup with the liquid flatjet system for L-edge x-ray absorption spectroscopy of transition metal complexes in solution. (B, C) Molecular structures of the studied complexes Mn^II(acac)₂ (B) and Mn^III(acac)₃ (C). (D) and (E) Transmission spectra of the pure solvent ethanol and 30 mM Mn^II(acac)₂ solution in ethanol, shown for the energy range of the oxygen K-edge (D) and the Mn L-edge (E), as acquired with 1 eV (“low res.”) and 0.1 eV step sizes (“high res.”), respectively. For comparison, the transmission curves in (D) and (E) were normalized with Beer-Lambert’s law to the thickness of the pure ethanol sample (2.44 μm).

For a spectrum scan, the monochromator was scanned in steps of 0.1 eV (1 s integration time per step) over the Mn L-edge region (630–660 eV). The O K-edge region (500–700 eV) was scanned (in 1 eV steps) to determine the sheet thickness with tabulated O K-edge absorption cross sections from Henke’s tables.^46–47 Typical acquisition times for a single-scan spectrum were around 10 min. The monochromator slit size was set to 120 μm or 150 μm, corresponding to bandwidths of 300 meV or 380 meV, respectively, at the Mn L-edge. The beamline flux was on the order of 1×10¹² photons/s (diode current ~20 μA) in the Mn L-edge spectral region. In case the spectrum and reference scans were recorded with different monochromator slit sizes w_s and w₀, respectively, the reference signal was rescaled with a linear factor w_s/w₀. This procedure was checked for consistency as shown in the Supporting Information (S.I.), section 1.1.

All diode signals were normalized by the storage ring current of the BESSY II synchrotron radiation facility. As in refs.^12–13, we have calibrated the axis of the incident photon energy to the L₃-edge maximum of a Mn²⁺_aq solution sample with a relative uncertainty of 50 meV with respect to the values reported in ref.⁴⁸ via the sharp Mn^II L₃ peak position at 639.7 eV. The incident x-ray flux was found to decrease with respect to time due to an increasing portion of the beam being clipped by the experimental chamber (see S.I., section 1.2.2 for details). We corrected for this in the data analysis with a spectrally constant attenuation factor Att. (0.4<Att.≤1) which reduces the original incident flux Φ₀(hν) to Φ_Att.(hν) = Att·Φ₀(hν). We retrieved this factor Att. from a least-squares fit of the uncorrected experimental transmission of the solvent to that expected from tabulated values.^46–47 From the same fit of transmission spectra T_L(hν), with fit parameters Att. and the sample thickness L, we retrieved the effective sample thickness for each spectrum scan. The fit regions were chosen such that no absorption resonances were included (see S.I., section 1.2.1). All transmission curves and further processed spectra shown in this paper were corrected by this fitted attenuation factor Att.. We note that with this procedure we lose information about the spectral intensity of the edge-jump on the high-energy side of the Mn L-edge absorption spectra. Further details on the data analysis are summarized in the S.I., section 1.

Density Functional Theory (DFT)

The molecular structures used for the restricted active space calculations (see below) were obtained from ground state density functional theory (DFT) calculations (using a DFT/B3LYP solvent optimization). The same geometries were also used for the RAS calculations in ref.¹³. The molecular structures of the two complexes are displayed in Figures 1B and 1C, where Mn^II(acac)₂ and Mn^III(acac)₃ have a nearly tetrahedral (T_d) Mn-O coordination symmetry and a Jahn-Teller distorted nearly D_4h Mn-O coordination symmetry^49–50, respectively. The structure of Mn^III(acac)₃, as reported in crystallographic investigations,⁵¹ comprises four short and two long Mn-O bond lengths of 1.935 and 2.11 Å. These agree well with our calculated bond lengths of 1.93/1.94 Å and 2.17 Å, with a slight overestimation of the long distances consistent with previous experience.⁵² Concerning the molecular structure of Mn^II(acac)₂ we are not aware of any crystallographic data since the compound crystallizes as Mn^II(acac)₂ trimers.⁵³ The reported crystal structure of such Mn^II(acac)₂ trimers exhibits a trigonal-prismatic D_3h-O_h-D_3h structure, resulting in a six-coordination of each Mn by six O atoms in a near octahedral geometry and Mn-O bond lengths between 2.1 and 2.2 Å.⁵³ Our Mn-O bond lengths of 2.06 Å for Mn^II(acac)₂ are consistent with this.

Restricted Active Space (RAS) Calculations

Ab-initio methods are uniquely beneficial compared to semi-empirical methods such as the crystal-field multiplet approach since they provide valuable predictive character and access to the spatially resolved charge and spin in the probed molecule.¹³ The restricted active space (RAS) approach has been shown to correctly treat the individual many-electron interactions contributing to K-edge spectroscopies^54–55 and Ledge spectroscopies involving the interactions with the 2p core hole.^{11, 13, 39–40, 43, 56} The ab-initio theoretical L-edge spectra presented here were obtained from RAS calculations including dynamic correlation performed with MOLCAS 7.9⁵⁷ at the RASPT2/ANO-RCC-VTZP level^{13, 42} (the sensitivity of the RAS results to different model choices is analyzed in ref.⁵⁸). The RAS calculations are based on the molecular geometries from the DFT/B3LYP solvent optimizations of the two complexes (see above). To save computational cost, the calculations for Mn^III(acac)₃ were performed on a truncated complex where six terminal methyl groups were replaced by hydrogen atoms, which did not notably change the spectrum. All calculations were performed in a solvent environment that was modeled using the polarized continuum model (PCM) for the solvent ethanol. In the RAS calculations, a minimal active space consisting of the five metal-3d dominated orbitals were placed in the RAS2 space. The Mn 2p orbitals were placed in the RAS3 space, allowing a maximum of five electrons (at least one hole) in the core excited states. All possible configurations that represent single core excitations were included. For Mn^II(acac)₂, 4;4;3;4 sextet states, 37;37;39;37 quartet states, and 72;72;69;72 doublet states were included for the a₁; b₁; a₂; b₂ irreducible representations in C_2v symmetry. For Mn^III(acac)₃, 1;2 septet, 37;38 quintet, 147;150 triplet and 111;114 singlet core-excited states were included for the two irreducible representations (a;b) in C₂ symmetry. To ensure that the hole is located in the Mn 2p orbitals (instead of the Mn 3p orbitals, upon ‘orbital rotation’), these orbitals were frozen in the RASSCF optimizations. RASPT2 calculations were performed using the default ionization potential electron affinity (IPEA) shift of 0.25 Hartree and an imaginary shift of 0.1 Hartree to reduce the occurrence of ‘intruder states’ in the core-excited states. Unlike in ref.⁴⁴, including dynamic correlation effects within the RASPT2-approach improved the spectrum quality of the Mn^III complex significantly as compared to RASSCF calculations (see Figure S9 in the S.I.). RAS spectra were calculated for T=300 K and were broadened with a Gaussian broadening of σ= 0.127 eV (0.3 eV FWHM) and 0.2 eV and 0.7 eV Lorentzian lifetime widths (FWHM) for the L₃ and L₂ edges, respectively.⁵⁹ This approach is the same as for the theoretical RAS spectra given in ref.¹³. For comparison to the calculated spectra in ref.¹³ we checked that changing the solvent from acetylacetone to ethanol has no effect on the calculated L-edge spectra (shape and energies of the spectra are indistinguishable for the different solvents described with continuum polarization models). The calculated incident photon energy axis was corrected to match experimental energies. The same shift of −3.09 eV was applied to the XAS spectra of both Mn^II(acac)₂ and Mn^III(acac)₃ calculated with RAS for matching the experimental L₃-edge maximum in Mn^II(acac)₂ from ref.¹³.

CFM and CTM Multiplet Theory

Crystal field multiplet (CFM)³⁷ and charge transfer multiplet (CTM)³⁸ calculations can provide important insights to the influence of specific effects to L-edge XAS, as they enable for systematically varying and “switching on and off” relevant interactions in L-edge XAS.^{7, 10, 37–38} CFM and CTM calculations of Mn L-edge spectra were implemented using the multiplet program by Thole et al.⁶⁰ and the CTM4XAS interface.⁶¹ All spectra were calculated for T=300 K. CFM and CTM spectra were broadened with 0.2 eV and 0.7 eV Lorentzian lifetime widths (FWHM) for the L₃ and L₂ edges, respectively,⁵⁹ and a Gaussian broadening of σ= 0.127 eV (0.3 eV FWHM) throughout, unless further specified. All CFM and CTM calculations are based on Slater integrals that were reduced to 80% of their Hartree-Fock atomic values. All CFM and CTM fit parameters are given in Table S1 in the S.I.. The parameters for the CTM fits of XAS are equivalent to those applied for the CTM fits of PFY-XAS spectra shown in ref.¹³. The energy axes of the final CFM and CTM spectra are corrected by constant offsets such that the L₃-edge maximum position coincides with that of the experimental spectrum, unless indicated otherwise. Shifts of −0.7 eV and −0.5 eV were applied to all CFM spectra of Mn²⁺ in tetrahedral (T_d) and Mn³⁺ in octahedral (O_h) symmetry, respectively, for all values of 10 Dq, to align the L₃-edge maxima of the best-fitting spectra to those in the experimental spectra. All CFM spectra of Mn²⁺ and Mn³⁺ calculated in D_4h symmetry were aligned to the L₃-edge absorption maxima of the experimental spectra.

III. Results and Discussion

Transmission XAS of Dilute Metal Complexes in Solution

In Figures 1D and 1E we show typical transmission spectra of Mn^II(acac)₂ at a concentration of 30 mM in ethanol. Fig 1E is a zoom of Figure 1D into the Mn L-edge spectral region. All transmission spectra in Figures 1D and 1E were normalized to the thickness L of a pure solvent ethanol sample (orange curve) at 2.44 μm, using Beer-Lambert’s law T_L(hν) = exp(−L/Λ(hν))= exp(−α(hν)·L), where hν is the incident photon energy, Λ(hν) is the attenuation length and α(hν) = Λ⁻¹ (hν) is the linear absorption coefficient.

The comparison of transmission curves for only the solvent (orange and black solid curves in Figures 1D and 1E) and for solution samples including the Mn^II(acac)₂ solute (solid blue curve in Figures 1D and 1E) illustrate that for organic solvents the spectral transmission in the soft x-ray range is governed by the light elements (here predominantly O K-edge absorption) of the solvent. The L-edge absorption signal of the dilute Mn complex represents small additional dips. This signal corresponds to the Mn 2p⁶3dⁿ→2p⁵3dⁿ⁺¹ absorption resonances with excitations to core-excited states where a Mn 2p electron is promoted to the 3d-derived orbitals. These resonances group into the Mn L₃- and L₂-edges, which are split by around 10 eV due to spin-orbit interaction in the presence of the 2p core hole in the XAS final states.⁶² Figure 1E reveals a splitting of each of the two L-edge features which is caused by crystal field atomic multiplet effects as well as charge-transfer interactions of the probed Mn atoms with the ligand oxygen atoms. We will address the details of these absorption features below.

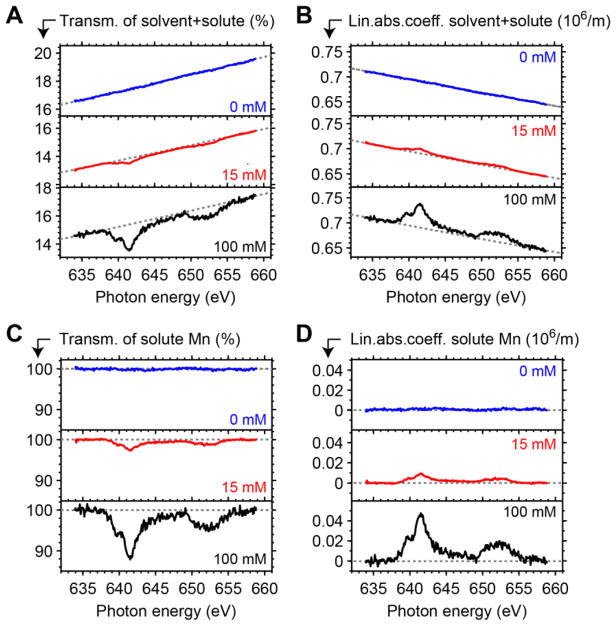
In Figure 2 we compare single-scan spectra of samples with variable concentrations of 0 mM (solvent only), 15 mM and 100 mM Mn^III(acac)₃ in ethanol. In Figure 2A, transmission spectra are shown, illustrating the influence of the solute concentration on the amplitude of the Mn L-edge spectral dip with respect to the overall transmission. The non-resonant parts of the spectra at 500–530 eV, 560–638 eV, and 658–700 eV were fitted with the tabulated transmission of the solvent ethanol(dotted lines).^46–47 This provides the crucial information of the employed sample thickness thereby determined to 2.5 μm, 2.9 μm, and 2.7 μm from top to bottom (see Materials and Methods and the S.I., section 1.2, for details). The dip amplitude of the Mn L₃-edge maximum increases when going from the 15 mM to the 100 mM sample (Mn L-edge absorption is evidently absent in the pure solvent). Figure 2B displays the corresponding linear absorption coefficients α(hν) of solute and solvent as calculated using Beer-Lambert’s law with the measured properties T_L(hν) and L.

Figure 2.

Single scan spectra for Mn L-edge XAS of Mn^III(acac)₃ in ethanol solution as measured with the transmission flatjet. In all panels the Mn concentration increases from 0 mM (blue) to 15 mM (red) and 100 mM (black). (A) Experimental transmission spectra with sample thicknesses L of 2.5 μm (blue), 2.9 μm (red) and 2.7 μm (black). Gray dotted lines denote the fitted transmission of the solvent, as extracted from Henke’s tables (see methods section). (B) Linear absorption coefficients α, as calculated from the data shown in (A). (C) Relative transmission dips associated with Mn L-edge absorption, obtained from division of the colored curves in (A) by the gray dotted solvent fits. (D) Linear absorption coefficients due to Mn L-edge absorption, obtained from subtraction of the gray dotted solvent fits from the colored curves in (B). The larger relative noise in the 100 mM data is due to a comparably unstable operation of the liquid flatjet during the scan.

In Figure 2C we show the relative transmission dips due to Mn L-edge absorption, that were obtained from division of the experimental transmission curves (Figure 2A) by the fitted solvent transmission (Figure 2A dotted curves). The peak amplitude of the relative transmission dips at the Mn L₃-edge increases from 3% to 12% when going from the 15 mM to the 100 mM sample. In Figure 2D we display the linear absorption coefficient α(hν) due to Mn L-edge absorption of only the solute. These curves were obtained from subtraction of the fitted solvent signal from the experimental curves in Figure 2B. The linear absorption coefficients of Mn peak around 1·10⁴ m⁻¹ and 5·10⁴ m⁻¹ for the 15 mM and 100 mM samples, respectively. The experimental ratio of peak intensities for the two single-scan spectra is around 5 and, thus, smaller than the expected ratio of 6.7 (=100/15). This deviation reflects the experimental uncertainties discussed in the following section.

Absolute X-ray Absorption Cross Sections

For an arbitrary solution sample containing i different molecular or atomic species with respective concentrations c_i, Beer-Lambert’s law connects the experimental linear absorption coefficient α(hν)= Σ_i α_i to the absorption coefficients α_i and absorption cross sections σ_i(hν) of the individual species i via α(hν) = Σ_i c_i·N_A·σ_i(hν), where N_A is Avogadro’s number. With this we retrieve the final absorption cross-section spectra in units of Mb (1 b=10⁻²⁸ m²), being thus independent from the experimental parameters.

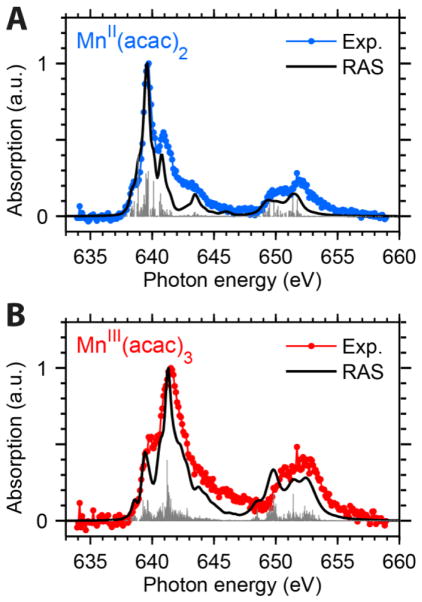
These absorption cross section spectra of Mn^II(acac)₂ and Mn^III(acac)₃ are shown in Figure 3A. The Mn^II(acac)₂ spectrum (blue) is averaged from 8 successive single-scan spectra (30 mM concentration). The Mn^III(acac)₃ spectrum (red) is averaged from 13 single-scan spectra of Mn^III(acac)₃ (two scans of a 100 mM sample and eleven runs of a 15 mM sample). The total acquisition time amounts to ~1.5 and ~2.5 hours for the averaged spectra of Mn^II and Mn^III, respectively.

Figure 3.

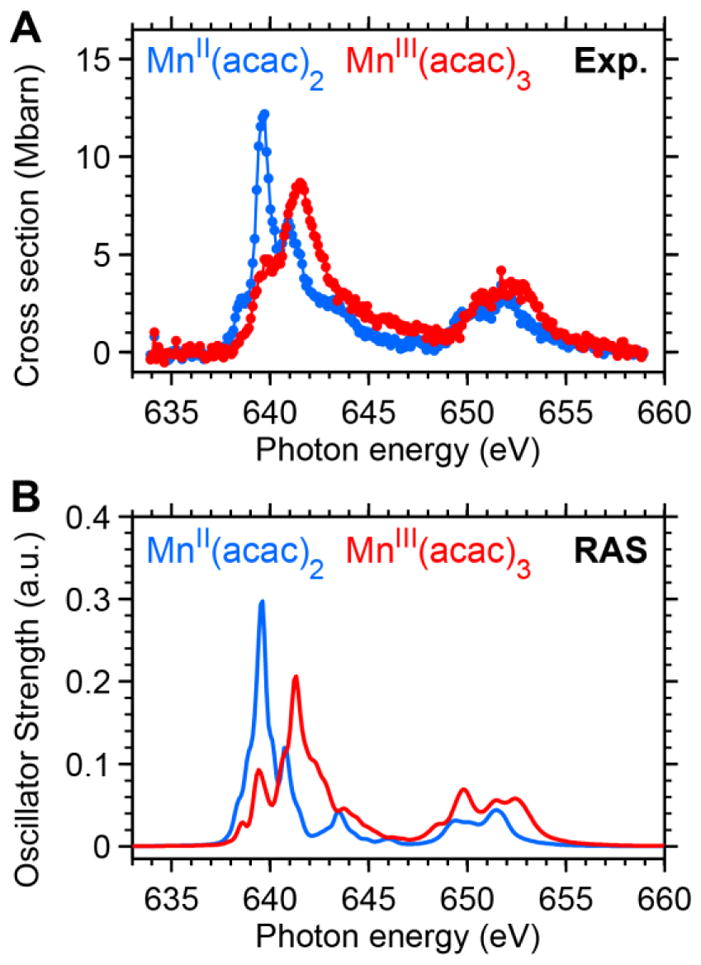
Comparison of absolute L-edge XAS absorption cross sections of Mn^II(acac)₂ and Mn^III(acac)₃ in solution from (A) experiment and (B) ab-initio restricted active space (RAS) theory. The experimental spectra are averaged over several single-scan spectra and were calibrated in analogy to the PFY-XAS spectra in ref. 13. Both RAS spectra were calibrated using the same energy shift for coinciding L₃-edge peak positions in the RAS and the experimental spectra of Mn^II(acac)₂. The absorption amplitudes of experimental and RAS spectra are quantified in Table S2 in the Supporting Information.

The direct comparison of the spectra in Figure 3A leads to a number of observations. First, the L₃-edge absorption maxima are shifted in energy with respect to each other by 1.9 eV. This agrees with the shift of 2.0 eV determined in a previous study of L-edge PFY-XAS spectra of Mn^II(acac)₂ and Mn^III(acac)₃ (ref.¹³). The shift is interpreted as a final state effect due to an increased affinity to 3d electrons in the core-excited XAS final states. Similar spectral shifts between 1.5 and 2 eV have been reported for other series of high-spin Mn complexes with various oxidation states.^{4, 12} A second observation concerns differences in the absolute absorption cross sections and associated absorption integral of the two molecular species. This provides quantitative information which is difficult to access in fluorescence yield detected XAS due to state-dependent fluorescence yield and which complements electron-yield detected XAS⁷. With 12.4±1.0 Mb the L₃-edge peak maximum of the Mn^II species is about 40% more intense than that of Mn^III at 8.8±1.9 Mb. The error bars reflect a combination of systematic uncertainties of the sample concentrations due to precipitation and statistical errors due to fluctuations in the jet thickness (see Figure S8 in the S.I.). Concomitant to the lower intensity at the L₃-edge maximum the Mn^III(acac)₃ spectrum appears broader with a more extended intensity distribution as compared to Mn^II(acac)₂. These differences in shape are a direct consequence of the increasing multiplet interactions when going from Mn^II to Mn^III (see refs.^62–63). With absolute cross sections we can also compare integrals of the L-edge absorption spectra for the two complexes. The total L-edge intensity is interpreted as proportional to the number of holes in the 3d-derived valence orbitals and their associated covalency⁷. Obtaining the integrated intensity in Mb·eV can therefore reveal information on the occupation number of these valence orbitals. We find (for integration over the full energy range shown in Figure 3A) absorption integrals of 48±11 Mb·eV for Mn^III(acac)₃ and 41.5±3.3 Mb·eV for Mn^II(acac)₂. The error bars reflect the uncertainty of the cross sections claimed above and comprise systematic uncertainties due to differences in the background subtraction scheme (linear background as applied here vs. edge-jump background as applied in ref.⁷). The ratio of our experimental spectrum areas is 1.16±0.28 for Mn^III/Mn^II and reflects the ratio of Mn^III/Mn^II 3d holes with 6/5=1.2 for Mn^III/Mn^II as expected for the Mn^III/Mn^II ground state configurations 3d⁴/3d⁵ with small contributions of metal-ligand covalent interactions. Within the error bars the experimental ratio therefore reflects the predominantly ionic character of Mn in Mn^III(acac)₃ and Mn^II(acac)₂. The transmission-mode spectra shown here thus allow to directly confirm simple but important expectations for L-edge XAS of Mn^II and Mn^III complexes: The overall spectrum intensity increases due to the increasing number of 3d holes but it is spectrally redistributed when going from Mn^II to Mn^III due to increasing multiplet splittings. The results of the numerical analyses in this paragraph are summarized in Table S2 in the S.I..

In experiments with smaller uncertainties in the Mn cross sections, transmission-mode measurements could be applied for the determination of the metal character (the degree of covalence) of the probed metal 3d-derived valence orbitals. This direct way of probing the relative number of holes in the metal 3d-derived orbitals with L-edge XAS is complementary to probing the relative number of electrons in the 3d-derived molecular orbitals via their np-character with valence-to-core Kβ_2,5 XES.⁶⁴ Beckwith et al. report a ratio of 1.45±0.10 for the spectrum areas of valence-to-core emission signals of Mn^III(acac)₃ as compared to Mn^II(acac)₂.⁶⁵ The discrepancy of this number with the expected ratio of electrons in the 3d-derived orbitals in the respective ground states (4/5=0.8 for Mn^III/Mn^II) was explained by the shorter Mn-ligand bond lengths in Mn^III(acac)₃ which “provide a mechanism for increased Mn-np mixing into the ligand orbitals”.⁶⁵ This points to a difference in the complementary sensitivity between L-edge XAS and Kβ_2,5 XES to metal-ligand bond lengths and orbital admixtures. In contrast to XES-based methods which probe differences in the ligand p-character of the 3d-derived orbitals, metal L-edge XAS provides a direct way for probing the metal-d character of the metal 3d-derived valence orbitals.

Absence of X-ray Induced Sample Damage

Due to their ionizing character, soft x-rays tend to modify the chemical structure of the probed samples. A major source of x-ray induced sample damage is the vast amount of electrons and radicals created upon ionization of the sample. X-ray spectroscopic signatures of such “beam damage” appear, for example, via the signature of a chemically reduced species. For a Mn^III sample one would expect the signature of a Mn^II species to appear in considerable amounts at x-ray doses on the order of 10⁶ Gy.^21–22 In case of insufficiently replenished samples such doses can quickly be reached at typical synchrotron radiation beamlines. For our experiment we estimate that the doses absorbed by the flatjet samples are on the order of ~20 Gy and thus five orders of magnitude below the critical threshold. We conclude that with our transmission flatjet we measure spectra unaffected by (dose-dependent) x-ray induced sample damage. We note that this could not be ensured in earlier L-edge spectroscopic studies of non-replenished solid Mn^III(acac)₃ samples.^66–67 Confirming results from ref.¹³, the much broader L₃-edge of the Mn^III(acac)₃ spectrum in refs.^66–67 compared to the spectrum reported here with considerable intensity at the peak location characteristic for Mn^II species indicates that the spectra in refs.^66–67 suffer from x-ray induced sample damage. We roughly estimate the relative Mn^II content in these experiments to several 10%.^66–67 Based on one of these sets of spectra recent restricted open-shell configuration interaction singlet (ROCIS) simulations of metal L-edge XAS of Mn^II(acac)₂ and Mn^III(acac)₃ show differences to both our experimental and RAS calculated spectra.^68–69

Spectrum Calculations with RAS

In Figure 3B we show Mn L-edge XAS spectra of Mn^II(acac)₂ and Mn^III(acac)₃ in ethanol solution as calculated with RAS theory, based on the molecular structures shown in Figures 1B and 1C. The relative energies and intensities of the two complexes are displayed as calculated. We find excellent agreement with our experimental spectra with respect to the overall shapes, the relative peak positions and the relative peak intensities in the individual spectra. The RAS spectra nicely reproduce the sharp and intense L₃-edge peak in Mn^II(acac)₂ as compared to the broad and less intense L₃-edge peak in Mn^III(acac)₃. The L₃-edge shift is underestimated by the RAS calculations by 16% (1.6 eV from RAS as compared to 1.9 eV from the experiment). The relative peak absorptions of Mn^III and Mn^II are reproduced within the experimental error bars by the ratio of 0.69 in the RAS calculations as compared to the experimental ratio of 0.71±0.15. The calculated ratio of 1.29 of the Mn^III/Mn^II spectrum areas from RAS is also within the experimental limits of 1.16±0.28 (see also Table S2 in the S.I.).. This indicates that the differences between the two complexes in terms of electronic structures and atomic multiplet effects are well accounted for in the RAS calculations.

In Figures 4A and 4B we compare calculated and measured spectra in more detail by also including the individual transitions as sticks in the calculated spectra. The agreement between calculated and measured spectra illustrates the quality of such state-of the art RAS spectral calculations. Overall the calculated spectral features appear too narrow compared to experiment and this could be due to the neglect of inhomogeneous broadening by structural fluctuations in the calculations. The largest discrepancies between theory and experiment, however, appear in the spectrum of Mn^II(acac)₂ between 641 and 644 eV, where the intensity is underestimated in the calculated spectrum, and, to a lesser extent, in the same region in the Mn^III(acac)₃ spectra. These high-energy sides of the L₃-edges were characterized before in Fe L-edge XAS as arising from excitations to charge-transfer (CT) states.⁷ At this point we can only speculate that the missing intensity in our RAS calculations is due to missing CT excitations as they include only the five active orbitals with metal 3d character and therefore do not take into account excitations to ligand-dominated orbitals, as required to describe the CT final states. RAS calculations can easily be extended with another five or even more valence orbitals. However, for ionic complexes the minimal active space of five metal 3d-derived orbitals is the most stable, ensuring consistent comparisons between the two complexes. Alternative implementations of ab-initio type calculations of L-edge XAS may include many more final states with CT character⁷⁰ and comparisons of the different approaches promises further insight.

Figure 4.

Direct comparison of normalized spectra of (A) Mn^II(acac)₂ and (B) Mn^III(acac)₃ in solution from experiment (blue and red) and RAS theory (black lines) on a RASPT2 level. The sticks denote the transitions to individual XAS final states underlying to the RAS spectra. The energy axis of both RAS spectra was aligned with the same energy shift for coinciding L₃-edge peak positions in the experimental and the RAS spectra of Mn^II(acac)₂.

L_3,2-edge Branching Ratios

The proportion of integral absorption areas of the Mn L₃ and L₂-edges in the spectra is often denoted the “branching ratio” (see refs.^{63, 71}). It reflects the statistical ratio of 2p_j=3/2→3d and 2p_j=1/2→3d transitions where j denotes the total angular momentum of the 2p hole. We determine the L₃ and L₂ absorption integrals over the energy ranges hν<647.5 eV and hν>647.5 eV for the Mn L₃ and L₂-edges, respectively, and obtain experimental branching ratios L₃/(L₃+L₂) of 0.72±0.02 for Mn^II(acac)₂ and 0.66±0.02 for Mn^III(acac)₃. The error bars account for the estimated deviation of branching ratios after linear background subtraction (as applied here) with respect to subtraction of an L_3,2-edge jump as applied in ref.⁷. These values agree well with those calculated in ref.⁶³ by Thole and van der Laan stating average branching ratios of 0.74 and 0.66 for atomic Mn^II and Mn^III, where a typical reduction factor 0.75 was applied to all Slater integrals.

The branching ratio extracted from the calculated RAS spectrum of Mn^II(acac)₂ amounts to 0.78 and thus significantly deviates from the experimentally determined branching ratio of 0.72 ±0.02. This reveals an overestimation of the L₃-edge intensity (or equivalently an underestimation of the L₂-edge) in the calculated with respect to the experimental spectrum. In contrast, for Mn^III(acac)₃ good agreement is found for the branching ratio of 0.65 in the RAS spectrum to that from experiment (0.66±0.02). The reason for the limited capability of RAS to consistently reproduce the branching ratio of Mn^II is not well understood, but could possibly be due to the perturbative treatment of the strong 2p spin-orbit coupling.

CFM Theory for Variable Ligand Field Splittings 10 Dq

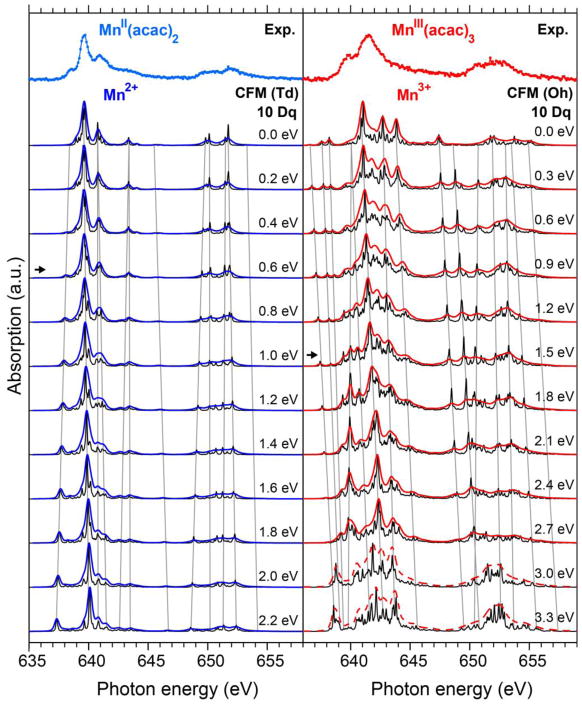
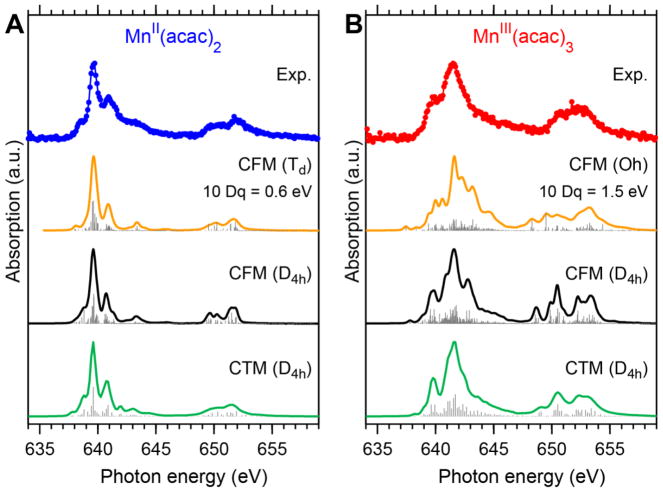
We use CFM calculations for a systematic study of the influence of the ligand field splitting 10 Dq in a cubic ligand environment on the L-edge XAS spectrum and we use the comparison of CFM and CTM to investigate the influence of CT states on the spectra. In Figure 5 we compare the experimental spectra to a series of theoretical spectra calculated with the CFM approach in T_d/O_h symmetry where we vary the ligand field splitting parameter 10 Dq. We track the energies of corresponding multiplet features with gray lines as 10 Dq is systematically increased.

Figure 5.

Comparison of experimental L-edge XAS spectra of Mn^II(acac)₂ (top left) and Mn^III(acac)₃ (top right) to crystal field multiplet (CFM) calculations (rows 2 to 13) with a variable ligand field splitting (LFS) for Mn²⁺ (left) in T_d symmetry and Mn³⁺ (right) in O_h symmetry. The red and blue spectrum curves in rows 2–13 were calculated with the broadenings similar to the experimental values (see methods section). The black curves are broadened with a Lorentzian width 0.1 eV (FWHM) and a Gaussian width σ=0.01 eV for better discrimination of the underlying multiplet features. The experimental spectra are best reproduced by the CFM spectra marked with arrows. All CFM spectra of Mn²⁺ and Mn³⁺ have been shifted by the same constant offsets of −0.7 eV and −0.5 eV, respectively.

The spectrum of Mn^II(acac)₂ in Figure 5 is qualitatively well described by the spectral multiplet features of a field-free Mn²⁺ ion (with 10 Dq=0). Apparently, however, no such agreement is found for the spectrum calculated for the field-free Mn³⁺ ion when compared to the experimental Mn^III(acac)₃ spectrum. Varying 10 Dq illustrates the influence of the Mn-O coordination geometry on the electronic structure⁷² and, more specifically, on the spectrum observable in Mn L-edge XAS.³⁷ For Mn²⁺ a weak pre-edge peak below the L₃-edge in Figure 5 splits off on the low energy side of the main L₃-edge maximum with increasing separation as 10 Dq is increased. With respect to this pre-edge peak, the best qualitative match to the experimental spectrum is found for 10 Dq=0.6 eV. Moreover, all other peaks in the L₃-edge seem to broaden when 10 Dq is increased. Varying 10 Dq for Mn³⁺ leads to dramatic redistribution of intensities in the spectra and, in particular, to the appearance of a strong pre-edge feature on the low energy side of the L₃-edge. The best qualitative match with experiment is found for 10 Dq=1.5 eV (the calculated CFM(T_d/O_h) spectra with shapes best matching experiment are marked with arrows in Figure 5). For both complexes these are the values where the L₃ pre-edge features and the “smooth” intensity distribution on the high-energy side of the L₃-edge best match those in the experimental spectra. Both observables seem to characteristically correlate with the values of 10 Dq. In particular the presence of a strong pre-edge feature at 1 to 2 eV below the L₃-edge maximum appears to be characteristic for the octahedral complex.

We can assess the fit results with information on the ligand field strength from UV-vis spectroscopic investigations where for Mn^III(acac)₃ optical absorption energies between 2.1 and 2.4 eV have been found for the ⁵T_2g→⁵E_g transitions.^73–74 This is roughly consistent with our approximate value for the ligand-field splitting of 10 Dq=1.5 eV found for Mn³⁺ in Mn^III(acac)₃. The 30–40% smaller value of 10 Dq from CFM theory compared to UV-vis may be explained with an “increased localization of the 3d states in the presence of the core hole” (ref.⁴ and ref.17 therein). We are not aware of any UV-vis data or values of the ligand field splittings in Mn^II(acac)₂ to which we could reference our value of 10 Dq, but the value is consistent with crystal-field theory that predicts 10 Dq of tetrahedral complexes to be 4/9 of the value of corresponding octahedral complexes.⁷²

We note that the simulated CFM spectra in Figure 5 for octahedrally coordinated Mn^III with 10 Dq changing from 2.7 eV to 3.0 eV illustrate the effect of an abrupt transition from a high-spin to a low-spin Mn³⁺ complex with S=2 and S=0 ground states, respectively. This is where the multiplet structures in both the L₃ and L₂-edges abruptly change. Such a high-spin to low-spin transition was reported to occur at around 10 Dq=3 eV for octahedrally coordinated Mn³⁺ (and also for tetrahedrally coordinated Mn²⁺).⁶² The CFM analysis can therefore be used to confirm the spin states of the Mn^II and Mn^III species in the ground states of Mn^II(acac)₂ and Mn^III(acac)₃ to be high spin.

With the above analysis we have identified the occurrence of a strong (weak) pre-edge feature at 1 to 2 eV below the L₃ absorption maximum to be characteristic for Mn coordinated in octahedral (tetrahedral) ligand fields. A similar yet more distinct pre-edge feature was observed by Pinjari et al.⁴⁰ in L-edge XAS of both high-spin and low spin Fe³⁺ ions in octahedral ligand fields (Fe³⁺ is isoelectronic to Mn²⁺ and has a similar L-edge spectral shape). In ref.⁴⁰ the calculated RAS ligand field is represented once by point charges and once by molecular ligands. The orbital-population analysis of these RAS spectra reveals differences in the assignment of the pre-edge feature. Importantly, for the high-spin Fe³⁺ ion in a point charge field, the pre-edge feature is predominantly assigned to one-electron transitions to the energetically low-lying t_2g-orbitals, while in the example of a molecular high-spin Fe³⁺ complex this assignment breaks down due to strong mixing of orbital contributions in the pre-edge feature. This latter observation agrees with findings from analyses of RAS calculated L-edge XAS spectra of Mn^II(acac)₂ and Mn^III(acac)₃ for orbital populations in the core-excited states¹³ where no particular assignment of peaks to specific orbital-excitations was found.

Spectrum Fits using CFM and CTM Theory

In Figure 6 we compare the best fitting CFM(T_d/O_h) spectra from Figure 5 to more quantitative multi-parameter fits that we performed within the CFM and CTM frameworks. With respect to the CFM model the CTM approach uses a valence bond configuration interaction model to include charge transfer (CT) states with energy separations Δ_CT and mixing parameters T.⁸ The CFM and CTM multi-parameter simulations were implemented in D_4h symmetry where additional parameters D_s and D_t include the energy splittings due to Jahn-Teller distortion.

Figure 6.

Comparison of experimental spectra of Mn^II(acac)₂ (A) and Mn^III(acac)₃ (B) in solution to the best fitting CFM(T_d/O_h) spectra (orange) (arrows in Fig. 5) and those fitted with CFM(D_4h) (black) and CTM(D_4h) (green). The sticks denote the transitions to individual XAS final states underlying to the calculated spectra. The energy axis of all CFM and CTM spectra was aligned to that of the experimental spectra for coinciding L₃-edge peak-maximum positions. All fit parameters are given in Table S1 in the Supporting Information.

In Figure 6 we observe that the best fitting spectra from our single-parameter CFM(T_d/O_h) fits show strong similarity to the spectra obtained from the multi-parameter CFM(D_4h) fits, yet with better qualitative agreement to the experimental spectra of Mn^II(acac)₂ and Mn^III(acac)₃. This concerns in particular the shape of the pre-edge features in both spectra. Yet, even better agreement to the experimental spectra is obtained for the CTM(D_4h) fits which involve up to 10 free parameters (see fit parameters in Table S1 in the S.I.), in particular for modeling the charge transfer states. The CTM model adds a dⁿ⁺¹L configuration to the single configuration ground state dⁿ and cdⁿ⁺²L to the cdⁿ⁺¹ configurations in the core-excited XAS final states (where L and c denote holes in the ligand and in the 2p core orbitals, respectively). This is known to produce CT excitations or CT core-excited states (shake-up states) to the high-energy side of the L₃ and L₂ edges, respectively.^{7–8, 10} Inclusion of charge transfer states improves the agreement of the calculated Mn^II spectrum at the “smooth” high-energy side of the L₃-edge (641–647 eV) with the experimental spectrum of Mn^II(acac)₂ (Figure 6A). Apparently, CT states add intensity in this spectral range which explicitly cannot be reproduced neither with the purely ionic CFM calculations nor with our RAS calculations. The CTM fit for Mn^III in Mn^III(acac)₃ in Figure 6B also shows a smoother flank on the high-energy side of the L₃-edge (642–647 eV) as compared to the CFM and the RAS calculations and in good agreement with the experimental spectrum.

The branching ratios of the Mn^III(acac)₃ CFM(D_4h) and CTM spectra amount to 0.65 and 0.67, respectively, which is in good agreement with the experimental value of 0.66±0.02. However, both CFM and CTM calculations overestimate the branching ratio in the spectrum of the Mn^II(acac)₂ complex (0.76 and 0.75 for CFM(D_4h) and CTM, respectively, as compared to 0.72±0.02 from experiment). This trend is the same as in the RAS calculations. We observe that for both systems including CT states affects the branching ratios only marginally.

Comparison to Partial Fluorescence-Yield XAS

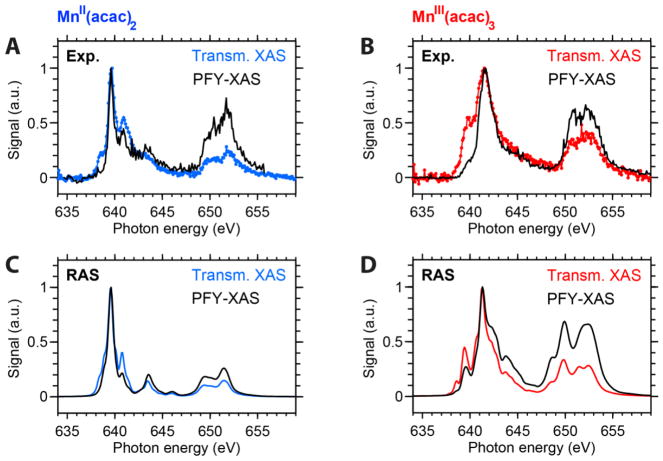
In transmission mode XAS the 2p⁶3dⁿ→2p⁵3dⁿ⁺¹ transitions (and their cross sections) are probed most directly, whereas PFY-XAS, measuring 3d-2p fluorescence intensity, introduces state-dependent fluorescence yield effects^{27, 31–33} due to spectrally variable fluorescence decay of core-excited XAS final states 2p⁵3dⁿ⁺¹ to valence excited PFY-XAS final states (2p⁶3dⁿ)^*. In Figures 7A and 7B we illustrate these effects by comparing the absorption spectra of Mn^II(acac)₂ and Mn^III(acac)₃ from transmission detected XAS with respect to PFY-detected XAS from ref.¹³. Note that the same absolute energy calibration for all experimental spectra was used and all spectra were normalized to the same intensity at the L₃ edge maximum. We identify almost all features of the transmission XAS spectra also in the PFY-XAS spectra and for each complex the specific energy of the features agree well.

Figure 7.

Comparison of experimental and RAS-theoretical x-ray absorption spectra in transmission mode (XAS) and in partial fluorescence yield mode (PFY-XAS) for Mn^II(acac)₂ and Mn^III(acac)₃ in solution samples. Experimental and RAS calculated PFY-XAS spectra (black) are copied from ref. 13. All spectra are normalized to their peak intensity. The transmission XAS spectra in (A) and (B) were taken from Fig. 3A, those in (C) and (D) from Fig. 3B. Notably, the energy position of the features is conserved for both detection modes.

The most apparent difference between the two detection modes is the enhancement or suppression of individual spectrum features due to state-dependent fluorescence yield. With all spectra normalized to their maximum intensity, for both complexes, this is most pronounced in a relative enhancement of the L₂-edge with respect to the L₃-edge in PFY-XAS as compared to transmission XAS. Quantitatively, in PFY-XAS the branching ratios for Mn^II(acac)₂ and Mn^III(acac)₃ are 0.49 and 0.50 as compared to 0.72 and 0.66 in transmission XAS, respectively. These observations of state-dependent fluorescence yield are consistent with earlier studies.^{31–33, 48}

Based on CFM analyses, Miedema et al. find that the 2p-3d exchange interaction in the XAS final states (quantified by the Slater integrals G_pd) is mainly responsible for differences in the L_3,2-edge branching ratios in PFY-XAS as compared to XAS and also for the suppression of the L₃ pre-edge⁷⁵ (herein called pre-edge peak). They argue that the exchange interaction orders the energy of XAS final states within the L-edge spectrum in accordance with their total angular momenta J, resulting in high-J states at the “low-energy side” (the pre-edge peak) of the L₃-edge and low-J states at the high energy side. The high-J states “tend to have lower fluorescence strengths, while there is no influence on the major (Auger) decay channel from these XAS final states”.⁷⁵ With this, the suppression of the pre-edge peak and the enhancement of the L₂-edge features in PFY-XAS as compared to XAS can be explained. As high-J states tend to have high total spin S, these findings are consistent with XAS spectrum analyses of Mn^II(acac)₂ and Mn^III(acac)₃ using RAS, revealing the ordering of XAS final states by their spin multiplicity (2S+1).¹³ Comparisons of the calculated PFY-XAS to the XAS spectra from RAS in Figures 7C and 7D reproduce all observations discussed above. This confirms that in our RAS approach the intra-atomic effects responsible for state-dependent fluorescence yield are taken into account albeit with deviations in the calculated relative XAS versus PFY-XAS intensities at the L₂-edge compared to experiment.

Potentials of the Method for Highly Dilute Samples and Table-Top X-ray Sources

Based on an extrapolation of our results we now discuss the application of L-edge XAS with a transmission flatjet to other experimental designs with, first, low sample concentrations on the order of 1 mM as achieved for many biologically relevant samples^{1, 12} and, second, with lower photon fluxes, as available for example from table-top soft x-ray sources.^76–83

An important factor delimiting the quality of a spectrum is the signal-to-noise ratio (S/N). From the absorption spectra shown in Figure 3A we estimate that the relevant multiplet structures of a Mn L-edge spectrum are minimally resolved, if features with absorption signals of 1 Mb have a S/N≥1. From our measurements we identify two terms contributing to the total noise N of a transmission spectrum, namely the experimental noise N_exp due to detection and x-ray source noise and the “jet-noise” N_jet in case of an unstable operation of the transmission flatjet. We illustrate the meaning of the experimental noise N_exp and jet noise N_jet upon comparison of two exemplary single-scan spectra, one with the best and one of with the worst S/N, namely that of 15 mM and that of 100 mM Mn^III(acac)₃ in Figure 2C, respectively. These spectra have noise levels (1σ) of around 0.1 % and 0.6 %, respectively. The 0.1 % noise is equal to the experimental noise N_exp=10⁻³, measured without any sample in the beam. This comparison implies that for a stable transmission flatjet N_exp dominates the total noise N (in particular if the influence of thickness variations in the transmission flatjet is negligible). The higher noise level in the spectrum of the 100 mM sample is due to the notably less stable operation of the liquid flatjet (e.g. due to precipitation of the sample) where N_jet becomes the predominant term to the total noise. A third term, the statistical noise or shot noise N_stat is negligible under our experimental conditions, but can gain predominant character if lower photon fluxes or larger sample thicknesses are used. While N_exp and N_jet are extracted from our experimental observations and are herein assumed to be constant, the shot noise ${\mathrm{N}}_{\text{stat}}=\sqrt{{\mathrm{p}}_{\text{out}}}$ is determined by the number of photons p_out=p_in·exp(−L/Λ_solv) to be detected by the photodiode. It is parametrized via the number of photons incident on the sample p_in, the sample thickness L and the attenuation length of the solvent Λ_solv (here Λ_ethanol at 640 eV equals 1.44 μm^46–47). In Figure 8A, N_stat was calculated for 10¹² photons per spectrum data point (corresponding to 1 s integration time with our experimental flux of 10¹² photons/s) and a lower number of 10⁴ photons per spectrum data point (which would correspond, e.g., to 1 s integration time with a flux of 10⁴ photons/s). For our experimental conditions (with sample thicknesses around 3 μm and 10¹² photons per data point) Figure 8A illustrates that N_stat≪(N_exp, N_jet), i.e. that our measured S/N is not limited by statistical noise but rather by the experimental or jet noise contributions, respectively.

Figure 8.

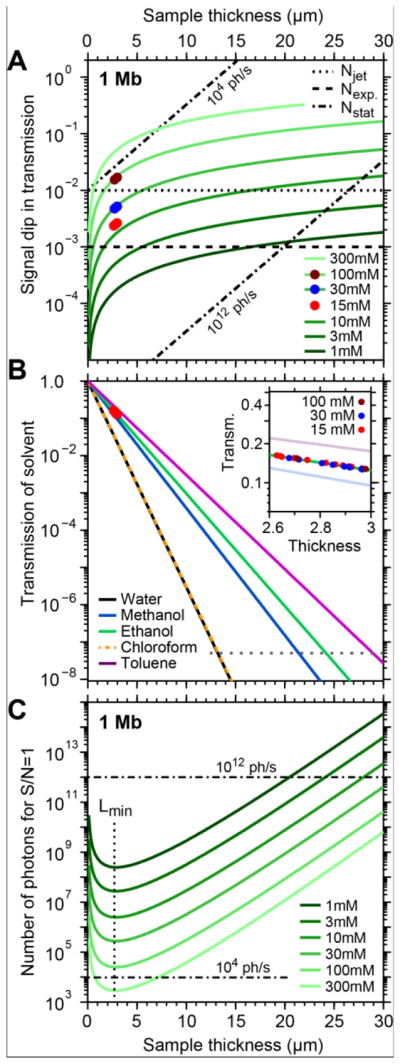
Comparison of signal and noise amplitudes for L-edge XAS of dilute Mn complexes under our experimental conditions and in the theoretical limit. (A) Expected vs. experimental signal dips in transmission for a 1 Mb absorption feature at the Mn L-edge. The expected curves were derived for 640 eV photon energy and the solvent ethanol, using Henke’s tables. The dashed/dotted lines assign the experimental and theoretical detection limits (see main text) for an acquisition time of 1 s per spectrum data point. (B) Transmission of typical solvents at the Mn L-edge (640 eV) with a magnification of the experimental range (inset). (C) Theoretical minimum number of incoming photons for detecting a 1 Mb absorption feature with S/N=1, here for statistical shot noise, using the solvent ethanol.

In Figure 8A we compare the expected amplitudes of the L-edge XAS signal dip S (green solid lines) of a 1 Mb feature for variable sample concentrations and sample thickness to the magnitudes of the noise terms N_exp, N_jet and N_stat (dashed, dotted and dash-dotted). The expected signal amplitudes S=T_dip(L, c)=[1-exp(−L·c·σ·N_A)] are derived from Beer-Lambert’s law. Our experimental 1 Mb signals (circle marks) measured with 10¹² photons/s and at thicknesses around 3 μm agree well with the calculated amplitudes. This is also consistent with previous work measured with the transmission flatjet.³⁶

Along the vertical axis of Figure 8A we observe that signal amplitudes decrease with decreasing concentrations and assuming a constant noise level this also implies that the S/N decreases. We can use this plot to estimate, for a given sample thickness, the feasibility of measuring meaningful Mn L-edge spectra (here in ethanol solution) of samples with different concentrations in the transmission flatjet, using the simple criterion S≥N where N is the dominant noise term. With this we expect that, assuming a stable flatjet (correspondingly with a dominant noise term N_exp) with a typical thickness of 3 μm, measurements for sample concentrations ranging from several 100 mM down to the order of 10 mM are feasible within a single scan.

For highly dilute biological samples with concentrations on the order of 1 mM with Figure 8A we expect that measuring a sufficiently resolved single-scan spectrum is unfeasible under our experimental conditions, since S<N_exp. At a sample thickness of around 3μm one would need to average around 25 single-scan spectra (each with S/N_exp=0.2) to increase the effective S/N to a minimum value of 1. In our experiment, this would correspond to around 4 h of data acquisition and a total sample consumption on the order of 1 liter, where we assume that no sample recycling unit is employed.³⁴ Sample consumption, however, is a limiting factor in spectroscopy of many precious samples such as biologically relevant complexes and metalloenzymes. Solutions of metalloproteins, in particular, are often available in volumes on the order of 1 ml only. Such measurements therefore rather require slowly flowing liquid jets with flow rates on the order of 1 μl/min¹² or sophisticated sample recovery systems for the transmission flatjet.³⁴ The latter would need to be optimized for recycling and rehydrating sensitive solution samples after exposure to vacuum and the probing x-rays to constantly guarantee unspoiled sample conditions.

Along the horizontal axis of Figure 8A the signal amplitudes increase with increasing sample thickness. If the dominant noise stays largely constant, a different way to increase S/N of low concentrated samples would therefore lie in increasing the sample thickness and therefore also S/N. However, this concept is limited by the increased absorption by the solvent, which leads to an increased shot noise N_stat and to a decreased detector signal, saturating close to the zero-level of the detector. The former effect is estimated in Figure 8A, where at large sample thicknesses we expect N_stat>S. The latter effect is illustrated in Figure 8B for some typical solvents, assuming our experimental conditions at 10¹² photons/s, where at thicknesses between 10 and 30 μm the transmitted signal (colored lines) dips below the detection limit of our detector (gray dotted line).

We now turn our discussion to applications of L-edge XAS on the transmission flatjet using table-top soft x-ray sources^{77, 79–83} which have mostly lower average flux than used in our study. For example, earlier implementations of soft x-ray sources based on high harmonic generation provide on the order of 10⁴ photons/s in the spectrum range and spectral bandwidth used in our study.^{76, 78} With Figure 8A we expect that reducing the photon flux delimits the parameter space where our method provides single-scan spectra with S/N>1, as the statistical noise N_stat is increased. For sample thicknesses around 3μm we expect this experimental feasibility for sample concentrations on the order of several 100 mM and larger.

The statistical noise N_stat defines the theoretical limits of experimental feasibility where all other noise sources are eliminated. We use it to calculate the minimum number of photons that is required per spectrum data point for recording L-edge XAS of Mn solution samples in a transmission flatjet under ideal conditions (stable flatjet in particular). In Figure 8C we plot this minimum number of incident photons p_min(L, c, Λ_solv) = [(1 − exp(−L·c·σ·N_A))² · exp(−L/Λ_solv)]⁻¹ for variable sample concentration and thickness. For these estimates we used Λ_ethanol(640 eV)=1.44 μm and used the above criterion that a 1 Mb feature is resolved with S/N_stat=1.

Three major observations can be made in Figure 8C. First, in an ideal experiment acquisition of Mn L-edge XAS in a transmission flatjet is most efficient at a sample thickness at L_min=2.9 μm (for ethanol) independent of the sample concentration. This coincides with the flatjet thicknesses used in our experiments. Our above discussion, however, shows that with our non-ideal experimental noise it is favorable to increase the sample thickness beyond L_min. Second, for a given photon number per spectrum data point one can read off the theoretical minimum in sample concentration which in an ideal experiment could be measured with S/N>1 in a single-scan. For example, for soft x-ray sources with a flux on the order of 10⁴ photons/s, this would be expected for sample concentrations on the order of a few 100 mM. Third, the figure shows that in an ideal experiment where only statistical noise contributes, measuring absorption spectra of samples with concentrations as low as 1 mM may be detectable already with 10⁹ photons per spectrum data point. Reaching such ideal experimental conditions will require further reduction of the experimental (detection and x-ray source) and jet-induced noise sources.

IV. Conclusions

In this paper we present results from L-edge x-ray absorption spectroscopy of dilute transition metal complexes in solution using a transmission flatjet. We show that this approach is ideally suited for probing dilute radiation sensitive transition metal complexes in solution, here for Mn^II(acac)₂ and Mn^III(acac)₃, as we strictly avoid x-ray induced sample damage with fast sample replenishment. We show that the method allows extracting important information on the absolute absorption cross sections. We use this to demonstrate that within the experimental uncertainty the integrated absorption cross sections of Mn^III with respect to Mn^II are consistent with the ratio expected from the number of holes in the 3d shells of the two systems. In future studies with better S/N this could be extended to assess the ionic or covalent character of the metal-ligand bonds. Our measured Mn L-edge peak cross-sections of 12 and 9 Mb for Mn^II(acac)₂ and Mn^III(acac)₃, respectively, can be used to plan future Mn L-edge experiments. Comparison of our experimental spectra to crystal field and charge transfer multiplet calculations shows that the occurrence of a weak/strong pre-edge peak at around 1 to 2 eV below the L₃ absorption maximum is characteristic for tetrahedral/(nearly) octahedral ligand environments in Mn^II and Mn^III. For the Mn^II complex and to a weaker extent for the Mn^III complex, we find evidence for charge transfer states on the high-energy side of the L₃-edge. We show that L-edge absorption spectra from ab-initio restricted active space calculations reproduce the experimental spectra with very good agreement with respect to shapes, relative absorption strengths, peak positions as well as the oxidation-state dependent Mn^II-Mn^III shift. The experimentally observed enhancement and suppression of features in fluorescence-detected x-ray absorption spectra (partial fluorescence yield) as compared to absorption cross section spectra due to state-dependent fluorescence yield is correctly reproduced by the RAS calculations. We discuss the potential of further L-edge XAS experiments of dilute 3d metal complexes in solution with a transmission flatjet. Under the present experimental conditions with a relative noise level of 10⁻³ in flux transmitted by the sample and at a high-brilliance undulator beamline at a synchrotron radiation source the approach is shown to be suited for studies of 3d transition metal complexes in solution with concentrations from several 100 mM to several 10 mM. We estimate the feasibility of transferring our approach to table-top soft x-ray sources with sample concentrations on the order of several 100 mM. We further expect that under the present conditions studies of biological samples with metal concentrations around 1 mM impose severe experimental challenges.