Abstract
In order to rationalize the influence of FeIII contamination on labeling with the 68Ga eluted from 68Ge/68Ga-generator, a detailed investigation was carried out on the equilibrium properties, formation and dissociation kinetics of GaIII- and FeIII-complexes of 1,4,7-triazacyclononane-1,4,7-tris(methylene[2-carboxyethylphosphinic acid]) (H6TRAP). The stability and protonation constants of the [Fe(TRAP)]3− complex were determined by pH-potentiometry and spectrophotometry by following the competition reaction between the TRAP ligand and benzhydroxamic acid (0.15 M NaNO3, 25°C). The formation rates of [Fe(TRAP)] and [Ga(TRAP)] complexes were determined by spectrophotometry and 31P-NMR spectroscopy in the pH range 4.5–6.5 in the presence of 5–40 fold HxTRAP(x−6) excess (x = 1 and 2, 0.15 M NaNO3, 25°C). The kinetic inertness of [Fe(TRAP)]3− and [Ga(TRAP)]3− was examined by the trans-chelation reactions with 10 to 20-fold excess of HxHBED(x−4) ligand by spectrophotometry at 25°C in 0.15 M NaCl (x = 0,1 and 2). The stability constant of [Fe(TRAP)]3− (logKFeL = 26.7) is very similar to that of [Ga(TRAP)]3− (logKGaL = 26.2). The rates of ligand exchange reaction of [Fe(TRAP)]3− and [Ga(TRAP)]3− with HxHBED(x−4) are similar. The reactions take place quite slowly via spontaneous dissociation of [M(TRAP)]3−, [M(TRAP)OH]4− and [M(TRAP)(OH)2]5− species. Dissociation half-lives (t1/2) of [Fe(TRAP)]3− and [Ga(TRAP)]3− complexes are 1.1 × 105 and 1.4 × 105 h at pH = 7.4 and 25°C. The formation reactions of [Fe(TRAP)]3− and [Ga(TRAP)]3− are also slow due to the formation of the unusually stable monoprotonated [*M(HTRAP)]2− intermediates [*logKGa(HL) = 10.4 and *logKFe(HL) = 9.9], which are much more stable than the [*Ga(HNOTA)]+ intermediate [*logKGa(HL) = 4.2]. Deprotonation and transformation of the monoprotonated [*M(HTRAP)]2− intermediates into the final complex occur via OH−-assisted reactions. Rate constants (kOH) characterizing the OH−-driven deprotonation and transformation of [* Ga(HTRAP)]2− and [*Fe(HTRAP)]2− intermediates are 1.4 × 105 M−1s−1 and 3.4 × 104 M−1s−1, respectively. In conclusion, the equilibrium and kinetic properties of [Fe(TRAP)] and [Ga(TRAP)] complexes are remarkably similar due to the close physico-chemical properties of FeIII and GaIII-ions. However, a slightly faster formation of [Ga(TRAP)] over [Fe(TRAP)] provides a rationale for a previously observed, selective complexation of 68GaIII in presence of excess FeIII.
Keywords: chelates, gallium, iron, thermodynamics, kinetics, reaction mechanism, positron emission tomography
Introduction
Due to the wealth of obtainable information resulting in a high diagnostic value, medical imaging plays an ever-increasing role in modern personalized healthcare. In this context, radionuclide based imaging modalities which exploit George Hevesy's tracer principle (Levi, 1976) allow for unique functional diagnostics, because they enable monitoring of biological processes without significant interference with the investigated subject owing to minuscule amounts of administered active compound. Although the majority of nuclear imaging procedures (estimated >85%) still are scintigraphic or single photon emission computed tomography (SPECT) scans relying on the gamma-emitter 99mTc, recent times have seen a strong surge in positron emission tomograpy (PET), following introduction of scanners capable of simultaneous functional and morphological imaging utilizing PET and computed tomography (CT) in 2001 (Beyer et al., 2000). While most PET investigations rely on the positron emitter 18F (more precisely, on the radiofluorinated glucose derivative [18F]2-fluoro-2-deoxy-d-glucose), some positron-emitting metal ion radionuclides have also received considerable attention in recent times (Wadas et al., 2010). Among these, 68Ga has arguably the highest value for preclinical and translational studies (Notni and Wester, 2018), mainly because it is obtained for a low price per dose from radionuclide generators. These small benchtop devices, which act as cyclotron-independent continuous on-site nuclide sources, contain 68Ge adsorbed on an inorganic matrix, such as SnO2 or TiO2, while decay of 68Ge produces 68GaIII which can be eluted with dilute HCl (Notni, 2012; Rösch, 2013). Notably, such eluate frequently contains small amounts of impurities originating from the sorbent (Simecek et al., 2013), such as TiIV but also FeIII, CuII, ZnII, or AlIII in form of their aqua or chlorido complexes.
68Ga-labeling of biomolecules usually requires prior decoration with a suitable multidentate ligand capable of binding the 68GaIII ion into a kinetically inert complex (Wadas et al., 2010) and a plethora of ligands have been proposed for this purpose (Frank and Patrick, 2010; Velikyan, 2011). Against the background of aforementioned metal ion impurities in the generator eluate, an investigation of the radionuclide complexation efficiency of certain macrocycle-based chelators, among them TRAP (Notni et al., 2014) and NOTA (Mariko and Susumu, 1977; Scheme 1) pointed at a markedly different influence of non-GaIII metal ions present in the 68GaIII solutions used for radiolabeling (Simecek et al., 2013). In particular, TRAP was shown to tolerate much higher concentrations of ZnII, CuII, and FeIII. Although highly similar structural features of [Fe(H3TRAP)] and [Ga(H3TRAP)] point at a close relation of both systems (Notni et al., 2010), it was found that even a threefold stoichiometric excess of FeIII over TRAP or its mono-conjugable congener NOPO (Simecek et al., 2014) did not result in a significant decrease of 68Ga incorporation, whereas labeling of NOTA was almost completely inhibited. Particularly in view of the known similarity of FeIII and GaIII, this discrepancy sheds a light on the mechanisms governing the superior 68Ga labeling properties of 1,4,7-triazacyclononanes bearing (methylene)phosphinic acid N-substituents (Notni et al., 2011). In order to gain a more detailed understanding, thermodynamics as well as formation and dissociation kinetic studies were performed for GaIII- and FeIII-complexes formed with TRAP and NOTA.
Scheme 1.
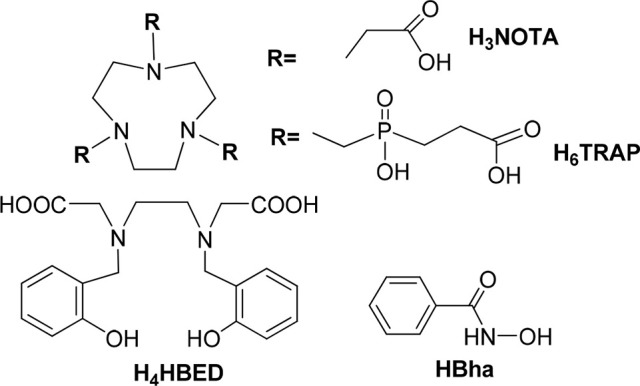
Structural formula of H3NOTA, H6TRAP, H4HBED and HBha chelates (H3NOTA: 1,4,7-triazacyclononane-1,4,7-triacetic acid; H6TRAP: 1,4,7-triazacyclononane-1,4,7-tris(methylene[2-carboxyethylphosphinic acid]); H4HBED: N, N′-Bis(2-hydroxybenzyl)ethylenediamine-N, N′-diacetic acid; HBha: benzhydroxamic acid).
Materials and methods
Materials
The chemicals used for the experiments were of the highest analytical grade. Ga(NO3)3 and Fe(NO3)3 were prepared by dissolving Ga2O3 (99.9%, Fluka) and Fe2O3 (99.9% Fluka) in 6M HNO3 and evaporating of the excess acid. The solid Ga(NO3)3 and Fe(NO3)3 were dissolved in 0.1 M HNO3 solution. The concentration of the Ga(NO3)3 and Fe(NO3)3 solutions were determined by complexometry with the use of standardized Na2H2EDTA in excess. The excess of the Na2H2EDTA was measured with standardized ZnCl2 solution and xylenol orange as indicator. The H+ concentration of the Ga(NO3)3 and Fe(NO3)3 solutions was determined by pH potentiometric titration in the presence of Na2H2EDTA excess. The concentration of the H6TRAP, H4HBED, benzohydroxamic acid (HBha) and H3NOTA (provided by Prof. Petr Hermann, Department of Inorganic Chemistry, Faculty of Science, Charles University, Prague, Czech Republic) was determined by pH-potentiometric titration in the presence and absence of a large (40-fold) excess of CaCl2. All the measurements were made at constant ionic strength maintained by 0.15 M NaNO3 or NaCl at 25°C.
Equilibrium studies
For determining the protonation constants of H6TRAP and H3NOTA ligands three parallel pH-potentiometric titration were made with 0.2 M NaOH in 0.002 M ligand solutions.
Stability constant of [Fe(Bha)]2+ complex was determined by spectrophotometry, studying the FeIII-HBha systems at the absorption band of FeIII-complex over the wavelength range of 400–800 nm in two sets of experiments. Individual samples were prepared in the first series in which the concentrations of FeIII and HBha was constant 0.2 and 2.0 mM, while that of the H+ was varied between 0.04 and 1.0 mM (eight samples, Figure S1). The H+ concentration in the samples was adjusted by addition of calculated amounts of 2.0 M HNO3. The ionic strength was constant in the samples with [H+] < 0.15 M ([H+]+[Na+] = 0.15 M). Samples were kept at 25°C for a week. Absorbance values were determined at 11 wavelengths (400, 415, 430, 445, 460, 475, 490, 505, 520, 535, and 550 nm). In the second set, spectrophotometric titrations were done with samples containing HBha ligand in 2.0 mM concentration, whereas the concentration of FeIII was varied between 0.1–0.3 mM (Figures S2–S4). The pH of the samples was adjusted using concentrated NaOH and HNO3 solutions in the pH range 1.7–11.0 (0.15 M NaNO3 and 25°C). For calculation of the equilibrium constants, the best fit of the absorbance–pH data was obtained by assuming formation of [Fe(Bha)]2+, [Fe(Bha)2]+, [Fe(Bha)3], and [Fe(Bha)2(OH)2]− species (Figure S5). The molar absorptivity of [Fe(Bha)]2+, [Fe(Bha)2]+, [Fe(Bha)3] and [Fe(Bha)2(OH)2]− species were also determined at the same 11 wavelengths in these experiments (Figure S6).
The stability constant of the [Fe(TRAP)]3− complex has been determined by spectrophotometry, using competition reactions between HTRAP5− and Bha− for FeIII at pH = 10.0. Concentration of [Fe(TRAP)]3− was 0.2 mM, while that of HBha was varied between 0.0 and 1.5 mM (6 samples). The samples were kept at 25°C for 2 weeks. Absorbance values of the FeIII-HTRAP5−-Bha− systems were determined at 11 wavelengths (400, 415, 430, 445, 460, 475, 490, 505, 520, 535, and 550 nm). The molar absorptivities of [Fe(TRAP)]3− and [Fe(TRAP)OH]4− in equilibrium solutions were determined by recording the absorption spectra of 0.1, 0.2, and 0.3 mM solution of [Fe(TRAP)]3− in the pH range 6.0–12.0. The molar absorptivity of [Fe(Bha)2(OH)2]− species was determined in the separate experiments. Absorbance and pH values were determined in the samples after equilibration (the time needed to reach the equilibria was determined by spectrophotometry). Spectrophotometric measurements were done using 1.0 cm cells with a Cary 1E spectrophotometer at 25°C. Protonation constants of the FeIII complex formed with TRAP6− were determined by direct pH-potentiometric titration at 1:1 metal to ligand ratios (both concentrations were 0.002 M). For calculation of the logKMHiL values, the mL base–pH data used were measured in the pH range 1.7 −12.0.
For pH measurements and titrations, a Metrohm 785 DMP Titrino titration workstation and a Metrohm-6.0233.100 combined electrode were used. Equilibrium measurements were carried out at a constant ionic strength (0.15 M NaNO3 or NaCl) in 6 mL samples at 25°C. Solutions were stirred and continuously purged with N2. Titrations were performed in a pH range of 1.7–12.0. KH-phthalate (pH = 4.005) and borax (pH = 9.177) buffers were used to calibrate the pH meter. For calculation of [H+] from measured pH values, the method proposed by Irving et al. was used (Irving et al., 1967). A 0.01 M HNO3 or HCl solution was titrated with the standardized NaOH solution in the presence of 0.15 M NaNO3 or NaCl. Differences between the measured (pHread) and calculated pH (–log[H+]) values were used to obtain the equilibrium H+ concentration from the pH values, measured in the titration experiments. For equilibrium calculations, the stoichiometric water ionic product (pKw) is also needed to calculate [H+] values in basic conditions. The VNaOH–pHread data pairs of the HNO3–NaOH or HCl–NaOH titration obtained in the pH range 10.5–12.0 have been used to calculate the pKw value (pKw = 13.84). For calculation of the equilibrium constants, the program PSEQUAD (Zekany and Nagypal, 1985) was used. The standard deviation (SD) of the equilibrium parameters calculated by the program PSEQUAD is defined by Equation (1)
| (1) |
where res, N, m, J and JT are the residual, number of fitted data, number of refined parameters, Jacobian matrix and the transpose of Jacobian matrix, respectively.
Kinetic studies
Formation kinetics of [Fe(TRAP)] and [Ga(TRAP)]
Formation rates of [Fe(TRAP)] were studied by spectrophotometry at 260 nm in the pH range of about 4.5–6.5. Kinetic studies were carried out with Cary 1E and Cary 100 Bio spectrophotometers, using cell holders thermostated to 25°C. The pre-thermostated solutions were mixed in tandem cells (l = 0.874 cm). Formation of FeIII complexes were studied in the presence of a 5- to 40-fold ligand excess in order to maintain pseudo-first-order conditions ([FeIII] = 0.1 mM). Pseudo-first-order rate constants (k = kobs) were calculated by fitting the absorbance values to the equation:
| (2) |
wherein A0, Ae, and At are the absorbance values at the start (t = 0 s), at equilibrium and at the time t of the reaction, respectively. Formation of [Ga(TRAP)]3− was monitored by 31P-NMR spectroscopy on the signal of the forming Ga(TRAP) complex. 31P-NMR spectra were recorded by a Bruker DRX 400 spectrometer (31P, 161.97 MHz, 9.4 T) equipped with Bruker VT-1000 thermocontroller, using a 5 mm broad band probe. Kinetic experiments were performed at a constant temperature of 25.0°C. The formation rates were studied in the pH range of about 4.5–6.3. For these experiments, Ga(NO3)3 and H6TRAP solutions were prepared in H2O (a capillary with D2O was used for lock). In all experiments, the concentration of GaIII was 1 mM, while that of the H6TRAP was varied between 5 and 30 fold excess in order to maintain pseudo-first-order conditions. Pseudo-first-order rate constants (k = kobs) were calculated by fitting the integral signal values to the Equation (2). The ionic strength of the solutions was kept constant at 0.15 M with NaNO3. To keep the pH values constant, N-methylpiperazine (pH range of 4.1–5.2) and piperazine (pH range of 4.7–6.6) buffers (0.01 M) were used.
Dissociation kinetics of Fe(TRAP) and Ga(TRAP)
The rates of the ligand exchange reactions of Fe(TRAP) and Ga(TRAP) with HxHBEDx−4 (x = 0,1 and 2) ligand were studied by following the formation of [Fe(HBED)]− and [Ga(HBED)]− complexes by spectrophotometry at 470 nm and 290 nm, respectively. All experiments were performed in the presence of 10- and 20-fold excess of HxHBEDx−4 (x = 1 and 2) in order to maintain pseudo-first order kinetic conditions ([Fe(TRAP)] = [Ga(TRAP)] = 0.2 mM). The pseudo-first-order rate constants (k = kd) were calculated by fitting the absorbance values to the Equation (2). Kinetic studies were performed with Cary 1E and Cary 100 Bio spectrophotometers, using cell holders thermostated to 25°C. The pre-thermostated solutions were mixed in tandem cells (l = 0.874 cm). The ionic strength of the solutions was kept constant at 0.15 M with NaCl. The ligand exchange reactions were followed at 25°C in the pH range 9.0–14.0. The OH− concentration at pH > 12 was adjusted by addition of calculated amounts of 4.0 M NaOH solution. Buffers were not used to keep the pH constant due to the high buffer capacity of the HxHBEDx−4 (x = 1 and 2) excess at pH < 12. Calculation of the kinetic parameters was performed with the Micromath Scientist computer program (version 2.0, Salt Lake City, UT, USA).
Results and discussion
Solution thermodynamics
Protonation equilibria of the TRAP6−, NOTA3− and Bha− ligands were studied by pH-potentiometry. The protonation constants (log) of ligands defined by Equation (3) are listed in Table 1 (standard deviations are shown in parentheses). The charges of ligands and complexes will be indicated when it is necessary.
Table 1.
Protonation constants of TRAP6−, NOTA3−, and Bha− ligands (25°C).
| I | log | log | log | log | log | log | Σlog | |
|---|---|---|---|---|---|---|---|---|
| TRAP6− | 0.15 M NaNO3 | 11.60(2) | 5.39(2) | 4.42(2) | 4.19(3) | 3.46(3) | 1.60(2) | 18.59 g |
| 0.15 M NaCla | 11.74 | 5.46 | 4.80 | 4.16 | 3.49 | 1.50 | 18.70 g | |
| 0.1 M Me4NCl b | 11.48 | 5.44 | 4.84 | 4.23 | 3.45 | 1.66 | 18.58 g | |
| NOTA3− | 0.15 M NaNO3 | 11.94(2) | 5.71(3) | 3.14(3) | 1.60(2) | – | – | 22.39 |
| 0.15 M NaCla | 12.16 | 5.75 | 3.18 | 1.90 | – | – | 22.99 | |
| 0.1 M KClc | 11.98 | 5.65 | 3.18 | – | – | – | – | |
| 0.1 M Me4NCld | 13.17 | 5.74 | 3.22 | 1.96 | – | – | 24.09 | |
| Bha− | 0.15 M NaNO3 | 8.53(3) | – | – | – | – | – | – |
| 0.2 M KCle | 8.69 | – | – | – | – | – | – |
Ref. (Baranyai et al., 2015);
Ref. (Notni et al., 2010);
Ref. (Clarke and Martell, 1991);
Ref. (Drahos et al., 2011);
Ref. (Farkas et al., 1998);
Total ligand basicity (Σlog) characterizes the sum of basicity of donor atoms;
The protonation constants of the acetate pendants (log, log and log) of TRAP6− were not considered in the calculation of Σlog values.
| (3) |
The protonation schemes of TRAP6− and NOTA3− ligands were well characterized by both spectroscopic and potentiometric methods (Bevilacqua et al., 1987; Geraldes et al., 1991; Notni et al., 2010). These studies reveal that the first and second protonations occur at two ring nitrogen atoms, whereas the third, fourth and fifth protonations occur at the carboxylate groups of NOTA3− and TRAP6−. The sixth proton of the TRAP6− ligand binds on the phosphinate oxygen atom. Interestingly, not all phosphinate groups are protonated, even under very acidic conditions (pH < 1), which is why they are still able to coordinate to metal ions. A comparison of protonation constants of TRAP6− and NOTA3− indicates that log value of TRAP6− is significantly lower than that of NOTA3− (Table 1). The lower first protonation constant of TRAP6− can be attributed to formation of a weaker H-bond between the protonated ring nitrogen and the phosphinate oxygens than that formed between the protonated ring nitrogen and the carboxylate oxygens in HNOTA2−. Comparison of the protonation constants obtained in 0.15 M NaNO3 or NaCl, 0.1 M KCl and 0.1 M Me4NCl solutions indicates that the log values of TRAP6− are independent of the ionic strength, whereas the log value of NOTA3− is significantly lower in the presence of K+ and Na+ ions, which can be attributed to formation of [K(NOTA)]2− and [Na(NOTA)]2− complexes. Total basicity of ligands (Σlog, Table 1) generally correlates with the stability constants (KML) of their metal complexes. (For the calculation of Σlog value of TRAP6−, the log values of the carboxylate groups were not considered because they do not participate in the coordination of metal ions). The Σlog values (Table 1) show that the total basicity of TRAP6− is significantly lower than that of NOTA3− because of the lower protonation constant of the ring nitrogen (log) and phosphinate oxygen atoms of the TRAP6− ligand. Therefore, lower stability constants should be expected for the TRAP6− complexes than those of NOTA3− complexes.
Stability and protonation constants of TRAP6− and NOTA3− complexes formed with FeIII were determined by pH-potentiometry and UV/Vis spectrophotometry. The stability and protonation constants of the metal complexes formed with the TRAP6− and NOTA3− ligands listed in Table 2 are defined by Equations (4–6):
Table 2.
Stability and protonation constants (logK) of FeIII and GaIII-complexes formed with TRAP6−, NOTA3−, and Bha− ligand (25°C).
| TRAP6− | NOTA3− | Bha− | ||||
|---|---|---|---|---|---|---|
| FeIII | GaIII | FeIII | GaIII | FeIII | ||
| I | 0.15 M NaNO3 | 0.1 M Me4NCla | 0.1 M KClb | 0.1 M Me4NClc | 0.15 M NaNO3 | 0.2 M KCld |
| ML | 26.73(8) | 26.24 | 28.3 | 29.60 | 10.80(2) | 11.08 |
| MHL | 5.07(2) | 5.18 | – | 0.9 | – | – |
| MH2L | 4.34(2) | 4.55 | – | – | – | – |
| MH3L | 3.20(2) | 3.77 | – | – | – | – |
| MH4L | – | 0.7 | – | – | – | – |
| M(L)OH | 9.76(2) | 9.84 | 9.12(4)e | 9.83 | – | – |
| ML2 | – | – | – | – | 9.03(2) | 10.12 |
| ML3 | – | – | – | – | 7.41(3) | 7.60 |
| logβFeL2(OH)2 | – | – | – | – | 6.68(5) | – |
| (4) |
| (5) |
| (6) |
wherein i = 1, 2, or 3. Since the [Fe(TRAP)]3− and [Fe(NOTA)] complexes are highly stable, formation of FeIII complexes was practically completed at about pH < 2.0. Therefore, from the data obtained by pH-potentiometric titrations performed at 1:1 metal to ligand concentration ratio, only the protonation constants of the [Fe(TRAP)]3− and [Fe(NOTA)] complexes could be calculated. In order to determine the logKFeL value, we studied the competition reactions between HTRAP5− and Bha− for FeIII [Equation (7)] by spectrophotometry in the wavelength range 400–800 nm. To calculate the stability constant of [Fe(TRAP)]3−, the equilibrium constants characterizing the species formed in the FeIII-HBha system have been determined from the data obtained by pH-potentiometric and spectrophotometric measurements (experimental detail and calculation procedures used for the characterization of FeIII-HBha system are summarized in the Supplementary information).
| (7) |
wherein x = 0 and 1. The pH of the samples was 10.0, when [Fe(TRAP)]3−, [Fe(TRAP)OH]4− and [Fe(Bha)2(OH)2]− were formed. Some characteristic absorption spectra of FeIII-HTRAP5−Bha− systems are shown in Figure 1.
Figure 1.
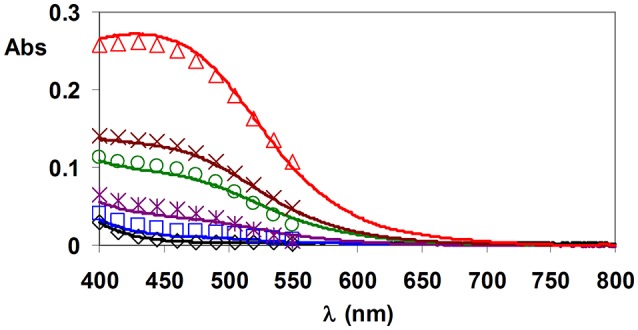
Absorption spectra of FeIII–HTRAP5−-Bha− equilibrium systems. Open symbols and solid lines represent experimental and calculated absorbance values, respectively. ([Fe(TRAP)(OH)x(−3−x)] = 0.2 mM, [HBha] = 0.0 mM (black). mM (blue), mM (purple), mM (green), mM (brown), and mM (red), x = 0 and 1, pH = 10.0, 0.15 M NaNO3, 25°C).
The stability and protonation constants of [Fe(TRAP)]3− complex have been calculated by the combination of the pH-potentiometric data obtained by the titration of [Fe(TRAP)]3− complex with NaOH solution in the pH range 1.7–12.0 (Figure S7) with the spectrophotometric data acquired at pH = 10.0 in FeIII-HTRAP5−–Bha− system (Figure 1). For calculation of the logKFeL value, protonation constants of Bha− (Table 1), the stability constant (Table 2) and the molar absorptivity of the [Fe(Bha)2(OH)2]− complex were used. Stability and protonation constants obtained for [Fe(TRAP)]3− are shown in Table 2.
Comparison of stability constants in Table 2 reveals that the logKML values of [Fe(TRAP)]3− and [Ga(TRAP)]3− complexes are essentially equal and 2–3 logK unit smaller than those of the corresponding NOTA3− complexes. The higher stability constant of [Fe(NOTA)] and [Ga(NOTA)] complexes can be attributed to higher total basicity of NOTA3−. The stability constant of [Fe(NOTA)] is about one logK unit lower than that of [Ga(NOTA)], which corresponds to a lower log value of NOTA3− obtained in 0.1 M KCl solution. The triazacyclononane macrocyclic ligands with carboxylate or phosphinate pendant arms show similar affinity to FeIII and GaIII, which is readily explained by the facts that Ga3+ and Fe3+ have similar ionic radii (0.62 Å and 0.65 Å, respectively), and share the same charge and preferred coordination number (CN = 6).
The species distribution diagram of the FeIII-TRAP6− system (Figure 2) shows that the FeIII complex is fully formed even at pH < 2 in the form of a tri-protonated [Fe(H3L)] species. Upon rising the pH from 2.0 to 7.0, stepwise deprotonation results in consecutive formation of [Fe(H2L)]− and [Fe(HL)]2−. Since the protonation constants characterizing the formation of the [Fe(HL)]2−, [Fe(H2L)]− and [Fe(H3L)] species are very similar to the log, log and log values of the free TRAP6− ligand, [Fe(TRAP)]3− is protonated on the non-coordinating carboxylate pendant arms. According to the known solid state structures of [Fe(H3TRAP)], the coordination environment of FeIII is characterized by the trigonal antiprismatic structure formed by the parallel ring-N3 and phosphinate-O3 planes, whereas the carboxylate groups are protonated and non-coordinated (the solid state structure of [Ga(H3TRAP)] complex is very similar to that of [Fe(H3TRAP)]) (Notni et al., 2010). The [Fe(TRAP)]3− complex predominates in the pH range 6.0–9.0. The pH-potentiometric titration data, obtained at pH > 8 for [Fe(TRAP)]3−, indicate a base-consuming process, which can be attributed to substitution of one of the phosphinate oxygens with a OH− ion in the coordination sphere of FeIII upon formation of the [Fe(TRAP)OH]4− species [Equation (6)]. Similar processes were also identified for [Ga(TRAP)]3−, [Fe(NOTA)] (Figure S8 and Table 2) and [Ga(NOTA)] complexes (Notni et al., 2010; Simecek et al., 2012).
Figure 2.
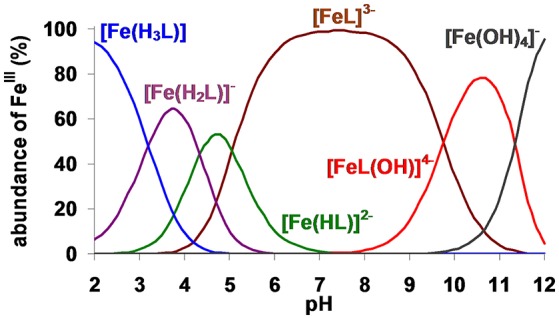
Species distribution of FeIII – TRAP6− system ([FeIII] = [TRAP6−] = 0.2 mM, 0.15 M NaNO3, 25°C).
Formation kinetics of Fe(TRAP) and Ga(TRAP) complexes
The formation reactions between NOTA and various metals, such as lanthanide(III) ions (LnIII) but also GaIII, are typically slow at pH around 2.0–5.0 (Brucher and Sherry, 1990; Morfin and Toth, 2011). Since formation of LnIII and GaIII complexes of open-chain ligands is generally fast, the slow formation kinetics of the NOTA complexes can be attributed to the rigidity of the triaza-cyclononane macrocycle. Incorporation of LnIII- and GaIII-ions into the preformed coordination cage of NOTA is slow because of formation of stable mono-protonated [*Ln(HNOTA)]+ and [*Ga(HNOTA)]+ intermediates, which has been confirmed earlier by spectrophotometry measurements (Brucher and Sherry, 1990) and 1H NMR spectroscopy(Morfin and Toth, 2011). Stability constants of such intermediates have furthermore been determined from kinetic data obtained by spectrophotometry (Brucher and Sherry, 1990) and 1H NMR spectroscopy (Morfin and Toth, 2011). In the intermediate, the proton is most likely attached to a macrocyclic nitrogen, and the electrostatic repulsion between the proton and a LnIII- or GaIII-ion can inhibit fast entrance of the metal ion into the coordination cage. Formation rates of the [Ln(NOTA)] and [Ga(NOTA)] complexes are directly proportional to the OH− concentration, meaning that a rate-determining OH− assisted deprotonation and rearrangement of the monoprotonated intermediate is followed by entrance of the LnIII- or GaIII-ion into the N3O3 coordination cage of NOTA3−(Brucher and Sherry, 1990; Morfin and Toth, 2011).
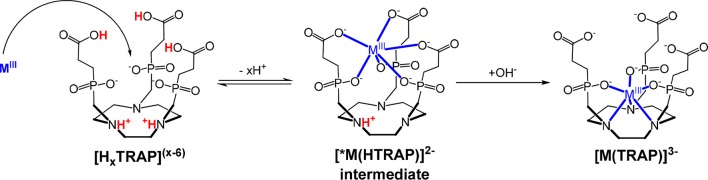
In the present work, formation kinetics of M(TRAP) complexes (MIII = FeIII and GaIII) have been studied by spectrophotometry on the absorption band of the forming Fe(TRAP) (λ = 260 nm) and by 31P-NMR spectroscopy following the integral value of the forming Ga(TRAP) complex in the pH range 4–6. UV-absorption as well as 31P-NMR spectra, recorded after mixing of solutions containing Fe(NO3)3 or Ga(NO3)3 with HTRAP5− as functions of time, are shown in Figures S9, S10. For the reaction mixture of FeIII-HTRAP5− at pH = 6.0, the absorption band observed between λ = 245–320 nm (Figure S9) can be explained by the formation of the intermediate. The absorbance values in the λ = 250–280 nm range increase with time, allowing for the conclusion that the intermediate is transformed into the final [Fe(TRAP)]3− in-cage complex. Formation of the intermediate in GaIII-TRAP reactions mixtures was previously proven by 31P- and 71 Ga-NMR spectroscopy (Notni et al., 2010). Based on the similarity of TRAP and NOTA, it can be assumed that protonation of the ring nitrogen below pH = 10.0 initially hampers the formation of in-cage TRAP complexes while the three carboxylate and three phosphinate oxygen atoms of HTRAP5− can be coordinated to the metal ions to form a mono-protonated [*M(HTRAP)]2− intermediate, in which the FeIII and GaIII -ion is situated outside of the coordination cage. To complete the complex formation, the proton has to be removed from the ring nitrogen via a OH−-assisted reaction, followed by the rearrangement of the intermediate to the final [Fe(TRAP)]3− and [Ga(TRAP)]3− complexes (Scheme 2).
Scheme 2.
Formation mechanism of [M(TRAP)]3− complexes.
The formation rates of [Fe(TRAP)]3− and [Ga(TRAP)]3− have been studied under pseudo-first-order conditions in the presence of high excess of HxTRAP(x−6) ([FeIII] = 1.0 × 10−4 M; [TRAP]t = 0.5–4.0 × 10−3 M; [GaIII] = 1.0 × 10−3 M; [HxTRAP]t = 5.0–30 × 10−3 M, x = 1 and 2). Under such conditions the rate of formation reactions can be expressed by Equation (8).
| (8) |
wherein [ML]t is the concentration of the [Fe(TRAP)]3− and [Ga(TRAP)]3− complexes, [MIII]t is the total concentration of species containing the FeIII and GaIII ions not bound to the HxTRAP(x−6) ligand, and kobs is a pseudo-first-order rate constant. As expected, the kobs vs. [HxTRAP]t curves (Figures 3, 4) are saturation curves indicating the formation of the [*M(HTRAP)]2− intermediates characterized by the stability constant defined by Equation (9).
Figure 3.
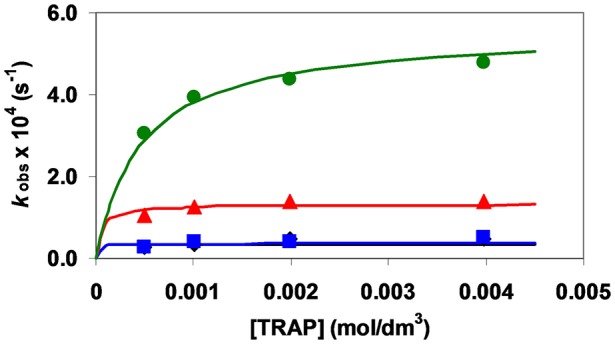
kobs pseudo-first order rate constants for the formation reaction of [Fe(TRAP)]3− as function of [HxTRAP]t ([FeIII] = 0.1 mM, pH = 4.5 ( ), 5.0 (
), 5.0 ( ), 5.5 (
), 5.5 ( ), and 6.0 (
), and 6.0 ( ), x = 1 and 2, 0.15 M NaNO3 and 25°C).
), x = 1 and 2, 0.15 M NaNO3 and 25°C).
Figure 4.
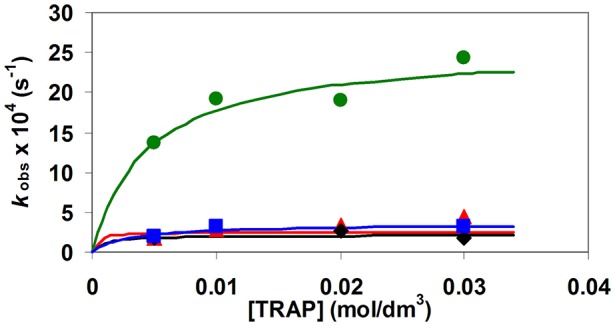
kobs pseudo-first order rate constants for the formation reaction of [Ga(TRAP)]3− as a function of [HxTRAP]t ([GaIII] = 1 mM, pH = 4.6 ( ), 5.0 (
), 5.0 ( ), 5.6 (
), 5.6 ( ), and 6.0 (
), and 6.0 ( ), x = 1 and 2, 0.15 M NaNO3 and 25°C).
), x = 1 and 2, 0.15 M NaNO3 and 25°C).
| (9) |
The rate-determining step of the reactions is the deprotonation and rearrangement of the [*M(HTRAP)]2− intermediates followed by the entrance of the metal ion into the coordination cage of the TRAP6− ligand:
| (10) |
wherein [*M(HTRAP)] is the concentration of [*M(HTRAP)]2− intermediate and kf is the rate constant characterizing the deprotonation and rearrangement of the intermediate to the [M(TRAP)]3− complex. In the pH range studied, the concentration of the non-complexed ligand ([TRAP]free) can be expressed by Equation (11) using the protonation constants of TRAP6− ligand (Table 1).
| (11) |
where αH = [H+]+[H+]2+…+[H+]5. Under the conditions used in our experiments (pH = 4.0–6.0), hydrolysis of FeIII and GaIII may occur by formation of [M(OH)]2+, [M(OH)2]+ and M(OH)3 species, i.e., OH− ions may compete with HxTRAP(x−6) for formation of [*M(HTRAP)]2− intermediate. Considering the hydrolysis of FeIII and GaIII, the total metal ion concentration can be expressed by Equation (12).
| (12) |
By taking into account the stability constant of the [*M(HTRAP)]2− intermediate [Equation (9)] and the equilibrium constants characterizing the hydrolysis of FeIII and GaIII (βx = [M(OH)x][H+]x/[MIII], x = 1, 2, and 3), the total metal ion concentration can be expressed as follows:
| (13) |
wherein αOH = /[H+] +/[H+]2+ /[H+]3 (log = −2.19; log = −5.67 and log = −12.0 for FeIII and log = −2.97; log = −5.92 and log = −8.2 for GaIII ion; Baes and Mesmer, 1976). Considering the protonation constants of TRAP6− (Table 1), the stability constant of the [*M(HTRAP)]2− intermediate [Equation (9)], the total concentration of the MIII ion [Equation (13)], the concentration of the non-complexed TRAPfree ligand [Equation (11) and Equation (10)], the pseudo-first order rate constant can be expressed by Equation (14).
| (14) |
The pseudo-first-order rate constants determined at various pH and [TRAP]t values (Figures 3, 4) were fitted to Equation (14) and the stability constant of the [*M(HTRAP)]2− intermediates [*KM(HL)] and the kf rate constants were calculated.
The stability constants of the [*Fe(HTRAP)]2− and [*Ga(HTRAP)]2− intermediates [log*KM(HL)] are 9.9 ± 0.1 and 10.4 ± 0.1, respectively. The log*KM(HL) values of the [*Fe(HTRAP)]2− and [*Ga(HTRAP)]2− intermediates are significantly higher than those of the mono-protonated [*Ga(HNOTA)]+ (log*KGa(HL) = 4.2), (Morfin and Toth, 2011) [*Ce(HNOTA)]+ (log*KCe(HL) = 3.2), (Brucher and Sherry, 1990) [*Gd(HNOTA)]+ (log*KGd(HL) = 3.6) (Brucher and Sherry, 1990) and [*Er(HNOTA)]+ (log*KEr(HL) = 3.8) (Brucher and Sherry, 1990) intermediates. In the [*Fe(HTRAP)]2− and [*Ga(HTRAP)]2− intermediates, FeIII and GaIII are presumably coordinated by three carboxylate and three phosphinate oxygen donor atoms, whereas the metal ions in [*M(HNOTA)]+ intermediates are coordinated by three carboxylate oxygen donor atoms, resulting in lower log*KM(HL) values.
The calculated kf rate constants obtained for formation of [Fe(TRAP)]3− and [Ga(TRAP)]3− complexes are shown in Figure 5 as functions of [OH−]. Kinetic data in Figure 5 show that the kf values increase monotonously with increasing OH− concentration, while interception of linear extrapolations at the origin indicates that under our experimental conditions, deprotonation and transformation of the [*M(HTRAP)]2− intermediate to the final [M(TRAP)]3− complex predominantly occurs by an OH−-catalyzed pathway. The kOH rate constants calculated from the slopes of the straight lines in Figure 5 are shown in Table 3.
Figure 5.
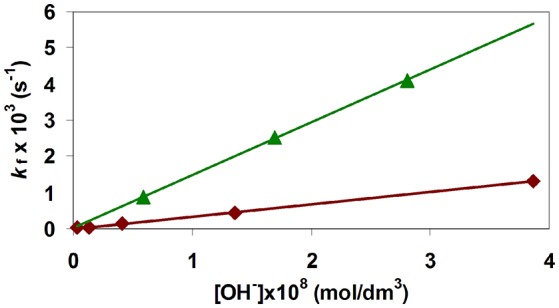
Formation rate constants (kf) for [ and [ as a function of [OH−].
Table 3.
Rate constants characterizing the formation (kOH) and dissociation (M(L)OHkOH, M(L)(OH)2kOH) of [Fe(TRAP)]3−, [Ga(TRAP)]3−, [Ga(NOTA)], and [Ln(NOTA)] complexes (25°C).
| Formation kinetics | Dissociation kinetics | |||||
|---|---|---|---|---|---|---|
| kOH /M−1s−1 | M(L)OHkOH/s−1 | M(L)(OH)2kOH/s−1 | logKM(L)(OH)2 | kd/s−1 at pH = 7.4 | t1/2/h at pH = 7.4 | |
| [Fe(TRAP)]3− | (3.37 ± 0.02) × 104 | (4 ± 1) × 10−7 | (5.2 ± 0.4) × 10−4 | 13.4 (1) | 1.8 × 10−9 | 1.1 × 105 |
| [Ga(TRAP)]3− | (1.47 ± 0.02) × 105 | (4.3 ± 0.5) × 10−7 | (3.8 ± 0.2) × 10−6 | 10.9 (1) | 1.4 × 10−9 | 1.4 × 105 |
| [Ga(NOTA)]a | 1.14 × 105 | – | – | – | – | – |
| [Ce(NOTA)]b | 6.3 × 107 | – | – | – | – | – |
| [Gd(NOTA)]b | 7.1 × 107 | – | – | – | – | – |
| [Er(NOTA)]b | 5.5 × 107 | – | – | – | – | – |
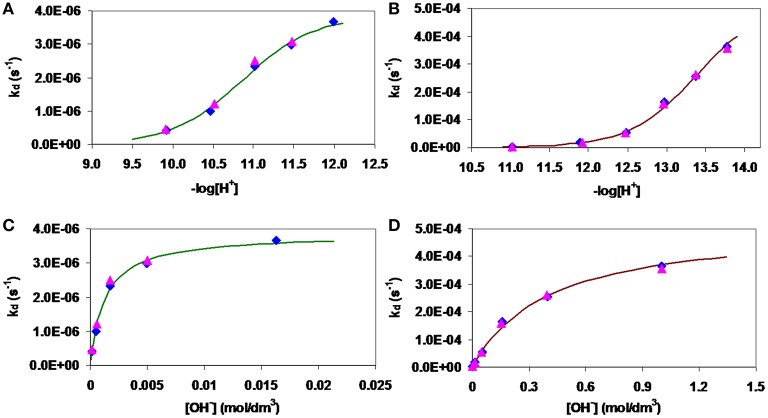
Comparison of the kOH rate constants presented in Table 3 shows that the formation rates of [Ga(TRAP)]3− and [Ga(NOTA)] complexes in this pathway are similar and about two orders of magnitude lower than those of [Ln(NOTA)] complexes. The results of the labeling experiments with the TRAP and NOTA chelates of 68GaIII at identical conditions (10 nM ligand, pH = 3.3 and 20 °C) shows that the formation rate of [68Ga(TRAP)]3− surpasses that of [68Ga(NOTA)] (Notni et al., 2010). The faster formation of [68Ga(TRAP)]3− can be explained by the higher stability [*KGa(HL)] and consequently the higher concentration of the kinetically active [*Ga(HTRAP)]2− intermediate that results in the more rapid formation of [68Ga(TRAP)]3− in the same labeling condition. On the other hand, the formation rate of [Fe(TRAP)]3− is about 3 times lower than that of Ga(TRAP), which allows to perform selective labeling of TRAP with 68GaIII even in presence of FeIII contaminations in the eluate.
Kinetic inertness and transchelation reaction of complexes
In order to compare the kinetic inertness, the rates of transchelation reactions of Fe(TRAP) and Ga(TRAP) complexes with HxHBEDx−4 (x = 0, 1 and 2) ligand were studied because of the high stability of the [Fe(HBED)]− and [Ga(HBED)]− complexes [logKFe(HBED) = 39.01, logKGa(HBED) = 38.51, 0.1 M KCl, 25°C, (Ma et al., 1994)]. The transchelation reactions were followed by spectrophotometry on the absorption band of the forming [Fe(HBED)]− and [Ga(HBED)]− complexes in the pH ranges 11.0–14.0 and 9.0–12.0, respectively. The absorption spectra of the protonated HHBED3− and H2HBED2− ligands and [Ga(HBED)]− complex are different, whereas that of the deprotonated HBED4− ligand and [Ga(HBED)]− complex are very similar. Therefore, the transchelation reactions of [Ga(TRAP)]3− with HHBED3− and H2HBED2− could be monitored by spectrophotometry only up to pH = 12.0 (HBED4−: log = 12.57(4), log = 11.41(3), log = 8.22(5), log = 4.73(6) and log = 1.45(6), 0.15 M NaCl, 25°C). Some characteristic absorption spectra of [Fe(TRAP)]3−-HxHBEDx−4 and [Ga(TRAP)]3−–HxHBEDx−4 (x = 0, 1 and 2) reacting systems are shown in Figures S11, S12, respectively. The transchelation reactions can be described by Equation (15)
| (15) |
wherein MIII is FeIII or GaIII, x = 0, 1 and 2 and y = 0 and 1. The rates of the transchelation reactions have been studied in the presence of 10- and 20-fold excess of HxHBED(x−4), so a pseudo-first order kinetic model can be applied and the rates of reaction Equation (15) can be expressed by Equation (16):
| (16) |
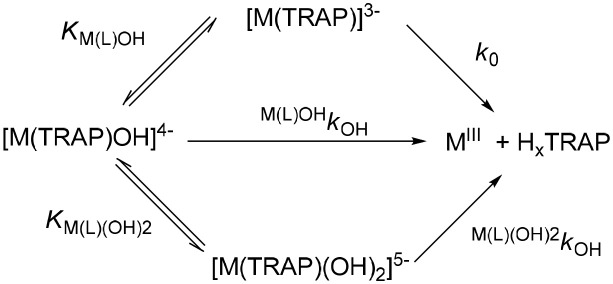
wherein kd is a pseudo-first-order rate constant, [M(TRAP)]t is the total concentration of [Fe(TRAP)]3− and [Ga(TRAP)]3− complexes. The pseudo-first-order rate constants (kd) characterizing the transchelation reactions of [Fe(TRAP)]3− and [Ga(TRAP)]3− with HxHBED(x−4) at different –log[H+] and [OH−] values are shown in Figure 6. The kinetic data presented in Figure 6 show that the kd values are independent of the concentration of HxHBED(x−4) and increase with –log[H+] and [OH−], indicating that the rate-determining step of the transchelation reactions is the dissociation of the [Fe(TRAP)]3− and [Ga(TRAP)]3− complexes, followed by fast reaction of free FeIII and GaIII with HxHBED(x−4). The kd values presented in Figure 6 show the similar behavior of [Fe(TRAP)]3− and [Ga(TRAP)]3− complexes in their transchelation reactions. The kd vs. –log[H+] and kd vs. [OH−] curves (Figure 6) obtained for [Ga(TRAP)]3− and [Fe(TRAP)]3− reach saturation of the kd values at [OH−] > 0.015 M and [OH−] > 1.0 M, respectively. Based on the species distribution of the GaIII-TRAP6− (Notni et al., 2010) and FeIII-TRAP6− (Figure 2) systems, the transchelation reaction of [Ga(TRAP)]3− and [Fe(TRAP)]3− with HxHBED(x−4) may occur by the spontaneous dissociation of [M(TRAP)]3− (k0) and [M(TRAP)OH]4− species (M(L)OHkOH), whereas the pH-independent dissociation rate (kd) of [M(TRAP)]3− under more basic conditions corresponds to formation [KM(L)(OH)2, Equation (17)] and slow dissociation of the bis(hydroxo) [M(TRAP)(OH)2]5− intermediate.
Figure 6.
Pseudo-first-order rate constants (kd) of the ligand exchange reactions of [] () and [] () wih HxHBED(x−4) as a function of –log[H+] and [OH−] (x = 0,1, and 2). Solid lines and symbols represent calculated and experimental kd pseudo-first-order rate constants, respectively. ([Ga(TRAP)] = [Fe(TRAP)] = 0.2 mM, [HxHBED] = 2.0 mM ( ), and 4.0 mM (
), and 4.0 mM ( ), 0.15 M NaCl, 25°C).
), 0.15 M NaCl, 25°C).
| (17) |
It can be assumed that in the [M(TRAP)(OH)2]5− intermediate, TRAP6− is coordinating via four donor atoms, whereas the remaining two coordination sites of GaIII and FeIII are occupied by two OH− ions. Hence, a spontaneous dissociation of the [M(TRAP)(OH)2]5− intermediates is more probable, which is reflected by the M(L)(OH)2kOH rate constants. The mechanisms of the transchelation reactions of [Fe(TRAP)]3− and [Ga(TRAP)]3− are summarized in Scheme 3.
Scheme 3.
Proposed mechanism of the dissociation of [Fe(TRAP)]3− and [Ga(TRAP)]3− complexes (x = 0 and 1).
By taking into account all possible pathways (Scheme 3), the dissociation rate of [Fe(TRAP)]3− and [Ga(TRAP)]3− can be expressed by Equation (18).
| (18) |
Considering the total concentrations of [Fe(TRAP)]3− and [Ga(TRAP)]3− ([ML]t = [ML]+[M(L)OH]+[M(L)(OH)2]) and the protonation constants of [M(L)OH]4− [KM(L)OH, Equation (6), Table 2) and [M(L)(OH)2]5− intermediates (KM(L)(OH)2, Equation (17)], the kd pseudo-first-order rate constants presented in Figure 6 can be expressed by Equation (19).
| (19) |
wherein k0, M(L)OHkOH and M(L)(OH)2kOH are the rate constants characterizing the spontaneous dissociation of [M(TRAP)]3−, and [M(TRAP)OH]4− complexes and [M(TRAP)(OH)2]5− intermediates, whereas KM(L)(OH)2 is the equilibrium constant characterizing the formation of the bis(hydroxo) [M(TRAP)(OH)2]5− intermediates.
The rate and protonation constants characterizing the transchelation reactions of [Fe(TRAP)]3− and [Ga(TRAP)]3− with HxHBED(x−4) have been calculated by fitting the kd values presented in Figure 6 to the Equation (19), and the resulting values are shown in Table 3. We obtained a very low value with a large error for k0; therefore, the spontaneous dissociation of [Fe(TRAP)]3− and [Ga(TRAP)]3− is negligible under our experimental conditions. The M(L)OHkOH rate constants characterizing the spontaneous dissociation of [Fe(TRAP)OH]4− and [Ga(TRAP)OH]4− complexes are very similar, which indicates that the kinetic inertness of [Fe(TRAP)OH]4− and [Ga(TRAP)OH]4− are comparable. Interestingly, the KM(L)(OH)2 protonation constants indicate that the formation of [Fe(TRAP)(OH)2]5− intermediate takes place at significantly higher –log[H+] values than that of [Ga(TRAP)(OH)2]5−. However, the M(L)(OH)2kOH rate constant of [Fe(TRAP)(OH)2]5− intermediate is about two orders of magnitude higher than that of [Ga(TRAP)(OH)2]5−, which indicates the considerably lower kinetic inertness of the [Fe(TRAP)(OH)2]5− intermediate.
In order to compare the kinetic inertness directly, the half-lifes (t1/2 = ln2/kd) of the dissociation reactions of [Fe(TRAP)]3− and [Ga(TRAP)]3− at pH = 7.4 have been calculated, utilizing the rate and equilibrium constants presented in Table 3. The t1/2 values of Fe(TRAP) and Ga(TRAP) are 1.1 × 105, and 1.4 × 105 h, respectively, which indicates a similar kinetic inertness of [Fe(TRAP)]3− and [Ga(TRAP)]3− due to comparable M(L)OHkOH rate constants of the [Fe(TRAP)OH]4− and [Ga(TRAP)OH]4− complexes. On the other hand, reliability of our kinetic data is supported by a good agreement of the dissociation half-life for [Ga(TRAP)]3− at pH = 11 determined in this study (t1/2 = 86 h) with the literature value of t1/2 ≈ 60 h (Notni et al., 2010).
Conclusion
Due to the availability of 68Ge/68Ga generators, recent years have seen an ever-growing interest in the radionuclide 68GaIII for PET examinations. The corresponding radiopharmaceuticals generally contain 68GaIII in form of chelates, for which purpose dedicated bifunctional chelators are usually conjugated to biological targeting vectors. The carrier-free 68GaIII obtained by acidic elution from the generator may contain some metal ions as impurities in trace amounts. These metal ions, like TiIV, FeIII, CuII, and ZnII, may compete with the 68GaIII for the chelator's binding sites. Hence, knowledge of the possible interactions of these ions and GaIII with chelates are highly important.
In this work, the interaction of GaIIII and FeIII ions with H6TRAP, a phosphinic acid analog of H3NOTA, were studied and compared. The stability constants of the [Ga(TRAP)]3− and [Fe(TRAP)]3− complexes were found to be very similar, as are their very low dissociation rates at physiological pH. The dissociation predominantly occurs via spontaneous dissociation of mono-hydroxo [M(TRAP)OH]4− complexes and bis(hydroxo) [M(TRAP)(OH)2]5− intermediates. Similarly to the respective NOTA complexes, formation of Ga(TRAP) and Fe(TRAP) is slow and occurs by formation of the monoprotonated [*M(HTRAP)]2− intermediates. The stability of these intermediates is very high, presumably because both the phosphinate and carboxylate groups of the ligand are coordinated. However, although we observed an extraordinary similarity of the thermodynamic and kinetic properties of the Ga(TRAP) and Fe(TRAP) complexes, there is a small but important difference between the two systems: the formation rate of Ga(TRAP) is approximately three times higher than that of the Fe(TRAP), which has implications for the influence of FeIII contaminations on 68Ga labeling of TRAP.
Apparently, the previously observed selectivity of TRAP for 68GaIII over FeIII is rooted in a totally different mechanism than the preference of TRAP for GaIII over CuII and ZnII (Simecek et al., 2013). Because Fe(TRAP) is formed more slowly than Ga(TRAP), formation of 68Ga(TRAP) is preferred and even a 3-fold excess of FeIII over TRAP does not substantially reduce the labeling yield. However, Fe(TRAP) is kinetically inert, and a higher excess of FeIII ultimately inhibits the 68GaIII incorporation due to an irreversible consumption of all available TRAP. On the other hand, the TRAP complexes of ZnII and CuII are formed much faster but they are not inert (Baranyai et al., 2015). Unlike FeIII, TRAP-bound CuII and particularly ZnII may therefore be readily displaced by GaIII (Simecek et al., 2013), driven by a much higher thermodynamic stability of [Ga(TRAP)]3− as compared to [Zn(TRAP)]4− and [Cu(TRAP)]4− (logKML of 26.24, 16.07, and 19.09, respectively) (Notni et al., 2010; Baranyai et al., 2015). Hence, in contrast to FeIII, even high concentrations of CuII and particularly that of ZnII do not completely inhibit 68Ga labeling of TRAP, likewise resulting in a pronounced tolerance of these potential contaminants. We conclude that even a phenomenon of elementary character, namely, the selectivity of TRAP for GaIII which manifests itself in a tolerance of remarkably high concentrations of different metal ion impurities during 68GaIII labeling, may rely on a variety of driving forces and molecular properties, thus requiring a detailed investigation of mechanistic details for thorough understanding.
Author contributions
AV and AF contributed to the equilibrium and kinetic characterizations; AW performed the ligand synthesis; EB, IT, AM, H-JW, JN, and ZB contributed to the evaluation of the physico-chemical parameters and to the manuscript preparation.
Conflict of interest statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest. The reviewer, FG, and handling Editor declared their shared affiliation.
Acknowledgments
Support by the Deutsche Forschungsgemeinschaft (grant #NO822/4-1 and SFB 824, project A10), the EU and the European Regional Development Fund (projects GINOP-2.3.2-15-2016-00008 and GINOP-2.3.3-15-2016-00004) are gratefully acknowledged. The project has been carried out in the frame of the EU COST Action CA15209: European Network on NMR Relaxometry.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/fchem.2018.00170/full#supplementary-material
References
- Baes C. F., Mesmer R. E. (1976). The Hydrolysis of Cations. New York, NY; London; Sydney; Toronto, ON: John Wiley & Son. [Google Scholar]
- Baranyai Z., Reich D., Vagner A., Weineisen M., Toth I., Wester H. J., et al. (2015). A shortcut to high-affinity Ga-68 and Cu-64 radiopharmaceuticals: one-pot click chemistry trimerisation on the TRAP platform. Dalton Trans. 44, 11137–11146. 10.1039/C5DT00576K [DOI] [PubMed] [Google Scholar]
- Bevilacqua A., Gelb R. I., Hebard W. B., Zompa L. J. (1987). Equilibrium and thermodynamic study of the aqueous complexation of 1,4,7-triazacyclononane-N,N',N”-triacetic acid with protons, alkaline-earth-metal cations, and copper(II). Inorg. Chem. 26, 2699–2706. 10.1021/ic00263a029 [DOI] [Google Scholar]
- Beyer T., Townsend D. W., Brun T., Kinahan P. E., Charron M., Roddy R., et al. (2000). A combined PET/CT scanner for clinical oncology. J. Nucl. Med. 41, 1369–1379. [PubMed] [Google Scholar]
- Brucher E., Sherry A. D. (1990). Kinetics of formation and dissociation of the 1,4,7-triazacyclononane-N,N',N"-triacetate complexes of cerium(III), gadolinium(III), and erbium(III) ions. Inorg. Chem. 29, 1555–1559. 10.1021/ic00333a022 [DOI] [Google Scholar]
- Clarke E. T., Martell A. E. (1991). Stabilities of the Fe(III), Ga(III) and In(III) chelates of N,N′,N″-triazacyclononanetriacetic acid. Inorg. Chim. Acta 181, 273–280. 10.1016/S0020-1693(00)86821-8 [DOI] [Google Scholar]
- Drahos B., Kubicek V., Bonnet C. S., Hermann P., Lukes I., Toth E. (2011). Dissociation kinetics of Mn2+ complexes of NOTA and DOTA. Dalton Trans. 40, 1945–1951 10.1039/c0dt01328e [DOI] [PubMed] [Google Scholar]
- Farkas E., Kozma E., Petho M., Herlihy K. M., Micera G. (1998). Equilibrium studies on copper(II)- and iron(III)-monohydroxamates. Polyhedron 17, 3331–3342. 10.1016/S0277-5387(98)00113-2 [DOI] [Google Scholar]
- Frank R., Patrick J. R. (2010). The renaissance of the 68Ge/68Ga radionuclide generator initiates new developments in 68Ga radiopharmaceutical chemistry. Curr. Top. Med. Chem. 10, 1633–1668. 10.2174/156802610793176738 [DOI] [PubMed] [Google Scholar]
- Geraldes C. F. G. C., Sherry A. D., Marques M. P. M., Alpoim M. C., Cortes S. (1991). Protonation scheme for some triaza macrocycles studied by potentiometry and NMR spectroscopy. J. Chem. Soc. Perkin Trans. 2, 137–146. 10.1039/p29910000137 [DOI] [Google Scholar]
- Irving H. M., Miles M. G., Pettit L. D. (1967). A study of some problems in determining the stoicheiometric proton dissociation constants of complexes by potentiometric titrations using a glass electrode. Anal. Chim. Acta 38, 475–488. 10.1016/S0003-2670(01)80616-4 [DOI] [Google Scholar]
- Levi H. (1976). George von Hevesy memorial lecture. George Hevesy and his concept of radioactive indicators in retrospect. Eur. J. Nucl. Med. 1, 3–10. 10.1007/BF00253259 [DOI] [PubMed] [Google Scholar]
- Ma R., Motekaitis R. J., Martell A. E. (1994). Stability of metal ion complexes of N,N′-bis(2-hydroxybenzyl)ethylenediamine-N,N′-diacetic acid. Inorg. Chim. Acta 224, 151–155. 10.1016/0020-1693(94)04012-5 [DOI] [Google Scholar]
- Mariko T., Susumu T. (1977). The preparation of trivalent metal chelates with some N3O3-type ligands. Bull. Chem. Soc. Jpn. 50, 3413–3414. 10.1246/bcsj.50.3413 [DOI] [Google Scholar]
- Morfin J. F., Toth E. (2011). Kinetics of Ga(NOTA) formation from weak Ga-citrate complexes. Inorg. Chem. 50, 10371–10378. 10.1021/ic201445e [DOI] [PubMed] [Google Scholar]
- Notni J. (2012). With Gallium-68 into a New Era? Nachr. Chem. 60, 645–649. 10.1515/nachrchem.2012.60.6.645 [DOI] [Google Scholar]
- Notni J., Hermann P., Havlickova J., Kotek J., Kubicek V., Plutnar J., et al. (2010). A triazacyclononane-based bifunctional phosphinate ligand for the preparation of multimeric 68Ga tracers for positron emission tomography. Chem. Eur. J. 16, 7174–7185. 10.1002/chem.200903281 [DOI] [PubMed] [Google Scholar]
- Notni J., Simecek J., Hermann P., Wester H. J. (2011). TRAP, a powerful and versatile framework for gallium-68 radiopharmaceuticals. Chem. Eur. J. 17, 14718–14722. 10.1002/chem.201103503 [DOI] [PubMed] [Google Scholar]
- Notni J., Simecek J., Wester H. J. (2014). Phosphinic acid functionalized polyazacycloalkane chelators for radiodiagnostics and radiotherapeutics: unique characteristics and applications. ChemMedChem. 9, 1107–1115. 10.1002/cmdc.201400055 [DOI] [PubMed] [Google Scholar]
- Notni J., Wester H.-J. (2018). Re-thinking the role of radiometal isotopes: towards a future concept for theranostic radiopharmaceuticals. J. Label. Compd. Radiopharm. 61, 141–153. 10.1002/jlcr.3582 [DOI] [PubMed] [Google Scholar]
- Rösch F. (2013). Past, present and future of 68Ge/68Ga generators. Appl. Rad. Isot. 76, 24–30 10.1007/978-3-642-27994-2_1 [DOI] [PubMed] [Google Scholar]
- Simecek J., Hermann P., Wester H. J., Notni J. (2013). How is 68Ga labeling of macrocyclic chelators influenced by metal ion contaminants in 68Ge/68Ga generator eluates? ChemMedChem. 8, 95–103. 10.1002/cmdc.201200471 [DOI] [PubMed] [Google Scholar]
- Simecek J., Schulz M., Notni J., Plutnar J., Kubicek V., Havlickova J., et al. (2012). Complexation of metal ions with TRAP (1,4,7-triazacyclononane phosphinic acid) ligands and 1,4,7-triazacyclononane-1,4,7-triacetic acid: phosphinate-containing ligands as unique chelators for trivalent gallium. Inorg. Chem. 51, 577–590. 10.1021/ic202103v [DOI] [PubMed] [Google Scholar]
- Simecek J., Zemek O., Hermann P., Notni J., Wester H. J. (2014). Tailored Gallium(III) chelator NOPO: synthesis, characterization, bioconjugation, and application in preclinical Ga-68-PET imaging. Mol. Pharm. 11, 3893–3903. 10.1021/mp400642s [DOI] [PubMed] [Google Scholar]
- Velikyan I. (2011). Positron emitting [68Ga]Ga-based imaging agents: chemistry and diversity. Med. Chem. 7, 345–379. 10.2174/157340611796799195 [DOI] [PubMed] [Google Scholar]
- Wadas T. J., Wong E. H., Weisman G. R., Anderson C. J. (2010). Coordinating radiometals of copper, gallium, indium, yttrium, and zirconium for PET and SPECT imaging of disease. Chem. Rev. 110, 2858–2902. 10.1021/cr900325h [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zekany L., Nagypal I. (1985). PSEQUAD, in Computational Methods for the Determination of Formation Constants, ed Leggett D. (Springer; ), 291–353. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.