Modeling quantum nuclei with perturbed path integral molecular dynamics

Here we combine perturbation theory with the Feynman–Kac imaginary-time path integral approach to quantum mechanics for modeling quantum nuclear effects.

Abstract

The quantum nature of nuclear motions plays a vital role in the structure, stability, and thermodynamics of molecules and materials. The standard approach to model nuclear quantum fluctuations in chemical and biological systems is to use path-integral molecular dynamics. Unfortunately, conventional path-integral simulations can have an exceedingly large computational cost due to the need to employ an excessive number of coupled classical subsystems (beads) for quantitative accuracy. Here, we combine perturbation theory with the Feynman–Kac imaginary-time path integral approach to quantum mechanics and derive an improved non-empirical partition function and estimators to calculate converged quantum observables. Our perturbed path-integral (PPI) method requires the same ingredients as the conventional approach, but increases the accuracy and efficiency of path integral simulations by an order of magnitude. Results are presented for the thermodynamics of fundamental model systems, an empirical water model containing 256 water molecules within periodic boundary conditions, and ab initio simulations of nitrogen and benzene molecules. For all of these examples, PPI simulations with 4 to 8 classical beads recover the nuclear quantum contribution to the total energy and heat capacity at room temperature within a 3% accuracy, paving the way toward seamless modeling of nuclear quantum effects in realistic molecules and materials.

1. Introduction

The reliability, efficiency, and predictive capabilities of electronic structure calculations for molecules and materials have been steadily improving over the past decade,1,2 in particular with the development of methods for the increasingly accurate description of non-covalent interactions in the context of density-functional approximations (DFA).3,4 State-of-the-art methods that treat the quantum-mechanical many-body nature of non-covalent interactions and tackle the self-interaction errors of DFA are nowadays able to yield predictions within the so-called “chemical accuracy” of 1 kcal mol^–1 for the binding energies of small molecules, supramolecular systems, as well as for the stability and polymorphism of molecular crystals.5 Such a level of accuracy is essential for predictive first-principles modeling for applications in pharmaceuticals, electronics, molecular sensing, and catalysis.6,7 However, at this level of accuracy of electronic structure calculations, another serious issue arises, namely the need to accurately account for the quantum nature of nuclear motions, which play a vital role in the structure, stability, and thermodynamic properties of molecular and condensed-matter systems.

The standard approach used to take nuclear quantum fluctuations (NQF) into account is the Feynman–Kac imaginary-time path integrals (PI) approach.8,9 This method maps a quantum system into P copies of classical subsystems (“beads”) interacting with each other via harmonic springs.10 The incorporation of PI molecular dynamics (MD) techniques into ab initio calculations offers a straightforward way to study NQF in different chemical and physical systems.11–27 Unfortunately, conventional PIMD simulations require an exceedingly large number of beads (P ≫ ℏω/k_BT) to accurately capture NQF, resulting in a considerable computational cost, even at room temperature, due to the rather high internal vibrational frequencies ω of many systems of interest.

The need for large P stems from the second-order expansion of the Boltzmann exp(–β(K + V)) operator utilized in conventional PIMD simulations, where β is the inverse temperature, and K and V are the kinetic and potential energy operators, respectively. While for P → ∞ convergence to full quantum statistics is guaranteed, this is not the case for the reasonable finite P. In this case, the properties obtained in conventional PI simulations are often far from the correct quantum result and effectively correspond to a semi-classical regime. More sophisticated and promising approaches have been developed.11,15,22,28–32 However, most of the higher-order approaches are inapplicable for molecular dynamics simulations. On the other hand, reweighting techniques and colored-noise thermostats either require extensive parameterization or compromise between accuracy and sampling of the phase space, which limits their applicability to realistic molecules and materials. Hence, the development of an accurate and efficient parameter-free method for NQF of realistic molecular systems at a finite temperature would be highly desirable.

In this article, we propose to combine quantum-mechanical perturbation theory with Feynman–Kac imaginary-time path integrals to calculate converged thermodynamic averages from semi-classical (small P) PI simulations. Our method requires the same ingredients as conventional PI simulations, but decreases the required number of classical beads by roughly an order of magnitude. A considerable advantage of the developed approach is that it can be incorporated with any kind of thermostat or barostat, as well as any phase-space sampling technique. The proposed method has been applied to study the thermodynamics of a quantum harmonic oscillator and double-well potential, as well as a q-TIP4P/F water model containing 256 water molecules within periodic boundary conditions and ab initio PIMD simulations for N₂ and C₆H₆ molecules at room temperature. This selected set of applications demonstrates the broad applicability of our developments to realistic molecules and materials described by complex interaction potentials. For all the studied systems, P = 4 to 8 is enough to recover the NQF contribution to the total energy and heat capacity within 3% of the fully converged quantum result within the developed approach.

2. Methods

We start by noting that the free energy of an arbitrary quantum system can be written as an expansion in powers of the reduced Planck's constant ℏ:33,34

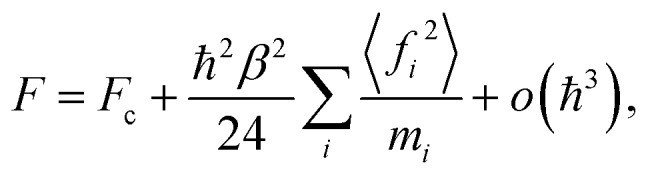1

where F_c is the classical free energy, m_i is a particle mass, f_i is the i-th force component, β = 1/k_BT is the inverse temperature, and … means thermodynamic averaging. The index i runs over all degrees of freedom in the system. The first non-vanishing non-classical term in eqn (1) is the Wigner correction35,36 which is proportional to ℏ² and does not depend upon the statistics of particles being equally applicable to both bosonic and fermionic systems. It is also proportional to f_i², which means that in strongly interacting systems the NQF can be important even at relatively high temperatures. In fact, for many real molecules the interatomic forces are rather strong. Thus, employing only the quasi-classical term in eqn (1) without accounting for the higher-order o(ℏ³) terms, which are unknown in the general case, usually leads to an overestimation of the free energy and, as a result, to wrong thermodynamic averages obtained from it.

The situation can be greatly improved by the generalization of eqn (1) to the case of the imaginary-time path integral approach. The auxiliary system which is constructed in the PI method has a temperature P times larger than the equilibrium temperature, where P is the number of beads. In the limit P → ∞ the quantum effects are fully recovered, while at finite P they are only partially captured. The contribution from the o(ℏ³) terms decreases as P grows, so an expression akin to that in eqn (1) should become increasingly more accurate. This allows us to treat the PI auxiliary system as a semi-classical one and use an analogue of eqn (1) to calculate its free energy, partition function and, as a result, all the thermodynamic averages.

To explain our proposal, we consider a quantum system consisting of a single particle in an external potential U. The PI partition function can be written as:

Z_PI = A∫dq₁…dq_P e^{–βU_eff({q_s})}, 2

where A is a normalization constant and U_eff is the effective potential,

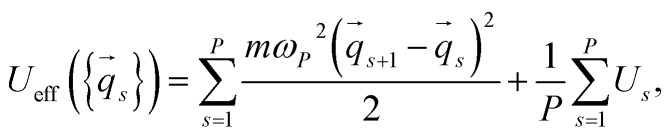3

where ω_P² = P/β² is the chain frequency, and q_s and U_s are the particle coordinate vector and the potential energy for the beads, respectively.

As follows from eqn (1) and (3), the quantum correction to the partition function can be written in the form:

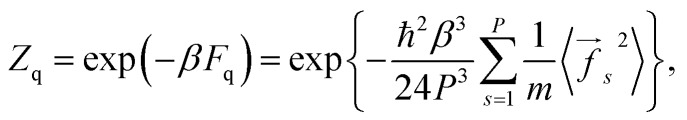4

where the averaged square forces f_s² are those of the conventional PI approach.

The multiplier P^–3 in eqn (4) appears due to the fact that the PI effective temperature is PT. The force f in eqn (4) is the same as in eqn (1). It does not include the coupling term arising from U_eff. Indeed, such a term gives non-zero coupling forces, even for non-interacting particles. Thus, its inclusion in f in eqn (4) would lead to a wrong non-zero free energy correction for a non-interacting system as well as a wrong translational motion of the center of mass of a multi-particle system in a zero external field.

As a result, the final expression for the perturbed path-integral (PPI) partition function is:

Z_PPI = Z_qZ_PI. 5

We remark in passing‡ that the same expression (5) for the partition function can be derived as a first-order cumulant expansion of the Takahashi and Imada (TI) scheme28 (see ESI†). This fact, however, does not answer the question of which partition function, TI or PPI, is more accurate at the finite number of beads and finite temperature relevant for the modeling of molecular systems. Our derivation, starting from the textbook eqn (1), unifies quantum-mechanical perturbation theory with the PI methodology in a transparent physical framework. As our applications will show, the developed PPI approach is more accurate and more efficient than PI simulations based on the TI scheme. Moreover, using the second-order cumulant expansion of the TI partition function reduces the accuracy when compared to the proposed PPI approach (see ESI†), clearly demonstrating the fundamental difference between the developed approach and the trivial cumulant expansion of the TI scheme.

From eqn (5) one can derive estimators for any thermodynamic quantity which can be computed using conventional PI trajectories, either during or a posteriori PI simulations. For the total energy E one obtains:

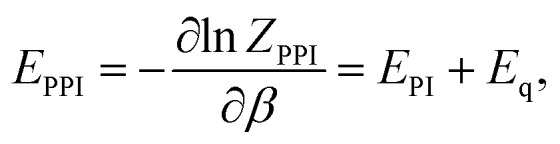6

where

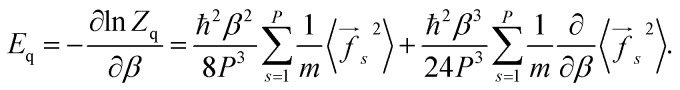7

The derivative of the average square force with respect to the inverse temperature can be found using eqn (2):

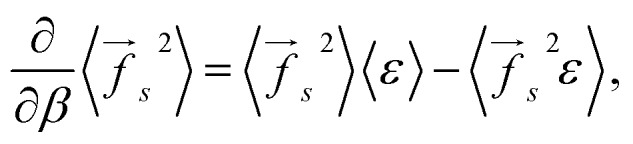8

where ε is the standard primitive energy estimator:

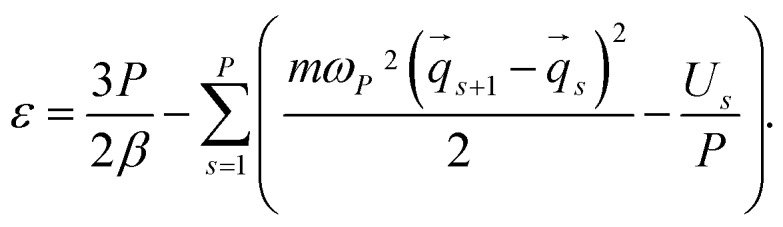9

Eqn (7) and (8) give the following expression for the total energy correction:

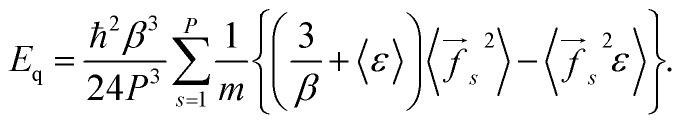10

The expression for the heat capacity C_q can be obtained as a temperature derivative of E_q (see ESI†).

In the general case, for an arbitrary function of coordinates λ(q), one can derive the improved estimator by using the following procedure. First, the potential energy is rewritten as U_i → U_i + αλ(q). Then the thermodynamic average for λ is:

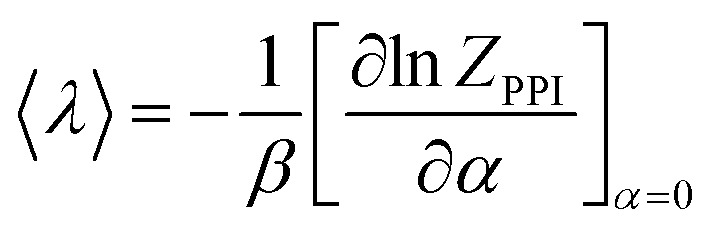11

Following the scheme for the derivation of the total energy, one obtains:

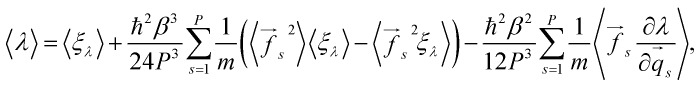12

where ξ_λ is the standard primitive estimator for λ in the conventional PI approach:

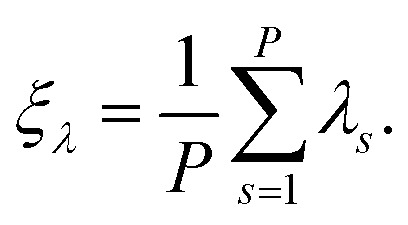13

The generalization to the case of the multi-particle system is trivial and requires a summation over all particles in the system.

In eqn (12), a potential difficulty could lie in obtaining the derivative ∂λ/∂q_s, contained in the last term. For some properties of interest, this derivative could be directly inaccessible, and might require approximations. In this work we concentrate our attention on the total energy and heat capacity, which require only information about particle coordinates, forces, and potential energies. Structural estimators, such as radial distribution functions, can also be derived in a tedious, but straightforward manner and will be published elsewhere.

3. Results and discussion

To demonstrate the performance of the developed method for both harmonic and anharmonic systems, we carried out PIMD simulations for a one dimensional (1D) quantum harmonic oscillator (QHO) and double-well potential (DWP):

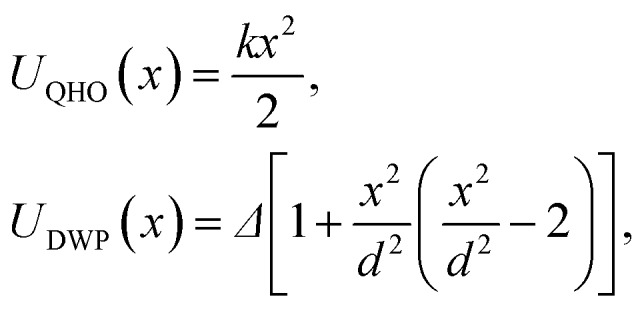14

where k is the stiffness of the QHO, Δ is the barrier height and 2d is the distance between the two minima in the DWP. At small and moderate Δ/T ratios, the DWP potential is strongly anharmonic, thus the combination of these two model systems represents two limiting cases of interest for real applications.

To avoid numerical errors due to the finiteness of the time step in PIMD simulations, we choose a value of the time step that gives 200 points per period of classical oscillation within the interaction potential. We use the following set of units and parameters for the QHO and DWP: ℏ = 1, k_B = 1, and m = 1.

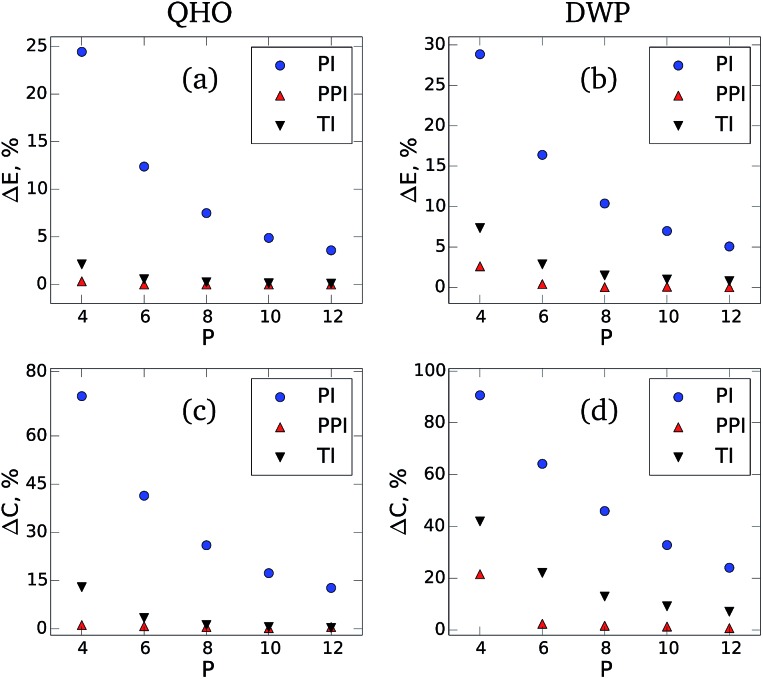
Fig. 1 shows the difference between the NQF contribution to the total energy [(a) and (b)] and the constant volume heat capacity [(c) and (d)] obtained for QHO and DWP from our method, conventional PIMD estimators, and TI simulations.28 The results are shown as a function of the number of beads with respect to the converged values. When using the developed estimators, both the total energy and heat capacity converge with a factor of eight fewer beads compared to the standard PIMD approach. The developed method also demonstrates noticeably faster convergence when compared to the high-order TI scheme.

Fig. 1. The relative error in the NQF contribution to the total energy [(a) and (b)] and constant volume heat capacity [(c) and (d)] of a 1D quantum harmonic oscillator (QHO) and double-well potential (DWP) at fixed temperature. The results are shown as a function of the number of beads with respect to the converged values. The blue circles are the results of the conventional PIMD approach (PI), the red triangles pointing up correspond to the developed method (PPI), and the black triangles pointing down are the results of the Takahashi and Imada (TI)28 Monte Carlo simulations. For both PI and PPI calculations we use the same PIMD trajectories. The parameters of the simulations are: k = 1 and T = 0.2 for QHO, and Δ = 1, d = 0.5, and T = 1.2 for DWP.

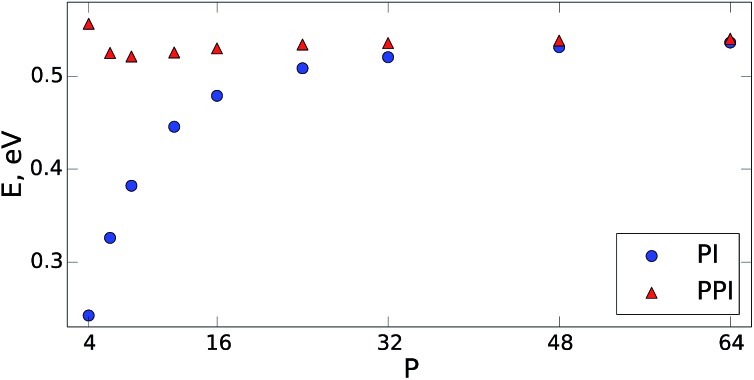
The PPI approach is equally applicable to arbitrarily large anharmonic systems described by complex intermolecular potentials. To demonstrate this, we carried out PIMD simulations for the q-TIP4P/F water model (which includes intermolecular Coulomb and Lennard-Jones terms)37 containing 256 water molecules in a periodic box at room temperature (300 K). We used the openMM code38 with a simulation time step of 0.5 femtoseconds. The performance of both methods for the NQF contribution to the total energy is shown in Fig. 2. The PPI approach recovers the correct quantum result, within a few percent, for P ≥ 6. For instance, for P = 6, the PI simulation underestimates the NQF contribution to the total energy by 29% while the developed approach gives less than 3% error. As demonstrated in Fig. 2, within the PPI method we require that the conventional PI simulations capture 60–70% of the NQF. For only a few beads (P < 4), the PPI approach would overestimate the energy, as expected for a quasi-classical formula. This is not a problem in practice, since large PPI contributions would simply indicate the need to increase P.

Fig. 2. The NQF contribution to the total energy (per molecule) of a q-TIP4P/F water model37 containing 256 water molecules within a periodic box. The results are shown as a function of the number of beads at 300 K. The blue circles are the results of the conventional PIMD approach (PI) and the red triangles show the performance of the developed method (PPI). For both PI and PPI calculations we use the same MD trajectories.

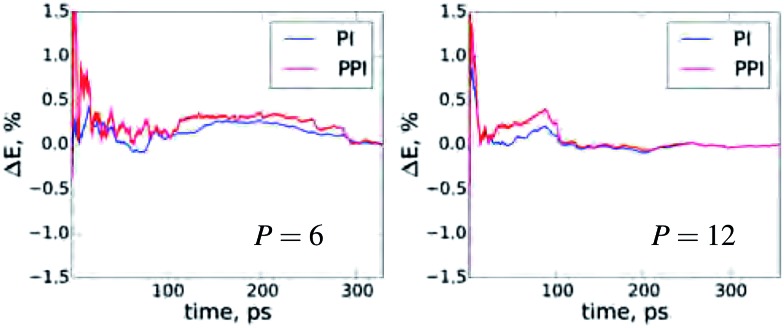
A very important aspect for PIMD simulations is the statistical convergence of the thermodynamic averages. Fig. 3 demonstrates the convergence of the NQF contribution to the total energy of the q-TIP4P/F water model, within the developed method, compared to the conventional PIMD for six and twelve beads. To have the same scale, we plot the difference between the results for the total energy as a function of the simulation time and the corresponding converged result for both methods. Obviously, the main issue with an increase in P is the convergence of the conventional virial total energy estimator. As follows from Fig. 2 and 3, for the values of P required for an accurate account of NQF, the statistical convergence of the developed method does not differ much from that of the standard PIMD simulations. We remark that throughout this work a simple white noise thermostat was employed to compare between methods. The use of more sophisticated thermostats is possible, and this would yield faster statistical convergence for both PPI and PI simulations.

Fig. 3. The deviation of the NQF contribution to total energy of the q-TIP4P/F water box containing 256 water molecules from the converged results as a function of the simulation time for P = 6 and 12. For details see Fig. 2.

Finally, we carried out ab initio PIMD simulations for N₂ and C₆H₆ molecules at room temperature. These were done using the i-PI code39 coupled with the FHI-aims40 code for DFT calculations with the PBE functional.41 The calculations were done for P = 4 and 8 using a time step of 0.2 femtoseconds. The results of the simulations are presented in Table 1.

Table 1. The NQF contribution to the total energy for N₂ and C₆H₆ molecules at room temperature in the conventional approach (PI), the developed method (PPI), and quantum harmonic approximation (QHA). The accuracy of the simulations is approximately 0.5 meV per atom.

P	N2 (in meV)		C6H6 (in meV)
	PI	PPI	PI	PPI
4	59.4	124.6	1081.8	2019.5
8	94.7	121.5	1549.8	1936.6
QHA	120.0		1933.9

Clearly, within the developed approach even for P = 4 one obtains results in a good agreement with the quantum harmonic approximation (QHA), while the conventional PIMD underestimates the NQF contribution by approximately 50%. For the molecules studied herein, the rather high internal vibrational frequencies make QHA a good reference for NQF at room temperature. For larger molecules with many anharmonic degrees of freedom, it is evident that the PPI approach will be significantly more accurate than QHA, and more efficient than conventional PI methods.

4. Conclusions

In summary, the developed parameter-free PPI approach to model nuclear quantum fluctuations considerably improves the efficiency of the path integral simulations. Using conventional PIMD trajectories, we are able to decrease the number of required beads by roughly an order of magnitude. The proposed method is not a re-weighting scheme and thus it does not suffer from the statistical convergence problem for large systems. It can also be systematically improved, either by employing higher-order corrections to the PI partition function or by using a high-order PI partition function as a starting point or both. The efficiency and accuracy of the PPI method can extend the applicability of PIMD simulations to study nuclear quantum fluctuations in increasingly realistic molecules and materials.