Gas Phase Kinetics of the OH+CH₃CH₂OH Reaction at Temperatures of the Interstellar Medium (T = 21-107 K)

Abstract

Ethanol, CH₃CH₂OH, has been unveiled in the interstellar medium (ISM) by radioastronomy and it is thought to be released into the gas phase after the warm-up phase of the grain surface, where it is formed. Once in the gas phase, it can be destroyed by different reactions with atomic and radical species, such as hydroxyl (OH) radicals. The knowledge of these rate coefficients at temperatures of the ISM is essential in the accurate interpretation of the observed abundances. In this work, we have determined the rate coefficient for the reaction of OH with CH₃CH₂OH (k(T)) between 21 and 107 K by employing the pulsed and continuous CRESU (Cinétique de Réaction en Ecoulement Supersonique Uniforme, which means Reaction Kinetics in a Uniform Supersonic Flow) technique. The pulsed laser photolysis technique was used for generating OH radicals, whose time evolution was monitored by laser induced fluorescence. An increase of approximately 4 times was observed for k(21 K) with respect to k(107 K). With respect to k(300 K), the OH-reactivity at 21 K is enhanced by two orders of magnitude. The obtained T-expression in the investigated temperature range is k(T)=(2.1±0.5)×10^-11(T/300 K)^{-(0.71±0.10)} cm³ molecule^-1 s^-1. In addition, the pressure dependence of k(T) has been investigated at several temperatures between 21 K and 90 K. No pressure dependence of k(T) was observed in the investigated ranges. This may imply that this reaction is purely bimolecular or that the high-pressure limit is reached at the lowest total pressure experimentally accessible in our system. From our results, k(T) at usual IS temperatures (~10-100 K) is confirmed to be very fast. Typical rate coefficients can be considered to range within about 4×10^-11 cm³ molecule^-1 s^-1 at 100 K and around 1×10^-10 cm³ molecule^-1 s^-1 at 20 K. The extrapolation of k at the lowest temperatures of the dense molecular clouds of ISM is also discussed in this paper.

1. Introduction

Ethanol (CH₃CH₂OH) is ubiquitous in the interstellar medium (ISM). This complex organic molecule (COM) has been detected in different objects of the ISM since 1975, when it was first detected by Zuckerman et al. in Sagittarius B2 (Sgr B2).¹ A summary of the observed total column densities of ethanol (N_CH3CH2OH) and its fractional abundances relative to H₂ in some IS objects is presented in Table 1.^1–14 As it can be seen, these abundances are very variable, even within the same source. The great variety of ethanol abundances implies that the chemistry of ethanol is greatly dependent on the source and its environment. In order to model and interpret the observed relative abundances of this COM, all depleting and formation processes must be considered in both grains and the gas phase. In the latter, one of the mechanisms that can deplete ethanol is the reaction with hydroxyl (OH) radicals (a major neutral radical observed in the ISM):

$${\text{OH}+\text{CH}}_{\text{3}}{\text{CH}}_{\text{2}}\text{OH}\to \text{Products}$$ (R1)

Table 1.

Observed column densities of CH₃CH₂OH (N_CH3CH2OH) and relative abundances (to H₂) in different astrophysical sources.

Source	NCH3CH2OH/cm-2	NCH3CH2OH/NH2	Reference
Sagittarius B2 (Sgr B2)	1015	10-9	[1]
	(0.8–4)×1017	(0.8–4)×10-7	[2]
Sagittarius A (Sgr A)	4.0×1015	4.0×10-8	[3]
W15M	1015	10-8	[4]
Orion KL	3.6×1016	3.6×10-7	[5]
G34.3+0.2	(2.5–8.8)×1015	(36-4.4)×10-9	[6]
G31.41+0.31	1.0×1018	8.4×10-9	[7]
Galactic center clouds	(0.068–12.7)×1014	6×10-8	[8]
Protostellar outflow L1157	1014	7×10-8	[9]
Serpens core (SMM1, SMM4, and SMM4-W)	(6–8)×1012	(6.4–3.6)×10-3 *	[10]
NGC 7129 FIRS 2 protostar	2.2×1016	1.10×10-8	[11]
NGC1333	5.1×1016		[12]
	4.4×1016
Bok globule B335	2.1×1015	3.8×10-9	[13]
C/2002 T7 comet	<1.9×1013		[14]

^*relative to methanol

The overall rate coefficient for reaction (R1), k(T), has been experimentally measured as a function of temperature (54-1297 K), although most of the studies were focused on temperatures of atmospheric and combustion interest.^15–22 At the ultra-cold temperatures of ISM (~10-100 K), k(T) values have to be provided for including them in astrochemical models, especially at temperatures close to 10 K. Caravan et al.²³ determined k(T) at temperatures between 54 K and 148 K. A significant increase of k(T) with respect to that at room temperature was observed, similar to former OH-reactions with other organic compounds investigated in our group^24–26 and by others.^23,27–29 As astrochemical models need the rate coefficients of reaction (R1) as close as 10 K to interpret the observed abundances of ethanol in IS dark molecular clouds, it is mandatory to explore the kinetics at lower temperatures than 54 K, which will also allow the verification of the observed reactivity trend down to temperatures of ~ 10 K.

In addition, Caravan et al.²³ reported that k(T) increases with total pressure (i.e. gas density, n) at temperatures higher than 80 K, while no dependence of k(T=54 K) with n was observed. These authors explained this pressure dependence of k(T) by the presence of a pre-reactive complex which can either stabilize by thermal collisions or dissociate into two products through H-abstraction quantum mechanical tunnelling.

Additional investigations on the temperature and pressure dependencies of k(T) are needed to provide a wider view of the chemical behaviour of this system in the ISM. Therefore, in this work, the rate coefficients k(T) have been determined between ca. 21 and 107 K using the pulsed and continuous CRESU (Cinétique de Réaction en Ecoulement Supersonique Uniforme, which means Reaction Kinetics in a Uniform Supersonic Flow) technique. The rate coefficients below 54 K are the first determinations of k(T) up to date. When possible, k(T) measurements were performed at different bath gas densities (n=(0.69-19.5)×10¹⁶ molecule cm^-3) for several fixed temperatures (ca. 21 K, 45 K, 50 K, 64 K, 69 K, 80 K and 90 K).

2. Experimental

The CRESU apparatus and all parts of the experimental system available in Ciudad Real were widely described elsewhere.^25,26,30,31 Therefore, only a brief is given below.

2.1. Operational conditions

In the CRESU technique, the ultra-low temperatures are achieved by the isentropic expansion of a gas mixture through a Laval nozzle from a high pressure reservoir (P_res) to a vacuum chamber (P_cham). In the present work, the method was mainly operated in pulsed mode, where the gas mixture is pulsed at 10 Hz by an aerodynamic chopper³¹ (rotary disk) placed in the divergent part of the nozzle. In some cases, it was also operated in the continuous mode by maintaining the disk open (see Table 2). The optimal working pressures P_cham and P_res for each Laval nozzle are summarized in Table 2. The temperature of the reservoir was kept constant in all experiments (T_res = 297±1 K). P_res was issued from the gas mixture formed by the OH-precursor (H₂O₂), the diluted ethanol, and the buffer gas (He, Ar, N₂ or a binary mixture He/N₂ or N₂/Ar), introduced into a 12 litres reservoir ended by the throat of the Laval nozzle. The resulting physical parameters (Mach number (M), hydrodynamic time (t_hydro), total gas density (n) and temperature in the jet (T)) are detailed in Table 2 for every flow condition optimised to generate a supersonic jet uniform in temperature and density for several tens of centimetres from the exit of the nozzle. This allows carrying out the kinetic experiments in a timescale of several hundreds of microseconds (see Table 2). The aerodynamical characterisation of the supersonic flow, issued from the expansion through the Laval nozzles used here, was previously described by Antiñolo et al.²⁴, Jiménez et al.^25,31 and Canosa et al.³⁰ The uniformity of T and n along the axis of the supersonic flow was verified by measuring the impact pressure with a Pitot tube as a function of the distance from the nozzle exit as described earlier.

Table 2.

Summary of the operating conditions employed in this work (buffer gas with their proportion in the mixture, pressure in the reservoir and in the chamber) and the resulting physical parameters (Mach number, hydrodynamic time, total gas density and temperature). The temperature of the reservoir was constant (T_res = 297±1 K). Uncertainties are ±1σ (standard deviation) and represent the fluctuations of physical parameters along the length of uniformity (i.e. hydrodynamic time) of the flow.

He%	% N2	% Ar	Pres/mbar	Pcham/mbar	M	thydro/µs	n / 1016 molecule cm-3	T/K
100			73.88	0.125	6.27 ± 0.10	165	3.37 ± 0.15	21.1 ± 0.6
100			147.76	0.280	6.05 ± 0.09	320	7.43 ± 0.32	22.5 ± 0.7
100			337.20	0.620	6.13 ± 0.21	238	16.65 ± 1.61	21.7 ± 1.4
100			173.32	1.100	4.65 ± 0.08	304	17.73 ± 0.86	36.2 ± 1.2
40*	60		127.05	0.296	5.02 ± 0.08	414	5.22 ± 0.33	42.6 ± 1.3
	100		31.17	0.050	5.26 ± 0.13	760	0.69 ± 0.08	45.5 ± 2.0
20	80		132.23	0.295	5.06 ± 0.08	560	4.23 ± 0.28	45.3 ± 1.3
	100		52.12	0.120	4.94 ± 0.10	768	1.50 ± 0.12	50.5 ± 1.4
	100*		136.24	0.279	4.88 ± 0.10	777	4.17 ± 0.35	51.6 ± 1.7
70	30		86.00	0.650	4.23 ± 0.07	273	8.33 ± 0.41	49.9 ± 1.4
		100	110.15	1.500	3.76 ± 0.02	990	19.52 ± 0.28	52.1 ± 0.5
	100*		41.70	0.180	4.25 ± 0.07	216	2.24 ± 0.15	64.1 ± 1.7
	30	70	112.60	1.670	3.60 ± 0.02	992	17.36 ± 0.29	64.4 ± 0.6
	100		50.57	0.360	4.04 ± 0.06	786	3.26 ± 0.19	69.5 ± 1.6
	40	60	110.53	1.690	3.55 ± 0.02	996	16.58 ± 0.27	68.8 ± 0.6
	100*		28.56	0.283	3.74 ± 0.03	297	2.45 ± 0.08	78.2 ± 1.0
	70	30	105.66	1.720	3.44 ± 0.02	775	14.49 ± 0.22	81.1 ± 0.5
	100		101.15	1.770	3.33 ± 0.01	674	13.09 ± 0.19	92.5 ± 0.5
	100		151.59	2.370	3.40 ± 0.02	610	18.24 ± 0.33	89.5 ± 0.6
	100		49.51	1.140	3.16 ± 0.01	841	7.67 ± 0.09	99.3 ± 0.4
	100		26.12	0.790	2.98 ± 0.01	382	4.90 ± 0.06	107.0 ± 0.5

^*continuous flow conditions

2.2. Absolute kinetic technique

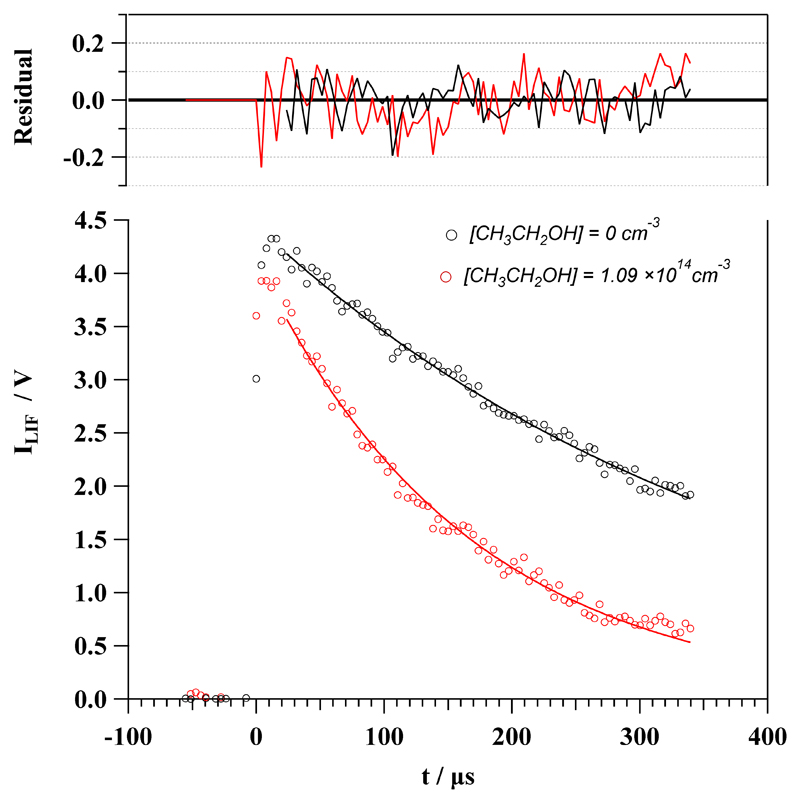
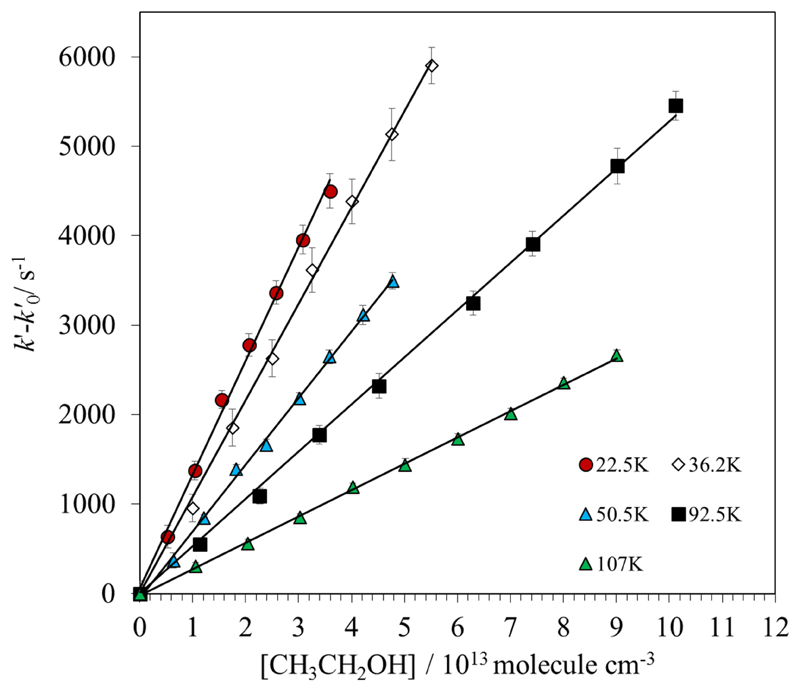
The PLP-LIF technique has been recently used in our laboratory for absolute kinetic studies of reactions between OH radicals and COMs at IS temperatures.^24–26 The OH radical was generated in situ along the jet by the photolysis of gaseous H₂O₂ at 248 nm by a KrF excimer laser. Gaseous H₂O₂ was introduced in the reservoir by flowing a portion of the buffer gas through a glass bubbler containing a commercial aqueous solution previously concentrated. Generated OH radicals were lost mainly by reaction with ethanol (in excess with respect to OH, i.e., under pseudo-first order conditions) and by reaction with the OH-precursor, H₂O₂ (also in excess), and other loss processes such as diffusion of OH radicals out of the detection zone. The temporal evolution of OH(X²Π) radicals was monitored by Laser Induced Fluorescence (LIF) at ca. 310 nm after excitation of OH at ca. 282 nm using a frequency doubled dye laser (Lambda Physik, model Scanmate) pumped by a Nd-YAG laser (Continuum, model Surelite). The LIF detection system consists of an optically fast telescope coupled to a filtered photomultiplier tube, PMT (Electron tube, model 9813B). The band pass filter was centered at 310 nm with a full width at half maximum (FWHM) of 10 nm. The optically fast telescope is comprised by two plano-convex lenses (70 mm diameter and 90 mm focal length) above the flow combined with a spherical mirror below the supersonic flow. The signal from the PMT was fed into a gated boxcar integration unit (Standford Research System, model SRS250) and the integrated signal was recorded and processed in a computer by a homemade LabView program. The timescale of the kinetic experiment was restricted by the length of uniformity of the supersonic flow. For that reason, the maximum reaction time is limited by the hydrodynamic time at each temperature (Table 2). The reaction time during the kinetic measurements was varied automatically by the LabView software changing the delay between the photolysis and the dye lasers from ca. 20-50 µs before the trigger of the photolysis laser (to record the background signal) to the hydrodynamic time. An example of the temporal profiles of the LIF signal from OH radicals recorded at 78.2 K in the absence and in the presence of ethanol (1.06×10¹⁴ molecule cm^-3) is depicted in Fig. 1. The fit to an exponential decay was done after rotational relaxation of OH radicals (typically 10-20 µs) and the pseudo-first order rate coefficient, k’, was obtained in the absence of ethanol $(k_0^{\prime })$ and at 8-9 ethanol concentrations, [CH₃CH₂OH], for each operating conditions. Concentrations of ethanol in the jet were checked by UV spectroscopy at 185 nm as described in the supplementary information. Knowing the [CH₃CH₂OH] is imperative to accurately determine the rate coefficient k(T) from the slope of k’ versus [CH₃CH₂OH] plots. A linear relationship between k’ and [CH₃CH₂OH] ensures the accomplishment of the pseudo-first order conditions. To compare different experiments at the same temperature, but with slightly different $k_0^{\prime }$ values, $k^{\prime }-k_0^{\prime }$ is plotted against [CH₃CH₂OH]. In Fig. 2, some examples of these plots are shown for several temperatures. The kinetic experiments (i.e. the full bimolecular plot) were repeated several times to check for reproducibility at each operating conditions, finding a very good agreement among the single k(T). A weighted average k(T) is listed in Table 3.

Fig 1.

Example of a temporal profile of the LIF signal from OH radicals recorded at 78.2 K in the absence (black circles) and presence (red circles) of ethanol. The upper panel shows the difference between the experimental I_LIF and the resulting from the fit.

Fig 2.

Pseudo-first order plots: $k^{\prime }-k_0^{\prime }$ versus ethanol concentration.

Table 3.

Average rate coefficients obtained at different total gas densities between 21 and 107 K.

Ttyp/K	Texp/K	Mode	Bath Gases	[CH3CH2OH]/1013 molecule cm-3	n/1016 molecule cm-3	k(T)/10-11 cm3 molecule-1 s-1
~ 21	21.1 ± 0.6	Pulsed	He	0.6-5.2	3.4	13.1±0.3
	22.5 ± 0.7	Pulsed	He	0.5-5.0	7.4	12.3±1.9
	21.7 ± 1.4	Pulsed	He	0.4-5.5	16.7	12.9±2.2
	36.2 ± 1.2	Pulsed	He	1.0-5.4	17.7	10.9±0.3
	42.6 ± 1.3	Continuous	N2/He	0.3-4.5	5.2	9.3±0.2
~ 45	45.3 ± 1.3	Pulsed	N2	0.5-4.7	0.7	8.4±0.8
	45.5 ± 2.0	Pulsed	N2/He	1.2-5.7	4.2	9.0±0.6
~ 50	50.5 ± 1.4	Pulsed	N2	0.6-4.8	1.5	7.5±0.2
	51.6 ± 1.7	Continuous	N2	0.2-2.0	4.2	7.2±1.0
	49.9 ±1.4	Pulsed	N2/He	1.5-6.1	8.3	8.0±0.3
	52.1 ± 0.5	Pulsed	Ar	0.2-0.6	19.5	7.4±0.8
~ 64	64.1 ± 1.7	Continuous	N2	0.4-4.6	2.2	6.7±0.1
	64.4 ± 0.6	Pulsed	N2/Ar	0.5-4.5	17.4	6.7±0.4
~ 70	68.8 ± 0.6	Pulsed	N2	1.3-10.0	3.3	4.2±0.1
	69.5 ±1.6	Pulsed	N2/Ar	0.6-4.8	16.6	4.5±1.2
~ 80	78.2 ± 1.0	Continuous	N2	0.7-10.9	2.5	3.0±0.5
	81.1 ± 0.5	Pulsed	N2/Ar	1.1-11.3	14.5	5.4±0.4
~ 90	89.5 ± 0.6	Pulsed	N2	0.9-10.1	13.1	5.4±0.4
	92.5 ± 0.5	Pulsed	N2	0.6-7.7	18.2	5.0±1.4
	99.3 ± 0.4	Pulsed	N2	0.9-8.9	7.7	4.3±0.1
	107.0 ± 0.5	Pulsed	N2	1.1-9.8	4.9	3.0±0.2

Uncertainties are ±1σ (standard deviation) for T and n and ±2σ for k(T). A conservative ±10% for taking into account the systematic errors has to be added in k(T).

2.3. Chemicals

He (99.999%, Praxair), N₂ (99.999%, Praxair) and Ar (99.999%, Praxair) were used as supplied. Liquid samples of CH₃CH₂OH (99.8%, Fluka) were degassed by repeated freeze-pump-thaw cycles prior to its use. Aqueous solution of H₂O₂ (Sharlab, initially at 50% w/w) was pre-concentrated.^31–34

3. Results and Discussion

3.1. k(T) as a function of total pressure

Several measurements of k(T) at different densities were performed at around 21, 45, 50, 64, 70, 80 and 90 K and are summarized in Table 3. The operation mode of the CRESU system is also specified in Table 3. Observation of consistent results between the pulsed and continuous modes at a constant temperature supports the robustness of the method. Given uncertainties are ±1σ for the temperature and density in the supersonic flow, whereas it corresponds to a ±2σ_stat statistical error for the rate coefficients. A systematic error σ_sys (±10%) has to be added to σ_stat of the rate coefficients in order to obtain the total uncertainty σ_tot on k measurements. The systematic error arises from any instrumental error such as calibrations of mass flow controllers or pressure gauges, which affect the determination of the gas concentrations and more particularly that of ethanol one. In this latter case, the UV experiment described in the supporting information gives a good evaluation of the systematic error concerning the dilution factor.

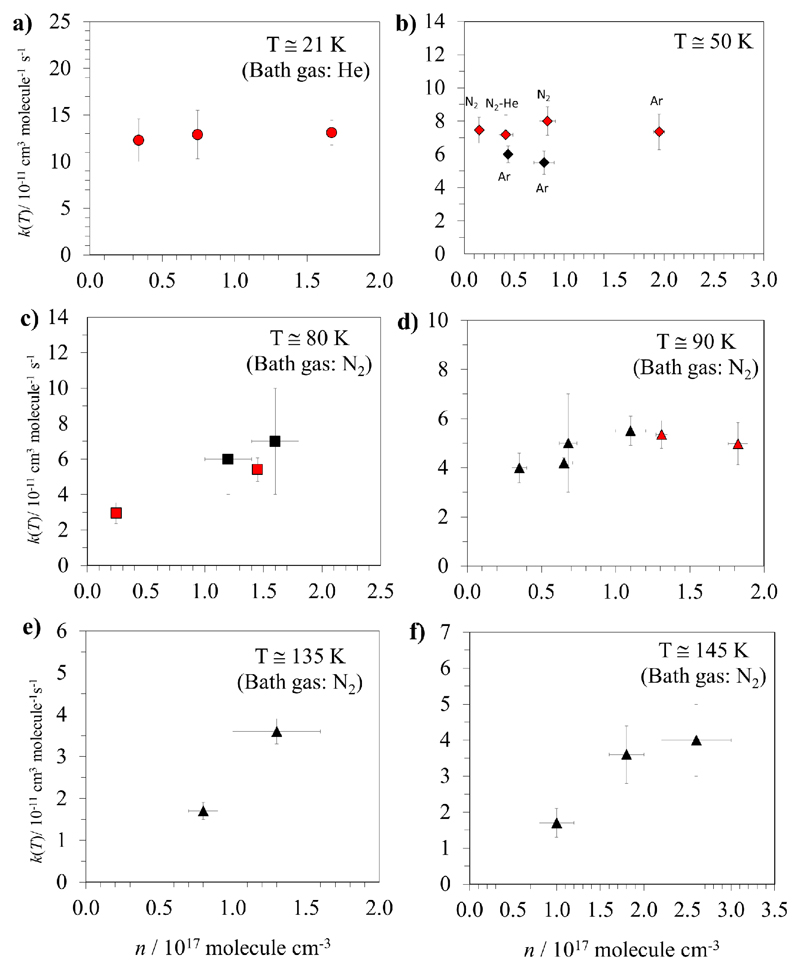
Figures 3 to 5 show our rate coefficient measurements including the total uncertainty σ_tot. In Fig. 3 we present our data as a function of the bath gas density for different temperatures: 21, 50, 80 and 90 K. We did not observe any pressure dependence of k(T~21K) between 3.4×10¹⁶ cm^-3 and 1.7×10¹⁷ cm^-3 (see Fig. 3a), implying that reaction (R1) at this temperature is purely bimolecular or, if it is a three-body reaction, the high-pressure limit is already reached. Unfortunately, experimentally the change in gas density is limited by the working conditions of the presently available Laval nozzle and the pumping capacity. At about 45 K, 64 K and 70 K, only two gas densities can be used and no dependence of k(T) was observed (see Table 3). The lowest n reached in our system is 6.9×10¹⁵ cm^-3 at ca. 45 K. At 50, 80 and 90 K, k(T) reported by Caravan et al.²³ are also included in Figs. 3b, 3c and 3d, respectively, to have a better global picture of the available experimental data to date. The buffer gas or gas mixtures used are also indicated in these plots. Even excluding the effect of the nature of the buffer gas, k(T~50 K) does not vary, within the experimental uncertainties, between 1.5×10¹⁶ and 1.9×10¹⁷ molecule cm^-3, i.e. when changing the density by one order of magnitude. This was also observed by Caravan et al.,²³ although they varied the gas density only by a factor of ~2. Nevertheless, at higher temperatures, Caravan et al.²³ claimed that there is a significant influence of gas density on k(T) at 85 K (range 82 – 89 K) and 140 K (range 133 – 148 K, see Figs. 3e and 3f). However, as shown in Figs. 3c and 3d, this p-dependence of k(T) is not evident. Considering the temperature spread around 80 K in the Leeds work, we have split in two figures their data with respect to their Fig. 4a (82 – 89 K range). This was done in order to minimize the temperature effect on the rate coefficient as experiments demonstrate a strong T-dependence for k(T). Excepting the rate coefficients gathered at ca. 80 K, no pressure dependence was observed in the available density range explored. An explanation could be that measurements were made in the high-pressure limit regime of the fall-off curve for T < 70 K. However, in this case we should have seen a pressure dependence at 90 K (86 – 92 K) as well as it seems to occur at 80 K (78 – 84 K). Even in this latter case, the pressure dependence is not clearly sustained because only the rate coefficient measured at 78 K is found to be somewhat lower. These experiments were repeated several times and the resulting k(T) was very reproducible, within the experimental uncertainties. In a pressure dependent process, the average collision energy transferred per collision between the pre-reactive excited complex and the bath gas depends on the nature of the bath gas and then this can influence the kinetics. All data gathered at ca. 80 K were obtained in N₂ with the exception of that measured at 81.1 K, where a mixture of 70% N₂ and 30% Ar was used. The agreement with the two encompassing k values obtained in Leeds using pure N₂ is an indication that the collision efficiency should be similar for N₂ and Ar in the present case. Taken as a whole, the present work does not agree with the Leeds conclusions. Additional investigations would be certainly worthwhile in order to disentangle this situation. For instance, even lower densities should be explored in order to see if a more evident decrease in the rate constant occurs. This however will require the building of new Laval nozzles working with larger pumping capacities.

Fig 3.

Rate coefficients k(T) obtained in this work (red symbols) together with those reported by the Leeds group²³ (black symbols) as a function of gas density for different temperatures.

Fig 5.

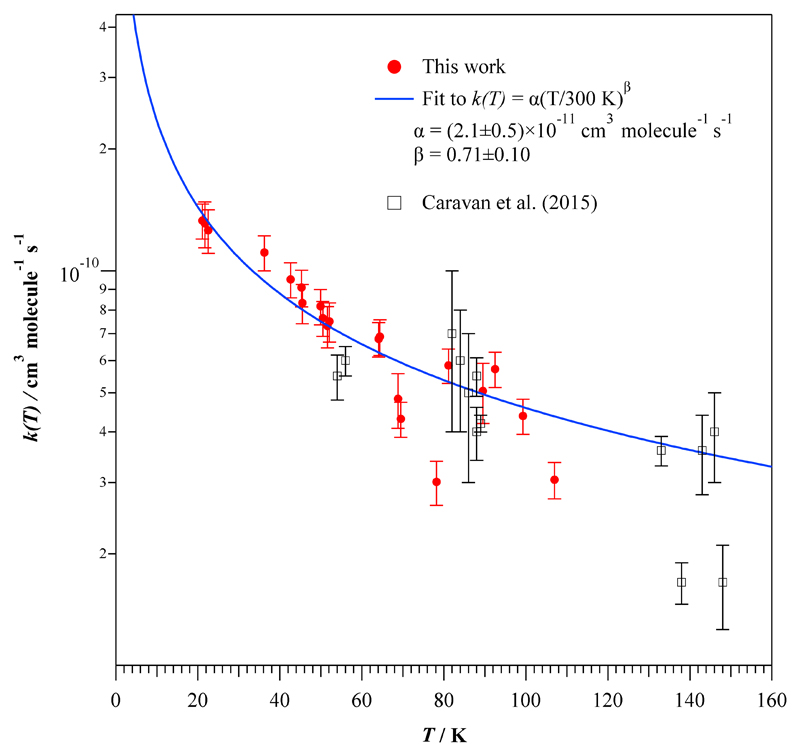
Temperature dependence of k(T) between 21 and 148 K. Solid line is the fit to our experimental data.

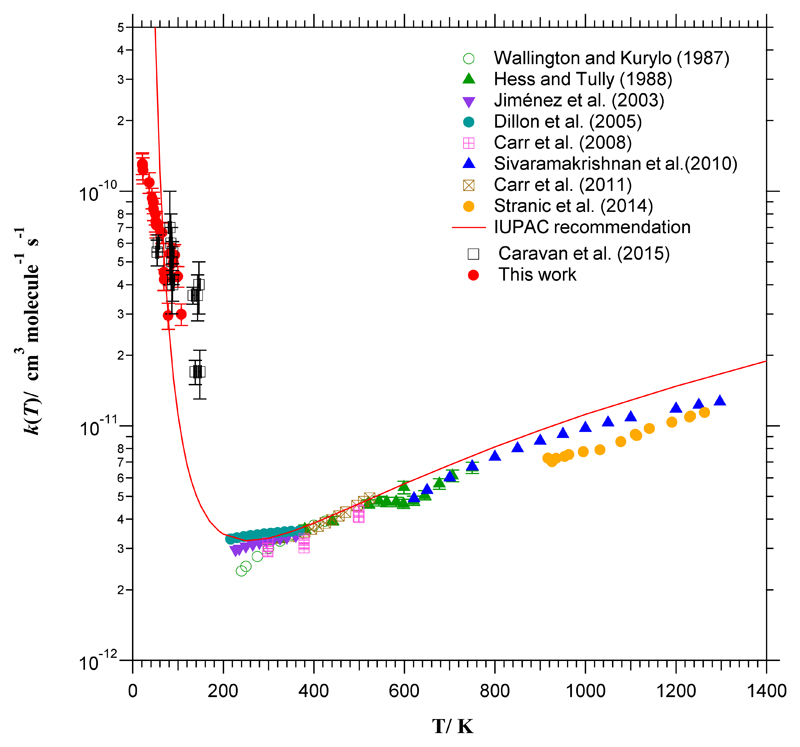
Fig 4.

Temperature dependence of k(T) in the whole T-range investigated experimentally (21-1300 K). The red curve is the T-expression for k(T) recommended by IUPAC panel.³²

3.2. Experimental temperature dependence of k(T)

The rate coefficients obtained as a function of temperature are listed in Table 3. As can be seen, k(T) increases more than four times from 107 K to 21 K. The enhancement of the OH-reactivity towards ethanol with respect to room temperature is around two orders of magnitude. Figure 4 shows the low-temperature rate coefficients from Table 3 together with the results from the literature above 54 K. As observed for other OH-reactions, the kinetic behaviour at T<200 K is opposite to that for higher temperatures, i.e. the k(T) versus T (or ln k versus 1/T in an Arrhenius form) plot presents a minimum rate coefficient between 200 and 300 K. No kinetic data are available between 148 K and 202 K to establish accurately this tendency. Further kinetic studies are desired in that temperature range.

As can be seen in Fig. 4, the T-expression recommended by IUPAC³² (k(T=216-599 K) = 6.70×10^-18 T² exp(511/T) cm³ molecule^-1 s^-1) is also depicted as a red curve. This three-parameter expression is based on the results from Hess and Tully,¹⁸ Wallington and Kurylo,²⁰ Jiménez et al.,¹⁹ and Dillon et al.¹⁷ Out of that temperature range, the preceding expression slightly overestimates the rate coefficient at T>600 K and clearly the IUPAC recommendation does not properly describe the behaviour of k(T) at temperatures below 200 K. The rate coefficient drastically increases in the region of astrochemical interest, predicting a k(T→0)→∞, which has no physical meaning.

The T-dependence expression commonly used in astrochemical models is a three-parameter expression:

$$k(T)=\alpha {\mathit{(}T/300\text{K})}^{\beta }\exp \mathit{(}-\gamma /T)$$ (E1)

When fitting our kinetic data to Eq. (E1) the uncertainty in α, β and γ parameters is found to be very large, predicting a maximum rate coefficient around 20 K and k(T→0)→0. The existence of the predicted maximum rate coefficient could be checked by performing future kinetic measurements at lower temperatures than 21 K. On the other hand, when assuming a barrierless process (γ = 0), then the resulting expression is:

$$k(T=21-107\text{K})=(2.1\pm 0.5)\times {10}^{-11}{(T/300\text{K})}^{-(0.71\pm 0.10)}{\text{cm}}^3{\text{molecule}}^{-1}{\text{s}}^{-1}$$ (E2)

where the uncertainties are the statistical errors (±2σ).Within the large uncertainties of k(T) reported by Caravan et al.²³, equation (E2) agrees fairly well with their data below 90 K and reproduces correctly part of their measurements at higher temperatures (see Fig. 5). As stated above, special care must be taken in the extrapolation at temperatures lower than 20 K. The extrapolated rate coefficient at 10 K from Eq. (E2) provides a value of (2.3±0.3)×10^-10 cm³ molecule^-1 s^-1. This value is significantly higher than the one used at 10 K by Acharyya et al.³³ in the modelling of ethanol in dense interstellar clouds. These authors considered a value of 0.6×10^-10 cm³ molecule^-1 s^-1 based on the initial experimental investigation from Caravan et al.²³ They also claimed that due to the uncertain extrapolation down to 10 K, the proposed value should be viewed as a lower limit at 10 K, in agreement with the present finding. However, increasing artificially their estimation by a factor of five did not lead to major effects in the astronomical conclusions. Finally, note that the presently proposed mathematical expression (E2) also predicts a k(T→0)→∞, which is not physically correct. For that reason, once again, it is mandatory to carry out additional experiments at even much lower temperatures than the present 21 K limitation.

3.3. Theoretical rate coefficients and branching ratios

Reaction (R1) can proceed via these three H-atom abstraction reactions forming water:

$$\text{OH}+{\text{CH}}_{\text{3}}{\text{CH}}_{\text{2}}\text{OH}\to {\text{H}}_{\text{2}}{\text{O}+\text{CH}}_{\text{3}}{\text{CH}}_{\text{2}}\text{O}$$ (R1a)

$$\to {\text{H}}_{\text{2}}{\text{O}+\text{CH}}_{\text{3}}\text{CHOH}$$ (R1b)

$$\to {\text{H}}_{\text{2}}{\text{O}+\text{CH}}_{\text{2}}{\text{CH}}_{\text{2}}\text{OH}$$ (R1c)

The branching ratio, BR, for each channel is not accurately known. A few theoretical investigations on reaction (R1) can be found in the literature.^21,34–37 All of them calculate the potential energy surface (PES) driving the reaction pathways (R1a-c) using differing methods and then evaluate k(T) through statistical methods including several variants of transition state (TS) and RRKM (Rice, Ramsperger, Kassel, Markus) theories. These calculations coincide in that three exit channels are likely after an OH radical collides with an ethanol molecule, corresponding to the three possible H-abstraction sites of CH₃CH₂OH (channels R1a-c). These routes go through a pre-reactive complex and a TS with a relatively low positive energy barrier with the exception of reaction (R1b) for which the transition state is localized a few tenth of kcal mol^-1 either higher^34,36 or lower^21,34,36 to the reactants reference energy according to the considered works. The highest barrier is always found for channel (R1a) and is about 3-4 kcal mol^-1. Consequently, channel (R1b) was found to be largely dominant at temperatures of 200 K and higher. With the exception of Elm et al.³⁷ who did only calculations at 298 K, branching ratios were obtained as a function of temperature and interestingly their temperature evolution differed from one study to another. Galano et al.³⁴ and Sivaramakrishnan et al.²¹ predicted a slight increase of BR for channels (R1a) and (R1c) when the temperature decreases from 500 to 250 K, whereas Xu et al.³⁵ and Zheng et al.³⁶ calculated that BR decreases with temperature (2400 – 200 K) reaching a value of less than 5% for channel (R1a) and less than 10% for channel R1c at 200 K. On the other hand, reaction (R1b) was found to account for about 90% of the whole process at 200 K in Xu et al.³⁵, Sivaramakrishnan et al.²¹ and Zheng et al.³⁶ studies. Branching ratio for reaction (R1b) was found to be in good agreement with the experimental work of Carr et al.¹⁶ in the temperature range 298 – 523 K who deduced the contributions of (R1b) and (R1c) to the title reaction from kinetic isotope effect. For reaction (R1c) agreement was less satisfactory excepting for Zheng et al. calculations. The partial and total rate coefficients were calculated and compared with the available experiments in the temperature range 200–1300 K. Several expressions were chosen to represent the temperature dependence of k(T). However, the following formula used by Zheng et al. can represent the four theoretical works:

$$k(T)=A{\left(\frac{T+T_0}{300}\right)}^n\exp \left(-\frac{E(T+T_0)}{R(T^2+T_0^2)}\right)$$ (E3)

where n, E and T₀ are adjusted parameters in order to fit the calculated values. In all cases but Zheng et al.³⁶ T₀ = 0 and the expression used by Galano et al.³⁴ considered n = 0 as well. With the exception of the expression found by Galano et al.³⁴, all other works agree well with the available experimental data. Extrapolation of the analytical expressions of k(T) to the ISM temperatures leads however to either non-physical results^21,35 or rate coefficients too low^34,36, about a factor 20-30 below the present experimental results at 20 K. None of these four theoretical investigations explores the possible pressure dependence of the rate coefficient. This aspect was modelled by Caravan et al.²³ to reinforce their experimental observations. These authors carried out a simulation based on an extended Lindemann-Hinshelwood model. Extrapolation to zero density showed that the simulation was not intercepting the rate coefficient axis at either 80 K or 140 K. Then, they concluded that reaction (R1) may proceed via two routes, namely stabilization of the pre-reactive complex from one side and tunnelling through the TS barrier from another side. Caravan et al.²³ also suggested that at low temperatures the branching ratios for the hydrogen abstraction channels depend on the barrier widths. Similar to the reaction of OH with methanol, they proposed that route (R1a) is expected to be the major bimolecular channel at low temperatures because the pathway leading to CH₃CH₂O + H₂O has the largest TS imaginary frequency. This would imply a dramatic change in the BRs between 200 K and 140 K (and below). Caravan et al.²³ attempted to detect CH₃CH₂O radical by laser induced fluorescence, but it was unsuccessful.

The routes leading to a stabilization of the pre-reactive complexes have never been investigated and the impact of a possible tunnelling effect at low temperatures is presently not quantified. It is worth noting here that finding a non-zero rate coefficient when extrapolating k(T) to zero density is not a sufficient argument to deduce that tunnelling is occurring. Sleiman et al.³⁸ recently detailed a counterexample, the CN + CH₃CN reaction. They found clear pressure dependences of k(T) at 52 and 132 K, with non-zero intercepts. Ab initio TST calculations using highly accurate thermochemical protocols showed that the CN + CH₃CN reaction was purely termolecular and tunnelling was insignificant. Complementary theoretical calculations at very low temperatures (presently limited to 200 K) would be of great help in the understanding of the mechanisms driving the reaction of OH with ethanol.

4. Conclusions

In this work, we present for the first time the pressure and temperature dependence of the rate coefficients for the OH+ethanol reaction at temperatures below 54 K. No evident pressure dependence of k(T) was observed in the gas density range investigated between 21 and 107 K, indicating that this reaction is either at the high-pressure limit or is purely bimolecular. The T-dependence of k(T) in that temperature range can be described by a two-parameter expression. From our results, the rate coefficient at 10 K – a typical temperature of dense molecular clouds in the ISM – obtained from extrapolation of the T-expression yields a value of (2.3±0.3)×10^-10 cm³ molecule^-1 s^-1, which can be used in the astrochemical modelling of ethanol in those environments, but considering that this rate coefficient must be checked experimentally and/or theoretically. In our group, we are currently developing a new set of Laval nozzles to cover the temperature range 10-20 K and 100-160 K as well, which is also an interesting T-range where just a few data are available for the title reaction.