Abstract
Recent studies have shown the value of using deep learning models for mapping and characterizing how the brain represents and organizes information for natural vision. However, modeling the relationship between deep learning models and the brain (or encoding models), requires measuring cortical responses to large and diverse sets of natural visual stimuli from single subjects. This requirement limits prior studies to few subjects, making it difficult to generalize findings across subjects or for a population. In this study, we developed new methods to transfer and generalize encoding models across subjects. To train encoding models specific to a target subject, the models trained for other subjects were used as the prior models and were refined efficiently using Bayesian inference with a limited amount of data from the target subject. To train encoding models for a population, the models were progressively trained and updated with incremental data from different subjects. For the proof of principle, we applied these methods to functional magnetic resonance imaging (fMRI) data from three subjects watching tens of hours of naturalistic videos, while a deep residual neural network driven by image recognition was used to model visual cortical processing. Results demonstrate that the methods developed herein provide an efficient and effective strategy to establish both subject-specific and population-wide predictive models of cortical representations of high-dimensional and hierarchical visual features.
Keywords: neural encoding, natural vision, deep learning, Bayesian inference, incremental learning
Introduction
An important area in computational neuroscience is developing encoding models to explain brain responses given sensory input (Trappenberg, 2009). In vision, encoding models that account for the complex and nonlinear relationships between natural visual inputs and evoked neural responses can shed light on how the brain organizes and processes visual information through neural circuits (Paninski et al., 2007; Naselaris et al., 2011; Chen et al., 2014; Cox and Dean, 2014; Kriegeskorte, 2015). Existing models may vary in the extent to which they explain brain responses to natural visual stimuli. For example, Gabor filters or their variations explain the neural responses in the primary visual cortex but not much beyond it (Kay et al., 2008; Nishimoto et al., 2011). Visual semantics explain the responses in the ventral temporal cortex but not at lower visual areas (Naselaris et al., 2009; Huth et al., 2012). On the other hand, brain-inspired deep neural networks (DNN) (LeCun et al., 2015), mimic the feedforward computation along the visual hierarchy (Kriegeskorte, 2015; Yamins and DiCarlo, 2016; Kietzmann et al., 2017; van Gerven, 2017), match human performance in image recognition (Krizhevsky et al., 2012; Simonyan and Zisserman, 2014; Szegedy et al., 2015; He et al., 2016), and explain cortical activity over nearly the entire visual cortex in response to natural visual stimuli (Yamins et al., 2014; Güçlü and van Gerven, 2015b, a; Wen et al., 2017, 2018; Eickenberg et al., 2017; Seeliger et al., 2017; Han et al., 2017; Shi et al., 2018).
These models also vary in their complexity. In general, a model that explains brain activity in natural vision tends to extract a large number of visual features given the diversity of the visual world and the complexity of neural circuits. For DNN, the feature space usually has a very large dimension in the order of millions (Krizhevsky et al., 2012; Simonyan and Zisserman, 2014; Szegedy et al., 2015; He et al., 2016). Even if the model and the brain share the same representations up to linear transform (Yamins and DiCarlo, 2016), matching such millions of features onto billions of neurons or tens of thousands of neuroimaging voxels requires substantial data to sufficiently sample the feature space and reliably train the transformation from the feature model to the brain. For this reason, current studies have focused on only few subjects while training subject-specific encoding models with neural responses observed from each subject given hundreds to thousands of natural pictures (Güçlü and van Gerven, 2015b; Eickenberg et al., 2017; Seeliger et al., 2017), or several to tens of hours of natural videos (Güçlü and van Gerven, 2015a; Wen et al., 2017, 2018; Eickenberg et al., 2017; Shi et al., 2018). However, a small subject pool incurs concerns on the generality of the conclusions drawn from such studies. Large data from single subjects are rarely available and difficult to collect especially for patients and children. It is thus desirable to transfer encoding models across subjects to mitigate the need for a large amount of training data from single subjects.
Transferring encoding models from one subject to another should be feasible if different subjects share similar cortical representations of visual information. Indeed, different subjects show similar brain responses to the same natural visual stimuli (Hasson et al., 2004; Lu et al., 2016), after their brains are aligned anatomically. The consistency across subjects may be further improved by functional alignment of fine-grained response patterns (Haxby et al., 2011; Conroy et al., 2013). Recent studies have also shown that encoding (Güçlü and van Gerven, 2015b; Wen et al., 2017) or decoding (Raz et al., 2017; Wen et al., 2017) models trained for one subject could be directly applied to another subject for reasonable encoding and decoding accuracies. Whereas these findings support the feasibility of transferring encoding and decoding models from one subject to another, it is desirable to consider and capture the individual variations in functional representations. Otherwise, the encoding and decoding performance is notably lower when the models are trained and tested for different subjects than for the same subject (Wen et al., 2017).
Beyond the level of single subjects, what is also lacking is a method to train encoding models for a group by using data from different subjects in the group. This need rises in the context of “big data”, as data sharing is increasingly expected and executed (Teeters et al., 2008; Van Essen et al., 2013; Paltoo et al., 2014; Poldrack and Gorgolewski, 2014). For a group of subjects, combining data across subjects can yield much more training data than are attainable from a single subject. A population-wise encoding model also sets the baseline for identifying any individualized difference within a population. However, training such models with a very large and growing dataset as a whole is computationally inefficient or even intractable with the computing facilities available to most researchers (Fan et al., 2014).
Here, we developed methods to train DNN-based encoding models for single subjects or multiple subjects as a group. Our aims were to 1) mitigate the need for a large training dataset for each subject, and 2) efficiently train models with big and growing data combined across subjects. To achieve the first aim, we used pre-trained encoding models as the prior models in a new subject, reducing the demand for collecting extensive data from the subject in order to train the subject-specific models. To achieve the second aim, we used incremental learning algorithm (Fontenla-Romero et al., 2013) to adjust an existing encoding model with new data to avoid retraining the model from scratch with the whole dataset. To further leverage both strategies, we employed functional hyper-alignment (Guntupalli et al., 2016) between subjects before transferring encoding models across subjects. Using experimental data for testing, we showed the merits of these methods in training the DNN-based encoding models to predict functional magnetic resonance imaging (fMRI) responses to natural movie stimuli in both individual and group levels.
Methods and Materials
Experimental data
In this study, we used the video-fMRI data from our previous studies (Wen et al., 2017, 2018). The fMRI data were acquired from three human subjects (Subject JY, XL, and XF, all female, age: 22–25, normal vision) when watching natural videos. The videos covered diverse visual content representative of real-life visual experience.
For each subject, the video-fMRI data was split into three independent datasets for 1) functional alignment between subjects, 2) training the encoding models, and 3) testing the trained models. The corresponding videos used for each of the above purposes were combined and referred to as the “alignment” movie, the “training” movie, and the “testing” movie, respectively. For Subjects XL and XF, the alignment movie was 16 minutes; the training movie was 2.13 hours; the testing movie was 40 minutes. To each subject, the alignment and training movies were presented twice, and the testing movie was presented ten times. For Subject JY, all the movies for Subjects XL and XF were used; in addition, the training movie also included 10.4 hours of new videos not seen by Subjects XL and XF, which were presented only once.
Despite their different purposes, these movies were all split into 8-min segments, each of which was used as continuous visual stimuli during one session of fMRI acquisition. The stimuli (20.3°×20.3°) were delivered via a binocular goggle in a 3-T MRI system. The fMRI data were acquired with 3.5 mm isotropic resolution and 2 s repetition time, while subjects were watching the movie with eyes fixating at a central cross. Structural MRI data with T1 and T2 weighted contrast were also acquired with 1 mm isotropic resolution for every subject. The fMRI data were preprocessed and co-registered onto a standard cortical surface template (Glasser et al., 2013). More details about the stimuli, data acquisition and preprocessing are described in our previous papers (Wen et al., 2017, 2018).
Nonlinear feature model based on deep neural network
The encoding models took visual stimuli as the input, and output the stimulus-evoked cortical responses. As shown in Fig. 1, it included two steps. The first step was a nonlinear feature model, converting the visual input to its feature representations; the second step was a voxel-wise linear response model, projecting the feature representations onto the response at each fMRI voxel (Kay et al., 2008; Naselaris et al., 2009; Nishimoto et al., 2011; Huth et al., 2012; Güçlü and van Gerven, 2015b, a; Wen et al., 2017, 2018; Eickenberg et al., 2017; Seeliger et al., 2017; Han et al., 2017; Shi et al., 2018). The feature model is described in this sub-section, and the response model is described in the next sub-section.
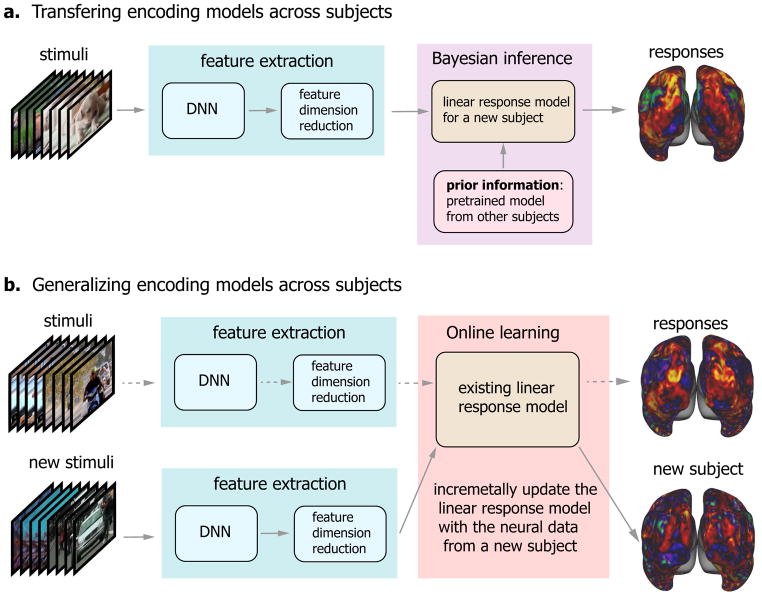
Figure 1. Schemes of transferring and generalizing DNN-based neural encoding models across subjects.
(a) Transferring encoding models across subjects. The encoding model comprises the nonlinear feature model and the linear response model. In the feature model, the feature representation is extract from the visual stimuli through the deep neural network (DNN), and followed by the feature dimension reduction. In the response model, the model parameters are estimated by using Bayesian inference with subject-specific neural data as well as a prior model trained from other subjects. (b) Generalizing encoding models across subjects. The dash arrows indicate the existing encoding model trained with the data from a group of subjects. The existing model can be incrementally updated by using the new data from a new subject with an online learning algorithm. In the scheme, the feature model is common any subjects and any stimuli, and the response model will be updated when new subject data is available.
In line with previous studies (Güçlü and van Gerven, 2015b, a; Wen et al., 2017, 2018; Eickenberg et al., 2017; Seeliger et al., 2017), a deep neural network (DNN) was used as the feature model to extract hierarchical features from visual input. Our recent study (Wen et al., 2018) has demonstrated that deep residual network (ResNet) (He et al., 2016), a specific version of the DNN, was able to predict the fMRI responses to videos with overall high and statistically significant accuracies throughout the visual cortex. Therefore, we used ResNet as an example of the feature model in the present study for transferring and generalizing encoding models across subjects. Briefly, ResNet was pre-trained for image recognition by using the ImageNet dataset (Deng et al., 2009) with over 1.2 million natural images sampling from 1,000 categories, yielding 75.3% top-1 test accuracy. The ResNet consisted of 50 hidden layers of nonlinear computational units that encoded increasingly abstract and complex visual features. The first layer encoded location and orientation-selective visual features, whereas the last layer encoded semantic features that supported categorization. The layers in between encoded increasingly complex features through 16 residual blocks. Passing an image into ResNet yielded an activation value at each unit. Passing every frame of a movie into ResNet yielded an activation time series at each unit, indicating the time-varying representation of a specific feature in the movie. In this way, the feature representations of the training and testing movies could be extracted, as in previous studies (Wen et al., 2017, 2018). Here, we extracted the features from the first layer, the last layer, and the output layer for each of the 16 residual blocks in ResNet (Wen et al., 2018).
Feature dimension reduction
The feature space encoded in ResNet had a huge dimension over 106. This dimensionality could be reduced since individual features were not independent. For this purpose, principal component analysis (PCA) was applied first to each layer and then across layers, as in previous studies (Wen et al., 2017, 2018). To define a set of principal components generalizable across various visual stimuli, a training movie as long as 12.54 hours was used to sample the original feature space. The corresponding feature representations were convolved with a canonical hemodynamic response function and then demeaned and divided by its standard deviation, yielding the standardized feature representation at each unit. Then, PCA was applied to the standardized feature representations from all units in each layer, as expressed as Eq. (1).
| (1) |
where stands for the standardized feature representation from layer l given a visual input x, Bl ∈ ℝpl×ql consists of the principal components (as unitary column vectors) for layer l, fl(x) ∈ ℝ1×ql is the feature representation after reducing the dimension from pl to ql.
Due to the high dimensionality of the original feature space and the large number of video frames, we used an efficient singular value decomposition updating algorithm (or SVD-updating algorithm), as used in prior studies (Zha and Simon, 1999; Zhao et al., 2006), to obtain the principal components Bl. Briefly, the 12.54-hour training movie was divided into blocks, where each block was defined as an 8-min segment (i.e. a single fMRI session). The principal components of feature representations were first calculated for a block and then were incrementally updated with new blocks. A minor distinction from the algorithms in (Zha and Simon, 1999; Zhao et al., 2006), we determined the number of principal components by keeping >99% variance of the feature representations of every block, rather than keeping a fixed number of components during every incremental update. See the SVD-updating algorithm in Supplementary Information for details.
Following the layer-wise dimension reduction, PCA was applied to the feature representations from all layers, by keeping the principal components that explained >99% variance across layers for every block of visual stimuli. The final dimension reduction was implemented as Eq. (2).
| (2) |
where stands for the feature representations concatenated across L layers, B1:L consists of the principal components of f1:L(x) given the 12.54-hour training movie, and f(x) ∈ ℝ1×k is the final dimension-reduced feature representation.
The principal components Bl and B1:L together defined a dimension-reduced feature space, and their transpose defined the transformation to the original feature space. So, given any visual stimulus x, its dimension-reduced feature representation could be obtained through Eqs. (1) and (2) with fixed Bl and B1:L. Once trained, the feature model including the feature dimension reduction, was assumed to be common to any subjects and any stimuli.
Voxel-wise linear response model
As the second part of the encoding model, a voxel-wise linear regression model was trained to predict the response rv(x) at voxel v evoked by the stimulus x. In some previous studies (Güçlü and van Gerven, 2015a; Wen et al., 2017; Eickenberg et al., 2017), the encoding model for each voxel was based on a single layer in DNN that was relatively more predictive of the voxel’s response than were other layers. Herein, we did not assume a one-to-one correspondence between a brain voxel and a DNN layer. Instead, the feature representations from all layers were used (after dimension reduction) to predict each voxel’s response to video stimuli. After training, the regression coefficients of voxel-wise response models could still reveal the differential contributions of the features in different DNN layers to each voxel (Wen et al., 2018; St-Yves and Naselaris, 2017).
Mathematically, the linear response model was expressed by Eq. (3).
| (3) |
where wv is a column vector of unknown regression coefficients specific to voxel v, and εv is the noise (unexplained by the model). Here, the noise was assumed to follow a Gaussian distribution with zero mean and variance equal to , i.e. .
Eq. (3) can be rewritten in vector/matrix notations as Eq. (4) for a finite set of visual stimuli (e.g. movie frames).
| (4) |
where F ∈ ℝn×k stands for the feature representations of n stimuli, rv ∈ ℝn×1 is the corresponding evoked responses, and .
To estimate the regression coefficients wv in Eq. (4), we used and compared two methods, both of which are subsequently described in a common framework of Bayesian inference. In the first method, we assumed the prior distribution of wv as a zero-mean multivariate Gaussian distribution without using any knowledge from a model pretrained with previous data from the same or other subjects (Sahani and Linden, 2003; Paninski et al., 2007). With such a zero-mean prior, we maximized the posterior probability of wv given the stimulus x and the fMRI response rv(x). In the second method, we assumed the prior distribution of wv as a multivariate Gaussian distribution, whereas the mean was not zero but proportional to the regression coefficients in the pretrained model. As such, the prior was transferred from existing knowledge about the model as learned from existing data or other subjects (hereafter we referred to this prior as the transferred prior). The first method was used for training subject-specific encoding models with subject-specific training data. The second method was what we proposed for transferring encoding models across subjects, as illustrated in Fig. 1a.
Training the response model with the zero-mean prior
From Eq. (4), the likelihood of the response rv given the unknown parameters wv and the known feature representations F followed a multivariate Gaussian distribution, as Eq. (5).
| (5) |
In the framework of Bayesian inference, wv was a multivariate random variable that followed a multivariate Gaussian distribution with a zero-mean, and an isotropic covariance , as expressed in Eq. (6).
| (6) |
The prior distribution was independent of the visual input and thus its feature representations, i.e. p(wv) = p(wv|F). Therefore, given F and rv, the posterior distribution of wv was written as Eq. (7) according to the Bayes’ rule.
| (7) |
where p(rv|F) was constant since rv and F were known.
According to Eqs. (5), (6) and (7), the Bayesian estimation of wv was obtained by maximizing the natural logarithm of its posterior probability, which was equivalent to minimizing the objective function as Eq. (8).
| (8) |
where . The analytical solution to minimizing (8) is as Eq. (9).
| (9) |
where G = [F]TF/n is the covariance matrix of F. Note that the above model estimation with zero-mean prior is simply a ridge regression estimator, i.e. least square regression with L2 regularization.
Training the response model with the transferred prior
If a pretrained model, , was available, we could use this model to derive more informative and precise prior knowledge about wv. Specifically, wv was assumed to follow a multivariate Gaussian distribution, of which the mean was (α is a non-negative factor) and the covariance was . The prior probability of wv was as Eq. (10).
| (10) |
Here, the prior was transferred from a pretrained model (namely the transferred prior), and was used to constrain the mean of the model to be trained with new data and/or for a new subject. According to Eqs. (5), (7) and (10), maximizing the posterior probability of wv was equivalent to minimizing the following objective function.
| (11) |
where . Note that if α = 0, this objective function becomes equivalent to Eq. (8). The objective function could be reformatted as Eq. (12), where a = αλ, b = (1 − α)λ, and c is a constant.
| (12) |
In this function, the first term stands for the mean square error of model fitting, the second term stands for the deviation from the prior model, , and the third term had a similar regularization effect as that in Eq. (8). Hence, the model estimation method is a ridge regression estimator with an extra term that constrains the estimated model to be close to a prior model. The analytical solution to minimizing (12) was as Eq. (13).
| (13) |
where G = [F]TF/n is the covariance matrix of F.
Choosing hyper-parameters with cross-validation
The hyper-parameters λ in Eq. (9) or (a, b) in Eq. (13) were determined for each voxel by four-fold cross-validation (Geisser, 1993). Specifically, the training video-fMRI dataset was divided into four subsets of equal size: three for the model estimation, and one for the model validation. The validation accuracy was measured as the correlation between the predicted and measured cortical responses. The validation was repeated four times such that each subset was used once for validation. The validation accuracy was averaged across the four repeats. Finally, the hyper-parameters were chosen such that the average validation accuracy was maximal.
Testing the encoding performance with the testing movie
Once voxel-wise encoding models were trained, we evaluated the accuracy of using the trained models to predict the cortical responses to the testing movies, which were not used for training the encoding models. The prediction accuracy was quantified as the correlation (r) between the predicted and observed fMRI responses at each voxel given the testing movie. Since the testing movie included five different 8-min sessions with entirely different content, the prediction accuracy was evaluated separately for each session and then averaged across sessions. The significance of the average voxel-wise prediction accuracy was evaluated with a block-permutation test (Adolf et al., 2014) with a block length of 30 seconds (corrected at false discovery rate (FDR) q < 0.01), as used in our prior study (Wen et al., 2017, 2018).
Evaluating the encoding models without any transferred prior
For a specific subject, when the voxel-wise encoding model was estimated without any prior information from existing models pre-trained for other subjects, the estimated model was entirely based on the subject-specific training data. In this case, we evaluated how the encoding performance depended on the size of the training data.
To do so, we trained the encoding models for Subject JY using a varying part of the 10.4-hour training data. The data used for model training ranged from 16 minutes to 10.4 hours. For such models trained with varying lengths of data, we tested their individual performance in predicting the responses to the 40-min testing movie. We calculated the percentage of predictable voxels (i.e. significant with the block-permutation test) out of the total number of cortical voxels, and evaluated it as a function of the size of the training data. We also evaluated the histogram of the prediction accuracy for all predictable voxels, and calculated the overall prediction accuracy in regions of interest (ROIs) (Glasser et al., 2016) by averaging across voxels within ROIs.
Evaluating the encoding models with the transferred prior
When the voxel-wise encoding model was trained with the prior transferred from a pretrained model, the parameters in the new model depended on both the pretrained model and the new training data. As such, one might not require so many training data to train the model as required without the transferred prior.
We used this strategy for transferring encoding models from one subject to another. Specifically, we trained the models from scratch based on the 10.4-hour training data from one subject (JY), and used the trained models as the model prior for other subjects (XF and XL). With this prior model from Subject JY, we trained the encoding models for Subject XF and XL based on either short (16 minutes, i.e. two 8-min sessions) or long (2.13 hours, i.e. 16 sessions) training data specific to them. Note that the movie used for training the prior model in Subject JY was different from either the training or testing movies for Subject XL and XF. With either short or long training data, we evaluated the encoding performance in predicting the responses to the testing movie for Subject XF and XL. For comparison, we also evaluated the encoding models trained with the same training data from Subject XF and XL without using any transferred knowledge from Subject JY, or the prior models from Subject JY without being retrained with any data from Subject XF and XL. The comparison was made with respect to the number of predictable voxels and the voxel-wise prediction accuracy (after converting the correlation coefficients to the z scores with the Fisher’s r-to-z transform). The model comparison was conducted repeatedly when the models under comparison were trained (or tested) with distinct parts of the training (or testing) movie. Between different models, their difference in encoding performance was tested for significance by applying one-sample t-test to the repeatedly measured prediction accuracy (corrected at false discovery rate (FDR) q<0.01).
We also conducted similar analyses by using Subject JY as the target subject, for whom the encoding models were trained with prior knowledge transferred from the encoding models trained with data from Subject XL or XF. Note that the prior models were trained with 1.87-hour training data, and then were refined with 16min data from the target subject. Note that the movie used for training the prior model was different from the movie for refining the prior model for the target subject.
Hyperalignment between subjects
We also explored whether transferring encoding models from one subject to another would also benefit from performing functional hyperalignment as an additional preprocessing step. Specifically, we used the searchlight hyperalignment algorithm (Guntupalli et al., 2016) to correct for the individual difference in the fine-scale functional representation beyond what could be accounted for by anatomical alignment (Glasser et al., 2013). Given the 16-min alignment movie, the fMRI responses within a searchlight (with a radius of 20mm) were viewed as a high-dimensional vector that varied in time. A Procrustes transformation (Schönemann, 1966) was optimized to align high-dimensional response patterns from one subject to another (Guntupalli et al., 2016).
To evaluate the effect of hyperalignment in transferring encoding models across subjects, we performed the searchlight hyperalignment from Subject JY to Subject XL and XF. Then we applied the functional hyperalignment to the encoding models trained for the source subject (Subject JY) to give rise to the prior models that were used for training the encoding models for the target subject (Subject XL or XF). The encoding performance of the resulting models was evaluated and compared with those without hyperalignment. The difference in the encoding performance was addressed with respect to the number of predictable voxels and the voxel-wise prediction accuracy, and was tested for significance with one-sample t-test corrected at false discovery rate (FDR) q<0.01.
Training group-level encoding models with online learning
Here, we describe an online learning algorithm (Fontenla-Romero et al., 2013) to train group-level encoding models based on different video-fMRI data acquired from different subjects, by extending the concept of online implementation for the Levenberg-Marquardt algorithm (Dias et al., 2004). The central idea is to update the encoding models trained with existing data based on the data that become newly available, as illustrated in Fig. 1b.
Suppose that existing training data are available for a set of visual stimuli, X0 (n0 samples). Let F0 be the corresponding feature representations after dimension reduction, be the responses at voxel v. Let be the regression parameters in the voxel-specific encoding models trained with F0 and according to Eq. (9). Given incremental training data, X1 (n1 samples), F1 and , the parameters in the updated encoding model can be obtained by minimizing the objective function below.
| (14) |
The optimal solution is expressed as Eq. (15).
| (15) |
where G0 = [F0]TF0/n0 and G1 = [F1]TF1/n1 are the covariance matrices of F0 and F1, respectively; G = (1 − θ)G0 + θG1 is their weighted sum where the parameter θ specifies the relative weighting of the new data and the previous data. See Derivation of group-level encoding models in Supplementary Information for the derivation of Eq. (15). In this study, θ was set as the ratio of the corresponding sample sizes, i.e. . As such, the samples in the new data were assumed to be as important as those in the previous data.
According to Eq. (15), the encoding model could be incrementally updated by incorporating new data without training the model from scratch. See Algorithm 1 for the updating rules. As more and more data was used for model training, the encoding model was expected to converge, as (G + λI)−1(G0 + λ0I) → I and θ → 0. When it was used to utilize the growing training data from different subjects, this algorithm converged to the group-level encoding models.
Algorithm 1.
Online learning algorithm for training population-based encoding models
| 1: | G0 ← 0, , n0 ← 0, λ0 = 0 |
| 2: | While new data* is available: X, , n1 |
| 3: | |
| 4: | F1 = DimensionReduction(ResNet(X)) |
| 5: | G1 = [F1]TF1/n1 |
| 6: | G = (1 − θ)G0 + θG1 |
| 7: | with cross validation |
| 8: | G0 ← G, , n0 ← n0 + n1, λ0 = λ |
| 9: | Output: wv |
X is the new visual stimuli, is the cortical response, and n1 is the number of samples
As a proof of concept, we trained group-level encoding models by incrementally updating the models with 16-min video-fMRI training data sampled from each of the three subjects in the group. Before each update, the incremental fMRI data was functionally aligned to the data already used to train the existing models (see Hyperalignment between subjects in Methods). After the encoding models were trained with all the training data combined across all the subjects, we evaluated their prediction performance given the testing movie for each subject. The prediction accuracy of the group-level encoding models was averaged across subjects. We then compared the prediction performance before and after every update by incorporating new data.
Results
In recent studies, DNNs driven by image or action recognition were shown to be able to model and predict cortical responses to natural picture or video stimuli (Khaligh-Razavi and Kriegeskorte, 2014; Yamins et al., 2014; Güçlü and van Gerven, 2015b, a; Cichy et al., 2016; Wen et al., 2017, 2018; Eickenberg et al., 2017; Seeliger et al., 2017). This ability rested upon encoding models, in which nonlinear features were extracted from visual stimuli through DNNs and the extracted features were projected onto stimulus-evoked responses at individual locations through linear regression. Herein, we investigated the amount of data needed to train DNN-based encoding models in individual subjects, and developed new methods for transferring and generalizing encoding models across subjects without requiring extensive data from single subjects.
Encoding performance depended on the size of the training data
In this study, we focused on a specific DNN (i.e. ResNet) – a feed-forward convolutional neural network (CNN) pre-trained for image recognition (He et al., 2016). The DNN included 50 successive layers of computational units, extracting around 106 non-linear visual features. This huge dimensionality could be reduced by two orders of magnitude, by applying PCA first to every layer and then across all layers. The reduced feature representations were able to capture 99% of the variance of the original features in every layer.
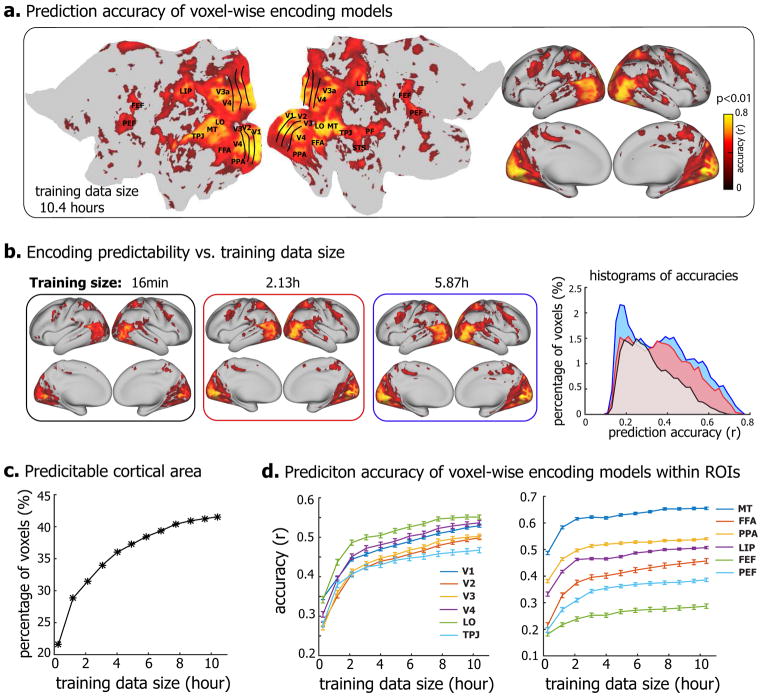
Despite the reduction of the feature dimensionality, training a linear regression model to project the feature representations onto the fMRI response at each voxel still required a large amount of data if the model was estimated solely based on the training data without any informative prior knowledge (Training the response model with the zero-mean prior in Methods). For such encoding models, we evaluated the effects of the size of the training data on the models’ encoding performance in terms of the accuracy of predicting the responses to the testing movie, of which the data were not used for training to ensure unbiased testing. When trained with 10.4 hours of video-fMRI data, the prediction accuracy of the encoding models was statistically significant (permutation test, FDR q<0.01) for nearly the entire visual cortex (Fig. 2.a). The number of predictable voxels and the prediction accuracy were notably reduced as the training data were reduced to 5.87 hours, 2.13 hours, or 16 minutes (Fig. 2.b). With increasing sizes of training data, the predictable areas increased monotonically, from about 20% (with 16-min of training data) to >40% (with 10.4-hour of data) of the cortical surface (Fig. 2.c). The average prediction accuracies, although varying across regions of interest (ROIs), showed an increasing trend as a growing amount of data were used for model training (Fig. 2.d). It appeared that the trend did not stop at 10.4 hours, suggesting a sub-optimal encoding model even if trained with such a large set of training data. Therefore, training encoding models for a single subject purely relying on training data would require at least 10 hours of video-fMRI data from the same subject.
Figure 2. DNN-based neural encoding models for Subject JY.
(a) Performance of neural encoding models (trained with 10.4-hour data) in predicting the cortical responses to novel testing movies. The accuracy is measured by the average Pearson’s correlation coefficient (r) between the predicted and the observed fMRI responses across five testing movies (permutation test, q<0.01 after correction for multiple testing using the false discovery rate (FDR) method). The prediction accuracy is visualized on both flat (left) and inflated (right) cortical surfaces. (b) Prediction accuracy of encoding models trained with less training data, i.e. 16min, 2.13h, and 5.87h. The right is the histograms of prediction accuracies. The x-axis is the prediction accuracy ranging from 0 to 0.8, divided into bins of length Δr = 0.02, the y-axis is the percentages of predictable voxels in the cortex within accuracy bins. (c) The percentage of predictable voxels as a function of training data size ranging from 16min to 10.4 hours. (d) ROI-level prediction accuracies as functions of the training data size. The error bar indicates the standard error across voxels.
Transferring encoding models across subjects
To mitigate this need for large training data from every subject, we asked whether the encoding models already trained with a large amount of training data could be utilized as the prior information for training the encoding models in a new subject with much less training data. To address this question, we used the encoding models trained with 10.4 hours of training data from Subject JY as a priori models for Subject XF and XL. A Bayesian inference method was used to utilize such prior models for training the encoding models for Subject XF and XL with either 16-min or 2.13-hour training data from these two subjects (see Training the response model with the transferred prior in Methods). The resulting encoding models were compared with those trained without using any prior models with the same amount of training data in terms of their accuracies in predicting the responses to the testing movie.
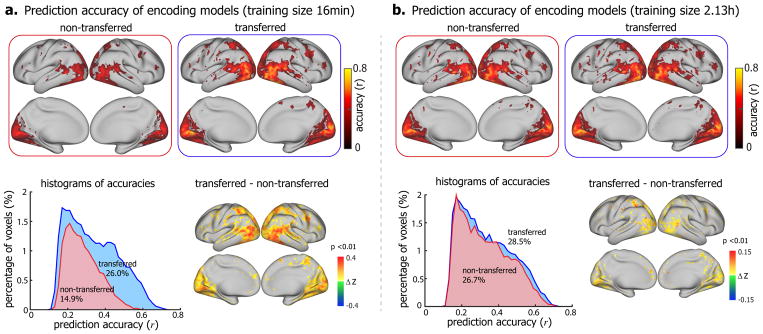
Fig. 3 shows the results for the model comparison in Subject XF. When the training data were as limited as 16 minutes, the encoding models trained with the prior modeled transferred from another significantly outperformed those without using the prior (Fig. 3.a). With the prior model, the predictable cortical areas were 26% of the entire cortex, nearly twice as large as the predictable areas without the prior (14.9% of the entire cortex). Within the predictable areas, the prediction accuracy was also significantly higher with the prior model (Δz = 0.155 ± 0.0006, one-sample t-test, p<10−5) (Fig. 3.a). The difference in voxel-wise prediction accuracy was significant (one-sample t-test, p<0.01) in most of the visual areas, especially for those in the ventral stream (Fig. 3.a). The advantage of using the prior model largely diminished when 2.13-hour training data were used for training the encoding models (Fig. 3.b). Although larger training data improved the model performance, the improvement was much more notable for the method when the prior model was not utilized. In that case, the predictable area increased from 14.9% to 26.7% of the cortex (p=6.5×10−5, paired t-test). When the prior model was utilized, the predictable area increased from 26.0% to 28.5% (p=0.017, paired t-test), and the prediction accuracy only improved marginally (Fig. 3.b). Similar results were observed when transferring from Subject JY to Subject XL (Supplementary Fig. S1), as well as across other pairs of subjects (Supplementary Fig. S2). It was noteworthy that the prediction accuracy of the transferred encoding model with 16-min fMRI data was comparable to the non-transferred models with 2.13-hour fMRI data (Fig. 3 and Supplementary Fig. S3).
Figure 3. Comparison between the encoding models that utilized the prior models transferred from a different subject (transferred) versus those without using any transferred prior (non-transferred).
Voxel-wise prediction accuracy of encoding models trained with 16min (a) and 2.13h (b) video-fMRI data (permutation test, corrected at FDR q<0.01). The top shows the voxel-wise prediction accuracy of the encoding models with the prior transferred from a pretrained model (right) and the encoding models without any transferred prior (left). The bottom left is the histograms of their respective prediction accuracies. The numbers are the total percentages of predictable voxels. The bottom right is the difference of prediction accuracy (Fisher’s z-transformation of r, i.e. z = arctanh(r)) between the encoding models with the transferred prior and those without any transferred prior (one-sample t-test, p<0.01). The figure shows the results for transferring from Subject JY to Subject XF, see Figure S1 and S2 for other subjects.
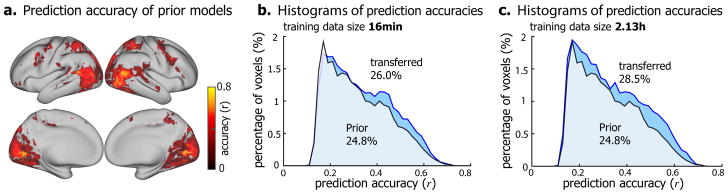
We also asked whether the better performance of the encoding models with the transferred prior was entirely attributable to the prior models from a different subject, or it could be in part attributable to the information in the training data specific to the target subject. To address this question, we directly used the prior models (trained with data from Subject JY) to predict the cortical responses to the testing movie in Subject XL and XF. Even without any further training, the prior models themselves yielded high prediction accuracy for widespread cortical areas in Subject XF for whom the models were not trained (Fig. 4.a). When the prior models were fine-tuned with a limited amount (16-min) of training data specific to the target subject, the encoding performance was further improved (Fig. 4.b). The improvement was greater when more (2.13-hour) training data were utilized for refining the encoding models (Fig. 4.c). Similar results were also observed in another subject (Supplementary Fig. S4). Hence, Bayesian inference to transfer encoding models across subjects could help train the encoding models for new subjects without requiring extensive training data from them. The subject-specific training data served to tailor the encoding models from the source subject towards the target subject.
Figure 4. Comparison between the encoding models that were refined from the prior models transferred from a different subject (transferred) versus the prior encoding models (prior).
(a) Voxel-wise prediction accuracy by directly using the prior encoding models (from Subject JY) to predict the responses to novel testing movies for Subject XF (permutation test, corrected at FDR q<0.01). (b) and (c) show the histograms of prediction accuracies of the encoding models that were transferred from the prior encoding models (blue) and the prior encoding models (green) trained with 16min (b) and 2.13h (c) training data, respectively. See Figure S4 for Subject XL.
Functional alignment better accounted for individual differences
Transferring encoding models across subjects were based on the assumption that the models and data from individual subjects were co-registered. Typically, the co-registration was based on anatomical features (i.e. anatomical alignment) (Glasser et al., 2013). We expected that searchlight hyperalignment of multi-voxel responses could better co-register the fine-grained representational space on the cortical surface (Guntupalli et al., 2016) to improve the efficacy of transferring the encoding models across subjects (see Hyperalignment between subjects in Methods).
Therefore, we performed searchlight hyperalignment such that Subject JY’s fMRI responses to the alignment movie were aligned to the other subjects’ responses to the same movie. After applying the same alignment to the encoding models trained for Subject JY, we used the aligned encoding models as the prior model for training the encoding models for Subject XF or XL with 16-min training datasets from each of them. It turned out that using the functional alignment as a preprocessing step further improved the performance of the transferred encoding models. For Subject XF, the model-predictable areas increased from 26% to 27.8% (p=9.7×10−4, paired t-test), and the prediction accuracy also increased, especially for the extrastriate visual areas (Fig. 5). Similar results were obtained for Subject XL (Supplementary Fig. S5).
Figure 5. Comparison of the encoding models that were transferred from prior models with anatomical versus functional alignment.
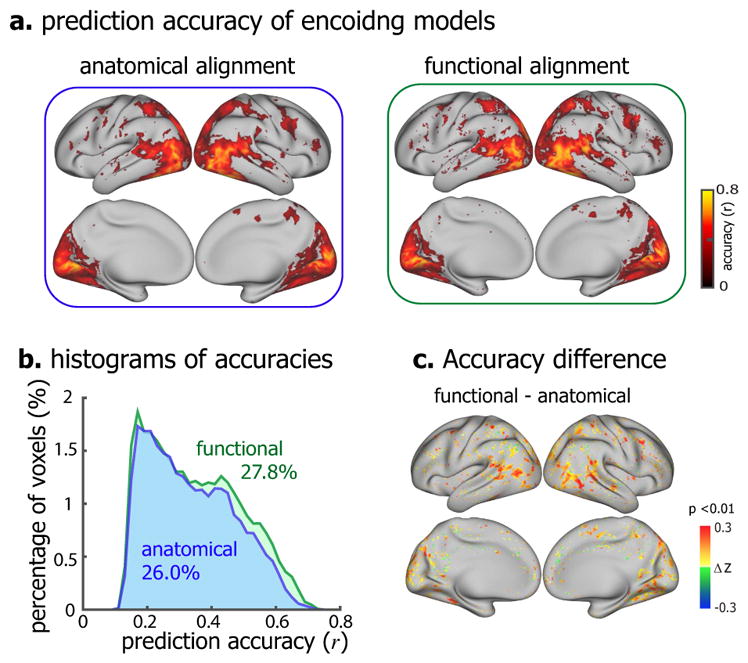
(a) Voxel-wise prediction accuracy of the encoding models based on anatomical alignment (left) and functional alignment (right) (permutation test, corrected at FDR q<0.01). (b) The histograms of prediction accuracies of anatomically aligned (blue) and functionally aligned (green) transferred encoding models. The colored numbers are the total percentages of predictable voxels. (c) The voxel-wise difference in prediction accuracy (Fisher’s z-transformation of r, i.e. z = arctanh(r)) between functional alignment and anatomical alignment (one-sample t-test, p<0.01). The figure shows the results for Subject XF, see Figure S5 for Subject XL.
Group-level encoding models
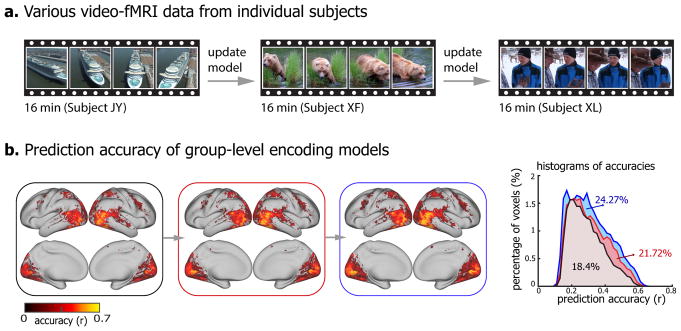
We further explored and tested an online learning strategy to train the encoding models for a group of subjects by incrementally using data from different subjects for model training (see Training group-level encoding models with online learning in Methods).
Basically, incremental neural data (16 minutes) was obtained from a new subject with new visual stimuli, and was used to update the existing encoding models (Fig. 6a). Such learning strategy allowed training group-level encoding models. The models significantly predicted the cortical response to novel testing movie for each subject (Fig. 6b). With every incremental update, the encoding models predicted wider cortical areas that increasingly covered 18.4%, 21.72%, and 24.27% of the cortex, and achieved higher prediction accuracies within the predictable areas (first update: Δz = 0.05 ± 0.0006, p<10−5; second update: Δz = 0.036 ± 0.00034, p<10−5, one-sample t-test) (Fig. 6.b). Meanwhile, the group-level encoding models exhibited similar predictability across individual subjects (Supplementary Fig. S6).
Figure 6. Group-level encoding models.
(a) Distinct video-fMRI dataset obtained from different subjects when watching different natural videos. (b) The voxel-wise prediction accuracy of group-level encoding models before and after every incremental update (permutation test, corrected at FDR q<0.01). The right is the histograms of prediction accuracies of incrementally updated encoding models. The colored numbers are the total percentages of predictable voxels. The testing accuracy is averaged across three subjects.
Discussion
In this article, we have described methods to transfer and generalize encoding models of natural vision across human subjects. Central to our methods is the idea of taking the models learnt from data from one subject (or a group of subjects) as the prior models for training the models for a new subject (or a new group of subjects). This idea allows to train subject-specific encoding models with a much less amount of training data than otherwise required if training the models from scratch without considering any pretrained model prior. The efficacy of this method, as demonstrated in this paper, suggests that different subjects share largely similar cortical representations of vision (Hasson et al., 2004; Haxby et al., 2011; Conroy et al., 2013; Chen et al., 2017). It has also led us to develop a method to train encoding models generalizable for a population by incrementally learning from different training data collected from different subjects.
The methods are described in the context of using DNN as a feature model, but they are also valuable and applicable to other models of visual or conceptual features (Kay et al., 2008; Naselaris et al., 2009; Nishimoto et al., 2011; Huth et al., 2012). In general, the larger the feature space is, the more data is required for training the model that relates the features to brain responses in natural vision. DNNs attempt to extract hierarchical visual features in many levels of complexity (Krizhevsky et al., 2012; Simonyan and Zisserman, 2014; Zeiler and Fergus, 2014; LeCun et al., 2015; Szegedy et al., 2015; He et al., 2016), and thus it is so-far most data demanding to model their relationships to the visual cortex. Nevertheless, DNNs are of increasing interest for natural vision (Cox and Dean, 2014; Khaligh-Razavi and Kriegeskorte, 2014; Yamins et al., 2014; Güçlü and van Gerven, 2015b, a; Kriegeskorte, 2015; Cichy et al., 2016; Wen et al., 2017, 2018; Eickenberg et al., 2017; Horikawa and Kamitani, 2017; Seeliger et al., 2017). Recent studies have shown that DNNs, especially convolutional neural networks for image recognition (Krizhevsky et al., 2012; Simonyan and Zisserman, 2014; He et al., 2016), preserve the representational geometry in object-sensitive visual areas (Khaligh-Razavi and Kriegeskorte, 2014; Yamins et al., 2014; Cichy et al., 2016), and predicts neural and fMRI responses to natural picture or video stimuli (Güçlü and van Gerven, 2015b, a; Wen et al., 2017, 2018; Eickenberg et al., 2017; Seeliger et al., 2017), suggesting their close relevance to how the brain organizes and processes visual information (Cox and Dean, 2014; Kriegeskorte, 2015; Yamins and DiCarlo, 2016; Kietzmann et al., 2017; van Gerven, 2017). DNNs also open new opportunities for mapping the visual cortex, including the cortical hierarchy of spatial and temporal processing (Güçlü and van Gerven, 2015b, a; Cichy et al., 2016; Wen et al., 2017; Eickenberg et al., 2017), category representation and organization (Khaligh-Razavi and Kriegeskorte, 2014; Wen et al., 2018), visual-field maps (Wen et al., 2017; Eickenberg et al., 2017), all by using a single experimental paradigm with natural visual stimuli. It is even possible to use DNNs for decoding visual perception or imagery (Wen et al., 2017; Horikawa and Kamitani, 2017). Such mapping, encoding, and decoding capabilities all require a large amount of data from single subjects in order to train subject-specific models. Results in this study suggest that even 10 hours of fMRI data in response to diverse movie stimuli may still be insufficient for DNN-based encoding models (Fig. 2). Therefore, it is difficult to generalize the models established with data from few subjects to a large number of subjects or patients for a variety of potential applications.
The methods developed in this study fill this gap, allowing DNN-based encoding models to be trained for individual subjects without the need to collect substantial training data from them. As long as models have been already trained with a large amount of data from existing subjects or previous studies, such models can be utilized as the prior models for a new subject and be updated with additional data from this subject. Results in this study demonstrate that with prior models, encoding models can be trained with 16-min video-fMRI data from a single subject to reach comparable encoding performance as the models otherwise trained with over two hours of data but without utilizing any prior models (Fig. 3). Apparently, data acquisition for 16 minutes readily fit into the time constraint of most fMRI studies. With the method described herein, it is thus realistic to train encoding models to effectively map and characterize visual representations in many subjects or patients for basic or clinical neuroscience research. The future application to patients with various cortical visual impairments, e.g. facial aphasia, has the potential to provide new insights to such diseases and their progression.
The methods developed for transferring encoding models across subjects might also be usable to transfer such models across imaging studies with different spatial resolution. The fMRI data in this study are of relatively low resolution (3.5mm). Higher resolution about 1mm is readily attainable with fMRI in higher field strengths (e.g. 7T or above) (Goense et al., 2016). Functional images in different resolution reflect representations in different spatial scales. High-field and high-resolution fMRI that resolves representations in the level of cortical columns or layers is of particular interest (Yacoub et al., 2008; Goense et al., 2016); but prolonged fMRI scans in high-field face challenges, e.g. head motion and susceptibility artifacts as well as safety concern of RF power deposition. Transferring encoding models trained with 3-T fMRI data in lower resolution to 7-T fMRI data in higher resolution potentially enables higher throughput with limited datasets. Note that transferring the encoding models is not simply duplicating the models across subjects or studies. Instead, new data acquired from different subjects or with different resolution serve to reshape the prior models to fit the new information in specific subjects or representational scales. It is perhaps even conceivable to use the method in this study to transfer encoding models trained with fMRI data to those with neurophysiological responses observable with recordings of unit activity, local field potentials, and electrocorticograms. As such, it has the potential to compare and converge neural coding in different spatial and temporal scales. However, such a potential is speculative and awaits verification in future studies.
This study also supports an extendable strategy for training population-wide encoding models by collecting data from a large group of subjects. In most of the current imaging studies, different subjects undergo the same stimuli or tasks with the same experiment paradigm and the same acquisition protocol (Hodge et al., 2016). Such study design allows for more convenient group-level statistics, more generalizable findings, and easier comparison across individuals. However, if one has to collect substantial data from each subject, it is practical too expensive or unrealistic to do so for a large number of subjects. An alternative strategy is to design a study for a large number of subjects, but only collect imaging data from subjects undergoing different visual stimuli, e.g. watching different videos. For the population as a whole, data with a large and diverse set of stimuli become available. The methods described herein lay the technical foundation to combine the data across subjects for training population-wide encoding models. This strategy may be further complemented by also using a small set of stimuli (e.g. 16-min video stimuli) common for all subjects. Such stimuli can be used to functionally align the data from different subjects to account for individual differences (Fig. 6) (Haxby et al., 2011; Conroy et al., 2013; Guntupalli et al., 2016). It also provides comparable testing data to assess individual differences.
In addition, our methods allow population-wide encoding models to be trained incrementally. For a study that involves data acquisition from many subjects, data are larger and growing. It is perhaps an unfavorable strategy to analyze the population data only after data are available from all subjects. Not only is it inefficient, analyzing the population data as a whole requires substantial computing resources – a common challenge for “big data”. Using online learning (Fontenla-Romero et al., 2013), the methods described herein allows models to be trained and refined as data acquisition progresses. Researchers can examine the evolution of the trained models, and decide whether the models have converged to avoid further data acquisition. As population-wide encoding models become available, it is more desirable to use them as the prior models for training encoding models for specific subjects, or another population. Population-wide models are expected to be more generalizable than models trained from one or few subjects, making the prior models more valid and applicable for a wide group of subjects or patients.
Beyond the methods described in this paper, the notion of transferring encoding models across subjects may be substantiated with further methodological development. In this study, the encoding parameters in the prior model was used to constrain the mean of the parameters in a new model, whereas the covariance of the parameters were assumed to be isotropic. As such, all the parameters were assumed to bear different means but the same variance while being independent of each other. The assumption of independence was valid, because the feature space was reduced to a lower dimension, and was represented by its (orthogonal) principal components. The assumption of isotropic variance might be replaced by a more general covariance structure, in which the prior variance is allowed to be different for the parameters of individual features. Although it is possible to estimate the prior variance from the data, it requires a larger amount of training data and iterative optimization to estimate both the model parameters and their prior (anisotropic) variances for the maximum posterior probability (Berger 2013). The demand for data and computation is what we aim to mitigate. Therefore, our assumption of isotropic variance is a legitimate choice, even though it may or may not be optimal.
In this paper, the method for transferring encoding models across subjects is described in the framework of Bayesian inference. Incorporating a pretrained model in the prior allows us to transfer the knowledge about encoding models from one subject to another subject. In the present study, we proposed a transferred prior that constrained the means of the encoding parameters to be close to those of a prior model, while assuming a priori Gaussian distribution for each parameter. Given these assumptions, the method is effectively ridge regression estimator with an extra L2-norm constraint for regularization, and the model estimation is thus linear and computationally efficient. Nevertheless, a more general description in the framework of Bayesian inference is useful for other model assumptions to be explored in future extension of this method.
In this study, we also assume a voxel-wise correspondence between one brain and another (Hasson et al., 2004). This assumption may not be optimal given the individual differences in the brain’s structure and function (Haxby et al., 2011; Conroy et al., 2013). In addition to anatomical alignment (Glasser et al., 2016), functional hyperalignment (Guntupalli et al., 2016) is helpful to partly account for the individual differences, before transferring voxel-wise encoding models across subjects. It is also likely helpful to statistically summarize the prior model across neighboring voxels, or in a region that contains the target voxel. Refinement of the algorithms for transferring encoding models awaits future studies.
In this study, a two-step PCA was used to reduce the dimension of the feature space prior to training the linear response model to relate visual features to brain responses. In the first step, PCA reduced the redundancy of features within each layer; in the second step, PCA reduced the feature space by taking into account the dependency of features in different layers. This strategy for dimension reduction was especially effective for estimating the encoding models with limited training data while mitigating the risk of overfitting (Wen et al., 2018; Shi et al., 2018). However, it should be noted that PCA is not a central to transferring encoding models across different subjects. What is central to this paper is the proposed cross-subject transferring and generalizing methods, which may be combined with other alternative methods for feature selection or dimension reduction (Li, 2004; Smith et al., 2014; St-Yves and Naselaris, 2017). In particular, Smith et al. has demonstrated that incremental PCA is more favorable for handling large and growing datasets than conventional PCA (Smith et al., 2014).
In this study, we collected video-fMRI dataset from three subjects. Although the number of the subjects seems small, the fMRI data from all three subjects reaches a total of 44.8 hours, which is very large and unique. The proposed methods for transferring and generalizing encoding models across subjects achieved consistent and significant results. As each subject watched five testing movies, each for 10 times, for a total of 6.7 hours, repeating this paradigm for a large number of subjects, although desirable, is not realistic within the scope of this project.
Lastly, this study focuses exclusively on natural vision. However, the methods developed are anticipated to serve well for more general purposes, including natural language processing, speech and hearing.
Supplementary Material
Voxel-wise prediction accuracy of encoding models trained with 16min (a) and 2.13h (b) video-fMRI data (permutation test, corrected at FDR q<0.01). The top shows the voxel-wise prediction accuracy of the encoding models with the prior transferred from a pretrained model (right) and the encoding models without any transferred prior (left). The bottom left is the histograms of their respective prediction accuracies. The numbers are the total percentage of predictable voxels. The bottom right is the difference of prediction accuracy (Fisher’s z-transformation of r, i.e. z = arctanh(r)) between the encoding models with the transferred prior and those without any transferred prior (one-sample t-test, p<0.01). The figure shows the results for transferring from Subject JY to Subject XL.
Voxel-wise prediction accuracy of encoding models trained with 16min video-fMRI data (permutation test, corrected at FDR q<0.01). Each row shows the voxel-wise prediction accuracy of the encoding models without any transferred prior (left), the encoding models with the prior transferred from a pretrained model (middle), and the histograms of their respective prediction accuracies. The numbers are the total percentage of predictable voxels.
Voxel-wise prediction accuracy of the encoding models that were transferred from prior models and trained with 16min training data (left) and the encoding models trained with 2.13h training data without any transferred prior (middle) (permutation test, corrected at FDR q<0.01). The right shows the histograms of their respective prediction accuracies.
(a) Voxel-wise prediction accuracy by directly using the prior encoding models (from Subject JY) to predict the responses to novel testing movies for Subject XL (permutation test, corrected at FDR q<0.01). (b) and (c) show the histograms of prediction accuracies of the encoding models that were transferred from the prior encoding models (blue) and the prior encoding models (green) trained with 16min (b) and 2.13h (c) training data, respectively. See Figure 4 for Subject XF.
(a) Voxel-wise prediction accuracy of transferred encoding models based on anatomical alignment (left) and functional alignment (right) (permutation test, corrected at FDR q<0.01). (b) The histograms of prediction accuracies of anatomically aligned (blue) and functionally aligned (green) transferred encoding models. The colored numbers are the total percentages of predictable voxels. (c) The voxel-wise difference in prediction accuracy (Fisher’s z-transformation of r, i.e. z = arctanh(r)) between functional alignment and anatomical alignment (one-sample t-test, p<0.01). The figure shows the results for Subject XL, see Figure 5 for Subject XF.
The group-level encoding models are trained with the data from three subjects (Subject JY, XF, and XL) by using online learning algorithm. Each panel shows the accuracy of such group-level encoding models in predicting the cortical responses to novel testing movie for each subject (permutation test, corrected at FDR q<0.01).
Acknowledgments
The authors are thankful to Dr. Xiaohong Zhu and Dr. Byeong-Yeul Lee for constructive discussion. The research was supported by NIH R01MH104402 and Purdue University.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Adolf D, Weston S, Baecke S, Luchtmann M, Bernarding J, Kropf S. Increasing the reliability of data analysis of functional magnetic resonance imaging by applying a new blockwise permutation method. Frontiers in neuroinformatics. 2014;8:72. doi: 10.3389/fninf.2014.00072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berger JO. Statistical decision theory and Bayesian analysis. Springer Science & Business Media; 2013. [Google Scholar]
- Chen J, Leong YC, Honey CJ, Yong CH, Norman KA, Hasson U. Shared memories reveal shared structure in neural activity across individuals. Nature neuroscience. 2017;20:115–125. doi: 10.1038/nn.4450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen M, Han J, Hu X, Jiang X, Guo L, Liu T. Survey of encoding and decoding of visual stimulus via FMRI: an image analysis perspective. Brain imaging and behavior. 2014;8:7–23. doi: 10.1007/s11682-013-9238-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cichy RM, Khosla A, Pantazis D, Torralba A, Oliva A. Comparison of deep neural networks to spatio-temporal cortical dynamics of human visual object recognition reveals hierarchical correspondence. Scientific reports. 2016:6. doi: 10.1038/srep27755. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Conroy BR, Singer BD, Guntupalli JS, Ramadge PJ, Haxby JV. Inter-subject alignment of human cortical anatomy using functional connectivity. NeuroImage. 2013;81:400–411. doi: 10.1016/j.neuroimage.2013.05.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cox DD, Dean T. Neural networks and neuroscience-inspired computer vision. Current Biology. 2014;24:R921–R929. doi: 10.1016/j.cub.2014.08.026. [DOI] [PubMed] [Google Scholar]
- Deng J, Dong W, Socher R, Li L, Li K, Fei-Fei L. Imagenet: A large-scale hierarchical image database. In Computer Vision and Pattern Recognition. CVPR 2009. IEEE Conference on; IEEE; 2009. pp. 248–255. [Google Scholar]
- Dias FM, Antunes A, Vieira J, Mota AM. Implementing the levenberg-marquardt algorithm on-line: A sliding window approach with early stopping. IFAC Proceedings Volumes. 2004;37:49–54. [Google Scholar]
- Eickenberg M, Gramfort A, Varoquaux G, Thirion B. Seeing it all: Convolutional network layers map the function of the human visual system. NeuroImage. 2017;152:184–194. doi: 10.1016/j.neuroimage.2016.10.001. [DOI] [PubMed] [Google Scholar]
- Fan J, Han F, Liu H. Challenges of big data analysis. National science review. 2014;1:293–314. doi: 10.1093/nsr/nwt032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fontenla-Romero Ó, Guijarro-Berdiñas B, Martinez-Rego D, Pérez-Sánchez B, Peteiro-Barral D. Online machine learning. Efficiency and Scalability Methods for Computational Intellect. 2013:27. [Google Scholar]
- Geisser S. Predictive inference. CRC press; 1993. [Google Scholar]
- Glasser MF, Sotiropoulos SN, Wilson JA, Coalson TS, Fischl B, Andersson JL, Xu J, Jbabdi S, Webster M, Polimeni JR. The minimal preprocessing pipelines for the Human Connectome Project. Neuroimage. 2013;80:105–124. doi: 10.1016/j.neuroimage.2013.04.127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glasser MF, Coalson TS, Robinson EC, Hacker CD, Harwell J, Yacoub E, Ugurbil K, Andersson J, Beckmann CF, Jenkinson M. A multi-modal parcellation of human cerebral cortex. Nature. 2016 doi: 10.1038/nature18933. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goense J, Bohraus Y, Logothetis NK. fMRI at high spatial resolution: implications for BOLD-models. Frontiers in computational neuroscience. 2016:10. doi: 10.3389/fncom.2016.00066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Güçlü U, van Gerven MA. Deep neural networks reveal a gradient in the complexity of neural representations across the ventral stream. Journal of Neuroscience. 2015a;35:10005–10014. doi: 10.1523/JNEUROSCI.5023-14.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Güçlü U, van Gerven MA. Increasingly complex representations of natural movies across the dorsal stream are shared between subjects. NeuroImage. 2015b doi: 10.1016/j.neuroimage.2015.12.036. [DOI] [PubMed] [Google Scholar]
- Guntupalli JS, Hanke M, Halchenko YO, Connolly AC, Ramadge PJ, Haxby JV. A model of representational spaces in human cortex. Cerebral cortex. 2016;26:2919–2934. doi: 10.1093/cercor/bhw068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Han K, Wen H, Shi J, Lu K, Zhang Y, Liu Z. Variational autoencoder: An unsupervised model for modeling and decoding fMRI activity in visual cortex. bioRxiv. 2017 doi: 10.1016/j.neuroimage.2019.05.039. doi: https://doi.org/10.1101/214247. [DOI] [PMC free article] [PubMed]
- Hasson U, Nir Y, Levy I, Fuhrmann G, Malach R. Intersubject synchronization of cortical activity during natural vision. science. 2004;303:1634–1640. doi: 10.1126/science.1089506. [DOI] [PubMed] [Google Scholar]
- Haxby JV, Guntupalli JS, Connolly AC, Halchenko YO, Conroy BR, Gobbini MI, Hanke M, Ramadge PJ. A common, high-dimensional model of the representational space in human ventral temporal cortex. Neuron. 2011;72:404–416. doi: 10.1016/j.neuron.2011.08.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He K, Zhang X, Ren S, Sun J. Deep residual learning for image recognition. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition; 2016. pp. 770–778. [Google Scholar]
- Hodge MR, Horton W, Brown T, Herrick R, Olsen T, Hileman ME, McKay M, Archie KA, Cler E, Harms MP. ConnectomeDB—sharing human brain connectivity data. Neuroimage. 2016;124:1102–1107. doi: 10.1016/j.neuroimage.2015.04.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horikawa T, Kamitani Y. Generic decoding of seen and imagined objects using hierarchical visual features. 2017;8:15037. doi: 10.1038/ncomms15037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huth AG, Nishimoto S, Vu AT, Gallant JL. A continuous semantic space describes the representation of thousands of object and action categories across the human brain. Neuron. 2012;76:1210–1224. doi: 10.1016/j.neuron.2012.10.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kay KN, Naselaris T, Prenger RJ, Gallant JL. Identifying natural images from human brain activity. Nature. 2008;452:352–355. doi: 10.1038/nature06713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khaligh-Razavi S-M, Kriegeskorte N. Deep supervised, but not unsupervised, models may explain IT cortical representation. PLoS Comput Biol. 2014;10:e1003915. doi: 10.1371/journal.pcbi.1003915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kietzmann TC, McClure P, Kriegeskorte N. Deep Neural Networks In Computational Neuroscience. bioRxiv. 2017:133504. [Google Scholar]
- Kriegeskorte N. Deep neural networks: a new framework for modeling biological vision and brain information processing. Annual Review of Vision Science. 2015;1:417–446. doi: 10.1146/annurev-vision-082114-035447. [DOI] [PubMed] [Google Scholar]
- Krizhevsky A, Sutskever I, Hinton GE. Imagenet classification with deep convolutional neural networks. Advances in neural information processing systems. 2012:1097–1105. [Google Scholar]
- LeCun Y, Bengio Y, Hinton G. Deep learning. Nature. 2015;521:436–444. doi: 10.1038/nature14539. [DOI] [PubMed] [Google Scholar]
- Li Y. On incremental and robust subspace learning. Pattern recognition. 2004;37(7):1509–1518. [Google Scholar]
- Lu KH, Hung SC, Wen H, Marussich L, Liu Z. Influences of High-Level Features, Gaze, and Scene Transitions on the Reliability of BOLD Responses to Natural Movie Stimuli. PloS one. 2016;11(8):e0161797. doi: 10.1371/journal.pone.0161797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Naselaris T, Kay KN, Nishimoto S, Gallant JL. Encoding and decoding in fMRI. Neuroimage. 2011;56:400–410. doi: 10.1016/j.neuroimage.2010.07.073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Naselaris T, Prenger RJ, Kay KN, Oliver M, Gallant JL. Bayesian reconstruction of natural images from human brain activity. Neuron. 2009;63:902–915. doi: 10.1016/j.neuron.2009.09.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nishimoto S, Vu AT, Naselaris T, Benjamini Y, Yu B, Gallant JL. Reconstructing visual experiences from brain activity evoked by natural movies. Current Biology. 2011;21:1641–1646. doi: 10.1016/j.cub.2011.08.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paltoo DN, Rodriguez LL, Feolo M, Gillanders E, Ramos EM, Rutter J, Sherry S, Wang VO, Bailey A, Baker R. Data use under the NIH GWAS data sharing policy and future directions. Nature genetics. 2014;46:934. doi: 10.1038/ng.3062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paninski L, Pillow J, Lewi J. Statistical models for neural encoding, decoding, and optimal stimulus design. Progress in brain research. 2007;165:493–507. doi: 10.1016/S0079-6123(06)65031-0. [DOI] [PubMed] [Google Scholar]
- Poldrack RA, Gorgolewski KJ. Making big data open: data sharing in neuroimaging. Nature neuroscience. 2014;17:1510–1517. doi: 10.1038/nn.3818. [DOI] [PubMed] [Google Scholar]
- Raz G, Svanera M, Singer N, Gilam G, Cohen MB, Lin T, Admon R, Gonen T, Thaler A, Granot RY, Goebel R. Robust inter-subject audiovisual decoding in functional magnetic resonance imaging using high-dimensional regression. Neuroimage. 2017;163:244–263. doi: 10.1016/j.neuroimage.2017.09.032. [DOI] [PubMed] [Google Scholar]
- Sahani M, Linden JF. Evidence optimization techniques for estimating stimulus-response functions. Advances in neural information processing systems. 2003:317–324. [Google Scholar]
- Schönemann PH. A generalized solution of the orthogonal Procrustes problem. Psychometrika. 1966;31:1–10. [Google Scholar]
- Seeliger K, Fritsche M, Güçlü U, Schoenmakers S, Schoffelen J-M, Bosch S, van Gerven M. Convolutional neural network-based encoding and decoding of visual object recognition in space and time. NeuroImage. 2017 doi: 10.1016/j.neuroimage.2017.07.018. [DOI] [PubMed] [Google Scholar]
- Shi J, Wen H, Zhang Y, Han K, Liu Z. Deep recurrent neural network reveals a hierarchy of process memory during dynamic natural vision. Human Brain Mapping. 2018 doi: 10.1002/hbm.24006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simonyan K, Zisserman A. Very deep convolutional networks for large-scale image recognition. 2014 arXiv preprint arXiv:14091556. [Google Scholar]
- Smith SM, Hyvärinen A, Varoquaux G, Miller KL, Beckmann CF. Group-PCA for very large fMRI datasets. Neuroimage. 2014;101:738–749. doi: 10.1016/j.neuroimage.2014.07.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- St-Yves G, Naselaris T. The feature-weighted receptive field: an interpretable encoding model for complex feature spaces. bioRxiv. 2017:126318. doi: 10.1016/j.neuroimage.2017.06.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szegedy C, Liu W, Jia Y, Sermanet P, Reed S, Anguelov D, Erhan D, Vanhoucke V, Rabinovich A. Going deeper with convolutions. Proceedings of the IEEE conference on computer vision and pattern recognition; 2015. pp. 1–9. [Google Scholar]
- Teeters JL, Harris KD, Millman KJ, Olshausen BA, Sommer FT. Data sharing for computational neuroscience. Neuroinformatics. 2008;6:47–55. doi: 10.1007/s12021-008-9009-y. [DOI] [PubMed] [Google Scholar]
- Tipping ME. Sparse Bayesian learning and the relevance vector machine. Journal of machine learning research. 2001 Jun;1:211–244. [Google Scholar]
- Trappenberg T. Fundamentals of computational neuroscience. OUP Oxford; 2009. [Google Scholar]
- Van Essen DC, Smith SM, Barch DM, Behrens TE, Yacoub E, Ugurbil K Consortium W-MH. The WU-Minn human connectome project: an overview. Neuroimage. 2013;80:62–79. doi: 10.1016/j.neuroimage.2013.05.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Gerven M. Computational Foundations of Natural Intelligence. bioRxiv. 2017:166785. doi: 10.3389/fncom.2017.00112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wen H, Shi J, Zhang Y, Lu K-H, Liu Z. Neural Encoding and Decoding with Deep Learning for Dynamic Natural Vision. Cerebral Cortex. 2017 doi: 10.1093/cercor/bhx268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wen H, Shi J, Chen W, Liu Z. Deep Residual Network Predicts Cortical Representation and Organization of Visual Features for Rapid Categorization. Scientific reports. 2018;8(1):3752. doi: 10.1038/s41598-018-22160-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yacoub E, Harel N, Uğurbil K. High-field fMRI unveils orientation columns in humans. Proceedings of the National Academy of Sciences. 2008;105:10607–10612. doi: 10.1073/pnas.0804110105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamins DL, DiCarlo JJ. Using goal-driven deep learning models to understand sensory cortex. Nature neuroscience. 2016;19:356–365. doi: 10.1038/nn.4244. [DOI] [PubMed] [Google Scholar]
- Yamins DL, Hong H, Cadieu CF, Solomon EA, Seibert D, DiCarlo JJ. Performance-optimized hierarchical models predict neural responses in higher visual cortex. Proceedings of the National Academy of Sciences. 2014;111:8619–8624. doi: 10.1073/pnas.1403112111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeiler MD, Fergus R. Visualizing and understanding convolutional networks. European conference on computer vision; Springer; 2014. pp. 818–833. [Google Scholar]
- Zha H, Simon HD. On updating problems in latent semantic indexing. SIAM Journal on Scientific Computing. 1999;21:782–791. [Google Scholar]
- Zhao H, Yuen PC, Kwok JT. A novel incremental principal component analysis and its application for face recognition. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics) 2006;36:873–886. doi: 10.1109/tsmcb.2006.870645. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Voxel-wise prediction accuracy of encoding models trained with 16min (a) and 2.13h (b) video-fMRI data (permutation test, corrected at FDR q<0.01). The top shows the voxel-wise prediction accuracy of the encoding models with the prior transferred from a pretrained model (right) and the encoding models without any transferred prior (left). The bottom left is the histograms of their respective prediction accuracies. The numbers are the total percentage of predictable voxels. The bottom right is the difference of prediction accuracy (Fisher’s z-transformation of r, i.e. z = arctanh(r)) between the encoding models with the transferred prior and those without any transferred prior (one-sample t-test, p<0.01). The figure shows the results for transferring from Subject JY to Subject XL.
Voxel-wise prediction accuracy of encoding models trained with 16min video-fMRI data (permutation test, corrected at FDR q<0.01). Each row shows the voxel-wise prediction accuracy of the encoding models without any transferred prior (left), the encoding models with the prior transferred from a pretrained model (middle), and the histograms of their respective prediction accuracies. The numbers are the total percentage of predictable voxels.
Voxel-wise prediction accuracy of the encoding models that were transferred from prior models and trained with 16min training data (left) and the encoding models trained with 2.13h training data without any transferred prior (middle) (permutation test, corrected at FDR q<0.01). The right shows the histograms of their respective prediction accuracies.
(a) Voxel-wise prediction accuracy by directly using the prior encoding models (from Subject JY) to predict the responses to novel testing movies for Subject XL (permutation test, corrected at FDR q<0.01). (b) and (c) show the histograms of prediction accuracies of the encoding models that were transferred from the prior encoding models (blue) and the prior encoding models (green) trained with 16min (b) and 2.13h (c) training data, respectively. See Figure 4 for Subject XF.
(a) Voxel-wise prediction accuracy of transferred encoding models based on anatomical alignment (left) and functional alignment (right) (permutation test, corrected at FDR q<0.01). (b) The histograms of prediction accuracies of anatomically aligned (blue) and functionally aligned (green) transferred encoding models. The colored numbers are the total percentages of predictable voxels. (c) The voxel-wise difference in prediction accuracy (Fisher’s z-transformation of r, i.e. z = arctanh(r)) between functional alignment and anatomical alignment (one-sample t-test, p<0.01). The figure shows the results for Subject XL, see Figure 5 for Subject XF.
The group-level encoding models are trained with the data from three subjects (Subject JY, XF, and XL) by using online learning algorithm. Each panel shows the accuracy of such group-level encoding models in predicting the cortical responses to novel testing movie for each subject (permutation test, corrected at FDR q<0.01).