A First Step Towards Behavioral Coaching for Managing Stress: A Case Study on Optimal Policy Estimation with Multi-stage Threshold Q-learning

Abstract

Psychological stress is a major contributor to the adoption of unhealthy behaviors, which in turn accounts for 41% of global cardiovascular disease burden. While the proliferation of mobile health apps has offered promise to stress management, these apps do not provide micro-level feedback with regard to how to adjust one’s behaviors to achieve a desired health outcome. In this paper, we formulate the task of multi-stage stress management as a sequential decision-making problem and explore the application of reinforcement learning to provide micro-level feedback for stress reduction. Specifically, we incorporate a multi-stage threshold selection into Q-learning to derive an interpretable form of a recommendation policy for behavioral coaching. We apply this method on an observational dataset that contains Fitbit ActiGraph measurements and self-reported stress levels. The estimated policy is then used to understand how exercise patterns may affect users’ psychological stress levels and to perform coaching more effectively.

Introduction

Psychological stress has long been shown as the source of unhealthy behaviors and in turn contributes to the increase of cardiovascular disease risk [1]. Public health experts have been advocating on the importance of behavioral factors on cardiovascular risk, which account for 41% of global cardiovascular disease burden [2, 3]. Improving on exercise behaviors, in particular, has been shown as a cost-effective solution compared to pharmacological treatments. Recent research has demonstrated the benefit of regular exercise and physical activities on reducing stress and improving emotional well-being [4, 5]. Yet its implementation often fails due to the lack of systematic monitoring for effective coaching. Early research in clinical decision support systems has attempted to integrate multimodal sensor input to start guiding the management of psychological stress. However, its clinical uptake has been slow due to the lack of intuitive reasoning and explanation capability [6].

In fact, the stress-behavior mechanistic pathway is a process that is highly individualized, in which interpretations of the environmental demand and adaptive capacity (“appraisals”) are important in determining psychological, behavioral, and physiological responses to stress [7]. Previous clinical trials have demonstrated the effectiveness of individualized stress management for obtaining certain goals, e.g., hypertension control [8]. The recent proliferation of mobile health and self-tracking mobile apps has offered new promise to further integrate daily monitoring data into the process of individualized stress management. However, a most recent review of existing stress management apps [9] has shown that there is still a lack of apps that can provide user behavior-oriented feedback such as prompting for a specific goal. Therefore, how to leverage individual observations to provide incremental micro-level feedback has been a key challenge to the development of behavioral coaching systems.

In many other domains, recent technological advances in mobile health have used smart phones and wearable devices to collect data and deliver interventions over time. Evidence has emerged for the potential of drawing sequential patterns from patient-reported outcomes (PRO) [10] and Ecological Momentary Assessments (EMA) [11] to make predictions and recommendations. This is favorable by behavior scientists and healthcare researchers, since mobile devices provide an interactive platform that has great potential to promote heath behaviors and achieve better health outcomes [12, 13]. Despite that simply measuring users’ calories intake and exercise patterns has only limited effect on outcomes, such as long-term weight loss [14], it still has been expected that the development of mobile-based behavioral coaching systems would be beneficial to understand the implicit user preferences and barriers so as to guide users for goal obtainment with personalized training plans. In addition, behavior interventions can be tailored based on users’ changing needs and ongoing performance. The delivery of such interventions has started being attempted in the area of substance use disorder [15], physical activity [16], mental health [17, 18] and diabetic self-management [19]. Yet the methodology is under development for these behavior intervention studies.

As a first step towards an interactive and personalized behavioral coaching system for stress management, we need to build on the observations of actions and self-reported outcomes over time to derive recommendations of beneficial behaviors and to guide users to achieve healthy outcomes. Intuitively, this can be represented as a sequential decision-making problem. Under similar problem specifications, reinforcement learning algorithms [20], for example Q-learning, can be applied to solve this problem by estimating an optimal policy, i.e., a set of decision rules for selecting actions that maximize long-range cumulative reward. However, the “black-box” nature of reinforcement learning algorithms makes it less appealing for stress management coaching systems that require explicit explanations for recommended actions -- as demonstrated in the previous clinical decision support research [6]. In many other fields, such as clinical trials, explicit explanations are also preferred for decision-making. Statistical methods have been developed for prescribing adaptive treatment regimes in clinical trials [21, 22, 23]. In this paper, we apply a Multi-stage Threshold Q-learning (MTQL) method and construct interpretable policies that map from subjects’ up-to-date observations to recommend actions adaptively for stress reduction coaching. We make model assumptions for the Q-leaning algorithm and incorporate a threshold-finding step to identify optimal sub-goals for recommendation. In the rest of this paper, we will first introduce the stress data used in the study and describe the MTQL method. Then we will demonstrate and discuss the interpretable policies derived from the MTQL method on the dataset.

Method

Data Collection

In this paper, the stress dataset used was collected in a longitudinal study during Jan 2014 to July 2015 from 79 subjects. The observations used to evaluate the MTQL method were from the first twelve weeks of the study. 75 subjects had complete data for that period of time.

Subjects in the study were healthy individuals aged 18 or older who responded to fliers posted throughout the buildings of Columbia University Medical Center and who on phone screening reported only intermittent engagement in exercise (exercise 6-11 times per month, not on a regular basis), had daily access to a computer with Internet, and had an iPhone or Android phone. Excluded were individuals who had previously been told by a healthcare professional to restrict physical activity, were deemed unable to comply with the protocol (either self-selected, by indicating during screening that he/she could not complete all requested tasks), were unavailable during the following continuous twelve months, had serious medical comorbidity that would compromise their ability to engage in usual physical activity, had occupational work demands that required rigorous activity or would make responding to the EMA dangerous, or were unable to read and speak English.

Physical activity was continuously and objectively measured using a wrist-based model of the Fitbit (Fitbit Flex; Fitbit, Inc., San Francisco, CA) [24]. The Fitbit Flex is a microelectromechanical triaxial accelerometer that tracks the wearer’s daily physical activity including steps, intensity of activities (sedentary, light, moderate, or vigorous) and energy expenditure. We and others have shown that the Fitbit Flex is a valid and reliable device for measuring physical activity in adults [25, 26].

Minute-by-minute activity data were extracted using Fitabase (Small Steps Labs, San Diego, California). We defined a “social day” as the period from 3am one day until 2:59am the next day. Non-wear was defined as greater than 60 consecutive minutes with fewer than 10 steps. Only days with a minimum of 10 hours of wear time were included in analyses. Each valid day was then classified as an exercise or non-exercise day. Our objective measure for exercise was defined as at least 24 minutes of moderate or vigorous physical activity (MVPA) within any consecutive 30-minute period, thereby allowing for up to 6 minutes of below threshold physical activity (e.g., rest). Such an instance is referred to as an “MVPA bout”. This definition was adapted from conventional accelerometer processing approaches used in many population-based studies [27, 28, 29] and suggested by best practice recommendations [30] wherein a healthful bout of physical activity is defined as a 10-minute or longer bout of MVPA with an allowance of 2 minutes below threshold (e.g. 8 out of 10 consecutive minutes). The 8 out of 10-minute bout was extrapolated to 30 minutes for the purposes of this study to be consistent with physical activity guidelines which recommend exercise in bouts of 10 minutes or more for at least 30 minutes a day, while accommodating interruptions.

An electronic diary that used the subject’s own iPhone or Android phone was used to capture momentary and summary aspects of their perceived stress. Each morning upon rising, the subject responded to a question on a browser asking them, “Overall, how stressful do you expect today to be?” answered on a scale from 0 (Not at all) to 10 (Extremely). Similarly, each evening, the subject responded to a question on a browser asking them, “Overall, how stressful was your day?”, answered on the same scale. In addition, the diary system was programmed to query the subject via text message or email 3 random times per day over their preset hours of wakefulness (e.g., 7am-10pm), with the specific time period programmed individually according to the subject’s own sleep schedule. Notifications were separated by at least 1 hour. Each of the 3 daytime momentary assessments included questions concerning key sources of stress (one screen listing sources of stress including work, argument, traffic, deadline trouble, paying bills, running late, none, or other, with the subject checking all that apply) [31], stress appraisal using the four-item Perceived Stress Scale [32]. Before each prompt, the subject responded to a question asking “how stressful did you feel?”, answered on the scale specified before. Data transmission was secured via SSL (i.e., https) and sent to a managed server.

The data used for the analyses includes duration of daily MVPA bouts, perceived stress levels, exogenous and environmental factors (such as day in a week, daylight time, temperature and precipitation).

Problem Formulation for the Multi-stage Threshold Q-learning Method

We observed a sequence of data discussed in the last section and aim to maximize the mean stress level reduction from baseline over a given time period. At baseline, the subjects’ characteristics and stress information were collected. We defined the baseline stress level as the mean stress level over the first four-week of the study. After four weeks, daily actions (e.g., MVPA pattern) and daily health outcomes (e.g., stress level) were observed at each stage. The action was binary and defined as if the mean duration of daily MVPA bout over the time period of the stage was greater than 30 minutes then the action was denoted as 1 otherwise 0. Mean stress level was used as the health outcome of interest, which was a continuous value ranging from 0 to 10. Everyday the stress level was assessed three times during the wakefulness time of the subjects and the overall stress level was assessed at the end of the day. If the value of the overall stress level was not missing, then the daily stress level was defined as the overall stress level. Otherwise, it was defined as the average of the stress levels assessed during the wakefulness time. The stress level at each stage was calculated by averaging over the daily stress level during the time period of the stage. In a T-stage study for each subject i, we observe the data:

{O_i1, A_i1, O_i2, A_i2,…, O_iT, A_iT, O_i(T+1)}

O_i1 is a baseline stress level, O_it, where 1 < t < T +1, is a stress level at the (t-1)-stage, and A_it is a binary action at the t-stage. Since stress levels were self-evaluated, subtracting the baseline stress level from the following stress levels evaluated helps to adjust for heterogeneity of self-evaluation across subjects. We define R_it = O_i1 − O_i(t+i) as the stress reduction from baseline at the t-stage, which is also the reward at the t-stage. We use H_it to denote historical information for subject i before the t-stage, for example H_il = {O_i1} and H_i2 = {0_i1, A_i1, O_i2}.

Q-learning is a commonly used method of reinforcement learning introduced by computer scientists to construct high quality policies [20]. Q-learning models the interaction between an agent and environment. In our setting, the agent refers to each subject in the study, and environment refers to the system of human body and external source of observations. The Q-learning algorithm uses a backward induction to estimate the optimal policy π, which consists of a sequence of decision rules π₁,…, π_T, under which the cumulative reward is maximized. At the t-stage, a decision rule π_t takes the historical information of a subject H_it as an input and outputs a recommended action A_it. The i-th subject with historical information H_it takes an action A_it and gains a reward R_it. In the computer science field, researchers focus on solving infinite time horizon decision-making problems [20], while in the statistical field, methodologies were developed to solve finite time horizon problems using statistical models [21–23, 33–36]. The MTQL method combines statistical methods with the Q-learning algorithm to construct interpretable decision rules. In the following, we use lower-case variables to denote the realizations of the corresponding upper-case random variables. We define a value function at the t-stage:

$$V_t\left({\text{h}}_t\right)=E_{\pi }\left({\displaystyle \sum _{k=0}^T{r}_{t+k}|{\text{h}}_t}\right)$$

Then the optimal value function is the one maximized over all possible policies π in the policy space Π, i.e., $V_t^{*}\left({\text{h}}_t\right)={\max }_{\pi \in \Pi }{V}_t\left({\text{h}}_t\right)$. We define the optimal Q function at the t-stage:

$$Q_t^{*}\left({\text{h}}_t,{\text{a}}_t\right)=E\left[r_t+V_{t+1}^{*}\left({\text{h}}_{t+1}\right)|{\text{h}}_t,{\text{a}}_t\right]$$

By definition, the relationship between a value function and a Q function is $V_t^{*}\left({\text{h}}_t\right)={\max }_{{\text{a}}_t}{Q}_t^{*}\left({\text{h}}_t,{\text{a}}_t\right)$, thus

$$Q_t^{\ast }\left({\text{h}}_t,{\text{a}}_t\right)=E\left[r_t+{\max }_{{\text{a}}_{t+1}}{Q}_{t+1}^{\ast }\left({\text{h}}_{t+1},{\text{a}}_{\text{t+1}}\right)|{\text{h}}_t,{\text{a}}_t\right]$$

The optimal Q function $Q_t^{\ast }$ (referred to as the Q function in the following) is estimated based on the Bellman equation [37] backwards through time. The optimal policy is defined as ${\pi }_t^{\ast }\left({\text{h}}_t\right)=\arg {\max }_{{\text{a}}_t}{Q}_t^{\ast }\left({\text{h}}_t,{\text{a}}_t\right)$.

In our proposed MTQL method, we assume a regression model for the Q function. The benefit of assuming a regression model is to make the estimated Q function and policy interpretable. A threshold-selection step is added into the learning process. The thresholds are set for the health outcome variables and selected by maximizing the expected cumulative reward. The estimated thresholds are considered as goal-setting options of the health outcome. To formulate the problem in mathematical terms, we define X_it as stress reduction from the previous stage, i.e., X_it = O_it − O_i(t+i), and define a dichotomized variable of X_it as I_it = l(X_it > c_t), where 1(·) is an indicator function and c_t is the threshold to be estimated. If X_it exceeds the threshold c_t, then I_it = 1, otherwise I_it = 0. The variable I_it indicates whether the change of stress level from the previous stage exceeds a threshold.

We illustrate the proposed method in multi-stage studies and discuss the effect of setting different numbers of stages on the expected health outcome. Our goal is to estimate a sequence of optimal decision rules that maximizes the mean stress reduction from baseline over a four-week period. This can be formulated as a four-stage study (T=4) with one week for each stage, or a two-stage study (T=2) with two weeks for each stage, or a one-stage study (T=1) with four weeks for one stage. We describe the variables used in modeling Q functions in Table 1.

Table 1.

List of variables used in modeling Q functions.

Variable name	Variable label
Y	Mean stress level reduction from baseline over a four-week period.
O1	Baseline stress level (mean stress level at the first four-week of the study).
At	Binary action at the t-stage, t = 1,…, T.
Rt	Stress level reduction from baseline at the t-stage, t = 1,…, T.
Xt	Stress level reduction from the previous stage at the t-stage, t = 1,…, T.
It	Indicator of whether Xt exceeds a threshold, t = 1,…, T.

The Q function consists of the main effect and the interaction effect. The interaction effect assesses the association of the historical information and the value of the Q function under different actions. We use H_t0 = (1, R₁, A₁, R₂, A₂,…, R_t) to denote the design matrix for the main effect and use H_tl = (1, I_t-l, A_t-1, I_t, I_t-1A_t-1, A_t-1I_t) to denote the design matrix for the interaction effect. Let θ_t be a vector of regression coefficients which consists of the coefficients of the main effect θ_t0 and the coefficients of the interaction effect θ_tl, i.e., θ_t = (θ_t0, θ_tl). The model of the Q function at the t-stage, for t = 2,…, 7, is of the formml:

$$Q_t\left({\text{h}}_t,{\text{a}}_t;{\text{θ}}_{\text{t}},{\text{c}}_t\right)={\text{h}}_{t0}{\text{θ}}_{t0}+\left({\text{h}}_{t1}{\text{a}}_t\right){\text{θ}}_{t1}$$

For the first stage (t = 1), let H₁₀ = (1, O₁ and H₁₁ = (1,1(O₁ > c₁), thus

$$Q_1\left({\text{h}}_t,{\text{a}}_t;{\text{θ}}_{\text{t}},{\text{c}}_t\right)={\text{h}}_{10}{\text{θ}}_{10}+\left({\text{h}}_{11}{\text{a}}_1\right){\text{θ}}_{11}$$

The optimal policy is estimated from the last stage to the first stage using a backward induction. The optimal policy at the t-stage is of the form:

$${\pi }_t^{\ast }\left({\text{h}}_{t1};{\text{θ}}_{t1},{\text{c}}_t\right)=\arg {\max }_{{\text{a}}_t}\left({\text{h}}_{t1}{\text{a}}_t\right){\text{θ}}_{t1}$$

The parameters of a policy consist of the regression parameter θ_t and the threshold parameter c_t. θ_t is estimated as a least square estimator. More specifically, at final stage T given an estimated threshold parameter ${\widehat{\text{c}}}_T$,

$${\widehat{\text{θ}}}_T=\arg {\min }_{{\text{θ}}_T}{\displaystyle \sum _{i=1}^n{\left(R_{iT}-Q_T\left({\text{h}}_{iT},{\text{a}}_{iT};{\text{θ}}_{\text{T}}\text{,}{\widehat{\text{c}}}_T\right)\right)}^2}$$

At a previous stage t:

$${\widehat{Y}}_{it}=R_{it}+{\max }_{a_{i\left(t+1\right)}}{Q}_{t+1}\left({\text{h}}_{i\left(t+1\right)},{\text{a}}_{i\left(t+1\right)};{\widehat{\text{θ}}}_{t+1},{\widehat{\text{c}}}_{t+1}\right)$$

$${\widehat{\text{θ}}}_t=\arg \min {\text{θ}}_t{{\displaystyle \sum _{i=1}^n\left({\widehat{Y}}_{it}-Q_t\left({\text{h}}_{iT},{\text{a}}_{iT};{\text{θ}}_{\text{T}}\text{,}{\widehat{\text{c}}}_T\right)\right)}}^2$$

The estimated threshold parameter ĉ_t is chosen as the one that maximizes the mean stress level reduction from baseline Y. We introduce an inverse probability weighting estimator (IPWE) [34], which is an expected outcome under a given policy. IPWE does not depend on model assumptions, thus is robust to model misspecification. It is used to evaluate the estimated parametric policies. IPWE is defined as

$$\frac{{\displaystyle {\sum }_{i=1}^n{W}_i{Y}_i}}{{\displaystyle {\sum }_{i=1}^n{W}_i}}$$

where the weight

$$W_i=\frac{{\Pi }_{k=1}^{T}1\left(a_{ik}={\pi }_k\left({\text{h}}_{ik};{\text{θ}}_k,{\text{c}}_k\right)\right)}{{\Pi }_{k=1}^T{p}_k\left(a_{ik}|{\text{h}}_{ik}\right)}$$

$p_t\left(a_{it}|{\text{h}}_{it}\right)$ is a propensity score estimated using logistic regression. The logistic regression model is built based on variable selection using P-value less than 0.2 as a criterion, and it contains the variables of stress level, action, gender and mean precipitation. The threshold parameter c_t is estimated using the genetic algorithm [38] to maximize the mean stress reduction from baseline. Genetic algorithm is a heuristic searching algorithm and has computational advantages for solving optimization problems.

Policy Estimation from the Observational Data

In the observational study, we consider a binary action of whether exercising more than 30 minutes daily on average (i.e., daily MVPA bout on average is greater than 30 minutes) over the time period of a stage, and define “active” as exercising more than 30 minutes daily on average, and “inactive” otherwise. The health outcome of our interest is the self-evaluated stress level on average over the time period of a stage. We use the data of the first four weeks of the study for assessing the baseline information, the data of the second four weeks as the training data and the data of the third four weeks as the test data. We apply the MTQL method on the training data to estimate the optimal policy and evaluate it on the test data. The estimated tree-structured policy is presented below in Figure 1–3 respectively. Our goal is to compare the expected outcomes estimated in a one-stage study, in a two-stage study and in a four-stage study in order to evaluate the effect of setting different numbers of intervention stages.

Figure 1.

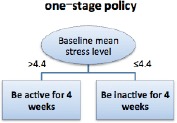
Estimated optimal policy for the one-stage study.

Figure 3.

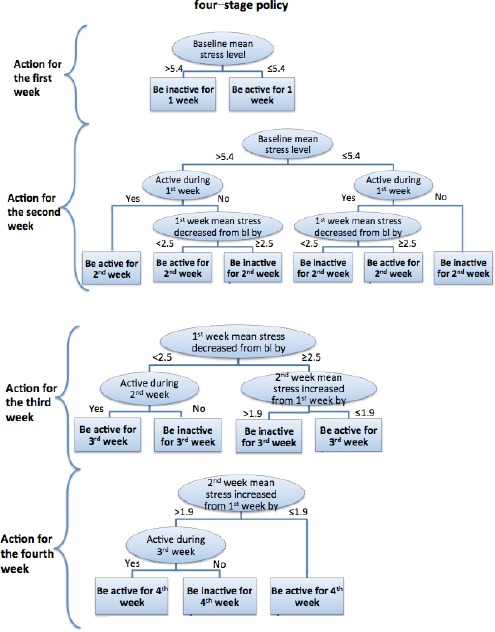
Estimated optimal policy for the four-stage study. Note: bl means baseline.

Results

Figure 1 shows the estimated optimal policy in a one-stage study over the time period of four weeks. That is, if a subject has perceived baseline stress level higher than 4.4 (on a scale of 0-10), then for obtaining the optimal stress reduction outcome, this subject should be recommended to stay “active” (i.e., exercising more than 30 minutes daily on average) in the next four weeks. This recommendation is similar to what has been offered by the existing stress management apps (as surveyed in [9]). The threshold learned here can help subjects and their care team to understand whether keeping active would be expected to yield a positive impact on the overall stress reduction for them.

As we expect that a fine-grained level of policy will reveal more actionable micro strategies for subjects and their care team, we further derive the optimal two- and four-stage policy from the data. Figure 2 shows the optimal policy estimated using the data of the first two weeks as one stage and the second two weeks as the other stage. The stress level 3.7 is learned as the baseline threshold to decide if we should recommend being active in the first two weeks, and 1.3 is learned as the threshold for the mean stress level increased from baseline to differentiate whether a target subject can potentially obtain an optimal outcome by adopting a sequential active-to-inactive strategy: i.e., staying active in the first two weeks, and then take a break in the next two weeks. For those subjects who have baseline stress level lower than or equal to 3.7, it would be important to observe whether being active in the first two weeks followed by an increase of mean stress level in the next two weeks. If the mean stress level increases greater than 1.3, then it is better not to suggest the active action any further to accommodate the individual behavioral preferences and barriers.

Figure 2.

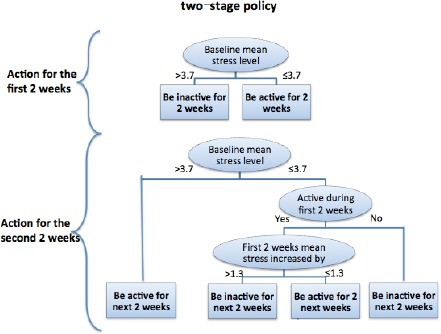
Estimated optimal policy for the two-stage study.

Figure 3 shows the finer-grained policy (one week as one stage) learned for making recommendations for subjects. It is important to know whether the target subject starts with a perceived mean stress level higher than 5.4, whether the subject is active during the first week and whether exercising helps reduce the subject’s mean stress level. The observed intermediate outcomes and actions would be important to determine whether to recommend being active or not in the next stage. To make the fourth stage recommendation, it is critical to keep observing for the mean stress level change in the second week and whether the user is active or not in the third week.

In addition to the empirical interpretation of the learned policy for curating actionable micro strategies, we are also interested in learning the quantifiable impact of a finer-grained policy on the overall outcome (i.e. the mean stress reduction from baseline). Applying the learned policies on the test data, the mean stress level reduction from baseline in the one-stage study is 0.04, the one in the two-stage study is 0.58, and the one in the four-stage study is 0.97. The distribution of the mean stress level reduction among the study subjects is shown in Figure 4. The estimated values of the mean stress level reduction based on different numbers of stages are indicated in Figure 4. The results show that dividing the study period into multiple stages and incorporating more sub-goals for micro-level feedback potentially help subjects achieving better stress reduction.

Figure 4.

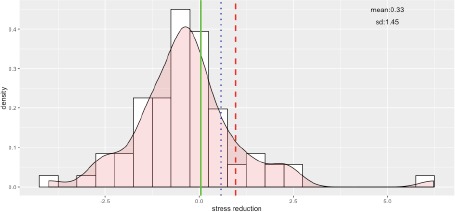
Histogram of the mean stress level reduction from baseline over a four-week period. The solid line is the mean stress level reduction following the estimated policy of the one-stage study; the dotted line is the one following the estimated policy of the two-stage study; the dashed line is the one following the estimated policy of the four-stage study.

Figure 4. Histogram of the mean stress level reduction from baseline over a four-week period. The solid line is the mean stress level reduction following the estimated policy of the one-stage study; the dotted line is the one following the estimated policy of the two-stage study; the dashed line is the one following the estimated policy of the four-stage study.

Discussion

There exist needs to propose new methods that can support the building of simple but interpretable decision making models and the discovery of optimal sub-goals so as to facilitate decision-making processes, instead of dictating interventions to subjects. In addition, a concern frequently raised for applying behavioral coaching is often that the evidence may not adequately reflect individual differences among users. In the past, psychologists and behavioral scientists have developed a variety of ideographic approaches for single-case experimental designs [39]. To extend the ideographic approach in experimental designs of intervention, researchers have further developed N-of-1 trials to help patients make health decisions that are informed by highly relevant, evidence-based information [40, 41, 42]. In this paper, we extend this school of thoughts to investigate how to further tie the insights learned from user-generated health data into an adaptive decision-making process. In particular, we develop a MTQL method to learn how to curate effective micro strategies for recommendations, with an implicit consideration of user preferences and barriers. The proposed method uses a simple form of regression models to approximate Q functions, and constructs an interpretable form of policies using the Q-learning algorithm. The policy learned using the MTQL method provides sub-goal setting options, which may affect the intervention process. In many other domains, such as tutoring, micro-level strategies have been validated to be beneficial in pragmatic settings [43, 44]. The proposed method in this paper provides a novel way to start exploring a more systematic monitoring and self-experimentation framework to derive sequential micro-level strategies for behavioral coaching.

Conclusion

In this paper we described a MTQL method to estimate the optimal policy in order to maximize the mean stress reduction for healthy adults over a four-week period. We implement the MTQL method on the stress data to illustrate the interpretability of the estimated policies and the way to provide recommendations based on the policies. The insights we gain from the stress data are three-fold: First, tracking whether intermediate stress reduction is achieved and what actions have been taken by a target user are important; the observations will affect the choice of different strategies of stress reduction in a longer term. Second, individualized stress management can benefit from the agility introduced by micro-level strategies. When we assume a finer-grained observation time unit, the system derives more effective micro-strategies that in turn lend support to subjects for achieving better stress reduction in a longer term. Moreover, when the system observes that a user has started going astray from his usual path, the system is still capable to find corresponding recommendations for this user for quick adaptation. Instead of insisting on the same recommendation for target users, the proposed approach is expected to be more flexible and effective in pragmatic settings. Last but not least, personal behavioral coaching recommendations have the potential to help managing people’s stress better by enabling more informed decision making. The derived insights are expected to benefit future collaborative care and self-care applications, such as sense making [19] and persuasive reminders [45]. These insights can also be used to provide feedback into adaptive N-of-1 trials [40, 41, 42] and self-experimentation [46]. Our work is a first step towards a behavioral coaching system, which can help consume systematic monitoring data of target users and transform the curated insights into micro-level feedback that can sequentially guide users through the care management process (or self-experimentation when applicable) to obtain the best possible outcome.