Learning Doctors’ Medicine Prescription Pattern for Chronic Disease Treatment by Mining Electronic Health Records: A Multi-Task Learning Approach

Abstract

Increasing learning ability from massive medical data and building learning methods robust to data quality issues are key factors toward building data-driven clinical decision support systems for medicine prescription decision support. Here, we attempted accordingly to address the factors using a multi-task neural network approach, benefiting from multi-task learning’s advantage in modeling commonalities to increase learning performance and neural network’s robustness to imprecise data. By mining electronic health record data, we learned medicine prescription patterns of multiple correlated antidiabetic agents in blood glucose control and antihypertensive drugs in blood pressure control scenarios. We achieved AUC increases of 0.02 to 0.06 in single drug prescription and an accuracy increase of 0.05 in prescription pattern prediction compared to logistic regression, demonstrating the efficacy of multi-task neural network approach in learning medicine prescription patterns.

Introduction

Clinical decision support systems (CDSSs) are health information technology systems that assist clinical decisionmaking tasks. CDSS can be broadly divided into two types of approaches: knowledge-based that relies on digitalized clinical guidelines, and data-driven that relies on gathering evidence from real-life medical data. Many publications convey the belief that CDSS, especially on electronic health record (EHR) platform, will provide decision support to achieve large gains in clinical performance, improving its quality, safety, and cost efficiency^1–3. The accumulation of EHR data has allowed us the opportunity to use big data analytics approaches for data-driven CDSS. Prior work on EHR data includes mining association rules and Bayesian networks between clinical orders and diagnoses^4,5. Datadriven CDSS from EHR can be regarded as learning from collective experience of many practitioners to automatically generate evidence for clinical decision support.

Though interest in data-driven CDSS has grown, its application remains limited. The reasons are primarily twofolds: the quality of data, and the ability to learn from data. EHR data suffers from three main data quality issues: incompleteness, inaccuracy, and inconsistency⁶. Incompleteness is reflected by missing values of many attributes. Inaccuracies are unavoidable during typing and are frequently caused by inappropriate use of ICD codes. Inconsistency is also reflected by the inconsistent ICD code use and the inconsistent value-unit match for laboratory tests. Apart from these EHR data quality issues, uncertainty and inconsistencies abound in clinical decision making due to a lack of consensus view on a same clinical condition and evidence to confirm or deny the efficacy of each view⁷, rendering each diagnosis, clinical order, and prescription less of a ground truth. Even with perfect data, the effectiveness of data-driven methods still depend on the capacity of machine learning algorithms to solve the problem.

In response to the limitations, efforts toward data-driven CDSS can be made from three perspectives: increasing data quality, increasing tolerance to data quality issues during learning, and increasing learning ability. The last two perspectives can be addressed in machine learning by using neural network. Neural networks have remarkable capability to derive meaning from imprecise or complicated data though suffering from a major disadvantage of difficulty in interpretation.

In this paper, we use neural networks to learn doctors’ medicine prescription patterns in chronic disease treatment by mining EHR data to benefit from neural network’s properties of robustness to imprecise data and capacity to learn complex tasks. Blood glucose control medication and blood pressure control medication in type 2 diabetes patients were considered. Seven types of antidiabetic agents were considered for blood glucose control: alpha-glucosidase inhibitors (AGIs), dipeptidyl peptidase-4 (DPP-4), thiazolidinediones (TZDs), biguanides, glinides, sulfonylureas, and insulin. Seven types of antihypertensive drugs were considered for blood pressure control: angiotensin-convertingenzyme inhibitors (ACEIs), alpha blockers, angiotensin II receptor blockers (ARBs), beta blockers, calcium channel blockers (CCBs), diuretics, and hydrochlorothiazide. In a typical medicine prescription for blood glucose control, a doctor can prescribe one to several of the seven kinds of drugs. Thus, to learn doctors’ prescription behavior, prescribing a certain kind of antidiabetic agent or not can be formulated into a binary classification problem, resulting in seven binary classifiers that can each be modeled by a neural network. In our observation, the prescription of the seven drugs are not mutually independent. To benefit from their commonalities while preserving the differences, a multitask learning approach was used to learn the prescription combination of the seven drugs. Multi-task learning has been applied in healthcare settings to solve various problems like disease risk prediction⁸, disease onset prediction⁹, and disease progression¹⁰ for its good representation learning capability. In antidiabetic agent prescription prediction, our multi-task neural network has shown AUC increases of 0.02 to 0.06 compared to logistic regression in the prediction of each single drug, and an accuracy increase of 0.05 in the prescription pattern prediction. In antihypertensive drug prescription prediction, the multi-task neural network has shown AUC increases of 0.02 to 0.03 compared to logistic regression in single drug prediction, though no accuracy increase in prescription pattern prediction was observed.

Our contribution is that we used a multi-task neural network approach to learn doctors’ medicine prescription pattern of multiple correlated drugs in blood glucose control and blood pressure control scenarios by mining EHR data, and has demonstrated its usefulness in solving these prescription problems.

Methods

Scenarios. Two scenarios were considered in this work: learning antidiabetic agent prescription for blood glucose control and learning antihypertensive drug prescription for blood pressure control. Data was each constructed and processed.

Data preparation. Deidentified EHR data of type 2 diabetes patients from Xiamen, China within a four-year period (August 2012 to April 2016) was used in this study. Each case is defined as a patient encounter that has a prescription of at least one of the drugs concerned. Features used are summarized in Table 1, including demographics, physical examinations, laboratory tests, recent prescriptions, and disease history. The prescription of each drug is concerned as a class label, resulting in seven class labels in each of the two scenarios.

Table 1:

Summary of features used in doctor’s medicine prescription pattern learning.

Category	Attribute	Type	Antidiabetic agent prescription	Antihypertensive drug prescription
Demographics	Gender	Categorical	Included	Included
	Age	Continuous	Included	Included
	Ethnic group	Categorical	Included	Included
	Education	Categorical	Included	Included
	Marriage	Categorical	Included	Included
	Occupation	Categorical	Included	Included
Physical examinations	Height	Continuous	Included	Included
	Weight	Continuous	Included	Included
	BMI	Continuous	Included	Included
	Blood pressure, systolic	Continuous	Included	Included
	Blood pressure, diastolic	Continuous	Included	Included
Laboratory tests	Serum creatinine level	Continuous	Included	Not included
	Fasting plasma glucose level	Continuous	Included	Not included
Recent prescriptions	Antidiabetic agents or Antihypertensive drugs	Boolean	AGIs	ACEIs
			DPP-4	Alpha blockers
			TZDs	ARBs
			Biguanides	Beta blockers
			Glinides	CCBs
			Sulfonylureas	Diuretics
			Insulin	Hydrochlorothiazide
Disease history	ICD codes	Boolean	862 codes	1,252 codes

Data imputation. In this work, missing values of categorical variables were imputed by randomly sampling a category from a discrete probability distribution calculated from non-missing values, while missing values of continuous variables were imputed by randomly sampling a number from a normal distribution fit with non-missing values.

Feature engineering. Demographics were first extracted and imputed. For physical examinations, the most recent ones before the patient encounter were used if multiple sets were available. The immediate ones after this patient encounter were used in the absence of previous ones. Missing values were imputed. In antihypertensive drug prescription prescription, cases with imputed blood pressures were excluded. Two laboratory tests were used for antidiabetic agent prescription since blood glucose level is a major indicator of such prescriptions, but were not used for antihypertensive drug prescription due to the rare availability of these tests. Test results within three months before or after the case were taken as valid. Only cases with valid test results were used for the antidiabetic agent prescription prediction. Disease history was constructed using ICD codes, where the ICD-10 coding hierarchy was collapsed to the first three characters. A case would be assigned a ‘1’ for a disease if the corresponding ICD code was observed within the past year.

Data summary. After feature engineering, only 4,480 cases remained for antidiabetic agent prescription prediction due to vast missing of laboratory test values, while 153,470 cases were preserved for antihypertensive drug prescription prediction. Antidiabetic agent prescription frequency and antihypertensive drug prescription frequency were each summarized in Table 2 and Table 3. Here, the antidiabetic agent prescription frequency is significantly different from that in the whole population before removing cases, as is evident from the high frequency of insulin use. This reflects a bias that cases with blood glucose levels recorded in the system may have more serious conditions compared to others.

Table 2:

Antidiabetic agents prescription frequency.

Drug	Prescription (count)	Prescription (%)
Individual drug count
AGIs	500	11.16%
DPP-4	9	0.20%
TZDs	183	4.08%
Biguanides	1,067	23.82%
Glinides	234	5.22%
Sulfonylureas	741	16.54%
Insulin	2,435	54.35%
Number of drugs count
One drug	3,883	86.67%
Two drugs	514	11.47%
Three drugs	74	1.65%
Four drugs	9	0.20%

Table 3:

Antihypertensive drugs prescription frequency.

Drug	Prescription (count)	Prescription (%)
Individual drug count
ACEIs	15,758	10.27%
Alpha blockers	2,365	1.54%
ARBs	52,698	34.34%
Beta blockers	29,855	19.45%
CCBs	90,068	58.69%
Diuretics	6,174	4.02%
Hydrochlorothiazide	9,401	6.13%
Number of drugs count
One drug	110,647	72.10%
Two drugs	34,091	22.21%
Three drugs	7,595	4.95%
Four drugs	1,138	0.74%

Drug dependency study. From statistics’ point of view, prescription of two drugs A and B are independent if their joint probability equals the product of their probabilities:

$$P\left(A\cap B\right)=P\left(A\right)P\left(B\right)$$ (1)

The dependency of drug A and B in this work is thus measured as:

$$dependency=\frac{P\left(A\cap B\right)}{P\left(A\right)P\left(B\right)}$$ (2)

It can be rewritten with conditional probabilities as:

$$dependency=\frac{P\left(A|B\right)}{P\left(A\right)}=\frac{P\left(B|A\right)}{P\left(B\right)}$$ (3)

This is equivalent to the support A provides for B, or the support B provides for A in the Bayesian interpretation, where a value larger than 1 indicates positive correlation, while a value smaller than 1 indicates negative correlation.

Baseline classifier. Logistic regression (LR) was used as the baseline classifier. The prescription of each drug is modeled by an LR, resulting in seven LR models in each scenario.

Multi-task learning. Multi-task neural networks were constructed as in Figure 1 for multi-task learning (MTL). Two intermediate components were illustrated: representation learning layers and classifier layers. A consensus representation relevant to the prescription tasks was learned in the representation learning layers. Out of the consensus representation, classifier layers were constructed for each classification task to make a distinction between the tasks while optimizing jointly a cost function considering the cost of all classification tasks. After training, the MTL model can intake the features and output the prediction of the seven drugs at the same time.

Figure 1.

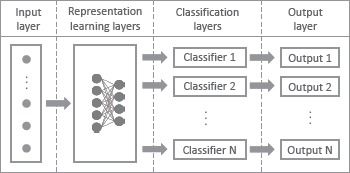
A schematic representation of multi-task neural network. For each instance, a set of features and several class labels for the tasks are used for training. Input layer is followed by representation learning layers to learn the common representations, then followed by multiple classifiers to deal with the distinctions, after which an output layer is constructed for each classifier.

Threshold selection. For both LR and MTL, the output is produced as the probability of a case to be positive (or ‘1’). A threshold translating a probability to a class was such selected as to maximize the F1 score (explained in Table 4).

Table 4:

Measurements used in this work.

Measurement	Description	Formula
True positive rate (TPR)	The proportion of positives correctly identified as such.	$TPR=\frac{truepositives}{allpositivecases}$
False positive rate (FPR)	The proportion of negatives wrongly categorized as positive.	$FPR=\frac{falsepositives}{allnegativecases}$
Receiver operating characteristic (ROC) curve	A curve created by plotting the TPR against the FPR at various thresholds.
Area under the curve (AUC)	Area under the ROC curve.
Precision	The proportion of predicted positives that are real positives.	$Precision=\frac{truepositives}{allpredicatedpositives}$
Recall	The same as TPR.	$$Recall=\frac{truepositives}{allpositivescases}$$
F1 score	A measure of a binary classifier’s accuracy.	$$F_1=2.\frac{precision\cdot recall}{precision\text{}+recall}$$
Jaccard similarity	A measure of similarity between two finite sample sets.	$$jaccard(A,B)=\frac{|A\cap B|}{|A\cup B|}$$
Odds ratio (OR)	A measure of how strongly the presence one property (A) is associated with the presence of another (B).	$$\begin{array}{l}{n}_{11}=|A\cap B|,n_{00}=|\neg A\cap \neg B|\\ n_{10}=|A\cap \neg B|,n_{01}=|\neg A\cap \neg B|\\ OR=\frac{n_{00}\cdot n_{11}}{n_{01}\cdot n_{10}}\end{array}$$
Wald confidence interval	Confidence interval of the OR.	$$\begin{array}{l}SE=\sqrt{\frac{1}{n_{11}}+\frac{1}{n_{10}}+\frac{1}{n_{01}}+\frac{1}{n_{00}}}\\ Lower95\%CI=exp(log(OR)-SE)\\ Upper95\%CI=exp(log(OR)+SE)\end{array}$$

Method assessment. In a typical run of the experiment, the input data is first split into training data (70%) and testing data (30%). Either LR or MTL is trained on training data, with its performance assessed on testing data. For LR, 50 runs were conducted in each scenario with different training/testing splits to account for split randomness. For MTL, 150 runs were conducted for each task, 3 runs each on the 50 different training/testing splits to account also for the randomness in neural network training. A list of measurements used in this work is summarized in Table 4. The performance of a classifier for single drug prescription prediction is evaluated by AUC. The performance in combined prescription prediction is firstly measured by average Jaccard similarity between the predicted and the actual prescription pattern. The performance in combined prescription is also measured by prediction accuracy, where a predicted prescription pattern is counted accurate only if single drug prediction is accurate for all seven drugs.

Statistical analysis. Prediction by MTL is called AI (artificial intelligence) prescription in contrary to doctor prescription. To explore the justification for AI prescription, we conducted statistical analysis to evaluate the importance of each disease in disease history to the prediction. The importance is assessed for each disease in the prescription of each drug, where having this disease or not is counted towards having this drug prescribed or not. Odds ratios and Wald confidence intervals were calculated as in Table 4. A disease is considered significant in the prescription of this drug if the confidence intervals do not span through 1, where an OR larger than 1 indicates the drug is associated with increased prescription of the drug and smaller than 1 otherwise.

Results

Drug dependency. In antidiabetic agent prescription, around 13% cases have more than one drug prescribed (Table 2). Dependency of antidiabetic agents is shown in Table 5. Many drug pairs show dependency other than 1, suggesting correlation between the drugs. As an example, the support glinides provides for AGIs is 2.46, suggesting elevated level of combined use. Also, the support sulfonylureas provides for insulin is 0.28, suggesting less combined use. DPP-4 has some large dependency values, probably a bias caused by its rare use. Similarly as in antihypertensive drug prescription, around 28% cases have more than one drug prescribed (Table 3). Dependency of antihypertensive drugs are summarized in Table 6, showing many dependency other than 1. These suggest the relatedness in prescribing the drugs, forming the basis for multi-task learning to model information sharing.

Table 5:

Dependency of antidiabetic agent prescription.

	AGIs	DPP-4	TZDs	Biguanides	Glinides	Sulfonylureas	Insulin
AGIs		3.25	1.18	0.80	2.46	1.42	0.89
DPP-4	3.26		4.08	1.07	8.35	1.11	0.83
TZDs	1.18	4.08		1.53	1.61	1.32	0.62
Biguanides	0.80	1.07	1.53		0.70	1.16	0.38
Glinides	2.46	8.35	1.61	0.70		0.59	1.79
Sulfonylureas	1.42	1.11	1.32	1.16	0.59		0.28
Insulin	0.89	0.83	0.62	0.38	1.79	0.28

Table 6:

Dependency of antihypertensive drug prescription.

	ACEIs	Alpha blockers	ARBs	Beta blockers	CCBs	Diuretics	Hydrochlorothiazide
ACEIs		0.56	0.87	2.04	1.55	0.83	0.75
Alpha blockers	0.56		1.21	1.19	0.67	2.68	1.73
ARBs	0.87	1.21		1.59	1.50	0.99	3.42
Beta blockers	2.04	1.19	1.59		1.90	1.36	1.01
CCBs	1.55	0.67	1.50	1.90		0.51	0.82
Diuretics	0.83	2.68	0.99	1.36	0.51		8.46
Hydrochlorothiazide	0.75	1.73	3.42	1.01	0.82	8.46

Performance comparison in antidiabetic agent prescription prediction: MTL vs LR. In LR, the prescription pattern is predicted by constructing an LR classifier for each drug and joining the predictions from them. MTL is capable of predicting prescription pattern together. Their performances are compared in Table 7. AUC is used to evaluate the prediction of each single drug, with its mean, standard deviation (SD), and maxima in all runs listed. For all the seven drugs, MTL has higher AUC than LR, with the highest increase in glinides, a mean AUC increase from 0.788 to 0.850. In the prediction of combined prescription, MTL has a mean Jaccard similarity of 0.600 compared to 0.569 achieved by LR. In terms of accuracy (percentage of predictions that have all seven drugs correctly predicted), MTL has an accuracy of 0.493 compared to 0.445 of LR.

Table 7:

Performance comparison of LR and MTL in antidiabetic agent prescription prediction.

		Single drug: AUC							Combined prescription
		AGIs	DPP-4	TZDs	Bigua-nides	Glinides	Sulfony-lureas	Insulin	Mean Jaccard similarity	Accuracy
LR	Mean	0.756	0.878	0.763	0.756	0.788	0.792	0.833	0.569	0.445
	SD	0.020	0.214	0.029	0.012	0.029	0.014	0.009
	Max	0.802	1	0.820	0.784	0.867	0.814	0.853
MTL	Mean	0.793	0.903	0.795	0.779	0.850	0.831	0.853	0.600	0.493
	SD	0.021	0.089	0.031	0.014	0.032	0.013	0.009
	Max	0.857	1	0.869	0.812	0.908	0.873	0.874

Performance comparison in antihypertensive drug prescription prediction: MTL vs LR. Similar comparison as in antidiabetic agent prescription prediction was conducted for antihypertensive drug prescription prediction, with performances summarized in Table 8. In single drug prediction, MTL has about 0.02 increase in AUC compared to LR in all seven drugs. However, MTL and LR have similar performance in combined prescription prediction, both mean Jaccard similarity and accuracy. This may be explained that though AUC is an important measure of binary classifier performance, it is difficult to be translated to a measure while solving a real-life problem since a threshold is needed to make a prediction based on the probability given. In this work, we selected the threshold that maximized the F1 score, bearing our intension to balance precision and recall. Under such selection, the accuracy of combined prescription prediction may well be the same between MTL and LR.

Table 8:

Performance comparison of LR and MTL in antihypertensive drug prescription prediction.

		Single drug: AUC							Combined prescription
		ACEIs	Alpha blockers	ARBs	Beta blockers	CCBs	Diuretics	Hydrochloro-thiazide	Mean Jaccard similarity	Accuracy
LR	Mean	0.847	0.938	0.856	0.820	0.844	0.892	0.855	0.714	0.596
	SD	0.003	0.007	0.002	0.003	0.001	0.005	0.004
	Max	0.852	0.950	0.860	0.827	0.847	0.904	0.865
MTL	Mean	0.872	0.955	0.877	0.846	0.859	0.915	0.880	0.719	0.594
	SD	0.003	0.005	0.002	0.002	0.002	0.004	0.004
	Max	0.878	0.967	0.883	0.852	0.864	0.924	0.892

Disease history relevant to insulin prescription. Disease onsets (denoted by ICD codes) within a year from the time of case were evaluated for their relevance to insulin prescription both by doctor and by AI. A list of ICD codes was identified as significant for doctor prescription and AI prescription. We first tried to figure out AI’s ability in capturing doctors’ intension for insulin use. AI made a successful capture if an ICD code significant to doctors’ prescription was also significant to AI’s prescription. We thus present Figure 2 for visualization. From the figure, the majority of the diseases significant to doctor’ prescription were also identified as significant in AI prescription (OR > 1 in Figure 2A or OR <1 in Figure 2B). A few exceptions were identified and summarized in Table 9. Out of the 121 ICD codes significant to increased doctor insulin prescription (OR >1), 15 (12.4%) were missed by AI prescription, suggesting AI’s ability in capturing most diseases. However, some potentially important diseases were missed, like high blood pressure, lipid disorder, and diseases related to eye, limb, and bone, raising more expectations on AI methods. Out of the 47 ICD codes significant to decreased doctor insulin prescription (OR <1), 10 (21.3%) were not significant to AI prescription, suggesting AI has denied the association between some diseases and decreased insulin use. Some of these diseases may not be related to decreased insulin use, like embedded and impacted teeth (K01), which suggests AI’s capability in reducing impact of less related features. We also tried to figure out AI’s inherent logic in prediction after learning from doctors’ prescription. AI prescription identified 147 ICD codes associated with increased insulin prescription, and 97 ICD codes associated with decreased insulin prescription. This number is greater than in doctor prescription, indicating that AI is inflating the importance of features in prediction to make a greater distinction between different predictions. Diseases significant only in AI prescription are listed in Table 9. However, the interpretation of the results are complicated, which are discussed in the discussion section.

Figure 2.

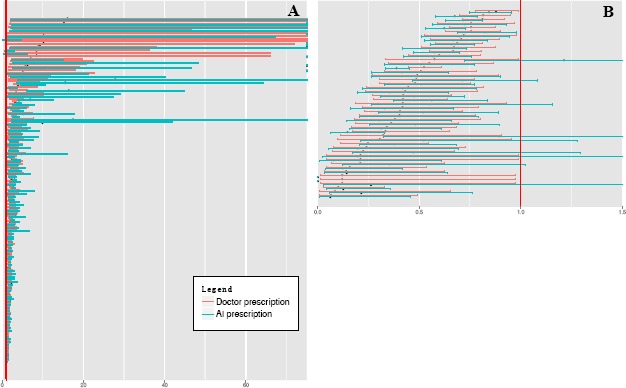
Characterizing ICD codes significant to doctor prescription of insulin and their corresponding significance in AI prescription. Odds ratios and confidence intervals of ICD codes that are significant to doctor prescription of insulin are plotted in A (odds ratio > 1) and B (odds ratio < 1). Each pink row represent an ICD code’s statistics, with the odds ratio plotted as a black dot and confidence interval plotted as a pink line. The blue line immediately below a pink line denotes the ICD code’s odds ratio (black dot) and confidence interval (blue line) in AI prescription of insulin. The red vertical lines represent the line of x=1. In A, confidence intervals beyond 75 are not explicitly plotted.

Table 9:

Comparison of the differential disease history-insulin prescription associations between doctor prescription and AI prescription.

	Odds ratio > 1		Odds ratio < 1
	Significant only in doctor prescription	Significant only in AI prescription	Significant only in doctor prescription	Significant only in AI prescription
Diabetes		E13
Heart-related		I50, I51
Cardiovascular disease		G45, I63, I64		I61
Eye-related	H20	H04
Kidney disease		N04, N05, N28
Limb-related	L97			G56
Bone-related	M81	M24, M75, M77, M91, S52, S63		M19, M25, M47, M48, M51
Infection		B35, J15		A15
High blood pressure	I10
Lipid disorder	E75, E78
Neoplasm		C20, C61, Z85	D23	D24, N63
Local codes		AVY	BGS, BRK	BEZ, BNW, ZYT
Other	D72, I84, J01, K04, K56, L73, L98, N30	D84, E03, E79, E87, G12, K08, K26, K58, K74, K81, L29, L30, M10, M32, M33, M35, M60, R04, R06, R21, R42, R53, S39, Z01, Z71	J43, J84, K01, K83, M61, M65	B90, C50, E02, G58, H60, H81, J05, J21, J94, L21, L70, L95, N86, T14, Z98

Discussion

Application of AI methods in clinical practices. While AI may never be able to act the role of human doctors completely, it can learn from doctors’ behavior to provide support for further actions. In this work, we present an effort toward learning doctor medicine prescription patterns. The potential application of such efforts in clinical practices is supporting doctors who have less experience, providing them with clinical decisions learned from other doctors’ experience. We are aware that a major critique of such AI methods is a lack of interpretability compared to clinical guidelines that can explicitly be formatted into a series of if-then rules.

Data quality. As mentioned in the introduction section, data quality is a limiting factor of the application of datadriven CDSS. Data quality issue in our work can be viewed from two perspectives. First, missing data. We encountered plenty of features with missing values in EHR. Mostly, we either imputed the missing values or discarded the feature. However, this is not a proper choice for features vital to drug prescription, blood glucose levels, for example. In our antidiabetic agent prescription problem, cases without blood glucose levels tested were discarded, resulting in extremely reduced number of cases. Second, it may be problematic to learn from doctors’ prescriptions without assessing effectiveness. The prescription of one doctor may not be proper, or may not be the only proper prescription. Some drugs may have highly overlapping functions and the choice is highly doctor-specific or hospital-specific. Under such circumstances, AI can hardly tell the differential use of the drugs. And unfairly in performance evaluation, the prediction of AI may be judged as wrong if it predicts a drug while the doctor used its counterpart.

Disease history as features for prediction. The use of demographics, physical examinations, laboratory tests and recent prescriptions in learning doctors’ prescription is less debatable as they are more or less self-evident. However, how to make use of disease history remains an open question. While many traditional studies pick only a few clinically relevant diseases in analysis, we include nearly all, benefiting from big data approaches’ merit of being able to learn feature importance and in the hope of finding hidden factors to better explain doctors’ behavior. Here we collapsed the ICD-10 code hierarchy to the first three characters since in real-life settings, the more detailed the ICD code goes, the less accurate it is. However, this collapse from the nomenclature point of view may not actually capture the hierarchy and relatedness of diseases, which, in itself, is a complex task. Moreover, since ICD-10 contains codes for not only diseases, but also signs and symptoms, abnormal findings, complaints, social circumstances, and external causes of injury or diseases, it is a rather mixed representation, which is currently not treated with special care.

Caveats of disease relevance to drug prescription. We have discussed about disease history relevant to insulin prescription in the results section. Several ICD codes were associated with increased or decreased insulin prescription either by doctor or by AI. However, the interpretation of the association should be made with caution. Some diseases associated with increased insulin use are potential complications of type 2 diabetes (N18: chronic kidney disease, and N19: unspecified kidney failure, for example), thus can be used as an indication of exacerbating disease condition and an indication of insulin use. Some diseases negatively associated with insulin use may not be a reason not to use insulin but a result of no previous insulin use. Taking elevated blood glucose level (R73) as such an example. Previous insulin use can decrease the onset of elevated blood glucose level, making the onset of it an indication of no previous insulin use and thus an indication of no insulin prescription. Some may have rather complex reasons. Vitamin B12 deficiency anemia (D51) is significantly correlated with decreased insulin use in both doctor and AI prescription. Existing studies have well demonstrated that long term metformin treatment increases the risk of vitamin B12 deficiency¹¹. This is also observed in our data that D51 is strongly associated with increased biguanides use (OR=12.88, 95% CI = [2.73, 60.76]). Besides, in out drug dependency study, use of biguanides decrease the use of insulin. These altogether lead D51’s association with decreased insulin use. As the same with all association studies, it is hard to infer causation from such results. After all, it is not necessary for big data analytics to know causation to infer decision.

Conclusion

In this paper, we use a multi-task neural network approach to learn doctor medicine prescription pattern of multiple correlated antidiabetic agents in blood glucose control and antihypertensive drugs in blood pressure control scenarios by mining EHR data. We have demonstrated that for single drug prescription, multi-task learning achieves 0.02 to 0.06.increases in AUC compared with logistic regression. In prescription pattern prediction, we achieved an accuracy increase of 0.05 in antidiabetic agent prediction, showing the efficacy of multi-task learning approach in learning doctor prescription patterns.