Can SNOMED CT Changes Be Used as a Surrogate Standard for Evaluating the Performance of Its Auditing Methods?

Abstract

We introduce RGT, Retrospective Ground-Truthing, as a surrogate reference standard for evaluating the performance of automated Ontology Quality Assurance (OQA) methods. The key idea of RGT is to use cumulative SNOMED CT changes derived from its regular longitudinal distributions by the official SNOMED CT editorial board as a partial, surrogate reference standard. The contributions of this paper are twofold: (1) to construct an RGT reference set for SNOMED CT relational changes; and (2) to perform a comparative evaluation of the performances of lattice, non-lattice, and randomized relational error detection methods using the standard precision, recall, and geometric measures. An RGT relational-change reference set of 32,241 IS-A changes were constructed from 5 U.S. editions of SNOMED CT from September 2014 to September 2016, with reversals and changes due to deletion or addition of new concepts excluded. 68,849 independent non-lattice fragments, 118,587 independent lattice fragments, and 446,603 relations were extracted from the SNOMED CT March 2014 distribution. Comparative performance analysis of smaller (less than 15) lattice vs. non-lattice fragments was also given to approach the more realistic setting in which such methods may be applied. Among the 32,241 IS-A changes, independent non-lattice fragments covered 52.8% changes with 26.4% precision with a G-score of 0.373. Even though this G-score is significantly lower in comparison to those in information retrieval, it breaks new ground in that such evaluations have never performed before in the highly discovery-oriented setting of OQA.

Introduction

Large, comprehensive terminological systems such as SNOMED CT [1] continue to evolve over time, with ontology quality assurance (OQA) an indispensable part of the terminology lifecycle [2]. OQA approaches typically involve the implementation of computational tools that translate ontological principles into specific rules and patterns [3]. Ontological systems are then audited using such tools to infer and flag out substructures violating such rules and patterns, pointing to potential errors to be corrected in the next release after validation and review.

Finding errors in existing ontologies is a creative discovery process. Because of the highly discovery-oriented nature of OQA, the performance measure of precision (i.e., the percentage of true errors among the candidates that have been examined) for auditing methods is neither an initial consideration nor as glorious to quantify, unlike the setting for information retrieval [4]. Similarly, recall, the percentage of errors discovered among all true errors (“the ground truth”), is impossible to measure because of the lack of ground truth: a complete, validated error list is impossible to construct, again because of the highly discovery-oriented nature of the task.

Nevertheless, reference standards, or benchmarking data sets with validated results, have played critical roles for advancing disciplines such as image analysis (e.g., Face Recognition Technology [5] and Wilt Dataset [6]) and information retrieval (e.g., The Text Retrieval Conference series (http://trec.nist.gov)), and would be an important resource for OQA. Despite the fact that it is impossible to obtain precision and recall measures for OQA methods in absolute terms, it may still be meaningful to investigate such measures relative to some “partial ground truth.”

The goals of this paper are twofold: to develop reference sets for evaluating the performance of OQA methods for SNOMED CT, and to demonstrate how such reference sets may be applied to evaluate the performance of lattice vs. non-lattice-based methods with randomized review as a background benchmark. We propose RGT, Retrospective Ground-Truthing, as a surrogate reference standard for evaluating the performance of automated OQA methods. The key idea of RGT is to leverage the cumulative SNOMED CT changes derived from its regular longitudinal distributions by the official SNOMED CT editorial board as a partial, surrogate reference standard. Three performance measure are proposed: RGT recall, RGT precision and RGT geometric mean (G-measure), formulated by adapting the standard measures using RGT relational changes derived from SNOMED CT U.S. distributions as the reference set.

We demonstrate the feasibility of this approach by constructing an RGT reference set for SNOMED CT relational changes and performing a comparative evaluation of the performances of lattice, non-lattice, and randomized relational error detection methods using the proposed RGT measures. A RGT relational-change reference of 32,241 IS-A changes were constructed from 5 versions of SNOMED CT from September 2014 to September 2016, with reversals and changes due to deletion or addition of new concepts excluded. 68, 849 independent non-lattice fragments, 118, 587 independent lattice fragments, and 446,603 relations were extracted from the U.S. version 20140301. Comparative performance analysis of smaller (less than 15) lattice vs. non-lattice fragments were also given to approach the more realistic setting in which such methods may be applied. Among the 32, 241 IS-A changes, independent non-lattice fragments covered 52.8% changes with 26.4% precision with a G-score of 0.373. Our results show that the non-lattice auditing method had significantly better overall performance for detecting incorrect and missing IS-A relations. With independent further work in the accurate identification of specific relational errors contained in individual fragments [7], non-lattice auditing method could prove to be a powerful, versatile approach to OQA.

1. Background

The Evolution of SNOMED CT. SNOMED CT [8] is the most comprehensive, multilingual clinical healthcare terminology in the world, developed by SNOMED International, the trading name of the International Health Terminology Standard Development Organization (IHTSDO). It provides a consistent representation of clinical content in electronic health records and has been used in more than fifty countries. It contains over 300,000 active concepts with unique numeric identifiers (SNOMED ID, or ID in short), organized into 19 hierarchies including Clinical Finding and Body Structure. To connect such concepts, over 1,500,000 relations, including IS-A (subtype) relationships and attribute relationships (e.g. associated morphology and finding site) [9], are constructed and maintained. Release Format 2 (RF2) [10] is used to support reference set creation.

For each version of SNOMED CT, RF2 provides a snapshot folder containing such items as: all active content (concepts, description, and relationships); a “delta” folder which includes identified new and changed content from previous snapshot version; and a “full” folder with the history of all content. Each relationship consists of numeric attributes, such as effectiveTime (date of change), active (“0” for not active, “1” for active), sourceId (the source concept of a relation), destinationId (the target concept of a relation), relationshipGroup, and typeId (relationship type). Ochs et al. [11] captured editing operations and created an easily understandable SNOMED CT “delta” set that included added relations and removed relations. An inactive relation in the “delta” with type IS-A can be treated as an IS-A relation deletion or an IS-A relation error in the prior version. Similarly, an active relation in the “delta” with type IS-A can be treated as an IS-A relation insertion or a missing IS-A relation in the prior version.

To illustrate, Fig. 1 displays a fragment in the SNOMED CT version 20140301 (left), which was changed in version 20160901 (right) with an IS-A deletion (dashed red line) and an IS-A addition (solid red line).

Figure 1.

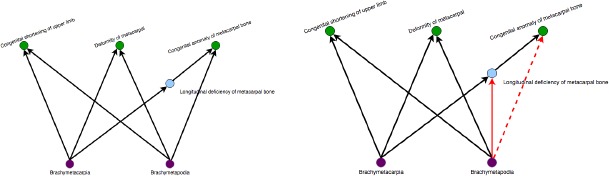
An example of SNOMED CT IS-A changes. A fragment in the SNOMED CT 20140301 release (left) was changed in the 20160901 release (right), with an IS-A deletion (dotted red) and an IS-A insertion (solid red).

Non-lattice Auditing. We review several related notions for non-lattice auditing (see more details in [12, 13]). The concepts and the IS-A relationship between concepts in an ontology such as SNOMED CT can be viewed as a partially ordered set (poset) L with a reflexive, transitive relationship ≤. That is, L is the set of concepts, and ≤ is the IS-A relationship. A concept (or element) u is called an upper bound of a subset X ⊆ L, if for each x ∈ X we have x ≤ u. A concept m is called a minimal upper bound of a subset X ⊆ L, if m is an upper bound of X, and for any n ≤ m such that x ≤ n for each x ⊆ X, we have m = n. We use mub(X) to denote the set of minimal upper bounds of X.

Dually, an element l ∈ L is called a lower bound of a subset X ⊆ L, if for each x ∈ X we have x ≥ l. An element m is called a maximal lower bound of a subset X ⊆ L, if m is a lower bound of X, and for any n ≥ m such that x ≥ n for each x ∈ X, we have m = n. We use mlb(X) to denote the set of maximal lower bounds of X.

A lattice pair is a pair of concepts that have a unique maximal lower bound (when the pair has any shared lower bound). For example, on the left of Fig. 2 (an induced subgraph of SNOMED CT, in the sense that all corresponding relations in SNOMED CT must be included in the subgraph when the nodes are included), the two concepts (in green) “Brain stem infarction” and “Cerebellar infarction” form a lattice pair: this pair has a unique minimal upper bound “Posterior cerebral circulation infarction” (in pink) and unique maximal lower bound “Claude’s syndrome” (in crimson). Thus this concept pair is a lattice pair. This fragment is called a lattice fragment.

Figure 2.

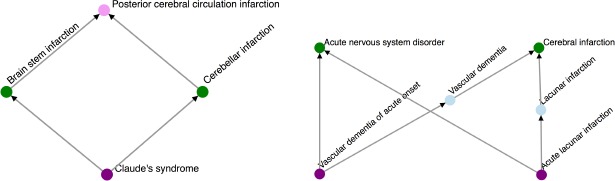
Examples of a lattice fragment (left) and a non-lattice fragment (right).

A non-lattice pair (a, b) is defined as a pair of concepts that have at least two maximal lower bounds, that is, the size of mlb{a, b} is greater than 1. For example, on the right of Fig. 2 (another induced subgraph of SNOMED CT), the concept pair “Acute nervous system disorder” and “Cerebral infarction” has two (hence not unique) maximal lower bounds: ‘Vascular dementia of acute onset’ and “Acute lacunar infarction.” Thus this concept pair is a non-lattice pair. This fragment (including the maximal lower bounds) is called a non-lattice fragment.

The Lattice-based Structural Auditing (LaSA) principle (a.k.a. non-lattice auditing [14]) provides a mathematically grounded, error-agnostic method for auditing biomedical ontologies. LaSA focuses on the order structure induced by the hierarchical relationship (IS-A) and requires that such a structure forms a lattice: every concept pair should not have more than one maximal lower bound. It extracts non-lattice pairs and generates non-lattice fragments, consisting of concepts in-between a maximal shared descendant and a member of the non-lattice pair. Non-lattice fragments are in conflict with the Fundamental Theorem of Formal Concept Analysis [15], which states that concept hierarchies derived from the duality of intension and extension always have their order structure being a (complete) lattice. In recent work, Cui et al. [7] provide a new method for mining non-lattice lexical patterns for detecting missing concepts and hierarchical relations in SNOMED CT. Evaluation using a random selected 100 fragments by experts, showed that non-lattice fragments have a high frequency of containing missing IS-A relationships.

2. Methods

We first construct a partial reference set focusing on two types of relational errors derived from the “delta” of SNOMED CT releases: incorrect IS-A relations represented by IS-A deletions, and missing IS-A relations as captured by ISA insertions. We then perform a comparative evaluation of lattice, non-lattice, and randomized relational auditing methods using the standard precision, recall, and geometric measures.

2.1. Constructing RGT

We use 5 versions (U.S. version 20140301 - U.S. version 20160901) of SNOMED CT for capturing relational changes (change numbers are shown in the second column in Table 1). We focus on erroneous and missing relations on shared concepts, so newly added relations that involve newly added concepts are ignored. An IS-A relational change (or IS-A change in short) with the same source and target concepts may have different “modualId”, which may cause a repeated count. Moreover, IS-A relations may be reversed back to a prior version as a part of the changes in later versions [16]. For example, relation “Streptococcal tonsillitis (ID 41582007) IS-A Tonsillitis (ID 90176007)” is deleted in the July 2014 version and added in the January 2016 version. To construct a robust reference set of relational changes, we perform three preprocessing steps:

Table 1:

SNOMED CT change statistics from U.S. version 20140901 to U.S. version 20160901.

SNOMED CT version	Relational changes	IS-A deletion	IS-A insertion
20140901	57,879	4,799	2,723
20150301	60,433	4,426	3,807
20150901	61,253	5,866	3,350
20160301	64,676	7,888	3,350
20160901	19,753	1,212	835
Cumulative	263,994	20,744	11,497

• Extracting only IS-A changes;

• Removing duplicated counts and reversed changes; and

• Removing IS-A changes that involve concepts not in the targeted SNOMED CT versions.

2.2. Extracting Independent Lattice and Non-lattice Fragments

We first extract all lattice and non-lattice fragments for the U.S. version 20140301 of SNOMED CT using our MapReduce pipeline [12], which consists two MapReduce phases to extract non-lattice fragments from large partially ordered ontological structures. The resulting fragments are not “independent” in the sense that one fragment may be contained in another, making further error detection intertwined, as well as violating the independent sampling assumption for statistical analysis. However, given a large collection of fragments, obtaining a reduced “independent” collection with exhaustive pairwise comparison is computationally prohibitive. To address this issue, we formulate the notion of independence as follows. For (induced and connected) fragments f₁ = (C₁, R₁) and f₂ = (C₂, R₂) where C₁ and C₂ are sets of concepts and R₁ and R₂ are sets of relations,

• we say that f₂ is a subfragment of f₁ if R₂ ⊆ R₁; and

• we say that f₁ and f₂ are independent f neither of them is a subgragment of the other.

For example, the non-lattice fragment in Fig. 3 shows the non-lattice fragment generated by the non-lattice pair “Pelvic injury” (ID 282771003) and “Closed fracture of hip” (ID 359817006) has a non-lattice subfragment generated by the non-lattice pair “Pelvic injury” (ID 282771003) and “Closed fracture of neck of femur” (ID 35982003).

Figure 3.

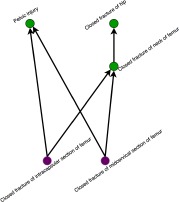
An example of a non-lattice

In general, a collection of fragments is called independent if each pair of fragments from the collection is independent.

Formally, for a non-lattice pair (a, b) and their maximal lower bounds mlb{a, b}, the non-lattice fragment determined by the pair (a, b) is defined as a subgraph containing the concepts between the pair (a, b) and any concept in mlb{a, b}. For a lattice pair (c, d), their only maximal lower bound is the unique element in mlb{c, d}, and their only minimun upper bound is the unique element in mub{c, d}, the lattice fragment determined by the pair (c, d) is defined as a subgraph containing the concepts between the pair (c, d) and the concept mlb{c, d}, combining the concepts between the pair (a, b) and the concept mub{a, b}. The MapReduce pipeline in [12] can be used to exhaustively detect nonlattice and lattice pairs. We further compute independent fragments using the generating pairs.

By definition, comparing all relations between every pair of fragments is required for constructing an dependent collection of non-lattice fragments. To reduce the computational cost involved, we propose an algorithm to detect all possible non-lattice subfragments for each given non-lattice fragment. Lattice fragment dependency can be computed in a similar way.

Let P be the set of all non-lattice pairs, and F be the set of all non-lattice fragments for a given SNOMED CT version. Every non-lattice fragment f_{(a, b)} ∈ F is generated by some non-lattice pair (a, b) ∈ P. Then f_{(x, y)} is subfragment of f_(a,b) if

• (x, y) ≠ (a, b), (x, y) ∈ P, {x, y} ⊆ f_(a,b); and

• for any relation (u, v) ∈ f_(x,y), we have (u, v) ∈ f_(a,b).

The second condition is required because a non-lattice pair may generate a non-lattice fragment without itself being a part of the fragment. For instance, the non-lattice fragment in Fig. 4 shows an independent non-lattice fragment generated by the non-lattice pair “Nonvenomous insect bite with infection” (ID 10461000) and “Infected insect bite of upper limb” (ID 283347003). This fragment contains another non-lattice pair “Nonvenomous insect bite of trunk with infection” (ID 19108007) and “Infected insect bite of upper limb” (ID 283347003), although this pair does not generate a subfragment of the displayed fragment.

Figure 4.

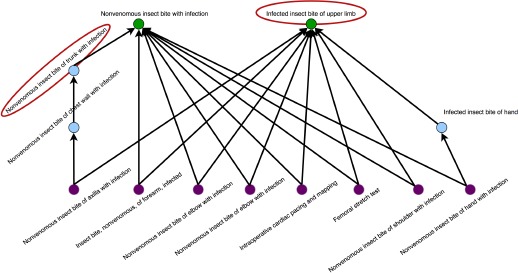
An example of an independent non-lattice fragment containing a non-lattice pair (in red circles) other than that pair generated the fragment. The non-lattice fragment generated by the pair in red is not contained in the displayed fragment.

2.3. Performance Measures

To the best of our knowledge, there are no existing measures for comparing distinct OQA methods. We introduce RGT recall, RGT precision, and RGT geometric mean to measure the performance of OQA methods, motivated by the precision and recall measures commonly used in information retrieval.

We consider an OQA method M as a group of fragments (in general terms as induced subgraphs). Each fragment may potentially capture some ontological errors that involve concepts as nodes and IS-A relations as edges. A fragment f is a graph consisting of a set of IS-A relations. The size of f is defined as the number of concepts involved in it.

We can view a benchmark of validated changes (i.e., ground truth) as a tuple ε = (E₀, E₁), where E₀ is the set of validated relational errors (where a relation deletion is indicated), and E₁ is the set of validated missing relations (where a relation insertion is indicated).

To evaluate the performance of M against ε, we can break the RGT measure of precision and recall into two categories: measures with respect to deletion, and measures with respect to insertion:

• The deletion recall is defined as the ratio

  $$\frac{\left|\left\{r\in E_0|\exists f\in M,r\in f\right\}\right|}{\left|E_0\right|};$$
• The deletion precision is defined as the ratio

  $$\frac{\left|\left\{f\in M|\exists r\in f,r\in E_0\right\}\right|}{\left|M\right|};$$
• The insertion recall is defined as the ratio

  $$\frac{\left|\left\{r\in M|\exists f\in M,r\in f\right\}\right|}{\left|E_1\right|};$$
• The insertion precision is defined as the ratio

  $$\frac{\left|\left\{f\in M|\exists r\in f,r\in E_1\right\}\right|}{\left|M\right|};$$

Note that while RGT recall is defined as a ratio of the number of relations, RGT precision is defined as a ratio of the numbers of fragments. One can combine precision and recall to obtain the geometric mean measure (G-measure) $\sqrt{\text{recall}\cdot \text{precision}}$. The G-measure shows a combined performance of precision and recall. The higher the G-measure, the greater the agreement between an OQA method and the SNOMED CT changes.

3. Results

Relational changes in SNOMED CT U.S. versions ranged from 19,753 in the 20160901 release to 64,676 in the 20160301 release (Table 1). All the changes were calculated based on the released “delta” set for each version. There has been a total of cumulative 263,994 relational changes from the 20140301 release to the 20160901 release, after removing relation reversals and duplicates. Therefore, the cumulative change is not a simple summation of the numbers in all prior changes.

We compared five auditing methods according to our formulation of each method as a collection of fragments. Non-lattice auditing consists of all non-lattice fragments and lattice auditing consists of all lattice fragments. Similarly, independent non-lattice auditing consists of all independent non-lattice fragments and independent lattice auditing consists of all independent lattice fragments. Additionally, single-edge auditing consists of all fragments made of a single relation (edge). This corresponds to randomized edge examination.

We used 20140301 release of SNOMED CT to generate non-lattice fragments, lattice fragments, and single-edge fragments. We also extracted all independent fragments from lattice and non-lattice fragments. To calculate the deletion recall using the RGT formulation, we collected the number of SNOMED CT IS-A deletions discovered through methods (numerator) and the number of 5 versions SNOMED CT IS-A deletion cumulation (denominator). The result is shown in Fig. 5 where the y axis is the numerator and the x axis is the denominator. The 5 numbers of cumulative IS-A deletion E₀ from 20140901 release to 20160901 release (4,799; 8,965; 13,844; 19,968; and 20,744) were computed in the same way as the last row in Table 1. For each of the 5 methods, the slope is the deletion recall, and the larger the slope, the better deletion recall the method has. The line of best fitting for each method is linear, which indicates that the deletion recall is stable with different numbers of SNOMED CT IS-A deletion for all methods. In other words, deletion recall for each method is almost a constant, e.g., the slope for single-edge is always 1 becauseits deletion recall is 100%. Such a feature indicates that deletion recall is a robust measure for OQA method evaluation. With such a feature, we may predict that the IS-A relations deletion recall relative to the ground truth for a method may be close to its deletion recall relative to SNOMED CT IS-A deletion.

Figure 5.

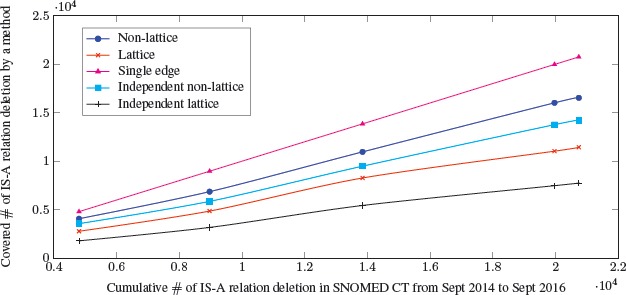
The slopes for RGT recall among the 5 auditing methods. Note that the recall for single edge is 1, matching the intuition.

We also divide lattice and non-lattice fragments into large sized groups and small sized groups for detailed comparison. We consider larger fragments those fragments with sizes larger or equal to 15, and small fragments those fragments with sizes smaller than 15. The second column in Table 2 presents the numbers of non-lattice and lattice fragments in each group obtained in SNOMED CT U.S. version 20140301, which is the denominator in the formulation of recision. The third column is the numbers of fragment hits (enumerator), the number of changes detected by the methods using cumulative SNOMED CT changes.

Table 2:

List of non-lattice and lattice fragments number and hits obtained in SNOMED CT version March 2014.

Method	Number of fragments	Number of hits
Non-lattice fragments	595,960	70,182
Independent non-lattice fragments	68,849	18,183
Independent non-lattice fragments with size ≤ 15	62,001	15,070
Independent non-lattice fragments with size > 15	6,848	3,113
Lattice fragments	835,015	82,801
Independent lattice fragments	118,587	20,552
Independent lattice fragments with size ≤ 15	113,248	18,641
Independent lattice fragments with size > 15	5,339	1,911

Fig. 6 displays the results for deletion recall and deletion precision. Fig. 7 displays the results for insertion recall and insertion precision. Table 3 displays the results for the G-measure for IS-A deletion, IS-A insertion, and the changes with respect to each method.

Figure 6.

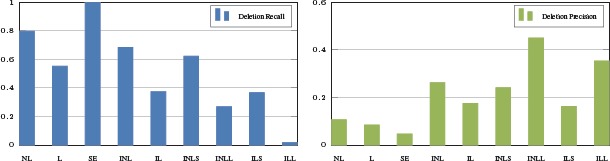
Deletion recall (left) and deletion precision (right) for each method. The methods are non-lattice (NL), lattice (L), single-edge (SE), independent non-lattice (INL), independent lattice (IL), independent non-lattice with fragments size ≤15 (INLS), independent non-lattice with fragments size >15 (INLL), independent lattice with fragments size ≤15 (ILS), independent lattice with fragments size >15 (ILL).

Figure 7.

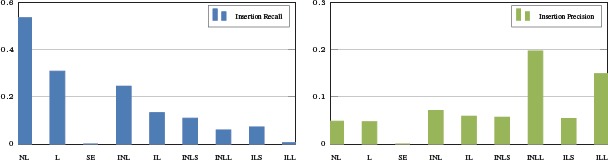
Insertion recall (left) and insertion precision (right) for each method. The methods are non-lattice (NL), lattice (L), single-edge (SE), independent non-lattice (INL), independent lattice (IL), independent non-lattice with fragments size ≤15 (INLS), independent non-lattice with fragments size >15 (INLL), independent lattice with fragments size ≤15 (ILS), independent lattice with fragments size >15 (ILL).

Table 3:

List of G-measures for various methods that detect SNOMED CT changes.

Method	Deletion	Insertion	Both
Non-lattice	0.291	0.160	0.288
Lattice	0.215	0.120	0.215
single-edge	0.216	0	0.173
Independent non-lattice	0.423	0.132	0.373
Independent lattice	0.255	0.089	0.226
Independent non-lattice small (size ≤ 15)	0.387	0.079	0.298
Independent non-lattice large (size > 15)	0.348	0.107	0.273
Independent lattice small (size ≤ 15)	0.244	0.062	0.190
Independent lattice large (size > 15)	0.076	0.026	0.061

The first three rows of Table 3 show that non-lattice auditing performs better than lattice auditing, which is much better than single-edge using G-measure. From Fig. 6 and Fig. 7, we can find the reason that non-lattice has a higher G-measure is non-lattice has higher deletion recall and insertion recall (79.9% and 53.4%) than lattice while they perform similarly in deletion precision and insertion precision, this means non-lattice auditing has better coverage on incorrect IS-A relational errors and missing IS-A relational errors.

Among all methods, independent non-lattice auditing performed the best on discovering incorrect IS-A relations with a 68.4% deletion recall and a 26.2% deletion precision. Only 68,849 independent non-lattice fragments (about 11% of all non-lattice fragments) exist in SNOMED CT version 20140301, and 62,001 (90%) of them are small sizes (≤ 15) so that they are amendable for human inspection. Our result indicates that independent non-lattice fragments could play significant role for detecting incorrect IS-A relations for SNOMED CT. However, independent non-lattice fragments failed to perform well on discovering missing IS-A relations, while non-lattice auditing returns the best G-measure in missing IS-A relation detection. We noticed that a missing relations is often needed to connect a concept inside an independent non-lattice fragment and another concept outside the independent non-lattice fragment. By this reason, larger non-lattice fragments with sub-fragments are able to catch such missing relationships. The scenario can also lead to undesirable insertion discovering result for independent non-lattice because missing relationships are only detected between concepts inside a fragment.

4. Discussion

Small G-scores. Compared with traditional informationl retrieval methods, the G-scores calculated in this paper are relatively low, even for the higher-performing non-lattice approaches. This should not be a concern for two reasons. One is that SNOMED CT change is continuing with each new release, and we are always dealing with parital ground truth. In lack of the existence of available complete ground truth set, the performances for any OQA methods would suffer. The second reason is that detecting ontology errors or defects is a highly discovery-oriented, and sometimes not even well-defined process. For the first time, this paper introduced a framework to provide the feasibility to calculate G-scores to enable the comparison of distinct OQA methods (but the comparative evaluation of some existing OQA methods may remain infeasible).

Comparison of methods between fragment sizes. By comparing methods with larger fragments sizes and smaller fragments sizes, methods with larger fragments always show better RGT precision than the methods with smaller fragments. It is intuitive that larger fragments have more concepts and relationships so that they have more possibility to contain errors. On the contrary, methods with smaller size fragments present better scores on RGT recall relative to deletion and insertion, which means SNOMED CT IS-A relationship changes are aggregated on small sizes of fragments.

Comparison of populations between methods. Independent non-lattice auditing performed best among the three evaluated methods, with merely 68,849 fragments. To demonstrate the statistical significance, we computed test statistic Z-scores on precision between non-lattice and lattice (35.5); independent non-lattice and independent lattice (46.8); independent non-lattice and single-edge (201.2); and independent lattice and single-edge (149.3). Independent non-lattice auditing departs the most in outcome from larger population sets consisting of individual IS-A relations.

Balance of RGT precision and recall. Our setup for ontology auditing methods to capture quality issues is analogus to capturing fishes using fishing nets. A single method provides a collection of fishing nets. The fishes are the cumulative changes approved by the SNOMED CT editoral panel that have been officially reflected the releases. The nets are the SNOMED CT subsets or fragments determined by a particular method. To illustrate the possibility in the extremes, a method may provide a single net, which is the entire graph of SNOMED CT (100% recall, 100% precision against RGT reference set). But this is useless since no progress is made in making “the haystack” smaller. Another method may provide the finest possible net, which consists of single IS-A relations. This is also useless since it is equivalent to random examination, because of the largest possible numbers of “fishing nets” used. A more useful method should balance the number of “nets” as well as the sizes of the “nets.” We believe this is achieved using independent non-lattice fragments with sizes not exceeding 15.

SNOMED CT changes vs. the ground truth of relational errors. The entirety of the ground truth of ontology errors is unknowable because the lack of a complete and validated error list is the inherent nature of the task for OQA. SNOMED CT changes is the most trustworthy error list since it has been generated by the world’s most authoratitive group - the SNOMED International Editorial Panel. However, there exist change reversals [16] that need to be accounted for, as is the case in this study.

Limitations of non-lattice auditing. Non-lattice auditing [14] is founded on the theory of formal concept analysis. This paper demonstrates a significant difference between the G-scores of lattice vs non-lattice based methods in their ability in capturing official SNOMED CT relational changes. However, knowing a non-lattice fragment contains a relational error and identifying this specific error remains two different matters, as each fragment still contains multiple relations. To address this issue, we developed data mining techniques [7] leverging structural and lexical information for automated detection of relational errors in non-lattice fragments. Further development of data mining techniqies combining a rich variety of information sources represent provide additional research opportunities in this area.

Changes in the number of non-lattice fragments between versions. The number of non-lattice fragments can be a significant measure to evaluate the quality of SNOMED CT. We computed the numbers of non-lattice fragments for 4 pairs of versions using shared common concepts between versions: 581,327 (version 20140301) and 575,927 (version 20140901), 562,819 (version 20140901) and 574,028 (version 20150301), 596,015 (version 20150301) and 587,263 (version 20150901), 610,785 (version 20150901) and 604,221 (version 20160301). We did not include the latest version in the comparison because of the sudden drop in the number of relational changes. 3 of 4 pairs showed a decrease of the number of non-lattice fragments. This may suggest that quality assurance work between these versions actually reduced the number of non-lattice fragments. However, the reasons for the unexpected increase in the 20150301 release may need further investigation.

SNOMED CT versions used for RGT. We used the latest five versions of SNOMED CT (the March 2017 version was released too late to be included in this study) for feasibility demonstration of our method. This choice was purely a matter of convenience and did not result from methodological or computational limitations of our approach. In fact, it would be desirable to use all the available SNOMED CT versions (in Release Format 1 as well as Release Format 2), with an appropriate starting release as the time-point for computing the fragments. One might only want to go so far to reach a point of reletively stable version (with the sizes of delta sets within a reasonable range). All the performance measures would only improve, as the RGT reference set will become larger. We also noted an abnormality in the sudden drop of relational changes in the 20160901 release, which needs further investigation.

5. Conclusion

This paper introduced an innovative notion of RGT reference set for SNOMED CT relational changes and performed a comparative evaluation of the performances of lattice, non-lattice, and randomized relational error detection methods using the newly introduced precision, recall, and geometric measures. An RGT relational-change reference set of 32,241 IS-A changes were constructed from 5 versions of SNOMED CT from September 2014 to September 2016, with reversals and changes due to deletion or addition of new concepts excluded. 68, 849 independent non-lattice fragments, 118,587 independent lattice fragments were extracted from the SNOMED CT March 2014 distribution. Comparative performance analysis of smaller (less than 15) lattice vs. non-lattice fragments were also given to reflect the more realistic setting in which such methods may be applied. Among the 32, 241 IS-A changes, independent non-lattice fragments covered 52.8% changes with 26.4% precision and a G-score of 0.373, showing non-lattice auditing as a superior approach than lattice auditing, confirming a theoretical predication implicitly given in [7, 14].