High-Speed “4D” Computational Microscopy of Bacterial Surface Motility

Abstract

Bacteria exhibit surface motility modes that play pivotal roles in early-stage biofilm community development, such as type IV pili-driven “twitching” motility and flagellum-driven “spinning” and “swarming” motility. Appendage-driven motility is controlled by molecular motors, and analysis of surface motility behavior is complicated by its inherently 3D nature, the speed of which is too fast for confocal microscopy to capture. Here, we combine electromagnetic field computation and statistical image analysis to generate 3D movies close to a surface at 5 ms time resolution using conventional inverted microscopes. We treat each bacterial cell as a spherocylindrical lens and use finite element modeling to solve Maxwell’s equations and compute the diffracted light intensities associated with different angular orientations of the bacterium relative to the surface. By performing cross-correlation calculations between measured 2D microscopy images and a library of computed light intensities, we demonstrate that near-surface 3D movies of Pseudomonas aeruginosa translational and rotational motion are possible at high temporal resolution. Comparison between computational reconstructions and detailed hydrodynamic calculations reveals that P. aeruginosa act like low Reynolds number spinning tops with unstable orbits, driven by a flagellum motor with a torque output of ~2 pN μm. Interestingly, our analysis reveals that P. aeruginosa can undergo complex flagellum-driven dynamical behavior, including precession, nutation, and an unexpected taxonomy of surface motility mechanisms, including upright-spinning bacteria that diffuse laterally across the surface, and horizontal bacteria that follow helicoidal trajectories and exhibit superdiffusive movements parallel to the surface.

Graphical Abstract

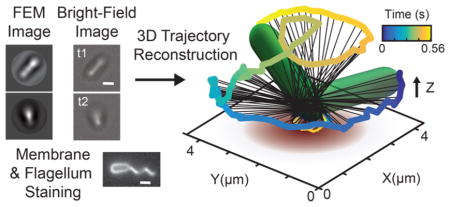
Biofilm communities are surface-associated microbial communities that are fundamental to the biology and ecology of bacteria in biomedical, environmental, and industrial contexts. During early stages of biofilm formation, bacteria adapt their motility appendages for surface sensing^1–3 and viscosity sensing.^4–7 It was recently shown that deletion of such appendages can even impact cell size homeostasis and metabolic diversity.⁸ They also develop a broad range of surface-specific motility strategies critical to the formation of biofilms. Pili are hairlike appendages (diameter ~5 nm) found on many bacterial species. Type IV pili (TFP) are molecular motors capable of generating motile forces via cycles of linear extension and retraction.^9–11 Motility behavior involving pili includes mannose-sensitive hemagglutinin (MSHA)-based “surface scanning” behavior that precedes commitment to bacterial surface attachment¹² and TFP-based “twitching” motility.^13–15 The latter motility mediates exopolysaccharide (EPS) “trail following” behavior via a perpendicular gradient chemotactic coupling,¹⁶ which ultimately forms the basis for the dynamical cooperative organization that forms microcolonies.^17–19 The flagellum is a whiplike appendage (diameter ~20 nm) driven by a rotary molecular motor. Examples of flagellum-mediated surface dynamics include “swarming”^20–24 motility and “spinning” motility,^25–28 first seen in classic experiments in which Escherichia coli are tethered to a surface by their flagellum.^27,29 Recent mathematical modeling has even revealed species-specific hydrodynamic behavior¹⁸ as well as synergistic dynamics due to pili and flagella interacting with surfaces in Vibrio cholerae.¹² However, detailed characterization of flagellum- driven motility behavior is complicated by the inherently 3D nature of the movement, the speed of which is too fast for conventional confocal microscopy to capture effectively. Specialized instrumentation based on holographic techniques^30–32 and correlative light and electron microscopy³³ has been used to obtain 3D information. Moreover, recent work has shown that it is possible to use comparisons of observed diffraction patterns with reference libraries to perform high-throughput tracking of swimming bacteria in 3D without specialized instrumentation.³⁴ Multiimaging modalities have proven valuable not only in the medical field, e.g., PET-CT, but also in cellular microscopy. For example, the combination of transmission electron microscopy (TEM) with confocal imaging, aided with 3D computational reconstructions, has allowed the detailed study of cilia in eukaryotic cells.³³

Here, we exploit electromagnetic field computation and statistical image analysis to make high-resolution near-surface (<4 μm) 3D movies at a 5 ms time resolution using images from conventional inverted microscopes. We treat each bacterial cell as a spherocylindrical lens and use finite element method (FEM) modeling to solve Maxwell’s equations for all diffracted light fields associated with different angular orientations of the bacterium relative to the surface. In this manner, a library of calculated microscopy images can be generated. Cross-correlation calculations between experimental 2D microscopy images and this image library allows for reconstruction of near-surface 3D movies of P. aeruginosa translational and rotational motion at high temporal resolution. We use this “4D” computational microscopy method to produce movies at 5 ms time resolution, but even finer resolutions are in principle possible. Comparisons between computational reconstructions and detailed hydrodynamic calculations reveal that P. aeruginosa act like spinning tops with unstable orbits in the low Reynolds number regime, driven by a flagellum motor with a torque output of ~2 pN μm, which is close to measured values for other species.²⁷ Interestingly, our analysis reveals that P. aeruginosa can undergo complex flagellum-driven dynamical behavior, including precession, nutation, and an unexpected taxonomy of surface motility modes, such as vertical-spinning bacteria with unanchored poles that transiently move on the surface. Moreover, we find that horizontal bacteria with canted flagella can move parallel to the surface with the two poles of the bacterium tracing out phase-shifted helical trajectories, resulting in efficient flagellum-driven superdiffusive surface motility. Surprisingly, these flagellum-based motility modes are reminiscent of various TFP-based movements (such as “walking” and “crawling”^14,28) that are associated with diffusive or superdiffusive motility.

RESULTS AND DISCUSSION

Finite Element Method Protocol for Calculated Microscopy Images

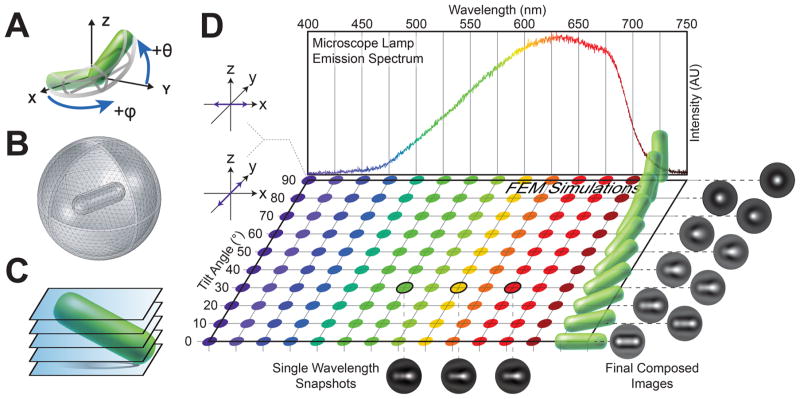
To generate a library of calculated microscopy images, the RF Module in COMSOL Multiphysics 5.0 is used to solve Maxwell’s equations for the electric field and light intensity distributions around the bacteria. Since the wavelength of light scattered (λ = 400–700 nm) is comparable with the size of the bacterium, a simple ray-optics calculation is insufficient and a full electromagnetic solution is required. The full electromagnetic theory captures diffractive effects that contribute to the observed light intensity. A 3 μm × 1 μm spherocylindrical model of P. aeruginosa is created within COMSOL (Figure 1A). The model bacterium is placed within a sphere of water of radius 3 μm, simulating the surrounding medium. A perfectly matched layer (PML) of width 0.2 μm is created to absorb outgoing radiation, allowing for truncation of the simulation volume (Figure 1B). The bacterium and surrounding water are meshed with a tetrahedral mesh of element size λ/5, and the PML is swept with quadrilateral elements of size λ/5. By meshing the entire simulation volume, we can obtain light-scattering fields across any arbitrary plane slicing through the volume (Figure 1C). Light intensity incident on these slices defines the computational microscopy images. To determine the dominant wavelengths in our microscope light source, we measure the emission spectrum of the halogen bulb (Figure 1D, top). The index of refraction of the bacterium is set to n₁ = 1.4,^35–37 consistent with prior measurements, while the index of the surrounding medium is set to that of water, n₂ = 1.33. Simulations were performed at an index of refraction ratio of n₁/n₂ = 1.05. We compute diffracted light fields across the dominant emission wavelengths (400–700 nm), two orthogonal polarizations (to simulate unpolarized light), and 10 different tilt angles (0–90°). A total of 260 distinct simulations are performed and composed into a look-up table of 10 final images corresponding to 10 different polar tilt angles (Figure 1D, right). Details of the COMSOL FEM simulation parameters and composition methodology of the simulated microscopy images are described in the Methods.

Figure 1.

Light-scattering simulations of tilted bacteria. (A) Modified spherical coordinate system used to specify the three-dimensional orientation of a tilted bacterium. θ represents the polar tilt angle measured with respect to the XY plane, and ϕ represents the azimuthal angle measured with respect to the positive X axis. (B) Diagram of the meshed simulation volume in FEM, including the bacterium, surrounding medium, and perfectly matched layer. The bacterium is modeled as a spherocylinder of length 3 μm and diameter 1 μm, which sits within a surrounding sphere of water with a radius of 3 μm. The perfectly matched layer is a thin outer shell of thickness 0.2 μm that absorbs light scattering off the artificial boundary. (C) Horizontal image slices obtained from the FEM-simulated light scattering. Multiple 2D slices spaced by Δd = 0.05 μm are taken from −2.5 μm below to +2.5 μm above the central plane (z = 0 μm). The final FEM image is a composite of these simulation slices. (D) We measured the spectral power distribution of our microscope light source to determine the dominant emission wavelengths (top). 260 total light-scattering simulations of tilted bacteria were conducted, spanning 10 different tilt angles (0–90°), 13 different wavelengths (400–700 nm), and two orthogonal light polarizations (purple arrows, left). Colors correspond to the wavelength of light used in the simulation, and the different tilt states are represented by the green spherocylinders. We show three example snapshots of FEM simulation results for bacteria tilted at 30° at wavelengths λ = 550, 600, and 650 nm averaged across polarizations (bottom). The final look-up table of composed images corresponding to each tilt angle (right) are obtained by summing over all simulated wavelengths according to the power spectrum and averaging the results for two orthogonal polarizations (left, purple arrows), which simulate unpolarized light.

“4D” Computational Microscopy Vector Parameters

In microscopy, increasing the spatial resolution in any dimension typically results in a trade-off in temporal resolution. The “4D” computational microscopy methods described here combines the high time and 2D (X–Y) resolution of the acquisition camera and the finite element method modeling results to calculate missing out-of-focus information (Z). To do this, we quantitatively compare the experimental images to our lookup table of computational microscopy images. Image processing and cell-tracking algorithms are adapted from previous work^12,14 and written in MATLAB R2015a (Mathworks). Briefly, all FEM-calculated images are imported into MATLAB as an image library. All experimental images are segmented and processed in a similar manner, and a normalized cross-correlation is performed between each experimental image and every simulated image in the library. The correlation values are stored in a 10 × 180 data matrix, which corresponds to 10 different polar tilt angles and 180 different azimuthal orientation angles of the bacterium. The full orientation (θ, ϕ) of the bacterium is numerically deduced from this correlation matrix. This process is repeated for every frame of the movie, and the resulting predicted angular coordinates, polar tilt angle θ and azimuthal orientation angle ϕ, are stored as a time series (a full description of the computational algorithms to calculate ϕ and θ is contained in the Methods).

Finally, the location of the contact point (cp) of the bacterium on the surface is identified. In bright-field (BF) microscopy, the bacterium approximates a lens which focuses the incident light to the focal plane on the surface with an intensity maximum located along the bacterium body axis. The contact point is calculated from the raw grayscale images by applying a 3 × 3 edge filter to identify the X–Y coordinate with the largest pixel intensity gradient along the body. Hence, the 3D conformation and trajectory of a motile bacterium on a surface can be comprehensively described by four parameters in time [θ(t), ϕ(t), X_cp(t), Y_cp(t)]. To qualitatively describe the polar tilt angle θ of the bacterium body, we use the following terminology. Since the Z-axis is normal to the surface, bacteria that have their long axis parallel to the Z-axis (θ = 90°) are referred to as tilted, upright, or vertical; bacteria with their long axis perpendicular to the Z-axis (θ = 0°) are referred to as either not tilted or horizontal (Figure 1A).

Free-Spinning Rod-Shaped Bacteria

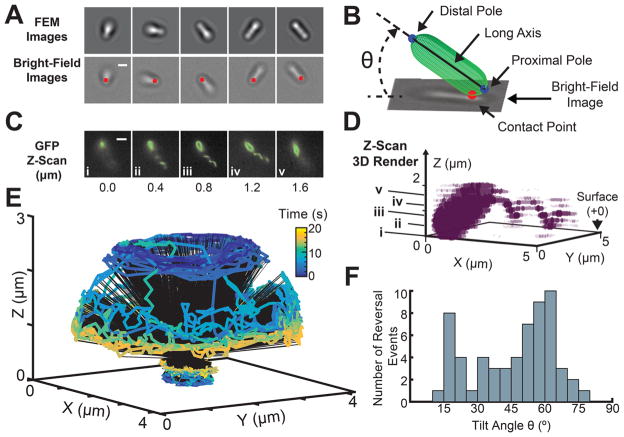
To reconstruct the 3D trajectory of the bacterium, the translational and rotational motions of each bacterium were tracked with the four parameters as a function of time [θ(t), ϕ(t), X_cp(t), Y_cp(t)]. Figure 2A shows five snapshots of measured BF images of a spinning bacterium and their corresponding FEM calculated images with maximal cross correlation values. The location of the contact point, [X_cp(t), Y_cp(t)], is labeled with a red dot for each bright-field image. To visualize the 3D trajectory, a spherocylinder was used to represent the bacterium body, and a 3D video of the motion was reconstructed (see the Methods). For visual clarity of the trajectory, only the poles, connected by the body long axis, are shown (Figure 2B, Supplementary Movie S1).

Figure 2.

3D reconstruction of the trajectory and flagellar orientation of a spinning bacterium. (A) Series of five sequential bright field snapshots (bottom) of a spinning bacterium are matched with their corresponding FEM simulated images (top) based on maximum cross-correlation value (2 μm scale bar). The location of the contact point is labeled with a red dot for each bright-field image. (B) Schematic of a reconstructed orientation and location for a bacterium bright-field image. A spherocylinder is used to visualize the long axis, distal, and proximal pole for each bacterium (see the Methods) (C) Location and orientation of the flagellum filament relative to the surface and the bacterium body is identified by fluorescence microscopy after staining of the cell membrane and flagellum. Parallel z-slices were taken at Δz = 0.2 μm, in the GFP channel, from the surface. A set of five sequential slices (z = 0.0, 0.4, 0.8, 1.2, and 1.6 μm) show that the flagellum is attached to the pole distal from the surface (3 μm scale bar). Furthermore, the flagellum axis is aligned at a non-zero angle with respect to the long axis of the body. The body–flagellum misalignment can be easily visualized in (D), the 3D render generated from the fluorescence z-scan (see the Methods). The (i–v) labeled points on z correspond to the (i–v) images in (C). (E) A 20 s reconstruction of the full 3D trajectory traced out by the poles of a single freely spinning bacterium. (F) Histogram of the tilt angles θ at which every detected reversal event occurred, generated using 60 reversals across 13 bacteria. 95% of the detected reversal events occur below a tilt angle θ = 70°.

Early work on the dynamics of bacterial flagellum motors leveraged the use of flagellum-specific antibodies to tether bacteria to surfaces, thereby making it possible to execute high precision measurements of angular speed and flagella-motor torque output.²⁶ Here, we aim to do something complementary by using techniques outlined above to monitor flagellum-mediated surface motility during early biofilm development.

To observe the geometric relationship between the flagellum and the bacterium body during surface movement, we carried out BF and fluorescence microscopy on a P. aeruginosa PA14 wild type (WT) strain with a cysteine mutation in the fliC gene to allow fluorescent labeling of the flagellum (Figure 2A–D). To see the location and orientation of the flagellum relative to the cell body, the cell membrane and the flagellum were fluorescently labeled with FM 1–43 FX membrane stain and Alexa Fluor 488 C5 Maleimide, respectively (see the Methods for details on the strain, stains, and imaging protocols). The bacteria were imaged on the glass surface with BF and fluorescence microscopy. First, high-speed BF imaging was conducted at 200 frames per second (fps) for 30–60 s. Then, fluorescent z-scans of the sample volume (Δz = 0.2 μm spaced slices) were taken at the end of the BF recording using a GFP filter. A 3D rendering of the entire bacterium and flagellum is recovered using this series of z-scans spanning 1.6 μm. This analysis reveals that the flagellum is distal to the surface and is not collinear with the body axis of the bacterium (Figure 2C,D). Thus, this is a system that has the potential for rich hydrodynamic behavior due to the asymmetry between the body and the flagellum.

Analyses of surface bacterial trajectories reveal that although several bacteria spin with their flagellum tethered to the surface, the majority of bacteria prefer to spin upright with the flagellated pole distal to the surface (Figure 2, Supplementary Figures S1–S3). For a subset of these bacteria, the cell body and flagellum rotate together in a synchronized propeller-like motion. From high-speed tracking of these spinning bacteria, we observe a rich hierarchy of motility patterns that are reminiscent of spinning tops with unstable orbits: Fast “tilt-up” and “tilt-down” transitions in θ while rotating azimuthally in ϕ, abrupt reversals of azimuthal rotations, and nutations with small and large radii (Supplementary Figures S1–S4).

Empirically, in the case of monotrichous P. aeruginosa PA14 moving freely on a surface with a free flagellum, we find that sudden changes in polar tilt angles θ can occur while bacteria are spinning azimuthally. A representative example of this behavior is seen in Figure 2E, which illustrates the tracking method. A reconstructed trajectory of the two poles over a 20 s time interval is color coded by the time index. To quantitatively map the rotational dynamics of the bacterium, we calculate the tilt states of the bacterium for t = 0–3 and t = 17–20 s. We define a tilt state θ̄(t₁, t₂) as the mean polar angle θ during a time window [t₁, t₂]. The bacterium begins at a tilt state of θ̄(0 s, 3 s) ≈53 ±4°, and spins down to a lower tilt state, θ̄(17 s, 20 s) ≈ 17 ± 4°. As the bacteria rotates in ϕ, it can have multiple or a single tilt states θ̄(t₁, t₂) making transitions between them, and/or have reversals of ϕ rotation direction. Interestingly, for bacteria examined here, 95% of detected reversal events occur below a polar tilt angle of 70° (Figure 2D). Trajectories showing reversal events are shown in Supplementary Figure S3. Reversals in the rotation of the flagellum motor are fundamental to bacterial chemotaxis.^25–27,29 In the case of P. aeruginosa, changes in the time structure of reversal behavior are observed for different diguanylate cyclase mutants.^1,38–40

To further dissect this phenomenon, we calculate the 3D angular speed of the bacterium over time from the time-series trajectory. Typically, angular velocities are calculated from the azimuthal rotational information. 3D orientations of spinning bacteria can be inferred from 2D projections of the cell body onto the surface, but the out-of-plane contribution to the angular speed is often neglected. This is compounded by the observation that some bacteria can dynamically change tilt states in the out-of-plane-direction (θ) while spinning azimuthally (ϕ). In fact, some bacteria often spend a significant amount of time spinning at near-vertical tilt angles (θ > 70°). Therefore, an accurate reconstruction of the bacterial angular trajectory in principle requires both the ϕ and θ components of motion. The FEM simulations enable high-resolution recovery of θ information, allowing for calculation of the true 3D angular speed. The true 3D angular speed, V_θϕ, of the bacterium is calculated as a function of the first derivatives of the polar and azimuthal angles:

$$V_{\theta \varphi }=\sqrt{{\left(\frac{\mathrm{d}\theta }{\mathrm{d}t}\right)}^2+{\text{sin}}^2\left(\frac{\pi }{2}-\theta \right){\left(\frac{\mathrm{d}\varphi }{\mathrm{d}t}\right)}^2}$$ (1)

By tracking the temporal evolution of both angular variables, we observe a mean angular speed of 2.18 ± 1.28 Hz, with a range of 0.68–4.38 Hz. These data afford us the opportunity to engage the nonequilibrium thermodynamics of the flagellum motor, which is beyond the scope of the present paper. We will present elsewhere a detailed analysis of the distribution of the observed nonequilibrium fluctuations of the angular velocity in the context of fluctuation theorems.

Hydrodynamic Modeling of Bacteria Spinning about Their Nonflagellated Pole

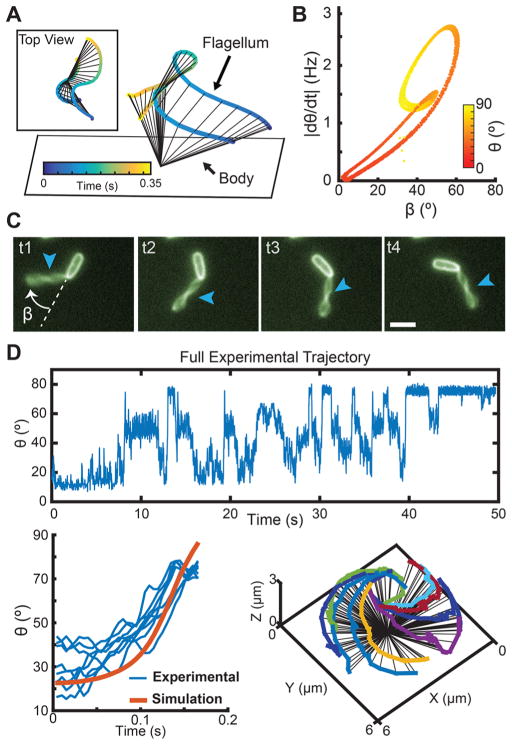
Based on the motility behavior observed in Figure 2E and the flagellum orientation and location in Figure 2D, it is interesting to examine whether the flagellum plays a role in achieving and maintaining a vertical orientation with respect to the surface, which is commonly observed during surface detachment. To answer this, we construct a hydrodynamic model (Figure 3). The PA14 spinning behavior shown in Figure 2E involves fast transitions in the polar tilt angle. Thus, a key question is how these instabilities arise in spinning bacteria at low Reynolds numbers. Previously, we studied the hydrodynamics of a spinning bacterium with a surface-tethered flagellum.¹⁸ Here, a cognate model is developed, in which the bacterium is attached to the surface by the nonflagellated pole, so that the spinning flagellum is driving the system from the distal pole. The cell body is modeled as a cylinder (with length 3 μm and radius 0.3 μm), and the flagellum as a helical filament (with wavelength 2 μm, total length 4 μm, radius 0.02 μm, and helix radius 0.4 μm). The flagellar hook, which is the flexible joint between the cell body and the flagellum, has a spring constant k that penalizes deviations from the preferred angle between the cell body axis and the flagellum axis.¹⁸ The flagellar motor exerts a torque τ at the base of the cell body, causing the flagellum to rotate relative to the body. The cell body is attached to the surface by fixing a point along the central long axis of the body 0.35 μm away from the nonflagellated pole, and the body does not counter-rotate in response to the flagellum rotation. The different spinning behaviors observed in the model depend on the ratio α = k/τ between the spring constant and the torque, rather than their individual absolute values; the absolute value of τ sets the time scale of the behavior.

Figure 3.

Misalignment between flagellum and cell body axes lead to fast transitions in tilt angle θ. (A) Simulated trajectory of a bacterium exploring a range of polar tilt angles. The proximal pole is touching the surface, while the flagellum is connected to the pole distal to the surface. Inset shows the top view of the simulated trajectory. (B) As the flagellum spins, the hook that connects it to the body allows it to adopt different angles with respect to the body. The resulting misalignment angle between the body long axis and the flagellum (β) oscillates between β = 1.7–61° as the body tilts up and down. Larger β angles between the body and the flagellum will generally yield faster polar tilt speeds, |dθ/dt|. (C) Fluorescent labeling of the body and flagellum allows for calculation of β as the body rotates on the surface, t1–t4 with times 0.0, 0.15, 0.30, and 0.45 s, respectively (3 μm scale bar). Arrows point to flagellum location. (D) Using cross-covariance (function “xcov” in MATLAB), a simulated rising trajectory (k = 4 pN μm, τ = 2 pN μm) of a bacterium rotating on a surface (orange) is used to identify similar rises in multiple experimentally tracked trajectories (blue). The identified trajectories that closely matched the hydrodynamic model are illustrated on the right.

In simulations of the hydrodynamic model, significant changes in the polar tilt angle θ can occur when the bacterium body axis and flagellum axis are not aligned with each other (Figure 3A). The resulting misalignment angle between the bacterium axis and the flagellum (β) oscillates between β = 1.7–61° as the body tilts up and down. Different values of β result in different polar tilt speeds, |dθ/dt|. The maximum misalignment angle is β_max = 61° with a tilt speed |dθ/dt| = 2.43 Hz, while the smallest angle is β_min = 1.7° with |dθ/dt| = 0.065 Hz. In general, larger polar tilt speeds, |dθ/dt|, correspond to greater misalignment angles β (Figure 3B). For the observed PA14 spinning bacteria, the misalignment angle is visualized by taking fluorescent images at 5 fps and keeping the focal plane fixed on the surface. At this frame rate sampling, it is possible to track the orientation of the body and flagellum for bacteria at near-horizontal spinning (Figure 3C). We observe a broad distribution of misalignment angles from β ~ 0° (collinear) to β ~ 180° (flagellum superimposed on the cell body). For most observed cases, bacteria tend to hold β constant during horizontal spinning (Supplementary Figure S5), which can be seen using the fast fluorescence imaging protocol. There are other cases where bacteria exhibit transitions between tilt angle states with different degrees of misalignment of the flagellum with respect to the body (Supplementary Figure S2), which can be seen using the BF/fluorescence imaging protocols explained earlier. Based on these data, we hypothesize that β may be important for tilt angle transitions and states.

The observed spinning behaviors in the model depend on the ratio between the flagellar hook spring constant and the flagellar torque (α = k/τ). By design, the time scale of the behaviors is directly proportional to the absolute torque. Thus, the time scales of the simulation and experimental trajectories can be aligned by selecting a proportional torque value. In this manner, the torque required for these spinning behaviors can be estimated simply by rescaling the time. Using cross-covariance, the full tilt angle history for a spinning bacterium is compared to a single simulated tilt angle rise for a range of time scales and torque values reported in literature.²⁷ For each set of simulated torque values, primary peaks from the cross-covariance output matrix are isolated and used to extract rises from the full experimental trajectory using a time window of the same size as the simulation rise time scale. The torque value and time scale that give the largest cross-covariance peak value (lowest error) are reported as the best match. The lower panel of Figure 3D shows the identified rises for the spinning bacterium using a set torque value of 2 pN μm, which is close to the reported values in the literature for flagella in other species.²⁷

Reconstruction of Flagellum-Driven Near-Surface Motility Modes of P. aeruginosa

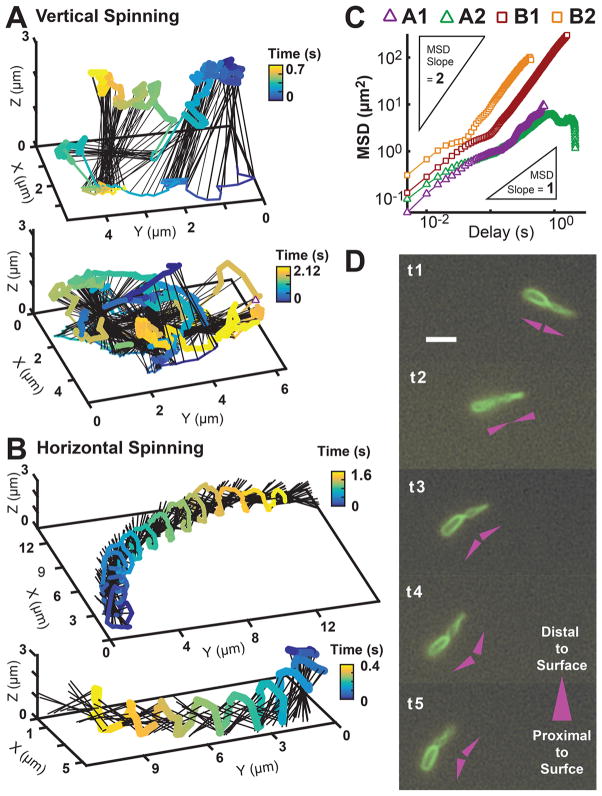
We use the above-described computational microscopy technique to reconstruct dynamics of two distinct categories of flagellum-driven near-surface motility modes with coupled translational and rotational motion. The first category can be roughly described as upright spinning with transverse diffusion and is similar to the free-spinning bacteria previously observed, except the pole in contact with the surface can “slip” and make significant lateral excursions. These excursions result in approximately diffusive motion on the surface. Figure 4A shows two examples of the reconstructed 3D trajectories for bacteria with this type of motility. The second category has trajectories analogous to those of the wobbly spirals of thrown footballs that are helicoidal with the principal axis parallel to the surface. This type of motion is highly superdiffusive, and the bacterial poles trace out out-of-phase helical trajectories while alternating contact with the surface. Figure 4B shows two examples of reconstructed 3D trajectories for bacteria exhibiting this type of motility, with additional trajectories in Supplementary Figure S6. Plots of the mean-squared displacement (MSD) curves for these two categories of motion are shown in Figure 4C. For upright spinning, the motion of the poles in contact with the surface is approximately diffusive, with MSD slopes ranging between 0.83 and 0.99. For horizontal spinning, the axial translation of the rotating body is highly superdiffusive, with the MSD slope of the contact point ranging between 1.45 and 1.50. By analyzing the traces of the poles, the helical trajectories are estimated to have a pitch between 0.9 and 5.0 μm/rev and an angular frequency between 11.1 and 33.3 Hz. An interesting observation is that these bacteria do not have their body and flagellar axes collinear with each other while they move in this helical fashion. Sequential fluorescent snapshots of labeled membrane and flagellum for this superdiffusive motion are shown in Figure 4D. We hypothesize that this angle between the bacterium body and flagellum may play a role on the pitch and angular frequency of this superdiffusive flagellum-driven surface motility.

Figure 4.

Bacteria exhibit diverse flagellum-driven translational and rotational motion while exploring surfaces during early biofilm formation. (A) Two reconstructed 3D trajectories of vertical-spinning bacteria, where the pole in contact with the surface can “slip” and make lateral excursions. These excursions result in relatively diffusive motion on the surface. (B) Two reconstructed 3D trajectories of horizontal-spinning bacteria, where the bodies’ spinning axes are predominantly parallel to the surface, their motion is highly superdiffusive, and their poles trace out a helical trajectory while alternating contact with the surface. (C) MSD versus time of the contact point for the four reconstructed trajectories in A and B. The vertical-spinning cells, A1 (top) and A2 (bottom), translate approximately diffusively on the surface with MSD slope of 0.99 and 0.83, respectively; horizontal-spinning cells, B1 (top) and B2 (bottom), translate superdiffusively with MSD slopes 1.45 and 1.48, respectively. Inset triangles represent the reference line slopes. (D) Sequential time-series snapshots, Δt = 0.12 s, of fluorescently labeled membrane and flagellum, for a horizontal-spinning cell moving on the surface. The head and flagellum maintain a misalignment angle β as it spins/translates. A diagram convention next to each snapshot illustrates the rotating V-shape maintained by the cell: The head and flagellum are each represented by a triangle pointing in the direction distal to the surface.

CONCLUSIONS AND PROSPECTS

The experimental technique outlined here is capable of reconstructing 3D phenomena near a surface with 5 ms time resolution. As a test case, we use this type of “4D” computational microscopy to study flagellum-driven bacterial motility near surfaces. We find two types of unanticipated flagellum-driven surface motions: vertical-spinning bacteria with unanchored poles that exhibit diffusive motion on the surface, and horizontal bacteria that are driven by the flagellum to execute purely superdiffusive motion on a surface. These fundamental flagellum-based motility mechanisms are reminiscent of various TFP-based movements (such as “walking” and “crawling”) that enforce diffusive or superdiffusive motility outcomes.²⁸

Studying spinning bacteria by tethering the flagellum to the surface has allowed for precise characterization of the flagellar rotary motor machinery.^25–27 Here, we expand our understanding of the hydrodynamic motility of the coupled flagellum-body system. The ability of monotrichous bacteria to stay surface bound while performing fast tilt angle changes and spinning reversals without an anchored flagellum suggests the presence of forces between the surface and the cell body. These may be especially important for the diffusive motion on the surface of vertically spinning bacteria. Moreover, the helical trajectories traced by the near-surface superdiffusive bacteria with a canted flagellum demonstrate the ability to use the flagellum not only as a simple propeller but as a more complex hydrodynamic appendage coupled to the cell body. In future work, it will be interesting to observe and model how these fundamental flagellum-driven surface movements are related to complex surface motility modes such as swarming, both the single cell version and the collective version, and how these motions are modified by structural modifications of the flagellum motor, such as stator changes.^{5,20–22,24,27,41} While the demonstration experiments here are performed on bacteria, it is clear that these computational microscopy techniques are generalizable to many species in microbiology.

METHODS

Experimental Imaging

P. aeruginosa strains PA14 wild-type (WT) with FliC modified to FliC^T394C were used in this study. PA14 were cultured in M63 medium supplemented with 1 mM magnesium sulfate, 0.2% glucose, and 0.5% casamino acids (CAA) overnight under shaking at 37 °C. M63 medium contained (per liter of deionized water) 3 g of potassium phosphate monobasic, 7 g of potassium phosphate dibasic, and 2 g of ammonium sulfate. Then a 1:50 dilution of cell culture was subcultured in a M63 medium, with reduced nutrients, with 1 mM magnesium sulfate, 0.05% glucose, and 0.25% CAA. The bacteria were subcultured to an OD₆₀₀ ~ 0.4. The cell culture was then diluted to an OD₆₀₀ in the range 0.01–0.03 in overnight medium described above, without CAA to minimize cross reaction with the dye.

Cell body membranes were stained using FM 1-43 FX (Life Technologies) at a concentration of 0.25 μg/mL. Flagella were stained using Alexa Fluor 488 C5 Maleimide (Molecular Probes) at concentration of 10 μg/mL. The dye was introduced after the last dilution. The bacteria were then injected into a sterile flow cell (ibidi sticky-Slide VI^0.4 with a glass coverslip) containing the same medium. The flow cell was attached to a heating stage set to 30 °C. After a brief incubation period (~1 min), the flow chamber was flushed with full overnight medium and then imaged.

Two separate imaging protocols were used to obtain the image data. The first imaging protocol involved fluorescence imaging for ~5 s at a single XYZ location. Fluorescence recordings used an Andor iXon EMCCD camera; images were taken with a 100 ms exposure (GFP filter with 456–490 nm excitation and 500–539 nm emission) at ~6.5 frames per second (fps) and a resolution of 1024 × 1024 pixels (0.065 μm/ pixel). This protocol was performed on an Olympus IX81 microscope equipped with a 100× oil objective, a 2× multiplier lens, and a Zero Drift Correction autofocus system.

The second imaging protocol involved high-speed bright-field imaging for ~30 s at a single XYZ location immediately followed by a fluorescence Z-scan imaging at the same XY location. High-speed bright-field recordings used a Phantom V12.1 high speed camera (Vision Research); images were taken with a 5 ms exposure at 200 fps and a resolution of 512 × 512 pixels (0.1 μm/pixel). Fluorescence Z-scan recordings used an Andor Neo sCMOS camera; images were taken with a 100 ms exposure (GFP filter with 456–490 nm excitation and 500–539 nm emission) at ~6.5 fps and a resolution of 2048 × 2048 pixels (0.0325 μm/pixel). Z-Scans were performed by scanning from the surface (+0 μm) to +4 μm above the surface at equal Δz spacings of 0.2 μm per picture. This protocol was performed on an Olympus IX83 microscope equipped with a 100× oil objective, a 2× multiplier lens, and a Zero Drift Correction autofocus system with both cameras simultaneously mounted on the microscope. These imaging protocols were repeated for multiple XYZ locations in the flow cell during the first 30 min after injection.

Construction of FliC^T394C Strains

In order to visualize flagella in P. aeruginosa, we introduced a T394C mutation in the flagellum protein FliC. This amino acid substitution is analogous to the T209C mutation in the Hag protein of Bacillus subtilis.⁴ To generate the mutant FliC^T394C construct, DNA fragments upstream and downstream of the fliC gene were PCR amplified from PA14 genomic DNA using the following primer pairs, respectively:

• FliC-up-for (tgtaaaacgacggccagtgccaagcttgcatgcctgcgacctcaacacctcgttgca)

• T394C-up-rev (gttctgggcgccgtcggcgcaggagatgtcgacgctggcaacgct)

• T394C-dn-for (agcgttgccagcgtcgacatctcctgcgccgacggcgcccagaac)

• FliC-dn-rev (ggaaacagctatgaccatgattacgaattcgagctccgcgctgatcgcactcttga)

The T394C codon mutation is underlined in the T394C-up-rev and T394C-dn-for primer sequences. The PCR products generated from these primer pairs were cloned into pMQ30 via homologous recombination in Saccharomyces cerevisiae InvSci (Invitrogen) as previously described.⁴² The resulting pMQ30-FliC^T394C plasmid was used to transform E. coli S17 via electroporation and was subsequently introduced into P. aeruginosa PA14 via conjugation. Integrants were selected with 30 μg/mL gentamicin and 20 μg/mL nalidixic acid. To evict the plasmid, bacteria were grown in 3 mL LB broth for 6 h at 37 °C, serially diluted with LB, spread on LB agar containing 10% sucrose and no salt, and then incubated at 30 °C overnight. Individual colonies were patched on LB plates and LB plates containing gentamicin to identify gentamicin-sensitive colonies that had evicted the plasmid. Colonies that had excised the plasmid were screened by PCR using primers T394C-check-for (cgacaagggtgtactgaccatca) and FliC-check-rev (gcgctcgccttgagaatgtct). PCR products were sequenced with primer T394C-check-for to determine which isolates had retained the allele encoding FliC^T394C.

COMSOL Finite Element Method Simulations

A typical size of a rodlike bacterium like P. aeruginosa is roughly 3 μm × 1 μm. We modeled the geometry of the bacterium as a spherocylinder consisting of the union of a cylinder and two spheres all with radius r = 0.5 μm (Figure 1A). The length of the cylinder can vary depending on the desired length of the bacterium. For a bacterium of length L = 3 μm, the cylinder has length L_c = L − 2r = 2 μm. The model bacterium is approximated as a spherocylinder of one dielectric medium embedded in the center of a larger sphere of radius 3 μm, which contains a different dielectric medium. The larger sphere has an outer layer of thickness 0.2 μm, which serves as a perfectly matched layer (PML) to absorb all outgoing radiation to avoid light reflection off the artificial boundary. This truncation of the simulation volume allows us to mimic scattering in an infinite domain without requiring meshing over an infinite volume, which is computationally unfeasible.

COMSOL utilizes a finite-element method (FEM) to spatially discretize the differential equations. The finite-element method requires a mesh to be defined on the geometry. We chose a free tetrahedral mesh on the bacterium and within the dielectric medium surrounding the bacterium (Figure 1B). The mesh in the PML was swept using quadrilateral elements from the inner to outer radius. We chose a mesh size of λ/5, which is fine enough to resolve the electric field on all surfaces but large enough to minimize system memory usage.

The emission spectrum of the halogen light source in the microscope was experimentally measured using an Ocean Optics USB400 Module and SpectraSuite software (Figure 1D). Since the dominant emission is in the 400–700 nm range, we simulated scattering of incident radiation in this range. FEM requires simulation of single wavelengths, so we composed simulations from multiple wavelengths weighted by the relative power of each wavelength in the emission spectrum (calculated from the SpectraSuite output). Since the experimental light source is incoherent, we simulated two incident fields with orthogonal polarizations. We define the first incident field E⃗₁ to be a linearly polarized plane wave in the ŷ direction with an initial value of E₀ = 100 V/m.

$${\overrightarrow{E}}_1=E_0\widehat{y}{\mathrm{e}}^{-i\overrightarrow{k}·\overrightarrow{r}}$$

We choose the second incident field E⃗₂ to have an orthogonal polarization in the x̂-ẑ plane, where θ is the defined polar tilt angle of the bacterium away from the X–Y plane.

$${\overrightarrow{E}}_2=E_0(\widehat{x}cos\theta -\widehat{z}sin\theta ){\mathrm{e}}^{-i\overrightarrow{k}·\overrightarrow{r}}$$

The wavevector is defined as

$$\overrightarrow{k}=-\frac{2\pi }{\lambda }(\widehat{x}sin\theta +\widehat{z}cos\theta )$$

These incident fields allowed us to span all possible polarizations and simulate the unpolarized light in our experimental setup. To reduce the computational complexity and decrease the modeling time required, we varied the angle of incidence of the incident radiation rather than tilting the bacteria in the simulation space. A simple coordinate rotation transform was used to obtain results for a tilted bacterium exposed to incident radiation parallel to the ẑ direction.

The equation solved to obtain the electric field is

$$\nabla \times \frac{1}{{\mu }_{\mathrm{r}}}(\nabla \times \overrightarrow{E})-k_0^2{\mathrm{\epsilon }}_{\mathrm{r}}\overrightarrow{E}=0$$

where the background radiation is defined as E⃗₁ and E⃗₂ from above and μ_r = 1.

The indices of refraction for the bacterium and the surrounding medium are set to mimic the true values from experiment. A typical imaging setup contains bacteria suspended in a surrounding medium of water-based media. A typical reported index of refraction of a bacterium was n₁ = 1.4.^35–37 As a first approximation, the differential contributions of the cell wall and membrane, attenuation effects, nonlinear contributions are all ignored. The index of refraction of the surrounding volume is chosen to be n₂ = 1.33. The simulation was performed at an index of refraction ratio of n₁/n₂ = 1.05/1. The surrounding sphere of water was assigned an index of refraction of n₂ = 1, while the bacterium interior was assigned a value of n₁ = 1.05 (Figure 1B). We found empirically that these conditions used in the simulations provide a good approximation of our experimental images.

A parametric sweep was performed over wavelengths λ = 400–700 nm in increments of 25 nm, polar tilt angles θ = 0–90° in increments of 10°, and the two defined orthogonal polarizations, E⃗₁ and E⃗₂ (260 total simulations) (Figure 1D). Simulations were carried out locally on a Dell XPS with a quad-core Intel Core i7 CPU with 32 GB of DDR3 RAM and remotely on a server running dual 8-core Intel Xenon E5-2630L CPUs with 384 GB of DDR3 RAM.

After simulation, the intensity is plotted for all points on the mesh with interpolation, where I ∝ |E⃗|². These files are then processed to obtain intensities projected onto successive parallel cut planes through the volume (Figure 1C).

Since we simulated light scattering of tilted bacteria by changing the angle of incidence of the light source, a coordinate transformation is performed to obtain the light intensity distribution in the experimental coordinates. We convolve the resulting scattered light fields with a rotation matrix to get new relative coordinates. The location of the imaging focal plane is defined to be the cut plane tangent to the bottom of the bacterium, which coincides with the experimental focal plane. For a bacterium tilted at angle θ, we define the central plane passing the origin with normal vector n̂= (sin θ, 0, cos θ), where θ is the polar tilt angle of the bacterium. We generate multiple 2D slices equally spaced by Δd = 0.05 μm parallel to the central plane at z = 0 μm, from −2.5 μm below to +2.5 μm above (Figure 1C). The output data vector is in the form of (x, y, z, |E|). This process is repeated for all combinations of wavelengths, tilt angles, and polarizations for several lengths of bacteria using COMSOL LiveLink for MATLAB.

Recomposition of Microscopy Images

An inherent limitation of COMSOL is that multiple slices data must be exported to a single CSV file. Thus, data at different z-slices are mixed up. To separate them, we rotated the x and z coordinate around the y axis by θ degrees clockwise keeping the aspect ratio constant, rounded the z coordinate to eliminate numerical errors caused by rotation, sorted all of the data according to the z coordinate, and classified them into different cut planes.

The resulting images of the light intensity distribution are processed to simulate imaging of bacteria on a surface. The optics of the microscope should be considered when reconstructing theoretical microscopy images because FEM does not adequately simulate all the optical transformations that occur within a microscope. We assume an ideal microscope and neglect nonlinear aberrations. We create an algorithm to postprocess the FEM simulation data to more realistically match the experimental images.

In our digital video microscopy, the numerical aperture (NA = 1.4) and high magnification (100×) of the objective creates a narrow depth of field, which is approximately 0.5 μm at λ = 600 nm. Thus, the image formed is the composition of the light intensity distribution in a thin three-dimensional optical volume around the object plane. According to the experimental setup, the object plane is at the bottom of the bacteria. For simplification, we selected slices within 0.4 μm of the object plane for image composition, neglecting the contribution of the out-of-focus slices that give blurred images. Since the typical focal length of a 100× objective is about 2 mm, the extended 3D tilted bacterium always lies within the regime of real images, and the differences in magnification for different parts of bacterium can be neglected. With all the simplifications and assumptions above, we utilized data from selected slices to compose images. The light intensity at (x,y) can be estimated from the electric field by I(x, y) = |E⃗(x, y)|², where the prefactor has been neglected since we only compare relative light intensity distributions. After the above procedure, we calculated the light intensity distribution function by linear interpolation. The grayscale value of each pixel is calculated by evaluating the sum of light intensity distribution functions for each of the selected slices at each point.

We chose a simple linear composition method based on several known characteristics of our experimental system. First, we composed images across a series of simulated wavelengths. This was done by calculating the relative weights of each simulated wavelength from the emission spectrum of the light source in our microscope. Second, we composed images across orthogonal polarizations, as described above. After these steps, the diffraction artifacts from the simulation patterns were almost entirely eliminated.

Image Analysis

Image processing and cell-tracking algorithms are adapted from previous work^12,14 and written in MATLAB R2015a (Mathworks). A description of the sequence of algorithms follows (Supplementary Figure S7).

Step A: Create Library of FEM Images

We imported all images into MATLAB as unsigned 8-bit integer (uint8) or unsigned 16-bit integer (uint16) arrays. The FEM simulation images have higher resolution than the experimental images, so we resized them using a bicubic interpolation with a scale factor of 0.055 and changed the resolution from 1001 × 1001 to 56 × 56 pixels. From the simulation, we observed that the best matching feature to the experimental bacterium projection profile is the dark shadows around the inner body. We segmented these shadows using a Gaussian filter, a high-pass filter, a second Gaussian filter, and an Otsu threshold. The high-pass filter used 5 × 5 is shown below:

$$\begin{array}{rrrrr}-1& -1& -1& -1& -1\\ -1& 0& 0& 0& -1\\ -1& 0& 16& 0& -1\\ -1& 0& 0& 0& -1\\ -1& -1& -1& -1& -1\end{array}$$

All of the nonshadow pixels were set to 130 intensity (about 50% of the 0–255 uint8 range). We observed the shadow pixels from the experimental images to be about 20% brighter than the shadow pixels from the FEM resized images; therefore, we increased the FEM shadows intensities by 15 units (uint8 range). To complete the library, we rotated the images by 360° in increments of 2° using a nearest neighbor interpolation.

Step B: Segmentation of Experimental Images

The experimental images were processed in a similar manner as the FEM images. We first cropped the high-speed videos of individual spinning bacteria using Phantom Camera Control software (Vision Research) and output as TIF stacks, which we then imported into MATLAB. We segmented the dark shadow around the bacterium’s body using the same procedure as mentioned previously, but with a 9 × 9 high-pass filter shown below:

$$\begin{array}{rrrrrrrrr}-1& -1& -1& -1& -1& -1& -1& -1& -1\\ -1& 0& 0& 0& 0& 0& 0& 0& -1\\ -1& 0& 0& 0& 0& 0& 0& 0& -1\\ -1& 0& 0& 0& 0& 0& 0& 0& -1\\ -1& 0& 0& 0& 32& 0& 0& 0& -1\\ -1& 0& 0& 0& 0& 0& 0& 0& -1\\ -1& 0& 0& 0& 0& 0& 0& 0& -1\\ -1& 0& 0& 0& 0& 0& 0& 0& -1\\ -1& -1& -1& -1& -1& -1& -1& -1& -1\end{array}$$

The nonshadow pixels are set to a 130 intensity value (uint8 range).

Step C: Normalized Cross-Correlation

Using the created FEM library of bacterial images, we performed a normalized cross-correlation between the experimental image and every image in the library. The normalized cross-correlation function is part of the MATLAB Image-Processing Toolbox (function name: normxcorr2.m). The maximum correlation value for each cross-correlation is stored; hence the output of this process is a 10 × 180 array of correlation values. This corresponds to 10 different tilt angles and the 180 azimuthal orientations (360° in increments of 2°).

Step D: Determining Azimuthal Orientation Angle Φ

In order to determine the azimuthal orientation angle of the bacterium, we performed a summation of the correlation values over the tilt angles. From the resulting curve, we found the azimuthal orientation with the maximum summed value. This azimuthal orientation is used as a reference to select a window of ±10° centered at this orientation, as well another window 180° away. Hence, we identified two sets of possible azimuthal orientations. From the selected azimuthal orientation windows, we identified the orientation with the greatest correlation coefficient per tilt angle. The window with the most members in the resulting set of 10 azimuthal orientations for all 10 tilt angles was used as the correct orientation window. Within the selected window, the mode is used as the true azimuthal orientation angle of the bacterium body.

Step E: Estimating Polar Tilt Angle θ

Once the azimuthal orientation was identified, we selected the ith column corresponding to such orientation. From the correlation profile at this orientation, we identified the tilt angle with the largest correlation. To better approximate a tilt angle, we used the neighboring two tilt angles.

$$\begin{gathered} \mathrm{\Phi }=[{\phi }_{i-1},{\phi }_i,{\phi }_{i+1}] \\ {C}_x=[c_{i-1},c_i,c_{i+1}] \end{gathered}$$

We sorted the arrays according to their correlation value in a descending order. We called the sorted arrays, Φ′ and C_x′ respectively. In addition, we used a Gaussian function with sigma 1 and mean 1 to give higher weight to the best correlated value. Hence, the estimated angle was computed as

$${\phi }_{\text{true}}=\sum _{j=1}^3{y}_j{c_j}^{\prime }{{\phi }_j}^{\prime }$$

where φ_j′ and c_j′ correspond to the jth element in the sorted arrays Φ′ and C_x′ respectively, and y_j follows:

$$y_j=\frac{1}{\sqrt{2\pi }}{e}^{-{(j-1)}^2/2}$$

In order to further estimate the tilt angle, we performed the same procedure to the smoothed profile of tilt angles. Finally, we averaged the estimated tilt angle from the raw and the smoothed profile for a final tilt angle estimation. Once we assigned an azimuthal orientation angle ϕ and a polar tilt angle θ to each frame, we converted them to 3-D Cartesian coordinates with the simple transform:

$$(x=Lcos\varphi cos\theta ,y=Lsin\varphi cos\theta ,z=Lsin\theta )$$

3D Movies of Bacteria Trajectories

The analysis of each experimental image outputs four parameters: contact point, tilt angle θ, orientation angle ϕ, and time. These fully define the geometry of the bacteria on the surface at each time point. We reconstructed the 3D trajectory assuming a spherocylinder with half-spheres of 0.5 μm radius on each end and a cylinder of 2 μm length and 0.5 μm radius in the middle. The contact point is the reference coordinate location of the bacteria on the surface. The spherocylinder is rotated by the estimated tilt angle θ and azimuthal orientation ϕ, with respect to the contact point. Based on the spherocylinder geometry, we obtained the distal and proximal poles to the glass surface plane. The 3D movies rendered from the experimental data show the trajectories of both poles, the cell body long axis and the contact point trace on the surface. See Figure 2B for a schematic on these features.

3D Render Using Wide-Field Fluorescence Z-Scans

The second imaging protocol mentioned in the Methods includes a z-scan of the fluorescently stained membrane and flagellum using the GFP channel. The scan was taken after continuous recording in the bright-field, using a high-speed camera (200 fps), since cells tend to stop spinning after a cumulative fluorescence exposure (~2 frames). Hence, the imaged cells remained virtually immobile through the scan, maintaining body tilt and orientation with respect to the surface. Using the Z-scan slices taken at equal Δz spacings of 0.2 μm per frame from the surface (+0 μm), we reconstructed a 3D render of the body and flagellum. The fluorescent images were first segmented using a Gaussian filter, a 31 × 31 high-pass filter, a second Gaussian filter, and an Otsu threshold. The lighted pixels for each binary image(z-slice) were plotted in MATLAB using built-in function scatter3.m, and the coordinates corresponded to the z-slice order and pixel resolution (0.0325 μm/pixel). Each marker represents a single pixel, with the marker size proportional to pixel intensity. The resulting is a 3D visualization of the body and flagellum from a wide-field fluorescence z-scan (see Figure 2C,D).

Hydrodynamic Model of a Spinning Bacterium without a Surface-Tethered Flagellum

We previously developed a hydrodynamic model to investigate the hydrodynamics of a spinning bacterium with a surface tethered flagellum.¹⁸ We adapted this model to study the hydrodynamics of a spinning bacterium that is attached to the surface by the nonflagellated pole, so that the spinning flagellum is driving the system from the distal pole. The cell body is modeled as a cylinder (with length 3 μm and radius 0.3 μm) and the flagellum as a left-handed helical filament (with wavelength 2 μm, total length 4 μm, radius 0.02 μm, and helix radius 0.4 μm). We used resistive force theory⁴³ (RFT) and the bipolar coordinate solution of the two-dimensional Stokes equations for a cylinder near a plane wall⁴⁴ to relate the angular velocities of each component of the bacterium to the torques from the flagellar motor, the viscous resistance from the fluid, and the flagellar hook which has a spring constant that resists bending from a preferred angle between the cell body and the flagellum.

In RFT, a filament is composed of many cylindrical elements of length δl. A resistance coefficient is associated with the component of force in the directions parallel and perpendicular to the filament: δF = δl(c_||u_|| + c_⊥u_⊥). The resistance coefficients for a helix close to a surface are c_|| ≈ 2πη/log(2d/r), c_⊥ ≈ 2c_||, where η is the bulk fluid viscosity, d is the distance of the filament from the surface, and r is the filament radius. The cylinder (cell body) is prevented from translations in the model, so only the perpendicular coefficient is required. For the cylinder, if the motion is parallel to the wall then c_⊥ = −4πη/(α − tanh α), and if the motion is perpendicular to the wall then c_⊥ = −4πη/α, where $\alpha =\sqrt{1-{(r/d)}^2}$.⁴⁴

The flagellar motor exerts a torque at the base of the cell body, causing the flagellum to rotate relative to the body. The cell body was attached to the surface by fixing a point along the central long axis of the body 0.35 μm away from the nonflagellated pole, and the body does not counter-rotate in response to the flagellum rotation. The total torque on the body Γ_b is

$${\mathrm{\Gamma }}_{\mathrm{b}}=-{\mathbf{M}}_{\mathrm{b}}{\mathbf{v}}_{\mathrm{b}}+\mathrm{\Gamma }{\widehat{\mathbf{n}}}_{\mathrm{b}}-k_{\mathrm{h}}\frac{{\widehat{\mathbf{n}}}_{\mathrm{f}}\times {\widehat{\mathbf{n}}}_{\mathrm{b}}}{\mid {\widehat{\mathbf{n}}}_{\mathrm{f}}\times {\widehat{\mathbf{n}}}_{\mathrm{b}}\mid }+\mathrm{\Lambda }{\widehat{\mathbf{n}}}_{\mathrm{b}}$$

M_b is the mobility matrix of the body due to viscous resistance; v_b is the angular velocity of the body; Γ is the torque exerted by the flagellar motor; n̂_b and n̂_f are orientations of the body and flagellum, respectively; k_h is the spring constant of the flagellar hook; Λ is the surface constraint on the body. The mobility matrix is calculated using RFT and results for a cylinder near wall.^43–45

The total torque on the flagellum Γ_f is

$${\mathrm{\Gamma }}_{\mathrm{f}}=-{\mathbf{M}}_{\mathrm{f}}{\mathbf{v}}_{\mathrm{f}}-\mathrm{\Gamma }{\widehat{\mathbf{n}}}_{\mathrm{b}}+k_{\mathrm{h}}\frac{{\widehat{\mathbf{n}}}_{\mathrm{f}}\times {\widehat{\mathbf{n}}}_{\mathrm{b}}}{\mid {\widehat{\mathbf{n}}}_{\mathrm{f}}\times {\widehat{\mathbf{n}}}_{\mathrm{b}}\mid }=0$$

M_f is the mobility matrix of the flagellum, which we obtain using RFT;^43,45 v_f is the angular velocity of the flagellum.

We solve for the angular velocities using the torque free condition on the flagellum and the torque-free condition on the combined body and flagellum in the directions perpendicular to the constraining torque. We include a short-range interaction between the bacterium and the surface to account for steric effects.

The different spinning behaviors observed in the model depend on the ratio between the spring constant and the torque, rather than their individual absolute values. The resultant model was used to consider how the free flagellum can affect the tilt angle that the bacterium makes with the surface during flagellum-mediated spinning.

Data and Code Availability

Raw microscope images and movies are available upon request by contacting the corresponding author. At present, the MATLAB code is in the alpha phase of development and not in a state ready for circulation. For information on the current phase of the MATLAB code contact the corresponding author.