An Automated Test Assembly Design for a Large-Scale Chinese Proficiency Test

The purpose of this brief report is to illustrate an automated test assembly design of parallel test forms for the Chinese Proficiency Tests Hanyu Shuiping Kaoshi (HSK). The test forms were assembled to match a seed test using the Maximum Priority Index (MPI; Chang, 2015; Cheng & Chang, 2009) approach. The new HSK, launched by Hanban¹ of China in 2009, is the most authoritative international standardized exam for non-native Chinese speakers. The HSK tests are administered either through paper-and-pencil or online testing format. Previously, HSK tests were assembled manually. However, the demand for HSK has soared in the recent years. A total of 1,068 testing centers have been established in countries around the world. In 2014, 432,245 people took the HSK test in 115 countries. To cater to this increasing demand of HSK administration, an automated test assembly (ATA) system was developed by the authors.

The HSK has six proficiency levels. A separate test blueprint has been developed for each of them. Each level’s test is comprised of two to three subtests with a mixture of item formats. For example, HSK Level 4 test consists of three subtests: listening, reading, and writing. Listening and reading subtests contain multiple-choice questions, whereas writing subtests comprise constructed response questions. The HSK content experts provide test blueprints for each level that delineate the required test sections, test length, word counts, vocabulary, content representation in terms of topics, maximum item pairwise overlap rate, and a reference form (i.e., the seed test). The parallel tests assembled at each level need to match (a) the level’s test blueprint, (b) the average discrimination statistic value (i.e., the point–biserial correlation) with the seed test, and (c) the average difficulty (in Classical Test Theory Scale) statistic value with the seed test.

An ATA program was developed by the authors to carry out the test assembly tasks. The program consists of three components: item pool preparation, parallel form generation, and the quality evaluation and test forms output.

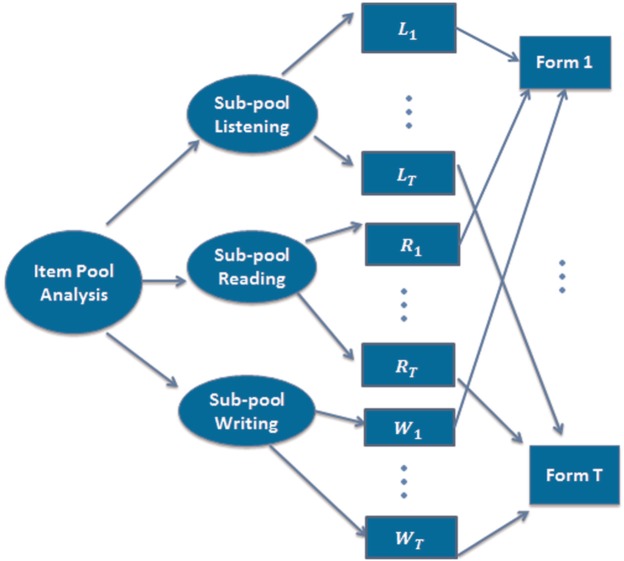
Figure 1 illustrates the first two components of the ATA program: item pool preparation and parallel form generation. The item pool for each level consists of items from the existing 2010 to 2013 HSK test forms collated from 33 administrations. In the item pool preparation, each level’s item pool is first partitioned into two or three sub-pools for the individual subtests. Then, a bottom-up strategy is used to assemble parallel test forms. With this strategy, each subtest is first assembled using items from the respective sub-pool based on subtest level blueprints as well as the target average discrimination and difficulty values matched to corresponding seed subtests. These assembled subtests are then mixed and matched to build parallel HSK-level test forms.

Figure 1.

The first two components of the ATA program: Item pool preparation and parallel form generation.

Note. ATA = automated test assembly.

The objective of subtest assembly is to minimize the difference in the difficulty and discrimination statistics between the assembled test forms and the seed tests while meeting the test blueprint requirements, termed non-statistical constraints. Because the items’ discrimination and difficulty statistics are computed based on classical test theory, a reliability-index-distance defined by Armstrong, Jones, and Wu’s (1992) is used as the distance function. Let p denote the difficulty statistic and r be the discrimination statistic. For items i and j, the distance between these two items is defined as

$$d_{ij}=\sqrt{{\lambda }_1{(p_i-p_j)}^2+{\lambda }_2{(r_i-r_j)}^2},$$

where ${\lambda }_1\ge 0,{\lambda }_2\ge 0,{\lambda }_1+{\lambda }_2=1$ are the adjustable weights for the difficulty and discrimination statistics. Similarly, this definition can be easily extended to a subtest. Suppose a subtest i in the seed test consists of two items with difficulty and discrimination parameters: $(p_{i1},r_{i1})$ and $(p_{i2},r_{i2})$, the distance between subtest i and a candidate subtest j with $(p_{j1},r_{j1})$ and $(p_{j2},r_{j2})$ is

$${d_{ij}}^{*}=\sqrt{{\lambda }_1({(p_{i1}-p_{j1})}^2+{(p_{i2}-p_{j2})}^2)+{\lambda }_2({({r_i}_1-r_{j1})}^2+{({r_i}_2-r_{j2})}^2)}.$$

The MPI is used to control both the statistical and the non-statistical constraints. Suppose that we need to select the item from the item pool that most closely matches item i in the seed test while satisfying k constraints, then the MPI index for the candidate item j in the item pool is given by

$$MP{I}_j=\frac{1}{d_{ij}}\underset{k=1}{\overset{K}{\Pi }}{(w_k{f}_k)}^{c_{jk}},$$

where $d_{ij}$ is the distance function that measures the closeness of items i and j in terms of difficulty and discrimination statistics as defined in Equation 1. $f_k$ measures the scaled “quota left” of constraint k. $c_{jk}$ indicates whether item j is related to constraint k: $c_{jk}=1$ indicating constraint k is relevant to item j, otherwise $c_{jk}=0$. $w_k$ is the weight for constraint k. In general, more important constraints will be assigned with larger weights.

An adapted heuristic algorithm based on Armstrong, Jones & Wu (1992) Phase II algorithm was developed to generate parallel test forms under the proposed criteria and restrictions. A most recently proposed algorithm by Chen (2016) also shares a similar idea. Suppose a subtest contains N items, and T parallel forms of this subtest need to be assembled. At the beginning, the total distance of each parallel subtest from the seed test is set to zero. The order of the N items in the subtest to be assembled is determined by a randomized procedure. Each time, according to this order, T items with the largest MPI values are selected from the corresponding sub-pools. This first set of T items is randomly assigned to the T subtest forms, and the total test distance for each form is updated. From the second set of T optimal items onward, first they are sorted in descending order by the MPI values, and then they are sequentially assigned to the list of T forms arranged in decreasing order of total test distance. After the assignment, the total distance of each parallel subtest from the seed test is updated again. The process continues until N items have been selected for each of the T parallel subtests.

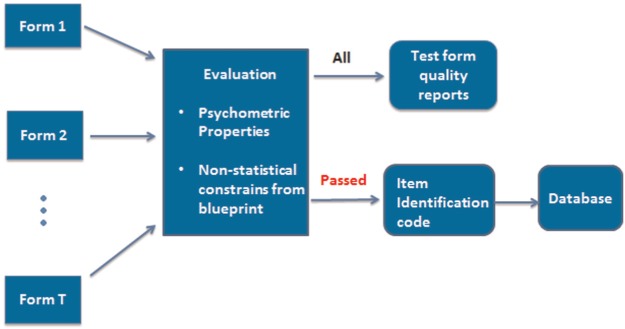
Because MPI is a heuristic method, it does not guarantee that every assembled form will meet all the constraints. Figure 2 presents the last component of the ATA program: quality evaluation and reporting of the assembled test forms. Quality reports containing information on the assembled forms’ average item difficulty and discrimination values as well as the degree to which they satisfy the required test blueprint are automatically generated and sent to HSK content experts. Moreover, based on the quality reports, the item identification codes of each qualified test form will be collated automatically into the system. The test administrator can then make use of this information to generate actual test forms.

Figure 2.

The last component of the ATA program: Quality evaluation and reporting of the assembled test forms.

Note. ATA = automated test assembly.

The ATA program was piloted using the test blueprints and item pools provided by Hanban. Table 1 documents the results for generating 50 parallel forms for HSK Levels 1 to 6 by using the ATA program as an example. The results demonstrated that the ATA program based on MPI was able to generate a reasonable number of qualified Hanyu Shuiping Kaoshi (HSK) test forms for all levels in a short time. The unsuccessful forms were primarily caused by the gap between the constraints from the blueprints and the supply of the item bank. The deviations of the item difficulty and discrimination values in the qualified forms from the corresponding seed tests were very small.

Table 1.

Results of Generating 50 Forms by the Proposed ATA Program.

HSK level	Number of items in the test	Time to generate a form (sec)	Successful assembly rate	Maximum deviation from the reference form
				Listening		Reading		Writing
				p	r	p	r	p	r
1	40	3.5	90%	.03	.04	.03	.02	—	—
2	60	13.4	84%	.02	.02	.05	.02	—	—
3	80	18.5	86%	.03	.04	.04	.06	—	—
4	100	22	88%	.05	.02	.04	.03	.03	.04
5	100	22.8	94%	.06	.05	.05	.05	.04	.06
6	100	12.8	100%	.05	.03	.04	.03	.01	.02

Note. p stands for difficulty statistic and r stands for the discrimination statistic. Computation time was recorded from the test run on a computer with Intel(R)-i5 2520M CPU with 4GB RAM memory. ATA = automated test assembly; HSK = Hanyu Shuiping Kaoshi.

The three components in the ATA program suggest a reasonable framework for practitioners who intend to develop their own ATA programs. In the future, in case item response theory item parameters may be used to replace the current classical test theory–based item statistics in Distance Function 1 or 2, the ATA program can be easily adjusted to accommodate the change. The randomization algorithm imbedded in the parallel subtest assembly process and the final mixing-and-matching step can ensure that the qualities of the assembled test forms are mostly balanced even with the “greedy” heuristic assembly approach. Finally, the quality reports generated by the ATA program not only suggest appropriate uses of the assembled test forms but also serve as useful references for content experts to revise the existing test blueprint or develop new versions.