Detecting Differential Item Functioning Using the Logistic Regression Procedure in Small Samples

Abstract

The logistic regression (LR) procedure for testing differential item functioning (DIF) typically depends on the asymptotic sampling distributions. The likelihood ratio test (LRT) usually relies on the asymptotic chi-square distribution. Also, the Wald test is typically based on the asymptotic normality of the maximum likelihood (ML) estimation, and the Wald statistic is tested using the asymptotic chi-square distribution. However, in small samples, the asymptotic assumptions may not work well. The penalized maximum likelihood (PML) estimation removes the first-order finite sample bias from the ML estimation, and the bootstrap method constructs the empirical sampling distribution. This study compares the performances of the LR procedures based on the LRT, Wald test, penalized likelihood ratio test (PLRT), and bootstrap likelihood ratio test (BLRT) in terms of the statistical power and type I error for testing uniform and non-uniform DIF. The result of the simulation study shows that the LRT with the asymptotic chi-square distribution works well even in small samples.

The logistic regression (LR) procedure (Swaminathan & Rogers, 1990) is a popular method for testing differential item functioning (DIF). In the LR procedure, an LR is used to model the probability of getting an item correct using a conditioning variable (e.g., observed total test score), a group membership, and an interaction between the conditioning variable and group membership. An item is said to show DIF if the regression coefficients related to the group membership or group–conditioning interaction are statistically significantly different from zero. The regression coefficients are usually estimated using the maximum likelihood (ML) estimation, and the statistical hypotheses about DIF are typically tested based on asymptotic distributions. However, in small samples, it is well known that the ML estimation may be biased (Cordeiro & McCullagh, 1991; Firth, 1993) and the asymptotic distributions may not work well (Davison & Hinkley, 1997; MacKinnon, 2009).

In the previous studies of DIF, it has been pointed out that the lack of robustness of the ML estimation and asymptotic assumption may limit the use of the LR procedure in small samples (Parshall & Miller, 1995; Swaminathan & Rogers, 1990). Therefore, it is important to determine the extent to which the traditional LR procedure based on the ML estimation and asymptotic assumption is valid in small samples. Also, it is worthwhile to examine whether other methods, such as the penalized maximum likelihood (PML) estimation, penalized likelihood ratio test (PLRT), and bootstrap likelihood ratio test (BLRT), could be considered as alternatives. The PML estimation is an estimation method developed to address the issue of potential bias of the ML estimation in small samples (Firth, 1993), and the PLRT compares the likelihoods of two nested models based on the PML estimation. In the BLRT, the likelihood ratio test (LRT) statistic is tested based on the empirical sampling distribution constructed from bootstrap samples, rather than the asymptotic sampling distribution derived from the asymptotic theory (Efron, 1979). The goal of this study is to compare the performances of the traditional LR procedure and the potential alternatives in small samples. More specifically, the traditional LR procedure based on the ML estimation and asymptotic assumption was compared with the LR procedures based on the PLRT and BLRT, especially in small samples, in terms of the statistical power and type I error rate for testing uniform and non-uniform DIF.

For more detailed discussion on the LR procedure, let us consider the following three LR equations (Fidalgo, Alavi, & Amirian, 2014):

$$\log \left(\frac{\mathrm{Pr}[u=1]}{1-\mathrm{Pr}[u=1]}\right)={\mathrm{\tau }}_0+{\mathrm{\tau }}_1\mathrm{\theta },$$

$$\log \left(\frac{\mathrm{Pr}[u=1]}{1-\mathrm{Pr}[u=1]}\right)={\mathrm{\tau }}_0+{\mathrm{\tau }}_1\mathrm{\theta }+{\mathrm{\tau }}_{2}g,$$

$$\log \left(\frac{\mathrm{Pr}[u=1]}{1-\mathrm{Pr}[u=1]}\right)={\mathrm{\tau }}_0+{\mathrm{\tau }}_1\theta +{\mathrm{\tau }}_{2}g+{\mathrm{\tau }}_3\mathrm{\theta }g,$$

where $u$ is the binary response to an item, $\mathrm{\theta }$ is the observed ability of an examinee (e.g., observed total test score), and $g$ is the group membership. The parameter ${\mathrm{\tau }}_2$ represents the group difference in the probability of getting an item correct, and ${\mathrm{\tau }}_3$ represents the interaction between the group membership and the observed ability. The LR procedure can be used to detect both uniform and non-uniform DIF. Several analytical strategies have been proposed in the literature, and choosing proper analytical strategies is important to maximize the performance of the LR procedure (Fidalgo et al., 2014). First, uniform and non-uniform DIF can be simultaneously tested by comparing the LR models represented by Equations 1 and 3. The null hypothesis of this test is $H_0:{\mathrm{\tau }}_2=0$ and ${\mathrm{\tau }}_3=0$, indicating there is no DIF. If the null hypothesis $H_0$ for an item is rejected, then the item is marked for further examination by content experts. The null hypothesis $H_0$ can be tested using both the LRT and Wald test. In general, under certain regularity conditions, the test statistics for the LRT asymptotically follow the chi-square distribution with the degrees of freedom equal to the difference in the number of parameters of the two nested models (Wilks, 1938). The LRT statistics for testing $H_0:{\mathrm{\tau }}_2=0$ and ${\mathrm{\tau }}_3=0$, therefore, asymptotically follow the chi-square distribution with the two degrees of freedom. It was also shown that the Wald test statistics for testing $H_0:{\mathrm{\tau }}_2=0$ and ${\mathrm{\tau }}_3=0$ asymptotically follow the chi-square distribution with the two degrees of freedom, under the assumption that the ML estimators for the parameters ${\mathrm{\tau }}_2$ and ${\mathrm{\tau }}_3$ asymptotically follow a multivariate normal distribution (Swaminathan & Rogers, 1990). Second, uniform and non-uniform DIF can be tested separately. The null hypothesis for testing uniform DIF is $H_0:{\mathrm{\tau }}_2=0$ and can be tested by comparing the LR models represented by Equations 1 and 2. If ${\mathrm{\tau }}_2\ne 0$ and ${\mathrm{\tau }}_3=0$, then an item is said to show uniform DIF because the relationship between the item response and group remains the same over the range of the ability of an examinee. However, the null hypothesis for testing non-uniform DIF is $H_0:{\mathrm{\tau }}_3=0$ and can be tested by comparing the LR models represented by Equations 2 and 3. If ${\mathrm{\tau }}_3\ne 0$, then an item is said to show non-uniform DIF because the relationship between the item response and group depends on the ability of an examinee. The LRT and Wald test are applicable for testing uniform and non-uniform DIF separately. For more detailed discussion on the analytical strategies for the LR procedure, readers are referred to Fidalgo et al. (2014) and Jodoin and Gierl (2001).

As can be seen from the discussion above, the hypothesis testings for the LR procedure typically depend on asymptotic sampling distributions. The LRT depends on the asymptotic chi-square distribution of the test statistics. Also, the Wald test is based on the asymptotic normality of ML estimators. In general, ML estimators have been widely used in many different settings because of the desirable asymptotic properties: The ML estimators are asymptotically unbiased and normally distributed. However, such nice asymptotic properties may not hold for small samples. The ML estimators have bias that increases with decreasing sample sizes, and such bias is usually known as finite or small sample bias. Therefore, in small samples, a bias correction for the ML estimators (e.g., the PML estimation) may be appreciable (Cordeiro & McCullagh, 1991; Firth, 1993). Also, the sampling distribution of the ML estimators may deviate from the normal distribution in small samples. In such a case, statistical inferences based on the non-parametric empirical sampling distribution (e.g., bootstrap) can be more accurate than statistical inferences based on the asymptotic normal distribution (MacKinnon, 2009).

In the specific context of DIF, previous studies have also concerned potential problems of testing DIF in small samples. Swaminathan and Rogers (1990) pointed out that the asymptotic result of an LR may not be a valid indicator of the presence of DIF in small samples. Mazor, Clauser, and Hambleton (1992) reported that more than 50% of the DIF items were missed when the Mantel–Haenszel (MH) procedure was used for samples of 500 or fewer examinees. Rogers and Swaminathan (1993) found that the distributional assumptions for the LR and MH procedures were less often met in small samples. Parshall and Miller (1995) compared the MH procedures based on the asymptotic chi-square distribution with the MH procedures based on the exact test. In their study, the performance of the MH procedures was extremely limited when the sample sizes of the focal groups were fewer than 100. Roussos and Stout (1996) compared the Simultaneous Item Bias Test (SIBTEST) and the MH procedure in small samples and found that two methods performed satisfactory in terms of type I error rates under all simulation conditions. Camilli (2006) also pointed out that the DIF test using the traditional LRT might be problematic in small samples.

Building on the previous studies, this study was designed to compare the performances of different statistical inferential methods for the LR procedure, especially in small samples. More specifically, the null hypothesis, which is $H_0:{\mathrm{\tau }}_2=0$ and ${\mathrm{\tau }}_3=0$, was tested using (a) the test statistic proposed by Swaminathan and Rogers (1990) under the assumption that the test statistic follows the asymptotic chi-square distribution with two degrees of freedom, (b) the LRT in which the LRT statistic comparing two likelihoods from the ML estimation is tested using the asymptotic chi-square distribution with two degrees of freedom, (c) the PLRT in which the PLRT statistic comparing two penalized likelihoods from the PML estimation is tested using the asymptotic chi-square distribution with two degrees of freedom, and (d) the BLRT in which the LRT statistic comparing two likelihoods from the ML estimation is tested using the bootstrap empirical sampling distribution. The next section briefly introduces the test statistic proposed by Swaminathan and Rogers (1990), PLRT, and BLRT, and this is followed by the section describing a Monte Carlo simulation study. Then, the results of the simulation study are presented and also discussed in the last two sections.

Method for Testing DIF

Swaminathan and Rogers (Wald Tests)

Swaminathan and Rogers (1990) assumed that the LR coefficients in Equation 1 follow a multivariate normal distribution:

$$\hat{\mathit{\tau }}~\mathrm{N}(\mathit{\tau },\sum ),$$

where $\mathit{\tau }=[{\mathrm{\tau }}_0,{\mathrm{\tau }}_1,{\mathrm{\tau }}_2,{\mathrm{\tau }}_3]$ and $\hat{\mathbf{\tau }}=[{\hat{\mathrm{\tau }}}_0,{\hat{\mathrm{\tau }}}_1,{\hat{\mathrm{\tau }}}_2,{\hat{\mathrm{\tau }}}_3]$ are the population regression coefficients in Equation 1 and their ML estimates, and ∑ is the population variance–covariance matrix of $\mathit{\tau }$. The null hypothesis for a DIF test, $H_0:{\mathrm{\tau }}_2=0$ and ${\mathrm{\tau }}_3=0$, was expressed as matrix form:

$$H_0:\mathit{C}\mathbf{\tau }=\mathbf{0},$$

where the $2\times 4$ matrix $\mathit{C}$ was defined as follows:

$$\mathit{C}=\left[\begin{array}{cccc}\hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \multicolumn{1}{c}{0}& \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right]$$

Then, it was shown that the null hypothesis can be tested using the following test statistic:

$${\chi }^2=\hat{\mathit{\tau }}\prime C(\mathit{C}\Sigma C{)}^{-1}\mathit{C}\hat{\tau },$$

which follows the chi-square distribution with two degrees of freedom.

The LRT

The LRT compares the fit of two competing models to test whether the observed difference in model fit of the two models is statistically significant. The two competing models are typically called the augmented model, which is a more complex one, and compact model, which is a less complex one. If the observed difference in model fit is statistically significant, the augmented model is preferred, whereas if the difference is not statistically significant, the compact model is preferred based on the principle of parsimony. The test statistic $G^2$ in the LRT is defined as the difference in the log-likelihoods of the two competing models:

$$G^2=-2\log L_C-(-2\log L_A),$$

where $L_C$ and $L_A$ represent the likelihoods of the compact and augmented models, respectively. Under the assumption that the two competing models are nested, it can be shown that the test statistic $G^2$ asymptotically follows the chi-square distribution with degrees of freedom equal to the difference in free parameters in the two nested models (Wilks, 1938). In our specific case, the LRT can be used to test DIF by comparing the likelihoods of two nested models, which are $\mathrm{logit}(\mathrm{Pr}[u=1])={\mathrm{\tau }}_0+{\mathrm{\tau }}_1\mathrm{\theta }$ and $\mathrm{logit}(\mathrm{Pr}[u=1])={\mathrm{\tau }}_0+{\mathrm{\tau }}_1\mathrm{\theta }+{\mathrm{\tau }}_{2}g+{\mathrm{\tau }}_3\mathrm{\theta }g$, using the chi-square distribution with two degrees of freedom.

The PLRT

The PML estimation was developed to address the issue of the finite sample bias of the ML estimation. The PML estimation removes the first-order bias from the ML estimation by using a penalized log-likelihood, which is just the traditional log-likelihood with a penalty. In the PML estimation, the penalty is given to the deviation from a desired outcome, and therefore, it will pull or shrink the PML estimates from the traditional ML estimates (Cole, Chu, & Greenland, 2014; Firth, 1993). In broad terms, the PML estimation is known as the regularized estimation, which improves the estimation using some form of additional information. In Bayesian perspective, penalizing the likelihood corresponds to specifying a prior distribution, and the penalized log-likelihood can be considered as a posterior distribution of the parameter of interest. For exponential family models, the PML estimation is equivalent to maximizing a likelihood that is penalized by the Jeffreys’ invariant prior (Firth, 1993; Heinze, 2006). The PML or Bayesian approach was used to obtain more stable parameter estimates in the item response theory (IRT; Mislevy, 1986; Swaminathan & Gifford, 1985). Recently, the PML estimation was used to obtain parameter estimates for the two-parameter logistic model (2PLM) in the IRT with only 20 examinees, with which the traditional ML estimation for the IRT may not be applicable (Paolino, 2013). Given the PML estimates, the PLRT compares the penalized likelihoods of two nested models.

The BLRT

In general, the bootstrap method may be considered as an alternative to the asymptotic approaches when the validity of the asymptotic approximation is suspect (Davison & Hinkley, 1997; MacKinnon, 2009). In the bootstrap method, bootstrap samples of size $n$ were taken from the original sample of size $n$ with replacement, and the sampling distribution of a statistic of interest is empirically constructed using the values of the statistic calculated for the bootstrap samples.

In the LRT, the $p$ value for testing a null hypothesis is obtained by comparing the observed value of the statistic of interest with the asymptotic distribution, which is the chi-square distribution in our case, whereas in the BLRT, the $p$ value is obtained by comparing the observed value of the statistic with the empirical sampling distribution constructed from the bootstrap samples. In this study, the BLRT was implemented as follows (Davison & Hinkley, 1997; Nylund, Asparouhov, & Muthén, 2007):

1. Fit a compact model, $\mathrm{logit}(\mathrm{Pr}[u=1])={\mathrm{\tau }}_0+{\mathrm{\tau }}_1\mathrm{\theta }$, and an augmented model, $\mathrm{logit}(\mathrm{Pr}[u=1])={\mathrm{\tau }}_0+{\mathrm{\tau }}_1\mathrm{\theta }+{\mathrm{\tau }}_{2}g+{\mathrm{\tau }}_3\mathrm{\theta }g$, to the original data to obtain the test statistic $G_{\mathrm{original}}^2=-2\log L_{\mathrm{C}}-(-2\log L_{\mathrm{A}})$, where $L_{\mathrm{C}}$ and $L_{\mathrm{A}}$ represent the likelihoods of the compact and augmented models obtained from the ML estimation.

2. Generate a bootstrap sample from the original data under the null hypothesis, and then calculate the $G_{\mathrm{boot}}^2$ statistic for the generated bootstrap sample. More specifically, generate a data set using the compact model with the parameters estimated in Step (a), and then fit both the compact and augmented models to the generated data set to compute the value of the $G_{\mathrm{boot}}^2$ statistic.

3. Repeat Step (b) $R$ times to construct the empirical sampling distribution of the $G_{\mathrm{boot}}^2$ statistic.

4. Calculate the bootstrap $p$ value by comparing the observed value of the $G_{\mathrm{original}}^2$ statistic obtained in Step (a) with the empirical sampling distribution of the $G_{\mathrm{boot}}^2$ statistic constructed in Step (c). More specifically, the bootstrap $p$ value can be calculated using the following equation: $p=(1+\#\{G_{\mathrm{boot}}^2\ge G_{\mathrm{original}}^2\})/(1+R)$, where $\#\{G_{\mathrm{boot}}^2\ge G_{\mathrm{original}}^2\}$ represents the number of bootstrap samples that produce the $G_{\mathrm{boot}}^2$ statistic greater than or equal to the value of $G_{\mathrm{original}}^2$ obtained in Step (a) (Davison & Hinkley, 1997). This bootstrap $p$ value is then used to determine whether the null compact model should be rejected in favor of the augmented model.

A Simulation Study

A Monte Carlo simulation in this study was designed to compare the performances of the aforementioned different statistical inferential methods for the LR procedure. The performances in small samples were particularly of interest because the asymptotic sampling distributions may not work well in small samples. The factors manipulated in this study were (a) the sample sizes of the reference and focal groups in DIF tests (50R/50F, 100R/100F, 150R/50F, 250R/250F, 450R/50F, and 500R/500F), (b) the effect sizes of DIF for a studied item based on the area between item response functions (0, 0.6, and 0.8), (c) the ability distributions of the focal group ($N(0,1)$ and $N(-1,1)$), and (d) the types of DIF (uniform and non-uniform). The number of items was fixed to 40 to represent a short but reliable standardized achievement test (Jodoin & Gierl, 2001). Among the 40 items, only one item was chosen to be a studied item. For each of the 72 simulation conditions ($6\times 3\times 2\times 2=72$), 1,000 data sets were replicated. For each data set, DIF for the studied item was tested using the aforementioned four different inferential approaches. The results of the BLRT could depend on the sizes of the bootstrap samples (MacKinnon, 2009), and therefore, both 1,000 and 10,000 bootstrap samples were sampled following the previously described procedure. This simulation study was performed using the R software package¹ (R Core Team, 2013). The following is the more detailed description about the simulation study.

In this simulation study, the sample size was the key factor because the focus of this study was to compare the performances of different inferential approaches for the LR procedure in small samples. The definition of smallness varied across different studies. Fidalgo, Ferreres, and MuÑiz (2004) examined the performance of the MH procedure in small samples with the sample sizes of 100, 150, 200, and 250. Parshall and Miller (1995) used 500R/25F, 500R/50F, 500R/100F, and 500R/200F to compare the performance of the exact and asymptotic MH procedures in small samples. The sample size requirements for Educational Testing Service (ETS) DIF analysis are at least 200 members in the smaller group and at least 500 in total (Zwick, 2012). In this present study, the performances of different inferential approaches were compared with the sample sizes of 50R/50F (total sample size $N$ = 100), 100R/100F ($N$ = 200), 150R/50F ($N$ = 200), 250R/250R ($N$ = 500), 450R/50F ($N$ = 500), and 500R/500F ($N$ = 1,000); 50R/50F ($N$ = 100) and 100R/100F ($N$ = 200) were chosen to represent small samples; 500R/500F ($N$ = 1,000) were chosen to represent large samples in which the asymptotic sampling distributions are expected to work well. Sample sizes of the focal group are often much smaller than those of the reference groups (Parshall & Miller, 1995); 100R/100F ($N$ = 200), 150R/50F ($N$ = 200), 250R/250R ($N$ = 500), and 450R/50F ($N$ = 500) were chosen to examine the differences in balanced and unbalanced sample sizes across the reference and focal groups.

The number of items was fixed to 40. Among the 40 items, only one item was simulated as a DIF item. The amount of DIF in the studied item was induced following Swaminathan and Rogers (1990) and Jodoin and Gierl (2001). To induce DIF, the item parameters of the three-parameter logistic model (3PLM) for the reference and focal groups were chosen such that pre-specified areas between the item response functions for the two groups were obtained based on the formula given by Raju (1988). More specifically, to induce uniform DIF, the item discrimination ($a$) and guessing ($c$) parameters in the 3PLM were fixed across the reference and focal groups, and the item difficulty parameters ($b$) for the two groups were chosen such that the areas between the item response functions for the two groups became 0.4 and 0.6 based on the following equation:

$$\mathrm{Area}=(1-c)|b_{\mathrm{F}}-b_{\mathrm{R}}|,$$

where $b_{\mathrm{R}}$ and $b_{\mathrm{F}}$ represent the item difficulty parameters for the reference and focal groups, respectively. To induce non-uniform DIF, the item difficulty ($b$) and guessing ($c$) parameters were fixed across the reference and focal groups, and the item discrimination parameters ($a$) for the two groups were chosen such that the areas between the item response functions for the two groups became 0.4 and 0.6 based on the following equation:

$$\mathrm{area}=(1-c)\left|\frac{2(a_{\mathrm{F}}-a_{\mathrm{R}})}{1.7a_{\mathrm{F}}{a}_{\mathrm{R}}}\ln 2\right|,$$

where $a_{\mathrm{R}}$ and $a_{\mathrm{F}}$ represent the item discrimination parameters for the reference and focal groups, respectively. Table 1 presents the specific values of item discrimination, difficulty, and guessing parameters used to induce uniform and non-uniform DIF for the studied item. For the non-DIF condition of the studied item to examine type I error rates, the item discrimination, difficulty, and guessing parameters of the studied item were fixed to 1.0, 0.0, and 0.2 across the reference and focal groups. For the remaining 39 items, item discrimination parameters were randomly sampled from 0.5 or 1.0, item difficulty parameters were randomly sampled from N(0,1), and item guessing parameters were fixed to 0.2.

Table 1.

Item Parameters of the 3PLM for R and F Groups.

DIF type	Area	$a_{\mathrm{R}}$	$b_{\mathrm{R}}$	$c_{\mathrm{R}}$	$a_{\mathrm{F}}$	$b_{\mathrm{F}}$	$c_{\mathrm{F}}$
Uniform	0.40	1.25	−0.25	0.20	1.25	0.25	0.20
Uniform	0.60	1.25	−0.38	0.20	1.25	0.38	0.20
Non-uniform	0.40	1.65	0.00	0.20	0.80	0.00	0.20
Non-uniform	0.60	0.79	0.00	0.20	0.45	0.00	0.20

Note. 3PLM = three-parameter logistic model; R = reference; F = focal; DIF = differential item functioning; a = discrimination parameter; b = difficulty parameter; c = guessing parameter.

The ability distributions of the reference and focal groups were also manipulated in this study. The ability distribution of the reference group was modeled as $N(0,1)$, and the ability distribution of the focal group was modeled as either $N(0,1)$ or $N(-1,1)$. These equal and unequal ability distributions across reference and focal groups were selected to reflect actual data encountered in practice and have been used in many other studies (Fidalgo et al., 2004; Zwick, 2012).

Results

The statistical power and type I error rate of the LR procedures based on four different inferential methods were calculated for each of the 72 simulation conditions. Tables 2 and 3 show the results for uniform and non-uniform DIF, respectively. In each table, the other simulation conditions, which are the sample size in reference ($n\mathrm{R}$) and focal ($n\mathrm{F}$) groups, effect size of DIF (effect size), and mean of the focal group (focal mean), are shown in the first four columns of the tables.

Table 2.

Statistical Power and Type I Error Rate of Different Inferential Methods for Uniform DIF.

$n\mathrm{R}$	$n\mathrm{F}$	Effect size	Focal mean	S&R	LRT	PLRT	BLRT1	BLRT2
50	50	0.0	0	0.038*	0.050***	0.045***	0.047***	0.048***
150	50	0.0	0	0.030*	0.041**	0.038*	0.036*	0.041**
100	100	0.0	0	0.038*	0.049***	0.042**	0.045***	0.048***
450	50	0.0	0	0.041**	0.056**	0.050***	0.049***	0.050***
250	250	0.0	0	0.052***	0.056**	0.053***	0.057**	0.056**
500	500	0.0	0	0.048***	0.048***	0.048***	0.049***	0.051***
50	50	0.4	0	0.119	0.144	0.133	0.134	0.141
150	50	0.4	0	0.182	0.190	0.186	0.179	0.185
100	100	0.4	0	0.228	0.247	0.231	0.233	0.239
250	250	0.4	0	0.552	0.559	0.554	0.552	0.554
450	50	0.4	0	0.219	0.231	0.233	0.217	0.228
500	500	0.4	0	0.841	0.843	0.841	0.840	0.841
50	50	0.6	0	0.252	0.310	0.277	0.282	0.302
150	50	0.6	0	0.413	0.420	0.421	0.401	0.403
100	100	0.6	0	0.535	0.552	0.544	0.537	0.547
450	50	0.6	0	0.529	0.513	0.538	0.492	0.510
250	250	0.6	0	0.930	0.937	0.932	0.935	0.935
500	500	0.6	0	0.999	0.999	0.999	0.999	0.999
50	50	0.0	−1	0.039*	0.055***	0.044**	0.051***	0.043**
150	50	0.0	−1	0.044**	0.053***	0.049***	0.051***	0.052***
100	100	0.0	−1	0.041**	0.053***	0.047***	0.048***	0.045***
450	50	0.0	−1	0.034*	0.041**	0.037*	0.037*	0.040**
250	250	0.0	−1	0.064*	0.067*	0.064*	0.061*	0.058**
500	500	0.0	−1	0.055***	0.059**	0.054***	0.058**	0.054***
50	50	0.4	−1	0.110	0.125	0.117	0.108	0.118
150	50	0.4	−1	0.151	0.159	0.158	0.153	0.155
100	100	0.4	−1	0.241	0.249	0.240	0.231	0.242
450	50	0.4	−1	0.196	0.212	0.211	0.196	0.209
250	250	0.4	−1	0.514	0.511	0.514	0.501	0.504
500	500	0.4	−1	0.791	0.802	0.800	0.793	0.800
50	50	0.6	−1	0.244	0.268	0.257	0.248	0.256
150	50	0.6	−1	0.365	0.372	0.372	0.353	0.368
100	100	0.6	−1	0.503	0.504	0.504	0.493	0.497
450	50	0.6	−1	0.416	0.417	0.422	0.396	0.411
250	250	0.6	−1	0.875	0.877	0.875	0.868	0.870
500	500	0.6	−1	0.991	0.991	0.991	0.991	0.991

Note. $n\mathrm{R}$ and $n\mathrm{F}$ represent sample sizes in reference and focal groups, respectively. S&R represents the test statistic proposed by Swaminathan and Rogers (1990). BLRT1 and BLRT2 used bootstrap samples of size 1,000 and 10,000, respectively. The *, **, and *** represent liberally [0.025, 0.075], moderately [0.040, 0.060], and strictly [0.045, 0.055] robust type I error (Bradley, 1978). The number highlighted with bold font represents the highest statistical power within each simulation condition. DIF = differential item functioning; S&R = Swaminathan & Rogers; LRT = likelihood ratio test; PLRT = penalized likelihood ratio test; BLRT = bootstrap likelihood ratio test.

Table 3.

Statistical Power and Type I Error Rate of Different Inferential Methods for Non-Uniform DIF.

$n\mathrm{R}$	$n\mathrm{F}$	Effect size	Focal mean	S&R	LRT	PLRT	BLRT1	BLRT2
50	50	0.0	0	0.029*	0.043**	0.033*	0.042**	0.044**
150	50	0.0	0	0.042**	0.053***	0.047***	0.045***	0.048***
100	100	0.0	0	0.057**	0.062*	0.060**	0.061*	0.058**
450	50	0.0	0	0.032*	0.050***	0.045***	0.047***	0.056 **
250	250	0.0	0	0.039*	0.040**	0.040**	0.041**	0.044**
500	500	0.0	0	0.053***	0.053***	0.053***	0.053***	0.052***
50	50	0.4	0	0.053	0.072	0.062	0.064	0.068
150	50	0.4	0	0.083	0.094	0.089	0.082	0.090
100	100	0.4	0	0.103	0.110	0.108	0.106	0.106
450	50	0.4	0	0.092	0.099	0.104	0.093	0.096
250	250	0.4	0	0.141	0.149	0.144	0.146	0.146
500	500	0.4	0	0.291	0.298	0.293	0.290	0.293
50	50	0.6	0	0.064	0.107	0.079	0.093	0.103
150	50	0.6	0	0.151	0.150	0.156	0.141	0.150
100	100	0.6	0	0.172	0.200	0.189	0.195	0.194
450	50	0.6	0	0.225	0.235	0.211	0.197	0.209
250	250	0.6	0	0.457	0.470	0.463	0.464	0.467
500	500	0.6	0	0.734	0.739	0.736	0.732	0.735
50	50	0.0	−1	0.045***	0.060**	0.052***	0.053***	0.054***
150	50	0.0	−1	0.046***	0.053***	0.051***	0.049***	0.052***
100	100	0.0	−1	0.047***	0.054***	0.052***	0.051***	0.052***
450	50	0.0	−1	0.041**	0.049***	0.048***	0.042**	0.043**
250	250	0.0	−1	0.046***	0.053***	0.049***	0.053***	0.054***
500	500	0.0	−1	0.054***	0.056**	0.054***	0.052***	0.053***
50	50	0.4	−1	0.062	0.080	0.071	0.072	0.078
150	50	0.4	−1	0.112	0.125	0.117	0.117	0.122
100	100	0.4	−1	0.099	0.112	0.101	0.108	0.110
450	50	0.4	−1	0.119	0.125	0.127	0.120	0.121
250	250	0.4	−1	0.164	0.171	0.166	0.169	0.169
500	500	0.4	−1	0.326	0.334	0.328	0.321	0.328
50	50	0.6	−1	0.098	0.137	0.114	0.120	0.125
150	50	0.6	−1	0.192	0.195	0.195	0.184	0.190
100	100	0.6	−1	0.198	0.232	0.209	0.213	0.219
450	50	0.6	−1	0.274	0.289	0.288	0.259	0.274
250	250	0.6	−1	0.514	0.533	0.517	0.527	0.530
500	500	0.6	−1	0.805	0.813	0.809	0.806	0.811

Note. $n\mathrm{R}$ and $n\mathrm{F}$ represent sample sizes in reference and focal groups, respectively. S&R represents the test statistic proposed by Swaminathan and Rogers (1990). BLRT1 and BLRT2 used bootstrap samples of size 1,000 and 10,000, respectively. The *, **, and *** represent liberally [0.025, 0.075], moderately [0.040, 0.060], and strictly [0.045, 0.055] robust type I error (Bradley, 1978). The number highlighted with bold font represents the highest statistical power within each simulation condition. DIF = differential item functioning; S&R = Swaminathan & Rogers; LRT = likelihood ratio test; PLRT = penalized likelihood ratio test; BLRT = bootstrap likelihood ratio test.

The type I error rate was calculated as the proportion of the replications that showed DIF when the effect size of DIF is zero. Bradley (1978) suggested liberal, moderate, and strict criteria of robustness. In Tables 2 and 3, the value of the type I error marked with *, **, and *** indicates that the type I error rate is liberally [0.025, 0.075], moderately [0.040, 0.060], and strictly [0.045, 0.055] robust based on the robustness criteria suggested by Bradley. All the four methods show strictly robust type I error rate in most of the cases when the sample sizes are 1,000 ($n\mathrm{R}=500$ and $n\mathrm{F}=500$). For sample sizes of less than 1,000, there seems to be no clear pattern in the results of type I error except that the test statistic proposed by Swaminathan and Rogers (1990; S&R) seems to show less robust type I error rate than other methods. The robustness of the type I error rate seems to be similar in the LRT, PLRT, and BLRT across different simulation conditions.

The statistical power was calculated as the proportion of the replications that showed DIF when the effect sizes of DIF are 0.4 and 0.6. In Tables 2 and 3, the numbers highlighted with bold font represent the highest statistical power within each simulation condition. Similar to the case of the type I error, all the four methods yield similar statistical power when the sample sizes are 1,000 ($n\mathrm{R}=500$ and $n\mathrm{F}=500$). For sample sizes of less than 1,000, the LRT shows the highest statistical power in most of the cases. For the BLRT, the BLRT with 10,000 bootstrap samples show slight higher performance than the BLRT with 1,000 bootstrap samples.

In addition to the comparisons among the four methods, several patterns can be identified across different simulation conditions in Tables 2 and 3. The statistical power of uniform DIF tests is higher than that of non-uniform DIF tests. The ability distributions of reference and focal groups seem to oppositely influence the statistical power in uniform and non-uniform DIF. In uniform DIF, the statistical power seems to be slightly higher when the ability distributions are the same, whereas in non-uniform DIF, the statistical power seems to be slightly higher when the ability distributions are different. Given the same sample size, the cases with the balanced sample sizes across reference and focal groups ($n\mathrm{R}=n\mathrm{F}=100$ or $250$) show higher statistical power than the unbalanced cases.

In Figure 1, the histograms and chi-square Q-Q plots of the LRT statistics calculated from the 10,000 bootstrap samples (i.e., empirical sampling distributions) are presented to compare the empirical and asymptotic sampling distributions for the sample sizes of $n\mathrm{R}=n\mathrm{F}=50$ and $n\mathrm{R}=n\mathrm{F}=500$. The histograms of the empirical sampling distributions appear to match well with the theoretical chi-square distribution with two degrees of freedom. However, the chi-square Q-Q plots reveal that, when the theoretical quantiles are large, sample quantiles are slightly greater than the theoretical quantiles, which suggests that the empirical sampling distributions have slightly thicker right tails than the theoretical chi-square distributions.

Figure 1.

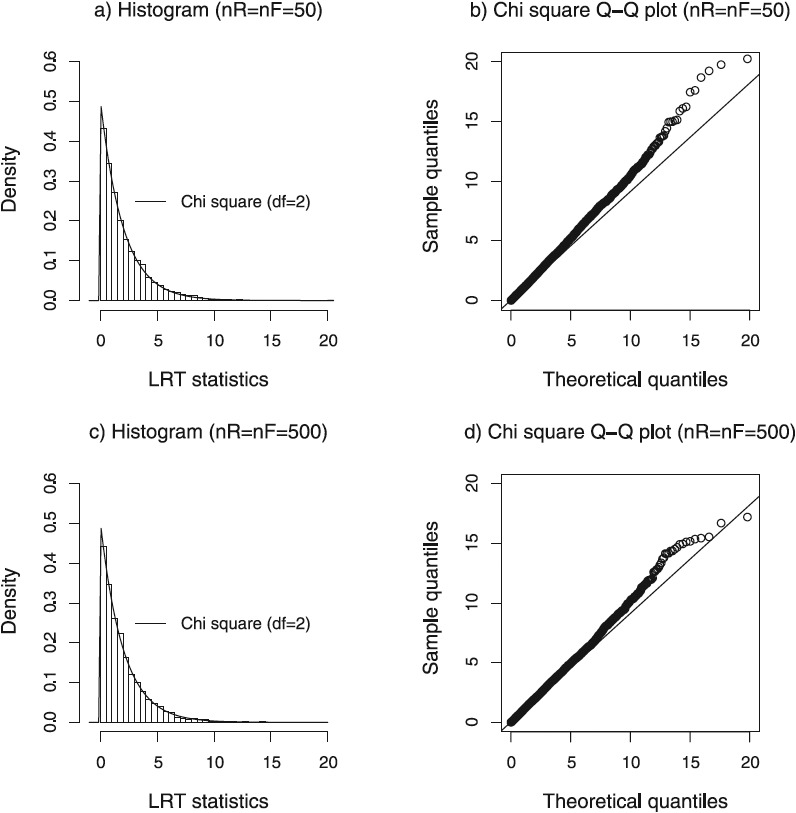
Histograms and chi-square Quantile-Quantile (Q-Q) plots.

Note. These histograms and chi-square Q-Q plots for $n\mathrm{R}$ = $n\mathrm{F}$ = 50 and $n\mathrm{R}$ = $n\mathrm{F}$ = 500 are presented to demonstrate the discrepancy between theoretical chi-square distributions with the degrees of freedom of 2 and empirical bootstrap sampling distributions. The histograms of the LRT statistics calculated from the 10,000 bootstrap samples appear to match well with the theoretical chi-square distributions represented by solid lines in figures. However, chi-square Q-Q plots show that, when the theoretical quantiles are large, sample quantiles are slightly greater than the theoretical quantiles, which suggests that the empirical bootstrap sampling distributions have slightly thicker right tails compared with the theoretical chi-square distributions. LRT = likelihood ratio test.

Discussion

The ML estimates are only asymptotically unbiased and normally distributed. Therefore, there have been concerns about testing DIF using the LR procedure based on the asymptotic properties of the ML estimates when sample sizes are small (Rogers & Swaminathan, 1993; Swaminathan & Rogers, 1990). Because the null hypothesis of the DIF test in the LR procedure involves the regression coefficients from the LR, the potential finite sample bias of the ML estimates may degrade the performance of the LR procedure in small samples. Moreover, the potential deviation of the true sampling distribution from the assumed asymptotic chi-square distribution also may degrade the performance of the LR procedure. This study examined whether the LR procedure based on the asymptotic properties of the ML estimates still produces satisfactory statistical power and type I error in small samples, and also whether the LR procedures based on the PLRT or BLRT may be considered as alternatives.

The simulation results in this study indicate that the LRT, in which the LRT statistic comparing two likelihoods from the ML estimation is tested using the asymptotic chi-square distribution with two degrees of freedom, show slightly better performance than other methods in terms of the statistical power although the difference in performance seems not to be so significant for practical purposes. The robustness of the type I error rate seems to be similar in the LRT, PLRT, and BLRT. According to the results, it seems that the LR procedure based on the asymptotic properties of the ML estimation still works well even in small samples, and therefore, the LR procedure based on the PLRT and BLRT may not need to be considered as alternative.

At this point, it may be worthwhile to discuss why the LR procedures based on the PLRT and BLRT show slightly lower performance in spite of the advantages that the PML may reduce the finite sample bias and the bootstrap method may capture the potential deviation of the true sampling distribution in small samples. The PML originally was developed to remove the first-order term from the asymptotic bias of the ML estimates by modifying the scoring function (Firth, 1993). However, there exists the trade-off between the bias and variance in resulting PML estimates (Fan & Tang, 2013). Firth (1993) pointed out that the merit of bias reduction in any particular problem needs to be compared with any sacrifice in precision that might result. In our specific problem, it seems that the merit of reducing bias of the PLM estimates is not appreciable compared with the sacrifice in precision.

However, the bootstrap hypothesis tests are often very reliable in many cases (Davidson & MacKinnon, 1999; Nylund et al., 2007; Park, 2003). However, this is not true in every case. As Davidson and MacKinnon (2007) pointed out, when the results from the bootstrap hypothesis test and asymptotic test are similar, we can be fairly confident that the asymptotic test is reasonably accurate. In such a case, it might be more reasonable to use the asymptotic test considering the computational cost for the bootstrap hypothesis test. Figure 1 shows the similarity in the sampling distributions of the asymptotic test and the bootstrap hypothesis test in our specific problem. Although the empirical sampling distributions constructed from the bootstrap samples seem to have slightly thicker right tails compared with the theoretical chi-square distributions, the two distributions appear to be similar for practical purposes. The discrepancy between the two distributions seems to decrease with the increasing sample sizes according to the chi-square Q-Q plots in Figure 1. This result is reasonable because the asymptotic assumptions should work well in large samples.

One of the factors that can influence the performance of the bootstrap hypothesis tests is the size of the bootstrap samples. It is known that the smaller is the size of the bootstrap samples, the less powerful is the test (Jockel, 1986). The simulation result in this study also shows that the performance of the bootstrap hypothesis test with the bootstrap sample sizes of 10,000 was slightly better than the one with the bootstrap sample sizes of 1,000 in terms of the statistical power. Another factor that can influence the performance of the bootstrap hypothesis tests is the data generation process for the bootstrap samples (MacKinnon, 2009). In this study, the original data were generated using the 3PLM in the IRT, whereas the bootstrap samples were generated using the LR equation with the coefficients satisfying the null hypothesis. The slightly lower performance of the BLRT may be due to this discrepancy in the data generation process. This study only tested a single data generation process and different data generation processes may yield different results, which could be the limitation of this study. However, considering the similarity in the sampling distributions of the asymptotic test and the bootstrap hypothesis test shown in Figure 1, it is expected that different data generation processes may not significantly change the results of this study.

In all, the LR procedure based on the asymptotic LRT seems to work well even in small samples. Although the results from the PLRT and BLRT were similar with the results from the asymptotic method in this study, the PLM and bootstrap method have outperformed the asymptotic method in the cases where the asymptotic assumptions are suspect. Therefore, investigating the applicability of the PLM and bootstrap method for such a case would be very interesting topics for future research in the area of measurements.