The $l_{z(p)}^{*}$ Person-Fit Statistic in an Unfolding Model Context

Abstract

Although person-fit analysis has a long-standing tradition within item response theory, it has been applied in combination with dominance response models almost exclusively. In this article, a popular log likelihood-based parametric person-fit statistic under the framework of the generalized graded unfolding model is used. Results from a simulation study indicate that the person-fit statistic performed relatively well in detecting midpoint response style patterns and not so well in detecting extreme response style patterns.

One of the goals of Item Response Theory (IRT) is to measure a latent variable for a set of subjects, based on the observed scores on a set of items. The positions of both the items and the subjects on the latent variable are assessed, thus providing users with rich information about the standing of the subjects on the latent variable of interest. IRT models are nowadays used in various applied settings, ranging from cognitive to psychological and personality measurement.

The most common unidimensional IRT models used, such as the 1-, 2-, and 3-parameter logistic models for dichotomous data (e.g., Embretson & Reise, 2000), are based on cumulative item response functions (IRFs). Cumulative IRFs imply that the probability of answering an item correctly (or of endorsing it) is expected to increase as the score on the latent variable increases. This model assumption is suitable, for example, in cognitive measurement, in which increasing knowledge is expected to be associated with a higher probability of answering an item correctly. Coombs (1964) referred to this underlying response process as being dominant.

There are, however, other settings where dominant models are not necessarily optimal. Measuring latent person characteristics such as preferences and attitudes provides two examples (e.g., Drasgow, Chernyshenko, & Stark, 2010; Hoijtink, 1993). The ideal point response process described by Coombs (1964) presented an alternative model approach in these settings. An ideal point process is based on the idea of a person endorsing an item to the extent that the person’s opinion is close to the item’s statement (Thurstone, 1928, 1929). Hence, what determines the probability of a person endorsing an item is the relative distance between the score of this person on the latent variable (say, ${\theta }_n$ for person n) and the item’s standing on the latent variable (say, ${\delta }_i$ for item i). As such, IRFs may peak at the value of the latent variable where ${\theta }_n={\delta }_i$, and the probability of endorsing the item may decrease as the latent score is further from ${\delta }_i$ in either direction. The so-called unfolding response models (Coombs, 1964) take the proximity between the persons and items into account and therefore allow for peaked IRFs.

Research concerning dominant models by far overwhelms that of unfolding models mostly because of the huge impact of the work of Rensis Likert (1932), but this state of affairs is not a settled issue (see the focal article by Drasgow et al., 2010 and the following replies for a very interesting discussion). Some of the most notorious IRT unfolding models available for either dichotomous or polytomous data include the logistic models of DeSarbo and Hoffman (1986), the squared simple logistic model (Andrich, 1988), the PARELLA model (Hoijtink, 1990, 1991), the (generalized) hyperbolic cosine model (Andrich, 1996; Andrich & Luo, 1993), and the generalized graded unfolding model (GGUM; Roberts & Laughlin, 1996; Roberts, Donoghue, & Laughlin, 2000). In this article, the author focuses on the GGUM (Roberts et al., 2000; Roberts & Laughlin, 1996). The GGUM is suitable for both dichotomous and polytomous data. Moreover, it also became popular due to available dedicated software (GGUM, Roberts, Fang, Cui, & Wang, 2006; see also Markov Chain Monte Carlo [MCMC] GGUM, Wang, de la Torre, & Drasgow, 2015).

The goal of this article is to adapt a popular polytomous person-fit statistic to the GGUM. Person-fit analysis comprises a broad set of statistical procedures aimed at detecting item response patterns that deviate from what would be expected based on the fitted model or on the groups of respondents. These atypical response patterns are often referred to as being aberrant or misfitting. An aberrant response pattern typically reflects idiosyncratic response behavior (such as guessing, carelessness, or sleepiness; Meijer, 1996). A latent trait estimate based on an aberrant response pattern may not accurately reflect the person’s true standing on the latent variable. Therefore, detecting this type of response patterns is an important step toward assuring the validity and the fairness of results. The importance of person-fit analysis is also recognized by the International Test Commission (2013).

To the author’s knowledge, there is no research on person-fit analysis with the popular GGUM. This article intends to start filling in this gap. The focus is on the popular $l_z^{*}$ person-fit statistic (Drasgow, Levine, & Williams, 1985; Snijders, 2001) and, in particular, on its recent extension to polytomous items (Sinharay, 2015). Henceforth, the latter shall be referred as the $l_{z(p)}^{*}$ person-fit statistic. The $l_{z(p)}^{*}$ statistic is based on the well-known standardized log likelihood statistic introduced by Drasgow et al. (1985), which has a long-standing relevance in person-fit research.

This article is organized as follows. In the next section, the details of both the GGUM and the $l_{z(p)}^{*}$ person-fit statistic are introduced. Then, the details of a simulation study that was conducted to study the performance of $l_{z(p)}^{*}$ under the framework of the GGUM are presented. The goal of this study is to understand how the Type I error and detection rates vary across several conditions. In particular, how the aberrant behavior was operationalized is explained. The “Results” section summarizes the relevant findings from the simulation study. Finally, some conclusions and new possible research directions are discussed.

The GGUM

Let $Z_i$ denote a random variable consisting of the score on item i ($i=1,\dots ,I)$, with possible observable response categories $z=0,1,\dots ,C_i$. $C_i$ equals 1 if item i is dichotomous and is larger than 1 if the item is polytomous. For simplicity, assume that the number of item response categories is the same across all items, so $C_i=C$ for all items. Score $z=0$ corresponds to the strongest level of disagreement with the item’s statement, and $z=C$ corresponds to the strongest level of agreement with the item’s statement. As noted before, denote the location of person n ($n=1,\dots ,N$) on the latent variable by ${\theta }_n$. The GGUM (Roberts et al., 2000) is given by the following equation:

$$P(Z_i=z|{\theta }_n)=\frac{f\left(z\right)+f(M-z)}{\sum _{w=0}^C[f\left(w\right)+f(M-w)]},$$

where

$$f\left(w\right)=\exp \left\{{\alpha }_i[w({\theta }_n-{\delta }_i)-\sum _{k=0}^w{\tau }_{\mathrm{ik}}]\right\}.$$

In Equation 1, $M=2C+1$. For item i, ${\alpha }_i$ is the discrimination parameter, ${\delta }_i$ is the location parameter, and ${\tau }_{\mathrm{ik}}(k=0,\dots ,M)$ are the threshold parameters. Parameter ${\tau }_{i0}$ is arbitrarily constrained to zero, and parameters ${\tau }_{\mathrm{ik}}$ ($k=1,\dots ,M$) are typically constrained such that

$${\tau }_{i(C+1)}=0\mathrm{and}{\tau }_{\mathrm{iz}}=-{\tau }_{i(M-z+1)}\mathrm{for}z=1,\dots ,C,$$

which implies that $\sum _{k=0}^z{\tau }_{\mathrm{ik}}=\sum _{k=0}^{M-z}{\tau }_{\mathrm{ik}}$, $z=0,\dots ,C$.

The GGUM is a divide-by-total model (Thissen & Steinberg, 1986). See Roberts et al. (2000) for more details on how the GGUM has been derived and on the interpretation of each model parameter. The GGUM is suitable for modeling the probability of endorsing an item based on the relative distance between a person’s location (${\theta }_n,n=1,\dots ,N$) and the item’s location (${\delta }_i,i=1,\dots ,I$): The smaller the distance between ${\theta }_n$ and ${\delta }_i$, the larger the probability given by Equation 1.

Figure 1 shows an example of the GGUM for a polytomously scored item with four observable response categories (“strongly against,”“against,”“in favor,”“strongly in favor”), thus $C=3$. The expected value of an observable response conditional on $\theta$ has also been superimposed (solid curve). As it can be readily seen, the curve of the expected value is peaked around 0, a consequence of the GGUM being based on the relative differences between the standing of the persons and the item.

Figure 1.

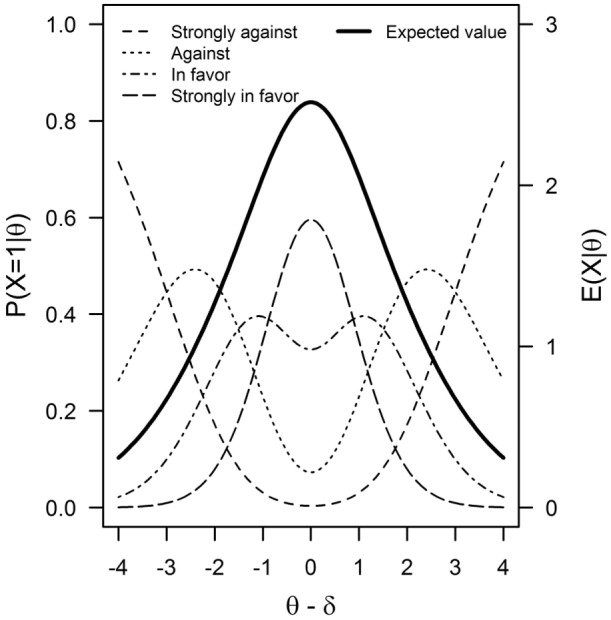
GGUM for an item with four observable response curves (from “strongly against” through “strongly in favor”).

Note. The item’s expected value conditional on $\theta$ is also shown (solid curve). The item parameters are ${\alpha }_i={\delta }_i=1$, ${\tau }_{\mathrm{ik}}=-3,-1.5,-.6,0,.6,1.5,3$. GGUM = generalized graded unfolding model.

The $l_z$ Person-Fit Statistic

Drasgow et al. (1985) introduced the most well-known person-fit statistic in use, usually referred to as the $l_z$ statistic. The fact that $l_z$ can be used for either dichotomous or polytomous items, as well as its purported asymptotic standard normal distribution (more about this below), partly explains the popularity that this person-fit statistic has enjoyed. The $l_z$ statistic is based on the standardized log likelihood of a response vector $\mathbf{X}=(X_1,X_2,\dots ,X_I)$. Denoting the probability $P(Z_i=z|\theta )$ by $P_{\mathrm{iz}}(\theta )$ (Drasgow et al., 1985),

$$l_z=\frac{l_0\left(\theta \right)-E\left(l_0\right)}{\sqrt{\mathrm{Var}\left(l_0\right)}},$$

where

$$l_0\left(\theta \right)=\log \left(L\left(\theta \right)\right),$$

$$L\left(\theta \right)=\underset{i=1}{\overset{I}{\Pi }}\sum _{z=0}^C{\gamma }_{\mathrm{iz}}{P}_{\mathrm{iz}}\left(\theta \right),$$

$$E\left(l_0\left(\theta \right)\right)=\sum _{i=1}^I\sum _{z=0}^C{P}_{\mathrm{iz}}\left(\theta \right)\log \left(P_{\mathrm{iz}}\left(\theta \right)\right),$$

and

$$\mathrm{Var}\left(l_0\left(\theta \right)\right)=\sum _{i=1}^I\sum _{z_1=0}^C\sum _{z_2=0}^C{P}_{i{z}_1}\left(\theta \right)P_{i{z}_2}\left(\theta \right)\log \left(P_{i{z}_1}\left(\theta \right)\right)\log (P_{i{z}_1}\left(\theta \right)/P_{i{z}_2}\left(\theta \right)).$$

Variable ${\gamma }_{\mathrm{iz}}$ is an indicator variable such that ${\gamma }_{\mathrm{iz}}=1$ if $X_i=z$ and 0 otherwise. In Equation 8, $z_1$ and $z_2$ denote the usual observable response categories (ranging between 0 and C). Small values of $l_z$ (say, below a prespecified threshold or cutoff value) are indicative of misfitting item response patterns.

The claim that $l_z$ is asymptotically standard normally distributed is only valid when true person parameters $\theta$ are used in the computations. However, in most practical applications, one only has access to estimated person parameters, say $\hat{\theta }$. In this case, it is well known that the asymptotic distribution of $l_z$ deviates from the standard normal distribution (Molenaar & Hoijtink, 1990; Nering, 1995, 1997; Reise, 1995). Snijders (2001) proposed a modified version of $l_z$, known as the $l_z^{*}$ statistic, that introduced a correction which resets the asymptotic distribution to be standard normal even when sample estimates of person parameters are used. Snijder’s correction applies only to dichotomously scored items. Recently, Sinharay (2015) generalized Snijders’ correction to polytomous items (and to mixed-format tests in general), which is the $l_{z(p)}^{*}$ statistic.

The goal of this study was to understand how the $l_{z(p)}^{*}$ statistic works in combination with the GGUM. The outcome was not clear to us beforehand, as there is no previous work on this topic (to the best of our knowledge). The author wanted to study Type I error rates as well as the power to detect aberrant response patterns under varying conditions. To this effect, a simulation study was carried out, the details of which are discussed next.

Simulation Study

Four factors were manipulated: Scale length (factor I with four levels: $I=10,20,40,100$), the proportion of aberrant items (factor AbI with three levels: $\mathrm{AbI}=.10,.20,.25$), the proportion of aberrant simulees (factor AbN with three levels: $\mathrm{AbN}=.05,.10,.20$), and the number of observable response categories (factor C with three levels: $C=3,5,7$, thus corresponding to 4, 6, and 8 observable response categories, respectively). Thus, in total, the simulation study consisted of 108 conditions. One hundred datasets were generated per condition, based on a fixed sample size of $N=1,000$ simulees per dataset.

The generation of model-fitting data closely followed previous research based on the GGUM (Roberts, Donoghue, & Laughlin, 2002; Tay, Ali, Drasgow, & Williams, 2011; Wang, Tay, & Drasgow, 2013). Item scores were randomly drawn from multinomial distributions based on the conditional probabilities given by Equation 1. For each replicated dataset, true $\alpha$ parameters were randomly drawn from a uniform distribution in the interval $(0.5,2.0)$. True $\delta$ parameters were randomly drawn from the standard normal distribution truncated between −2.0 and 2.0.¹ True person parameters $\theta$ were randomly drawn from the standard normal distribution. Finally, the true ${\tau }_{\mathrm{iC}}$ parameter was randomly drawn from a uniform distribution in the interval $(-1,-.4)$, and the remaining threshold parameters were recursively generated by means of the following equation:

$${\tau }_{i(k-1)}={\tau }_{\mathrm{ik}}-0.25+e_{i(k-1)},\mathrm{for}k=C,C-1,\dots ,2,$$

where $e_{i(k-1)}$ is an error term randomly drawn from a $N(0,0.04)$ distribution.

Two types of responding styles (i.e., systematic tendencies to respond to rating scales independently of the content; Paulhus, 1991) were considered in this study. Extreme responding style (ERS) is based on the person’s propensity to choose extreme answer options (coded 0 or C), and midpoint responding style (MRS) is based on the person’s propensity to choose middle answer options (say, between floor $(C/2)$ and ceiling $(C/2)$ for $C=3,5,7$, as in this simulation study). These responding styles have been a topic of interest on a wide range of fields, such as marketing (e.g., Peterson, Rhi-Perez, & Albaum, 2014), selection (e.g., Levashina, Weekley, Roulin, & Hauck, 2014), or clinical psychology (e.g., Forand & DeRubeis, 2014), among others (Kieruj & Moors, 2010; von Davier & Khorramdel, 2013; Worthy, 1969). The author decided to focus on these two types of responding style for simplicity, although other options would also be possible (e.g., acquiescence, disacquiescence, varying response range, or noncontingent responding; Baumgartner & Steenkamp, 2001).

For each replication in a condition, aberrantly responding simulees were randomly selected from the sample of N simulees available. A proportion AbI of item scores was generated to mimic ERS for half of the aberrantly responding simulees $(N\times \mathrm{AbN})/2$, while for the other half a proportion AbI of item scores was generated to mimic MRS. Also, the subset of items whose scores were generated to reflect either ERS or MRS was randomly selected from the total set of items for each simulee. To simulate ERS, midpoint response categories were randomly selected from each response vector, and the scores were changed to the corresponding extreme answer option with probability 1. To simulate MRS, extreme response categories were randomly selected, and the scores were changed to the corresponding midpoint answer option with probability 1. Table 1 summarizes this procedure.

Table 1.

Operationalization of ERS and MRS.

Observable response categories	ERS	MRS
$C=3$: 0, 1, 2, 3	$1\to 0$	$0\to 1$
	$2\to 3$	$3\to 2$
$C=5$: 0, 1, 2, 3, 4, 5	$2\to 0$	$0\to 2$
	$3\to 5$	$5\to 3$
$C=7$: 0, 1, 2, 3, 4, 5, 6, 7	$3\to 0$	$0\to 3$
	$4\to 7$	$7\to 4$

Note. ERS = extreme responding style; MRS = midpoint responding style.

The entire simulation study can be summarized in seven steps: (a) generate GGUM-fitting data, (b) generate GGUM-misfitting data (ERS and MRS) for adequate proportions of persons and items, (c) estimate item and person parameters, (d) control the quality of the estimated parameters, (e) look at model fit, (f) compute $l_{z(p)}^{*}$ for each simulee and decide which simulees to flag as displaying aberrant responding style, and (g) evaluate Type I error and detection rates. Step 3 was performed for the datasets without any aberrant item score (after Step 1) and with aberrant item scores (after Step 2). The goal was to compare both sets of parameter estimates to assess the impact of the operationalization of both ERS and MRS. The author hoped this impact would be small, otherwise the performance of the $l_{z(p)}^{*}$ statistic might have been overly affected by the incidence of aberrant responding style in the data (see St-Onge, Valois, Abdous, & Germain, 2011, for an interesting discussion about this problem in a different context). Below, perfect model-fitting data are generically referred to as “${\mathrm{Data}}_{\mathrm{fit}}$” and data that included misfitting score patterns as “${\mathrm{Data}}_{\mathrm{misfit}}$.”

In Step 4, the estimated parameters based on ${\mathrm{Data}}_{\mathrm{fit}}$ and based on ${\mathrm{Data}}_{\mathrm{misfit}}$ are compared with the true parameters. The author looked at the bias (BIAS = $\sum _{t=1}^T({\hat{\gamma }}_t-{\gamma }_t^{\mathrm{TRUE}})/T$), the mean absolute deviation (MAD = $\sum _{t=1}^T|{\hat{\gamma }}_t-{\gamma }_t^{\mathrm{TRUE}}|/T$), and the correlation (COR = $\mathrm{cor}({\hat{\gamma }}_t,{\gamma }_t^{\mathrm{TRUE}})$, $t=1,\dots ,T$) between true and estimated parameters, for each set of estimated parameters $\{{\hat{\gamma }}_t\}$, across conditions. Here, ${\gamma }_t$ stands for any of GGUM’s parameters (${\alpha }_i$,${\delta }_i$,${\tau }_{\mathrm{ik}}$, and ${\theta }_n$) and T is the corresponding number of parameters (I, I, $I\times C$, and N, respectively). Moreover, ANOVA models were fitted based on four factors: The number of items I, the number of answer options C, the proportion of aberrant item scores AbI, and the proportion of simulees providing aberrant item scores AbN. The goal was to understand the strength and direction of each effect on the BIAS, MAD, and COR, and to make sure that the effects were comparable across the two types of datasets (including and excluding aberrant response patterns).

In Step 5, the INFIT (weighted mean square error) and the OUTFIT (unweighted mean square error) statistics (Wright & Masters, 1982, 1990) were computed, as originally suggested by Roberts et al. (2000). Denote the score of person n ($n=1,\dots ,N$) on item i ($i=1,\dots ,I$) by $z_{\mathrm{ni}}$. Using Equation 1, the expected value and the variance of $z_{\mathrm{ni}}$ are, respectively, computed as

$$E_{\mathrm{ni}}=\sum _{z=0}^{C}z{P}_{\mathrm{iz}}\left({\theta }_n\right)\mathrm{and}{V}_{\mathrm{ni}}=\sum _{z=0}^C{(z-E_{\mathrm{ni}})}^2{P}_{\mathrm{iz}}\left({\theta }_n\right).$$

The formulas for INFIT and OUTFIT for item i are then given by

$$\mathrm{OUTFI}{\mathrm{T}}_i=\frac{1}{N}\sum _{n=1}^N{\left(\frac{z_{\mathrm{ni}}-E_{\mathrm{ni}}}{\sqrt{V_{\mathrm{ni}}}}\right)}^2,\mathrm{INFI}{\mathrm{T}}_i=\frac{\sum _{n=1}^N{(z_{\mathrm{ni}}-E_{\mathrm{ni}})}^2}{\sum _{n=1}^N{V}_{\mathrm{ni}}}.$$

Under the null hypothesis of model fit, both test statistics are chi-square distributed with N degrees of freedom. Furthermore, the adjusted ${\chi }^2$ degrees of freedom ratios (${\chi }^2/\mathrm{df}$; Chernyshenko, Stark, Chan, Drasgow, & Williams, 2001; Drasgow, Levine, Tsien, Williams, & Mead, 1995; LaHuis, Clark, & O’Brien, 2011) were also computed. These chi-square statistics are based on expected frequencies that depend on the estimated item parameters and the distribution of $\theta$. The formula for the unadjusted statistic for item i is

$${\chi }_i^2=\sum _{z=0}^C\frac{{(O_{\mathrm{iz}}-{\tilde{E}}_{\mathrm{iz}})}^2}{{\tilde{E}}_{\mathrm{iz}}},\mathrm{with}{\tilde{E}}_{\mathrm{iz}}=N\int P_{\mathrm{iz}}\left(\theta \right)\varphi \left(\theta \right)d\theta ,$$

where $O_{\mathrm{iz}}$ is the observed frequency of endorsing answer option z for item i, and $\varphi (\theta )$ denotes the standard normal density. The ${\chi }^2$ tests of Equation 12 apply to single items (also referred to as “singlets”). Drasgow et al. (1995) advised generalizing the procedure above to doublets (i.e., pairs) and triplets of items to better evaluate model (mis)fit. The procedure requires choosing subsets of suitable doublets and triplets based on the items’ difficulty, as the total number of options increases rapidly as the number of items increases (see Drasgow et al., 1995, and the MODFIT program for more details; Stark, 2001). Finally, the ${\chi }^2$ statistics of Equation 12 are adjusted to a sample size of 3,000 (Drasgow et al., 1995; LaHuis et al., 2011) by means of the formula

$${\chi }_i^2/\mathrm{df}=\frac{3,000({\chi }_i^2-\mathrm{df})}{N}+\mathrm{df},$$

where df is the adequate number of degrees of freedom (dependent on the number of singlets/doublets/triplets). The common heuristic used is that values of ${\chi }^2/\mathrm{dfs}$ larger than 3 are indicative of model misfit. In this simulation, the integral in Equation 12 (and its natural generalization to doublets and triplets) was evaluated by numerical quadrature using 61 equally spaced points between −3 and +3. After analyzing the results of INFIT, OUTFIT, and MODFIT, the author hoped to find as least misfitting items as possible.

The value of $l_{z(p)}^{*}$ was computed for each simulee in Step 6.² It was necessary to estimate a cutoff value for $l_{z(p)}^{*}$ to have a decision rule to flag each response pattern as either aberrant or not. Some preliminary analyses indicated that the nominal cutoff value derived from the standard normal distribution, which is valid only asymptotically, was not appropriate for the number of items that were considered in this simulation, possibly except for $I=100$. Further details concerning this issue will be presented in the “Results” section, based on the data generated for this study. Instead of using nominal cutoff values, person-based cutoff values (e.g., de la Torre & Deng, 2008; Sinharay, 2016; van Krimpen-Stoop & Meijer, 1999) were estimated as follows. For each simulee in each dataset, 100 GGUM-fitting item response patterns were generated based on the model parameters that were estimated from ${\mathrm{Data}}_{\mathrm{misfit}}$ and on the person’s estimated $\theta$. The values of $l_{z(p)}^{*}$ were computed for these perfectly fitting response patterns, and the cutoff value was estimated by the 5% quantile of this distribution. The Type I error rate in Step 7 was computed as the sample proportion of “normal” simulees with an associated $l_{z(p)}^{*}$ value smaller than the estimated cutoff value. The detection rate of ERS (MRS) was computed as the sample proportion of ERS (MRS) simulees with an associated $l_{z(p)}^{*}$ value smaller than the estimated cutoff value.

The parameters of the GGUM were estimated using the marginal maximum likelihood (MML) algorithm of Roberts et al. (2000). All the code, including the MML algorithm used to estimate the GGUM parameters, the model fit statistics, and the $l_{z(p)}^{*}$ person-fit statistic, was written in R (R Core Team, 2016).

Results

Model Fit

Table 2 summarizes the results concerning the BIAS, MAD, and COR measures, averaged across all conditions and replications. First, all sets of estimated parameters were always strongly linearly related to the true values (typically correlations above .94). For both the location and the person parameters, the estimated parameters based on data including misfitting item response patterns (${\hat{\delta }}_{\mathrm{misfit}}$ and ${\hat{\theta }}_{\mathrm{misfit}}$, respectively) and based on model-fitting data (${\hat{\delta }}_{\mathrm{fit}}$ and ${\hat{\theta }}_{\mathrm{fit}}$, resp.) were very close. For example, the absolute differences in BIAS or MAD between ${\hat{\delta }}_{\mathrm{fit}}$ and ${\hat{\delta }}_{\mathrm{misfit}}$ and between ${\hat{\theta }}_{\mathrm{fit}}$ and ${\hat{\theta }}_{\mathrm{misfit}}$ were at most 0.1 in more than 97% replications across all conditions. Moreover, $\hat{\delta }$ and $\hat{\theta }$ were on average unbiased based on either ${\mathrm{Data}}_{\mathrm{fit}}$ or ${\mathrm{Data}}_{\mathrm{misfit}}$. Furthermore, the BIAS and the MAD of the $\theta$ estimates were compared based on ${\mathrm{Data}}_{\mathrm{misfit}}$ between the “normal” and the “aberrant” simulees to make sure that this operationalization of aberrant behavior did not systematically bias the estimation of $\theta$ for the aberrant simulees. The author found that differences in BIAS were very small (between −0.02 and 0.01 across replications). In terms of MAD, the MAD of the $\theta$ estimates of the aberrant simulees were typically larger (mean difference of 0.04), and the MAD did increase with the proportion of misfitting items, AbI. However, these differences were relatively small (all mean differences in MAD were smaller than 0.15).

Table 2.

Assessing the Quality of the Estimated GGUM Parameters.

	${\mathrm{Data}}_{\mathrm{fit}}$			${\mathrm{Data}}_{\mathrm{misfit}}$
Parameter	BIAS	MAD	COR	BIAS	MAD	COR
${\alpha }_i$
M	−0.03	0.09	0.98	−0.09	0.12	0.97
SD	0.06	0.03	0.02	0.08	0.06	0.02
$R^2$	0.96	0.80		0.88	0.77
${\eta }_I^2$	0.96	0.80		0.64	0.42
${\eta }_C^2$	0.60	0.02		0.75	0.56
${\eta }_{\mathrm{AbI}}^2$				0.42	0.29
${\eta }_{\mathrm{AbN}}^2$				0.63	0.50
${\delta }_i$
M	−0.01	0.09	1.00	−0.01	0.09	1.00
SD	0.11	0.15	0.03	0.11	0.15	0.04
$R^2$	0.54	0.64		0.54	0.54
${\eta }_I^2$	0.54	0.60		0.53	0.50
${\eta }_C^2$	0.02	0.23		0.02	0.14
${\eta }_{\mathrm{AbI}}^2$				0.01	0.01
${\eta }_{\mathrm{AbN}}^2$				0.01	0.01
${\tau }_{\mathrm{ik}}$
M	−0.05	0.12	0.94	−0.03	0.12	0.93
SD	0.06	0.04	0.03	0.05	0.03	0.04
$R^2$	0.90	0.90		0.78	0.87
${\eta }_I^2$	0.89	0.82		0.74	0.60
${\eta }_C^2$	0.51	0.80		0.08	0.83
${\eta }_{\mathrm{AbI}}^2$				0.15	0.06
${\eta }_{\mathrm{AbN}}^2$				0.29	0.13
${\theta }_n$
M	0.00	0.17	0.98	0.00	0.17	0.98
SD	0.07	0.19	0.02	0.07	0.19	0.03
$R^2$	0.03	0.84		0.08	0.86
${\eta }_I^2$	0.02	0.83		0.04	0.86
${\eta }_C^2$	(*)	0.09		(*)	0.13
${\eta }_{\mathrm{AbI}}^2$				0.01	(*)
${\eta }_{\mathrm{AbN}}^2$				0.04	0.01

Note. The mean and standard deviation (SD) values reported are across all conditions and replications. The ${\eta }^2$ values are based on four-way fixed-effects ANOVA models which only include main effects. The star symbol “(*)” denotes effect sizes smaller than 0.01. GGUM = generalized graded unfolding model; BIAS = bias; MAD = mean absolute deviation; COR = correlation.

On the contrary, Table 2 also shows that the estimation of the discrimination parameters $\alpha$ and the threshold parameters $\tau$ from ${\mathrm{Data}}_{\mathrm{misfit}}$ was affected by factors AbI and AbN (the larger the AbI and AbN, the worse the BIAS and MAD values). Also, estimates ${\hat{\alpha }}_{\mathrm{Misfit}}$ were slightly underestimated on average. However, the absolute differences in BIAS or MAD between ${\hat{\alpha }}_{\mathrm{Fit}}$ and ${\hat{\alpha }}_{\mathrm{Misfit}}$ and between ${\hat{\tau }}_{\mathrm{Fit}}$ and ${\hat{\tau }}_{\mathrm{Misfit}}$ were at most 0.2 in more than 96% replications across all conditions.

In terms of model fit for the datasets that include aberrant item score patterns, INFIT flagged 5% or more of the items of a dataset as misfitting on 0.6% of all replications, so it was very conservative. OUTFIT flagged 5% or more of the items of a dataset as misfitting on 6.4% of all replications, which is slightly above the nominal 5% significance level used in the analyses. In particular, OUTFIT was affected by increasing proportions of aberrant simulees in the data (${\eta }^2=.26$), but the proportion of items flagged as misfitting was still relatively low. Furthermore, results based on MODFIT showed that no fit issues occurred for small to moderate number of items ($I=10,20,40$): The percentage of flagged singlets, doublets, and triplets was lower than 5% in 79 of 81 conditions. However, in the 27 conditions based on $I=100$ items, most singlets and doublets were flagged, indicating misfit. The author speculates that MODFIT may be too sensitive for larger number of items, at least in the GGUM framework. To check this, the MODFIT results were also looked at based on ${\mathrm{Data}}_{\mathrm{fit}}$, as a term of comparison. The author confirmed that, also for the GGUM-fitting data, MODFIT flagged most singlets and doublets when $I=100$, indicating misfit.

Summarizing, the author concludes that operationalization of ERS and MRS did not greatly distort the estimation of the model parameters, as intended. Moreover, the checks of model fit based on INFIT, OUTFIT, and MODFIT seem to indicate that the prevalence of misfitting items was low, with the exception of the datasets based on $I=100$, according to MODFIT. The latter finding might, however, be explained by an unusual sensitivity of MODFIT to larger number of items, at least under the GGUM framework.

Cutoff Values

The estimated person-based cutoff values were compared with the (asymptotic) nominal cutoff value to reinforce the decision of estimating cutoff values in this study. At a 5% significance value, the nominal cutoff value is equal to −1.64. The estimated cutoff values, averaged across all replications and conditions based on the same number of items, were equal to −1.78 ($\mathrm{SD}=.0019$) for $I=10$, −1.73 ($\mathrm{SD}=.0019$) for $I=20$, −1.69 ($\mathrm{SD}=.0015$) for $I=40$, and −1.66 ($\mathrm{SD}=.0015$) for $I=100$. Hence, on average, the estimated cutoff values do seem to get closer to the nominal value as the number of items increases, as expected, but not as quickly as desired. The differences between the estimated and the nominal cutoff value were deemed too large to be ignored except when $I=100$, which again helps understanding why we did not rely on the asymptotic nominal approximation. It is interesting to observe that the nominal cutoff value, −1.64, is more conservative than the average estimated cutoff. As a result, both the Type I error and the power rates discussed below, which are based on estimated cutoff values, are actually smaller in comparison with what would be expected based on the nominal cutoff value.

Type I Error

The author started by analyzing the Type I error rates for model-fitting data only, based on factors I and C (thus, with the constraint $\mathrm{AbN}=\mathrm{AbI}=0$), on a separate small simulation. The goal was to ascertain that the detection method was working as expected, namely, by incorrectly flagging about 5% (the nominal Type I error rate) of the simulees. This was found to be approximately the case. The procedure was slightly conservative (mean Type I error rate equal to .04, SD = .01), with the observed mean Type I error rate closer to the nominal 5% value as the number of items increased.

The analysis of the Type I error rates in the full simulation study indicated that the $l_{z(p)}^{*}$ statistic was very conservative. The mean Type I error rate across conditions and replications was equal to .03 (SD = .01), for a nominal 5% error rate, which is slightly below the Type I error rates found based on model-fitting data only. A four-way ANOVA including main effects only (I, C, AbI, AbN) indicated that all factors had a strong effect on the Type I error rates—$F(9,98)=75.28$, $p<.001$, adjusted $R^2=.86$; ${\eta }_p^2=.07,.78,.50,.70$ for effects I, C, AbI, and AbN, respectively. The error rates tended to decrease with C, AbI, AbN, and I.

Detection of ERS and MRS Patterns

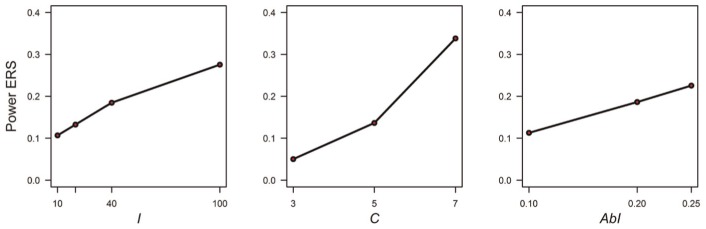
The detection rates of the ERS answer patterns were relatively low. The mean ERS detection rate across conditions and replications was .17 (first and third quartiles = .06 and .22, respectively). For most conditions (92 in the 108 total), not more than 30% of the ERS patterns were detected by the $l_{z(p)}^{*}$ person-fit statistic. Table 3 displays the results. It can be seen from this table that the best detection rates mostly concern conditions associated to a large number of items ($I=40,100$) and answer options ($C=7$), with a moderate to large proportion of aberrant item scores ($\mathrm{AbI}=.20,.25$). A four-way ANOVA including main effects only (I, C, AbI, AbN) indicated that all factors had a moderate to strong effect on the detection rates of the ERS patterns—$F(9,98)=26.95$, $p<.001$, adjusted $R^2=.69$; ${\eta }_{\mathrm{p}}^2=.32,.62,.20,.11$ for effects I, C, AbI, and AbN, respectively. Typically, the detection rates of the ERS patterns increased with I, AbI, and especially with the number of answer options C (see Figure 2). The latter result makes sense because the evidence for ERS becomes stronger when the middle and the extreme answer options are further apart from one another (i.e., as C increases). The detection rates of ERS patterns slightly decreased as the proportion of aberrantly responding simulees AbN increased, thus indicating that the performance of $l_{z(p)}^{*}$ can suffer in cases of large proportions of aberrant respondents in the sample (St-Onge et al., 2011).

Table 3.

Detection Rates for ERS Patterns.

			Detection rate
C	AbN	AbI	$I=10$	$I=20$	$I=40$	$I=100$
3		.10	.05	.04	.05	.05
	.05	.20	.05	.06	.06	.06
		.25	.07	.06	.06	.05
		.10	.05	.05	.05	.05
	.10	.20	.06	.06	.05	.05
		.25	.06	.05	.05	.05
		.10	.05	.04	.05	.04
	.20	.20	.05	.05	.05	.04
		.25	.05	.05	.04	.03
5		.10	.08	.09	.10	.14
	.05	.20	.08	.13	.18	.26
		.25	.15	.16	.23	.36
		.10	.08	.08	.10	.12
	.10	.20	.10	.12	.16	.21
		.25	.12	.14	.19	.29
		.10	.07	.07	.09	.10
	.20	.20	.08	.09	.11	.14
		.25	.10	.11	.13	.16
7		.10	.13	.15	.24	.40
	.05	.20	.20	.30	.51	.81
		.25	.29	.39	.63	.90
		.10	.12	.14	.20	.36
	.10	.20	.17	.28	.42	.68
		.25	.25	.34	.51	.81
		.10	.10	.11	.16	.25
	.20	.20	.13	.19	.28	.46
		.25	.16	.23	.32	.55

Note. Detection rates larger than .30 are marked in bold. ERS = extreme responding style.

Figure 2.

Effect of the number of items (I), the number of answer options (C), and the proportion of aberrant item scores in the response pattern (AbI) on the detection rates of ERS patterns.

Note. ERS = extreme responding style.

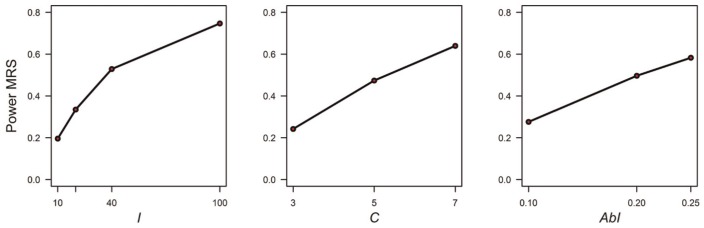
In contrast, the detection rates of the MRS patterns were higher in comparison with the ERS condition. The mean MRS detection rate across conditions and replications was .45 (first and third quartiles = .17 and .72, respectively). A four-way ANOVA including main effects only (I, C, AbI, AbN) indicated that all factors had a moderate to strong effect on the detection rates of the MRS patterns—$F(9,98)=124.70$, $p<.001$, adjusted $R^2=.91$; ${\eta }_{\mathrm{p}}^2=.85,.78,.69,.07$ for effects I, C, AbI, and AbN, respectively. The detection rates increased with I, AbI, andC, as shown in Figure 3.

Figure 3.

Effect of the number of items (I), the number of answer options (C), and the proportion of aberrant item scores in the response pattern (AbI) on the detection rates of MRS patterns.

Note. MRS = midpoint responding style.

The difference between the detection rates associated to ERS and MRS patterns may be partly explained by the proportion of extreme item scores ($=0,C$) and midpoint item scores (= floor(C/2), ceiling(C/2)) in the randomly generated GGUM-fitting data. The model-fitting item scores were generated based on Equation 1, with model parameters randomly drawn from probability distributions as explained in the description of the simulation study. For each generated GGUM-fitting dataset, the ratio of the number of generated extreme item scores to the number of generated midpoint item scores (denote this ratio by ${\varphi }_{\mathrm{E}/\mathrm{M}}$) was computed. It was verified that ${\varphi }_{\mathrm{E}/\mathrm{M}}$ (averaged over replications) ranged from 1.40 through 1.89. The effect of the number of answer options C on ${\varphi }_{\mathrm{E}/\mathrm{M}}$ was very strong—$F(2,105)=15,698.14$, $p<.001$, ${\eta }^2=1.00$—see Figure 4. This implies that the proportion of generated extreme scores exceeded the proportion of generated midpoint scores, a fact that was exacerbated with the increase of C. A consequence is that MRS is more prone to be detected, because response patterns are largely dominated by the extreme scores, and therefore midpoint answer options are more “unexpected.” Equivalently, ERS is less prone to be detected, since the proportion of extreme item scores in the data is already large. The author believes that this property of the data influenced the detection rates found for both the ERS and the MRS type of patterns.

Figure 4.

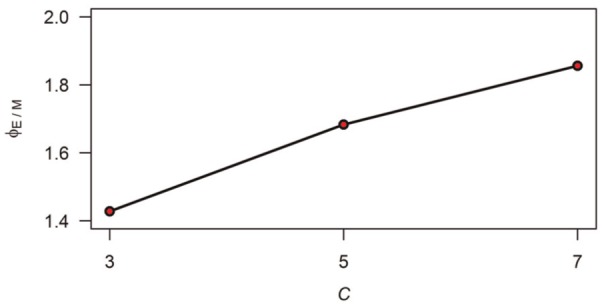
Effect of the number of answer options, C, on the ratio of the number of generated extreme item scores to the number of generated midpoint item scores, ${\varphi }_{\mathrm{E}/\mathrm{M}}$.

Furthermore, as suggested by an anonymous reviewer, it is also possible that the bias of the estimated parameters played a role in the difference of results between detecting ERS and MRS patterns. To check this, the effects of I, C, AbI, and AbN on the detection rates from a main-effects four-way ANOVA were compared with the same effects in regression models that further included the mean bias (across replications) of parameters ${\alpha }_i$, ${\delta }_i$, ${\tau }_{\mathrm{ik}}$, and ${\theta }_n$. It was concluded that the bias of parameters ${\delta }_i$ and ${\theta }_n$ had a negligible effect on the detection rates of either ERS or MRS (by considering a regression model based on factors I, C, AbI, AbN, mean ${\delta }_i$ bias, and mean ${\theta }_n$ bias). However, the inclusion of the mean bias of parameters ${\alpha }_i$ and ${\tau }_{\mathrm{ik}}$ (thus, considering the regression model based on factors I, C, AbI, AbN, mean ${\alpha }_i$ bias, and mean ${\tau }_{\mathrm{ik}}$ bias) greatly decreased the effect of AbN for detecting both ERS and MRS patterns (the effect of AbN based on the four-way ANOVA, given by ${\eta }_{\mathrm{p}}^2=.11$ for ERS and ${\eta }_{\mathrm{p}}^2=.07$ for MRS, decreased to ${\eta }_{\mathrm{p}}^2=.004$ and ${\eta }_{\mathrm{p}}^2=.01$, respectively, in the new regression model). Also, in the ERS case, the effect of I was also greatly reduced (from ${\eta }_{\mathrm{p}}^2=.32$ to ${\eta }_{\mathrm{p}}^2=.03$). These results seem to suggest that the detection rates of ERS were more strongly affected by the bias of the estimated parameters in comparison with the MRS case. This finding may also help explaining, at least partly, the difference of the results between both types of aberrant behavior.

Discussion

The measurement of personality traits, preferences, and attitudes typically involve response processes that require some sort of “introspection” (Drasgow et al., 2010, p. 467). This type of response is not always perfectly captured by dominant response models, and unfolding models may be better suited in some situations (see, for example, Weekers & Meijer, 2008). The lack of published research concerning person-fit analytical approaches suitable to unfolding models is striking. This article attempts to shed some light on this important topic.

We have applied the $l_{z(p)}^{*}$ person-fit statistic based on the GGUM. The results of this study indicated that the procedure was conservative (low Type I empirical error rates) and that the detection of midpoint response style patterns was promising in some conditions. The detection rates of extreme response style patterns were more modest, except for conditions associated to large number of items and answer options and to relatively large proportions of aberrant item scores. As previously explained, the author believes that this finding was related to the prevalence of extreme item scores in the generated data.

There are many open questions that deserve investigation. For example, it is unclear how other person-fit statistics (see Karabatsos, 2003 and Meijer & Sijtsma, 2001 for overviews of available procedures, and Tendeiro, Meijer, & Niessen, 2015 for an R implementation of most statistics) would perform under the unfolding framework. Also, it would be interesting to extend these analyses to other types of responding styles (Baumgartner & Steenkamp, 2001) and to unfolding models other than the GGUM. Furthermore, in this study, the number of answer options was kept constant throughout the set of items. Research based on mixed-format instruments would be of great value. These questions open interesting possibilities for future research in this field.