Multidimensional Computerized Adaptive Testing for Classifying Examinees With Within-Dimensionality

Abstract

A classification method is presented for adaptive classification testing with a multidimensional item response theory (IRT) model in which items are intended to measure multiple traits, that is, within-dimensionality. The reference composite is used with the sequential probability ratio test (SPRT) to make decisions and decide whether testing can be stopped before reaching the maximum test length. Item-selection methods are provided that maximize the determinant of the information matrix at the cutoff point or at the projected ability estimate. A simulation study illustrates the efficiency and effectiveness of the classification method. Simulations were run with the new item-selection methods, random item selection, and maximization of the determinant of the information matrix at the ability estimate. The study also showed that the SPRT with multidimensional IRT has the same characteristics as the SPRT with unidimensional IRT and results in more accurate classifications than the latter when used for multidimensional data.

Computerized adaptive testing (CAT) estimates ability precisely or makes accurate classification decisions while minimizing test length. Much is known about unidimensional CAT (UCAT), and several classification methods are available (Eggen, 1999; Spray, 1993; Weiss & Kingsbury, 1984). However, knowledge about multidimensional CAT (MCAT) is still expanding, and classification methods are available only for some situations.

Seitz and Frey (2013) developed a multidimensional classification method that makes a decision for each dimension for items that are assumed to measure only one trait. Spray, Abdel-Fattah, Huang, and Lau (1997) investigated classification testing for items that are assumed to measure multiple traits and concluded that this was not feasible. A new method was developed to make decisions for items that measure multiple traits. The advantages of making multidimensional classification decisions are that the multidimensional structure of the data is respected, adaptive testing principles can be used, and test length is reduced even more than in MCAT for estimating ability.

Item response theory (IRT), which is often used for CAT, is discussed in the “Multidimensional Item Response Theory” section of this article. IRT relates the score on an item, based on the item parameters, and the examinee’s ability (van der Linden & Hambleton, 1997). In multidimensional IRT (MIRT), multiple person abilities describe the skills and knowledge the person brings to the test (Reckase, 2009). Classification methods are then discussed. These methods decide whether testing can be finished and which decision is made about the examinee’s level (e.g., insufficient/sufficient). A new classification method for MCAT is proposed. Item-selection methods are discussed in the “Item-Selection Methods” section of this article. These methods select the items based on a statistical criterion or on the examinee’s responses to previously administered items. New item-selection methods are proposed for multidimensional computerized classification testing (MCCT). The efficiency and effectiveness of the new classification and selection methods are shown using simulations in the “Simulation Study” section. In the “Discussion and Conclusion” section, remarks are made about MCCT and directions for future research.

Multidimensional Item Response Theory

CAT requires a calibrated item pool suitable for the specific test for which the model fit is established, item parameter estimates are available, and items with undesired characteristics are excluded (van Groen, Eggen, & Veldkamp, 2014a). MIRT assumes that a set of $p$ abilities accounts for the examinee’s responses to the items. The multidimensional dichotomous two-parameter logistic model (Reckase, 1985) describes the probability of a correct answer to item $i$ by

$${\mathrm{P}}_i\left(\mathbf{\theta }\right)=\mathrm{P}(X_i=1|{\mathbf{a}}_i,d_i,\mathbf{\theta })=\frac{\exp ({\mathbf{a}}_i^{\prime }\mathbf{\theta }+d_i)}{1+\exp ({\mathbf{a}}_i^{\prime }\mathbf{\theta }+d_i)}.$$

${\mathrm{P}}_i(\mathbf{\theta })$ is the probability of a correct answer $X_i=1$, ${\mathbf{a}}_i$ is the vector of the discrimination parameters, $d_i$ denotes the easiness of the item, and $\mathbf{\theta }$ is the vector of the ability parameters. Items with multiple nonzero parameters ${\mathbf{a}}_i$ measure multiple abilities, the so-called within-item dimensionality (W.-C. Wang & Chen, 2004). If just one discrimination parameter is nonzero for all items, this is called between-item dimensionality. Item parameter estimates are assumed to be precise enough to fix them during testing (Veldkamp & van der Linden, 2002).

The likelihood of a set of observed responses ${\mathbf{x}}_j$ to items $i=1,\dots ,k$ for examinee $j$ with ability ${\mathbf{\theta }}_j$ is the product of the probabilities for the responses (Segall, 1996):

$$L({\mathbf{\theta }}_j|{\mathbf{x}}_j)=\underset{i=1}{\overset{k}{\Pi }}{\mathrm{P}}_i{\left({\mathbf{\theta }}_j\right)}^{x_{\mathrm{ij}}}{\mathrm{Q}}_i{\left({\mathbf{\theta }}_j\right)}^{1-x_{\mathrm{ij}}},$$

where ${\mathrm{Q}}_i({\mathbf{\theta }}_j)=1-{\mathrm{P}}_i({\mathbf{\theta }}_j)$. The values $\hat{\mathbf{\theta }}=({\hat{\theta }}_1,\dots ,{\hat{\theta }}_p)$ that maximize the likelihood function become the ability estimate for ${\mathbf{\theta }}_j$ (Segall, 1996). An iterative search procedure, such as the Newton–Raphson method, is used because the equations for finding maximum likelihood (ML) estimates have no closed-form solution (Segall, 1996). This procedure is described for weighted maximum likelihood (WML) in the appendix. WML estimation, as developed by Tam (1992), reduces the bias in the ML estimates.

Classification Methods

Classification methods determine whether testing can be stopped and which decision is made before the maximum test length (van Groen et al., 2014a). The existing literature about classification methods for MCAT is described, and then a new classification method is proposed.

Existing Multidimensional Classification Methods

Two studies about making classification decisions using MIRT exist. These studies concern MCAT with multiple unidimensional decisions for between-dimensionality (Seitz & Frey, 2013) and the use of the sequential probability ratio test (SPRT) for within-dimensionality (Spray et al., 1997).

MCAT for between-dimensionality

Seitz and Frey (2013) used the SPRT to make multiple unidimensional decisions using the fact that, for between-dimensionality, the multidimensional two-parameter logistic model is a combination of UIRT models (W.-C. Wang & Chen, 2004). Seitz and Frey implemented the SPRT for each dimension. The SPRT (Wald, 1947/1973) was applied to classification testing using IRT by Reckase (1983). A cutoff point is set for the SPRT between adjacent levels with a surrounding indifference region. The region accounts for the uncertainty of the decisions, owing to measurement error, for examinees with an ability close to the cutoff point (Eggen, 1999). Two hypotheses are formulated for the cutoff point, ${\theta }_c$, using the boundaries of the indifference region (Eggen, 1999):

$${\mathrm{H}}_0:{\theta }_j<{\theta }_c-\delta ;$$

$${\mathrm{H}}_a:{\theta }_j>{\theta }_c+\delta ,$$

in which $\delta$ is half the size of the indifference region. The likelihood ratio between the likelihoods after $k$ items for the bounds of the region is calculated (Eggen, 1999):

$$\mathrm{LR}({\theta }_c+\delta ;{\theta }_c-\delta )=\frac{\mathrm{L}({\theta }_c+\delta ;{\mathbf{x}}_j)}{\mathrm{L}({\theta }_c-\delta ;{\mathbf{x}}_j)},$$

in which $\mathrm{L}({\theta }_c+\delta ;{\mathbf{x}}_j)$ and $\mathrm{L}({\theta }_c-\delta ;{\mathbf{x}}_j)$ are calculated using the unidimensional version of Equation 2. Decision rules are used to decide to continue testing or to decide that the student’s ability is below or above the cutoff point (Eggen, 1999):

$$\begin{array}{c}\mathrm{administer}\mathrm{another}\mathrm{item}\mathrm{if}\beta /(1-\alpha )<\mathrm{LR}({\theta }_c+\delta ;{\theta }_c-\delta )<(1-\beta )/\alpha ;\hfill \\ \mathrm{ability}\mathrm{below}{\theta }_c\mathrm{if}\mathrm{LR}({\theta }_c+\delta ;{\theta }_c-\delta )\le \beta /(1-\alpha );\hfill \\ \mathrm{ability}\mathrm{above}{\theta }_c\mathrm{if}\mathrm{LR}({\theta }_c+\delta ;{\theta }_c-\delta )\ge (1-\beta )/\alpha ,\hfill \end{array}$$

where $\alpha$ and $\beta$ specify the acceptable classification error rates (Spray et al., 1997). A maximum test length is set to ensure that testing stops at some point (Eggen, 1999). At this point, the examinee passes the test if the log of Equation 5 is larger than the midpoint of the log of the interval on the first line of Equation 6 (Eggen, 1999) if no decision has been made yet.

Seitz and Frey (2013) implemented the SPRT by setting cut scores, ${\theta }_{\mathrm{cl}}$, for all dimensions $l=1,\dots ,p$, with surrounding indifference regions. The SPRT is calculated for each dimension $p$ using

$$\mathrm{LR}({\theta }_{\mathrm{cl}}+\delta ;{\theta }_{\mathrm{cl}}-\delta )=\frac{\mathrm{L}({\theta }_{\mathrm{cl}}+\delta ,{\hat{\mathbf{\theta }}}_{\mathrm{jc}-l},\mathbf{x})}{\mathrm{L}({\theta }_{\mathrm{cl}}-\delta ,{\hat{\mathbf{\theta }}}_{\mathrm{jc}-l},\mathbf{x})},l=1,\dots ,p,$$

in which ${\theta }_{\mathrm{cl}}-\delta$ and ${\theta }_{\mathrm{cl}}+\delta$ are imputed for dimension $l$ and ${\hat{\mathbf{\theta }}}_{\mathrm{jc}-l}$ denotes the provisional estimates for all dimensions except dimension $l$. Because no decision is required on the other dimensions when making the decision for dimension $l$, ability estimates are imputed for the other dimensions (Seitz & Frey, 2013). In the case of between-dimensionality, Equation 7 reduces to

$$\mathrm{LR}({\theta }_{\mathrm{cl}}+\delta ;{\theta }_{\mathrm{cl}}-\delta )=\frac{\mathrm{L}({\theta }_{\mathrm{cl}}+\delta ;{\mathbf{x}}_j)}{\mathrm{L}({\theta }_{\mathrm{cl}}-\delta ;{\mathbf{x}}_j)},l=1,\dots ,p.$$

If the items load on multiple dimensions, Seitz and Frey’s (2013) method cannot be used because the ratio does not reduce to Equation 8. Furthermore, the method requires an additional decision rule if a decision on all or a set of dimensions is to be obtained. This implies that Seitz and Frey’s method can be used only for between-dimensional tests with no decisions based on multiple or all dimensions.

MCAT for within-dimensionality

Spray et al. (1997) investigated the possibility of using the SPRT for MCAT. They specified a passing rate on a reference test with a standard setting method and obtained an equivalent latent passing score by solving for $\mathbf{\theta }$. The ability values that resulted in the passing rate defined the curve in the multidimensional space that divided the space into two mutually exclusive regions (Spray et al., 1997). Surrounding this curve, the curves denoting the indifference region were formed. According to Spray et al. (1997), the ability values that satisfied these curves did not necessarily result in constant probability values for each item. This implies that the likelihood ratio cannot be updated with a unique value for each item; thus, the SPRT cannot be extended to MCAT.

A Classification Method for Within-Dimensionality

Because the SPRT requires unique values for updating the ratio, a method should be developed that results in unique values if the SPRT is to be applied. The reference composite (RC; Reckase, 2009; M. Wang, 1985, 1986) reduces the multidimensional space to a unidimensional line. By using the RC, the likelihood ratio can be updated with unique values after an extra item is administered.

RC

The RC relates the multidimensional abilities to a unidimensional line in the multidimensional space (Reckase, 2009). This line describes the characteristics of the discrimination parameter matrix for the item set. All $\mathbf{\theta }$ points can be projected on the RC. Using projection, examinees are ranked on the RC. A higher RC value denotes a student who is more able than a lower RC value. Ability as projected on the RC is called proficiency $\xi$. The direction of the RC is given by the eigenvector of the $\mathbf{aa}\mathbf{\prime }$ matrix that corresponds to the largest eigenvalue of this matrix (Reckase, 2009). The $p$ elements of the eigenvector are the direction cosines ${\alpha }_{\xi l}$ for the angle between the RC and the dimension axes. The line is drawn in the multidimensional space through the origin with the direction cosines specifying the precise position. To calculate ${\xi }_j$, a line $L_j$ is drawn through the $\mathbf{\theta }$ point and the origin (Reckase, 2009). The length of ${\mathrm{L}}_j$ for examinee $j$ from the origin to the ${\hat{\mathbf{\theta }}}_j$ point is

$${\mathrm{L}}_j=\sqrt{\sum _{l=1}^p{\hat{\theta }}_{\mathrm{jl}}^2},$$

and the direction cosines for the line are calculated using (Reckase, 2009)

$$\cos {\alpha }_{\mathrm{jl}}=\frac{{\hat{\theta }}_{\mathrm{jl}}}{{\mathrm{L}}_j},l=1,\dots ,p,$$

in which ${\alpha }_{\mathrm{jl}}$ is the angle between axis $l$ and ${\mathrm{L}}_j$. The angle, ${\alpha }_{j\xi }={\alpha }_{\mathrm{jl}}-{\alpha }_{\xi l}$, between ${\mathrm{L}}_j$ and the RC is used to calculate the estimated proficiency ${\hat{\xi }}_j$ on the RC (Reckase, 2009):

$${\hat{\xi }}_j={\mathrm{L}}_j\cos {\alpha }_{j\xi }.$$

Multidimensional decision making using the RC

Using the RC, abilities can be ranked on a unidimensional line. The position of the RC is fixed before administration based on all items in the item pool. By fixing the RC, ability is measured on the same scale for all examinees, and cutoff points can be set.

The SPRT requires specifying a cutoff point, ${\xi }_c$, and the surrounding indifference region. The cutoff point and ${\delta }^{\xi }$ are set on the RC. The boundaries of the indifference region are transformed to $\mathbf{\theta }$ points using

$${\mathbf{\theta }}_{{\xi }_{c+\delta }}=\cos {\mathbf{\alpha }}_{\xi }\times ({\xi }_c+{\delta }^{\xi });$$

$${\mathbf{\theta }}_{{\xi }_{c-\delta }}=\cos {\mathbf{\alpha }}_{\xi }\times ({\xi }_c-{\delta }^{\xi }),$$

where ${\mathbf{\alpha }}_{\xi }$ includes all angles between the RC and the dimension axis. The likelihood ratio in Equation 5 becomes

$$\mathrm{LR}({\mathbf{\theta }}_{{\xi }_{c+\delta }};{\mathbf{\theta }}_{{\xi }_{c-\delta }})=\frac{\mathrm{L}({\mathbf{\theta }}_{{\xi }_{c+\delta }};{\mathbf{x}}_j)}{\mathrm{L}({\mathbf{\theta }}_{{\xi }_{c-\delta }};{\mathbf{x}}_j)},$$

which can be used to make classification decisions with the following decision rules:

$$\begin{array}{c}\mathrm{administer}\mathrm{another}\mathrm{item}\mathrm{if}\beta /(1-\alpha )<\mathrm{LR}({\mathbf{\theta }}_{{\xi }_{c+\delta }};{\mathbf{\theta }}_{{\xi }_{c-\delta }})<(1-\beta )/\alpha ;\hfill \\ \mathrm{ability}\mathrm{below}{\xi }_c\mathrm{if}\mathrm{LR}({\mathbf{\theta }}_{{\xi }_{c+\delta }};{\mathbf{\theta }}_{{\xi }_{c-\delta }})\le \beta /(1-\alpha );\hfill \\ \mathrm{ability}\mathrm{above}{\xi }_c\mathrm{if}\mathrm{LR}({\mathbf{\theta }}_{{\xi }_{c+\delta }};{\mathbf{\theta }}_{{\xi }_{c-\delta }})\ge (1-\beta )/\alpha .\hfill \end{array}$$

Item-Selection Methods

Selecting the correct items is important, because items that are too hard or too easy or provide little information result in tests that do not function well (Reckase, 2009). Several methods are available for MCAT (e.g., Luecht, 1996; Reckase, 2009; Segall, 1996) and for unidimensional computerized classification testing (UCCT; for example, Eggen, 1999; Spray & Reckase, 1994). However, item-selection methods for MCCT are scarce. Seitz and Frey (2013) selected items using Segall’s (1996) method for MCAT for estimating ability. This method is discussed in the next section. Item-selection methods for UCCT are described, and then these methods are adapted for MCCT using Segall’s method.

An Item-Selection Method for MCAT for Ability Estimation

The method that maximizes the determinant of the Fisher information matrix was developed for MCAT to estimate ability (Segall, 1996). This matrix is a measure of the information in the observable variables on the ability parameters (Mulder & van der Linden, 2009). The elements of $p\times p$ matrix $\mathbf{I}(\mathbf{\theta })$ for dimensions $l$ and $m$ are defined as follows (Tam, 1992):

$$\mathrm{I}({\theta }_l,{\theta }_m)=\sum _{i=1}^k\frac{\frac{\partial }{\partial {\theta }_l}{\mathrm{P}}_i\left(\mathbf{\theta }\right)\times \frac{\partial }{\partial {\theta }_m}{\mathrm{P}}_i\left(\mathbf{\theta }\right)}{{\mathrm{P}}_i\left(\mathbf{\theta }\right){\mathrm{Q}}_i\left(\mathbf{\theta }\right)}=\sum _{i=1}^k{a}_{\mathrm{il}}{a}_{\mathrm{im}}{\mathrm{P}}_i\left(\mathbf{\theta }\right){\mathrm{Q}}_i\left(\mathbf{\theta }\right).$$

Segall’s (1996) method is based on the relationship between the information matrix and the estimates’ confidence ellipsoid (Reckase, 2009). The method selects the item that results in the largest decrement in the volume of the confidence ellipsoid (Segall, 1996). As the size of the confidence ellipsoid can be approximated by the inverse of the information matrix, the item is selected that maximizes (Segall, 1996)

$$maxdet(\sum _{i=1}^k\mathrm{I}({\hat{\mathbf{\theta }}}_j,x_{\mathrm{ij}})+\mathrm{I}({\hat{\mathbf{\theta }}}_j,x_{k+1,j})),\mathrm{for}k+1\in V_{k+1},$$

which is the determinant of the information matrix of the administered items and the potential item $k+1$. The next item is administered that, when added to the information matrix, results in the largest determinant of the matrix. This implies that the volume of the confidence ellipsoid is minimized (Reckase, 2009).

Item-Selection Methods for UCAT for Classification Testing

In UCCT, two methods are commonly used in addition to random selection. The first method maximizes Fisher information at the ability estimate by minimizing the confidence interval around the ability estimate using

$$max{\mathrm{I}}_i\left({\hat{\theta }}_j\right),\mathrm{for}i\in {\mathrm{V}}_a,$$

where ${\mathrm{V}}_a$ denotes the set of items still available for administration. The second method maximizes Fisher information at the cutoff point, which results in

$$max{\mathrm{I}}_i\left({\theta }_c\right),\mathrm{for}i\in {\mathrm{V}}_a.$$

In unidimensional settings with the SPRT, maximizing information at the cutoff point is considered the most efficient (Eggen, 1999; Spray & Reckase, 1994).

Item-Selection Methods for MCAT for Classification Testing

Segall’s (1996) method selects the item with the largest determinant of the information matrix at the ability estimate. This method can also be used for MCCT. This method will be referred to as the method that maximizes the determinant of the information matrix at the ability estimate. The method is adapted to select items that maximize on some fixed point on the RC, analogous to the methods for UCCT.

The first new item-selection method for MCCT maximizes the determinant of the information matrix at the projected ability estimate. The rationale is that interest is limited here to the points that fall on the RC but not on the other points in the multidimensional space. The ability estimate is estimated using WML estimation (see the appendix). The estimate can be projected on the RC using Equation 11. To calculate $\mathrm{I}$, ${\hat{\xi }}_j$ is transformed to its corresponding point in the multidimensional space using ${\mathbf{\theta }}_{{\hat{\xi }}_j}=\cos {\mathbf{\alpha }}_{\xi }\times {\hat{\xi }}_j$. The selection function becomes

$$maxdet(\sum _{i=1}^k\mathrm{I}({\mathbf{\theta }}_{{\hat{\xi }}_j},x_{\mathrm{ij}})+\mathrm{I}({\mathbf{\theta }}_{{\hat{\xi }}_j},x_{k+1,j})),\mathrm{for}k+1\in V_{k+1}.$$

The second new item-selection method for MCCT maximizes the determinant of the information matrix at the cutoff point on the RC. This value is on the RC but has to be transformed to the multidimensional $\mathbf{\theta }$ space using

$${\mathbf{\theta }}_c=\cos {\mathbf{\alpha }}_{\xi }\times {\xi }_c.$$

The resulting objective function is

$$maxdet(\sum _{i=1}^k\mathrm{I}({\mathbf{\theta }}_c,x_{\mathrm{ij}})+\mathrm{I}({\mathbf{\theta }}_c,x_{k+1,j})),\mathrm{for}k+1\in V_{k+1}.$$

Simulation Study

The effectiveness and the efficiency of the classification and item-selection methods were investigated using simulations. The results with MCCT were evaluated on well-known characteristics of the unidimensional SPRT. A well-known characteristic of the unidimensional SPRT is that increasing $\alpha$ and $\beta$ often does not influence the accuracy, but shortens the test considerably (Eggen & Straetmans, 2000). Increasing $\delta$ also results in shorter tests, but does not influence accuracy (Eggen & Straetmans, 2000). The three discussed item-selection methods were compared with random selection. It was expected that maximizing the determinant of the information matrix at the ability estimate, the projected ability estimate, or the cutoff point would result in shorter and more accurate tests than random selection.

Simulation Design

An item pool from the ACT Assessment Program, which was used by Ackerman (1994) and Veldkamp and van der Linden (2002), was used to evaluate MCCT. The item pool consisted of 180 items, previously calibrated with a two-dimensional compensatory IRT model with within-dimensionality using NOHARM II (Fraser & McDonald, 1988). The fit of the MIRT model was established (Veldkamp & van der Linden, 2002). The means of the discrimination parameters were 0.422 and 0.454 with standard deviations 0.268 and 0.198. The observed correlation between the parameters was .093, which is explained by the orthogonal constraint in the calibration. The mean of the easiness parameter was −0.118 with a standard deviation of 0.568. The matrix of the discrimination parameters resulted in angles between the Dimension Axes 1 and 2 with the RC of 44.621 and 45.379 degrees.

Simulations were run for four item-selection methods: random selection (RA) and maximization of information at the cutoff point (CP), the projected ability estimate (PA), and the ability estimate (AE). The maximum test length was set at 50 items, following Veldkamp and van der Linden (2002). The acceptable decision error rates $\alpha$ and $\beta$ were set at 0.05 and 0.10 with $\delta =0.1,0.2,\mathrm{and}0.3$. The chosen values for $\alpha$ and $\beta$ are commonly found in UCCT. In each condition, 1,000 simulees were generated from a multivariate standard-normal distribution. The correlation between the dimensions was varied, $\rho =0.0,0.3,\mathrm{and}0.6$. The cutoff point was set at $0.0$ on the RC, which implied ${\mathbf{\theta }}_{{\xi }_c}=\{0.0,0.0\}$, which was the midpoint of the ability distribution. Each simulation condition was replicated 100 times.

A well-known characteristic of the unidimensional SPRT is that as ability becomes closer to the cutoff point, the test length increases (Eggen & Straetmans, 2000), and the proportion of correct decisions (PCD) nears 0.5 (van Groen & Verschoor, 2010). Additional simulations were run to investigate the effect of the distance between ability and the cutoff point. This study used 372,100 simulees: 100 at each of 61 evenly spaced points on ${\theta }_1$ from $-3$ to $3$ with the same number of points on ${\theta }_2$. The maximum test length was set at 50 items. $\alpha =\beta =0.10$, $\delta =0.20$, the cutoff point was set at $0.0$, and the items were selected by CP.

The classifications using multidimensional and unidimensional IRT were compared in a third simulation series. Although a two-dimensional model was required for model fit, which implied the use of MCCT, a comparison was made with UCCT. One hundred thousand simulees were generated using a multivariate standard-normal distribution with $\rho =0.0$. For each simulee, 180 responses were generated. The cutoff point for the true classification of each simulee was set at the 50th percentile of the observed proficiency distribution on the RC. These true proficiencies were computed based on the true abilities. The same cutoff point was used as the cutoff point for the MCCT. This observed distribution was also used to compute $\delta$ for the MCCT. In all, 1.25, 2.50, and 5.00 percentile points were added and subtracted from the cutoff point to compute $\delta$. $\alpha$ and $\beta$ were set at 0.05 and 0.10. Because the size of the indifference regions and the cutoff points are different in the third simulation series, the results for these simulations are not necessarily comparable with the results of Simulation Series 1 and 2. After 180 responses were generated per simulee, a maximum of 50 items were selected for each simulee RA, AE, and CP.

The classifications with multidimensional and unidimensional IRT were compared. Unidimensional item parameters were obtained for the generated multidimensional data set using BILOG. The cutoff point and $\delta$ were generated using the 50th percentile of the estimated ability distribution based on 180 items per simulee. $\delta$ was calculated using this distribution, and the same percentile points as for MCAT were added and subtracted. Comparability between the UCAT and MCAT simulations was ensured by using the same distribution percentiles to compute the cutoff points and the values for $\delta$. Items were selected in the unidimensional case by RA, AE, and CP.

Dependent Variables

The efficiency of MCCT was evaluated with the average test length (ATL), which was calculated per condition as the mean test length over 100 replications with each 1,000 simulees. Although reducing the test length reduces respondent burden, test development costs, and test administration costs, effectiveness was considered more important. Effectiveness was investigated using the PCD, which was calculated per condition as the mean of the PCD for each simulation over 100 replications. The PCD compared the true classification based on the true proficiency, with the decision by the SPRT. The PCD for UCCT compared the true classifications based on the proficiency on the RC with the observed classifications.

Simulation Results

Table 1 presents the ATL for different SPRT settings and the four selection methods. The performance of RA, AE, PA, and CP was evaluated. RA resulted in the highest ATL. CP resulted in the lowest ATL. An increase in $\alpha$ and $\beta$ decreased the ATL with several items. An increase in $\delta$ resulted in a lower ATL. If $\rho$ was increased, the ATL decreased.

Table 1.

Average Test Length for Different SPRT Settings and Item-Selection Methods.

$\rho =.05$	$\alpha =0.05$			$\alpha =0.10$
	$\delta =0.1$	$\delta =0.2$	$\delta =0.3$	$\delta =0.1$	$\delta =0.2$	$\delta =0.3$
Random item selection
0.0	50.000	48.404	43.598	49.916	45.303	38.431
0.3	49.999	47.778	42.383	49.850	44.217	36.949
0.6	49.998	47.186	41.324	49.752	43.218	35.725
Item selection by maximization at the ability estimate
0.0	49.996	43.165	35.065	48.792	37.411	28.624
0.3	49.993	41.819	33.541	48.341	35.918	27.318
0.6	49.989	40.785	32.310	47.887	34.674	26.188
Item selection by maximization at the projected estimate
0.0	49.990	43.362	35.359	48.898	37.673	28.893
0.3	49.992	43.911	35.965	49.165	38.261	29.824
0.6	49.981	43.045	34.890	48.952	37.160	28.739
Item selection by maximization at the cutoff point
0.0	49.531	40.851	32.337	47.269	34.733	25.840
0.3	49.234	39.264	30.660	46.268	33.022	24.230
0.6	48.901	37.815	29.120	45.399	31.541	22.956

Note. SPRT = sequential probability ratio test; $\rho$ = correlation between the abilities; $\alpha =\beta$ = acceptable error rates; $\delta$ = distance between the cutoff point and the boundary of indifference region.

The effectiveness of the classification method is shown in Table 2. The PCD is given for simulations with different SPRT settings and four item-selection methods. RA was the least accurate method. The PCD was lower for the simulations with $\alpha =\beta =.05$ than was specified beforehand. The simulations with the other three item-selection methods were more accurate, and the differences between them were negligible. $\alpha$, $\beta$, and $\delta$ appeared to have no influence on the PCD. If the $\rho$ was higher, the PCD was higher.

Table 2.

Proportion of Correct Decisions for Different SPRT Settings and Item-Selection Methods.

$\rho$	$\alpha =0.05$			$\alpha =0.10$
	$\delta =0.1$	$\delta =0.2$	$\delta =0.3$	$\delta =0.1$	$\delta =0.2$	$\delta =0.3$
Random item selection
0.0	0.865	0.866	0.868	0.866	0.867	0.867
0.3	0.880	0.882	0.882	0.883	0.882	0.882
0.6	0.892	0.894	0.893	0.893	0.893	0.890
Item selection by maximization at the ability estimate
0.0	0.895	0.896	0.897	0.895	0.896	0.895
0.3	0.908	0.907	0.906	0.909	0.908	0.908
0.6	0.918	0.917	0.918	0.916	0.915	0.915
Item selection by maximization at the projected estimate
0.0	0.896	0.895	0.895	0.897	0.895	0.894
0.3	0.903	0.901	0.904	0.904	0.904	0.901
0.6	0.910	0.912	0.912	0.912	0.912	0.911
Item selection by maximization at the cutoff point
0.0	0.898	0.896	0.898	0.897	0.898	0.897
0.3	0.909	0.910	0.909	0.908	0.910	0.909
0.6	0.919	0.920	0.918	0.917	0.919	0.919

Note. SPRT = sequential probability ratio test; $\rho$ = correlation between the abilities; $\alpha =\beta$ = acceptable error rates; $\delta$ = distance between the cutoff point and boundary of the indifference region.

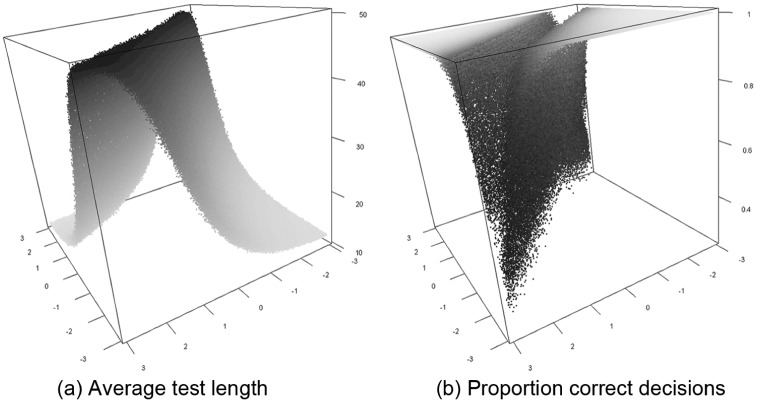
Simulations were run to investigate whether the ATL and the PCD depended in the same way on the distance between ability and the cutoff point as in UCAT. In Figure 1, the ATL and the PCD are shown for different combinations of ability. The ATL increased considerably when the projection of the ability on the RC was close to the cutoff point and the PCDs decreased considerably and became close to 0.50 or lower.

Figure 1.

Average test length and proportion of correct decisions with maximization at the cutoff point.

The ATL is shown in Table 3 for simulations in which classifications with UCAT and MCAT were compared for tests with a flexible test length. The ATL for the UCAT simulations was often lower than for the MCAT simulations. RA resulted in the highest ATL and CP in the lowest ATL. As shown in Table 4, the shorter UCAT tests were accompanied by a lower PCD than for MCAT. The decisions with MCAT and an information-based item-selection approach resulted in 5% higher accuracy than in UCAT. MCAT combined with CP resulted in the most accurate decisions followed by AE. RA resulted in 3% less accurate decisions for MCAT. In contrast, RA resulted in the most accurate decisions for UCAT, followed by CP.

Table 3.

Average Test Length for Different SPRT Settings for UCCT and MCCT.

Condition	$\alpha =0.05$			$\alpha =0.10$
	${\delta }^{*}=1.25$	${\delta }^{*}=2.50$	${\delta }^{*}=5.00$	${\delta }^{*}=1.25$	${\delta }^{*}=2.50$	${\delta }^{*}=5.00$
Random item selection
MIRT	50.000	50.000	49.961	50.000	50.000	49.378
UIRT	50.000	50.000	49.772	50.000	50.000	48.474
Item selection by maximization at the ability estimate
MIRT	50.000	50.000	49.384	50.000	50.000	46.280
UIRT	50.000	50.000	48.044	50.000	49.979	45.116
Item selection by maximization at the cutoff point
MIRT	50.000	50.000	47.944	50.000	49.945	44.041
UIRT	50.000	49.855	43.902	50.000	48.730	38.366

Note. Simulations for classifications with UIRT and MIRT with a flexible test length. SPRT = sequential probability ratio test; UCCT = unidimensional computerized classification testing; MCCT = multidimensional computerized classification testing; MIRT = multidimensional item response theory; UIRT = unidimensional item response theory; $\alpha =\beta$ = acceptable error rates; ${\delta }^{*}$ = percentile point that was used to calculate the boundary of the indifference region.

Table 4.

Proportion of Correct Decisions for Different SPRT Settings for UCCT and MCCT.

Condition	$\alpha =0.05$			$\alpha =0.10$
	${\delta }^{*}=1.25$	${\delta }^{*}=2.50$	${\delta }^{*}=5.00$	${\delta }^{*}=1.25$	${\delta }^{*}=2.50$	${\delta }^{*}=5.00$
Random item selection
MIRT	0.865	0.866	0.865	0.866	0.865	0.865
UIRT	0.850	0.851	0.851	0.848	0.850	0.850
Item selection by maximization at the ability estimate
MIRT	0.894	0.894	0.894	0.894	0.894	0.894
UIRT	0.837	0.838	0.837	0.837	0.837	0.837
Item selection by maximization at the cutoff point
MIRT	0.895	0.895	0.895	0.895	0.895	0.895
UIRT	0.845	0.845	0.845	0.845	0.845	0.845

Note. Simulations for classifications with UIRT and MIRT with a flexible test length. SPRT = sequential probability ratio test; UCCT = unidimensional computerized classification testing; MCCT = multidimensional computerized classification testing; MIRT = multidimensional item response theory; UIRT = unidimensional item response theory; $\alpha =\beta$ = acceptable error rates; ${\delta }^{*}$ = percentile point that was used to calculate the boundary of the indifference region.

Discussion of the Results

The main aim of the simulations was to investigate whether typical SPRT characteristics for UCAT also applied to the SPRT for MCAT. An increase of $\alpha$ and $\beta$ in the SPRT for UCAT led to shorter tests, but accuracy was not influenced (Eggen & Straetmans, 2000). The simulations with the SPRT for MCAT demonstrated similar effects on the PCD and the ATL. Another characteristic of the SPRT is that if the indifference region is increased, the ATL decreases, and the PCD is not influenced (Eggen & Straetmans, 2000). The same was found for the SPRT for MCAT. A third characteristic typical of the SPRT is inaccuracy if ability approaches the cutoff point (van Groen & Verschoor, 2010). The simulations showed that the tests were considerably longer if the distance between the cutoff point and proficiency on the RC became very small. In MCAT, this finding applied to all ability values that resulted in proficiency on the RC that was close to the cutoff point.

The simulation results were in line with previous unidimensional findings by Spray and Reckase (1994), Eggen (1999), and Thompson (2009), in which item selection by CP was the most efficient. Selecting items using the CP on the RC resulted in MCAT in the shortest tests. As expected, the other methods outperformed RA.

In the third series, the SPRT for MCAT was compared with the SPRT for UCAT. It might be unexpected that the SPRT resulted, on average, in shorter tests in UCAT. This can be explained by the simpler structure of the likelihoods that are used for the SPRT. The CP resulted in the shortest tests for UCAT and MCAT. Although a reduced test length has a practical value, accuracy is often considered to be more important. MCAT resulted in more accurate decisions than UCAT. For MCAT, the CP resulted, as expected, in the most accurate decisions followed by the AE. Surprisingly, RA resulted in the most accurate classification decisions with the SPRT for UCAT. This is probably the result of optimization at incorrect points on the scale by the information-based methods or the reduced test length. Given the importance of making accurate decisions, if an MIRT model improves model fit for a specific data set, these item parameters should be used to make classifications instead of unidimensional parameters.

Discussion and Conclusion

A classification method was developed to make classification decisions in tests with items that are intended to measure multiple traits. The method can be used in testing situations in which the construct of interest is modeled using an MIRT model. A RC is constructed in the multidimensional space and is used to make classification decisions with the SPRT.

Segall’s (1996) item-selection method was adapted to select items that had the largest determinant of the information matrix at either the cutoff point or the current projected ability estimate. The methods use the $\mathbf{\theta }$-point that corresponds to the intended point on the RC.

For item-selection methods that use an ability estimate, WML estimation was used. WML estimates (Tam, 1992) have a smaller bias than ML estimates. The Newton–Raphson method was used to find the estimates (see the appendix).

Simulations were used to investigate the ATL, the PCD, and the characteristics of the classification method. The efficiency and the accuracy were compared for different item-selection methods and different settings for the classification method. Independent of the settings for the SPRT, the classification method resulted in accurate decisions.

The differences in efficiency and effectiveness between the item-selection methods are small. The settings of the classification method had more influence on the ATL than on the PCD. Tests could be shortened considerably without much effect on the accuracy of the decisions. It was shown that the new classification method had the same characteristics as the unidimensional SPRT; when the projection of ability on the RC becomes close to the cutoff point, test length increases, and the PCD nears 0.5. The settings of the new SPRT had the same influence as in unidimensional IRT.

When compared with the SPRT with unidimensional IRT, the SPRT with MIRT resulted in longer tests but decisions that are more accurate. Given the importance of making accurate classification decisions, the SPRT should be used with MIRT when model fit for the data set is improved by MIRT.

Future Directions and Further Remarks

If the items load on one dimension, the new classification method cannot be used. If each item measures just one dimension, the non-diagonal elements of the $\mathbf{aa}\mathbf{\prime }$ matrix are zero. The eigenvalues and the eigenvectors of such a matrix do not make sense, and its classifications are solely based on the most discriminating dimension. Thus, Seitz and Frey’s (2013) classification method could be used to make classifications for each dimension or the expanded version (van Groen, Eggen, & Veldkamp, 2014b) of that method for making classifications on the entire test.

Simulations were run with an item pool that was calibrated with a two-dimensional model. The classification method can be applied to models with additional dimensions. A fixed test length can also be used.

Decisions were made based on the total set of items administered. Reckase (2009) showed that RCs can be constructed for underlying domains as well. Investigating whether it is possible to classify on these domains as well would be interesting. Such classifications can provide information regarding the level of the examinees for the underlying domains.

The current version of the SPRT is used to classify into one of two levels. It is expected that the method can be adapted to classify examinees into one of multiple levels, such as basic, proficient, and advanced.

The simulations used an item bank in which the dimensions were restricted to be orthogonal at each other. The SPRT can also be used if orthogonality is not assumed. The effects of fitting an orthogonal model and a non-orthogonal model to the same data set should be investigated, and the best fitting model should be used.

A WML estimator was used in the current study. The effectiveness and efficiency of the estimator have not been intensively studied and should be compared with other estimators. If this estimator is used for other studies, the researchers should investigate the appropriateness of using the estimator for their study.

In testing programs, constraints have to be met for the test content, and attention has to be paid to item exposure. The effects of content and exposure control should be investigated before the classification method for within-dimensionality is applied in actual testing programs.

Appendix

Weighted Maximum Likelihood (WML) Estimation

Ability can be estimated using WML. Tam (1992) developed a WML estimator for multidimensional item response theory (MIRT) based on Warm’s (1989) unidimensional WML estimator. It reduces the bias in the estimates (Tam, 1992). In WML estimation, the following equations are solved (Tam, 1992):

$$\frac{\partial }{\partial \mathbf{\theta }}\left[\ln \mathrm{L}(\mathbf{\theta }|\mathbf{x})\right]+\frac{\partial }{\partial \mathbf{\theta }}\left[\ln w\left(\mathbf{\theta }\right)\right]=0,$$

in which the first part denotes the derivatives of the natural logarithm of Equation 2 and the second part the weights that reduce the bias in the estimates. The set of likelihood equations is (Segall, 1996)

$$\frac{\partial }{\partial \mathbf{\theta }}\left[\ln \mathrm{L}(\mathbf{\theta }|\mathbf{x})\right]=\left[\begin{array}{c}\hfill \frac{\partial }{\partial {\theta }_1}\ln \mathrm{L}(\mathbf{\theta }|\mathbf{x})\hfill \\ \multicolumn{1}{c}{⋮}\\ \multicolumn{1}{c}{\frac{\partial }{\partial {\theta }_p}\ln \mathrm{L}(\mathbf{\theta }|\mathbf{x})}\end{array}\right].$$

In the two-parameter MIRT model, the partial derivatives for ${\theta }_l$ reduce to

$$\frac{\partial }{\partial {\theta }_l}[\ln \mathrm{L}(\mathbf{\theta }|\mathbf{x})]=\sum _{i=1}^k{a}_{\mathrm{il}}[x_i-P_i(\mathbf{\theta })]l=1,\dots ,p,$$

in which $a_{\mathrm{il}}$ denotes the discrimination parameter for dimension $l$ for item $i$.

The weighting function that Tam (1992) developed is given by

$$\frac{\partial }{\partial \mathbf{\theta }}\left[\ln w\left(\mathbf{\theta }\right)\right]=-\mathbf{I}\left(\mathbf{\theta }\right)\times \mathbf{B}\left(\mathbf{\theta }\right),$$

in which $\mathbf{B}(\mathbf{\theta })$ denotes the factor that reduces the bias. This factor for dimension $l$ is given by (Tam, 1992)

$$\mathrm{B}({\theta }_l)=\frac{-\mathrm{J}({\theta }_l)}{2\mathrm{I}{({\theta }_l,{\theta }_l)}^2}l=1,\dots ,p,$$

where $\mathrm{J}({\theta }_l)$ is an element of a $p\times 1$ matrix $\mathbf{J}$ (Tam, 1992):

$$\mathrm{J}\left({\theta }_l\right)=\sum _{i=1}^k\frac{(\frac{\partial }{\partial {\theta }_l}{\mathrm{P}}_i\left(\mathbf{\theta }\right)\times \frac{{\partial }^2}{\partial {\theta }_l^2}{\mathrm{P}}_i\left(\mathbf{\theta }\right))}{{\mathrm{P}}_i\left(\mathbf{\theta }\right){\mathrm{Q}}_i\left(\mathbf{\theta }\right)}=\sum _{i=1}^k{a}_{\mathrm{il}}^3{\mathrm{P}}_i\left(\mathbf{\theta }\right){\mathrm{Q}}_i{\left(\mathbf{\theta }\right)}^2-a_{\mathrm{il}}^3{\mathrm{P}}_i{\left(\mathbf{\theta }\right)}^2{\mathrm{Q}}_i\left(\mathbf{\theta }\right).$$

The set of Equations A1 that has to be solved becomes

$$\sum _{i=1}^k{a}_{\mathrm{il}}[x_{\mathrm{ij}}-{\mathrm{P}}_i\left(\mathbf{\theta }\right)]-\sum _{m=1}^p[\mathrm{I}({\theta }_l,{\theta }_m)\times \frac{-\mathrm{J}\left({\theta }_m\right)}{2\mathrm{I}{({\theta }_m,{\theta }_m)}^2}]=0l=1,\dots ,p.$$

The equations for finding the (W)ML estimates have no closed-form solution; therefore, an iterative numerical procedure is used (Segall, 1996). The Newton–Raphson (NR) method and the false positioning method were used here. Segall (1996) used NR to find ML estimates. To find the WML estimates, the procedure was adapted to include the weighting part of Equation A7. The NR method does not converge when the second derivatives of the functions are infinite (Hambleton & Swaminatan, 1985). As an indication of a possible lack of convergence, the difference between iterations is used. A small comparison study showed that the NR method resulted in estimates that were more accurate than those provided by the false positioning method. However, if the NR method did not converge, the estimation algorithm was switched toward the false positioning method. The estimation method also changed if the iteration difference was very large. Both methods are described next.

WML Estimation Using the NR Method

The update function for the NR method for iteration $j+1$ has the general form (Segall, 1996):

$${\mathbf{\theta }}^{(j+1)}={\mathbf{\theta }}^{\left(j\right)}-{\Delta }^{\left(j\right)},$$

in which ${\Delta }^{(j)}$ is described by Segall (1996) as

$${\Delta }^{\left(j\right)}=\frac{f\left(\mathbf{\theta }\right)}{\frac{\partial }{\partial \mathbf{\theta }}\left[f\left(\mathbf{\theta }\right)\right]},$$

in which

$$f\left(\mathbf{\theta }\right)=\frac{\partial }{\partial \mathbf{\theta }}\left[\ln \mathrm{L}(\mathbf{x}|\mathbf{\theta })\right]+\frac{\partial }{\partial \mathbf{\theta }}\left[\ln w\left(\mathbf{\theta }\right)\right],$$

and

$$\frac{\partial }{\partial \mathbf{\theta }}\left[f\left(\mathbf{\theta }\right)\right]=\frac{{\partial }^2}{\partial {\mathbf{\theta }}^2}\left[\ln \mathrm{L}(\mathbf{x}|\mathbf{\theta })\right]+\frac{{\partial }^2}{\partial {\mathbf{\theta }}^2}\left[\ln w\left(\mathbf{\theta }\right)\right].$$

The elements of the second partial derivative for dimension $l$ of the likelihood part in Equation A11 are given by

$$\frac{{\partial }^2}{\partial {\theta }_l^2}\left[\ln \mathrm{L}(\mathbf{\theta }|\mathbf{x})\right]=\frac{\partial }{\partial {\theta }_l}\left[\sum _{i=1}^k{a}_{\mathrm{il}}[x_{\mathrm{ij}}-{\mathrm{P}}_i\left(\mathbf{\theta }\right)]\right]=\sum _{i=1}^k-a_{\mathrm{il}}^2{\mathrm{P}}_i\left(\mathbf{\theta }\right){\mathrm{Q}}_i\left(\mathbf{\theta }\right)l=1,\dots ,p,$$

and the elements of the second partial derivative of the weighting part become

$$\begin{array}{c}\multicolumn{1}{c}{\frac{{\partial }^2}{\partial {\theta }_l^2}\left[\ln w\left(\mathbf{\theta }\right)\right]=\frac{\partial }{\partial {\theta }_l}\left[\sum _{m=1}^p\left(\frac{\mathbf{I}({\theta }_l,{\theta }_m)\times -\mathbf{J}\left({\theta }_m\right)}{2\mathbf{I}{({\theta }_m,{\theta }_m)}^2}\right)\right]}\\ \multicolumn{1}{c}{=\sum _{m=1}^p\frac{2\mathbf{I}({\theta }_l,{\theta }_m)\mathbf{J}\left({\theta }_m\right)\frac{\partial }{\partial {\theta }_l}\left[\mathbf{I}({\theta }_m,{\theta }_m)\right]}{2\mathbf{I}{({\theta }_m,{\theta }_m)}^3}}\\ \multicolumn{1}{c}{-\sum _{m=1}^p\frac{\frac{\partial }{\partial {\theta }_l}\left[\mathbf{I}({\theta }_l,{\theta }_m)\right]\mathbf{J}\left({\theta }_m\right)\mathbf{I}({\theta }_m,{\theta }_m)}{2\mathbf{I}{({\theta }_m,{\theta }_m)}^3}}\\ \multicolumn{1}{c}{-\sum _{m=1}^p\frac{\mathbf{I}({\theta }_l,{\theta }_m)\frac{\partial }{\partial {\theta }_l}\left[\mathbf{J}\left({\theta }_m\right)\right]\mathbf{I}({\theta }_m,{\theta }_m)}{2\mathbf{I}{({\theta }_m,{\theta }_m)}^3}.}\end{array}$$

The remaining elements of Equation A13 are specified by

$$\begin{array}{c}\multicolumn{1}{c}{\frac{\partial }{\partial {\theta }_l}\left[\mathbf{I}({\theta }_l,{\theta }_m)\right]=\sum _{i=1}^k\frac{\partial }{\partial {\theta }_l}\left[a_{\mathrm{il}}{a}_{\mathrm{im}}{\mathrm{P}}_i\left(\mathbf{\theta }\right){\mathrm{Q}}_i\left(\mathbf{\theta }\right)\right]}\\ \multicolumn{1}{c}{=\sum _{i=1}^k{a}_{\mathrm{il}}^2{a}_{\mathrm{im}}{\mathrm{P}}_i\left(\mathbf{\theta }\right){\mathrm{Q}}_i{\left(\mathbf{\theta }\right)}^2-a_{\mathrm{il}}^2{a}_{\mathrm{im}}{\mathrm{P}}_i{\left(\mathbf{\theta }\right)}^2{\mathrm{Q}}_i\left(\mathbf{\theta }\right),}\end{array}$$

and

$$\begin{array}{c}\multicolumn{1}{c}{\frac{\partial }{\partial {\theta }_l}\left[\mathbf{I}({\theta }_m,{\theta }_m)\right]=\sum _{i=1}^k\frac{\partial }{\partial {\theta }_l}\left[a_{\mathrm{im}}^2{\mathrm{P}}_i\left(\mathbf{\theta }\right){\mathrm{Q}}_i\left(\mathbf{\theta }\right)\right]}\\ \multicolumn{1}{c}{=\sum _{i=1}^k{a}_{\mathrm{il}}{a}_{\mathrm{im}}^2{\mathrm{P}}_i\left(\mathbf{\theta }\right){\mathrm{Q}}_i{\left(\mathbf{\theta }\right)}^2-a_{\mathrm{il}}{a}_{\mathrm{im}}^2{\mathrm{P}}_i{\left(\mathbf{\theta }\right)}^2{\mathrm{Q}}_i\left(\mathbf{\theta }\right),}\end{array}$$

and

$$\frac{\partial }{\partial {\theta }_l}\left[\mathbf{J}\left({\theta }_m\right)\right]=\sum _{i=1}^k{a}_{\mathrm{il}}{a}_{\mathrm{im}}^3{\mathrm{P}}_i\left(\mathbf{\theta }\right){\mathrm{Q}}_i{\left(\mathbf{\theta }\right)}^3-4a_{\mathrm{il}}{a}_{\mathrm{im}}^3{\mathrm{P}}_i{\left(\mathbf{\theta }\right)}^2{\mathrm{Q}}_i{\left(\mathbf{\theta }\right)}^2+a_{\mathrm{il}}{a}_{\mathrm{im}}^3{\mathrm{P}}_i{\left(\mathbf{\theta }\right)}^3{\mathrm{Q}}_i\left(\mathbf{\theta }\right).$$

The iterations of the NR procedure continue until the iteration differences become very small (e.g., 0.0001). If the NR method does not converge, the false positioning method can be used.

WML Estimation Using the False Positioning Method

Another numerical iterative procedure for finding the WML estimates is the false positioning method, or regula falsi. This method searches iteratively on an interval consisting of a set of two reasonable values for $\mathbf{\theta }$ (van Ruitenburg, 2006) for each dimension; for example, the vector ${\mathbf{\theta }}_{\mathbf{l}}=-5$ contains reasonable values for the left boundary of the interval and ${\mathbf{\theta }}_{\mathbf{r}}=5$ for the right boundary. The derivative of the WML Equation A10 is calculated for each dimension $m$ using

$$\frac{\partial }{\partial {\theta }_{\mathrm{ml}}}f\left(\mathbf{\theta }\right)=\frac{\partial }{\partial {\theta }_{\mathrm{ml}}}\left[\ln \mathrm{L}(\mathbf{\theta }|\mathbf{x})\right]+\frac{\partial }{\partial {\theta }_{\mathrm{ml}}}\left[\ln w\left(\mathbf{\theta }\right)\right]m=1,\dots ,p,$$

and

$$\frac{\partial }{\partial {\theta }_{\mathrm{mr}}}f\left(\mathbf{\theta }\right)=\frac{\partial }{\partial {\theta }_{\mathrm{mr}}}\left[\ln \mathrm{L}(\mathbf{\theta }|\mathbf{x})\right]+\frac{\partial }{\partial {\theta }_{\mathrm{mr}}}\left[\ln w\left(\mathbf{\theta }\right)\right]m=1,\dots ,p.$$

In each iteration, a straight line is drawn through the points $({\theta }_{\mathrm{ml}};\frac{\partial }{\partial {\theta }_{\mathrm{ml}}}f(\mathbf{\theta }))$ and $({\theta }_{\mathrm{mr}};\frac{\partial }{\partial {\theta }_{\mathrm{mr}}}f(\mathbf{\theta }))$ for each dimension $m$ (van Ruitenburg, 2006). A new replacement point ${\mathbf{\theta }}_s$ is determined for each dimension based on the point where the line meets the dimension axis using (Press, Flannery, Teukolsky, & Vetterling, 1989)

$${\theta }_{\mathrm{ms}}={\theta }_{\mathrm{ml}}-\frac{\frac{\partial }{\partial {\theta }_{\mathrm{ml}}}\left[f\left({\theta }_{\mathrm{ml}}\right)\right]({\theta }_{\mathrm{mr}}-{\theta }_{\mathrm{ml}})}{\frac{\partial }{\partial {\theta }_{\mathrm{mr}}}\left[f\left({\theta }_{\mathrm{mr}}\right)\right]-\frac{\partial }{\partial {\theta }_{\mathrm{ml}}}\left[f\left({\theta }_{\mathrm{ml}}\right)\right]}m=1,\dots ,p.$$

The slopes are calculated at point ${\mathbf{\theta }}_s$ for all dimensions:

$$\frac{\partial }{\partial {\theta }_{\mathrm{ms}}}f\left(\mathbf{\theta }\right)=\frac{\partial }{\partial {\theta }_{\mathrm{ms}}}\left[\ln \mathrm{L}(\mathbf{\theta }|\mathbf{x})\right]+\frac{\partial }{\partial {\theta }_{\mathrm{ms}}}\left[\ln w\left(\mathbf{\theta }\right)\right]m=1,\dots ,p.$$

If the slope for dimension $m$ is positive, point ${\theta }_{\mathrm{ms}}$ replaces the left boundary on the interval for dimension $m$. If the slope is negative, the right boundary is replaced. After replacement, a new point ${\theta }_{\mathrm{ms}}$ is calculated. Iteratively, the procedure is repeated until the size of the interval becomes very small (e.g., $<0.0001$) for each dimension. The point ${\theta }_{\mathrm{ms}}$ is then used as the ability estimate.