New Item Selection Methods for Cognitive Diagnosis Computerized Adaptive Testing

Abstract

This article introduces two new item selection methods, the modified posterior-weighted Kullback–Leibler index (MPWKL) and the generalized deterministic inputs, noisy “and” gate (G-DINA) model discrimination index (GDI), that can be used in cognitive diagnosis computerized adaptive testing. The efficiency of the new methods is compared with the posterior-weighted Kullback–Leibler (PWKL) item selection index using a simulation study in the context of the G-DINA model. The impact of item quality, generating models, and test termination rules on attribute classification accuracy or test length is also investigated. The results of the study show that the MPWKL and GDI perform very similarly, and have higher correct attribute classification rates or shorter mean test lengths compared with the PWKL. In addition, the GDI has the shortest implementation time among the three indices. The proportion of item usage with respect to the required attributes across the different conditions is also tracked and discussed.

Recent developments in psychometrics put an increasing emphasis on formative assessments that can provide more information to improve learning and teaching strategies. In this regard, cognitive diagnosis models (CDMs) have been developed to detect mastery and nonmastery of attributes or skills in a particular content area. In contrast to the unidimensional item response models (IRTs), CDMs provide a more detailed evaluation of the strengths and weaknesses of students (de la Torre, 2009). Computerized adaptive testing (CAT) has been developed as an alternative to paper-and-pencil test, and provides better ability estimation with a shorter and tailored test for each examinee (Meijer & Nering, 1999; van der Linden & Glas, 2000). Most of the research in CAT has been conducted in the traditional IRT context. However, a small number of research has recently been done in the context of cognitive diagnosis computerized adaptive testing (CD-CAT; e.g., Cheng, 2009; Hsu, Wang, & Chen, 2013; McGlohen & Chang, 2008; Wang, 2013; Xu, Chang, & Douglas, 2003).

One of the main components of CAT is the item selection method. By choosing more appropriate methods, better estimates of the examinees’ abilities or attribute vectors can be expected. Because of the discrete nature of attributes, some of the concepts in traditional CAT such as Fisher information are not applicable in CD-CAT. The goal of this study is to introduce two new indices, the modified posterior-weighted Kullback–Leibler index (MPWKL) and the generalized deterministic inputs, noisy “and” gate (G-DINA) model discrimination index (GDI), as item selection methods in CD-CAT, and evaluate their efficiency under the G-DINA framework. Their efficiency is compared with the posterior-weighted Kullback–Leibler index (PWKL; Cheng, 2009). The effects of different factors are also investigated: The item quality is manipulated, reduced versions of the G-DINA model are used for generating item response data, and fixed-test lengths and minimum of the maximum (minimax) of the posterior distribution of attribute vectors (Hsu et al., 2013) are used as stopping rules in the test administration. With respect to the stopping rules, the former provides a comparison of the efficiency of the three indices under different fixed-test lengths, whereas the latter provides tailored tests with different test lengths for each examinee.

The remaining sections of the article are laid out as follows: The next section gives a background in the G-DINA model and its reduced versions. In addition, the item selection indices are discussed, and the use of the GDI as an item selection method is illustrated. In the “Simulation Study” section, the design and the results of the simulation study are presented, and the efficiency of the indices under different conditions is compared. Finally, “Discussion and Conclusion” section presents with a discussion of the findings of this work and directions for future research.

CDMs

CDMs aim to determine whether examinees have or have not mastered a set of specific attributes. The presence or absence of the attributes is represented by a binary vector. Let α_i = {$\mathrm{\alpha }$_ik} be the examinee’s binary attribute vector for $k=1,2,\dots ,K$ attributes. The kth element of the vector is 1 when the examinee has mastered the kth attribute, and it is 0 when the examinee has not mastered it. Similarly, let X_i = {x_ij} be the binary response vector of examinee i for a set of J items in which $i=1,2,\dots ,N$ and $j=1,2,\dots ,J$. In CDM, the required attributes for each item are represented in a Q-matrix (Tatsuoka, 1983), which is a J×K matrix. The element of the jth row and the kth column, q_jk, is 1 if the kth attribute is required to answer the jth item correctly, and 0 otherwise.

A general CDM called generalized deterministic inputs, noisy “and” gate (G-DINA) model was proposed by de la Torre (2011). It is a generalization of the deterministic inputs, noisy “and” gate (DINA; de la Torre, 2009; Haertel, 1989; Junker & Sijtsma, 2001) model, and it relaxes some of the strict assumptions of the DINA model. Instead of two, the G-DINA model partitions examinees into $2^{K_j^{*}}$ groups, where $K_j^{*}$ is the number of required attributes for item j. The mathematical representation of the model consists of the combination of the baseline probability, the main effects due to the attribute k, the interaction effects due to the attributes k and k′ (k≠k′), and other higher order interaction effects (for more details, see de la Torre, 2011).

A few of commonly encountered CDMs are constrained versions of, and therefore, are subsumed by the G-DINA model (de la Torre, 2011). These include the DINA model, the deterministic input, noisy “or” gate (DINO; Templin & Henson, 2006) model, and the additive CDM (A-CDM; de la Torre, 2011). As constrained CDMs, the DINA model assumes that lacking one of the required attributes is as the same as lacking all of the required attributes; the DINO model assumes that having one of the required attributes is as the same as having all of the required attributes; and the A-CDM assumes that the impacts of mastering the different required attributes are independent of each other.

CAT

CAT has become a popular tool to estimate examinees’ ability levels with shorter test lengths. The main goal of CAT is to construct an optimal test for each examinee. Appropriate items to each examinee’s ability level are selected from an item bank, and the ability level is estimated during or end of the test administration. Therefore, different tests including different items with different lengths can be created for different examinees. Weiss and Kingsbury (1984) listed the components of CAT, which include item selection method and calibrated item pool. In addition, CAT can be used with different psychometric frameworks such as IRT or CDM. The Fisher information statistic (Lehmann & Casella, 1998) is widely used in the traditional CAT; however, it cannot be applied in CD-CAT because it requires continuous ability levels, whereas the attribute vectors in cognitive diagnosis are discrete. Fortunately, the Kullback–Leibler (K-L) information, which is an alternative information statistic, can work under both continuous and discrete cases. This study focuses on item selection methods in the cognitive diagnosis context, which include K-L–based indices.

The PWKL

The K-L information is a measure of distance between the two probability density functions, f(x) and g(x), where f(x) is assumed to be the true distribution of the data (Cover & Thomas, 1991). The function measuring the distance between f and g is given by

$$K(f,g)=\int \left[\log \left(\frac{f\left(x\right)}{g\left(x\right)}\right)\right]f\left(x\right)\mathrm{d}x.$$

Larger information allows easier differentiation between the two distributions or likelihoods (Lehmann & Casella, 1998). Xu et al. (2003) used the K-L information as an item selection index in CD-CAT. Cheng (2009) proposed the PWKL, which computes the index using the posterior distribution of the attribute vectors as weights. Her simulation study showed that the PWKL outperformed the K-L information in terms of estimation accuracy. The PWKL is given by

$${\mathrm{PWKL}}_j\left({\stackrel{⌢}{\mathbf{\alpha }}}_i^{\left(t\right)}\right)=\sum _{c=1}^{2^K}\left[\sum _{x=0}^1\log \left(\frac{P\left(X_j=x|{\stackrel{⌢}{\mathbf{\alpha }}}_i^{\left(t\right)}\right)}{P\left(X_j=x|{\mathbf{\alpha }}_c\right)}\right)P\left(X_j=x|{\stackrel{⌢}{\mathbf{\alpha }}}_i^{\left(t\right)}\right){\mathrm{\pi }}_i^{\left(t\right)}\left({\mathbf{\alpha }}_c\right)\right],$$

where P(X_j = x|α_c) is the probability of the response x to item j given the attribute vector α_c, and ${\pi }_i^{(t)}({\mathbf{\alpha }}_c)$ is the posterior probability of examinee i given the responses to the t items. The posterior distribution after tth response can be written as

$${\pi }_i^{\left(t\right)}\left({\mathbf{\alpha }}_c\right)\propto {\pi }_i^{\left(0\right)}\left({\mathbf{\alpha }}_c\right)L({\mathbf{X}}_i^{\left(t\right)}|{\mathbf{\alpha }}_c),$$

where ${\mathbf{X}}_i^{(t)}$ is the vector containing the responses of examinee i to the t items, ${\mathrm{\pi }}_i^{(0)}({\mathbf{\alpha }}_c)$ is the prior probability of α_c, and $L({\mathbf{X}}_i^{(t)}|{\mathbf{\alpha }}_c)$ is the likelihood of ${\mathbf{X}}_i^{(t)}$ given the attribute vector α_c. The (t+ 1)th item to be administered is the item that maximizes the PWKL.

The MPWKL

The PWKL is calculated by summing the distances between the current estimate of the attribute vector and the other possible attribute vectors using the K-L information, and it is weighted by the posterior distribution of the attribute vectors. By using the current estimate ${\stackrel{⌢}{\mathrm{\alpha }}}_i^{(t)}$, it assumes that the point estimate is a good summary of the posterior distribution ${\mathrm{\pi }}_i^{(t)}(\mathrm{\alpha })$. However, this may not be the case particularly when the test is still relatively short. Instead of using a point estimate, the new PWKL propose modifying by considering the entire posterior distribution, which involves 2^K attribute vectors. The resulting new index can be referred to as the MPWKL and can be computed as

$${\mathrm{MPWKL}}_{\mathrm{ij}}^{\left(t\right)}=\sum _{d=1}^{2^K}\left[\sum _{c=1}^{2^K}\left[\sum _{x=0}^1\log \left(\frac{P(X_j=x|{\mathbf{\alpha }}_d)}{P(X_j=x|{\mathbf{\alpha }}_c)}\right)P(X_j=x|{\mathbf{\alpha }}_d){\mathrm{\pi }}_i^{\left(t\right)}\left({\mathbf{\alpha }}_c\right)\right]{\mathrm{\pi }}_i^{\left(t\right)}\left({\mathbf{\alpha }}_d\right)\right].$$

Compared with the PWKL, by using the posterior distribution, the MPWKL does not require estimating the attribute vector ${\mathbf{\alpha }}_i^{(t)}$. Using an estimate in the numerator of Equation 2 is tantamount to assigning a single attribute vector (i.e., ${\stackrel{⌢}{\mathbf{\alpha }}}_i^{(t)}$) a probability of 1, which may not accurately describe the posterior distribution at the early stages of the testing administration. In contrast, the numerator in Equation 3 considers all the possible attribute vectors, and weights them accordingly, hence, the extra summation and posterior probability. Because the MPWKL uses the entire posterior distribution ${\mathrm{\pi }}_i^{(t)}(\mathbf{\alpha })$ rather than just an estimate ${\stackrel{⌢}{\mathbf{\alpha }}}_i^{(t)}$, it can be expected to be more informative than the PWKL.

The GDI

The GDI, which measures the (weighted) variance of the probabilities of success of an item given a particular attribute distribution, was first proposed by de la Torre and Chiu (2010) as an index to implement an empirical Q-matrix validation procedure. However, in this article, the index is used as an item selection method for CD-CAT. To define the index, let the first $K_j^{*}$ attributes be required for item j, and define ${\mathbf{\alpha }}_{\mathrm{cj}}^{*}$ as the reduced attribute vector consisting of the first $K_j^{*}$ attributes, for $c=1,2,\dots ,2^{K_j^{*}}$. For example, if a q-vector is defined as (1,1,0,0,1) for $K_j^{*}=3$ number of required attributes, the reduced attribute vector is ($\mathrm{\alpha }$₁,$\mathrm{\alpha }$₂,$\mathrm{\alpha }$₅). Also, define $\mathrm{\pi }({\mathbf{\alpha }}_{\mathrm{cj}}^{*})$ as the probability of ${\mathbf{\alpha }}_{\mathrm{cj}}^{*}$, and $P(X_{\mathrm{ij}}=1|{\mathbf{\alpha }}_{\mathrm{cj}}^{*})$ as the success probability on item j given ${\mathbf{\alpha }}_{\mathrm{cj}}^{*}$. The GDI for item j is defined as

$${\varsigma }_j^2=\sum _{c=1}^{2^{K_j^{*}}}\pi \left({\mathbf{\alpha }}_{\mathrm{cj}}^{*}\right){[P(X_{\mathrm{ij}}=1|{\mathbf{\alpha }}_{\mathrm{cj}}^{*})-{\overline{P}}_j]}^2,$$

where ${\overline{P}}_j=\sum _{c=1}^{2^{K_j^{*}}}\mathrm{\pi }({\mathbf{\alpha }}_{\mathrm{cj}}^{*})P(X_{\mathrm{ij}}=1|{\mathbf{\alpha }}_{\mathrm{cj}}^{*})$ is the mean success probability. In CD-CAT applications, the posterior probability of the reduced attribute vector ${\pi }_i^{(t)}({\mathbf{\alpha }}_{\mathrm{cj}}^{*})$ is used in place of $\mathrm{\pi }({\mathbf{\alpha }}_{\mathrm{cj}}^{*})$. This implies that the discrimination of an item is not static, and changes as the posterior distribution changes with t. The GDI measures the extent to which an item can differentiate between the different reduced attribute vectors based on their success probabilities, and is minimum (i.e., equal to zero) when $P(X_{\mathrm{ij}}=1|{\mathbf{\alpha }}_{1j}^{*})=P(X_{\mathrm{ij}}=1|{\mathbf{\alpha }}_{2j}^{*})=P(X_{\mathrm{ij}}=1|{\mathbf{\alpha }}_{2^{K_j^{*}}j}^{*})={\overline{P}}_j$ (or, trivially, when the posterior distribution is degenerate). It also attaches greater importance to reduced attribute vectors with higher π(·). As such, a larger GDI indicates a greater ability to differentiate between reduced attribute vectors that matter. The GDI is computed for each candidate item in the pool, and the candidate item with the largest GDI is selected.

The GDI has two important properties. First, instead of the original attribute vector, α_c, it uses the reduced attribute vector, ${\mathrm{\alpha }}_{\mathrm{cj}}^{*}$. Consequently, the GDI can be implemented more efficiently than can the PWKL or MPWKL. For example, if K = 5 and $K_j^{*}=2$, computing the GDI involves $2^{K_j^{*}}=4$ terms, whereas the PWKL and MPWKL involve 2^K = 32 and 2^K× 2^K = 1,024 terms, respectively.

Second, the GDI takes both the item discrimination and the posterior distribution into account. This property is illustrated using the example in Table 1. It involves K = 3, and six items, three of which are of low discrimination (LD), and the other three are of high discrimination (HD). For the low-discriminating items, the difference between the lowest and the highest probabilities of success is .4; for the high-discriminating items, this difference is .8. In addition, these items involve one of the following q-vectors: q₁₀₀, q₁₁₀, and q₁₁₁. Four distributions are considered: (1) all attribute vectors are equally probable, as in, π(α_c) = 0.125; in (2), (3), and (4), the attribute vector, namely, (1,0,0), (1,1,0), or (1,1,1), respectively, has a probability of .965 and was deemed dominant, whereas each of the remaining attribute vectors has a probability of .005. In Condition 1, the impact of the posterior distribution is discounted, whereas in Conditions 2, 3, and 4, one-attribute vector is highly dominant. In this table, the GDI was computed using the DINA model.

Table 1.

GDIs for Different Distribution, Item Discrimination, and Q-Vectors.

Condition	Dominant	Low discrimination			High discrimination
	α	q 100	q 110	q 111	q 100	q 110	q 111
1	None	0.090	0.068	0.039	0.160	0.120	0.070
2	(1,0,0)	0.007	0.004	0.002	0.013	0.006	0.003
3	(1,1,0)	0.007	0.010	0.002	0.013	0.019	0.003
4	(1,1,1)	0.007	0.010	0.012	0.013	0.019	0.022

Note. Numbers in bold represent the highest GDI in each condition for fixed item discrimination. GDI = G-DINA model discrimination index; G-DINA = generalized DINA; DINA = deterministic inputs, noisy “and” gate.

Several results can be noted. First, for a fixed q-vector, the high-discriminating items had higher GDI values compared with the low-discriminating items regardless of the posterior distribution. Second, when there was no dominant attribute vector, one-attribute items had the highest GDI values for a fixed item discrimination. In contrast, when one-attribute vector was highly dominant, the items with q-vectors matching the dominant attribute vectors had the highest GDI values. Finally, it can also be observed that the low-discriminating items with q-vectors that match the dominant attribute vectors can at times be preferred over the high-discriminating items with q-vectors that do not. For example, for attribute vector (1,1,0), the GDI for the low-discriminating item with q₁₁₀ is 0.010. This is higher than the GDI for the high-discriminating item with q₁₁₁, which is 0.003.

Based on the properties of the three indices discussed earlier, the authors expect the GDI and the MPWKL will be more informative than the PWKL. In addition, they expect the GDI to be faster than the PWKL in terms of implementation time, which in turn will be faster than MPWKL.

Simulation Study

The simulation study aimed to investigate the efficiency of the MPWKL and the GDI compared with the PWKL under the G-DINA model context considering a variety of factors, namely, item quality, generating model, and test termination rule. The correct attribute and attribute vector classification rates, and a few descriptive statistics (i.e., minimum, maximum, mean, and coefficient of variation [CV]), of the test lengths were calculated based on the termination rules to compare the efficiency of the item selection indices. In addition, the time required to administer the test was also recorded for each of the item selection indices. Finally, the item usage in terms of the required attributes was tracked and reported in each condition.

Design

Data generation

Different item qualities and reduced CDMs were considered in the data generation. First, due to documented impact of item quality on attribute classification accuracy (e.g., de la Torre, Hong, & Deng, 2010), different item discriminations and variances were used in the data generation. Two levels of item discrimination, HD and LD, were combined with two levels of variance, high variance (HV) and low variance (LV), in generating the item parameters. Thus, a total of four conditions, HD-LV, HD-HV, LD-LV, and LD-HV, were considered in investigating the impact of item quality on the efficiency of the indices. The item parameters were generated from uniform distributions. For HD items, the highest and lowest probabilities of success, P(0) and P(1), were generated from distributions with means of .1 and .9, respectively; for LD items, these means were 0.2 and 0.8. For HV and LV items, the ranges of the distribution were 0.1 and 0.2, respectively. The distributions for P(0) and P(1) under different discrimination and variance conditions are given in Table 2. The mean of the distribution determines the overall quality of the item pool, whereas the variance determines the overall quality of the administered items.

Table 2.

Item Parameters.

Item quality	P(0)	P(1)
HD-LV	U(0.05, 0.15)	U(0.85, 0.95)
HD-HV	U(0.00, 0.20)	U(0.80, 1.00)
LD-LV	U(0.15, 0.25)	U(0.75, 0.85)
LD-HV	U(0.10, 0.30)	U(0.70, 0.90)

Note. HD-LV = high discrimination–low variance; HD-HV = high discrimination–high variance; LD-LV = low discrimination–low variance; LD-HV = low discrimination–high variance.

Second, to investigate whether the efficiency of the indices is consistent across different models, item responses were generated using three reduced models: the DINA model, the DINO model, and the A-CDM. For the DINA and DINO models, the probability of success was set as shown in Table 2. For the A-CDM, in addition to the success probabilities given in Table 2, intermediate success probabilities were obtained by allowing each of the required attributes to contribute equally. The four item qualities and three reduced models resulted in the 12 conditions of the simulation study. The number of attributes was fixed to K = 5.

To design a more efficient simulation study, only a subset of the attribute vectors was considered. The six attribute vectors were α₀ = (0, 0, 0, 0, 0), α₁ = (1, 0, 0, 0, 0), α₂ = (1, 1, 0, 0, 0), α₃ = (1, 1, 1, 0, 0), α₄ = (1, 1, 1, 1, 0), and α₅ = (1, 1, 1, 1, 1), representing no mastery, mastery of a single attribute only, mastery of two attributes only, and so forth. For each attribute vector, 1,000 examinees were generated for a total of 6,000 examinees in each condition.

Test termination rules

Two test termination rules were considered in the simulation study: fixed-test lengths and minimax of the posterior distribution of the attribute vectors. The former allowed for a comparison of the efficiency of the indices with respect to classification accuracy when the CAT administration was stopped after a prespecified test length was reached for each examinee; the latter allowed for the comparison of the efficiency of the indices in terms of test lengths when the CAT administration was terminated after the largest posterior probability of an attribute vector was at least as large as a prespecified minimax value, which corresponds to the first criterion by Hsu et al. (2013). Three fixed-test lengths, 10, 20, and 40 items, were considered for the first termination rule, and four minimax values, 0.65, 0.75, 0.85, and 0.95, were used for the second rule.

Item pool and item selection methods

The Q-matrix was created to have 40 items from each of 2^K− 1 = 31 possible q-vectors, resulting in 1,240 items in the pool. Three different item selection indices were considered: PWKL, MPWKL, and GDI. For greater comparability, the first item administered to each examinee was chosen at random, and this item was fixed across the three indices. In the case of PWKL, when ${\stackrel{⌢}{\mathbf{\alpha }}}_i^{(t)}$ was not unique, a random attribute vector was chosen from the modal attribute vectors.

Let $\mathrm{\alpha }$_ikl and ${\hat{\mathrm{\alpha }}}_{\mathrm{ikl}}$ be the kth true and estimated attribute in attribute vector l for examinee i, respectively. For each of the six attribute vectors considered in this design, the correct attribute classification (CAC) rates, and the correct attribute vector classification (CVC) rates were computed as

$$\mathrm{CA}{\mathrm{C}}_l=\frac{1}{1,000}\sum _{i=1}^{1,000}\sum _{k=1}^{5}I[{\mathrm{\alpha }}_{\mathrm{ikl}}={\hat{\mathrm{\alpha }}}_{\mathrm{ikl}}],$$

and

$$\mathrm{CV}{\mathrm{C}}_l=\frac{1}{1,000}\sum _{i=1}^{1,000}\underset{k=1}{\overset{5}{\Pi }}I[{\mathrm{\alpha }}_{\mathrm{ikl}}={\hat{\mathrm{\alpha }}}_{\mathrm{ikl}}],$$

where $l=0,1,\dots ,5$, and I is the indicator function. Using appropriate weights (described later), the CAC and CVC were computed assuming the attributes were uniformly distributed for the fixed-test length conditions. The minimum, maximum, mean, and CV of the test lengths were calculated, again with appropriate weights where needed, when the minimax of the posterior distribution was used as the stopping criterion. This study focused on attribute vectors that were uniformly distributed. To accomplish this, the results based on the six attribute vectors needed to be weighted appropriately. For K = 5, the vector of the weights are 1/32, 5/32, 10/32, 10/32, 5/32, and 1/32, which represented the proportions of zero-, one-, two-, three-, four-, and five-attribute mastery vectors among the 32 attribute vectors. CV was calculated by taking the ratio of the standard deviation to the mean.

Results

Fixed-Test Length

The sampling design of this simulation study can allow for results to be generalized to different distributions of the attribute vectors. This study focused on attribute vectors that were uniformly distributed. To demonstrate the efficiency of using such a design, a small study comparing two sampling procedures for the DINA model with HD-LV items was carried out. In the first procedure, which is the current sampling design, only six selected attribute vectors, each with 1,000 replicates, were used; in the second procedure, 32,000 attribute vectors were generated uniformly. The CAC and the CVC in the former and the latter were computed using weighted and simple averages, respectively. Table 3 shows that despite working with fewer attribute vectors, using selected attribute vectors can give the CAC and the CVC that were almost identical to those obtained using a much larger sample drawn randomly, and this was true across the different test lengths. These findings can be expected to hold across other CDMs and item qualities.

Table 3.

Classification Accuracies Based on Two Sampling Procedures.

		CAC		CVC
Item quality	J	Weighted	Simple	Weighted	Simple
HD-LV	10	0.969	0.969	0.875	0.876
	20	0.999	0.999	0.996	0.996
	40	1.000	1.000	1.000	1.000

Note. CAC = correct attribute classification; CVC = correct attribute vector classification; HD-LV = high discrimination–low variance.

For all conditions, the CAC rates were, as expected, higher than the CVC rates, but both measures showed similar patterns. For this reason, only the CVC rates were reported in this article. However, the results in their entirety can be requested from the first author. The CVC results using fixed-test lengths as a stopping rule under the different factors are presented in Table 4 for all the generating models. Differences in the CVC rates were evaluated using two cut points, 0.01 and 0.10. Differences below 0.01 were considered negligible, between 0.01 and 0.10 were considered slight, and above 0.10 were considered substantial.

Table 4.

CVC Rates.

		DINA			DINO			A-CDM
Item quality	J	PWKL	MPWKL	GDI	PWKL	MPWKL	GDI	PWKL	MPWKL	GDI
HD-LV	10	0.752	0.878	0.887	0.749	0.855	0.849	0.839	0.817	0.826
	20	0.989	0.996	0.996	0.986	0.995	0.996	0.992	0.992	0.991
	40	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
HD-HV	10	0.854	0.979	0.981	0.870	0.979	0.981	0.963	0.967	0.962
	20	0.999	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
	40	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
LD-LV	10	0.454	0.589	0.604	0.441	0.551	0.557	0.515	0.524	0.511
	20	0.814	0.892	0.890	0.803	0.872	0.871	0.855	0.857	0.859
	40	0.987	0.995	0.995	0.984	0.993	0.992	0.987	0.990	0.990
LD-HV	10	0.569	0.723	0.719	0.596	0.703	0.704	0.658	0.666	0.660
	20	0.917	0.962	0.962	0.924	0.969	0.966	0.948	0.953	0.951
	40	0.999	1.000	0.999	1.000	1.000	1.000	0.998	0.999	0.999

Note. CVC = correct attribute vector classification; DINA = deterministic inputs, noisy “and” gate; DINO = deterministic input, noisy “or” gate; A-CDM = additive CDM; CDM = cognitive diagnosis model; PWKL = posterior-weighted Kullback–Leibler index; MPWKL = modified posterior-weighted Kullback–Leibler index; GDI = G-DINA model discrimination index; G-DINA = generalized DINA; HD-LV = high discrimination–low variance; HD-HV = high discrimination–high variance; LD-LV = low discrimination–low variance; LD-HV = low discrimination–high variance.

Using the DINA and the DINO as generating models in conjunction with a short test length (i.e., 10 items), the differences in the CVC rates of the MPWKL and the GDI were mostly negligible regardless of the item quality. The only exception is the one condition, with 10 LD-LV items, where the CVC rate of the GDI was slightly higher than the MPWKL. Under the same conditions, the CVC rates of the two indices were substantially higher than the PWKL regardless of the item quality. When the test lengths were longer (i.e., 20- and 40-item tests), all of the three indices generally performed similarly using the DINA and DINO models. However, in one condition (i.e., 20-item test with LD items and the DINA model), the MPWKL and the GDI had slightly higher CVC rates compared with the PWKL.

Using the A-CDM as a generating model, the three indices had mostly similar CVC rates. Interestingly, using 10-item tests with HD-LV items, the PWKL had slightly higher CVC rates compared with the MPWKL and the GDI.

Additional findings can be culled from Table 4. First, as expected, increasing the test length improved the classification accuracy regardless of the item selection index, item quality, and generating model. Using a long test (i.e., 40-item test) provided a CVC rate of almost 1.00 for all of the indices. However, a clear distinction can be seen on the efficiency of the indices when shorter test lengths, in particular 10-item test, were used. For example, using the DINA model and HD-LV items, the 10-item test yielded a maximum CVC rate of 0.89 for the MPWKL and the GDI. In comparison, the PWKL had only a CVC rate of 0.75 under the same condition.

Second, the item quality had an obvious impact on the CVC rates: higher discrimination and higher variance resulted in higher classification accuracy. As can be seen from the results, HD items resulted in better rates compared with LD items regardless of the variance. Similarly, items with HV showed higher classification rates compared with LV items. Consequently, HD-HV items had the best classification accuracy, whereas LD-LV items had the worst classification accuracy regardless of the item selection index and generating model. To illustrate, using the DINA model and a 10-item test, the highest and the lowest CVC rates of 0.98 and 0.60, were obtained with HD-HV and LD-LV items, respectively, for both the MPWKL and GDI; in comparison, the CVC rates were 0.85 and 0.45 for HD-HV and LD-LV items, respectively, for the PWKL.

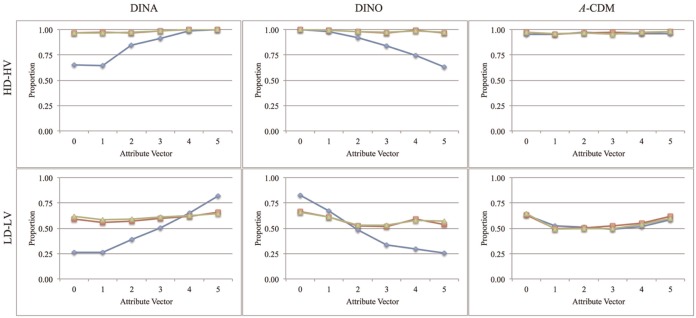
To investigate how the item selection indices behaved for different attribute vectors, the CVC rates for each attribute vector were calculated. Only the results for 10-item test with HD-HV and LD-LV items are presented (see Figure 1). Across the different item quality conditions, the CVC rates of the MPWKL and GDI were more similar for the different attribute vectors, whereas they were more varied for the PWKL. A few conclusions can be drawn from this figure. First, for HD-HV items, the indices performed similarly for α₄ and α₅ when the DINA model was used. However, under the same condition, the MPWKL and the GDI had higher CVC rates compared with the PWKL for the other four attribute vectors. Using the same item quality, the indices performed similarly for α₀ and α₁ when the DINO model was used; however, the CVC rates using the PWKL were lower for α₂, α₃, α₄, and α₅ compared with the other two indices. It can also be noted that the classification accuracy of the PWKL was more varied than those of the MPWKL and GDI across the attribute vectors. As can be seen from the graphs, the CVC rate of the PWKL could range from around 0.65 to 1.00, whereas these rates were mostly 1.00 for the MPWKL and the GDI. The three indices had almost the same results when the A-CDM was involved.

Figure 1.

CVC rates for six selected attribute vectors, J = 10.

Note. Blue, red, and green lines represent the PWKL, MPWKL, and GDI, respectively. CVC = correct attribute vector classification; PWKL = posterior-weighted Kullback–Leibler index; GDI = G-DINA model discrimination index; G-DINA = generalized DINA; DINA = deterministic inputs, noisy “and” gate; DINO = deterministic input, noisy “or” gate; A-CDM = additive CDM; CDM = cognitive diagnosis model; HD-HV = high discrimination–high variance; LD-LV = low discrimination–low variance.

Second, although the CVC rates were lower, the results for LD-LV items were similar to those for HD-HV items. The MPWKL and the GDI had higher CVC rates than the PWKL for α₀, α₁, α₂, and α₃ when the DINA model was used. In contrast, the PWKL outperformed the MPWKL and GDI for α₄ and α₅ in the same condition. Using the same item quality and the DINO model, the PWKL had higher CVC rates for α₀ and α₁. However, the MPWKL and GDI had higher rates for the other four attribute vectors. Again, the CVC rates of the PWKL had higher variability (0.26-0.82) compared with those of the MPWKL and the GDI (0.56-0.65). Finally, the efficiency of the indices was similar for the A-CDM, but the extreme attribute vectors α₀ and α₅ can be better estimated than the remaining attribute vectors.

Minimax of the Posterior Distribution

For a fixed minimax of the posterior distribution, descriptive statistics of the test lengths are shown in Tables 5 to 7 for the DINA, DINO, and A-CDM, respectively. Differences in the mean were evaluated using two cut points, 0.5 and 1, and differences below 0.5 were considered negligible, between 0.5 and 1 slight, and above 1 substantial.

Table 5.

Descriptive Statistics of Test Lengths Using the DINA Model.

		PWKL				MPWKL				GDI
Item quality	π(αc|Xi)	Minimum	Maximum	M	CV	Minimum	Maximum	M	CV	Minimum	Maximum	M	CV
HD-LV	0.65	3	25	8.26	0.28	3	16	6.69	0.13	3	14	6.67	0.13
	0.75	3	28	8.92	0.28	4	18	7.32	0.17	4	19	7.34	0.16
	0.85	3	32	10.08	0.27	4	22	8.83	0.19	4	24	8.87	0.19
	0.95	4	35	12.05	0.25	4	26	10.99	0.19	4	31	10.99	0.19
HD-HV	0.65	2	19	7.76	0.22	2	14	6.55	0.11	2	10	6.52	0.12
	0.75	2	22	7.96	0.22	2	14	6.58	0.11	2	11	6.60	0.11
	0.85	2	23	8.45	0.22	2	14	6.72	0.10	2	14	6.73	0.10
	0.95	2	23	9.36	0.21	2	17	7.51	0.12	2	18	7.22	0.11
LD-LV	0.65	4	48	13.48	0.37	5	32	11.41	0.30	5	34	11.46	0.30
	0.75	4	50	15.21	0.36	6	40	13.02	0.29	6	38	13.08	0.29
	0.85	5	55	17.11	0.35	6	53	14.95	0.30	6	55	15.00	0.30
	0.95	5	73	21.43	0.32	7	56	19.40	0.28	7	64	19.46	0.28
LD-HV	0.65	3	35	10.45	0.32	4	28	8.60	0.24	4	28	8.57	0.24
	0.75	4	36	11.71	0.32	5	29	9.86	0.26	5	31	9.93	0.26
	0.85	4	42	13.41	0.31	5	32	11.78	0.26	5	32	11.77	0.26
	0.95	4	49	15.70	0.29	6	43	14.13	0.25	6	42	14.17	0.25

Note. DINA = deterministic inputs, noisy “and” gate; PWKL = posterior-weighted Kullback–Leibler index; MPWKL = modified posterior-weighted Kullback–Leibler index; GDI = G-DINA model discrimination index; G-DINA = generalized DINA; CV = coefficient of variation; HD-LV = high discrimination–low variance; HD-HV = high discrimination–high variance; LD-LV = low discrimination–low variance; LD-HV = low discrimination–high variance.

Table 7.

Descriptive Statistics of Test Lengths Using the A-CDM.

		PWKL				MPWKL				GDI
Item quality	π(αc|Xi)	Minimum	Maximum	M	CV	Minimum	Maximum	M	CV	Minimum	Maximum	M	CV
HD-LV	0.65	6	13	6.99	0.10	6	13	6.92	0.08	6	12	6.93	0.08
	0.75	6	14	7.86	0.14	7	14	7.75	0.12	7	15	7.76	0.12
	0.85	9	18	9.98	0.14	9	19	9.74	0.13	9	20	9.79	0.13
	0.95	11	25	12.84	0.16	11	26	12.82	0.15	11	26	12.84	0.15
HD-HV	0.65	6	10	6.83	0.08	6	7	6.75	0.06	6	7	6.70	0.07
	0.75	6	14	7.18	0.12	6	8	6.83	0.06	6	8	6.80	0.06
	0.85	6	17	7.87	0.15	6	11	7.18	0.07	6	11	7.04	0.06
	0.95	6	17	8.71	0.16	6	15	8.79	0.09	7	16	8.79	0.10
LD-LV	0.65	10	32	12.67	0.21	10	30	12.65	0.22	10	29	12.62	0.22
	0.75	11	33	14.66	0.23	11	34	14.67	0.23	11	34	14.64	0.23
	0.85	12	50	17.80	0.24	12	49	17.84	0.24	12	52	17.82	0.24
	0.95	16	59	24.41	0.23	16	74	24.39	0.23	16	74	24.37	0.23
LD-HV	0.65	8	22	9.04	0.17	8	21	9.04	0.17	8	18	9.03	0.17
	0.75	9	26	11.25	0.19	9	24	11.30	0.19	9	24	11.26	0.19
	0.85	11	27	13.29	0.19	11	32	13.20	0.18	11	29	13.20	0.18
	0.95	13	39	17.43	0.20	13	38	17.49	0.19	13	41	17.48	0.20

Note. A-CDM = additive CDM; CDM = cognitive diagnosis model; PWKL = posterior-weighted Kullback–Leibler index; MPWKL = modified posterior-weighted Kullback–Leibler index; GDI = G-DINA model discrimination index; G-DINA = generalized DINA; DINA = deterministic inputs, noisy “and” gate; CV = coefficient of variation; HD-LV = high discrimination–low variance; HD-HV = high discrimination–high variance; LD-LV = low discrimination–low variance; LD-HV = low discrimination–high variance.

Table 6.

Descriptive Statistics of Test Lengths Using the DINO Model.

		PWKL				MPWKL				GDI
Item quality	π(αc|Xi)	Minimum	Maximum	M	CV	Minimum	Maximum	M	CV	Minimum	Maximum	M	CV
HD-LV	0.65	3	24	8.37	0.28	3	24	6.89	0.15	3	19	6.83	0.15
	0.75	3	27	9.08	0.28	4	27	7.58	0.18	4	21	7.58	0.18
	0.85	3	29	10.32	0.27	4	28	8.91	0.19	4	23	8.89	0.19
	0.95	4	34	12.23	0.25	4	30	11.09	0.20	4	27	11.04	0.20
HD-HV	0.65	2	17	7.78	0.23	2	10	6.60	0.11	2	10	6.53	0.11
	0.75	3	18	8.04	0.22	3	13	6.71	0.10	3	10	6.60	0.11
	0.85	3	22	8.61	0.23	3	14	7.24	0.10	3	11	6.80	0.10
	0.95	3	26	9.51	0.22	3	17	8.10	0.10	3	20	7.66	0.11
LD-LV	0.65	4	49	13.73	0.35	5	40	11.88	0.29	5	37	11.85	0.29
	0.75	4	50	15.43	0.34	6	43	13.61	0.29	6	43	13.61	0.29
	0.85	5	59	17.41	0.33	6	57	15.57	0.30	6	62	15.60	0.30
	0.95	5	67	21.83	0.31	7	69	20.10	0.29	7	68	20.07	0.29
LD-HV	0.65	3	32	10.45	0.31	4	24	8.81	0.23	4	24	8.75	0.23
	0.75	4	33	11.79	0.30	5	36	10.18	0.25	5	29	10.08	0.25
	0.85	4	36	13.45	0.30	5	36	12.13	0.24	5	42	12.11	0.25
	0.95	5	45	15.75	0.28	6	40	14.40	0.25	6	43	14.35	0.26

Note. DINO = deterministic input, noisy “or” gate; PWKL = posterior-weighted Kullback–Leibler index; MPWKL = modified posterior-weighted Kullback–Leibler index; GDI = G-DINA model discrimination index; G-DINA = generalized DINA; DINA = deterministic inputs, noisy “and” gate; CV = coefficient of variation; HD-LV = high discrimination–low variance; HD-HV = high discrimination–high variance; LD-LV = low discrimination–low variance; LD-HV = low discrimination–high variance.

Using the DINA and DINO models, the mean test lengths of the MPWKL and the GDI were generally similar (i.e., the differences were negligible), and they were substantially shorter compared with the test lengths of the PWKL. This was true regardless of the minimax value and item quality. The largest mean test length differences occurred when LD-LV items were involved—these differences were greater than 2.0 and 1.8 for the DINA and DINO models, respectively. However, when the A-CDM was used, all the three indices performed similarly except in the HD-HV and 0.85 minimax value condition, where the PWKL had a slightly longer test length compared with the MPWKL and GDI.

It can also be noted that, as expected, increasing the minimax value resulted in longer test lengths regardless of the item selection index, item quality, and generating model. The change in the mean test length as a result of increasing the minimax value from 0.65 to 0.95 was substantial for all of the conditions except for one—there was only a slight change when the MPWKL and the GDI were used with HD-HV items. In addition, as in the fixed-test length, the item quality had an impact on the efficiency of the indices: Using items with higher discrimination or higher variance resulted in shorter tests. Consequently, HD-HV and LD-LV items had the shortest and the longest tests, respectively. In this study, using the minimax value of 0.95, GDI, and DINA model, HD-HV items resulted in tests with a mean of 7.22; in contrast, for LD-LV items, this mean was 19.46. Finally, generating model can have an impact on the mean test lengths, but this moderated by the choice of the item selection index—with the GDI, the DINA or DINO models consistently required shorter tests than the A-CDM, but this pattern was not as obvious with the other two indices.

Other findings can be gleaned from Tables 5 to 7. First, the minimum test lengths of the three indices were similar for most of the conditions. Second, increasing the minimax of the posterior distribution generally resulted in higher minimum and maximum test lengths, especially at the two extreme minimax values. However, using HD-HV items with the DINA model, the minimum values remained the same for the three indices. Third, the item quality had an impact on the minimum, maximum, and CV of the test lengths: HD-HV items provided the smallest minimum, maximum, and CV values, whereas LD-LV items provided the largest statistics for all of the indices. Finally, using the A-CDM, the indices had the smallest maximum and CV values; however, they had the highest minimum test lengths compared with the DINA and DINO models.

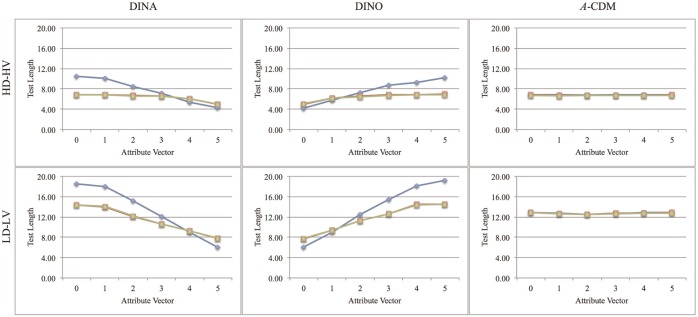
The mean test lengths for each attribute vector were calculated, and the results using HD-HV and LD-LV items, and 0.65 as the minimax value are shown in Figure 2. For the DINA model, the PWKL required longer tests, on the average, for the attribute vectors α₀, α₁, and α₂ compared with the MPWKL and GDI; however, these two indices required longer tests for α₅. In contrast, the MPWKL and GDI required longer tests for α₀, and the PWKL required longer tests for α₂, α₃, α₄, and α₅ with the DINO as the generating model. Using the A-CDM, the mean test lengths were similar for each attribute vector.

Figure 2.

Mean test lengths for six selected attribute vectors, π(α_c|X_i) = 0.65.

Note. Blue, red, and green represent the PWKL, MPWKL, and GDI, respectively. PWKL = posterior-weighted Kullback–Leibler index; GDI = G-DINA model discrimination index; G-DINA = generalized DINA; DINA = deterministic inputs, noisy “and” gate; DINO = deterministic input, noisy “or” gate; A-CDM = additive CDM; CDM = cognitive diagnosis model; HD-HV = high discrimination–high variance; LD-LV = low discrimination–low variance.

Item Usage

To gain a better understanding of how different models utilize the items in the pool, the overall item usage in terms of the number of required attributes was recorded for each condition. Only the results for the fixed-test lengths with HD-HV and LD-LV items are shown in Table 8.

Table 8.

The Proportion of Overall Item Usage.

			PWKL					MPWKL					GDI
			Number of required attributes
True Model	Item quality	J	1	2	3	4	5	1	2	3	4	5	1	2	3	4	5
DINA	HD-HV	10	0.25	0.45	0.23	0.06	0.01	0.38	0.27	0.31	0.02	0.01	0.34	0.34	0.28	0.03	0.01
		20	0.25	0.48	0.22	0.04	0.01	0.27	0.39	0.30	0.03	0.01	0.27	0.37	0.29	0.05	0.02
		40	0.28	0.49	0.18	0.04	0.01	0.24	0.44	0.27	0.05	0.01	0.24	0.39	0.30	0.05	0.01
	LD-LV	10	0.26	0.30	0.34	0.08	0.02	0.50	0.30	0.16	0.03	0.01	0.52	0.29	0.15	0.03	0.01
		20	0.29	0.34	0.28	0.07	0.02	0.37	0.35	0.23	0.04	0.01	0.38	0.34	0.22	0.05	0.01
		40	0.25	0.34	0.31	0.08	0.02	0.27	0.35	0.30	0.07	0.02	0.28	0.35	0.29	0.07	0.02
DINO	HD-HV	10	0.26	0.44	0.23	0.07	0.01	0.30	0.38	0.27	0.04	0.01	0.36	0.28	0.30	0.05	0.01
		20	0.25	0.44	0.24	0.06	0.01	0.28	0.40	0.26	0.06	0.01	0.23	0.41	0.26	0.08	0.02
		40	0.24	0.46	0.24	0.05	0.01	0.21	0.49	0.23	0.06	0.01	0.22	0.41	0.29	0.07	0.01
	LD-LV	10	0.23	0.32	0.32	0.11	0.02	0.46	0.32	0.17	0.04	0.01	0.49	0.30	0.16	0.04	0.01
		20	0.27	0.33	0.29	0.09	0.02	0.35	0.36	0.22	0.05	0.01	0.37	0.34	0.22	0.05	0.01
		40	0.22	0.36	0.30	0.10	0.02	0.26	0.37	0.27	0.08	0.02	0.26	0.37	0.27	0.08	0.02
A-CDM	HD-HV	10	0.92	0.03	0.03	0.02	0.00	0.92	0.03	0.03	0.02	0.00	0.92	0.03	0.03	0.02	0.00
		20	0.95	0.02	0.02	0.01	0.00	0.96	0.02	0.02	0.01	0.00	0.96	0.02	0.02	0.01	0.00
		40	0.93	0.06	0.01	0.00	0.00	0.96	0.03	0.01	0.00	0.00	0.98	0.01	0.01	0.00	0.00
	LD-LV	10	0.92	0.03	0.03	0.02	0.00	0.92	0.03	0.03	0.02	0.00	0.92	0.03	0.03	0.02	0.00
		20	0.96	0.02	0.02	0.01	0.00	0.96	0.02	0.02	0.01	0.00	0.96	0.02	0.02	0.01	0.00
		40	0.98	0.01	0.01	0.00	0.00	0.98	0.01	0.01	0.00	0.00	0.98	0.01	0.01	0.00	0.00

Note. PWKL = posterior-weighted Kullback–Leibler index; MPWKL = modified posterior-weighted Kullback–Leibler index; GDI = G-DINA model discrimination index; G-DINA = generalized DINA; DINA = deterministic inputs, noisy “and” gate; DINO = deterministic input, noisy “or” gate; A-CDM = additive CDM; CDM = cognitive diagnosis model; HD-LV = high discrimination–low variance; HD-HV = high discrimination–high variance; LD-LV = low discrimination–low variance; LD-HV = low discrimination–high variance.

For the DINA and DINO models, items that required one, two, and three attributes were generally used more often compared with those which required four and five attributes regardless of the item selection index and item quality. The PWKL mostly used two-attribute items for the same models except in one condition, where a 10-item test with LD-LV items and the DINA were used. The MPWKL and GDI had a similar pattern of item usage (i.e., one-attribute items were mostly used for 10- and 20-item tests with LD-LV items) across different test lengths and item qualities for the DINA except in one condition where a 10-item test with HD-HV items was used. However, for the A-CDM, one-attribute items were mostly used with a proportion of at least 0.92 regardless of the item selection index and item quality.

To get a deeper understanding of the differences in item usage among the models, the items were grouped based on their required attributes. To accomplish this, an additional simulation study was carried out using the same factors except for one: item quality. For this study, the lowest and highest success probabilities were fixed across all of the items, specifically, P(0) = .1 and P(1) = .9. This design aimed to eliminate the effect of the item quality on item usage. Due to the space constraint, only the results for the GDI, 20-item test, and α₃ are shown in Figure 3. Overall, the DINA model showed the following pattern of item usage: It uses items that required the same attributes as the examinee’s true attribute mastery vector, and items that required single attributes which were not mastered by the examinee. For α₃, the DINA model used the items that required (1,1,1,0,0), and items that required either (0,0,0,1,0) or (0,0,0,0,1). In contrast, the DINO showed a different pattern of item usage: It uses items that required the same attributes as the examinee’s true nonmastery vector, and items that required single attributes, which were mastered by the examinee. Again for α₃, the DINO model used items that required (0,0,0,1,1) and items that required (1,0,0,0,0), (0,1,0,0,0), and (0,0,1,0,0). The A-CDM used items that required single attributes regardless of the true attribute vector. The same pattern was observed for the other attribute vectors.

Figure 3.

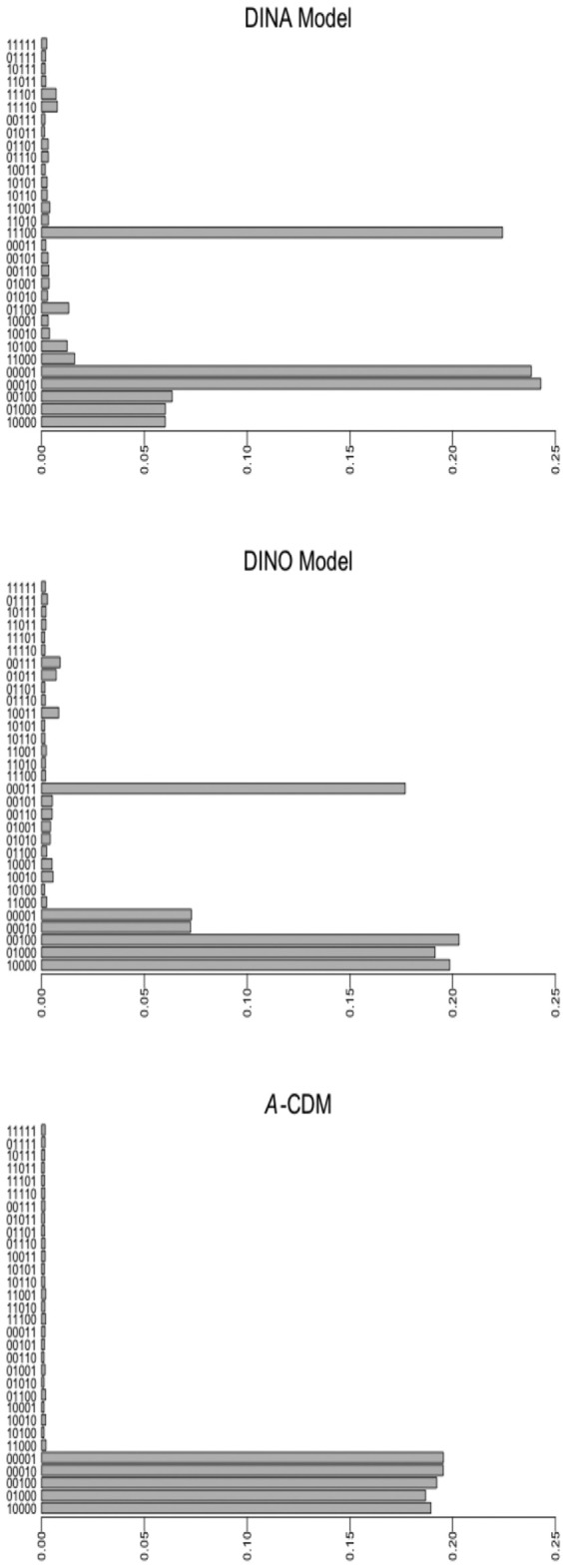
Overall proportion of item usage for α₃, GDI, and J = 20.

Note. GDI = G-DINA model discrimination index; G-DINA = generalized DINA; DINA = deterministic inputs, noisy “and” gate; DINO = deterministic input, noisy “or” gate; A-CDM = additive CDM; CDM = cognitive diagnosis model.

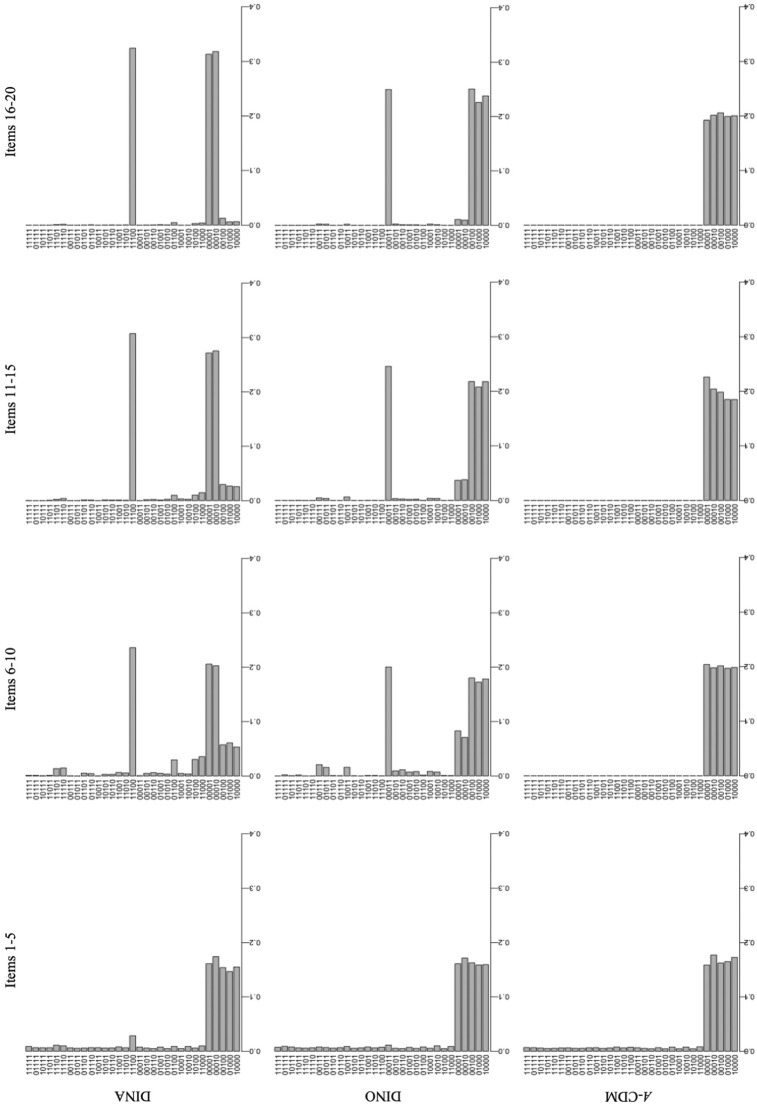
To further investigate how the models converged into those patterns of item usage, the test administrations were divided into periods each comparing of five items. The item usage was recorded in each period. Only the results for the GDI, 20-item test, and α₃ are shown (refer to Figure 4). In the first period, which includes the first five items, one-attribute items were used mostly regardless of the generating model and examinees’ true attribute vector. In the second, third, and fourth periods (items from 6 to 10, 11 to 15, and 16 to 20, respectively), the most common item types gradually became more similar to the previous patterns of item usage for the DINA and DINO models. However, the A-CDM favored one-attribute item at the rate of almost 1.00 in each period. Again, the same pattern was observed for the other attribute vectors in this study.

Figure 4.

The proportion of item usage in different periods for α₃, GDI, and J = 20.

Note. GDI = G-DINA model discrimination index; G-DINA = generalized DINA; DINA = deterministic inputs, noisy “and” gate; DINO = deterministic input, noisy “or” gate; A-CDM = additive CDM; CDM = cognitive diagnosis model.

Average Time

The average item administration time per examinee was recorded separately for each index. The CAT administration code was written in Ox (Doornik, 2011) and run on a computer with processor of 2.5 GHz. Only the average times in milliseconds using 10 HD-LV items and the DINA model are shown in Table 9. The table shows that the MPWKL was the slowest, and the GDI was the fastest index in terms of the administration time: the PWKL, the MPWKL, and the GDI took 6.43, 20.18, and 4.53 ms, respectively. In other words, the GDI was 4.45 faster than the MPWKL, and 1.42 faster than the PWKL. As mentioned earlier, the GDI works with the reduced attribute vectors, and involves fewer terms compared with the PWKL and the MPWKL. The dimensions in the PWKL and the MPWKL grow exponentially as the number of attribute K increases. However, the GDI does not have the same problem as long as the number of required attributes $K_j^{*}$ remains small. The advantage of the GDI can be expected to be more apparent with the A-CDM because mostly one-attribute items are picked by the different indices.

Table 9.

Average Test Administration Time per Examinee (J = 10, HD-LV, and DINA).

	PWKL	MPWKL	GDI
Time (in ms)	6.43	20.18	4.53
Ratio (relative to GDI)	1.42	4.45	—

Note. HD-LV = high discrimination–low variance; DINA = deterministic inputs, noisy “and” gate; PWKL = posterior-weighted Kullback–Leibler index; MPWKL = modified posterior-weighted Kullback–Leibler index; GDI = G-DINA model discrimination index; G-DINA = generalized DINA.

Discussion and Conclusion

Compared with traditional unidimensional IRT models, CDMs provide more information that can be used to inform instruction and learning. These models can reveal examinees’ strengths and weaknesses by diagnosing whether they have mastered a specific set of attributes. CAT is a tool that can be used to create tests tailored for different examinees. This allows for a more efficient determination of what students know and do not know. In this article, two new item selection indices, the MPWKL and the GDI, were introduced, and their efficiency was compared with the PWKL. In addition, a more efficient simulation design was proposed in this study. This design can allow for results to be generalized to different distributions of attribute vectors, despite involving a smaller sample size.

Based on the factors manipulated in the simulation study, the two new indices performed similarly, and they both outperformed the PWKL in terms of classification accuracy and test length. The study also showed that items with HD or HV provided better classification rates or shorter test lengths. Moreover, generating models can have an impact on the efficiency of the indices: For the DINA and DINO models, the results were more distinguishable; however, the efficiency of the indices was essentially the same for the A-CDM, except in a few conditions.

Although this study showed that the proposed indices, particularly the GDI, are promising, more research needs to be done to determine their viability. First, some constraints on the design of the Q-matrix and the size of the item pool need to be investigated. The Q-matrix in this study involved all the possible q-vectors. However, in practice, this may not be the case, particularly, when the CDMs are retrofitted to existing data. Therefore, it would be important to examinee how the indices perform when only a subset of the q-vectors exists in the pool. The current study uses a large item pool, which may not be always possible in real testing situations. Considering smaller item pools, with or without constraints on the Q-matrix specifications, can lead to a better understanding of how the proposed indices perform under more varied conditions.

Second, although diagnostic assessments are primarily designed for low-stakes testing situations, their use for high-stakes decisions cannot be totally precluded. Because test security is a critical issue in high-stakes testing situations, item exposure in CD-CAT needs also to be controlled. At present, there are procedures for item exposure control in the context of CD-CAT. For example, Wang, Chang, and Huebner (2011) proposed item exposure control methods for fixed-test lengths in CD-CAT. However, the performance of these methods with the proposed indices has yet to be investigated. In addition, controlling the exposure of the items with the MPWKL and the GDI can also be examined when different termination rules are involved.

Third, each data set was generated using a single CDM in this study. However, as with previous indices, the MPWKL and the GDI are sufficiently general that it can simultaneously be applied to any CDMs subsumed by the G-DINA model. As such, it would be interesting to examine how the new indices will perform when the item pool is made up of various CDMs, which reflects what can be expected in practice—different items might require different processes (i.e., CDMs). Finally, to keep the scope of this work manageable, a few simplifications about factors affecting the performance of CD-CAT indices were made. These include fixing the number of attributes, using a single method in estimating the attribute vectors, and assuming that the item parameters were known. To obtain more generalizable conclusions, future research should consider varying these factors.