Abstract
Differential item functioning (DIF) occurs when people with the same proficiency have different probabilities of giving a certain response to an item. The present study focused on an assumption implicit in popular methods for DIF testing that has received little attention in published literature (item residual homogeneity). The assumption is explained, a strategy for detecting violations of it (i.e., item residual heterogeneity) is illustrated with empirical data, and simulations are carried out to evaluate the performance of binary logistic regression, two-group item response theory (IRT), and the Mantel–Haenszel (MH) test in the presence of item residual heterogeneity. Results indicated that heterogeneity inflated Type I error and attenuated power for logistic regression, and attenuated power and produced biased estimates of the latent focal group mean and standard deviation for two-group IRT. The MH test was robust to item residual heterogeneity, probably because it does not use the logistic function.
Keywords: differential item functioning, DIF, logistic regression, heterogeneity
For a test to be valid, the probability of responding in a particular category to each item should be the same for all respondents with the same level of the construct measured by the items (θ). If people with the same θ value have different response probabilities for an item, the item displays differential item functioning (DIF). To ensure valid assessment, it is important to test for DIF and eliminate or model it.
Several popular methods for DIF testing make an implicit assumption that the groups have equivalent variability on the underlying continuum of response to the item (this is different from equal variability on θ). It is realistic to expect this assumption to be violated in some cases. For example, in comparisons between people with and without cognitive symptoms of psychological disorders, those with the symptoms may experience more internal distractions like intrusive thoughts than people without the symptoms, leading to greater item residual variance.
Methods for testing DIF that use the logistic function (e.g., logistic regression) assume item residual homogeneity and are likely to mislead researchers if the assumption is violated. There is literature about this assumption in the context of comparing groups with logistic regression more generally (e.g., Allison, 1999; Hoetker, 2007; Long, 2009; Mood, 2010; Williams, 2009), but it has not been addressed in the context of DIF. When the assumption is violated, logistic regression coefficients and their standard errors (SEs) are biased (Allison, 1999; Long, 2009; Mood, 2010; Williams, 2009, 2011).
In the present article, the authors explain item residual heterogeneity, present an empirical example showing that this type of heterogeneity can exist in real data, and use simulations to evaluate how item residual heterogeneity affects DIF testing with (a) two-group logistic item response modelling with likelihood ratio testing (IRT-LR; Thissen, Steinberg, & Gerrard, 1986; Thissen, Steinberg, & Wainer, 1988, 1993), (b) the Mantel–Haenszel (MH) test (Holland, 1985; Holland & Thayer, 1988; Mantel & Haenszel, 1959), and (c) binary logistic regression (Bennett, Rock, & Kaplan, 1987; Swaminathan & Rogers, 1990).
Item Residual Heterogeneity and DIF Testing
The authors focus on binary responses and logistic regression for simplicity but the issue of item residual heterogeneity is also relevant with ordinal and nominal item responses and with latent variable models that use the logistic function. Some of the issues to be explained in the following have been mentioned in the context of categorical latent variable modeling (e.g., Muthén & Asparouhov, 2002) using Mplus. The “theta approach” (p. 9) implemented in Mplus for categorical latent variable modeling with the logistic function is closely related to what is described here.
Binary logistic regression is a linear model for the latent outcome, with predictors in xi (1 ×p), their corresponding coefficient estimates in (p× 1), and observations i = 1, 2, . . . N. The problem to be discussed here affects both regression coefficients and odds ratios, because odds ratios are a simple transformation of . Let refer to a continuous variable assumed to underlie binary yi, where τ is a threshold such that yi = 1 if ( = xiβ+εi) > τ and yi = 0 if ( = xiβ+εi) ≤τ. In this case, binary logistic regression is equivalent to a linear model for , where εi follows the continuous standard logistic distribution, which has mean = 0 and variance = . The variance of the outcome is fixed and not separately identified as in the general linear model.
Although homoscedasticity is a consideration in linear regression and linear latent variable models for continuous data, the problem described here is a more complicated variation of heteroscedasticity because of the categorical responses. In linear models with an observed outcome, both error variance and model-explained variance can be estimated, with the homoscedasticity assumption needed for accurate SEs with ordinary least squares estimation. When the outcome is latent, the error and model-explained variances are not both separately identified, so the error variance is fixed to . This means that all observations are presumed to have the same (standard logistic) residual variance. Thus, when logistic regression is used to compare groups, members of all groups are presumed to have the same residual variance. This is the variance of , not the variance of θ, as manipulated previously in DIF research (e.g., Monahan & Ankenmann, 2005; Pei & Li, 2010).
Usually, the total variance in is partitioned into model-explained variance (i.e., ) and . Thus, when two groups are compared using regression coefficients, each group is assumed to have error variance equal to . That means the scale of is for each group, which is inconsequential if the residual variance is homoscedastic. However, if the residual variance actually differs between groups, may appear group discrepant due to group-discrepant scaling. Thus, a group difference in residual variance can be misinterpreted as a group difference in predictor effects. This implies that conclusions about DIF can be misleading when the groups differ in item residual variance.
Researchers typically do not know in advance of an analysis whether the item residual variances for two groups are equal. It is easy to imagine realistic situations when groups would differ in item residual variance. The underlying response process for an item may be more homogeneous for a reference group of Caucasian native English-speaking Americans than for a group of nonnative English-speaking “Asians,” grouped together to make an adequate sample size for the analysis, which may refer to people from any part of China, Japan, Korea, and so on. The next section describes an empirical analysis demonstrating item residual heterogeneity in empirical data.
Empirical Evidence of Item Residual Heterogeneity
The data examined here were used in previous research (Woods, Oltmanns, & Turkheimer, 2009). In the present analysis, binary (true–false) item responses given on the 18-item Workaholic subscale of the 375-item Schedule for Nonadaptive and Adaptive Personality (SNAP; Clark, 1996) by Air Force recruits (N = 2,026) are tested for heterogeneity between gender groups (1,265 male, 761 female). Ten items are tested, with the same 8 items that were empirically identified as anchors by Woods et al. (2009) treated as designated anchors here.
The goal is to test for item residual heterogeneity. Few methods are available for this purpose. Here, the authors model the mean and variance simultaneously with a double generalized linear model (e.g., DGLM; Smyth & Verbyla, 1999) using the dglm R package (Dunn & Smyth, 2012). The authors are essentially using a logistic regression model set up for DIF testing (item response predicted from summed score, gender, and their interaction) while modeling the variances. An important limitation is that if heterogeneity is present, the coefficients in the mean model remain biased by the variance difference between groups and do not provide an adjusted DIF test. Details have been omitted to save space; please see the Online Appendix for more about this analysis and the full table of results.
Five items showed statistically significant variance heterogeneity for men versus women with the following effect sizes (γsex) = 0.13 (SE = 0.07) for Item 1, −0.13 (0.07) for Item 111, 0.13 (0.07) for Item 180, 0.16 (0.07) for Item 192, 0.17 (0.07) for Item 227. More research is needed to determine the practical importance of the magnitude of these effects. The point here is to show that statistically significant heterogeneity can be apparent in an empirical data set. As a result, naïve DIF results using popular methods are likely to be misleading for those items.
DIF Methods Included in the Present Simulations
Binary Logistic Regression for DIF Testing
The basic DIF model for comparing two groups with respect to a binary item response is
where pij = probability that person i responds 1 (correct, true, etc.) to Item j, through = estimated parameters, and x2 = group. The summed score, x1, is a proxy for θ and in the present study consists of scores on anchor items, plus the studied item (the studied item is included for better group matching, see Millsap, 2011, p. 239).
There are different ways to carry out the DIF testing (Millsap, 2011; Swaminathan & Rogers, 1990). Here, the authors carry out an omnibus test that is significant in the presence of uniform DIF, non-uniform DIF, or both, by comparing the model from Equation 1 to the baseline model: using a LR test (which indicates DIF when significant).
DIF is not mentioned in the literature on residual variance heterogeneity in group comparisons with logistic regression, but DIF testing is just a particular way of interpreting such analyses. Thus, the prior literature indicating that there is bias in regression coefficients and SEs under heterogeneity (Allison, 1999; Long, 2009; Mood, 2010; Williams, 2009, 2011) suggests that DIF testing with logistic regression will be inaccurate in the presence of heterogeneity.
IRT-LR
IRT-LR is a procedure wherein LR tests from nested two-group unidimensional IRT models are used to test items individually for DIF (Thissen et al., 1986, 1988, 1993). Almost any item response function (IRF) can be used, and the IRF may vary over items in the same analysis. No explicit estimation of the latent construct, θ, is needed; θ is a random latent variable treated as missing using Bock and Aitkin’s (1981) scheme for marginal maximum likelihood implemented with an expectation maximization algorithm. The mean and variance of θ are fixed to 0 and 1 (respectively) for the reference group to identify the scale, and estimated for the focal group as part of the DIF analysis. Anchor items are used to link the metric of θ for the two groups. Item parameters for all anchors are constrained equal between groups in all models.
In the present research, the authors use the omnibus test with the 2PL model (Birnbaum, 1968), designed to identify uniform DIF, non-uniform DIF (Camilli & Shepard, 1994, p. 59; Mellenbergh, 1989), or both. A model with all parameters for the studied item constrained equal between groups is compared with a model with all parameters for the studied item permitted to vary between groups. The LR test statistic is negative twice the difference between the optimized log likelihoods, which is approximately χ2-distributed (df = the difference in free parameters). Statistical significance indicates the presence of DIF.
The authors found no literature on item residual heterogeneity with IRT-LR and no application that mentioned checking for assumptions about equal group residual variances. Because IRT-LR uses the logistic function, they expect inaccuracy in the presence of item residual heterogeneity.
MH for DIF Testing
The MH statistic tests for association between binary group and binary item response, holding constant the continuous matching variable, for which the authors use the sum of scores on anchor items, including the studied item. Items are tested one at a time, and statistical significance is evidence of uniform DIF. The MH statistic (without the sometimes-included continuity correction) is, , where m is a score on the matching criterion (m = 1, 2, . . ., M), nm11 is the number of people in Group 1 who gave Response 1, E and var are the expected value and variance under the null hypothesis of independence (no DIF): , , and nm is the number of people at level m of the matching criterion. Under the null hypothesis, QMH is distributed χ2(df = 1).
The authors found no mention of item residual heterogeneity for the MH test in the literature. The MH test may be considered a restricted case of logistic regression with a binary predictor and binary outcome, not requiring all the assumptions of the generalized linear model framework. Nevertheless, the MH does not use the logistic function and is therefore likely robust to violations of item residual heterogeneity for group comparisons. The authors hypothesized that the MH would be unaffected by heterogeneity in the simulations.
Simulation Methods
Design
There were (2 × 2 × 2 × 4) 32 conditions (500 replications each), varying according to (a) whether DIF was simulated in the discrimination parameters, (b) the scale length (20 or 40 items), (c) the percent of items on the test with DIF (15% or 30%), and (d) the amount of item residual heterogeneity (none, focal = 2× reference, focal = 3× reference or focal = 4× reference). The rationale for (a) is that generating data from the one-parameter logistic (1PL) model for both groups permits conditions with no assumption violations for logistic regression and the MH test, necessary for isolating the effects of item residual heterogeneity. However, including conditions with DIF in the discrimination parameters improves generalizability. The scale lengths and DIF contamination percentages were chosen based on what is realistic for empirical data sets. Because there is not empirical research to guide what might be realistic amounts of item residual variance in a DIF context with an IRT model, the heterogeneity values used here were selected fairly arbitrarily for this preliminary study.
Data Generation
In each condition, data for the reference (R) group were generated from the 1PL model. To create conditions with and without a residual variance difference between groups, the 1PL model was reparameterized to the latent variable form. In other words, consider a typical form of the 1PL, , equivalently expressed in logit form, ; then equivalently express it with a latent outcome and a standard logistic distributed error term: . For the simulations, the generating model was = aiR(θ−biR) +εi for the R group and = aiF(θ−biF) +σiεi for the focal (F) group, with σi used to impose the multiplicative residual variance difference, which varied over simulation conditions (σi = either 1 (no difference), 2, 3, or 4).
The item residual variance (εi) in each model was distributed standard logistic, L(0, ), and computed as εi = log(unif/(1 − unif)), where “unif” is a random number from a uniform (0,1) distribution (logistic formula obtained from Johnson, Kotz, & Balakrishnan, 1995). The outcome was dichotomized for each group by comparing it with a random uniform (0,1) draw; if was greater than the draw, the generated item response was 1, otherwise it was 0.
Sample sizes were selected to be on the larger end of what is seen in this literature to provide plenty of power, and the R and F groups were set to unequal values, which is typically observed: NR = 1,000 and NF = 800. The latent variable was drawn from N(0,1) for the R group, and N(0.8, 1) for the F group; 0.8 is in the range of mean differences observed in applications.
R-group item parameters were drawn from distributions. The discrimination parameter was held constant over items but drawn from N(1.7, SD = 0.1), so that it was different for every replication. The difficulty parameters were drawn from unif(−2,2), as done by Li, Brooks, and Johanson (2012). F-group parameters were defined in relation to R-group parameters. For DIF-free items, aiF = aiR and biF = biR. For items with uniform or non-uniform DIF, biF = biR−δi with δi determined by a random draw (u) from a unif(0,1) distribution such that if (u1≤ .33) then δi = .3; else if ((u1 > .33) and (u1≤ .66)) then δi = .5; else if ((u1 > .66) and (u1≤ 1.0)) then δi = .7. For items with non-uniform DIF, aiF = aiR−γi, with γi determined by a separate unif(0,1) draw: if (u2≤ .2) then γi = .3, else if ((u2 > .2) and (u2≤ .4)) then γi = .4, else if ((u2 > .4) and (u2≤ .6)) then γi = .5, else if ((u2 > .6) and (u2≤ .8)) then γi = .6, else if ((u2 > .8) and (u2≤ 1.0)), then γi = .7.
DIF Testing
A C++ program simulated data, operated SAS (version 9.3) proc logistic for logistic regression and the MH test, operated IRTLRDIF (v2.0b, Thissen, 2001), and processed the output. All data sets were tested once with logistic regression, the MH, and IRT-LR, respectively. For each simulated test, there was one set of DIF-free anchor items used for all procedures. There were five anchors for 20-item scales and 10 anchors for 40-item scales. The authors used only DIF-free anchor items to avoid misspecification in the matching criterion. The matching criterion for logistic regression and the MH was the sum of item scores for the DIF-free anchors, plus the studied item. The same DIF-free anchors were specified as the designated set for IRT-LR. All procedures tested each studied item individually for DIF.
Outcomes
The primary outcomes of interest were statistical power for the studied items with DIF and the Type I error for the studied items without DIF. These were calculated as the proportion of items in 500 replications for which the DIF test was significant (α = .05).
Simulation Results
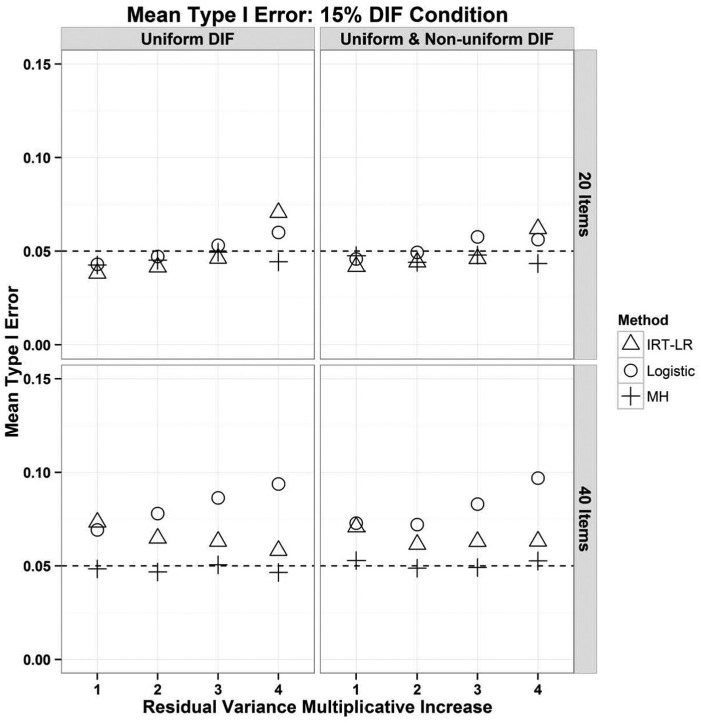
Figure 1 shows the Type I error rates for the three methods with and without non-uniform DIF for both scale lengths and 15% DIF. Item residual heterogeneity was either 1× (absent), 2×, 3×, or 4× greater for the F versus R group. A dashed line is drawn at the nominal alpha level. The pattern of results was nearly identical with 30% DIF in the data; results with 30% are available in the Online Appendix.
Figure 1.
Type I error rates (averaged over items) for logistic regression (o), IRT-LR (Δ), and the MH test (+) with 15% of items functioning differently.
Note. DIF = differential item functioning; IRT-LR = item response theory–likelihood ratio; MH = Mantel–Haenszel.
As expected, Type I error for the MH was near the nominal level regardless of the item residual variance difference. The MH shows this robustness to item residual heterogeneity probably because it does not use the logistic function.
For logistic regression, the trend was not perfectly linear but there was a general trend for Type I error to become inflated as the item residual variance increased. This was expected because of the prior literature on group comparisons with logistic regression under heterogeneity. The relationship between item residual heterogeneity and Type I error inflation was stronger with 40 versus 20 items. Perhaps this was because longer tests provide overall more information from the data, having more items with heterogeneity, more items with DIF, and more DIF-free anchor items to define the construct.
For IRT-LR, Type I error tended to increase with increases in item residual heterogeneity and became a little inflated with the greatest amount of item residual heterogeneity. This was true, however, only for 20-item tests. For 40-item tests, there was no systematic relationship between item residual heterogeneity and Type I error, and Type I error was a little inflated even in the absence of heterogeneity. Inflation in the absence of heterogeneity may have been due to inflation of the familywise error rate. The authors did not correct for inflation in this study using, for example, the Benjamini–Hochberg (1995) method (Thissen et al., 2002; Williams, Jones, & Tukey, 1999). Overall, the finding that heterogeneity was not systematically related to Type I error for IRT-LR surprised the authors.
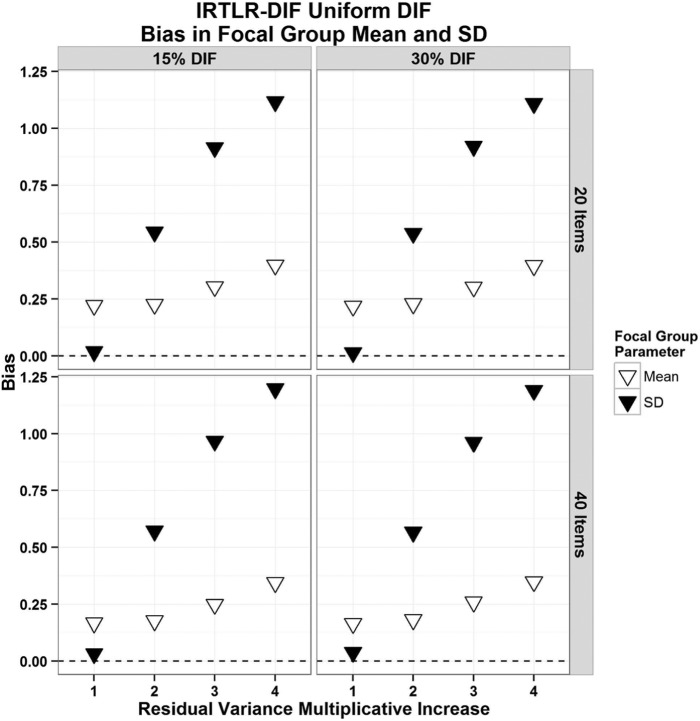
In light of the findings, the authors speculated that item residual heterogeneity was producing biased average estimates of the F-group latent mean and SD for IRT-LR instead of Type I error inflation. The IRT-LR DIF test compares two models that are identical except that one model estimates one set of parameters for the studied item and the other model estimates two sets of parameters for the studied item. Thus, the DIF test is primarily a function of the difference in item parameter estimates for the studied item, and its accuracy is primarily influenced by the accuracy of those estimates (as well as the distributional assumption for the LR statistic). Inaccuracy in the latent mean and SD are not reflected in the DIF test.
Figure 2 shows average F-group estimates of the latent mean and SD from IRT-LR with varying levels of item residual heterogeneity. The case of uniform DIF is shown but results were virtually identical for non-uniform DIF. For both scale lengths and either percentage of DIF items, there was a noticeable tendency for bias in estimates of the F-group latent mean to increase with increases in item residual heterogeneity. More striking was the extreme increase in bias of the estimated F-group latent SD as item residual heterogeneity increased. Thus, it appears that when the logistic function is used in a model with a latent predictor, the heterogeneity gets mostly absorbed into the latent variable instead of the parameter estimates.
Figure 2.
Bias in estimation of the latent mean (∇) and SD (▼) for the focal group, with 20 or 40 items and 15% or 30% of items functioning differently.
Note. The case of uniform DIF is shown but results were virtually identical for non-uniform DIF. IRT-LR = item response theory–likelihood ratio; DIF = differential item functioning.
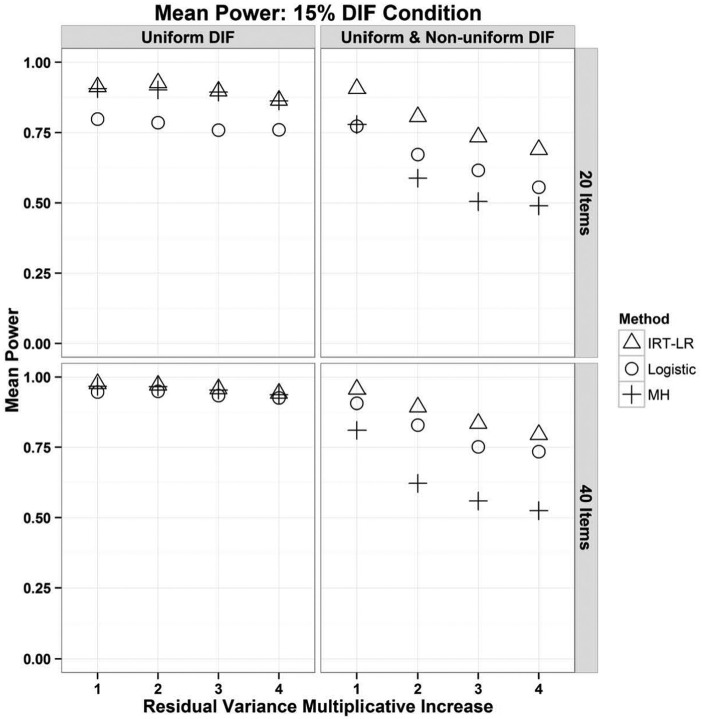
Figure 3 shows the statistical power rates for the three methods with and without non-uniform DIF for both scale lengths and 15% DIF. The pattern of results was nearly identical with 30% DIF in the data; results with 30% are available in the Online Appendix. With uniform DIF only, the power was high, similar for all methods (though a little bit lower for logistic regression with 20 items), and not very sensitive to item residual heterogeneity. Results for non-uniform DIF were striking: With all three methods, power declined as item residual heterogeneity increased. This was true even when Type I error had increased for those same conditions.
Figure 3.
Statistical power rates (averaged over items) for logistic regression (ö¢), IRT-LR (Δ), and the MH test (+) with 15% of items functioning differently.
Note. DIF = differential item functioning; IRT-LR = item response theory–likelihood ratio; MH = Mantel–Haenszel.
Recall that the MH test is theoretically matched to the research question of uniform DIF and not that of non-uniform DIF. Consistently, the MH test showed high power for uniform DIF and the lowest power of all methods for non-uniform DIF. However, item residual heterogeneity further attenuated power for non-uniform DIF, perhaps because item residual heterogeneity increases heterogeneity of the odds ratios, exacerbating the assumption violation already present for the MH in the case of non-uniform DIF. An additional possibility is that power was attenuated because, in this study, non-uniform DIF introduced measurement error for the DIF methods that condition on summed scores.
For logistic regression, the power attenuation observed for non-uniform DIF was expected because of the prior literature on group comparisons with logistic regression under heterogeneity. The only surprise was that it was not also observed in the absence of non-uniform DIF. Perhaps this was because the summed score is sufficient for the latent variable in the case of uniform DIF in this study, whereas non-uniform DIF introduced measurement error.
Power was highest for IRT-LR compared with the other methods, perhaps because it most closely matched the data-generating model. Because Type I error had not been systematically related to item residual heterogeneity for IRT-LR, the authors did not expect an association for power either. It was surprising that power was associated with heterogeneity in the presence of non-uniform DIF (this was not true for uniform DIF only). Tests simulated with non-uniform DIF had a larger overall DIF problem compared with those with uniform DIF only. Perhaps item residual heterogeneity is more likely to produce power attenuation for IRT-LR (or one of the other methods), in the presence of stronger DIF effects.
Discussion
The present study addressed item residual heterogeneity: one way an item can differ between groups that cannot be identified by popular DIF testing methods. Heterogeneity therefore represents model misfit, especially for models using the logistic function. When the possibility of item residual heterogeneity is ignored, misleading results about DIF can result. The present simulations evaluated logistic regression, IRT-LR, and the MH test to examine how or whether item residual heterogeneity influenced Type I error and power for DIF testing. Conditions varied according to the scale length, percent of items on the test with DIF, whether DIF was simulated in the discrimination parameters, and the amount of item residual heterogeneity.
As expected, the presence of item residual heterogeneity led to misleading DIF test results with logistic regression. Logistic regression should not be used if item residual heterogeneity is hypothesized or detected in prior analyses. IRT-LR was also detrimentally affected by item residual heterogeneity, just not in the way the authors predicted. Although IRT-LR may be robust to heterogeneity in certain research contexts (e.g., DIF testing with large samples, where the F-group mean and SD estimates are not interpreted), it cannot be unreservedly recommended when item residual heterogeneity is hypothesized or detected in prior analyses.
The best way to manage item residual heterogeneity may be to avoid it, perhaps through greater standardization of test administration procedures. Regardless, researchers will need empirical evidence about whether they have avoided it. Checking the item residual homogeneity assumption is difficult because most methods require constraining regression coefficients or factor loadings equal for the groups to test it, which is not generally any more tenable of an assumption than equal item residual variances. As an example, the “theta parameterization” in Mplus software (for use with latent variable models and ordinal or binary responses) permits a residual variance difference between groups but only conditional on group-equivalent thresholds and loadings (Muthén & Asparouhov, 2002).
One exception is a DGLM, as mentioned earlier in this article, wherein the mean and the variance are modeled simultaneously. These models can be used to identify significant differences in item residual variance, thereby checking the homogeneity assumption. Use of a DGLM is recommended prior to DIF testing with logistic regression or IRT-LR for checking the item residual homogeneity assumption.
When item residual heterogeneity is hypothesized due to the data-collection methodology, or detected empirically from a DGLM (or both), researchers could use the MH to test for DIF. As expected, the MH test was robust to item residual heterogeneity, showing nominal Type I error and high power for uniform DIF. This is presumably because it does not use the logistic function. However, it is important to remember that the MH test has limitations. Measurement error is not modeled, and valid application is for uniform DIF only whereas non-uniform DIF is common in real data. The Breslow–Day (BD) test (Breslow & Day, 1980) can be used with the MH to evaluate non-uniform DIF. In future research, it will be interesting to evaluate the robustness of the BD test to item residual heterogeneity.
Limitations and Future Research
This is just the first study about item residual heterogeneity and DIF testing. Future applications are needed to evaluate the extent and pervasiveness of item residual heterogeneity in empirical data sets. This can be done with a DGLM, though it would be a boon if other methods can be identified or developed for testing heterogeneity, which do not require alternative unrealistic assumptions. The present simulation conclusions should be replicated, extended, and re-evaluated with different types of simulated data. Item residual heterogeneity is a type of model misfit, so exploration of how it interacts with other types of model misfit is warranted. Also related to the issue of fit, data were generated for the present simulations using an IRT model, but two of the three DIF-testing methods evaluated here were not IRT-based. The data generation procedures could be varied in future simulations. Experimental research is needed to learn about how item writing or test administration procedures may produce or avoid item residual heterogeneity. The performance under heterogeneity of many other DIF-testing methods could be evaluated in future research.
One limitation of the present simulations is that effect sizes were not examined. Although effect sizes are important in research, the authors focused here on Type I error and power because many DIF-testing contexts use only binary decision making about including or excluding items. Also, the metrics of the effect sizes corresponding to the three methods the authors focused on are not all comparable with each other, or with the true effect size. Nevertheless, it would be useful to evaluate the accuracy of DIF effect size estimates in future research. Relatedly, the authors found differences in power attenuation for conditions with uniform versus non-uniform DIF that may have been due to differences in the overall amount of DIF in the data. It will be interesting in future research to systematically examine whether the amount of simulated DIF moderates the detrimental effects of item residual heterogeneity.
Supplementary Material
Footnotes
Authors’ Note: The first author is jointly appointed in Psychology and the Center for Research Methods and Data Analysis at the University of Kansas.
Declaration of Conflicting Interests: The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Funding: The author(s) received no financial support for the research, authorship, and/or publication of this article.
Supplemental Material: The online appendix is available at http://apm.sagepub.com/supplemental
References
- Allison P. D. (1999). Comparing logit and probit coefficients across groups. Sociological Methods & Research, 28, 186-208. [Google Scholar]
- Benjamini Y., Hochberg Y. (1995). Controlling the false discovery rate: A practical and powerful approach to multiple testing. Journal of the Royal Statistical Society, Series B, 57, 289-300. [Google Scholar]
- Bennett R. E., Rock D. A., Kaplan B. A. (1987). SAT differential item performance for nine handicapped groups. Journal of Educational Measurement, 24, 41-55. [Google Scholar]
- Birnbaum A. (1968). Some latent trait models. In Lord F. M., Novick M. R. (Eds.), Statistical theories of mental test scores (pp. 395-479). Reading, MA: Addison & Wesley. [Google Scholar]
- Bock R. D., Aitkin M. (1981). Marginal maximum likelihood estimation of item parameters: An application of the EM algorithm. Psychometrika, 46, 443-459. [Google Scholar]
- Breslow N. E., Day N. E. (1980). Statistical methods in cancer research: Vol. 1—The analysis of case-control studies. Lyon, France: International Agency for Research on Cancer. [PubMed] [Google Scholar]
- Camilli G., Shepard L. A. (1994). Methods for identifying biased test items. Thousand Oaks, CA: Sage. [Google Scholar]
- Clark L. (1996). SNAP Manual for administration, scoring, and interpretation. Minneapolis: University of Minnesota Press. [Google Scholar]
- Dunn P. K., Smyth G. K. (2012). Package dglm: Double generalized linear models (version 1.6.2) [R software]. Retrieved from http://cran.us.r-project.org/
- Hoetker G. (2007). The use of logit and probit models in strategic management research: Critical issues. Strategic Management Journal, 28, 331-343. [Google Scholar]
- Holland P. W. (1985). On the study of differential item performance without IRT. In Proceedings of the 17th Annual Conference of the Military Testing Association (Vol. 1, pp. 282-287). San Diego, CA: Navy Personnel Research and Development Center. [Google Scholar]
- Holland P. W. (1990). On the sampling theory foundations of item response theory models. Psychometrika, 55, 577-601. [Google Scholar]
- Holland P. W., Thayer D. T. (1988). Differential item performance and the Mantel-Haenszel procedure. In Wainer H., Braun H. I. (Eds.), Test validity (pp. 129-145). Hillsdale, NJ: Erlbaum. [Google Scholar]
- Johnson N., Kotz S., Balakrishnan N. (1995). Continuous univariate distributions (Vol. 2, 2nd ed.). New York, NY: Wiley. [Google Scholar]
- Li Y., Brooks G. P., Johanson G. A. (2012). Item discrimination and Type I error in the detection of differential item functioning. Educational and Psychological Measurement, 72, 847-861. [Google Scholar]
- Long J. S. (2009). Group comparisons in logit and probit using predicted probabilities. Retrieved from http://www.indiana.edu/~jslsoc/research_groupdif.htm
- Mantel N., Haenszel W. (1959). Statistical aspects of the analysis of data from retrospective studies of disease. Journal of the National Cancer Institute, 22, 719-748. [PubMed] [Google Scholar]
- Mellenbergh G. J. (1989). Item bias and item response theory. International Journal of Educational Research, 13, 127-143. [Google Scholar]
- Millsap R. E. (2011). Statistical approaches to measurement invariance. New York, NY: Taylor & Francis. [Google Scholar]
- Monahan P. O., Ankenmann R. D. (2005). Effect of unequal variances in proficiency distributions on Type-I error of the Mantel-Haenszel chi-square test for differential item functioning. Journal of Educational Measurement, 42, 101-131. [Google Scholar]
- Mood C. (2010). Logistic regression: Why we cannot do what we think we can do, and what we can do about it. European Sociological Review, 26, 67-82. [Google Scholar]
- Muthén B., Asparouhov T. (2002). Latent variable analysis with categorical outcomes: Multiple group and growth modeling in Mplus (Mplus Web Notes: No. 4 [version 5]). Retrieved from http://www.statmodel.com/examples/webnote.shtml#web4
- Pei L., Li J. (2010). Effects of unequal ability variances on the performance of logistic regression, Mantel-Haenszel, SIBTEST IRT, and IRT likelihood ratio for DIF detection. Applied Psychological Measurement, 34, 453-456. [Google Scholar]
- Smyth G. K., Verbyla A. P. (1999). Adjusted likelihood methods for modeling dispersion in generalized linear models. Environmetrics, 10, 695-709. [Google Scholar]
- Swaminathan H., Rogers H. J. (1990). Detecting differential item functioning using logistic regression procedures. Journal of Educational Measurement, 27, 361-370. [Google Scholar]
- Thissen D. (2001). IRTLRDIF v2.0b: Software for the computation of the statistics involved in item response theory likelihood-ratio tests for differential item functioning. Documentation for computer program [Computer software and manual]. Chapel Hill: L. L. Thurstone Psychometric Laboratory, University of North Carolina. [Google Scholar]
- Thissen D., Steinberg L., Gerrard M. (1986). Beyond group-mean differences: The concept of item bias. Psychological Bulletin, 99, 118-128. [Google Scholar]
- Thissen D., Steinberg L., Kuang D. (2002). Quick and easy implementation of the Benjamini-Hochberg procedure for controlling the false positive rate in multiple comparisons. Journal of Educational and Behavioral Statistics, 27, 77-83. [Google Scholar]
- Thissen D., Steinberg L., Wainer H. (1988). Use of item response theory in the study of group difference in trace lines. In Wainer H., Braun H. (Eds.), Test validity (pp. 147–169). Hillsdale, NJ: Erlbaum. [Google Scholar]
- Thissen D., Steinberg L., Wainer H. (1993). Detection of differential item functioning using the parameters of item response models. In Holland P. W., Wainer H. (Eds.), Differential item functioning (pp. 67-113). Hillsdale, NJ: Erlbaum. [Google Scholar]
- Williams R. (2009). Using heterogeneous choice models to compare logit and probit coefficients across groups. Sociological Methods & Research, 37, 531-559. [Google Scholar]
- Williams R. (2011, September). Comparing logit and probit coefficients between models and across groups. Colloquium presented at the University of Kansas, Lawrence. [Google Scholar]
- Williams V. S. L., Jones L. V., Tukey J. W. (1999). Controlling error in multiple comparisons, with examples from state-to-state differences in educational achievement. Journal of Educational and Behavioral Statistics, 24, 42-69. [Google Scholar]
- Woods C. M., Oltmanns T. F., Turkheimer E. (2009). Illustration of MIMIC-model DIF testing with the schedule for nonadaptive and adaptive personality. Journal of Psychopathology and Behavioral Assessment, 31, 320-330. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.