Exploring Rubric-Related Multidimensionality in Polytomously Scored Test Items

Abstract

Test items scored as polytomous have the potential to display multidimensionality across rating scale score categories. This article uses a multidimensional nominal response model (MNRM) to examine the possibility that the proficiency dimension/dimensional composite best measured by a polytomously scored item may vary by score category, an issue not generally considered in multidimensional item response theory (MIRT). Some practical considerations in exploring rubric-related multidimensionality, including potential consequences of not attending to it, are illustrated through simulation examples. A real data application is applied in the study of item format effects using the 2007 administration of Trends in Mathematics and Science Study (TIMSS) among eighth graders in the United States.

Constructed response (CR) items have become increasingly popular in standardized testing, with many tests now using both multiple-choice and CR formats. The combination of item types has led to dimensionality studies of construct equivalence across format types, yielding varying results (see, for example, Rodriguez, 2003; Thissen, Wainer, & Wang, 1994; Wang, Drasgow, & Liu, 2016). As CR items are frequently scored using partial credit, the use of multidimensional item response theory (MIRT) models requires models that can accommodate more than two score categories per item.

In MIRT settings, it is not always clear how partial credit items should be scored with respect to the different underlying proficiency dimensions. Many unidimensional IRT models applied to polytomously scored items can be viewed as special cases of a nominal response model (NRM; Bock, 1972) that apply fixed interval scoring of the items (see Muraki, 1992; Thissen & Steinberg, 1986). The assumption of fixed equal-interval scoring is generally carried over to multidimensional extensions of these models as well (e.g., Yao & Schwarz, 2006), where items are also assumed to measure a consistent proficiency dimension, or composite of dimensions, across score categories. This assumption of a constant proficiency composite is also present in other multidimensional models applied to polytomously scored items, such as the multidimensional graded response model (Muraki & Carlson, 1993), as well as the traditional multiple common factor model (Thurstone, 1947). Reckase (2009), however, has noted the potential for different skills to be associated with different scores on an item. He presents a hypothetical scenario in which the rubric for scoring a writing sample might at lower item score levels distinguish with respect to simple writing mechanic skills, but at higher item scores in terms of organization and style of writing (Reckase, 2009, pp. 110-111). If such skills are statistically distinguishable, an item scored in this way might be viewed as displaying multidimensionality across the rating scale. As Reckase (2009) noted, such occurrences are not captured in previously described MIRT models, and represent a potential place for new model development.

The goal of this article is to illustrate the capability of a multidimensional nominal response model (MNRM; Thissen, Cai, & Bock, 2010) to capture the situation considered by Reckase (2009). Relative to previous models that have allowed for different proficiencies across score categories (e.g., Kelderman & Rijkes, 1994), the approach in this article is exploratory with respect to the scoring of items across dimensions, as the potential for rubric-related multidimensionality could also emerge in conditions where the nature of the underlying proficiency dimensions is unknown. An example might be a mathematics test containing partial credit word problems. Such applied problems frequently introduce a language-related statistical dimension (Wu & Adams, 2006), especially when the ability to interpret what is being asked has the potential to interfere with measuring the examinee mathematics proficiency. In such a case, a score of partial credit versus no credit may be highly related to language proficiency, as the inability to process the item may preclude obtaining even partial credit, while higher score categories (i.e., the distinction between full and partial credit) may be more related to mathematics problem solving. Importantly, such differences across score categories may be present even though the scoring rubric does not make apparent the different proficiencies involved.

The NRM and Special Cases

The NRM (Bock, 1972) is frequently presented as a model for item score categories with an unknown (or only partially known) ordering. The model expresses the probability of scoring in category k (= 1, . . . , K) on an item j as

$$P\left(U_j=k|\theta \right)=\frac{\exp \left(a_{jk}\theta +c_{jk}\right)}{{\displaystyle \sum _{h=1}^K\exp \left(a_{jh}\theta +c_{jh}\right)}},$$

where $\mathrm{\theta }$ denotes a person proficiency level, $a_{\mathrm{jk}}$ denote item category slope parameters, and $c_{\mathrm{jk}}$ are category intercept parameters. For statistical identification, constraints must be imposed across category parameters within each item, usually either an effect coding constraint (i.e., $\sum _k{a}_{\mathrm{jk}}=0$ and $\sum _k{c}_{\mathrm{jk}}=0$ for each item j), or a statistically equivalent first category constraint (i.e., $a_{j1}=0;c_{j1}=0$ for each item j). A useful feature of the NRM relates to its category slope parameters $a_{j1},a_{j2},\dots ,a_{\mathrm{jK}}$, which define the scoring of the item. This feature is useful not just when the score categories are nominal but also, as in the case of partial credit items, when the ordering is known but the relative spacing of categories is not.

In the unidimensional case, models such as the partial credit model (PCM; Masters, 1982) and generalized partial credit model (GPCM; Muraki, 1992) have been considered as special cases of the NRM in which the scoring is defined using specified (and typically equally spaced) values for the score categories (Thissen & Steinberg, 1986). The GPCM can be written as

$$P(U_j=k|\mathrm{\theta })=\frac{\exp \{a_j^{*}\left[(k-1)\mathrm{\theta }\right]-\sum _{t=1}^k{d}_{\mathrm{jt}}\}}{\sum _{h=1}^K\exp \{a_j^{*}\left[(h-1)\mathrm{\theta }\right]-\sum _{t=1}^h{d}_{\mathrm{jh}}\}},$$

where $a_j^{*}$ is an item discrimination parameter, and $d_{\mathrm{jk}}$ represent category threshold parameters, with $d_{j1}$ = 0 for each j. The PCM is a special case of Equation 2, where $a_j^{*}$ = 1 for all j. When applying the first category constraint of the nominal model mentioned above, the GPCM can thus be viewed as a special case of Equation 1, where $a_{j1}=a_j^{*}0,a_{j2}=a_j^{*}1,\dots ,a_{\mathrm{jK}}=a_j^{*}(K-1)$ and $d_{\mathrm{jk}}=c_{\mathrm{jk}}-c_{j,k-1}$ for all k > 1, while the PCM is a special case where also $a_{j1}=0,a_{j2}=1,\dots ,a_{\mathrm{jK}}=K-1$ (Thissen & Steinberg, 1986). As the category slopes define the scoring of the item with respect to the latent trait, both the PCM and GPCM can be seen as assuming fixed interval-level scoring across score categories that is equal (up to a proportionality constraint defined by the item discrimination parameter in the GPCM) across items.

Multidimensional Extensions of the Nominal Model

Some recent applications of the nominal model have considered its generalization to multiple traits or proficiencies (Bolt & Johnson, 2009; Falk & Cai, 2016; Thissen et al., 2010). The MNRM expresses the probability of scoring in category k as

$$P(U_j=k|{\mathrm{\theta }}_1,{\mathrm{\theta }}_2,\dots ,{\mathrm{\theta }}_M)=\frac{\exp (a_{\mathrm{jk}1}{\mathrm{\theta }}_1+a_{\mathrm{jk}2}{\mathrm{\theta }}_2+\dots +a_{\mathrm{jkM}}{\mathrm{\theta }}_M+c_{\mathrm{jk}})}{\sum _{h=1}^K\exp (a_{\mathrm{jh}1}{\mathrm{\theta }}_1+a_{\mathrm{jh}2}{\mathrm{\theta }}_2+\dots +a_{\mathrm{jhM}}{\mathrm{\theta }}_M+c_{\mathrm{jh}})},$$

where $\mathbf{\theta }={\mathrm{\theta }}_1,{\mathrm{\theta }}_2\dots ,{\mathrm{\theta }}_M$ denote M latent person proficiencies, $a_{\mathrm{jk}1},a_{\mathrm{jk}2},\dots ,a_{\mathrm{jkM}}$ denote the corresponding item category slope parameters for item j and category k, and $c_{\mathrm{jk}}$ are category intercept parameters. As for the unidimensional model, for identification purposes, either effect coding constraints, that is, $\sum _k{a}_{\mathrm{jkm}}=0$ and $\sum _k{c}_{\mathrm{jk}}=0$, or first category constraints, that is, $a_{j1m}=0;c_{j1}=0$, are imposed on the category parameters for each item j and for each dimension m.θ is arbitrarily assigned a mean of 0 and an identity covariance matrix. In this article, θ is also assumed to be multivariate normal.

As in the unidimensional case, multidimensional extensions of the PCM and GPCM can be viewed as special cases of the MNRM (Thissen et al., 2010). Under the MNRM, there are potentially distinct $a_{\mathrm{jk}1},a_{\mathrm{jk}2},\dots ,a_{\mathrm{jkM}}$ across items, score categories and dimensions. As mentioned earlier, most applications of MIRT with polytomous items assume constant scoring across dimensions, at least up to a proportionality constraint. Under the multidimensional PCM (MPCM; Yao & Schwarz, 2006), for example, the probability of scoring in category k is expressed as

$$P(U_j=k|{\mathrm{\theta }}_1,{\mathrm{\theta }}_2,\dots ,{\mathrm{\theta }}_M)=\frac{\exp [(k-1)(a_{j1}^{*}{\mathrm{\theta }}_1+a_{j2}^{*}{\mathrm{\theta }}_2+\dots +a_{\mathrm{jm}}^{*}{\mathrm{\theta }}_M)-\sum _{t=1}^k{d}_{\mathrm{jt}}]}{\sum _{h=1}^K\exp [(h-1)(a_{j1}^{*}{\mathrm{\theta }}_1+a_{j2}^{*}{\mathrm{\theta }}_2+\dots +a_{\mathrm{jm}}^{*}{\mathrm{\theta }}_M)-\sum _{t=1}^h{d}_{\mathrm{jh}}]},$$

where ${\mathbf{a}}_{\mathrm{j}}^{*}=(a_{j1}^{*},a_{j2}^{*},\dots ,a_{\mathrm{jm}}^{*})$ is now a vector of dimension-specific item discrimination parameters. Because the vector is constant across score categories, and is multiplied by category scores of 0, . . . , K − 1 for all dimensions, the resultant scoring is equivalent across dimensions up to a multiplicative constant. For example, if for a given item j the scoring with respect to Dimension 1 is 0, $a_{j1}^{*}$, 2 $a_{j1}^{*}$, . . . (K − 1) $a_{j1}^{*}$, then the scoring with respect to Dimension 2 is the same vector multiplied by $a_{j2}^{*}/a_{j1}^{*}$.

This proportionality constraint can also be understood in relation to direction of measurement, where the vector of category slopes is viewed geometrically (see, for example, Ackerman, 1994; Reckase, 1985). The MPCM assumes that the direction of best measurement stays constant across successive score categories, a direction represented by ${\mathrm{a}}_{\mathrm{j}}^{*}$. As for the GPCM, the thresholds of the MPCM are a function of the category intercepts of the MNRM, that is, $d_{\mathrm{jk}}=c_{j,k+1}-c_{\mathrm{jk}}$, where $d_{j1}=0$.

Thissen et al. (2010) considered a multidimensional nominal model in which category scoring is estimated as under the unidimensional nominal model, but is assumed to be constant across dimensions. Like the MPCM, the model assumes that the measurement direction is constant within an item, but with flexibility in terms of the ordering and spacing of the intermediate score categories. Despite the increased flexibility afforded by the Thissen et al. (2010) model, it does not address the scenario presented by Reckase (2009) in which a single item distinguishes between different dimensions or dimensional composites across score categories. This possibility is considered in the next section.

Dimension-Specific Item Scoring and the Multidimensional Nominal Response Model

Recent applications of the MNRM (e.g., Bolt & Johnson, 2009; Falk & Cai, 2016) have illustrated value in allowing the score category slopes to differ across latent traits. Kelderman and Rijkes (1994) have also presented a model with dimension-specific scoring in the form of an MPCM where differences between successive score categories were specified to either measure or not measure particular proficiency dimensions. In this article, the possibility of empirically estimating the category slopes within the MNRM is considered, as typically occurs for the NRM. Importantly, the estimated scoring can vary across dimensions, and is therefore freed from the proportionality constraint of the MPCM. This type of modeling resembles closely how optimal scaling can be applied within principal components analysis (see, for example, Meulman, Van der Kooij, & Heiser, 2004). We discuss some implications of the relationship with this method in discussion.

Of course, a significant issue related to dimension-specific scoring is the large number of model parameters introduced. The model may become particularly unwieldy for items having many score categories and/or dimensions. Category slope parameters may be estimated poorly unless sample sizes are large. In addition, when applied in a purely exploratory fashion, there is a similar rotational indeterminacy as occurs in traditional exploratory factor analysis (Bolt & Johnson, 2009). As a result, restricted versions of the model in Equation 3 would be desirable in many settings. For example, when a consistent scoring rubric is applied across items, it may be reasonable to apply equality constraints across items (i.e., $a_{1\mathrm{km}}=a_{2\mathrm{km}}=\dots =a_{\mathrm{Jkm}}$) for each category k and each dimension m. To the extent that the resulting estimates might also be viewed as defining a type of “average” across items scored using a common rating scale, the estimates may inform how the individual categories of the score scale tend to differentially distinguish across dimensions, as in the example of Reckase (2009). Another useful form of constraint are zero constraints, particularly as imposed for a given item j on a particular dimension m (e.g., $a_{j1m}=a_{j2m}=\dots =a_{\mathrm{jKm}}=0$). Zero constraints function in the same way as zero loading constraints in confirmatory factor analysis, and can reflect settings in which the dimensions are defined only by select items. Finally, monotonicity constraints across categories within an item for a given dimension m (i.e., $a_{j1m}\le a_{j2m}\le \dots \le a_{\mathrm{jKm}}$) are also considered. Monotonicity constraints may be sensible where the score categories possess a known ordering, as in partial credit scoring. Such an application in a real data example is considered shortly.

Another potential advantage of the more flexible MNRM approach relates to how the resulting category estimates can be interpreted. Specifically, the difference in category slopes for successive score categories along a given proficiency dimension indicates how well the successive score categories measure that dimension. Consider, for example, a three-category item with category slopes of 0, 0.7, 2.0 on Proficiency Dimension 1, and 0, 0.8, 1.0 on Proficiency Dimension 2 (or equivalently using effects coding, −0.9, −0.2, and 1.1 on Dimension 1 and −0.6, 0.2, and 0.4 on Dimension 2). When viewed in terms of item discrimination (as in the GPCM), these vectors inform about measurement of the underlying dimensions both in an absolute and relative sense. In this instance, based on the relative differences in the category slope estimates across dimensions, it can be seen that the first pair of categories measures more Dimension 2 than Dimension 1, specifically, (.8 − 0) / (.7 − 0) = .8 / .7 = 1.14 times greater, while the second pair of successive categories measures more Dimension 1 than Dimension 2, specifically, (2.0 − .7) / (1.0 − .8) = 1.3 / .2 = 6.5 times greater. When combined with information provided by the corresponding threshold estimate ($d_{\mathrm{jk}}=c_{j,k+1}-c_{\mathrm{jk}}$), an item vector representation like that presented by Reckase (1985) and discussed by Ackerman (1994) can be provided for each pair of successive score categories within an item, as illustrated below.

Estimation of an MNRM can be implemented using Latent Gold syntax (Vermunt & Magidson, 2008) through the specification of continuous factors using the Cluster module (see Supplementary Appendix). The use of Latent Gold for this purpose is discussed in the next section.

Simulation Illustrations

The purpose of these simulation illustrations is to demonstrate how rubric-related multidimensionality can in fact go undetected when applying traditional psychometric procedures for evaluating multidimensionality. In this article, two examples are considered; additional analyses reflecting alternative simulation conditions and results are provided in the online Supplementary Appendix. In the first example, an item response dataset is simulated for 2,000 examinees administered 20 items each having three score categories. Two underlying proficiency dimensions are assumed and responses using Equation 3 are simulated. A two-step process is taken to generate category slope parameters for each item. An initial item discrimination (slope) parameter for each item was first generated as $s_j~\mathrm{Uniform}(.8,1.5)$, with the corresponding category slope vectors of Equation 3 then defined as a_j1 = (0, s_j, s_j) for Dimension 1, and as a_j2 = (0, 0, s_j) for Dimension 2. This approach constrains the directions of measurement associated with each pair of successive score categories to be the same across items, while allowing the amount of discrimination to vary across items. Next, for item category intercept parameters, $c_{j1}=0$, $c_{j2}~\mathrm{Uniform}(-2,2)$ and $c_{j3}~\mathrm{Uniform}(-2,2)$ are generated. Finally, person parameters were generated as bivariate normal, with a mean vector of 0, variances of 1, and a correlation of .3, so as to make the multidimensionality introduced substantial.

In a second example, data to four-category items are simulated such that the first pair of successive categories (1 to 2) reflect Dimension 1, the second pair of categories (2 to 3) an equal composite of Dimensions 1 and 2, and the third pair of categories (3 to 4) Dimension 2. Responses for 2,000 examinees to 20 items are again simulated using an MNRM, where initial item discrimination (slope) parameters for each dimension are generated as $s_j~\mathrm{Uniform}(.8,1.5)$, but now with the corresponding category slopes of Equation 3 defined as a_j1 = (0, 1.0*s_j, 1.71*s_j, 1.71*s_j) and a_j2 = (0,0,.71*s_j,1.71*s_j). For item category intercept parameters, $c_{j1}=0$, $c_{j2}~\mathrm{Uniform}(-2,2)$, $c_{j3}~\mathrm{Uniform}(-2,2)$ and $c_{j4}~\mathrm{Uniform}(-2,2)$ are generated. Person parameters were again simulated as bivariate normal, with a mean vector of 0, variances of 1, and a correlation of .3. In contrast to the first simulation example, the second example simulates a condition in which the distinction between Score Categories 1 and 2 again reflects Dimension 1, while Score Categories 2 and 3 now reflect an equally weighted composite of Dimensions 1 and 2, and score categories 3 and 4 reflect Dimension 2. (Note that the use of the coefficients .71 and 1.71 make the multidimensional discrimination provided by the distinction between Score Categories 2 and 3 equal to the other successive score categories.)

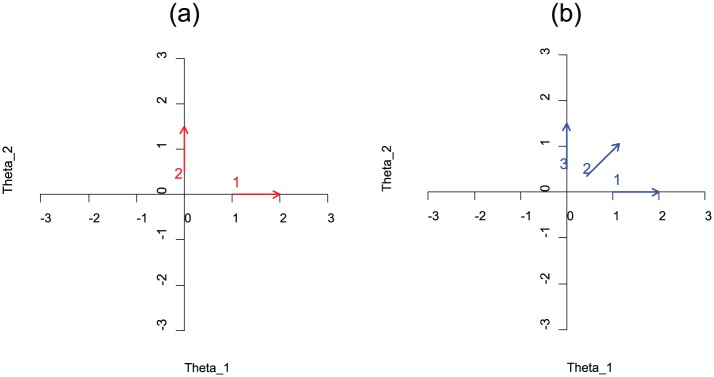
As described earlier, the nature of the multidimensionality simulated in these examples can also be illustrated graphically (Ackerman, 1994). Figure 1a and 1b illustrates item vector plots for hypothetical items from each of Simulations 1 and 2. Each item vector corresponds to a pair of successive score categories, implying each item in the first dataset can be displayed using two vectors, and each item in the second dataset by three vectors. The tail of the vector is positioned $d_{j,k+1}=(c_{j,k+1}-c_{\mathrm{jk}})$ units from the origin, while each vector has a direction and length defined by the category slope differences (i.e., $a_{j,k+1,1}-a_{\mathrm{jk}1},a_{j,k+1,2}-a_{\mathrm{jk}2}$) for k = 1, . . . , K− 1. As the MNRM reduces to a multidimensional two-parameter logistic model (M2PL) when considering only a single pair of successive score categories, the interpretation parallels that of the M2PL vectors (Ackerman, 1994; Reckase, 1985), except now it relates to the conditional probability of scoring in the higher of two successive item score categories. Specifically, the direction of the vector defines the direction in the two-dimensional proficiency space at which the conditional probability surface maximally increases, and the length of the vector reflects the rate of increase. The tail of the vector corresponds to that location in the space at which the maximal increase occurs.

Figure 1.

Item Category Vector Plots, Simulation Datasets 1(a) and 2(b).

Note that in both simulations, the generated item vectors for the same pair of successive categories are all oriented in the same directions across items; however, the items vary with respect to the locations of their vector tails (i.e., thresholds) and vector lengths (magnitude of discrimination). As illustrated in Figure 1, in the three category items, the first vector for each item is positioned in the direction of ${\mathrm{\theta }}_1$ and the second vector in the direction of ${\mathrm{\theta }}_2$. For the four-category items, the first vector is positioned in the direction of ${\mathrm{\theta }}_1$, the second vector in a direction the reflects an equal composite of ${\mathrm{\theta }}_1$ and ${\mathrm{\theta }}_2$, and the third vector in the direction of ${\mathrm{\theta }}_2$.

As noted above, the two datasets are intended to illustrate how a rubric-based multidimensionality of the kind simulated here can go undetected using traditional factor-analytic and MIRT-based dimensionality procedures. A common approach to inspecting multidimensionality considers principal component eigenvalues based on an inter-item correlation matrix. For example, the ratio of first-to-second eigenvalues, or the number of eigenvalues above 1, are common criteria for evaluating unidimensionality (Hattie, 1985). The first five eigenvalues for Dataset 1 were 4.933, .988, .913, .910, and .876; for Dataset 2, they were 7.412, 1.039, .870, .794, and .771. Thus, by both eigenvalue criteria, there would appear to be in both datasets strong support for unidimensionality. Maximum-likelihood factor loadings based on a single factor model are between .22 and .57 across variables for Dataset 1 and between .43 and .67 for Dataset 2. Consequently, applying traditional factor analysis techniques to these data would appear to quite clearly support the use of unidimensional item response models, and miss the presence of the multidimensionality simulated.

Datasets 1 and 2 were also analyzed using Latent Gold (Vermunt & Magidson, 2008) which allows for specification of not only the MNRM but also various comparison models. Unidimensional (1D), two-dimensional (2D), and three-dimensional (3D) models were fit to the datasets in which the variables (items) were specified as either “ordinal” or “nominal” and for which the item (category) slopes were or were not constrained to be equal across items. In Latent Gold, specification of an item variable as ordinal implies fixed equal-interval score categories, with a potentially varying (item)-specific slope (discrimination) parameter. Models with an ordinal specification are equivalent to a GPCM, or MPCM in the multidimensional case. Specification of an item variable as nominal implies estimated item score category slopes for each category within each dimension using effect coding constraints, equivalent to the MNRM. For models in which equal item constraints were imposed (referred to as “Equal Items” models), either the item category slope parameters (in the nominal case) or the item discrimination parameters (in the ordinal case) are constrained to be equal across all items; the category threshold/intercept parameters always freely vary across both items and categories. For the nominal models, in each case monotonicity constraints were also imposed on the score category functions for each item with respect to each dimension, that is, $a_{j,1,m}\le a_{j,2,m}\le a_{j,3,m}$ for Dataset 1, and $a_{j,1,m}\le a_{j,2,m}\le a_{j,3,m}\le a_{j,4,m}$ for Dataset 2. Such constraints allow the comparison of nominal models against ordinal models to relate only to the spacing of score categories and not their ordering.

Tables 1 and 2 displays the corresponding log-likelihood values for each the resulting twelve models fit, and the corresponding log-likelihood-based model comparison criteria for each model as provided by Latent Gold. These include the Bayesian Information Criterion (BIC), the Akaike Information Criterion (AIC), the AIC3, and the Consistent version of the AIC (CAIC). Each criterion introduces a model complexity penalty based on the number of parameters that permits a more meaningful statistical comparison across models. For each criterion, the model that performed the best is identified in bold.

Table 1.

Model Comparison Indices for Simulation Datasets 1 and 2: Simulation Dataset 1.

Model	Log-likelihood	Log-prior	Log-posterior	#pars	BIC	AIC	AIC3	CAIC
1D-ordinal, equal item	−38,320.9	−23.7	−38,344.6	41	76,953.4	76,723.7	76,764.7	76,994.4
1D-ordinal	−38,166.4	−24.0	−38,190.3	60	76,788.8	76,452.7	76,512.7	76,848.8
2D-ordinal, equal item	−38,320.5	−25.1	−38,345.6	42	76,960.2	76,725.0	76,767.0	77,002.2
2D-ordinal	−38,117.8	−25.7	−38,143.5	80	76,843.7	76,395.6	76,475.6	76,923.7
3D-ordinal, equal item	−38,320.5	−25.6	−38,346.0	43	76,967.8	76,726.9	76,769.9	77,010.8
3D-ordinal	−38,025.5	−35.0	−38,060.5	100	76,811.0	76,250.9	76,350.9	76,911.0
1D-nominal, equal itema	−37,686.3	−24.2	−37,710.6	41	75,684.3	75,454.7	75,495.7	75,725.3
1D-nominala	−37,533.6	−24.5	−37,558.1	61	75,530.9	75,189.3	75,250.3	75,591.9
2D-nominal, equal itema	−36,313.8	−28.1	−36,341.9	42	72,946.9	72,711.6	72,753.6	72,988.9
2D-nominala	−36,080.6	−28.5	−36,109.1	82	72,784.6	72,325.3	72,407.3	72,866.6
3D-nominal, equal itema	−36,329.6	−28.4	−36,357.9	43	72,986.0	72,745.1	72,788.1	73,029.0
3D-nominala	−36,083.6	−28.9	−36,112.5	101	72,934.8	72,369.1	72,470.1	73,035.8

Note. Boldfaced values indicate best model. BIC = Bayesian Information Criterion; AIC = Akaike Information Criterion; CAIC = Consistent version of the AIC.

^aWith monotonicity constraints applied. pars = Number of parameters.

Table 2.

Model Comparison Indices for Simulation Datasets 1 and 2: Simulation Dataset 2.

Model	Log-likelihood	Log-prior	Log-posterior	#pars	BIC	AIC	AIC3	CAIC
1D-ordinal, equal item	−38,016.6	−32.2	−38,048.8	61	76,496.8	76,155.1	76,216.1	76,557.8
1D-ordinal	−37,890.0	−32.5	−37,922.5	80	76,388.2	75,940.1	76,020.1	76,468.2
2D-ordinal, equal item	−37,855.1	−36.1	−37,891.2	62	76,181.5	75,834.3	75,896.3	76,243.5
2D-ordinal	−37,698.1	−37.0	−37,735.1	100	76,156.3	75,596.2	75,696.2	76,256.3
3D-ordinal, equal item	−37,854.0	−36.5	−37,890.5	63	76,186.8	75,834.0	75,897.0	76,249.8
3D-ordinal	−37,685.6	−37.6	−37,723.2	120	76,283.3	75,611.2	75,731.2	76,403.3
1D-nominal, equal itema	−37,976.2	−32.3	−38,008.5	63	76,431.2	76,078.4	76,141.4	76,494.2
1D-nominala	−37,831.3	−32.6	−37,863.9	120	76,574.7	75,902.6	76,022.6	76,694.7
2D-nominal, equal itema	−37,594.0	−36.9	−37,630.9	66	75,689.6	75,320.0	75,386.0	75,756.6
2D-nominala	−37,418.4	−37.5	−37,455.9	173	76,151.8	75,182.8	75,355.8	76,324.8
3D-nominal, equal itema	−37,589.7	−37.2	−37,626.9	69	75,703.9	75,317.4	75,386.4	75,772.9
3D-nominala	−37,367.8	−38.3	−37,406.1	233	76,506.6	75,201.6	75,434.6	76,739.6

Note. Boldfaced values indicate best model. BIC = Bayesian Information Criterion; AIC = Akaike Information Criterion; CAIC = Consistent version of the AIC.

^aWith monotonicity constraints applied. pars = Number of parameters.

Several aspects of the model comparison criteria across analyses provide insight. First, when making ordinal assumptions regarding the score categories, the presence of multidimensionality is either missed, or appears small/negligible. A comparison of the 1D-ordinal models (either with or without equality constraints) against the corresponding 2D- and 3D-ordinal models shows the 1D model to be preferred in Simulation Dataset 1. In Simulation Dataset 2, the 2D-ordinal model is preferred, but the difference between the 1D and 2D solutions is more substantial in the nominal models. Such results appear largely consistent with the factor-analytic results reported earlier. By contrast, when making nominal-level assumptions, the superiority of the 2D-nominal models over the corresponding 1D- and 3D-nominal models is much clearer, a result consistently observed across all four model comparison criteria.

As a general tool for exploring rubric-related multidimensionality, the analyses of both datasets make clear how the detection of multidimensionality really only emerges under the nominal models. Moreover, the 2D-nominal models emerge as statistically superior to all of the models under consideration. Due to the relatively small amounts of between-item variability simulated in the category slopes (uniform between .8 and 1.5), it is not surprising that the Equal Items models are at times found to be the best models.

To examine recovery of the simulated category slope estimates, the resulting category slope estimates and standard errors for the 2D-nominal equal items model for each dataset are shown in Table 3. The results suggest the ability of the model to effectively recover the relative spacing across categories of the slope estimates as simulated. In Dataset 1, it is apparent that Dimension 1 is measured only by the distinction between Categories 1 and 2, while only Dimension 2 is measured by the distinction between Categories 2 and 3. Similarly, for Dataset 2, the distinction between Categories 1 and 2 reflects only Dimension 1, while the distinction between Categories 2 and 3 is approximately equally sensitive to both Dimensions 1 and 2, and the distinction between Categories 3 and 4 is largely sensitive to only Dimension 2.

Table 3.

Estimates of Two-Dimensional Nominal Category Slopes (${\hat{a}}_{\mathrm{jk}}s$), Equal Items Model, Simulation Datasets 1 and 2.

	Dataset 1		Dataset 2
Category	Dimension 1	Dimension 2	Dimension 1	Dimension 2
1	−0.71 (.02)	−0.44 (.01)	−1.51 (.04)	−0.60 (.02)
2	0.36 (.01)	−0.44 (.01)	−0.33 (.02)	−0.60 (.02)
3	0.36 (.01)	0.89 (.02)	0.76 (.02)	0.09 (.02)
4			1.08 (.04)	1.11 (.03)

Although not shown here, results for the 2D-nominal models without the Equal Item constraint in terms of their recovery of the category slopes at the item level were also inspected. The correlations between the true and estimated category slopes were quite high (.96, .96 for Datasets 1 and 2, respectively) and the root mean square errors (RMSEs) were reasonably low (.09 and .12 for Datasets 1 and 2, respectively), suggesting reasonably good recovery.

Taken together, these results illustrate a couple of important considerations in the application of the MNRM in the possible presence of rubric-related multidimensionality. The first is the potential for multidimensionality to uniquely emerge when specifying a nominal model. Such a result can be attributed to the fact that when the nature of the multidimensionality relates to differences across score categories (what the authors refer to as rubric-related multidimensionality), the multidimensionality is missed when treating the score categories as fixed equal-interval values. The second is the potential of a 2D-nominal model to not only identify the correct dimensionality but also determine the relative spacing of score categories across dimensions. As the relative spacing of score category slopes determines measurement direction, the model makes it possible to consider how the item score categories differentially reflect the underlying proficiencies.

Real Data: Eighth Grade 2007 Trends in Mathematics and Science Study (TIMSS) Science and Math, United States

Our real data example considers item response data from the TIMSS 2007 assessment administered to 7,377 eighth graders in the United States. A total of 214 math items (116 MC, 98 CR) and 222 science items (104 MC, 118 CR) were administered. In both science and math subject areas, all multiple-choice items and a portion of the CR items were scored as correct/incorrect (0/1), while other CR items were scored as partial credit (0,1,2). For math, 22 of the CR items were partial credit, while for science, 21 were partial credit. Each student was administered two blocks of items from each subject area; each block is approximately 15 items in length. Overall, each item from the test is administered to approximately 1,000 respondents, so the data structure contains a large number of structural missings. However, due to overlap of items across administered blocks, a concurrent calibration of items within each subject area was used in the current analyses.

We considered a series of two-dimensional models in which all items loaded on a first general factor, but only the CR items (both binary and partial credit) loaded onto an orthogonal second factor. Therefore, the first factor is interpreted as a content factor (Math or Science) and the second factor as a CR format factor. The CR format factor might be viewed as reflecting aspects of performance on CR items, that is, the ability to explain reasoning, to show work, and so on, that are unique to CR items and how they are scored.

To verify the presence of multidimensionality and to explore different assumptions about the CR partial credit items, similar models were fit to those considered in the simulation analyses. The authors considered 1D models in which all items only loaded on a general factor, and a 2D model of the form described above. The authors also considered models in which the partial credit items were either treated as ordinal or nominal, and for which the item (category) slopes were either freely estimated or constrained to be equal across items (Equal Items models). For each model, the items scored as binary were always specified as nominal, although an ordinal specification would be statistically equivalent.

Tables 4 and 5 present the model comparison results. Across all eight models, the preferred models are consistently the 2D models, suggesting a detectable distinction between the CR and MC items. In this analysis, unlike the simulation illustrations, the multidimensionality is apparent under both ordinal and nominal conditions. The better-fitting models are also clearly those that allow the slope parameters to vary across items as opposed to the Equal Items models. However, the model comparison indices are inconsistent regarding a preference for nominal versus ordinal treatment of partial credit CR items. For Math, the AIC prefers the nominal model while the BIC, AIC3, and CAIC prefer the ordinal model; for Science, the AIC and AIC3 prefer the nominal model, while the BIC and CAIC prefer the ordinal model.

Table 4.

Model Comparison Indices for TIMSS 2007 Eighth-Grade Math and Science Items, U.S. Students: TIMSS Math (N = 7377).

Model	Log-likelihood	Log-prior	Log-posterior	#pars	BIC	AIC	AIC3	CAIC
1D-ordinal, equal CR item	−120,369.4	−159.6	−120,528.9	429	244,559.5	241,596.7	242,025.7	244,988.5
1D-ordinal	−120,181.2	−160.2	−120,341.5	450	2,443,702	241,262.5	241,712.5	244,820.3
2D-ordinal, equal CR itema	−119,702.9	−168.5	−119,871.4	506	243,912.3	240,417.8	240,923.8	244,418.3
2D-ordinala	−119,367.8	−170.5	−119,538.3	544	243,580.5	239,823.6	240,367.6	244,124.5
1D-nominal, equal CR item	−120,369.1	−159.5	−120,528.6	430	244,567.8	241,598.2	242,028.2	244,997.8
1D-nominal	−120,133.6	−160.3	−120,293.9	472	244,470.8	241,211.1	241,863.1	244,942.8
2D-nominal, equal CR itema	−119,709.8	−168.9	−119,878.7	507	243,935.1	240,433.7	240,940.7	244,442.1
2D-nominala	−119,311.2	−171.0	−119,482.2	583	243,814.7	239,788.4	240,371.4	244,397.7

Note. Boldfaced values indicate best model. TIMSS = Trends in Mathematics and Science Study; BIC = Bayesian Information Criterion; AIC = Akaike Information Criterion; CAIC = Consistent version of the AIC; CR = constructed response.

^aWith monotonicity constraints applied.

Table 5.

Model Comparison Indices for TIMSS 2007 Eighth-Grade Math and Science Items, U.S. Students: TIMSS Science (N = 7377).

Model	Log-likelihood	Log-prior	Log-posterior	#pars	BIC	AIC	AIC3	CAIC
1D-ordinal, equal CR item	−132,753.8	−164.0	−132,917.7	448	267,497.5	266,403.5	266,851.5	269,945.5
1D-ordinal	−132,505.2	−168.2	−132,673.5	468	269,178.5	265,946.5	266,414.5	269,646.5
2D-ordinal, equal CR itema	−132,345.5	−171.2	−132,516.7	543	269,527.1	265,777.1	266,320.1	270,070.1
2D-ordinala	−131,084.2	−197.6	−131,281.8	581	267,342.9	263,330.5	263,911.5	267,923.9
1D-nominal, equal item	−132,679.7	−163.9	−132,933.6	447	269,520.4	266,433.3	266,880.3	269,967.4
1D-nominal	−134,194.2	−167.1	−134,361.3	482	272,681.1	269,352.4	269,834.4	273,163.1
2D-nominal, equal CR itema	−132,332.9	−171.8	−132,504.6	547	269,537.4	265,759.7	266,306.7	270,084.4
2D-nominala	−130,993.6	−200.6	−131,194.2	613	267,446.7	263,213.2	263,826.2	268,059.7

Note. Boldfaced values indicate best model. TIMSS = Trends in Mathematics and Science Study; BIC = Bayesian Information Criterion; AIC = Akaike Information Criterion; CAIC = Consistent version of the AIC; CR = constructed response.

^aWith monotonicity constraints applied.

Closer inspection of the model parameter estimates under the 2D-nominal models provides insight into causes of the divergence across criteria. Although it would appear that the ordinal assumptions are suitable for many items, for a select number of items they are not. To explore this further, the category slope estimates for the 2D-nominal equal items model are first considered, as shown in Table 6. For both the math and science datasets, it appears the category slopes estimates reflect an approximately equal spacing with respect to Dimension 1 (the content—Math or Science—dimension), but a slightly unequal spacing with respect to Dimension 2 (the CR dimension). For math, it appears there is a slightly larger relative difference between Categories 1 and 2 on Dimension 2, while for Science the larger relative difference is between Categories 2 and 3. Consequently, it would seem that on average there is a difference across content areas in how Dimension 2 functions in relation to the score categories.

Table 6.

Estimates of Category Slopes (${\hat{a}}_{\mathrm{jk}}s$) and Standard Errors, 2D-Nominal Equal Items Model, TIMSS Math and Science Data, Eighth Grade, United States (N = 7,377).

	Math		Science
Category	Dimension 1	Dimension 2	Dimension 1	Dimension 2
1	−0.77 (.02)	−0.28 (.03)	−0.66 (.02)	−0.37 (.03)
2	−0.00 (.02)	0.07 (.03)	0.03 (.01)	−0.08 (.02)
3	0.78 (.02)	0.21 (.03)	0.63 (.02)	0.45 (.03)

Note. TIMSS = Trends in Mathematics and Science Study.

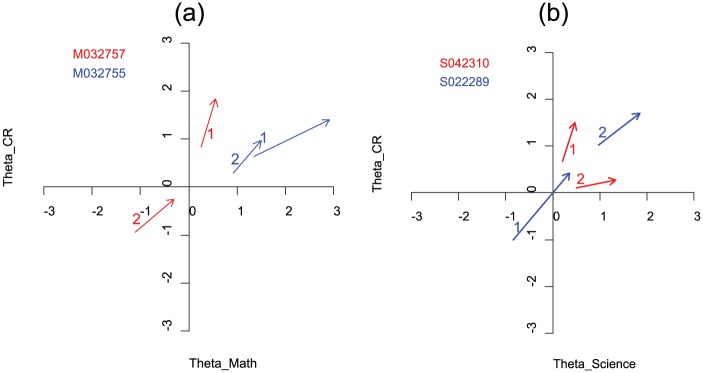
However, the superiority of the 2D-nominal model (without equal items) over the 2D-nominal with equal items model suggests allowing for differences in the category slopes across items. For illustration, a couple of example items from each content area involving items that have been released by TIMSS (see http://timssandpirls.bc.edu/timss2007/items.html and http://timssandpirls.bc.edu/timss2011/international-released-items.html) in examining these results are considered. In each case, the released information provides not only the items but also a description of criteria used for assigning partial (1) and full credit (2) to the items. Tables 7 and 8 present estimates from the 2D-nominal models for four example items, two from science and two from math. Corresponding item vector plots based on the estimates are shown in Figure 2a and 2b. For the two math items, Item M032757 demonstrates much greater variability in the angular directions of its two vectors compared with M032755. Item M032757 is an algebra item involving the presentation of patterns of tiles arranged in the form of squares. The problem itself involves identifying the sequential pattern that would permit calculation of the number of internal squares as the overall square increases in size. The problem requires identifying the next two values in the sequence. Partial credit is awarded if one of the two subsequent values is correctly provided. The item vectors for this item would suggest that obtaining partial versus no credit distinguishes mainly with respect to the CR format dimension, while full versus partial credit distinguishes mainly with respect to the math dimension. A reasonable explanation for this result is the potential for multiple strategies in solving the item, only one of which actually involves algebra. One likely strategy is to construct (draw) the squares that are next in the sequence and count the number of squares of each type. The other likely strategy will write out the algebraic equation and solve it to determine the next two values in the sequence. In the presence of two such strategies, it would seem highly plausible that the first strategy will be more prone to a type of mistake that would lead to one correct and one incorrect answer in regard to the subsequent two values. The latter strategy, if implemented correctly, will lead to both answers being solved correctly. It thus seems very natural that full credit would inform much more about mathematics proficiency than partial credit, explaining the disproportionate difference between the full and partial credit scores on the math dimension relative to the format dimension.

Table 7.

Multidimensional Nominal Category Estimates (${\hat{a}}_{\mathrm{jk}}s$) and Standard Errors for Example Items From TIMSS Math and Science Test: Math Items.

	M032757			M032755
Category	a1	a2	c	a1	a2	c
0	−0.47 (.09)	−0.88 (.15)	−0.18 (.10)	−1.24 (.11)	−0.56 (.10)	1.79 (.11)
1	−0.17 (.09)	0.10 (.15)	−0.96 (.10)	0.33 (.10)	0.19 (.10)	−.44 (.12)
2	0.64 (.07)	0.78 (.13)	1.15 (.07)	0.91 (.13)	0.37 (.12)	−1.35 (.16)

Note. TIMSS = Trends in Mathematics and Science Study.

Table 8.

Multidimensional Nominal Category Estimates (${\hat{a}}_{\mathrm{jk}}s$) and Standard Errors for Example Items From TIMSS Math and Science Test: Science Items.

	S042310			S022289
Category	a1	a2	c	a1	a2	c
0	−0.45 (.07)	−0.61 (.15)	−0.41 (.08)	−1.09 (.16)	−1.26 (.35)	−0.47 (.20)
1	−0.19 (.06)	0.22 (.11)	0.08 (.06)	0.11 (.08)	0.17 (.20)	1.24 (.15)
2	0.64 (.06)	0.39 (.12)	0.34 (.06)	0.98 (.13)	1.09 (.31)	−0.76 (.18)

Note. TIMSS = Trends in Mathematics and Science Study.

Figure 2.

Item Category Vector Plots, TIMSS Math and Science Items.

Note. Trends in Mathematics and Science Study.

By contrast, Item M032755 appears to measure a similar composite of dimensions across categories. This item, while similarly consisting of two parts and awarding partial credit for answering correctly one of the two parts, is less integrated, and yields partial credit if one of the two parts is answered correctly. Consequently, the observation of a similar measurement direction for both vectors is much more intuitive.

The two science items provide a similar contrast. Item S042310 shows substantial variability in the direction of its two vectors, while the vectors of Item S022289 are more consistent. As for M032757, inspection of the item and scoring associated with S042310 provides a likely explanation for the different directions of its vectors. In Item S042310, a diagram showing two sets of planted seeds is provided, one of which is planted under conditions of low soil nutrients and dim light, the other under conditions of high soil nutrients and bright light. The student is asked which of the two plants will grow taller and to explain why. Partial credit can be obtained simply for identifying that the latter plant will grow taller but without explanation, a result that could by random guessing be achieved with 50% probability and absent any scientific knowledge. By contrast, the full credit response must provide the scientific reason, and thus would seem more aligned with actual measurement of science proficiency.

Item S022289, by contrast, simply asks the student to provide two reasons a human’s heart beats faster with exercise. Full credit is provided if explanations related to both the physiological needs of the body and the role of the circulatory system are identified, partial credit if only one of the two explanations is provided. Like Item M032755, the sensitivity of the partial credit to no credit distinction in relation to the substantive content (in this case science proficiency) is much more apparent, and the consistency of measurement direction for both vectors of this item would appear consistent with expectations.

Conclusion and Discussion

In contexts of multidimensionality, items scored as partial credit may measure different dimensional composites across score categories (Reckase, 2009). In this article, the authors illustrate how a multidimensional nominal model can be used for exploratory study of this issue. As shown in two simulation illustrations, the actual presence of rubric-based multidimensionality can be missed when applying traditional MIRT models, such as the multidimensional PCM (Yao & Schwarz, 2006). To the extent that multidimensionality can facilitate meaningful diagnostic reports of test performances, the failure to detect it can be consequential. Use of the proposed approach may also be useful in validating individual test items, as well as the scoring applied to items in partial credit settings.

The primary goal of this article was to illustrate the potential of an MNRM in capturing conditions in which rubric-related multidimensionality may be present, Additional study is needed regarding the wide range of dimensionality conditions that are likely to be encountered in practice and the capability of an MNRM under such conditions. In many settings the nature of multidimensionality related to scoring rubrics will not be consistent across items, and will also occur in the presence of other forms of multidimensionality related to item characteristics. Future simulation work might also examine the psychometric requirements in terms of sample size and item score distributions needed for good recovery of the item category slopes.

As noted earlier, there is a close relationship between the form of IRT modeling considered in this article and optimal scaling applications as are sometimes applied with principal components analysis. As the latter methodology is less computationally intensive, a useful practical strategy may be to use an optimal scaling approach initially to explore whether dimension-based scoring appears to be important, and to follow-up with a model based approach only if so. Additional study of the relationship between these methodologies although beyond the scope of the current article, may be useful.

Further attention to multidimensionality related to item scoring in the study of item format effects would seem to be warranted. It is possible, for example, that how partial credit items are scored may play in role in understanding the heterogeneity seen in format effect correlations observed across studies (Rodriguez, 2003). Applications to other tests would also be useful. In the current TIMSS tests studied, the use of fixed equal-interval scoring for the PCMs generally appears appropriate, with a small number of individual items that showed differences. It is conceivable, for example, with tests of reading such as the Progress in International Reading Literacy Study (PIRLS) that partial credit items may display differential sensitivity to passage-based versus reading comprehension dimensions across score categories.