Critical Values for Yen’s Q₃: Identification of Local Dependence in the Rasch Model Using Residual Correlations

Abstract

The assumption of local independence is central to all item response theory (IRT) models. Violations can lead to inflated estimates of reliability and problems with construct validity. For the most widely used fit statistic Q₃, there are currently no well-documented suggestions of the critical values which should be used to indicate local dependence (LD), and for this reason, a variety of arbitrary rules of thumb are used. In this study, an empirical data example and Monte Carlo simulation were used to investigate the different factors that can influence the null distribution of residual correlations, with the objective of proposing guidelines that researchers and practitioners can follow when making decisions about LD during scale development and validation. A parametric bootstrapping procedure should be implemented in each separate situation to obtain the critical value of LD applicable to the data set, and provide example critical values for a number of data structure situations. The results show that for the Q₃ fit statistic, no single critical value is appropriate for all situations, as the percentiles in the empirical null distribution are influenced by the number of items, the sample size, and the number of response categories. Furthermore, the results show that LD should be considered relative to the average observed residual correlation, rather than to a uniform value, as this results in more stable percentiles for the null distribution of an adjusted fit statistic.

Introduction

Statistical independence of two variables implies that knowledge about one variable does not change the expectations about another variable. Thus, test items, $X_1,\dots ,X_I$, are not independent, because a student giving a correct answer to one test item would change the expectation of his or her probability of also giving a correct answer to another item in the same test. A fundamental assumption in the Rasch (1960) model and in other item response theory (IRT) models is that item responses are conditionally independent given the latent variable:

$$P(X_1=x_1,\dots ,X_I=x_I|\theta )=\underset{i=1}{\overset{I}{\Pi }}P(X_i=x_i|\theta ).$$

The items should only be correlated through the latent trait that the test is measuring (Lord & Novick, 1968). This is generally referred to as local independence (Lazarsfeld & Henry, 1968).

The assumptions of local independence can be violated through response dependency and multidimensionality, and these violations are often referred to under the umbrella term of “local dependence” (LD). Both of these situations yield interitem correlations beyond what can be attributed to the latent variable, but for very different reasons. Response dependency occurs when items are linked in some way, such that the response on one item governs the response on another because of similarities in, for example, item content or response format. A typical example is where several walking items are included in the same scale. If a person can walk several miles without difficulty, then that person must be able to walk 1 mile, or any lesser distance, without difficulty (Tennant & Conaghan, 2007). This is a structural dependency which is inherent within the items, because there is no other logical way in which a person may validly respond. Another form of LD could be caused by a redundancy–dependency, where the degree of overlap within the content of items is such that the items are not independent (i.e., where the same question is essentially asked twice, using slightly different language or synonymous descriptive words). Yen (1993) offered an in-depth discussion of ways that the format and presentation of items can cause LD.

Violation of the local independence assumption through multidimensionality is typically seen for instruments composed of bundles of items that measure different aspects of the latent variable or different domains of a broader latent construct. In this case, the higher order latent variable alone might not account for correlation between items in the same bundle.

Violations of local independence in a unidimensional scale will influence estimation of person parameters and can lead to inflated estimates of reliability and problems with construct validity. Consequences of LD have been described in detail elsewhere (Lucke, 2005; Marais, 2009; Marais & Andrich, 2008a; Scott & Ip, 2002; Yen, 1993). Ignoring LD in a unidimensional scale thus leads to reporting of inflated reliability giving a false impression of the accuracy and precision of estimates (Marais, 2013). For a discussion of the effect of multidimensionality on estimates of reliability, see Marais and Andrich (2008b).

Detecting LD

One of the earliest methods for detecting LD in the Rasch model is the fit measure Q₂ (van den Wollenberg, 1982), which was derived from contingency tables and used the sufficiency properties of the Rasch model. Kelderman (1984) expressed the Rasch model as a log-linear model in which LD can be shown to correspond to interactions between items. Log-linear Rasch models have also been considered by Haberman (2007) and by Kreiner and Christensen (2004, 2007), who proposed to test for LD by evaluating partial correlations using approach similar to the Mantel–Haenszel analysis of differential item functioning (DIF; Holland & Thayer, 1988). The latter approach is readily implemented in standard software such as SAS or SPSS. Notably, Kreiner and Christensen (2007) argued that the log-linear Rasch models proposed by Kelderman that incorporate LD still provide essentially valid and objective measurement and described the measurement properties of such models. Furthermore, a way of quantifying LD has been proposed by Andrich and Kreiner (2010) for two dichotomous items. It is based on splitting a dependent item into two new ones, according to the responses to the other item within the dependent pair. LD is then easily quantified by estimating the difference d between the item locations of the two new items. However, Andrich and Kreiner do not go on to investigate whether d is statistically significant. For the partial credit model (Masters, 1982) and the rating scale model (Andrich, 1978), a generalized version of this methodology exists (Andrich, Humphry, & Marais, 2012).

Beyond the Rasch model, Yen (1984) proposed the Q₃ statistic for detecting LD in the three parameter logistics (3PL) model. This fit statistic is based on the item residuals,

$$d_i=X_i-E(X_i|\hat{\theta }),$$

and computed as the Pearson correlation (taken over examinees),

$$Q_{3,\mathrm{ij}}=r_{d_i{d}_j},$$

where $d_i$ and $d_j$ are item residuals for items i and j, respectively. This method is often used for the Rasch model, the partial credit model, and the rating scale model.

Chen and Thissen (1997) discussed X² and G² LD statistics that, although not more powerful than the Q₃, have null distributions very similar to the chi-square distribution with one degree of freedom. Other methods for detecting LD are standardized bivariate residuals for dichotomous or multinomial IRT models (Maydeu-Olivares & Liu, 2015), the use of conditional covariances (Douglas, Kim, Habing, & Gao, 1998), or the use of Mantel–Haenszel type tests (Ip, 2001). Tests based on parametric models are also a possibility: Glas and Suarez-Falcon (2003) proposed Lagrange multiplier (LM) tests based on a threshold shift model, but bifactor models (Liu & Thissen, 2012, 2014), specification of other models that incorporate LD (Hoskens & De Boeck, 1997; Ip, 2002), or limited information goodness-of-fit tests (Liu & Maydeu-Olivares, 2013) are also possible.

The Use of the Q₃ Fit Statistic

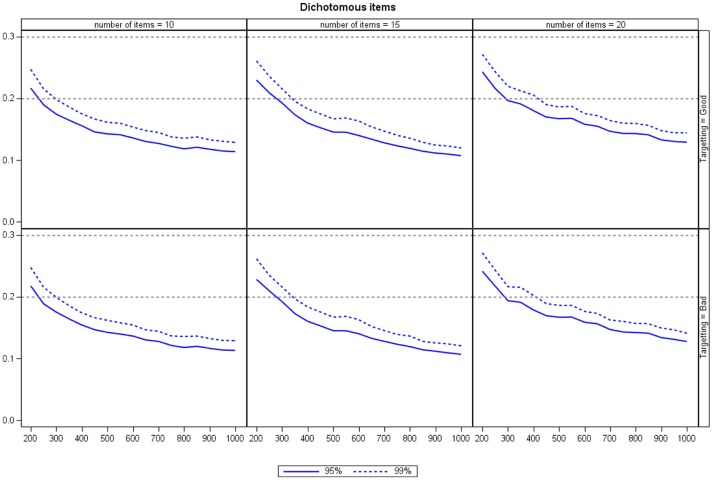
Yen’s Q₃ is probably the most often reported index in published Rasch analyses due to its inclusion (in the form of the residual correlation matrix) in widely used software such as RUMM (Andrich, Sheridan, & Luo, 2010). Yen (1984) argued that if the IRT model is correct, then the distribution of the Q₃ is known, and proposed that p values could be based on the Fisher (1915)z-transform. Chen and Thissen (1997) stated, “In using Q₃ to screen items for local dependence, it is more common to use a uniform critical value of an absolute value of 0.2 for the Q₃ statistic itself” (pp. 284-285). They went on to present results showing that, although the sampling distribution under the Rasch model is bell shaped, it is not well approximated by the standard normal distribution, especially in the tails (Chen & Thissen, 1997, Figure 3).

Figure 3.

The empirical 95th and 99th percentiles in the empirical distribution of Q_3,* for dichotomous items.

Note. Gray horizontal dashed lines indicate 0.2 and 0.3, respectively.

In practical applications of the Q₃ test statistic researchers will often compute the complete correlation matrix of residuals and look at the maximum value:

$$Q_{3,\max }={max}_{i>j}{Q}_{3,\mathrm{ij}}.$$

Critical Values of Residual Correlations

When investigating LD based on Yen’s Q₃, residuals for any pair of items should be uncorrelated, and generally close to zero. Residual correlations that are high indicate a violation of the local independence assumption, and this suggests that the pair of items have something more in common than the rest of the item set have in common with each other (Marais, 2013).

As noted by Yen (1984), a negative bias is built into Q₃. This problem is due to the fact that measures of association will be biased away from zero even though the assumption of local independence applies, due to the conditioning on a proxy variable instead of the latent variable (Rosenbaum, 1984). A second problem is that the way the residuals are computed induces a bias (Kreiner & Christensen, 2011). Marais (2013) recognized that the sampling properties among residuals are unknown; therefore, these statistics cannot be used for formal tests of LD. A third, and perhaps the most important, problem in applications is that there are currently no well-documented suggestions of the critical values which should be used to indicate LD, and for this reason, arbitrary rules of thumb are used when evaluating whether an observed correlation is such that it can be reasonably supposed to have arisen from random sampling.

Standards often reported in the literature include looking at fit residuals over the critical value of 0.2, as proposed by Chen and Thissen (1997). For examples of this, see Reeve et al. (2007); Hissbach, Klusmann, and Hampe (2011); Makransky and Bilenberg (2014); and Makransky, Rogers, and Creed (2014). However, other critical values are also used, and there seems to be a wide variation in what is seen as indicative of dependence. Marais and Andrich (2008a) investigated dependence at a critical value of 0.1, but a value of 0.3 has also often been used (see, for example, das Nair, Moreton, & Lincoln, 2011; La Porta et al., 2011; Ramp, Khan, Misajon, & Pallant, 2009; Røe, Damsgård, Fors, & Anke, 2014), and critical values of 0.5 (Davidson, Keating, & Eyres, 2004; Ten Klooster, Taal, & van de Laar, 2008) and even 0.7 (González-de Paz et al., 2015) can be found in use.

There are two fundamental problems with this use of standard critical values: (a) there is limited evidence of their validity and often no reference of where values come from, and (b) they are not sensitive to specific characteristics of the data.

Marais (2013) not only identified that the residual correlations are difficult to directly interpret confidently when there are fewer than 20 items in the item set but also stated that the correlations should always be considered relative to the overall set of correlations. This is because of the magnitude of a residual correlation value, which indicates LD will vary depending on the number of items in a data set. Instead of an absolute critical value, Marais (2013) suggested that residual correlation values should be compared with the average item residual correlation of the complete data set to give a truer picture of the LD within a data set. It was concluded that when diagnosing response dependence, item residual correlations should be considered relative to each other and in light of the number of items, although there is no indication of a relative critical value (above the average residual correlation) that could indicate LD.

Thus, under the null hypothesis, the average correlation of residuals is negative (cf. Marais, 2013) and, ideally, observed correlations between residuals in a data set should be evaluated with reference to this average value. Marais proposes to evaluate them with reference to the average of the observed correlations rather than the average under the null hypothesis. Thus, following Marais, the average value of the observed correlations could be considered:

$${\overline{Q}}_3={\left(\begin{array}{c}\hfill I\hfill \\ \multicolumn{1}{c}{2}\end{array}\right)}^{-1}\sum _{i>j}{Q}_{3,\mathrm{ij}},$$

where $\left(\begin{array}{c}\hfill I\hfill \\ \multicolumn{1}{c}{2}\end{array}\right)$ is the number of item pairs and defines the test statistic:

$$Q_{3,*}=Q_{3,\max }-{\overline{Q}}_3,$$

that compares the largest observed correlation with average of the observed correlations.

The problem with the currently used critical values is that they are neither theoretically nor empirically based. Researchers and practitioners faced with making scale validation, and development decisions need to know what level of LD could be expected, given the properties of their items and data.

A possible solution would be to use a parametric bootstrap approach and simulate the residual correlation matrix several times under the assumption of fit to the Rasch model. This would provide information about the level of residual correlation that could be expected for the particular case, given that the Rasch model fits. To the authors’ knowledge, there is no existing research that describes how important characteristics such as the number of items, number of response categories, number of respondents, the distribution of items and persons, and the targeting of the items affect residual correlations expected, given fit to the Rasch model. In the current study, the possibility of identifying critical values of LD is investigated by examining the distribution of Q₃ under the null hypothesis, where the data fit the model. This is done using an empirical example along with a simulation study.

Given the existence of the wide range of fit statistics with known sampling distributions outlined above, it is surprising that Rasch model applications abound with reporting of Q₃ using arbitrary cut-points without theoretical or empirical justification. The reason for this is that the theoretically sound LD indices are not included in the software packages used by practitioners. For this reason, this article presents extensive simulation studies that will (a) illustrate that Q₃ should be interpreted with caution and (b) allow researchers to know what level of LD could be expected, given properties of their items and data. Furthermore, these simulation studies will be used to study whether the maximum correlation, or the difference between the maximum correlation and the average correlation, as suggested by Marais (2013), is the most informative. Thus, the objectives of this article are (a) to provide an overview of the influence of different factors upon the null distribution of residual correlations and (b) to propose guidelines that researchers and practitioners can follow when making decisions about LD during scale development and validation. Two different situations are addressed: first, the situation where the test statistic is computed for all item pairs and only the strongest evidence (the largest correlation) is considered, and second, the less common case where only a single a priori defined item pair is considered.

Simulation Study

Methods

The simulated data sets used are as follows: (a) I dichotomous items simulated from

$$P(X_i=x|\theta )=\frac{\exp \left(x(\theta -{\beta }_i)\right)}{1+\exp (\theta -{\beta }_i)}(i=1,\dots ,I),$$

with evenly spaced item difficulties ${\beta }_i$ ranging from −2 to 2,

$${\beta }_i=2\left(\frac{i-1}{I-1}\right)(i=1,\dots ,I),$$

or (b) I polytomous items simulated from

$$P(X_i=x|\theta )=\frac{\exp \left(\sum _{h=1}^x(\theta -{\beta }_{\mathrm{ih}})\right)}{1+\sum _{l=1}^3\exp \left(\sum _{h=1}^l(\theta -{\beta }_{\mathrm{ih}})\right)}(x=0,1,2,3;i=1,\dots ,I),$$

with item parameters defined by

$${\beta }_{\mathrm{ih}}=2\left(\frac{i-1}{I-1}\right)+(h-1)(i=1,\dots ,I;h=1,2,3).$$

The person locations were simulated from a normal distribution with mean $\mathrm{\mu }$ and SD 1. All combinations of the four conditions—(a) number of items (I = 10, 15, 20), (b) number of persons (N = 200, 250, . . . , 1,000), (c) number of response categories (two, four), and (d) mean value in the distribution of the latent variable $\mathrm{\theta }$ ($\mathrm{\mu }$ = 0, 2)—were simulated. This yielded 204 different setups, and for each of these, 10,000 data sets were simulated and the steps followed to find the empirical 95th and 99th percentiles:

1. Estimating item parameters using pairwise conditional estimation (Andrich & Luo, 2003; Zwinderman, 1995),

2. Estimating person parameters using weighted maximum likelihood (WML; Warm, 1989),

3. Computing the residuals (Equation 2),

4. Computing the empirical correlation matrix,

5. Extracting the largest value from the correlation matrix.

Note that only data sets under the null hypothesis are simulated; there is no LD in the simulated data sets.

Results

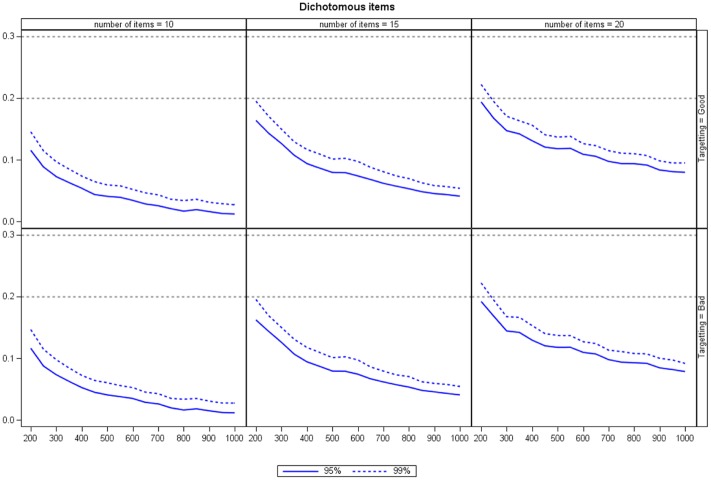
Figure 1 reports the empirical 95th and 99th percentiles in the empirical distribution of the maximum residual correlation for dichotomous items. The top panel shows $\mathrm{\mu }$ = 0 (labeled “good targeting”) and the bottom panel shows $\mathrm{\mu }$ = 2 (labeled “bad targeting”). The reason for this labeling is that the average of the item locations (the item difficulties) is zero.

Figure 1.

The empirical 95th and 99th percentiles in the empirical distribution of Q_3,max for dichotomous items.

Note. Gray horizontal dashed lines indicate 0.2 and 0.3, respectively.

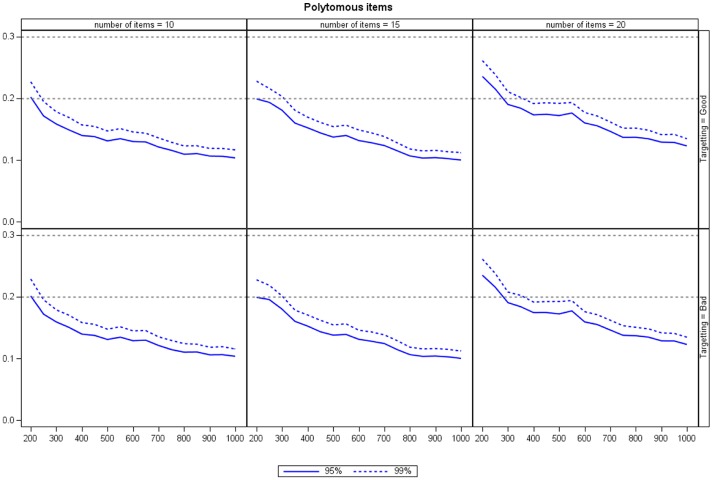
The percentiles decrease as the sample size increases, and they increase with the number of items. The latter finding is hardly surprising in a comparison of the maximum of 45, 105, and 190 item pairs, respectively. However, it is evident that the targeting does not have an impact on the percentiles. Figure 2 reports the empirical 95th and 99th percentiles in the empirical distribution of the maximum residual correlation for polytomous items. Again the top panel labeled “good targeting” shows $\mathrm{\mu }$ = 0 and the bottom panel labeled “bad targeting” shows $\mathrm{\mu }$ = 2.

Figure 2.

The empirical 95th and 99th percentiles in the empirical distribution of Q_3,max for polytomous items.

Note. Gray horizontal dashed lines indicate 0.2 and 0.3, respectively.

For N = 200, some of these percentiles were very large. Again, the percentiles decrease as sample size increases and the mean $\mathrm{\mu }$ had little impact on the percentiles.

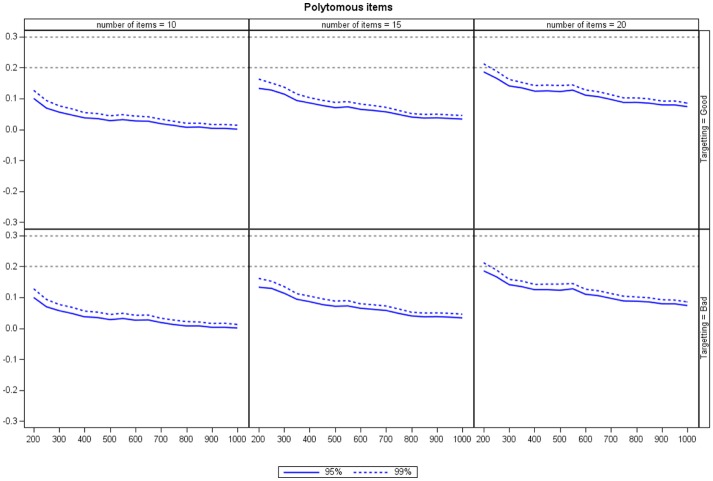
When item pairs are considered individually and computed the empirical distribution Q₃ for selected item pair, there was quite a big difference across item pairs and, again, the percentiles decrease as sample size increases while the mean $\mathrm{\mu }$ had little impact on the percentiles. Comparing the percentiles in the distribution of the correlation for a single a priori specified item pair shows that percentiles increase with the number of items (results not shown). Thus, the above finding that the percentiles in the distribution of the maximum correlation increase with the number of items is not solely due to the increase in the number of item pairs. Figures 3 and 4 show the empirical distribution of Q_3,* for dichotomous and polytomous items, respectively.

Figure 4.

The empirical 95th and 99th percentiles in the empirical distribution of Q_3,* for polytomous items.

Note. Gray horizontal dashed lines indicate 0.2 and 0.3, respectively.

When using Q_3,* rather than Q_3,max, there is a smaller effect of the number of items, but again the critical values decrease as sample size increases.

Makransky and Bilenberg Data

Methods

The empirical data example uses the Attention Deficit Hyperactivity Disorder Rating Scale–IV (ADHD-RS-IV), which has been validated using the Rasch model in a sample consisting of 566 Danish schoolchildren (52% boys), ranging from 6 to 16 years of age (M = 10.98) by Makransky and Bilenberg (2014). The parent and teacher ADHD-RS-IV (Barkley, Gwenyth, & Arthur, 1999) which is one of the most frequently used scales in treatment evaluation of children with ADHD consists of 26 items which measure across three subscales: Inattention, Hyperactivity/Impulsivity, and Conduct Problems. Parents and teachers are independently asked to rate children on the 26 items on a 4-point Likert-type scale, resulting in six subscales (three with ratings from parents and three with ratings from teachers). In this study, the authors will specifically focus on the nine items from the teacher ratings of the Hyperactivity/Impulsivity subscale. They attempted to find the empirical residual correlation critical value that should be applied to indicate LD. They did this by simulating data sets under the Rasch model, that is, data sets without LD. Using an implementation in SAS (Christensen, 2006), the simulation study was conducted by simulating 10,000 data sets under the Rasch model and, for each of these, performing the Steps (i) to (v) outlined above to find the empirical 95th and 99th percentiles.

Results

In this section, the authors describe an empirical example where they illustrate the practical challenge of deciding whether or not the evidence of LD provided by the maximum value Q_3,max of Yen’s (1984)Q₃ is large enough to violate the assumptions of the Rasch model. Makransky and Bilenberg (2014) reported misfit to the Rasch model using a critical value of 0.2 to indicate LD. Using this critical value, they identified LD between Item 2 (“Leaves seat”) and Item 3 (“Runs about or climbs excessively”) where Q₃ was 0.26, and also between Item 7 (“Blurts out answers”) and Item 8 (“Difficulty awaiting turn”) where Q₃ was 0.34 (Table 1).

Table 1.

The Observed Residual Correlation Matrix in the Makransky and Bilenberg (2014) Data for the Teacher Ratings of Hyperactivity/Impulsivity in the ADHD-RS-IV.

Item	1	2	3	4	5	6	7	8	9
1. Fidgets or squirms	1.00
2. Leaves seat	.12	1.00
3. Runs about or climbs excessively	.03	.26	1.00
4. Difficulty playing quietly	−.05	−.04	.04	1.00
5. On the go	−.09	−.25	−.02	−.14	1.00
6. Talks excessively	−.20	−.25	−.26	−.21	.03	1.00
7. Blurts out answers	−.34	−.26	−.23	−.25	−.18	.00	1.00
8. Difficulty awaiting turn	−.29	−.21	−.23	−.24	−.19	−.12	.34	1.00
9. Interrupts	−.20	−.12	−.14	−.14	−.24	−.32	.12	.12	1.00

Note. Boldface indicates values above 0.1. ADHD-RS-IV = Attention Deficit Hyperactivity Disorder Rating Scale–IV.

They were able to explain the LD based on the content of the items, for example, that students would have to leave their seat to run about or climb excessively within a classroom environment, where students are usually required to sit in their seat, and they went on to adjust the scale based on these results. Thus, the observed value of Q_3,max is 0.34, and as the average correlation ${\overline{Q}}_3$ in Table 1 is −0.12, the observed value of Q_3,* is 0.46.

As described above, there are examples in the literature where this procedure has been used with critical values of Q₃ ranging from 0.1 to 0.7. The choice of the critical value has implications for the interpretation of the measurement properties of a scale. This will, in turn, impact upon any amendments that might be made, as well as the conclusions that are drawn. Using a critical value of 0.3 would lead to the conclusion that the residual correlation value of 0.26 identified between Items 2 and 3 is not in violation of the Rasch model. A critical value of 0.7 would lead to the conclusion that there is no LD in the scale. Alternatively, a critical value of 0.1 would result in the conclusion that three additional pairs of items also exhibit LD within this data set.

Based on the estimated item and person parameters in the Makransky and Bilenberg data, 10,000 data sets from a Rasch model were simulated without LD, computed residuals, and their associated correlations. The empirical distribution of the maximum value Q_3,max based on these 10,000 data sets is shown in Figure 5.

Figure 5.

The empirical distribution of Q_3,max based on 10,000 data sets simulated using item and person parameters from the Makransky and Bilenberg (2014) data.

The 95th and 99th percentiles in this empirical distribution were 0.19, and 0.24, respectively, indicating that Makransky and Bilenberg were correct in concluding that Q_3,max = 0.34 indicated misfit. Using the parametric bootstrap results reported in Figure 1, Makransky and Bilenberg could have rejected the assumption of no LD with a p value of <.001. For nine items (as in the Makransky and Bilenberg data), there are 36 item pairs, and based on the simulated data sets, the authors are able to determine critical values for Yen’s Q₃ for each item pair. If a hypothesis about LD had been specified a priori for a single item pair (e.g., between Items 2 and 3), then it would make sense to compare the observed correlation with a percentile in the empirical distribution of correlations for this item pair. In Table 2, the median and four empirical percentiles are shown.

Table 2.

Empirical 95th and 99th Percentiles in the Empirical Distribution of the Correlations of Residuals.

				Percentile
Item 1	Item 2	Median	IQR	95th	99th
1	2	−0.07	−0.11 to −0.02	0.06	0.12
	3	−0.06	−0.11 to −0.02	0.06	0.12
	4	−0.08	−0.13 to −0.02	0.06	0.12
	5	−0.07	−0.12 to −0.02	0.06	0.13
	6	−0.07	−0.11 to −0.02	0.07	0.14
	7	−0.07	−0.12 to −0.02	0.06	0.12
	8	−0.07	−0.12 to −0.02	0.06	0.13
	9	−0.07	−0.12 to −0.02	0.06	0.13
2	3	−0.08	−0.12 to −0.03	0.05	0.10
	4	−0.09	−0.15 to −0.04	0.05	0.10
	5	−0.08	−0.13 to −0.03	0.06	0.13
	6	−0.08	−0.13 to −0.03	0.06	0.12
	7	−0.08	−0.13 to −0.03	0.05	0.12
	8	−0.08	−0.12 to −0.03	0.05	0.12
	9	−0.08	−0.13 to −0.03	0.05	0.12
3	4	−0.10	−0.15 to −0.05	0.03	0.09
	5	−0.08	−0.13 to −0.03	0.05	0.11
	6	−0.07	−0.13 to −0.02	0.06	0.12
	7	−0.08	−0.13 to −0.03	0.05	0.11
	8	−0.08	−0.13 to −0.03	0.05	0.11
	9	−0.08	−0.13 to −0.03	0.05	0.11
4	5	−0.09	−0.15 to −0.04	0.05	0.12
	6	−0.08	−0.14 to −0.03	0.06	0.12
	7	−0.10	−0.15 to −0.04	0.04	0.11
	8	−0.09	−0.15 to −0.04	0.05	0.10
	9	−0.09	−0.15 to −0.04	0.05	0.12
5	6	−0.08	−0.13 to −0.02	0.06	0.13
	7	−0.08	−0.13 to −0.03	0.06	0.12
	8	−0.08	−0.13 to −0.03	0.06	0.13
	9	−0.09	−0.14 to −0.03	0.06	0.13
6	7	−0.08	−0.13 to −0.02	0.06	0.13
	8	−0.08	−0.13 to −0.02	0.06	0.13
	9	−0.08	−0.13 to −0.02	0.06	0.13
7	8	−0.08	−0.13 to −0.03	0.06	0.12
	9	−0.08	−0.13 to −0.03	0.06	0.12
8	9	−0.08	−0.13 to −0.03	0.06	0.12

Note. Based on 10,000 data sets simulated under the Rasch model using estimated parameters from the Makransky and Bilenberg (2014) data. IQR = interquartile range.

Table 2 illustrates that the median value of the Q₃ test statistic for any item pair is negative. Table 2 further outlines the critical values that could be used for tests at the 5% and 1% level, respectively, if the hypothesis about LD was specified a priori for an item pair. These values ranged from 0.05 to 0.07 with a mean of 0.06 for the 95th, and from 0.09 to 0.14 with a mean of 0.12 for the 99th percentiles. As no a priori hypotheses about LD were made in the Makransky and Bilenberg study, the results indicate that the conclusions made using a critical value of 0.2 were reasonable. As the simulation performed is based on the estimated item and person parameters in the Makransky and Bilenberg data, it can be viewed as a parametric bootstrap approach.

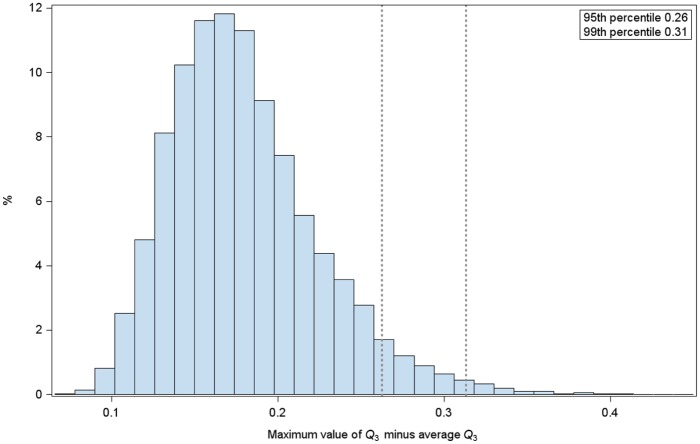
The empirical distribution of Q_3,* (the difference between Q_3,max and the average correlation ${\overline{Q}}_3$) based on these 10,000 data sets is shown in Figure 6.

Figure 6.

The empirical distribution of Q_3,* based on 10,000 data sets simulated using item and person parameters from the Makransky and Bilenberg (2014) data.

As the average value ${\overline{Q}}_3$ is negative, it is not surprising that the distribution of the Q_3,* is shifted to the right compared with the distribution of Q_3,max. The relevant critical value for a test at the 5% level is 0.26, and the relevant critical value for a test at the 1% level is 0.31. The observed value of the average correlation being ${\overline{Q}}_3=-.12$, as computed from Table 1, we see that $Q_{3,*}=0.46$. Based on this, Makransky and Bilenberg were correct in concluding that LD exists in the data.

Formally, the results in Figures 1 and 2 would enable us to reject the overall hypothesis about absence of LD and conclude that there is LD for the Item Pair 7 and 8. Of course, a parametric bootstrap approach like this could be extended from looking at the maximum value Q_3,max to looking at the empirical distribution of largest and the second largest Q₃ value. Makransky and Bilenberg report that LD between the items was successfully dealt with by combining the item pairs with LD into single combination items, and evaluating fit for the resulting seven-item scale. They further argue that item deletion is not desirable because the Hyperactivity/Impulsivity subscale in the ADHD-RS-IV is “. . . developed to assess the diagnosis in the DSM-IV and DSM-5, and the elimination of the items would decrease the content validity of the scale” (Makransky & Bilenberg, 2014, p. 702). A third alternative is to model the LD using log-linear Rasch models (Kelderman, 1984). Table 3 outlines the result obtained using item deletion and combining items, respectively. Item fit was evaluated using comparison of observed and expected item-restscore correlation (Kreiner, 2011), while Andersen’s (1973) conditional likelihood ratio test was used to evaluate scale fit.

Table 3.

Evaluation of Item and Scale Fit in Four Models With Item Deletion and a Model With Item Combination: The Makransky and Bilenberg Data.

		Deleting items
	Original scale	2 and 7	3 and 7	2 and 8	3 and 8	Combining items
Item fit
1. (Fidgets or squirms)	0.981	0.880	0.251	0.697	0.428	0.297
2. (Leaves seat)	0.989		0.558		0.695	0.650
3. (Runs about or climbs excessively)	0.005	0.008		0.009
4. (Difficulty playing quietly)	0.001	0.010	0.016	0.005	0.010	0.037
5. (On the go)	0.716	0.123	0.208	0.180	0.319	0.168
6. (Talks excessively)	0.030	0.124	0.171	0.108	0.150	0.345
7. (Blurts out answers)	0.023			0.116	0.095	0.735
8. (Difficulty awaiting turn)	0.394	0.761	0.613
9. (Interrupts)	0.772	0.996	0.782	0.854	0.906	0.196
Scale Fit	0.036	0.019	0.218	0.002	0.045	0.081

Note. Boldface indicates p < .05. Item fit evaluated using comparison of observed and expected item-restscore correlations, total fit based on Andersen’s (1973) conditional likelihood ratio test, p values reported.

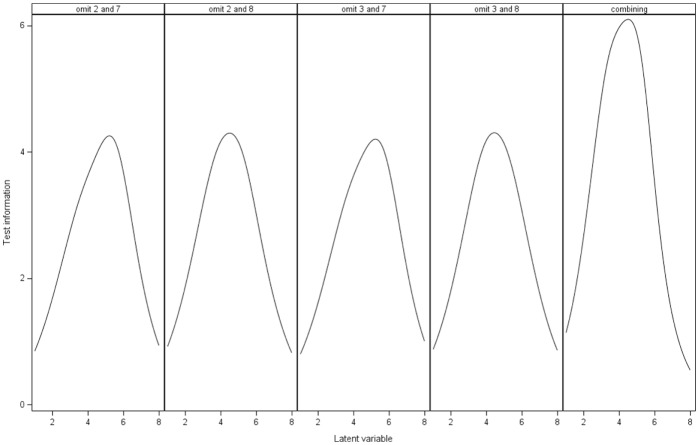
Based on the results in Table 3, we see that combining items yields the best item and scale fit. The four models are also compared with respect to the test information function (Figure 7).

Figure 7.

The test information in four models with item deletion and in the model with item combination.

Figure 7 shows that combining items yields the highest test information.

Discussion

Local independence implies that, having extracted the unidimensional latent variable, there should be no leftover patterns in the residuals (Tennant & Conaghan, 2007). The authors simulated the distribution of residuals that can be expected between two items when the data fit the Rasch model under a number of different conditions. In all instances, the critical values used to indicate LD were shown to be lower when there are fewer items, and more cases within a data set. Similar patterns were observed for dichotomous and polytomous items.

In the first part of this study, empirical percentiles were reported from the empirical distribution of the Q_3,max test statistic and the Q_3,* test statistic. We reported critical values across a number of situations with differing numbers of items, response options, and respondents and with different targeting. Each of these conditions was based on 10,000 data sets simulated under the Rasch model. The outlined parametric bootstrap method could be applied on a case-by-case basis to inform research about a reasonable choice of cut-point for the maximum value of the Q_3,max and for the Q_3,* test statistics. The second part of this study made it clear that the critical value of the Q_3,max test statistic depends heavily on the number of items, but that the Q_3,* test statistics are more stable.

In the second part of this study, the empirical 95th and 99th percentiles were reported from the empirical distribution of the maximum value Q_3,max of Yen’s (1984)Q₃ test statistic in 10,000 data sets, which were simulated under the Rasch model using the estimated item and person parameters from the Makransky and Bilenberg (2014) data. Based on this, a critical value of 0.19 was observed at the 95th percentile, and a critical value of 0.24 was observed at the 99th percentile. As the observed value was $Q_{3,\max }=0.34$, it is reasonable to conclude that there is LD in the data set.

Having disclosed evidence of LD when it is found to exist, several ways of dealing with it have been suggested. These include the deletion of one of the LD items or by fitting the partial credit model to polytomous items resulting from summation locally dependent Rasch items (Andrich, 1985; Kreiner & Christensen, 2007; Makransky & Bilenberg, 2014). Other approaches include using testlet models (Wang & Wilson, 2005; Wilson & Adams, 1995) or a bifactor model (Reise, 2012). In the analysis of the Makransky and Bilenberg (2014) data, we found that combining items yielded the best item and scale fit and the highest test information.

Summary and Recommendations

In summary, several methods for identifying LD have been suggested, but the most frequently used one appears to be Yen’s Q₃ based on computing residuals (observed item responses minus their expected values), and then correlating these residuals. Thus, in practice, LD is identified through the observed correlation matrix of residuals based on estimated item and person parameters, and residual correlations above a certain value are used to identify items that appear to be locally dependent.

It was shown that a singular critical value for the Q_3,max test statistics is not appropriate for all situations, as the range of residual correlations values is influenced by a number of factors. The critical value which indicates LD will always be relative to the parameters of the specific data set, and various factors should be considered when assessing LD. For this reason, the recommendation by Marais (2013) was that LD should be considered relative to the average residual correlation, and thus that the Q_3,* test statistic should be used. For neither of the test statistics, a single stand-alone critical value exists.

Despite no single critical value being appropriate, the simulations show that the Q_3,* critical value appears to be reasonably stable around a value of 0.2 above the average correlation. Within the parameter ranges that were tested, any residual correlation >0.2 above the average correlation would appear to indicate LD, and any residual correlation of independent items at a value >0.3 above the average would seem unlikely.

Finch and Jeffers (2016) proposed a permutation test for LD based on the Q₃ and found it to have good Type I error control, while also yielding more power for detecting LD than the use of the 0.2 cut-value. Bootstrapping and determining critical values for the Q₃ is one option, but using one of the statistics with known null distribution listed in the introduction is a better option. For researchers for whom these tests are not available, the results presented in Figures 3 and 4 yield guideline for choosing a critical value of the Q_3,max and the results presented in Figures 5 and 6 yield guideline for choosing a critical value of the Q_3,* for certain data structure situations, and the parametric bootstrap approach outlined illustrates how a precise critical value can be ascertained. A complete summary of the simulation studies is available online on the home page (http://publicifsv.sund.ku.dk/~kach/Q3/critical_values_Yens_Q3.html).