Abstract
Cognitive diagnostic modeling in educational measurement has attracted much attention from researchers in recent years. Its applications in real-world assessments, however, have been lagging behind its theoretical development. Reasons include but are not limited to requirement of large sample size, computational complexity, and lack of model fit. In this article, the authors propose to use the support vector machine (SVM), a popular supervised learning method to make classification decisions on each attribute (i.e., if the student masters the attribute or not), given a training dataset. By using the SVM, the problem of fitting and calibrating a cognitive diagnostic model (CDM) is converted into a quadratic optimization problem in hyperdimensional space. A classification boundary is obtained from the training dataset and applied to new test takers. The present simulation study considers the training sample size, the error rate in the training sample, the underlying CDM, as well as the structural parameters in the underlying CDM. Results indicate that by using the SVM, classification accuracy rates are comparable with those obtained from previous studies at both the attribute and pattern levels with much smaller sample sizes. The method is also computationally efficient. It therefore has great promise to increase the usability of cognitive diagnostic modeling in educational assessments, particularly small-scale testing programs.
Keywords: support vector machine, cognitive diagnosis, small sample size, supervised learning
Introduction
The past decade has seen rapid growth of theoretical development and application of diagnostic classification models (DCMs), also known as cognitive diagnostic models (CDMs). The popularity of the CDMs has been prompted by increasing pressure in the field of educational assessment to provide fine-grained, formative feedback to test takers. In contrast to item response theory (IRT) models which assume a continuous latent trait or multiple continuous latent traits, CDMs assume a latent cognitive profile that represents mastery status on a set of specific, discrete skills or attributes. An attribute is a task, subtask, cognitive process, or skill involved in answering an item. Using the CDMs, students can be provided estimates of their latent cognitive profiles, that is, estimates of their mastery or nonmastery status on these attributes, as opposed to just a total score or several subscores. This way CDMs enable stakeholders to better understand each student’s strengths and weaknesses.
There is a myriad of CDMs. Most of them can be considered constrained or restricted latent class models as discussed in Chiu, Douglas, and Li (2009).1 These models require the Q-matrix (Tatsuoka, 1983), which is a J×K matrix, with entry indicating item () measures the kth attribute or skill (), and otherwise. The Q-matrix is often determined prior to the analysis by content experts. This is similar to confirmatory factor analysis where the factor loading structure is predetermined before fitting the model. CDMs are also confirmatory in that certain rules are imposed to combine the latent attributes to yield response probabilities. Based on these rules, the CDMs can be largely divided into two categories: compensatory and noncompensatory. The compensatory models are those allowing a higher value on one attribute to compensate lower values on other attributes. In Appendix A (available online), two models are specifically covered: the Deterministic Input, Noisy “And” Gate (DINA) model (Haertel, 1989; Junker & Sijtsma, 2001; Macready & Dayton, 1977) and the Deterministic Input, Noisy “Or” Gate (DINO) model (Templin & Henson, 2006). The DINA model is a well-known noncompensatory model, whereas the DINO model belongs to the compensatory category.
The ultimate goal of cognitive diagnostic modeling is to estimate the latent cognitive profile or mastery profile for each test taker, . Following the notation of McGlohen and Chang (2008), for the ith examinee, the latent master profile is , where indicates that the ith examinee masters the kth attribute and otherwise. Given the CDM and the Q-matrix, one can estimate structural parameters for items and for each test taker from the N×J item response matrix, where N is the number of test takers.
As noted in Chiu and Köhn’s (2015) and Köhn, Chiu, and Brusco’s (2015) studies, likelihood-based estimation has been the predominant method of fitting cognitive diagnosis models to educational test data. For example, expectation maximization (EM) or Markov Chain Monte Carlo (MCMC) procedures have been developed to estimate structural parameters in the CDMs (de la Torre, 2009, 2011; DiBello, Roussos, & Stout, 2007; von Davier, 2008). Köhn et al. (2015) enumerated a number of challenges of applying these procedures. For example, these procedures require large sample sizes to reach stable and reliable estimates. In addition, they are susceptible to model misspecification or misfit. In practice, the underlying true model is never known. If the model is misspecified, the test takers are likely to be erroneously classified. In fact, it is difficult to identify the model that best fits the data, and it is not uncommon that a single parametric CDM is oversimplified and not flexible enough to fit all items on a test (Liu, 2015). Misspecification of the Q-matrix also results in inaccurate estimation of the latent cognitive profiles (e.g., Y. Chen, Liu, Xu, & Ying, 2015; Liu, 2015; Liu, Xu, & Ying, 2012).
Other issues of the likelihood-based estimation approaches include computational complexity, dependence on starting values, and local maxima. These drawbacks pose serious challenges to the application of CDMs to small-scale testing programs. The AP-CAT system, a National Science Foundation (NSF)-funded computerized adaptive testing (CAT) program for Advanced Placement (AP) Statistics that purports to provide formative feedback to high school students, is an example. The AP classes are typically small. With a sample size of around 300 students (Whitney, Cheng, Brodersen, & Hong, under review), it is difficult to apply even the simplest CDMs.
In light of these drawbacks, researchers have proposed several alternative procedures, generally falling under the category of unsupervised learning methods, such as K-means clustering (e.g., Chiu et al., 2009), and supervised learning methods, such as neural networks (e.g., Shu, Henson, & Willse, 2013). Unsupervised learning methods do not classify examinees into labeled categories; that is, mastery versus nonmastery. Therefore, the quality of classification is measured by an indicator of agreement between partitions, for example, the adjusted rand index (ARI; Chiu et al., 2009), instead of the rate of correct classifications. For the purpose of classifying examinees into masters and nonmasters, supervised learning methods are more suitable.
In this article, the authors propose to use support vector machine (SVM), a supervised learning approach, to perform cognitive diagnosis for each test taker. To date, little research has been done using supervised learning methods in cognitive diagnostic assessment except for the following two studies: Shu et al. (2013), a full research paper on applying neural network to cognitive diagnosis, and Kuang, Ding, and Xu (2010), a five-page conference proceeding on applying SVM. The present article differs from both in important ways: First, Shu et al. (2013) and Kuang et al. (2010) both adopted the attribute hierarchical method (AHM) by Gierl and colleagues (Gierl, 2007; Gierl, Zheng, & Cui, 2008), so that diagnostic class membership of examinees in their training datasets was “determined theoretically” rathan than empirically. Furthermore, in both studies the examinees were not classified attribute by attribute but pattern-wise. Third, the focus of Shu et al. (2013) is on recovering the structural parameters of items, and Kuang et al. (2010) on recovering the Q-matrix. In contrast, the primary focus of the current study is on classifying examinees on each attribute, and the diagnosis of examinees in the training dataset can be obtained empirically and not necessarily error free. The mastery profile of each student may come from expert rating and/or teacher focus group. It is possible to allow the use of auxiliary data explicitly or implicitly in labeling the training sample. For instance, a teacher may be very familiar with a student through daily interactions, and his or her labeling of the student on an attribute may not rely solely on the item response data. Moreover, the present method does not rely on a known Q-matrix (Köhn et al., 2015) and would not try to recover one. Therefore, the current study makes distinct contribution to our understanding of using supervised learning methods for cognitive diagnosis.
The rest of the article is organized as follows: First, the general idea of SVM will be introduced, and then how to apply SVM to classify examinees in terms of their mastery status on each attribute will be discussed. Then, a simulation study is carried out to investigate the performance of a linear-kernel SVM in classifying examinees, given very small sample sizes. Findings and their implications to educational research are discussed at the end.
Method: SVM and Its Application to Cognitive Diagnosis
As mentioned earlier, the goal of cognitive diagnosis was to obtain the mastery profile of each student, which is essentially a collection of the mastery status (represented by 0 or 1) on a number of attributes. By classifying a student in terms of his or her mastery status on each attribute, one is able to get the mastery profile for him or her. This is the idea underlying the application of SVM to cognitive diagnosis.
SVM is a well-known supervised classification method that is widely used in data mining and artificial intelligence research and applications (Boser, Guyon, & Vapnik, 1992; Hastie, Tibshirani, & Friedman, 2009; Tan, Steinbach, & Kumar, 2005; Vapnik, 1998). The algorithm tries to find the maximum-margin hyperplane as the classification boundary, by which all data points in the multidimensional space can be classified into two groups, as they fall on one of the two sides of the hyperplane. Assume that there is a training sample of M subjects with continuous response data collected on J items. The data can be projected into a J-dimensional space. The subject s in the training sample, , , can be represented as one point in the J-dimensional space. The subjects belong to two groups, in the present case, masters and nonmasters, denoted by or , respectively.
Suppose that the two groups are linearly separable; that is, there exists at least one hyperplane, such that it clearly bisects two groups of data points. In the case where such multiple hyperplanes exist, the optimal hyperplane will be one that yields the largest distance to both groups. This is because a decision hyperplane that is too close to the training data points will be sensitive to any slight noise or perturbation, and consequently likely to result in a large classification error.
Suppose a hyperplane, or classification boundary, in the J-dimensional space that clearly bisects the two groups is
where and are the parameters to determine the position of the hyperplane.Two margin hyperplanes that are parallel to the boundary hyperplane can be found, one on each side of the boundary hyperplane. These margin hyperplanes can be represented as follows:
where is a constant. With appropriate rescaling of both sides of Equation 2, the margin hyperplanes can be expressed as follows:
where = and . Therefore, the distance between the two margin hyperplanes, a.k.a. the margin, is
The optimal decision boundary is one that leads to the largest distance between two margin hyperplanes, that is, one that maximizes d, while satisfying the constraints that the two margin hyperplanes clearly bisect the two groups of data points, that is, making no classification error in the training sample. This is equivalent to maximizing d under the constraints of
These constraints could be reexpressed as for .
In practice, two groups may not be linearly separable, and a soft-margin approach can be used in this case to allow for some classification errors in the training sample. Even if two groups are linearly separable, a soft-margin approach is recommended to avoid overfitting. This is done by introducing positive-valued slack variables to the constraints:
Finding the optimal decision boundary is equivalent to finding the parameters and that maximize the distance in Equation 4 under the constraint (Equation 6). However, to minimize prediction error, a parameter can be imposed to penalize large values of slack variables. The resulting new objective function becomes , and the optimal hyperplane minimizes this function while satisfying Equation 6. The value of can be chosen based on the cross-validation.
In this study, instead of relying on the conventional likelihood-based method, the problem of estimating the latent class of each examinee is converted into finding the best boundary that separates the two groups, that is, masters versus nonmasters, for each attribute. A test taker’s responses to a J-item test can be treated as data points in a J-dimensional space. For dichotomous items, the possible value along each coordinate is either 0 or 1. Given the M test takers in the training sample whose cognitive profiles have been identified by experts, for each attribute, there are M data points in the J-dimensional space, some identified as “masters of this attribute” or “non-masters of the attribute” by the experts. In total, K SVM models will be built, one for each attribute. For a new test taker (who is not in the training sample), each one of the K SVM models will be applied to determine whether he or she masters the attributes or not.
Note that the SVM described above uses a linear kernel (see Equation 1, a linear function), and the resulting boundary between two classes is a hyperplane. Nonlinear kernels will result in hypersurfaces, for example, hyperspheres. To select an appropriate tuning parameter and the best kernel, one can use cross-validation to minimize prediction error.
A preliminary study is performed to select the kernel and the tuning parameter through 10-fold cross-validation. In -fold cross-validation, the entire training sample is divided into equal-sized subsets. One subset will be used to validate the model, while the remaining subsets are used to train the model. Each subset will be used as the validation dataset once. The overall misclassification rate is calculated as the total classification errors divided by total sample size. The choice of is arbitrary, although 10-fold cross-validation is the most common when the training sample size is large enough. Hence, is chosen for this study. If the sample size is very small, one could use leave-one-out (LOO) cross-validation instead. LOO uses data points (in the present case, test takers) as the training data and the one data point left to test the model. In this study, 10-fold cross-validation is used for the model validation.
Through cross-validation, preliminary results of the present study indicate that when using DINA and DINO as the underlying simulation models, linear-kernel SVM performs better than some commonly used nonlinear kernels. The parameter is also varied, and found to work well in most conditions. Hence in the simulation study, to classify each simulee on their mastery status on an attribute, linear-kernel soft-margin SVM is used with the tuning parameter set at .1. It is expected that in some circumstances, nonlinear kernel may perform better than the linear kernel, and a different may lead to better prediction accuracy. An additional issue to consider is the class imbalance problem. Class imbalance problem occurs when one class is substantially larger than the other; for example, when the masters substantially outnumber nonmasters. In the presence of class imbalance, the model may be biased toward the majority class. To solve this problem, one could oversample from the smaller class. Another solution is to factor the class size in the classification algorithm, for instance, using cost-sensitive learning and boosting (Japkowicz & Stephen, 2002).
Simulation Design and Results
The present study’s research question is whether SVM provides a viable alternative to conventional likelihood-based methods in performing cognitive diagnosis, particularly in situations where it is challenging to utilize the latter; for example, when the sample size is small and/or computational resources are scarce. Most research of SVM has to date centered around continuous data. In the context of testing, item response data are often dichotomous. Therefore, another goal of the current study is to find out whether SVM performs well with dichotomous data.
A simulation study was therefore conducted to examine the performance of SVM in performing cognitive diagnosis when the training sample size is small. Item response data are generated from the DINA and DINO models, respectively. Details of the two models are provided in Appendix A. Both models relate item responses to the attributes probabilistically, and both include two structural parameters for each item; that is, “slipping” () and “guessing” () for item . They represent the probability of getting an item correctly or incorrectly by chance. The two models differ in the combination rules of the attributes: The DINA model employs the “AND” rule and the DINO model the “OR” rule.
As indicated earlier, in this simulation study, linear-kernel soft-margin SVM is used with the tuning parameter set at .1. The test length is set at 30, and the number of attributes is 6. These two numbers are consistent with previous studies on cognitive diagnosis (e.g., Cheng, 2009; Wang, 2013). The tetrachoric s are 0, .1, or .2. If the correlation is 0, the elements of Q-matrix will be independent of each other. Each item has a 20% chance of measuring a specific attribute. If the correlation was nonzero, the Q-matrix is generated using the R package “bindata” developed by Leisch, Weingessel, and Hornik (1998), which can generate columns of 0/1’s with desired correlation.
The slipping parameter and guessing parameter under the DINA and DINO models are set at .05, .1, or .2. Furthermore, experts might not provide perfectly reliable judgments in practice. Therefore, it is imperative to consider errors in the training data. Errors in the training data will affect the resulting SVM models. In this study, error rates at 0%, 10%, 20%, or 30% are simulated. Training data with high expert judgment error rate are expected to lead to less accurate SVM decision boundaries, and subsequently higher misclassification rate.
Five item response matrices, each with examinees, are generated based on the and the under both the DINA and DINO models. The is simulated following Wang (2013) to maintain the correlation among attributes at the same level as in the Q-matrix; that is, at 0, or .1, or .2. For each item response matrix, of the 5,000 examinees are randomly selected to be the training sample. In this study, is set to be 10, 20, 30, 50, 100, or 150. The numbers are chosen to test small-sample scenarios on purpose, which is one of the advantages for SVM. The remaining examinees, that is, , will be used as the testing samples. Furthermore, to avoid the class imbalance problem, a constraint is added to the random selection process: The number of examinees who master the attribute of interest should be within the range [/3, 2/3]. For each response matrix, the simulation will be replicated 20 times for each M. Therefore, in total, results from replications are available for analysis. The prediction accuracy is calculated by comparing the model-predicted mastery status against their true mastery status on each attribute. The average accuracy rate is then calculated across all attributes.
Overall, there are 432 conditions: 2 (generating models) (correlations among attributes) (levels of slipping and guessing) (levels of error rates) (training sample sizes). By simulating data from both DINA and DINO models, one is able to evaluate the performance of SVM under different underlying models, compensatory or noncompensatory. This is very important, because the underlying model is always unknown in practice. If SVM only works well with one particular type of model, its application would be rather limited. Many past studies assume that the attributes are uncorrelated. For example, Cheng (2009, 2010) and Wang, Chang, and Huebner (2011) generated independent attributes in their simulation studies. However, recent studies have shown increasing awareness of possible covariation among the attributes and have taken that into account in the simulation design (e.g., Wang, Chang, & Douglas, 2012; Wang, Zheng, & Chang, 2014). Therefore, correlated attributes are considered in addition to the case where they are independent. Simulating varying levels of slipping and guessing is consistent with prior studies, and allows us to examine the performance of SVM in the presence of noise. Considering errors in the training sample enables the evaluation of SVM’s capacity of working with imperfect labeling, which is more realistic than assuming that training data are error free. An important goal of the current study was to find out whether SVM provides a viable alternative to conventional likelihood-based methods when the sample size is small or the ratio of sample size to the number of attributes is small. Hence, varying levels of sample size are included in the simulation study.
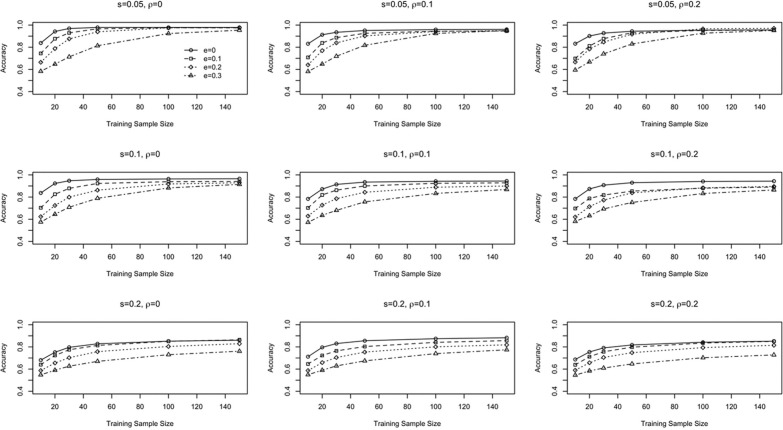
To evaluate the performance of SVM under these conditions, the average classification accuracy is summarized at both the attribute and the pattern levels for each condition. Figure 1 shows the average classification accuracy at the attribute level when the generating model is the DINA model. It contains nine subfigures. From the top to the bottom row, slipping and guessing increase from .05 to .2. From the left to the right column, the correlation among attributes increases from 0 to .2. Within each subfigure, the horizontal axis represents the training sample size, which goes from 10 to 150. The vertical axis represents the classification accuracy. Different levels of error rates in the training sample are reflected in each subfigure by different curves.
Figure 1.
Attribute-level classification accuracy rate under the DINA model using SVM.
Note. DINA = Deterministic Input, Noisy “And” Gate; SVM = support vector machine.
In Figure 1, going from top to bottom, it is clear that with the increase of slipping and guessing, the classification accuracy drops, which is expected. Going from left to right, when the correlation among attributes increases, the change in classification accuracy is fairly small. Within each subfigure, as the training sample size increases, the classification accuracy increases. As the error rate in the training sample goes up, the classification accuracy goes down. In general, the top left subfigures show the highest classification accuracy, whereas the bottom right subfigure shows the lowest classification accuracy. Within each subfigure, the classification accuracy is the highest when the training sample is large and contains little error. The results are very promising. The bottom right subfigure shows that even when the slipping and guessing parameters are set at .2, and the error rate in the training sample is .2, the classification accuracy can reach .8 as long as the sample size is 100 or above. Note that such a sample size is very small compared with conventional methods that require thousands of subjects to obtain reliable model parameter estimates. If the slipping and guessing parameters are smaller than .2 and/or the error rate drops, the sample size requirement can be even further relaxed. For example, when slipping and guessing parameters are set at .1, and the error rate in the training sample remains .2, the classification accuracy already exceeds .8 given a training sample size of 50. In the best scenario, for tests with slipping and guessing parameters of .05 (this requirement almost precludes multiple-choice items), and a training sample without error, the classification accuracy is higher than .9 for a sample size of 20 (see the top left subfigure). If the training sample contains 10% of error, a training sample of around 30 students will be needed to reach classification accuracy higher than .9. This means, if experts can be found to provide very accurate diagnosis for a very small group of students based on a well-designed test, this small group can be used to build very accurate SVMs to classify the remaining large number of students whose cognitive profiles are unknown.
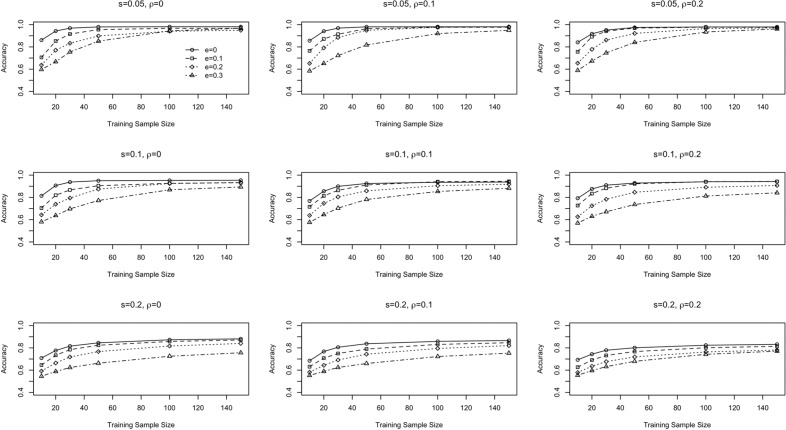
Figure 2 is presented in the same way as Figure 1, for the condition that the underlying model is the DINO model. The pattern is very similar. When the slipping and guessing parameters are at a moderate level, and the training sample contains 20% of error, the classification accuracy still reaches .8 given a sample size of 50 (see the center subfigure). In the best scenario, when the slipping and guessing parameters are set at .05, and the training sample contains no error, the classification accuracy can be .9 with a training sample size of 20 (see the top left subfigure). Comparison between Figures 1 and 2 reveals that SVM works slightly better when the underlying model is the DINA model.
Figure 2.
Attribute-level classification accuracy rate under the DINO model using SVM.
Note. DINO = Deterministic Input, Noisy “Or” Gate; SVM = support vector machine.
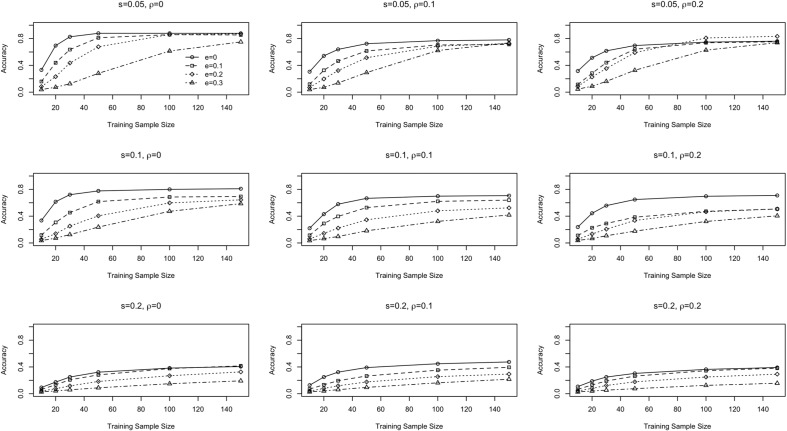
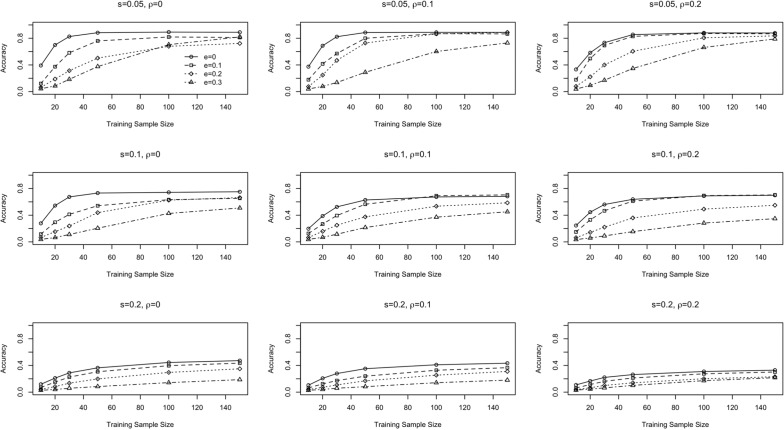
Figures 1 and 2 summarize the classification accuracy at the attribute level. At the pattern level, a diagnosis is considered accurate only when the mastery status of all six attributes is correctly labeled. From this perspective, the classification accuracy must be lower than the one at the attribute level. Figure 3 shows the classification accuracy at the pattern level when the underlying model is the DINA model. The top left subfigure shows that when the sample size is 150, the pattern-level classification accuracy reaches around 80% when the error rate in training sample is low. As slipping and guessing go up, the pattern-level classification accuracy quickly drops. The lowest pattern-level classification accuracy is between .2 and .4 with a training sample size of 150, which occurs in the bottom right subfigure, where the guessing and slipping parameters are set at .2, and the error rate in the training sample can be up to 20%. This is not surprising, given previous studies with similar conditions (e.g., Cheng, 2009; Wang, 2013). For example, in Cheng (2009) the pattern-level accuracy was reported to be between .3 and .5 for a 24-item, six-attribute test (Cheng, 2009), when the attribute-level accuracy is mostly between 70s and 90s. It was a computerized adaptive test in which the item selection algorithm was designed to efficiently make classification decisions. The item parameters were derived from a calibration sample of 2,000 examinees. Given the results from that study, the pattern-level accuracy rate based on the SVM method in the current study is well expected and encouraging, as it is based on training sample sizes of 150 or lower and a linear test. Figure 4 summarizes the pattern-level classification accuracy when the underlying model is DINO. The trend is largely the same as discussed above when the underlying model is the DINA model.
Figure 3.
Pattern-level classification accuracy rate under the DINA model using SVM.
Note. DINA = Deterministic Input, Noisy “And” Gate; SVM = support vector machine.
Figure 4.
Pattern-level classification accuracy rate under the DINO model using SVM.
Note. DINO = Deterministic Input, Noisy “Or” Gate; SVM = support vector machine.
Summary and Discussion
In this article, the utility of the SVM, a widely used supervised learning method, was explored to perform cognitive diagnosis on each attribute. The SVM approach is particularly helpful when the sample size is too small for conventional likelihood-based methods to work effectively. A simulation study was designed to examine its performance in terms of classification accuracy at the attribute level and at the pattern level when the training sample size ranges between 10 and 150. The simulation study also considers the following factors: the underlying model, the error rate in the training sample, the item quality (as reflected in the slipping and guessing parameters), and the correlation among attributes.
Overall, the study finds great potential of using SVM for cognitive diagnosis when the sample size is small. The performance at the attribute level is impressive. For example, the classification accuracy reaches .9 or above with a training sample of only 30 examinees in the presence of 10% error in the diagnosis of the training sample, and slipping and guessing are set at .05. Therefore, as long as experts can provide accurate diagnosis for a very small group of students based on a well-designed test, this small training sample can be used to build SVM models, one for each attribute, to classify the remaining large number of students whose cognitive profiles are unknown. The classification accuracy is on par with what has been reported in previous studies given similar test length and number of attributes, but those studies employed likelihood-based methods where large sample size is required and the estimation of latent profiles is computationally intensive.
It is important to note that here SVM is used with dichotomous items. In reality, SVM is usually used with continuous data. The fact that SVM performs well with dichotomous data is very encouraging, and it is expected to work better with polytomous items. An interesting and important follow-up study is therefore to examine the performance of SVM, given polytomous data. Meanwhile, this study uses SVM to make binary decision on each attribute; that is, mastery versus nonmastery. To address the issue of granularity in the attributes, CDMs allowing polytomous attributes have been developed, for example, the polytomous Generalized DINA (pG-DINA) model (J. Chen & de la Torre, 2013), the polytomous log-linear cognitive diagnostic model (LCDM; Templin & Bradshaw, 2014), and the general diagnostic model (GDM) for polytomous attributes (von Davier, 2008). J. Chen and de la Torre (2013) gave an example of three classes for each attribute: nonmastery, Level 1 mastery, and Level 2 mastery. Thus far, the authors of the present study have been unaware of any development in using SVM to make multiclass decisions for cognitive diagnosis, and it will be another interesting direction to pursue. The use of SVM for such multiclass decisions has been well documented in the literature (e.g., Mayoraz & Alpaydin, 1999), so the extension can be rather straightforward.
In addition to these exciting directions, several limitations of the current study that can be addressed in follow-up studies can be pointed out: First, albeit showing promises in this study, SVM is not without its limitations. The choice of a kernel function (e.g., linear vs. nonlinear), the tuning parameter in a soft-margin SVM, and the cross-validation method, as well as possible overfit under a small sample size, can all influence the outcome. The authors of the present study caution against blindly applying SVM without examining the default options or performing appropriate cross-validation.
Second, in this study training errors are introduced in a completely random fashion, meaning that even if an examinee answers all questions correctly, there is still a certain probability (e.g., 20% if the error rate is .2) for him or her to be classified as a nonmaster of an attribute and vice versa. Obviously, training points with such errors will have a substantial impact on the decision boundary. With a more realistic error generating mechanism, the proposed method is expected to work even better.
Furthermore, there exist numerous other classifiers that can perform classification in the context of cognitive diagnosis; for example, logistic regression. One logistic regression model can be fit for each attribute to the training data. The dependent variable is the master/nonmaster diagnosis provided by the teachers. The independent variables are the item responses. The model derived from the training sample can then be used on new test takers to determine if they are masters or nonmasters of an attribute. The present simulation study did include logistic regression for comparison. Logistic regression is chosen for two reasons: First, it is widely known and applied in social sciences. Second, it is closely linked to SVM, as both can be viewed as taking a probabilistic model and minimizing certain loss functions based on the likelihood ratio.2 Results are annexed in Appendix B for brevity of the article (Figures B1-B4). The results indicate that the performance of logistic regression is inferior to SVM at the same sample size, particularly when the training sample contains error. It is also important to note that logistic regression requires a sample size at least larger than the number of parameters, in this case . For this reason, logistic regression is not used with very small sample sizes such as or 20 or 30. The performance of other classifiers remains to be investigated in the future.
Last but not the least, in this study, it is showed that SVM provides a viable option to perform cognitive diagnosis when the sample size is inadequate for CDM fitting and calibration. Data are generated from two CDMs with small sample sizes. But what if CDMs do not fit? In the presence of model misspecification, even if the sample size is adequate, the resulting item parameter estimates would be biased and would subsequently lead to classification errors. SVM may provide a solution when the CDM is misspecified, as it bypasses CDM fitting. These are certainly worthy directions to pursue in future studies.
Acknowledgments
The authors would like to thank the editors and two anonymous reviewers for their constructive feedback.
General cognitive diagnostic models (CDMs) that combine latent trait(s) and latent classes, for example, the higher order model proposed by de la Torre and Douglas (2004), are exceptions.
As a reviewer kindly pointed out, the soft-margin support vector machine (SVM) is theoretically connected to regularized logistic regression (Hastie, Tibshirani, & Friedman, 2009). Limited by the space and scope, that comparison will be left to another study.
Declaration of Conflicting Interests: The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Funding: The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: The project is supported by the National Science Foundation under Grant DRL-1350787.
Supplemental Material: Supplementary material is available for this article online.
References
- Boser B. E., Guyon I., Vapnik V. (1992). A training algorithm for optimal margin classifiers. In Proceedings of the Fifth Annual Workshop on Computational Learning Theory ACM Press. doi: 10.1145/130385.130401 [DOI] [Google Scholar]
- Chen J., de la Torre J. (2013). A general cognitive diagnostic model for expert-defined polytomous attributes. Applied Psychological Measurement, 37, 419-437. doi: 10.1177/0146621613479818 [DOI] [Google Scholar]
- Chen Y., Liu J., Xu G., Ying Z. (2015). Statistical analysis of Q-matrix based diagnostic classification models. Journal of the American Statistical Association, 110, 850-866. doi: 10.1080/01621459.2014.934827 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng Y. (2009). When cognitive diagnosis meets computerized adaptive testing: CD-CAT. Psychometrika, 74, 619-632. doi: 10.1007/s11336-009-9123-2 [DOI] [Google Scholar]
- Cheng Y. (2010). Improving cognitive diagnostic computerized adaptive testing by balancing attribute coverage: The modified maximum global discrimination index method. Educational and Psychological Measurement, 70, 902-913. doi: 10.1177/0013164410366693 [DOI] [Google Scholar]
- Chiu C.-Y., Douglas J. A., Li X. (2009). Cluster analysis for cognitive diagnosis: Theory and applications. Psychometrika, 74, 633-665. doi: 10.1007/s11336-009-9125-0 [DOI] [Google Scholar]
- Chiu C.-Y., Köhn H.-F. (2015). A general proof of consistency of heuristic classification for cognitive diagnosis models. British Journal of Mathematical and Statistical Psychology, 68, 387-409. doi: 10.1111/bmsp.12055 [DOI] [PubMed] [Google Scholar]
- de la Torre J. (2009). DINA model and parameter estimation: A didactic. Journal of Educational and Behavioral Statistics, 34, 115-130. doi: 10.3102/1076998607309474 [DOI] [Google Scholar]
- de la Torre J. (2011). The generalized DINA model framework. Psychometrika, 76, 179-199. doi: 10.1007/s11336-011-9207-7 [DOI] [Google Scholar]
- de la Torre J., Douglas J. A. (2004). Higher-order latent trait models for cognitive diagnosis. Psychometrika, 69, 333-353. [Google Scholar]
- DiBello L. V., Roussos L. A., Stout W. F. (2007). Review of cognitively diagnostic assessment and a summary of psychometric models. In Rao C. R., Sinharay S. (Eds.), Handbook of Statistics: Vol. 26. Psychometrics (pp. 979-1030). Amsterdam, The Netherlands: Elsevier. doi: 10.1016/S0169-7161(06)26031-0 [DOI] [Google Scholar]
- Gierl M. (2007). Making diagnostic inferences about cognitive attributes using the rule-space model and attribute hierarchy method. Journal of Educational Measurement, 44, 325-340. doi: 10.1111/j.1745-3984.2007.00042.x [DOI] [Google Scholar]
- Gierl M., Zheng Y., Cui Y. (2008). Using the attribute hierarchy method to identify and interpret cognitive skills that produce group differences. Journal of Educational Measurement, 45, 65-89. [Google Scholar]
- Haertel E. H. (1989). Using restricted latent class models to map the skill structure of achievement items. Journal of Educational Measurement, 26, 301-321. [Google Scholar]
- Hastie T., Tibshirani R., Friedman J. (2009). The elements of statistical learning (2nd ed.). New York, NY: Springer. [Google Scholar]
- Japkowicz N., Stephen S. (2002). The class imbalance problem: A systematic study. Intelligent Data Analysis, 6, 429-449. [Google Scholar]
- Junker B. W., Sijtsma K. (2001). Cognitive assessment models with few assumptions, and connections with nonparametric item response theory. Applied Psychological Measurement, 25, 258-272. [Google Scholar]
- Köhn H.-F., Chiu C.-Y., Brusco M. J. (2015). Heuristic cognitive diagnosis when the Q-matrix is unknown. British Journal of Mathematical and Statistical Psychology, 68, 268-291. doi: 10.1111/bmsp.12044 [DOI] [PubMed] [Google Scholar]
- Kuang Z., Ding S., Xu Z. (2010, April). Application of support vector machine to cognitive diagnosis. Paper presented at the 2010 Asia-Pacific Conference on Wearable Computing Systems. doi: 10.1109/APWCS.2010.8 [DOI] [Google Scholar]
- Leisch F., Weingessel A., Hornik K. (1998). On the generation of correlated artificial binary data (Working Paper Series, SFB ‘Adaptive Information Systems and Modelling in Economics and Management Science’). Vienna, Austria: Vienna University of Economics. [Google Scholar]
- Liu J. (2015, July). Regularized latent class analysis with application in cognitive diagnosis. Paper presented at the International Meeting of Psychometric Society, Beijing, China. [Google Scholar]
- Liu J., Xu G., Ying Z. (2012). Data-driven learning of Q-matrix. Applied Psychological Measurement, 36, 548-564. doi: 10.1177/0146621612456591 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Macready G. B., Dayton C. M. (1977). Use of probabilistic models in the assessment of mastery. Journal of Educational Statistics, 2, 99-120. [Google Scholar]
- Mayoraz E., Alpaydin E. (1999). Support vector machines for multi-class classification. In Mira J., Sanchez-Andres J. (Eds.), International Work Conference on Artificial Neural Networks, Alicante, Spain, (Vol. 2, 833-842). Berlin: Springer. [Google Scholar]
- McGlohen M., Chang H.-H. (2008). Combining computer adaptive testing technology with cognitive diagnostic assessment. Behavior Research Methods, 40, 808-821. doi: 10.3758/BRM.40.3.808 [DOI] [PubMed] [Google Scholar]
- Shu Z., Henson R., Willse J. (2013). Using neural network analysis to define methods of DINA model estimation for small sample sizes. Journal of Classification, 30, 173-194. doi: 10.1007/s00357-013-9134-7 [DOI] [Google Scholar]
- Tan P.-N., Steinbach M., Kumar V. (2005). Introduction to data mining (1st ed.), Boston, MA: Addison-Wesley. [Google Scholar]
- Tatsuoka K. K. (1983). Rule space: An approach for dealing with misconceptions based on item response theory. Journal of Educational Measurement, 20, 345-354. [Google Scholar]
- Templin J. L., Bradshaw L. (2014). Hierarchical diagnostic classification models: A family of models for estimating and testing attribute hierarchies. Psychometrika, 79, 317-339. doi: 10.1007/s11336-013-9362-0 [DOI] [PubMed] [Google Scholar]
- Templin J. L., Henson R. A. (2006). Measurement of psychological disorders using cognitive diagnosis models. Psychological Methods, 11, 287-305. doi: 10.1037/1082-989X.11.3.287 [DOI] [PubMed] [Google Scholar]
- Vapnik V. (1998). Statistical learning theory. New York, NY: John Wiley. [Google Scholar]
- von Davier M. (2008). A general diagnostic model applied to language testing data. British Journal of Mathematical and Statistical Psychology, 61, 287-301. doi: 10.1348/000711007X193957 [DOI] [PubMed] [Google Scholar]
- Wang C. (2013). Mutual information item selection method in cognitive diagnostic computerized adaptive testing with short test length. Educational and Psychological Measurement, 73, 1017-1035. doi: 10.1177/0013164413498256 [DOI] [Google Scholar]
- Wang C., Chang H., Douglas J. (2012). Combining CAT with cognitive diagnosis: A weighted item selection approach. Behavior Research Methods, 44, 95-109. [DOI] [PubMed] [Google Scholar]
- Wang C., Chang H., Huebner A. (2011). Restrictive stochastic item selection methods in cognitive diagnostic CAT. Journal of Educational Measurement, 48, 255-273. [Google Scholar]
- Wang C., Zheng C., Chang H. (2014). An enhanced approach to combine item response theory with cognitive diagnosis in adaptive testing. Journal of Educational Measurement, 51, 358-380. [Google Scholar]
- Whitney B., Cheng Y., Brodersen A., Hong M. (under review). The survey of student engagement in statistics: Preliminary development and validation.