Evaluating Anchor-Item Designs for Concurrent Calibration With the GGUM

Abstract

Concurrent calibration using anchor items has proven to be an effective alternative to separate calibration and linking for developing large item banks, which are needed to support continuous testing. In principle, anchor-item designs and estimation methods that have proven effective with dominance item response theory (IRT) models, such as the 3PL model, should also lead to accurate parameter recovery with ideal point IRT models, but surprisingly little research has been devoted to this issue. This study, therefore, had two purposes: (a) to develop software for concurrent calibration with, what is now the most widely used ideal point model, the generalized graded unfolding model (GGUM); (b) to compare the efficacy of different GGUM anchor-item designs and develop empirically based guidelines for practitioners. A Monte Carlo study was conducted to compare the efficacy of three anchor-item designs in vertical and horizontal linking scenarios. The authors found that a block-interlaced design provided the best parameter recovery in nearly all conditions. The implications of these findings for concurrent calibration with the GGUM and practical recommendations for pretest designs involving ideal point computer adaptive testing (CAT) applications are discussed.

Pretesting large pools of items with large samples of respondents is time-consuming, expensive, and may be seen as so burdensome by respondents that data quality is jeopardized. A common pragmatic solution is to divide item pools among pretest groups and use concurrent calibration strategies (e.g., Bock & Zimowski, 1997) with anchor items to put parameter estimates on a common scale. Concurrent calibration using anchor items has proven to be an effective alternative to separate calibration and linking for developing large item banks based on its parameter estimation accuracy (e.g., Hanson & Béguin, 2002; Kim & Cohen, 2002). In principle, estimation methods that have proven effective with dominance item response theory (IRT) models, such as the three-parameter logistic (3PL) model, should also lead to accurate parameter recovery with ideal IRT point models, but surprisingly little research has been devoted to this issue.

Unlike dominance models, ideal point models allow non-monotonic item response functions (IRFs) because they assume a respondent endorses or agrees with an item only if he or she is located “near” an item on the trait continuum. That is, the probability of endorsement decreases as the distance between a respondent’s location (i.e., trait level) and an item’s location increases. The generalized graded unfolding model (GGUM; Roberts, Donoghue, & Laughlin, 2000) is perhaps the most widely used ideal point model in research and practice settings (e.g., Carter, Guan, Maples, Williamson, & Miller, 2015; Drasgow et al., 2012; Stark et al., 2014). Previous studies examining parameter recovery with the GGUM have exclusively focused on single-group estimation (e.g., de la Torre, Stark, & Chernyshenko, 2006; Roberts et al., 2000; Roberts & Thompson, 2011), and multi-group data have been dealt with only using separate calibration and linking strategies (e.g., Carter & Zickar, 2011; Koenig & Roberts, 2007; Seybert, Stark, & Chernyshenko, 2013). The authors questioned whether concurrent calibration would be an alternative strategy for multi-group analysis with the GGUM, given the “tradeoffs” that sometimes occur between delta and tau parameters due to indeterminacies (Seybert & Stark, 2012). Moreover, the authors wanted to know what would be the most effective anchor-item design for GGUM multi-group estimation if software could be developed.

The current study describes research leading to the development of Markov chain Monte Carlo (MCMC) concurrent calibration software for the GGUM and a simulation study that examined the accuracy of item and person parameters recovery under various conditions, including different anchor-item designs and respondent subpopulations in horizontal and vertical linking scenarios. MCMC estimation was chosen because it does not require the complicated derivatives associated with marginal maximum likelihood (MML) methods, and standard errors can be computed readily from MCMC output across iterations (e.g., Patz & Junker, 1999). Before describing the MCMC algorithms and the simulation study, the GGUM ideal point IRT model and concurrent calibration with various anchor-item designs are reviewed.

GGUM

Roberts et al. (2000) developed the GGUM for dichotomous and ordered polytomous responses. Like other ideal point models, the GGUM assumes the probability of a positive (agree) response decreases as a function of the distance between a person and an item. Letting ${\theta }_i$ represent a respondent’s trait level or standing on the trait continuum and ${\delta }_j$ represent the location or extremity of an item on that continuum, then the probability of respondent i endorsing item j is highest when ${\theta }_i={\delta }_j$, and the probability decreases as $|{\theta }_i-{\delta }_j|$ increases. More specifically, GGUM response probabilities are given by the following equation:

$$\mathrm{P}[Z_j=z|{\theta }_i]=\frac{\exp \left({\alpha }_j[z({\theta }_i-{\delta }_j)-\sum _{k=0}^z{\tau }_{\mathrm{jk}}]\right)+\exp \left({\alpha }_j[(M_j-z)({\theta }_i-{\delta }_j)-\sum _{k=0}^z{\tau }_{\mathrm{jk}}]\right)}{\sum _{w=0}^{C_j}\exp \left({\alpha }_j[w({\theta }_i-{\delta }_j)-\sum _{k=0}^w{\tau }_{\mathrm{jk}}]\right)+\exp \left({\alpha }_j[(M_j-w)({\theta }_i-{\delta }_j)-\sum _{k=0}^w{\tau }_{\mathrm{jk}}]\right)},$$

where

$Z_j$ = an observed response to the jth item with z = 0, 1, 2, . . ., $C_j$

${\theta }_i$ = the location of the ith respondent’s location on the latent continuum

${\alpha }_j$ = the discrimination of jth item

${\delta }_j$ = the location of jth item on the latent continuum

${\tau }_{\mathrm{jk}}$ = the location of the kth subjective response category threshold of the jth item

z = 0 represents the strongest level of disagreement

z = $C_j$ represents the strongest level of agreement for the jth item

$M_j$ = 2 $C_j$+ 1, and w is a convenient index of summation.

The reader is referred to Roberts et al. (2000) for more details about the GGUM.

For illustration, Figure 1 presents GGUM IRFs (i.e., expected value functions) for two four-option polytomous items. The first item has a discrimination parameter $\alpha$ = 2, location parameter $\delta$ = 0, and category threshold parameters, ${\tau }_1$ = −1.8, ${\tau }_2$ = −1.1, ${\tau }_3$ = −0.5. The second item has the same delta and tau parameters but $\alpha$ = 0.5. The location of the peak on the latent trait continuum is determined by the location parameter $\delta$. In this example, $\delta$ = 0 for both items, indicating that the items reflect intermediate or moderate levels of the latent trait. In accordance with ideal point assumptions, respondents possessing intermediate trait levels have the highest probability of agreement. That is, the IRFs peak at $|\mathrm{\theta }-\mathrm{\delta }|$, which leads to unimodal, bell-shaped curves.

Figure 1.

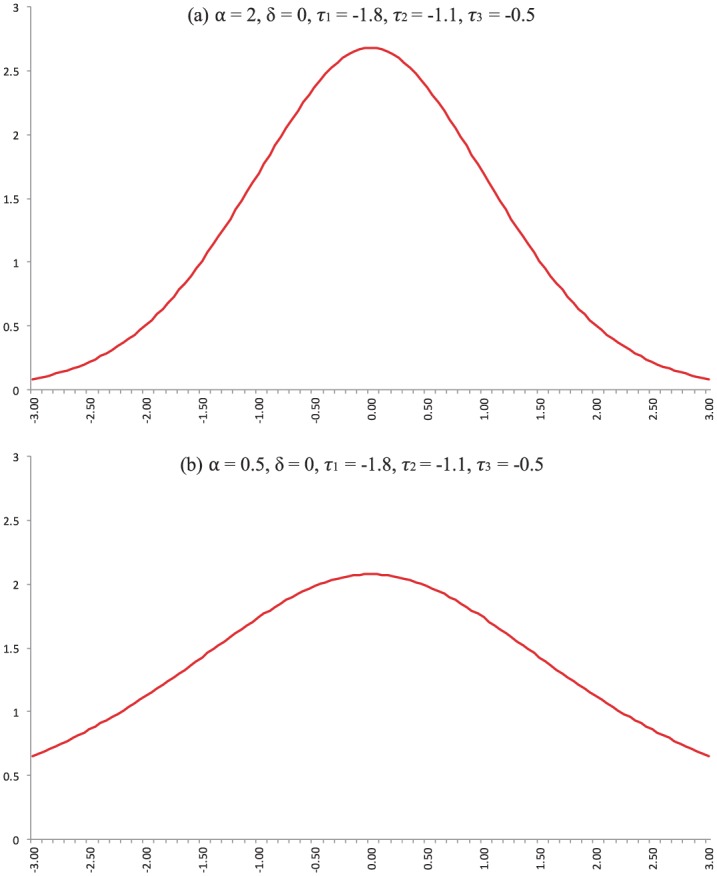
Item response functions (IRFs) of the generalized graded unfolding model (GGUM) for polytomous four-option items.

Note also that Item 1 has a taller and more peaked IRF than Item 2. As explained by Roberts et al. (2000), the steepness or flatness of IRFs depends on the item discrimination parameter as well as the distance between subjective response category thresholds (Roberts et al., 2000). Here, Item 1 has a larger discrimination parameter ($\alpha$ = 2 vs. $\alpha$ = 0.5), which leads to a steeper IRF.

Concurrent Calibration and Anchor-Item Designs

Over the past few decades, various data collection methods and statistical methods have been proposed to equate tests. The non-equivalent group with anchor test (NEAT) design is widely used in large-scale assessment. Under a NEAT design, two forms are administered in two different populations, and the forms are “linked” via a common set of anchor items. Several possible anchor-item designs have been proposed (García-Pérez, Alcalá-Quintana, & García-Cueto, 2010; Petersen, Kolen, & Hoover, 1989; Vale, 1986). Three anchor-item designs considered in this research are shown in Figure 2. The situation demonstrates three groups with set(s) of anchor items. In a standard anchor design, as displayed in Figure 2(a), each pair of forms administered to groups of respondents is separately anchored. In other words, two different sets of anchor items are administered to Groups 1 and 2 and Groups 2 and 3, respectively. Figure 2(b) displays a common-item anchor design. In this design, a single set of anchor items is administered to all three groups. Finally, as shown in Figure 2(c), block-interlaced anchor design sets the scale of measurement using a cyclical approach involving three distinct sets of anchor items for Groups 1 and 2, Groups 2 and 3, and Groups 3 and 1.

Figure 2.

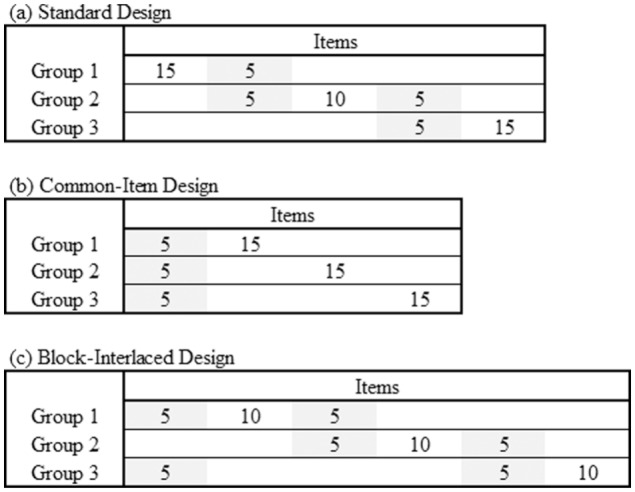
Sketch of data array for three anchor-item designs: (a) two sets of anchor items administered to Groups 1 and 2 and Groups 2 and 3, respectively, (b) a single set of anchor items administered to all groups, (c) similar to (a), except Groups 1 and 3 have an additional set of anchor items.

Note. Highlights are anchor items.

In concurrent calibration, item parameters are estimated simultaneously using a combined data set, with responses to the items that were unique to each group treated as missing for respondents that did not receive them. The anchor items establish the metric and eliminate the need for a subsequent linear transformation to put all the parameters on a common scale and make the forms interchangeable. Latent trait difference among the groups receiving the different forms can be examined by designating one group as a reference group, which is typically assumed to have a standard normal trait distribution, and freely estimating the mean and variance of the trait distributions in the groups receiving the other forms.

To date, researchers have examined the performance of concurrent calibration under dominance IRT models (e.g., Hanson & Béguin, 2002; Kim & Cohen, 1998; Petersen, Cook, & Stocking, 1983). However, for ideal point IRT models, no multi-group estimation software has been developed and released. Consequently, options for concurrent calibration have been limited for practitioners and applied researchers seeking to develop large item banks or alternate forms. The purpose of this research, therefore, was to develop an MCMC concurrent calibration program for the GGUM and evaluate the effectiveness of different anchor-item designs, via a Monte Carlo study, to provide guidance and recommendations. The next section describes the simulation study details and estimation procedures.

Method

Simulation Conditions

A simulation study was conducted to examine parameter recovery with different anchor-item designs and respondent subpopulations in horizontal and vertical linking scenarios. Four independent variables were manipulated: three anchor-item designs (standard, common-item, and block-interlaced); four samples size per group (100, 200, 400, and 800); two subpopulation trait distributions—three equivalent groups with N(0, 1), a base group with N(0, 1), and two non-equivalent groups with N(−0.5, 1); and two data types (dichotomous and polytomous four-option). There were a total of 3 × 4 × 2 × 2 = 48 conditions, with 50 replications per condition. (Note that for the conditions involving a sample size of 800 per group, only 30 replications were run due to long runtimes.)

Anchor-item design

Concurrent calibration with respondents from different subpopulations requires anchoring items to establish a common metric for the parameter estimates (García-Pérez et al., 2010; Kolen & Brennan, 2014). In this study, it was assumed that three groups of respondents were administered unique 20 items with subsets of items in common (anchor items). As shown in Figure 2, five items were used for anchoring between two groups. In the standard design conditions, the last five items for Group 1 were the same as the first five items for Group 2 and similarly for Groups 2 and 3. In the common-item design conditions, the first five items were common to each group. Finally, the block-interlaced design incorporated a “circular” anchoring approach, where the last five items for one group served as the first five items for the next group, with the last five items for Group 3 being the same as the first five items for Group 1, thus completing the circle 1-2-3-1. Note that total numbers of anchor items for the block-interlaced, standard, and common-item designs are 15, 10, and 5, respectively.

Sample size

Each form was administered to a different subpopulation of respondents, with the number respondents per group set at 100, 200, 400, or 800; thus the total sample sizes for concurrent calibration were 300, 600, 1,200, and 2,400, respectively. Note that a total sample of 300 is small for the GGUM, considering that previous single-group GGUM estimation studies have suggested that 400 or more respondents are required for accurate item parameter recovery (e.g., de la Torre et al., 2006; Roberts & Thompson, 2011). The large-sample conditions were included in this study because GGUM single-group MML item parameter estimation has been shown to improve substantially as sample size increases to 750 (Roberts, Donoghue, & Laughlin, 2002). Moreover, in the large-sample conditions, the efficacy of the various anchor-item designs should be most apparent.

Subpopulation trait distribution

Two subpopulation scenarios were considered in this study (equivalent groups vs. non-equivalent groups). In the equivalent groups scenario, the respondents were sampled from the same population distribution, which was assumed to be N(0, 1). In the non-equivalent groups scenario, it was assumed that the respondents from Group 1 were sampled randomly from a N(0, 1) population, but the respondents from Groups 2 and 3 were sampled from a different subpopulation having a N(−0.5, 1) trait distribution. It is generally known that non-equivalent group conditions pose greater challenges for item parameter estimation (Kolen, 2003).

Data type

Parameter recovery was examined using dichotomous and polytomous four-option responses. Both formats were examined here because research by Roberts and Thompson (2011) showed that bias and standard error decrease as the number of response categories increases.

Data Generation

Generating parameters

True item parameters for the simulation study were generated as in previous single-group GGUM estimation studies (e.g., Roberts et al., 2002; Roberts & Thompson, 2011). The location parameters (${\delta }_j$) were generated using an equal-spacing strategy reflecting the Thurstonian principle of attitude scale construction (Thurstone, 1928). The generating ${\delta }_j$ parameters ranged from −2.0 to 2.0, equally spaced on the trait continuum. The discrimination parameters (${\alpha }_j$) were randomly chosen from a uniform distribution ranging from 0.5 to 2. In the equivalent groups scenario, the true person parameters (${\theta }_i$) for all three groups were randomly sampled from a N(0, 1) distribution. In the non-equivalent groups scenario, the parameters for Group 1 (the base group) were randomly sampled from a N(0, 1) distribution, but the person parameters for Groups 2 and 3 were randomly sampled from a N(−0.5, 1) distribution. The true threshold parameters (${\tau }_{\mathrm{jk}}$) were generated with a recursive equation as follows:

$${\tau }_{\mathrm{jk}-1}={\tau }_{\mathrm{jk}}-0.25+e_{\mathrm{jk}-1},\mathrm{for}k=2,3,\dots ,C$$

where $e_{\mathrm{jk}-1}$ represents a random error generated from a N(0, .04) distribution, and C represents the total number of response categories. This equation was applied independently for each item, using C = 2 and C = 4 for the dichotomous and polytomous four-option conditions, respectively. Starting values (${\tau }_{\mathrm{jC}}$) for the recursion involving each item were randomly generated from a uniform distribution (−1.5, −0.5). This recursive equation produces practical threshold parameters, and it has been used in subsequent GGUM studies (Roberts et al., 2002).

Response data generation

Using the generating item parameters described above, response data were simulated as follows. In dichotomous conditions, a response was scored 1 if the GGUM probability exceeded a randomly sampled uniform (0, 1) number and 0 otherwise. In the polytomous conditions, a response was scored 3 if a randomly sampled uniform (0, 1) number exceeded the sum of the GGUM probabilities for Categories 0, 1, and 2. If the random number was less than the sum of the GGUM probabilities for Categories 0, 1, and 2 but greater than the sum for Categories 0 and 1, then the response was scored 2, and so forth. A C++ program was developed for this GGUM data generation.

Parameter Estimation

A multi-group MCMC algorithm was developed for GGUM concurrent calibration. Prior distributions for the item parameters (${\alpha }_j$, ${\delta }_j,{\tau }_{\mathrm{jk}}$) were based on a four-parameter beta distribution, Beta ($\nu ,\omega$, a, b). The four-parameter beta was selected for its flexibility; it can mimic widely used distributions, such as the normal or lognormal, by modifying its shape (a, b) and range ($\nu$, $\omega$) parameters (Zeng, 1997). As in de la Torre et al. (2006), the four-parameter beta priors for alpha, delta, and tau, respectively, were {1.5, 1.5, .25, 4}, {2, 2, −5, 5}, and {2, 2, −6, 6}. For the person parameters (${\theta }_i$), a N(0, 1) prior was used.

On each replication, item and person parameters were estimated using Metropolis–Hastings within Gibbs sampling (Patz & Junker, 1999), implemented in an Ox (Doornik, 2009) computer program. The initial values were generated separately for each parameter. The initial alphas were fixed at 1 across all items and groups of respondents. The initial deltas were generated using the method described by Roberts and Laughlin (1996). Applying that method separately for each respondent group produced three sets of deltas for the anchor items, which were averaged to obtain a single initial delta for each item to start the concurrent calibration. The initial values for tau parameters were randomly selected from a uniform (−2, −1) distribution. For person parameters, the initial values were randomly sampled from a N(0, 1) distribution. A C++ program was developed to generate the initial parameter values as described above.

Item and person parameters were estimated by averaging the posterior samples after a burn-in period. Standard errors of parameter estimates were obtained by computing the standard deviation of the posterior samples. A total of 20,000 samples were drawn from each of five independent chains after a burn-in period of 10,000 iterations. The number of iterations and burn-in period were determined based on a convergence check by Gelman–Rubin’s $\hat{R}$ statistics (Gelman & Rubin, 1992). $\hat{R}$ statistics were computed for item parameters, and $\hat{R}$ values less than 1.2 were viewed as a practical indication of convergence (de la Torre, Ponsoda, Leenen, & Hontangas, 2012).

Examining Estimation Accuracy

For GGUM item parameters, root mean square error (RMSE) and bias statistics were computed to investigate the accuracy of parameter estimates across simulation conditions. RMSE and bias statistics were calculated as follows:

$$\mathrm{RMSE}=\sqrt{\frac{\sum _i{({\hat{\mu }}_i-{\mu }_i)}^2}{I}},$$

$$\mathrm{Bias}=\frac{\sum _i{\hat{\mu }}_i-{\mu }_i}{I},$$

where, ${\mu }_i$ is the generating parameter, ${\hat{\mu }}_i$ is the estimated parameter, and $I$ is the total number of items or respondents. RMSE and bias were computed for each replication, and then averaged across replications. In addition, posterior standard deviations (PSD) for each parameter estimate were computed for item parameters. PSD estimates were calculated by taking the square root of the variance of the posterior samples after burn-in. For person parameters, correlations (CORR) between generated and estimated latent trait parameters in addition to RMSE and bias were calculated.

Results

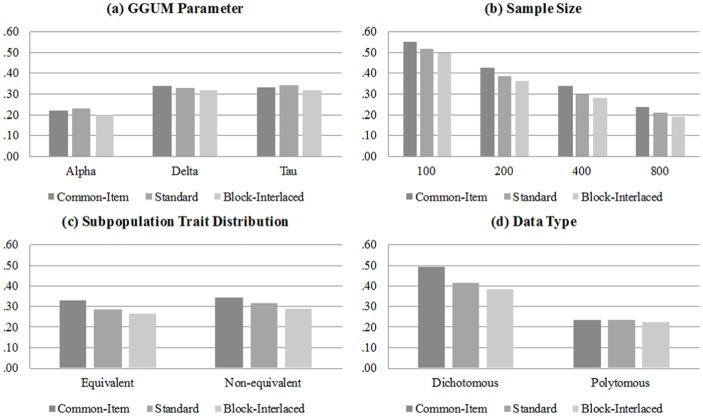
Table 1 presents the average RMSEs, and biases for the individual simulation conditions to allow an examination of overall GGUM parameter recovery with the three anchor-item designs. In addition, Figure 3 shows histograms for average PSD estimates of the GGUM concurrent calibration with three anchor-item designs, organized by levels of simulation conditions. For the polytomous four-option data type, note that ${\tau }_{j1}$, ${\tau }_{j2}$, and ${\tau }_{j3}$ were averaged to allow direct comparisons with the dichotomous findings.

Table 1.

Accuracy of Parameter Estimates for GGUM Concurrent Calibration With Three Anchor-Item Designs.

			Dichotomous								Polytomous
			α		δ		τ		θ		α		δ		τ		θ
Dist.	Design	N	RMSE	Bias	RMSE	Bias	RMSE	Bias	RMSE	Bias	RMSE	Bias	RMSE	Bias	RMSE	Bias	RMSE	Bias
Equivalent	Common-item	100	.59	.40	.84	.17	.63	−.37	.62	.17	.30	−.20	.47	.22	.48	−.01	.31	.16
		200	.42	.23	.56	.14	.61	−.40	.56	.04	.30	−.25	.44	.06	.48	−.10	.29	.04
		400	.30	.14	.51	.17	.40	−.24	.54	.07	.20	−.15	.28	.11	.31	−.11	.26	.08
		800	.21	.08	.49	.14	.34	−.13	.53	.07	.13	−.09	.18	.09	.27	−.09	.25	.07
	Standard	100	.59	.41	.52	.14	.64	−.39	.53	.17	.31	−.22	.48	.21	.48	.00	.31	.16
		200	.40	.22	.45	.07	.62	−.42	.46	.04	.30	−.26	.46	.06	.45	−.09	.29	.04
		400	.28	.14	.39	.07	.41	−.26	.45	.08	.21	−.17	.30	.11	.30	−.10	.26	.07
		800	.19	.07	.32	.06	.35	−.12	.45	.08	.14	−.10	.18	.11	.26	−.09	.25	.07
	Block-interlaced	100	.57	.39	.49	.14	.57	−.34	.52	.17	.29	−.19	.45	.19	.48	.01	.31	.16
		200	.37	.18	.41	.03	.55	−.37	.45	.04	.28	−.23	.43	.05	.44	−.09	.29	.04
		400	.27	.14	.39	.04	.38	−.22	.30	−.11	.18	−.13	.28	.07	.30	−.10	.26	.07
		800	.18	.07	.30	.05	.32	−.13	.45	.08	.13	−.09	.18	.07	.24	−.08	.24	.08
Non-equivalent	Common-item	100	.54	.31	.68	.16	.88	−.60	.47	.05	.36	−.31	.65	.07	.56	−.21	.31	.16
		200	.42	.22	.67	.16	.61	−.40	.64	−.12	.28	−.24	.46	−.10	.47	−.08	.31	−.11
		400	.28	.12	.54	.14	.58	−.28	.55	−.05	.25	−.21	.41	.04	.32	−.13	.34	−.04
		800	.18	.03	.41	.10	.41	−.21	.49	−.05	.18	−.14	.24	.02	.26	−.16	.27	−.05
	Standard	100	.54	.32	.59	.09	.87	−.63	.46	.05	.37	−.31	.66	.06	.56	−.20	.35	.05
		200	.40	.21	.44	−.02	.62	−.44	.47	−.11	.29	−.25	.48	−.09	.45	−.10	.31	−.11
		400	.27	.11	.38	.02	.57	−.34	.45	−.05	.25	−.22	.37	.01	.32	−.14	.29	−.05
		800	.17	.03	.31	−.02	.43	−.25	.45	−.05	.19	−.16	.27	.02	.25	−.15	.27	−.05
	Block-interlaced	100	.51	.28	.69	.15	.85	−.63	.45	.06	.36	−.31	.69	.06	.58	−.23	.35	.05
		200	.33	.15	.41	−.04	.55	−.38	.46	−.11	.27	−.22	.44	−.13	.42	−.09	.30	−.11
		400	.23	.07	.36	−.01	.46	−.29	.44	−.05	.21	−.18	.33	−.01	.38	−.15	.28	−.05
		800	.16	.01	.29	.01	.34	−.21	.45	−.05	.15	−.13	.24	.02	.23	−.17	.26	−.05

Note. GGUM = generalized graded unfolding model; Dist. = subpopulation trait distribution conditions; Design = anchor-item design; N = sample size per group; RMSE = root mean square error; Bias = bias of estimates; Equivalent = trait distribution for all groups is N(0, 1); Non-equivalent = trait distribution for Group 1 is N(0, 1) and trait distribution for Groups 2 and 3 is N(−0.5, 1).

Figure 3.

Average PSD estimates of GGUM concurrent calibration with three anchor-item designs.

Note. PSD = posterior standard deviation; GGUM = generalized graded unfolding model.

The detailed results in Table 1 and graphical representations in Figure 3 show that the block-interlaced design consistently produced better parameter recovery in all conditions. For instance, the block-interlaced design yielded marginal RMSEs for alpha, delta, and tau were .28, .40, and .44, respectively, across conditions, whereas the corresponding values were .31, .41, and .47 for the standard design and .31, .49, and .48 for the common-item design. Moreover, as shown in Figure 3, results by levels of simulation conditions indicate that the block-interlaced design yielded smaller PSD than the other two anchor-item designs. As expected, the accuracy of parameter estimation with GGUM concurrent calibration increased as sample size increased. The results for anchor-item design were the same across sample sizes, with the block-interlaced design performing slightly better in each case. Overall, parameter estimates of the GGUM were recovered well with sample sizes of 800 per group (e.g., RMSEs for alpha, delta, and tau were .13, .18, and .24 for the block-interlaced design in the equivalent group polytomous condition). Between the equivalent and non-equivalent group conditions, the non-equivalent group showed relatively higher RMSEs and Bias of parameter estimates as shown in Table 1. The effect of anchor-item designs, described above, was observed in both cases. Furthermore, as shown in Table 1, polytomous data led to better concurrent calibration results, a finding which is consistent with single-group estimation research by Roberts et al. (2002) and Roberts and Thompson (2011). Although not shown in Table 1 due to space limitations, the CORR of theta parameters ranged from .97 to 1 across simulation conditions.

Table 2 displays the extent to which the mean and standard deviation of the subpopulation trait distributions were recovered. The reported values are the estimated subpopulation means and standard deviations for Groups 2 and 3 and their corresponding RMSEs. Note that by reporting the actual parameter estimates, the bias results are apparent. Overall, all anchor-item designs produced results close to the expected values, N(0, 1) for equivalent group conditions and N(−0.5, 1) for non-equivalent conditions. For example, in the non-equivalent dichotomous 400 per group condition, population means averaged across Groups 2 and 3 were −.34, −.51, and −.52 for the common-item, standard, and block-interlaced designs, respectively; and the corresponding standard deviations were .93, .97, and .93.

Table 2.

Parameter Recovery of Subpopulation Ms and SDs for Groups 2 and 3.

			Dichotomous								Polytomous
			Subpopulation M				Subpopulation SD				Subpopulation M				Subpopulation SD
			Group2		Group3		Group2		Group3		Group2		Group3		Group2		Group3
Dist.	Design	N	RMSE	Est.	RMSE	Est.	RMSE	Est.	RMSE	Est.	RMSE	Est.	RMSE	Est.	RMSE	Est.	RMSE	Est.
Equivalent	Common-item	100	.28	.19	.18	.09	.19	.83	.13	.90	.20	.20	.09	−.07	.36	1.35	.39	1.38
		200	.27	.10	.27	.07	.14	.87	.12	.90	.10	−.09	.17	−.17	.31	1.31	.38	1.37
		400	.27	.17	.23	.18	.15	.85	.14	.87	.04	.03	.07	.07	.22	.83	.20	.87
		800	.20	.08	.20	.09	.14	.90	.13	.95	.03	.01	.05	.02	.11	.94	.18	.88
	Standard	100	.21	.18	.13	−.04	.20	.81	.19	.87	.23	.19	.17	−.09	.35	1.32	.52	1.38
		200	.11	−.08	.15	−.14	.12	.92	.14	.96	.10	−.08	.20	−.13	.31	1.28	.42	1.32
		400	.06	.04	.11	.10	.14	.88	.14	.89	.02	.02	.06	.12	.13	1.09	.26	1.12
		800	.02	.01	.04	.04	.13	.92	.12	.92	.01	.01	.03	.03	.19	.90	.18	.92
	Block-interlaced	100	.19	.19	.10	−.03	.20	.81	.15	.84	.20	.22	.11	−.13	.32	1.35	.39	1.51
		200	.10	−.07	.16	−.07	.11	.89	.08	.90	.08	−.09	.14	−.18	.28	1.31	.33	1.42
		400	.05	.03	.11	.09	.13	.87	.12	.87	.04	.01	.12	.05	.10	.60	.12	.64
		800	.02	.01	.05	.05	.09	.95	.07	.96	.03	.02	.08	.01	.06	.95	.05	.97
Non-equivalent	Common-item	100	.54	−.25	.42	−.39	.33	.69	.15	.87	.11	−.59	.31	−.80	.26	1.26	.45	1.45
		200	.61	−.15	.38	−.28	.13	.89	.15	.87	.13	−.62	.31	−.80	.36	1.36	.33	1.32
		400	.33	−.35	.35	−.32	.09	.92	.10	.93	.13	−.41	.15	−.38	.20	.81	.20	.82
		800	.26	−.45	.27	−.54	.10	.95	.10	.95	.12	−.48	.13	−.46	.16	.94	.16	.94
	Standard	100	.19	−.36	.16	−.45	.29	.75	.21	.85	.12	−.59	.33	−.79	.26	1.26	.46	1.46
		200	.11	−.47	.13	−.58	.08	.95	.15	.94	.13	−.61	.29	−.78	.39	1.34	.40	1.31
		400	.08	−.53	.09	−.49	.07	.97	.13	.97	.06	−.64	.09	−.60	.16	1.21	.13	1.21
		800	.05	−.50	.06	−.49	.06	.96	.09	.96	.06	−.48	.05	−.47	.08	.94	.10	.96
	Block-interlaced	100	.18	−.37	.48	−.50	.27	.72	.21	.81	.11	−.60	.30	−.81	.26	1.25	.47	1.45
		200	.06	−.45	.11	−.56	.07	.94	.09	.87	.12	−.62	.28	−.78	.34	1.39	.31	1.40
		400	.06	−.54	.05	−.50	.05	.95	.06	.90	.14	−.45	.10	−.42	.21	.87	.22	.90
		800	.07	−.54	.05	−.50	.07	.98	.07	.98	.05	−.50	.03	−.47	.10	.95	.11	.95

Note. Dist. = subpopulation trait distribution conditions; Design = anchor-item design; N = sample size per group; RMSE = root mean square error; Est. = parameter estimates; Equivalent = trait distribution for all groups is N(0, 1); non-equivalent = trait distribution for Group 1 is N(0, 1) and trait distribution for Groups 2 and 3 is N(−0.5, 1).

Discussion

This study sought to expand the options available to practitioners by developing an MCMC program for the GGUM concurrent calibration and exploring the efficacy of different anchor designs in conjunction with subpopulation trait distributions, sample sizes, and data types. The key findings were as follows. First, parameters of the GGUM were estimated well with samples of 800 per group, which is consistent with previous studies (e.g., Roberts et al., 2002). Second, block-interlaced design performed best—yielding the smallest RMSE, bias, and PSD values across conditions. Because block-interlaced design involves the largest total number of anchor items, this finding suggests that using more sets of anchor items can yield more accurate parameter estimates with multiple forms. Third, means and standard deviations of trait distributions in Groups 2 and 3 were well-recovered with all anchor designs, which indicates that the algorithm developed for this study provides an effective alternative to separate calibration and linking with the GGUM (the program may be obtained from the authors upon request).

Given that existing software (GGUM2004; Roberts, Fang, Cui, & Wang, 2006) also allows for limited concurrent calibration, the authors additionally compared the performance of concurrent calibration for GGUM2004, which performs MML estimation, and the developed MCMC program. Because GGUM2004 is limited to a maximum of 2,000 respondents, a three-group concurrent calibration with a sample size of 400 per group (N = 1,200) was initially conducted. However, GGUM2004 did not converge due to missing values, so a two-group concurrent calibration using a sample size of 800 per group (N = 1,600) was conducted. The results are presented in Table 3. The authors found that the developed MCMC program outperformed MML for the conditions where distributions of multiple groups were different and data were coded dichotomously. For example, for the dichotomous non-equivalent group conditions, RMSEs of alpha, delta, and tau parameters were .18, .76, and .73 for MML, whereas the corresponding values were .16, .32, and .35 for MCMC. This occurs primarily due to the absence of prior distributions in the MML. In general, dichotomous data often yield “trade-off” estimates of delta and tau parameters using MML. That is, the response probability of the GGUM is virtually unchanged even though the parameters have drifted away from their true values. More extreme dichotomous items and smaller sample sizes yield more substantially biased estimates using MML (Roberts & Thompson, 2011). MCMC generally performs better than MML with dichotomous data for this reason. However, as was shown by Roberts and Thompson (2011), marginal maximum a posteriori (MMAP) estimation may outperform MCMC. In addition, GGUM2004 assumes the population trait distribution is N(0, 1) for all respondent groups, and this could lead to biased estimates with concurrent calibration when the trait distributions differ across groups. The current MCMC program provides a more general alternative for estimation that allows means and standard deviations of trait distributions to vary across groups receiving alternate forms, in addition to allowing a user to manipulate the prior distributions on all GGUM item parameters.

Table 3.

Accuracy of Parameter Estimates for GGUM Two-Group Concurrent Calibration Using MML and MCMC (N = 800).

	α			δ			τ			θ
Estimation method	RMSE	Bias	SE/PSD	RMSE	Bias	SE/PSD	RMSE	Bias	SE/PSD	RMSE	Bias	SE/PSD
Dichotomous
MML	.18	.02	.20	.76	.43	4.32	.73	−.35	4.39	.40	.23	.43
MCMC	.16	.02	.17	.32	−.03	.29	.35	−.18	.32	.36	−.08	.34
Polytomous
MML	.10	.03	.09	.25	.23	.14	.14	.00	.20	.26	.22	.21
MCMC	.16	−.13	.09	.22	.01	.14	.28	−.17	.19	.22	−.07	.18

Note. SE is for MML and PSD is for MCMC. GGUM = generalized graded unfolding model; MML = marginal maximum likelihood; MCMC = Markov chain Monte Carlo; RMSE = root mean square error; bias = bias of estimates; PSD = posterior standard deviation; SE = standard error.

This study had some limitations. Only 50 replications were run in most conditions (and 30 in some) due to long MCMC runtimes. In this study, one replication with 30,000 iterations took 90 min with a total sample size of 300 and 50 items on a 3.0-GHz personal computer, and longer runtimes can be expected if substantially larger samples or more items are used. At present, MML or MMAP concurrent calibration methods would be much more time efficient (Roberts & Thompson, 2011). In addition, this study did not manipulate the standard deviation of theta in the non-equivalent group conditions. Future studies could examine the effects of different standard deviations of respondent groups, which is perhaps more common in work or educational settings. Finally, the concurrent calibration method may not be an ideal approach for some practical situations. For example, in a situation where a researcher can access an item parameter bank, but not the responses used to calibrate items for that bank, it is more efficient to calibrate new items in a single sample along with a few anchors from the bank.

Nonetheless, the results of this study provide valuable information about how to structure pretest data collections with the GGUM, and possibly other ideal point IRT models, which are being considered for large-scale testing programs. The authors hope the concurrent calibration software developed for this study will prove useful to applied researchers and expand research possibilities with ideal point IRT models.