Plausible-Value Imputation Statistics for Detecting Item Misfit

Abstract

When tests consist of a small number of items, the use of latent trait estimates for secondary analyses is problematic. One area in particular where latent trait estimates have been problematic is when testing for item misfit. This article explores the use of plausible-value imputations to lessen the severity of the inherent measurement unreliability in shorter tests, and proposes a parametric bootstrap procedure to generate empirical sampling characteristics for null-hypothesis tests of item fit. Simulation results suggest that the proposed item-fit statistics provide conservative to nominal error detection rates. Power to detect item misfit tended to be less than Stone’s ${\chi }^{2*}$ item-fit statistic but higher than the $S-X^2$ statistic proposed by Orlando and Thissen, especially in tests with 20 or more dichotomously scored items.

Item response theory (IRT) is a model-based statistical analysis paradigm useful for understanding response data in educational and psychological tests (Hambleton & Swaminathan, 1985). Models are constructed based on prior knowledge about the theoretical response processes that the items are expected to follow. These hypothesized IRT models are then fitted to suitable sample data, drawn from the population from which the test should be calibrated, to obtain estimates of the respective population parameters. However, as with all statistical models, the degree to which IRT models are useful for drawing inferences is contingent upon the degree of fit with the data. Misfitting models will generally lead to biased parameter estimates or inappropriate inferences, which may be especially bad in IRT applications because models are often formed so that subsequent latent trait estimates can be obtained more accurately than traditional scoring methods (Lord, 1980). Therefore, it is important to investigate goodness-of-fit techniques to evaluate whether the selected models adequately reflect the observed data.

Evaluating the goodness-of-fit for IRT models can take on many different forms. For instance, models may be evaluated based on whether residual covariation (i.e., local dependence) exists between item pairs both locally (e.g., Chen & Thissen, 1997) and globally (e.g., Maydeu-Olivares & Joe, 2005). Because pairwise covariation is the focus of local dependence–based measures, these IRT-based fit statistics have similar interpretations to the fit statistics and residual diagnostic methods common in structural equation modeling (Bollen, 1989). Alternatively, and arguably more importantly, individual items may be tested to determine whether the select item response functions appropriately reflect the underlying functional relationship with the latent traits (e.g., Bock, 1972; Orlando & Thissen, 2000; Yen, 1981). This class of fit statistics evaluates whether a given item response function is underfitting the functional form present in the response data, thereby misrepresenting the true functional variability.

In this article, the authors propose a simple yet novel procedure that addresses the inherent measurement imprecision when computing the two-step item-fit statistics proposed by Bock (1972), Yen (1981), and McKinley and Mills (1985). The proposed statistics use plausible-value (PV) imputations (Mislevy, 1991) and parametric bootstrap techniques (Hope, 1968) to account for uncertainty in the latent trait estimates and sampling variability present in shorter tests and smaller sample sizes. Monte Carlo simulations are used to evaluate the Type I error rates under a variety of testing conditions to determine whether the error rates are influenced by sample size, test length, and complexity of IRT models fitted to dichotomous response data. Finally, power rate estimates are compared with the existing $Q_1$ (Yen, 1981), $S-X^2$ (Orlando & Thissen, 2000), and ${\chi }^{2*}$ (Stone, 2000) statistics by investigating simulation conditions adapted from the Monte Carlo simulation conditions investigated by Orlando and Thissen (2000, 2003) for dichotomous IRT models.¹

Item-Fit Statistics for IRT Models

Determining how well an item response model fits the sampled data generally requires the comparison between model-implied expected values and observed item response characteristics for each item of interest. To accomplish this task, researchers such as Bock (1972), Yen (1981), and McKinley and Mills (1985) have proposed a family of two-step methods for investigating item misfit. These two-step approximations involve the computation of individual estimates of the latent trait values ($\theta$) to be used to construct expected counts of responses. These expected counts are then compared with commensurate counts of observed data, and the discrepancy between the values is typically compared with a theoretical ${\chi }^2$ distribution.

Before introducing further details regarding the family of two-step item-fit statistics, it is first important to understand how $\hat{\theta }$ estimates are typically obtained in practice. For each response pattern $\mathbf{y}$ containing J elements (one element for each item), the posterior probability of $\theta$ is defined as

$$P(\theta |\mathbf{y},\hat{\mathbf{\Psi }})=\frac{P(\mathbf{y}|\theta ,\mathbf{\Psi })P\left(\theta \right)}{\int P(\mathbf{y}|\theta ,\mathbf{\Psi })P\left(\theta \right)},$$

where $\hat{\mathbf{\Psi }}$ represents a vector of item parameters, $P(\mathbf{y}|\theta ,\mathbf{\Psi }\mathbf{)}$ is the likelihood function implied by the IRT probability functions and observed response pattern, and $P(\theta )$ is the prior distribution of $\theta$ (in many IRT applications, this is typically based on a $\mathcal{N}(0,1)$ density function). Computing the mean of Equation 1 (using numerical integration techniques) leads to the expected a posteriori (EAP) estimate of $\theta$, while locating the mode provides a maximum a posteriori (MAP) estimate (Bock & Mislevy, 1982). When the prior distribution of $\theta$ is not assumed to be known, then $P(\theta )=1$ for all $\theta$ values, and maximizing Equation 1 leads to the maximum-likelihood (ML) estimate of $\theta$. Finally, the associated sampling variability of the estimates is typically expressed as the standard deviation (or, less formally, the standard error) of Equation 1 for EAP estimates and as $(-\frac{{\partial }^2}{{\partial }^2\theta }\ln [P(\theta |\mathbf{y},\mathbf{\Psi }\mathbf{)}{\mathbf{])}}^{\mathbf{-}1\mathbf{/}2}$ for the ML or MAP estimates (Bock & Mislevy, 1982).

Turning now to the two-step item-fit statistics for IRT models, the process required to obtain observed and expected item response counts is as follows:

1. Fit the select IRT models to an $\mathrm{N}\times \mathrm{J}$ matrix of response data, typically with ML or MAP estimation techniques (e.g., Bock & Aitkin, 1981), to obtain a vector of item-parameter estimates $\hat{\mathbf{\Psi }}$.

2. Obtain estimates of ${\hat{\theta }}_i$ for each of the N item response patterns by setting $\mathbf{\Psi }\mathbf{=}\hat{\mathbf{\Psi }}$ in Equation 1. The collection of these estimates can be expressed as the vector $\hat{\mathbf{\theta }}$.

3. Rank all the $\hat{\mathbf{\theta }}$ elements from lowest to highest and partition the sorted vector into B discrete subgroups with $n_b$ participants in each subgroup. Analogously, the associated item responses for the jth item of interest are assigned to their subgroup according to where the associated ${\hat{\mathbf{\theta }}}_i$ values were assigned.

4. For each distinct bundle b, the number of individuals who answered the kth response category is obtained for all K categories ($O_{\mathrm{bk}}$). The expected count for the bth bundle and kth category ($E_{\mathrm{bk}}(\hat{\mathbf{\theta }})$) is obtained by computing $n_b$ times the item probability function given a $\theta$ location representing the central tendency of the bth bundle of ${\hat{\theta }}_i$ terms (typically the mean or median of the latent trait estimates).

This procedure generates B discrete sets of observed and expected response counts for each bundle and response category combination for a given item under investigation. When testing multiple items in the sample data, the computation and sorting of $\hat{\mathbf{\theta }}$, as well as the sorting of the rows in the sampled data, need only be performed once.

Bock (1972), Yen (1981), and McKinley and Mills (1985) have argued that the discrepancy between $O_{\mathrm{bk}}$ and $E_{\mathrm{bk}}(\hat{\mathbf{\theta }})$ can be evaluated with Pearson’s and likelihood-ratio-based ${\chi }^2$ tests. For example, Yen’s $Q_1$ item-fit statistic can be expressed as

$$Q_1=Q_1\left(\hat{\mathbf{\theta }}\right)=\sum _{b=1}^{10}\sum _{k=0}^{K-1}\frac{{(O_{\mathrm{bk}}-E_{\mathrm{bk}}\left(\hat{\mathbf{\theta }}\right))}^2}{E_{\mathrm{bk}}\left(\hat{\mathbf{\theta }}\right)},$$

which is a variant of Pearson’s ${\chi }^2$ test. The $Q_1$ statistic fixes the number of subgroups to 10 and uses the mean of the $\hat{\theta }$ estimates within each subgroup as a representation of the bundle’s central tendency. Bock’s version of this fit statistic slightly differs from $Q_1$ in that it allows the size of B to vary by constructing the subgroups according to fixed $n_b$ sizes, and uses the median of the $\hat{\theta }$ estimates instead of the mean. In this article, we will only focus on the $Q_1$ variant of Pearson’s ${\chi }^2$ test; however, the methods presented will also be applicable to Bock’s implementation, as well as McKinley and Mills’s (1985) likelihood-ratio-based $G^2$ statistic.

Limitations of Item-Fit Statistics Based on $\hat{\mathbf{\theta }}$ Estimates

Several authors have emphasized that caution should be used when interpreting the two-step family of item-fit statistics. The two-step item-fit statistics are generally influenced by the number of subgroups that have been constructed (Reise, 1990), the precision with which the item-parameter estimates are obtained (Orlando & Thissen, 2000), whether the model-implied expected values are too small (Agresti, 2002), and the consequences of replacing expected values with values implied by prediction estimates (i.e., using $E_{\mathrm{bk}}(\hat{\mathbf{\theta }})$ as a proxy for $E_{\mathrm{bk}}(\mathbf{\theta }\mathbf{)}$; Agresti, 2002). Furthermore, the question of which $\hat{\theta }$ estimator to use also influences the results (Chalmers, 2016a; Chalmers, Counsell, & Flora, 2016). Using prior distributions to obtain Bayesian estimates introduces a bias toward the mode of the prior distribution, particularly at the extreme ends of the latent trait distribution (Bock & Mislevy, 1982), while omitting a prior distribution (e.g., ML estimation) will tend to have the exact opposite effect.

Most importantly, however, Stone and Hansen (2000) stressed that “the problem with the goodness-of-fit statistics [based on $\theta$ estimates] may be due to the precision or uncertainty with which $\theta$ is estimated” (p. 986). To elaborate on this statement, and assuming for the moment that $\hat{\mathbf{\Psi }}=\mathbf{\Psi }$, the precision with which $\hat{\theta }$ values are obtained is intimately related to the accuracy with which individuals are correctly classified into their population-based subgroups. This result implies that the larger the imprecision in $\hat{\theta }$, the less likely the individuals will be correctly classified. A subtle consequence of this feature is that individuals are classified more accurately as the number of items in the test increases; in the limiting case, where $\underset{J\to \infty }{lim}\hat{\theta }=\theta$, each participant will be correctly classified in their respective population subgroup. Clearly, however, this property is not useful if the length of the test is too small or if $\hat{\mathbf{\Psi }}$ is an inaccurate representation of $\mathbf{\Psi }$.

The simulation study investigated by Orlando and Thissen (2000) highlights the severity of using these two-step item-fit statistics in shorter tests. In their simulation study, the authors investigated Type I error rate estimates (at $\alpha =.05$) for $G^2$ and $Q_1$ when studying the 1-, 2-, and 3-parameter logistic models (1PLM, 2PLM, and 3PLM, respectively; Hambleton & Swaminathan, 1985) for tests of length 10, 40, and 80 with $N=1,000$. The authors reported that when the test length was 10, the Type I error rate estimates for $G^2$ and $Q_1$ were all greater than 0.95, regardless of the IRT model studied. Furthermore, even when the test length was increased to 40 items, the error rates were still unacceptably liberal (ranging from 0.14 to 0.37, where rates were higher for $G^2$). Only when the test length reached 80 items were the error rates reasonably close to the nominal $\alpha$ for the $Q_1$ statistic; however, $G^2$ still tended to demonstrate liberal error detection rates.

Generating Uncertainty With PV Imputations

As is clear from the previous section, sampling variability of the $\hat{\theta }$ estimates is not included in the computations of the two-step item-fit statistics. However, the imprecision in $\hat{\theta }$ estimates for secondary analyses is not a new concept in the psychological measurement literature. In particular, measurement precision issues have been emphasized in large-scale assessment applications, such as National Assessment of Educational Progress (NAEP), where a smaller number of items are often administered. For these types of data, analysts are often interested in drawing inferences regarding the distribution of $\mathbf{\theta }$ by using $\hat{\mathbf{\theta }}$ as a suitable proxy (Mislevy, 1991).

However, inferences that utilize the $\hat{\mathbf{\theta }}$ values—even those as simple as estimating the variance of $\mathbf{\theta }$—will necessarily lead to biased estimates when $\hat{\mathbf{\theta }}$ is unreliable (for further discussion and examples, see Mislevy, Beaton, Kaplan, & Sheehan, 1992).

To account for the inherent measurement uncertainty in $\hat{\mathbf{\theta }}$, Mislevy (1991) recommended sampling from the posterior probability functions directly to obtain filled-in datasets containing PV instantiations of the missing data elements. After complete datasets are filled in, Rubin’s (1987) imputation methodology can be used to aggregate the sampling variability due to the missing data components. More specifically, after M complete datasets are constructed via imputation methods, these datasets can be used within M identically formed secondary analyses, and the variance components can be combined using Rubin’s data aggregation formulae.

Mislevy’s (1991) important insight in the development of PV imputations in IRT applications was to use the model-implied posterior response functions directly as a means to quantify uncertainty about the parameter estimates. Adopting this methodology for the $\hat{\theta }$ estimates, suitable samples can be obtained from Equation 1 to obtain M independent PV sets from the posterior distribution. Although there are several algorithms that can be used to obtain samples from these posterior distributions, the sampling form can be greatly simplified if the posterior distributions can be reasonably approximated by a Gaussian distribution (e.g., see Chang & Stout, 1993). If this assumption is viable, then PVs can be obtained by drawing from all N response patterns to obtain a complete set of PVs, ${\mathbf{\theta }}^{*}$.

PV Imputations for Item-Fit Statistics

Returning now to the topic of item misfit, Stone and Hansen (2000) have asserted that “. . . if the uncertainty with which $\theta$ is estimated can be accounted for, a chi-square goodness-of-fit statistic could be used with shorter tests” (p. 986). As is clear from the description above, the use of PV imputations has been introduced precisely to account for measurement uncertainty in each $\hat{\theta }$ estimate for secondary analyses. Therefore, PV imputations may provide a simple but effective means to improve the two-step item-fit statistics, particularly in shorter tests.

After obtaining M-PV sets of latent trait estimates ${\mathbf{\theta }}_1^{*},{\mathbf{\theta }}_2^{*},\dots ,{\mathbf{\theta }}_M^{*}$, the PV version of $Q_1$ can be expressed as

$$\mathrm{PV}-Q_1=\frac{Q_1\left({\mathbf{\theta }}_1^{*}\right)+Q_1\left({\mathbf{\theta }}_2^{*}\right)+\cdots +Q_1\left({\mathbf{\theta }}_M^{*}\right)}{M}.$$

The df associated with $\mathrm{PV}-Q_1$ has a similar form, where $d{f}_{\mathrm{PV}}=(d{f}_1+d{f}_2+\cdots +d{f}_M)/M$. This measure represents the average of the $Q_1$ statistic and their associated df given the M-independently drawn ${\mathbf{\theta }}^{*}$ sets. An average df estimate is used to control for instances where the $Q_1$ statistic has model-implied expected values that are too small, resulting in bundles that should be collapsed or omitted. According to these equations, as $M\to \infty$, the associated sample estimates will converge to the population statistic expressed in Equation 3 with degrees of freedom $d{f}_{\mathrm{PV}}$. When investigating this measure empirically, it has been found that as few as 30 imputations are required to obtain sufficient stability in the p values; however, more imputations can be drawn, if desired.

The benefit of the PV imputation variant of $Q_1$ is that it explicitly includes the imprecision of the $\hat{\theta }$ estimates as a source of variation in the computations. In practice, there are two scenarios that make $\mathrm{PV}-Q_1$ appealing for detecting item misfit. First, when the test length approaches $\infty$, all associated $\widehat{\mathrm{SE}}(\hat{\theta })\to 0$; hence, each draw will be exactly equal to their expected value (i.e., are equal to the corresponding EAP values). This implies that $\mathrm{PV}-Q_1$ will have the same asymptotic conclusions reached when using point estimates of $\theta$ in longer tests when the item-parameter estimates are accurate. Next, in situations where $\mathbf{y}$ contains few responses, the PV imputations will accommodate for the measurement uncertainty because the imputed values have a larger amount of sampling variation, thereby forcing the individuals to be stochastically classified into a wider number of subgroups. This feature is important because the upward bias borne from using point estimates of $\theta$ can be largely avoided.

In theory, the $\mathrm{PV}-Q_1$ item-fit statistic should perform better at controlling Type I error rates than $Q_1$ in shorter tests due to averaging over multiple samples with comparable misclassification accuracies. Unfortunately, however, the distribution of $\mathrm{PV}-Q_1$ will not be exactly ${\chi }^2$ with degrees of freedom $d{f}_{\mathrm{PV}}$ in smaller sample sizes and shorter tests. While PV imputations generally address the issue of measurement precision in the $\hat{\theta }$ estimates within a given sample, they do not address the problem of treating the $\hat{\mathbf{\Psi }}$ estimates as the population parameters $\mathbf{\Psi }$ (Tsutakawa & Johnson, 1990). The next section focuses on one possible method to account for sampling variability in the item-parameter estimates.

Parametric Bootstrap to Approximate the Sampling Distribution

To obtain a more appropriate sampling distribution for $\mathrm{PV}-Q_1$, a parametric bootstrap technique (also known as Monte Carlo sampling; Hope, 1968) is adopted to approximate the null sampling distribution (Efron & Tibshirani, 1998). The parametric bootstrap involves constructing independent random samples implied by the population generating functions, computing the statistic of interest on each respective sample, and comparing the empirical distribution of this statistic with the value obtained from the original dataset.

For the current application regarding $\mathrm{PV}-Q_1$, the parametric bootstrap algorithm is implemented as follows:

1. Fit the select IRT models to the original dataset and obtain the associated p value for the $\mathrm{PV}-Q_1$ statistic. Call this value $p_{\mathrm{PV}-Q_1}$.

2. Next, draw N independently distributed $\theta$ values (where N is the sample size of the original dataset) from the latent trait distribution that matches the original modeling assumptions (typically, $\theta ~\mathcal{N}(0,1)$).

3. Using the parameter estimates from the original fitted model, as well as the newly drawn $\theta$ values, generate a new sample dataset.

4. Using the new dataset, fit the same IRT models to obtain new parameter estimates.

5. Compute $\mathrm{PV}-Q_1$ and the associated p value for this new model, and store the p value into the vector ${\mathbf{p}}_{\mathrm{PV}-Q_1}$.

6. Repeat Steps 2 to 5 R times until a sufficient number of simulated datasets have been analyzed.

After the parametric bootstrap scheme is complete, the ${\mathbf{p}}_{\mathrm{PV}-Q_1}$ vector can be compared with $p_{\mathrm{PV}-Q_1}$ to determine how likely the original p value was compared with an empirical sample of values where the null hypothesis is exactly true. Specifically, the empirical p value estimate is obtained with the formula:

$$\mathrm{PV}-Q_1^{*}=\frac{1+I(p_{\mathrm{PV}-Q_1}>{\mathbf{p}}_{\mathrm{PV}-Q_1})}{1+R},$$

where $I(.)$ is an indicator function that computes the frequency with which $p_{\mathrm{PV}-Q_1}$ is greater than the Monte Carlo simulated p values (Davison & Hinkley, 1997). Note that the proposed parametric bootstrap procedure uses the p values rather than the observed $\mathrm{PV}-Q_1$ values. The authors recommend using p values to account for the possibility of omitting bundles with small expected values within the simulated datasets (as well as in the original observed statistic). When bundles are removed, the magnitude of $\mathrm{PV}-Q_1$ will vary as a function of the number of bundles remaining, while the p values will be implicitly adjusted through the changes in the df.

Similarity to Stone’s ${\chi }^{2*}$ Statistic

The proposed PV imputation statistics share some similarity to the ${\chi }^{2*}$ measure described by Stone (2000). Stone argued that the uncertainty in $\hat{\theta }$ can be addressed by comparing a model-implied table of pseudo-counts created in the “Expectation” step of the Expectation–Maximization (EM; see Bock & Aitkin, 1981) algorithm with similarly constructed expected values at the associated quadrature nodes. By integrating over the latent trait distribution to compute pseudo-count terms over a range of quadrature nodes, and comparing these values with model-implied expected values at the same quadrature node locations, a variant of Pearson’s ${\chi }^2$ measure (termed ${\chi }^{2*}$) could be computed. Stone (2000) further noted that the values in the expected table of pseudo-counts are unfortunately not independent; therefore, the distribution of ${\chi }^{2*}$ is not strictly ${\chi }^2$ distributed with the usual df. To account for this effect, Stone (2000) implemented a Monte Carlo simulation strategy to obtain the empirical sampling variability of the observed ${\chi }^{2*}$ values.

The $\mathrm{PV}-Q_1$ statistic has a similar purpose to ${\chi }^{2*}$ in that it is developed to account for uncertainty in the $\hat{\theta }$ estimates by utilizing information from the posterior probability functions. Both approaches also require Monte Carlo sampling techniques to better approximate the respective sampling distributions, and therefore tend to be more computationally demanding. However, where these approaches differ is the manner in which the posterior information about $\hat{\theta }$ is captured. $\mathrm{PV}-Q_1$ focuses on information from the N independent posterior probability functions for each sampled response pattern to account for the associated measurement uncertainty in each response pattern. The ${\chi }^{2*}$ statistic, on the contrary, compares model-implied expected values with information at different quadrature locations in the table of correlated pseudo-counts, thereby avoiding the need to classify individuals to population subgroups. These approaches are indeed quite different because the goal of $\mathrm{PV}-Q_1$ is to stochastically classify the N individuals into the population subgroups while the goal of ${\chi }^{2*}$ is to avoid the need for classification altogether.

Unfortunately, one negative consequence when using quadrature nodes across a range of $\theta$ values is that small expected values are likely to arise. To avoid this issue, Stone (2000) suggested that smaller ranges of $\theta$ should be used to reduce the likelihood of small expected values (e.g., between $-2\le \theta \le 2$); hence, the full range of $\theta$ is not used to detect the item misfit. In practice, this property could be problematic because item misfit may only be detected based on the information at the extreme ends of the $\theta$ distribution (e.g., when fitting a 2PLM to data generated from a 3PLM; cf. Orlando & Thissen, 2000). In addition, the range of $\theta$ may require further modifications to avoid sparse categories, depending on the total sample size or distribution of the response patterns. Unfortunately, however, the range of the $\theta$ quadrature nodes must be selected a priori and cannot be varied within each Monte Carlo sample.

Monte Carlo Simulations

To investigate the properties of $\mathrm{PV}-Q_1$ and $\mathrm{PV}-Q_1^{*}$, and to contrast these statistics with $Q_1$, ${\chi }^{2*}$, and the $S-X^2$ statistic, Monte Carlo simulations based on the designs investigated by Orlando and Thissen (2000, 2003) were constructed. The reason for basing the simulations on these two studies in particular was to reinvestigate whether $Q_1$ can be improved by using the proposed augmented schemes under similar design conditions. However, certain modifications were made to make the presentation slightly more consistent. In particular, the completely crossed simulation design presented by Orlando and Thissen (2000) was not utilized because the power conditions were less realistic (for a discussion of this, see Orlando & Thissen, 2003). Instead, we investigated only the Type I error conditions from their stimulation study where the IRT models were generated and fitted using the same 1PLM, 2PLM, and 3PLM. In addition, we explored the item-fit statistics when the test length contained 20 items, investigated Type I error and power rates with sample sizes of 500, and in the following power analysis simulations we removed the $N=2,000$ conditions used by Orlando and Thissen (2003) because the authors reported that detection rates were at or very close to 1.

Item response data were generated and analyzed using the mirt package (Version 1.17.1; Chalmers, 2012) and customized R functions (R Core Team, 2016) while the Monte Carlo simulation code was organized with the SimDesign package (Chalmers, 2016b; Sigal & Chalmers, 2016). Models were estimated using marginal MAP with the EM algorithm and terminated when all parameter estimates were less than |.0001| across successive EM iterations. To be consistent with Orlando and Thissen (2000, 2003), EAP estimates of $\hat{\theta }$ were obtained for $Q_1$ where the prior distribution was assumed to be $\mathcal{N}(0,1)$. To ensure that the $E_{\mathrm{bk}}(\hat{\mathbf{\theta }})$ values were not too small to distort $Q_1$ and $\mathrm{PV}-Q_1$, subgroups with any $E_{\mathrm{bk}}(\hat{\mathbf{\theta }})<2$ were omitted from the computations and the df were adjusted accordingly. $S-X^2$ was also adjusted when expected values were less than 1 by implementing the collapsing method described by Orlando and Thissen (2000). With respect to $\mathrm{PV}-Q_1$ and $\mathrm{PV}-Q_1^{*}$, 100 sets of PVs were drawn from a Gaussian distribution with the mean and standard deviation values equal to their respective EAP and posterior standard deviation estimates for each response pattern. For Stone’s ${\chi }^{2*}$ measure, 11 quadrature nodes, evenly spaced across the range $-2\le \theta \le 2$ (cf. Stone, 2000), were used to compute the table of expected pseudo-counts. Finally, a total of 1,000 parametric bootstrap samples were constructed for each of the $\mathrm{PV}-Q_1^{*}$ and ${\chi }^{2*}$ statistics to adequately approximate the empirical sampling distributions.

Type I Error Rates

Type I error rates were obtained by simulating and fitting data to the correct 1PLM, 2PLM, and 3PLM response functions. The 3PLM was generated using the slope-intercept form:

$$P(y=1|a,d,g)=g+\frac{1-g}{1+\exp (-(a\theta +d))},$$

where $P(y=0|a,d,g)=1-P(y=1|a,d,g)$. The 3PLM reduces to 2PLM when $g=0$ and further reduces to 1PLM when the a terms are constrained to be equal across all J items. In the following simulations, all a parameters were drawn from a log-normal $(0,0.5)$ distribution (for 1PLM, only one slope parameter was drawn and used for all J items), d’s from a normal $(0,1)$ distribution, g’s from a logit-normal $(-1.1,0.5)$ distribution, and $\theta$’s from a normal $(0,1)$ distribution. To ensure that models converged within a reasonable number of EM iterations, parameters were estimated with the prior distribution functions: $\mathcal{N}(0,1.5)$ for the d parameter (all models), $\mathcal{N}(1.1,0.6)$ for the a parameters (2PLM and 3PLM only), and $\mathcal{N}(-1.1,0.5)$ for the logit of the g parameters (3PLM only).

Type I error rates were estimated by simulating each condition 200 times and obtaining the p values for the first 10 items. Each p value was then compared with the nominal $\alpha$ level, and the average number of p values less than $\alpha$ was computed to represent the estimated error detection rate. Type I error rate estimates for all 24 simulation conditions are displayed in Table 1.

Table 1.

Estimated Type I Error Rates for Data Generated and Fitted by the 1PLM, 2PLM, and 3PLM.

n	IRT model	Test length	$S-X^2$	$Q_1$	$\mathrm{PV}-Q_1$	$\mathrm{PV}-Q_1^{*}$	${\chi }^{2*}$
500	1PLM	10	0.083	0.798	0.004	0.037	0.044
		20	0.062	0.362	0.007	0.038	0.054
		40	0.059	0.140	0.008	0.039	0.055
		80	0.046	0.077	0.014	0.042	0.047
	2PLM	10	0.054	0.773	0.000	0.013	0.060
		20	0.040	0.188	0.000	0.013	0.060
		40	0.038	0.070	0.000	0.038	0.053
		80	0.043	0.050	0.006	0.042	0.060
	3PLM	10	0.093	0.896	0.000	0.008	0.056
		20	0.065	0.422	0.001	0.020	0.062
		40	0.059	0.155	0.001	0.037	0.055
		80	0.050	0.080	0.003	0.050	0.064
1,000	1PLM	10	0.066	0.968	0.004	0.032	0.046
		20	0.067	0.590	0.004	0.033	0.055
		40	0.059	0.206	0.012	0.045	0.045
		80	0.053	0.106	0.022	0.045	0.053
	2PLM	10	0.043	0.913	0.000	0.017	0.061
		20	0.050	0.434	0.000	0.033	0.060
		40	0.052	0.103	0.000	0.050	0.053
		80	0.041	0.055	0.002	0.047	0.057
	3PLM	10	0.087	0.962	0.000	0.005	0.049
		20	0.063	0.686	0.000	0.021	0.054
		40	0.054	0.237	0.000	0.037	0.049
		80	0.047	0.086	0.001	0.038	0.060

Note. 1PLM = 1-parameter logistic model; 2PLM = 2-parameter logistic model; 3PLM = 3-parameter logistic model; IRT = item response theory.

Simulation results

Beginning with $Q_1$ and $S-X^2$, the Type I error rate estimates largely agreed with the simulation results presented by Orlando and Thissen (2000). Tests with more items resulted in better rates for $Q_1$, while $Q_1$ was influenced by sample size; specifically, smaller sample sizes resulted in lower Type I error rates. The $S-X^2$ statistic also behaved relatively well across the simulation conditions. In addition, and as noted in Orlando and Thissen’s (2003) simulation study, $S-X^2$ performed inconsistently when only 10 items were fitted. We observed the same phenomenon in our simulations, particularly when fitting the 1PLM when $N=500$ and with the 3PLM when $N=500$ or 1,000. In general, the $S-X^2$ statistic has a tendency to be slightly liberal in tests with only 10 items, though this effect appears to be moderated by sample size and may disappear in larger samples.

Regarding $\mathrm{PV}-Q_1$ and $\mathrm{PV}-Q_1^{*}$, these fit statistics were consistently either conservative or close to the nominal $\alpha$ and were influenced by the type of IRT models and test length studied. The general trend was that longer tests resulted in rates closer to the nominal $\alpha$, and more complex IRT models led to more conservative error rates. $\mathrm{PV}-Q_1^{*}$ was much closer to the nominal $\alpha$ compared with $\mathrm{PV}-Q_1$ and was able to achieve reasonable error rates around 40 or more items for all IRT models studied (according to Bradley’s, 1978, “liberal” Type I error criteria). For simpler IRT models, Bradley’s (1978) criteria were achieved by $\mathrm{PV}-Q_1^{*}$ using 10 items with 1PLMs and 20 items with 2PLMs. Overall, $\mathrm{PV}-Q_1$ demonstrated very conservative detection rates that will likely have a negative consequence on the power to detect item misfit, especially in shorter tests.

Finally, ${\chi }^{2*}$ demonstrated Type I error rates close to the nominal $\alpha$ level in all conditions studied. Based on Type I error control alone, it appears that ${\chi }^{2*}$ would provide the most consistent performance in practice, especially compared with the competing item-fit statistics that were investigated in this study.

Power Rates

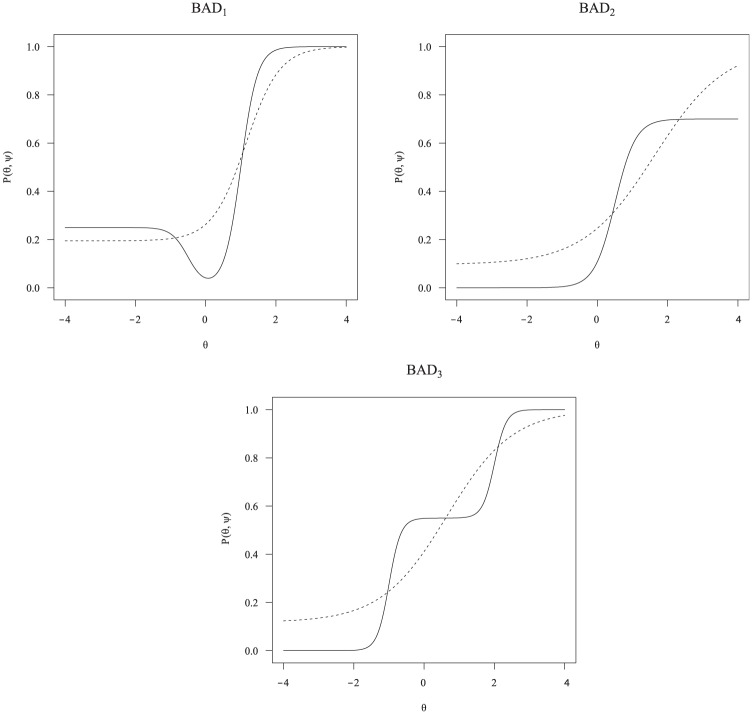
To determine the power for detecting item misfit, the authors reinvestigated the three atypical IRT models studied by Orlando and Thissen (2003). The respective items are labeled $\mathrm{BA}{\mathrm{D}}_1$, $\mathrm{BA}{\mathrm{D}}_2$, and $\mathrm{BA}{\mathrm{D}}_3$, where response data were generated from the models:

$$\mathrm{BA}{\mathrm{D}}_1=\frac{c}{1+\exp (1.7a[\theta -(b-d)])}+\frac{1}{1+\exp (-1.7a[\theta -b])},$$

where $a=2.5$, $b=1$, $c=0.25$, and $d=1.5$;

$$\mathrm{BA}{\mathrm{D}}_2=\frac{d}{1+\exp (-1.7a[\theta -b])},$$

where $a=2$, $b=0.5$, and $d=0.7$; and

$$\mathrm{BA}{\mathrm{D}}_3=\frac{x}{1+\exp (-1.7a[\theta -b])}+\frac{y}{1+\exp (-1.7a[\theta -(b+d)])},$$

where $a=3.5$, $b=-1$, $d=3$, $x=0.55$, and $y=0.45$.

Each atypical response curve can be seen in Figure 1 along with fitted 3PLM probability functions generated from parameters corresponding to an MAP discrepancy function within the range, $\theta =[-4,4]$. See the discussion by Orlando and Thissen (2003) for further details regarding these models and selected parameter values.

Figure 1.

Three types of misfitting items studied in the power analysis simulation (solid) with a fitted 3PLM response function (dashed).

Note. 3PLM = 3-parameter logistic model.

The simulation conditions investigated contained four test lengths (10, 20, 40, and 80) with two sample sizes (500 and 1,000) and three atypical items. Tests were generated such that J− 1 items were 3PLMs while one item was generated according to one of the atypical response functions. Each item was fitted using the 3PLM using the same prior parameter distributions described at the beginning of this section. Power rates estimated from 500 Monte Carlo simulated datasets are located in Table 2. Finally, to facilitate interpretation based on the information from the previous section, power rates that were paired with Type I error rate estimates greater than 0.075 are presented in bold font.

Table 2.

Power Rate Estimates for Three Types of Misfitting Items.

n	Item	Test length	$S-X^2$	$Q_1$	$\mathrm{PV}-Q_1$	$\mathrm{PV}-Q_1^{*}$	${\chi }^{2*}$
500	$\mathrm{BA}{\mathrm{D}}_1$	10	0.770	0.998	0.016	0.406	0.882
		20	0.940	1.000	0.490	0.972	0.996
		40	0.914	1.000	0.926	1.000	1.000
		80	0.844	0.996	0.988	1.000	1.000
	$\mathrm{BA}{\mathrm{D}}_2$	10	0.484	1.000	0.404	0.890	1.000
		20	0.330	0.970	0.272	0.996	1.000
		40	0.254	0.842	0.678	0.998	0.998
		80	0.254	0.806	0.834	0.992	1.000
	$\mathrm{BA}{\mathrm{D}}_3$	10	0.248	0.988	0.042	0.588	0.804
		20	0.358	0.952	0.390	0.942	0.968
		40	0.414	0.972	0.828	0.986	0.990
		80	0.362	0.988	0.986	1.000	1.000
1,000	$\mathrm{BA}{\mathrm{D}}_1$	10	0.946	1.000	0.166	0.688	0.984
		20	0.998	1.000	0.886	0.998	1.000
		40	1.000	1.000	1.000	1.000	1.000
		80	0.998	1.000	1.000	1.000	1.000
	$\mathrm{BA}{\mathrm{D}}_2$	10	0.704	1.000	0.638	0.928	1.000
		20	0.584	1.000	0.880	0.996	1.000
		40	0.634	0.998	0.988	1.000	1.000
		80	0.516	0.984	0.996	1.000	1.000
	$\mathrm{BA}{\mathrm{D}}_3$	10	0.482	1.000	0.314	0.878	0.976
		20	0.690	1.000	0.890	0.998	1.000
		40	0.800	1.000	0.996	1.000	1.000
		80	0.778	1.000	1.000	1.000	1.000

Simulation results

As expected, increasing the sample size from 500 to 1,000 increased the detection rates for all statistics investigated. As well, the detection rates in Table 2 demonstrate that $Q_1$ generally has the highest power to detect item misfit. However, given the liberal Type I error rates for the $Q_1$ statistic, this behavior is to be expected and unfortunately cannot be relied upon. $Q_1$’s power tended to decrease as the test length increased largely because the liberal nature of the statistic progressively was less prevalent as measurement precision improved. That being said, our simulation results agree with Orlando and Thissen’s (2003) conclusion that $Q_1$ is only a reliable fit detection statistic for dichotomous response models when $\theta$ is estimated from more than 80 observed dichotomous item responses.

With respect to the $S-X^2$ statistic, there was no systematic trend according to test length; estimated power rates could either increase or decrease with different test lengths. These results were likely caused by the necessity for collapsing small expected values in the associated number-correct response tables because of the likelihood of observing small expectations in longer tests. For $\mathrm{BA}{\mathrm{D}}_2$, this has particularly negative consequences because the discrepancy between the population generating model and the fitted 3PLM mainly occurs in upper and lower $\theta$ locations (see Figure 1); hence, when high and low sum scores are collapsed toward the center of the distribution, there is less information to detect this particular type of misfit. The effect of varying test length requires further investigation because there is a mixed consensus regarding whether $S-X^2$ is positively (Orlando & Thissen, 2003), negatively (Glas & Suárez-Falcón, 2003; LaHuis, Clark, & O’Brien, 2011; Wells & Bolt, 2008), or unaffected (Kang & Chen, 2008; Orlando & Thissen, 2000) by different test lengths.

Finally, $\mathrm{PV}-Q_1^{*}$ almost universally demonstrated higher power rates than $S-X^2$, despite its slightly conservative Type I error rates in shorter tests, while ${\chi }^{2*}$ demonstrated the highest power rate estimates of all the statistics studied. Regarding $\mathrm{PV}-Q_1^{*}$, only for $\mathrm{BA}{\mathrm{D}}_1$ with 10 items was the $S-X^2$ statistic more powerful than $\mathrm{PV}-Q_1^{*}$. However, given the slightly inflated Type I error rates for this condition, the $S-X^2$ statistic may not be the most optimal choice when testing goodness-of-fit in 10 item tests. $\mathrm{PV}-Q_1$, $\mathrm{PV}-Q_1^{*}$, and ${\chi }^{2*}$ demonstrated higher power rates as the test length and sample size increased; however, the more conservative nature of $\mathrm{PV}-Q_1$ was reflected in the power to detect misfit. In general, the $\mathrm{PV}-Q_1$ statistic likely will be of little use when only 10 items are modeled, especially in smaller sample sizes. When 20 or more items are fitted, $\mathrm{PV}-Q_1$ will achieve reasonable power that is often higher than $S-X^2$, especially in larger sample sizes. These fit statistics results generally indicate that focusing on the item response functions directly provides more information about item misfit compared with expected values generated from conditional sum scores.

Discussion

In this article, the authors explored the use of PV imputations in the context of testing IRT models for goodness-of-fit in individual items. PV imputations were implemented to improve the inherent measurement imprecision in the $\hat{\theta }$ estimates required for the $Q_1$ fit statistic (Yen, 1981), which the authors termed $\mathrm{PV}-Q_1$. To further account for using item-parameter estimates as a proxy for the respective population parameters, we adopted a parametric bootstrap procedure to generate an empirical sampling distribution for the proposed $\mathrm{PV}-Q_1$ statistic and termed this detection statistic $\mathrm{PV}-Q_1^{*}$. The two proposed item-fit statistics, as well as the previously proposed $Q_1$, ${\chi }^{2*}$, and $S-X^2$ fit statistics, were investigated in a Monte Carlo simulation study based on the conditions investigated by Orlando and Thissen (2000, 2003). These simulations were used to determine how well the PV imputation technique improved upon the $Q_1$ statistic, and, relative to previously established item-fit statistics, how effective the $\mathrm{PV}-Q_1$ family of item-fit statistics was at detecting true item misfit.

Simulation results revealed that the Type I error rates were reasonably close to the nominal $\alpha$ for $\mathrm{PV}-Q_1^{*}$. One potential reason why $\mathrm{PV}-Q_1^{*}$ demonstrated more conservative Type I error rates for the 2PLM and the 3PLM, particularly in shorter tests, may be due to the Gaussian approximation of the posterior response functions used to generate the PVs. While Chang and Stout (1993) have noted that the standard error of the $\theta$ estimates will be asymptotically sufficient to approximate the sampling variability of each estimate, this approximation may not be as effective in shorter tests. Hence, in shorter tests, the PV-based item-fit statistics may benefit from more intensive Markov chain Monte Carlo sampling techniques to obtain better samples from the posterior distribution. However, this topic was outside the scope of this article and should be investigated in future simulation studies.

The simulation results also showed that the error detection rates for $\mathrm{PV}-Q_1$ were highly conservative. In practice, however, conservative detection statistics still have their uses if they demonstrate sufficient power rates and are easy to obtain. For example, if in practice an analyst were to observe a $p<.05$ result with the $\mathrm{PV}-Q_1$ statistic, then they can be confident that the item is truly misfitting; compared with the original $Q_1$ statistic, this type of interpretation is clearly not possible due to the uncontrollably high false detection rates. Results suggested that the $\mathrm{PV}-Q_1^{*}$ statistic has more favorable Type I error control than $Q_1$, thereby demonstrating more interpretable (and often higher) power to detect item misfit across a variety of conditions.

Of the statistics that $\mathrm{PV}-Q_1$ and $\mathrm{PV}-Q_1^{*}$ were compared with, ${\chi }^{2*}$ demonstrated the best Type I error control and power in every simulation condition studied. This suggests that the most optimal approach to detect item misfit may be to use the IRT probability functions directly, along with a method to account for uncertainty in $\theta$, while avoiding the need for a binning technique to create suitable observed and expected frequency tables. However, both ${\chi }^{2*}$ and $\mathrm{PV}-Q_1^{*}$ require parametric bootstrapping to be adopted to draw adequate inferences, making efficient use of these statistics more difficult, while the use of $\mathrm{PV}-Q_1$ alone does not require parametric bootstrapping and is therefore considerably easier to compute.

This study demonstrated that combining PVs and a parametric bootstrap technique will generally improve the inferences drawn by the two-step item-fit statistics. In particular, Type I error rates will be improved to be either highly conservative when using PVs alone ($\mathrm{PV}-Q_1$) or closer to the nominal rate when parametric bootstrapping is used ($\mathrm{PV}-Q_1^{*}$). As was demonstrated, power to detect item misfit is often considerably higher than the competing $S-X^2$ statistic when the IRT functions are directly used to determine misfit (excluding $Q_1$, due to its problematic Type I error rates), and, unlike $S-X^2$, these fit statistics do not show any signs of liberal detection rates or decreases in power as the test length increases. In fact, $\mathrm{PV}-Q_1$ and $\mathrm{PV}-Q_1^{*}$ tended to dramatically increase in their efficiency to detect misfit as sample size and test length increased. Based on these results, we recommend using $\mathrm{PV}-Q_1$ and $S-X^2$ when the test length contains 20 or more items for a quick but less powerful test of item misfit, and ${\chi }^{2*}$, followed by $\mathrm{PV}-Q_1^{*}$, when parametric bootstrapping is computationally feasible (i.e., when the computational demands are not too high, the likelihood of obtaining local minimums in the bootstrap samples is small, etc.).

General Benefits of the PV Item-Fit Statistics

In addition to the improved Type I error control and effective power to detect misfit, there are other practical benefits to using these PV-based item-fit statistics. First, fit statistics that are based on two-step estimates are generally efficient to compute in datasets that contain large degrees of missing data. This feature is particularly appealing in datasets where missingness is included by design, such as when multiple test forms are administered for vertical linking designs (Kolen & Brennan, 2004). Because each item is tested independently, it is only a matter of plugging the values into the suitable formula after the $\hat{\theta }$ values (or sets of PVs) are obtained. Compared with $S-X^2$, which currently requires that the total scores are suitable representations of all response patterns (and therefore require datasets with no missing responses), the PV-based item-fit statistics provide the desirable feature of being effective in datasets with large amounts of missing data. This important property is shared by the ${\chi }^{2*}$ statistic as well.

Another practical benefit to the PV augmented versions of $Q_1$ is that a number of commercial (e.g., BILOG-MG; Zimowski, Muraki, Mislevy, & Bock, 2003) and open-source (e.g., mirt; Chalmers, 2012) IRT software already support the computation of EAP estimates, their associated standard errors, and the $Q_1$ fit statistic. Because these subroutines have been previously constructed, all of the necessary tools are readily available to implement the proposed measures. The only missing element required to compute $\mathrm{PV}-Q_1$ and $\mathrm{PV}-Q_1^{*}$ from these IRT software packages is a suitable function that (a) imports the results from these IRT software packages, (b) generates the PVs and associated parametric bootstrap samples, and (c) passes the PVs and sampled datasets back to the respective estimation software to collect the necessary item-fit statistic information.

Limitations and Future Directions

With respect to the computational considerations required, $\mathrm{PV}-Q_1^{*}$ and ${\chi }^{2*}$ are more time-consuming to compute than the simpler $\mathrm{PV}-Q_1$ and $Q_1$ statistics, and also require that the respective Monte Carlo samples are well behaved (i.e., no local minimum or nonconvergence issues). However, given that parametric bootstrap samples are completely independent across replications, the required computational time can be greatly decreased by capitalizing on modern multicore architecture systems. By implementing the parametric bootstrap draws in parallel across available computing cores, the total time required to obtain the required empirical samples can be decreased at a rate proportional to the number of cores available. In addition, it may be possible to adopt a strategy similar to Stone’s (2000) parametric bootstrap approximation to obtain a suitable df estimate for the observed $\mathrm{PV}-Q_1$ values, thereby also reducing the computational time.

We anticipate that $\mathrm{PV}-Q_1$ will generally demonstrate conservative Type I error rates across a wide variety of empirical settings, while $\mathrm{PV}-Q_1^{*}$ will provide error rates that are reasonably close to the nominal $\alpha$, particularly when the distribution of $\theta$ is correctly specified. However, if the distribution of $\theta$ is misspecified (e.g., the latent trait values are from a bimodal instead of a normal distribution), the outlined parametric bootstrap procedure may not behave as optimally as demonstrated in this article. While determining the robustness of item-fit statistics to misspecification was outside the purpose of this article, this area of research is nevertheless important and should be considered in future studies (see Stone, 2003, for an example of this type of analysis).

Finally, several questions remain regarding the detection properties of item misfit statistics for IRT models, especially for the newly proposed $\mathrm{PV}-Q_1$ and $\mathrm{PV}-Q_1^{*}$ statistics. Future research should investigate how these statistics perform when fitting polytomous IRT models, the consequences of including multiple items that contain misfit, the effects of temporarily removing misfitting items to improve the ${\mathbf{\theta }}^{*}$ imputations (specifically for power conditions), the effects of varying the shape of the latent trait distribution used to generate the data, how improving the precision of $\hat{\theta }$ by including fixed-effect covariants (Adams, Wilson, & Wu, 1997; Chalmers, 2015) affects the power to detect misfit and Type I error control, and so on. These and other research areas should also be investigated for competing item-fit statistics to determine their general robustness and efficiency so that practitioners can make informed decisions regarding which statistics they should adopt in their item analysis work.