Cell size control and gene expression homeostasis in single-cells

Abstract

Growth of a cell and its subsequent division into daughters is a fundamental aspect of all cellular living systems. During these processes, how do individual cells correct size aberrations so that they do not grow abnormally large or small? How do cells ensure that the concentration of essential gene products are maintained at desired levels, in spite of dynamic/stochastic changes in cell size during growth and division? Both these questions have fascinated researchers for over a century. We review how advances in singe-cell technologies and measurements are providing unique insights into these questions across organisms from prokaryotes to human cells. More specifically, diverse strategies based on timing of cell-cycle events, regulating growth, and number of daughters are employed to maintain cell size homeostasis. Interestingly, size homeostasis often results in size optimality – proliferation of individual cells in a population is maximized at an optimal cell size. We further discuss how size-dependent expression or gene-replication timing can buffer concentration of a gene product from cell-to-cell size variations within a population. Finally, we speculate on an intriguing hypothesis that specific size control strategies may have evolved as a consequence of gene-product concentration homeostasis.

Graphical abstract

Cell-size regulation: going beyond phenomenological models

Size plays an important role in cellular processes and functions of a cell [1], and therefore should be actively maintained. Indeed, cell size distribution of proliferating cells is known to be stable through generations, suggesting regulation of growth and division to correct deviations from a desired cell size. Earlier attempts towards understanding cell size control was based on population-averaged data on model organisms, bacteria and yeast, and led to proposition of phenomenological models of cell size control. In particular, three models were hypothesized: Timer – a constant time between successive divisions, Sizer – cell division upon attainment of a critical size, and Adder – a constant size addition between consecutive generations. However, validation of these in various organisms remained inconclusive. With recent advances in single-cell technologies, high throughput measurements of cell size over several cell-cycles of individual cells can be made, generating correlation data between different parameters such as cell size at birth, growth rate, cell size at division, division time, etc. This data has stimulated reexamination of phenomenological models of cell size homeostasis.

For a broad range of microbes, an individual cell grows exponentially over time with a constant growth rate per size [2, 3]. A Timer based mechanism to control division can thus be precluded since it cannot achieve size homeostasis, in the sense that, the cell-to-cell size variations will grow unboundedly with time [4^•, 5]. Consistent with it, analysis of data for several bacterial species reveals a negative correlation between division time and cell size at birth, implying presence of a size control during cell-cycle. Further investigation reveals the phenomenological strategy: size added from birth to division is uncorrelated with cell size at birth, which is inconsistent with a Sizer model and validates an Adder model (Fig. 1a) [6, 7, 8, 9, 10, 11, 12]. Existence of such phenomenological models, however, only provides limited perspective since it does not specify how other landmark cell-cycle events (e.g., initiation of DNA replication, assembly of division apparatus) are coordinated with division, and whether the size control is applied from birth to division or between two other cell-cycle events.

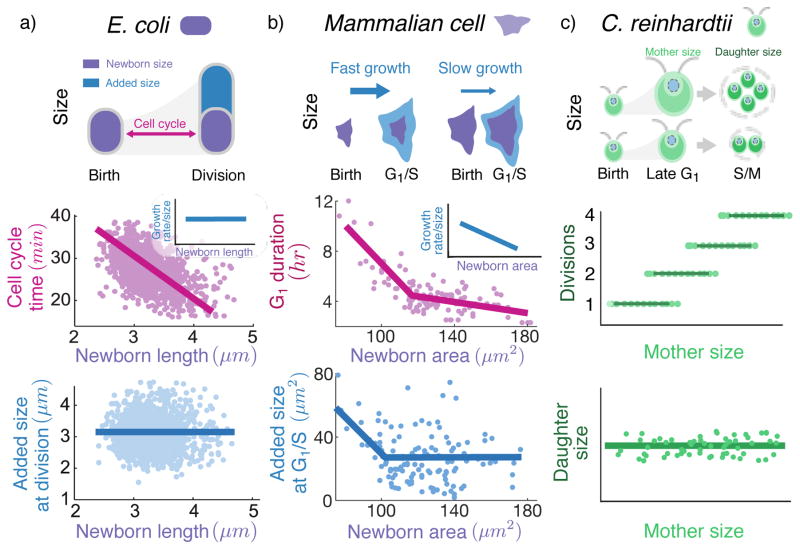
Figure 1. Diverse strategies based on regulating timing of cell-cycle events, growth rate, and number of daughters per mother cell are exploited for maintaining cell size homeostasis.

a) An E. coli cell grows exponentially in size (cell length used as a proxy for size) during the cell-cycle. At the single-cell level, the cell-cycle duration sharply decreases with increasing newborn size so as to add a fixed size from birth to division (corresponding to the Adder model; data taken from Fig. 4A and Fig. 2F of [7]). In contrast, the growth rate (normalized by size) is uncorrelated with size (Fig. 4C of [7]). b) Unlike E. coli, mammalian cells exhibit size-dependent growth during G₁, with larger newborns growing slower as compared to small newborns. The timing of the G₁ phase exhibits a strong negative correlation with newborn size (cell surface area used as a proxy for size), and the correlation becomes weaker for larger cells (data on Rat Basophilic Leukemia cells taken from Fig. 4C of [27]). The added size from birth to G₁/S transition decreases with newborn size (corresponding to a Sizer or size-checkpoint model) for small cells, but is independent of size for larger newborns (corresponding to the Adder model; Fig. 5A of [27]). c) The unicellular alga C. reinhardtii grows exponentially in size during the G₁ period (in presence of light) and then undergoes rapid alternating series of divisions (S phases and mitoses or S/M) to produce 2ⁿ daughters. At single-cell level, the number of division cycles n increases with mother cell size ([28]) such that the average daughter cell size is held approximately constant (see Fig. 4 of [29]).

Studies on E. coli have proposed several formulations that couple initiation of DNA replication to division while being consistent with an Adder between birth and division. One model postulates that size control is primarily exerted over the timing of initiation of DNA replication such that a constant volume per origin of replication is added between two consecutive initiation events. The corresponding division is assumed to occur a fixed time (C+D period; C–time to replicate DNA, D–time between end of replication to division) after initiation [13, 14, 15]. Another proposition, which suggests that initiation of DNA replication occurs at a constant size per origin and C+D period depends upon the growth rate, shows that the Adder model is valid only for fast growth rates and the size control behaves as a Sizer for slow growth conditions [16^•]. A third model argues that for slow growing cells, size control is exerted at two sub-periods (the time from birth to initiation, and the D period) whereas the C period resembles a Timer [17]. So far none of these models have been conclusively validated or falsified, and it would be worthwhile to carry out experiments to this end.

Similar couplings between important cell-cycle events and division have been explored in other organisms as well. For C. crescentus, pre-constriction and post-constriction periods have been examined for size control, showing that it obeys a mixer model wherein the time until constriction acts as a Timer followed by the post-constriction period regulated via an Adder [18^•]. Likewise, the cell-cycle of budding yeast has been investigated by dividing it in two distinct periods: time until G₁/S transition, and time from the G₁/S transition to division. Despite having an overall Adder between birth to division [19, 20^•], independent control of both these periods is proposed. In particular, the first period is shown to be dependent upon the size of mother cell, and the second period is controlled by the size of the daughter [20^•]. Collectively, dissecting the cell-cycle in biologically relevant periods for various organisms provides key insights in to how division might be coordinated with other events.

An important step moving forward is to understand molecular mechanisms that implement size control over timing of cell-cycle events. To this end, two generic themes have been proposed. One approach is to accumulate a protein in size dependent manner up to a threshold. Some notable examples of this include FtsZ to control Z-ring formation, [21, 22], DnaA to control timing of initiation in E. coli [13], and Cdc25 to regulate timing of mitotic entry in S. pombe [23^•]. Another way to implement a size control over timing is to dilute a protein until a critical level as cell grows in size. A prominent example of this strategy is Whi5 for control of G₁ duration in S. cerevisiae [19, 20•, 24, 25]. Interestingly, an alternative model shows that an Adder-like behavior can also arise from a very different mechanism of maintaining a constant surface area to volume ratio [26^•]. Apparently, the nutrient intake imposes constraints on this ratio by affecting the synthesis of surface material. The candidate molecules that carry out such function have not been identified yet. It is plausible that molecular players underlying important cell-cycle events interact with each other, and therefore an overarching framework may emerge with further research.

How is size control implemented in multicellular organisms? Arguably, these organisms operate in a more complex environment than bacteria and budding yeast; thus, size control strategies adopted by their cells are expected to be affected by physical constraints and thereby be relatively more complicated. Recent data indeed suggests that mammalian cells have different size control strategy in the G₁ duration than budding yeast. This strategy phenomenologically resembles a Sizer for small cells, but Adder for larger cells [27]. Examining the data further reveals that for mammalian cells, not only the time spent in G₁, but also the growth rate are negatively correlated with size at birth [27] (Fig. 1b). This observation has been strengthened by recent work showing size-dependent regulation of growth rate [30, 31]. The molecular underpinnings of growth rate control are not well understood, although access to nutrients and physical constraints are expected to play an important role.

In a stark contrast to size control on timing of cell-cycle events and growth rate, the green alga C. reinhardtii controls the number of daughter cells it produces upon division in a size controlled manner. It has a prolonged G₁ phase in which the size of a newborn cell increases by several folds. The cell then undergoes multiple divisions producing 2ⁿ daughter cells. The number of divisions n, on average, is large for large mother cells, so that the daughter cells are close to a target size (Fig. 1c) [28, 29]. The molecular mechanism for regulating the number of divisions in C. reinhardtii is suggested to rely on concentration dilution. Here, a cyclin dependent kinase CDKG1 is produced towards the end of G₁ phase and its production depends on the size of the cell. With each division, this protein is degraded and further divisions stop once its concentration goes below a threshold [28].

Why do organisms control size?

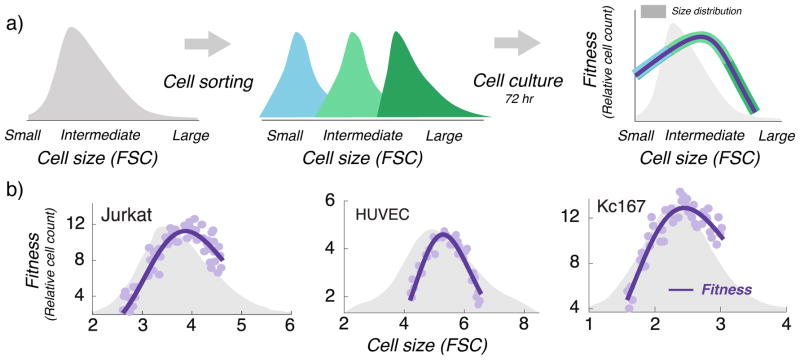
Recent experiments in proliferating animal cells unravel an interesting connection between cell size homeostasis and cellular fitness. By sorting a population of growing cells based on their sizes, it was shown that cellular proliferation (i.e., fitness) is low for small and large cells, but high at intermediate sizes [32^••, 33] (Fig. 2). The decrease in the fitness for large cells could not be attributed to higher cell-death since the apoptosis rates here were similar for large and average–sized cells. Notably, a similar optimality also exists for mitochondrial activity (metabolism) of cells [33]. Since the metabolism is linked to the growth, it is not too surprising that existence of an optimal size can be theoretically shown to arise from joint regulation of timing and growth [34].

Figure 2. An optimal cell size maximizes fitness within a population of mammalian cells.

a) Using forward scatter intensity (FSC) as a proxy for cell size [32^••, 35], flow cytometry is used to sort an original unsynchronized cell population (grey) into several subpopulations with different cell sizes. Each subpopulation is cultured for 72 hrs (approximately 3 – 5 cell generations), and fitness is quantified by measuring the relative change in cell count. Interested readers are referred to the material and methods of [32^••] for further details. b) Measured fitness is plotted as a function of the average subpopulation FSC at the time of sorting for three different cell types: Jurkat cells (human T lymphocyte cell line), HUVEC (human umbilical vein endothelial cells; a primary cell line) and Kc167 (a widely used Drosophila cell line). Original cell size distribution is shown in grey.

Do unicellular organisms also have an optimal size for a given growth condition? Intuitively, a bigger bacterial cell will divide faster and thus its proliferation would be higher than a smaller cell. However, the fact that the average bacterial cell size grows exponentially with growth rate (per size) imposed by the nutrients suggests that there may be a specific target cell size for the given environment [36], which may be determined by several factors such as the surface to volume ratio [26^•], availability of fatty acids [37], etc. Observing an optimal size in bacteria via experiment such as [32^••] is perhaps hard because of a narrow range of cell sizes as compared to mammalian cells. It would be interesting to see results of competition between mutants with artificially large sizes, such as those obtained by expression of useless proteins in [21].

Living with size variations: gene expression homeostasis

Going beyond cell size homeostasis, single-cell approaches are also elucidating mechanisms for gene-product concentration homeostasis. In particular, how is the concentration of given RNA/protein buffered to random or cell-cycle dependent fluctuations in cell size. This problem is especially acute for mammalian cells, where individual synchronized cells from the same population, exposed to identical nutrients, exhibit a six-fold variation in size [38^••]. Since rates of intercellular biochemical processes typically depend on the concentration of molecular species, cells must maintain concentration levels despite dramatic single-cell size deviations from the population average. Adding to size variations, unsynchronized cells also differ in the number of gene copies, and it is unclear to what degree expression is compensated for gene dosage across organisms.

In principle, one can envision different strategies for maintaining a desired gene-product concentration: size-dependent regulation of synthesis and/or decay rates with perfect gene dosage compensation, or scaling of gene dosage with cell size accompanied by size-independent expression per gene copy (Fig. 3). Prior investigations on inferring these mechanisms have relied on bulk-assay expression measurement utilizing cell size mutants, or altering size through small-molecules drugs [39, 40]. Instead of artificially changing the average cell size, exploiting natural intracellular size variations within a population provides a more physiologically perturbation-free setting to study concentration homeostasis. Building up on this theme, recent works have used mRNA fluorescence in situ hybridization (RNA FISH) to count mRNAs inside individual cell along with precise cell size measurement within a population of mammalian cells [38^••, 41]. For most genes, mRNA copy numbers scale linearly with size, implying a gene-specific mRNA concentration set point (Fig. 4a). Intriguingly, the data further points to gene dosage compensation - two similarly sized cells in G₁ and G₂ phase will have same number of mRNAs, on average [38^••, 42^•]. While this mRNA count vs. size scaling observed in diverse mammalian cell types seems intuitive and also previously reported in bulk-assay experiments [40], its mechanistic underpinnings and molecular implementations remained elusive. Measurements of promoter activity of individual gene copies in single cells revealed for the first time that concentration homeostasis is orchestrated through modulation of the transcriptional burst size - with increasing cell size more RNA polymerases initiate transcription when the gene randomly switches to an active state (Fig. 4b). In contrast, gene dosage compensation occurs through the burst frequency (i.e., how often a gene become active) which is approximately halved upon gene duplication during the S phase. It is interesting to note that similar size-dependent transcription rates have recently been found in A. thaliana [43], suggesting the homeostasis principles uncovered through single-cell measurements are broadly applicable to animal and plant cells.

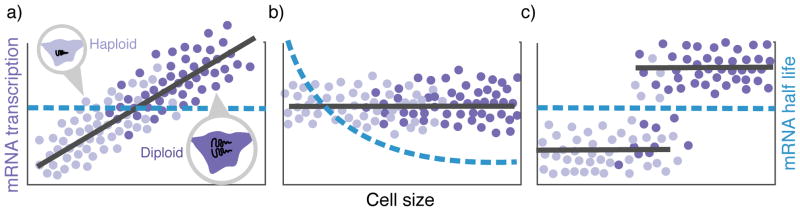
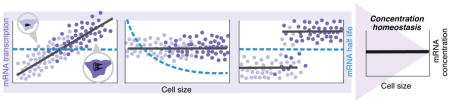
Figure 3. Potential mechanisms driving gene-product concentration homeostasis demonstrated at the RNA level.

a) The rate of transcription (number of mRNAs synthesizes per unit time) of an individual gene increases proportionally with size in single cells, with a size-invariant decay rate. Both haploid (light violet) and diploid (vilot) cells exhibit similar scaling due to gene dosage compensation. b) The transcription rate is independent of gene dosage and cell size, and the mRNA stability (decay rate) decreases with cell size to maintain a fixed concentration. c) The rate of transcription is size-independent and increases by approximately 2-fold upon gene replication. A strong coupling between cell size and gene dosage leads to concentration homeostasis. Unlike the first two strategies, here homeostasis is not perfect as mRNA concentrations will decrease with increasing size for fixed ploidy.

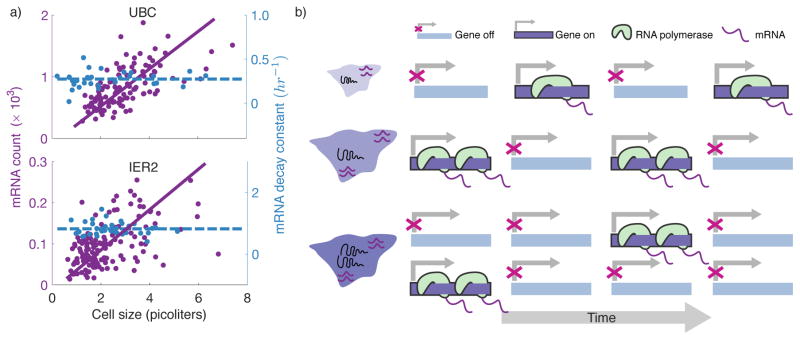
Figure 4. Mammalian cells maintain mRNA concentrations independent of size through modulation of transcriptional burst size and frequency with cell size.

a) The mRNA copy numbers measured via RNA FISH for two genes (UBC and IER2) scale linearly with size across single cells from the same population, while the mRNA half-lives are independent of size (Fig. 3A and 3B of [38^••]). Both chosen mRNAs are relatively unstable, and hence mRNA count is a proxy for de novo transcription rate. b) Schematic of a promoter switching between transcriptionally inactive and active states. The linear scaling of transcription rate with size results from a higher burst size (the number of mRNAs synthesized from the active state) in larger cells. Upon gene replication, the fraction of time the promoter in ON is approximately halved leading to gene dosage compensation [38^••]. As a consequence, two similarlysized cells in G₁ and G₂ will have the same mRNA count.

Studies in budding yeast show similarities and striking differences with their mammalian counterparts. For example, as in mammalian cells, gene-dosage compensation occurs during the S-phase of S. cerevisiae, wherein incorporations of acetylated histones into newly replicated regions leads to suppressed transcription per gene copy [44^••]. However, unlike mammalian cells, nascent transcription rates for RNA polymerase II genes have been reported to be size-independent in budding yeast [45^••]. This implies that a newborn yeast cell growing in G₁ will have reduced mRNA synthesis with increasing size, in the sense of mRNAs added per volume per unit time. Intriguingly, this decreased synthesis rate is compensated by a corresponding change in RNA stability to maintain mRNA concentration [45^••]. Previously, mRNA degradation rate modulation as a function of growth rate/temperature (which should indirectly affect the cell-size) has also been observed in yeast cells [46, 47, 48, 49]. In this case, the transcription-degradation cross talk for concentration homeostasis is hypothesized to occur through molecular factors that continuously shuttle between the nucleus/cytoplasm to coordinate and participate in both transcription and decay processes [50]. While transcription of RNA polymerase II genes is size-independent, transcription of ribosomal RNAs via RNA polymerase I is size-dependent [45^••], and this latter mechanism maybe critical in maintaining a fixed concentration of ribosomes.

In contrast to eukaryotic cells, the bacterial cells do not seem to compensate for DNA dosage [51]. In this case, gene-product concentrations decrease with increase in size for fixed ploidy, suggesting that a strong coupling between gene-dosage and cell size can lead to near-constant gene product concentrations. In agreement with this, [52^•] has shown that cyanobacteria cells are able to maintain concentration of proteins by scaling their gene dosage with cell size. (Fig. 3c). A related issue is how change in gene dosage affects concentration of its products through the cell-cycle. Intuitively, the gene product concentration is expected to decrease until associated gene duplicates (based on its location on the chromosome) and increase back thereafter [53]. Since genes located at different places on the chromosome are duplicated at different times, such imbalance in gene dosage is utilized by B. subtilis for coordination of sporulation [54]. It is also worth noting that the bacterial cell size distribution is quite narrow, hinting that the scaling DNA dosage with cell size may suffice to maintain near constant gene product concentrations for some genes strategically placed on the chromosome. Recent experiments on E. coli indeed suggest that the fluctuations in protein level are not very large (about 4%) for several genes and a near constant concentration is maintained during the cell-cycle [55]. These fluctuations may be further suppressed via autoregulation which is a prevalent feedback mechanism in prokaryotes.

Outlook

Despite considerable leapfrogging due to single-cell technologies, we are far from a full grasp over size regulation and expression homeostasis. For example, coordination of critical cell-cycle events with division cycle in various organisms, and their mechanistic underpinnings still remain unresolved. Identifying how cell-size control is applied on genome replication in prokaryotes is also closely linked to gene product concentration homeostasis since replication time of a gene of interest affects concentration profiles of its products over the cell-cycle. Given the physiological relevance of concentration homeostasis, could it be that size control over replication timing is exerted to ensure a constant concentration? Speculating even further, is it possible that the size control strategies are a mere consequence of maintaining gene product concentrations? A theory driven experimental investigation in these issues would certainly be useful. Further, in context of size homeostasis, how mammalian cells achieve size homeostasis is beginning to unfold only now. Mechanistic insights into how growth rate is regulated in these cells are critically required. Since size control is intimately tied with activation of competence in bacteria upon usage of antibiotics [56], a better understanding of size homeostasis would go a long way in therapeutics and drive new targets for drugs development for tuberculosis [12, 57]. Regarding concentration homeostasis, the relationship between mRNA concentration homeostasis and protein concentration homeostasis is not established as such; specifically it is not known whether both are simultaneously exhibited. It can be argued that protein concentration homeostasis can be achieved regardless of mRNA concentration homeostasis by changing translation and/or protein degradation rates with cell size. Simultaneous measurements of both mRNA and protein numbers of a given gene of interest would shed light into this issue. Another question of interest is to ask why some organisms (particularly prokaryotes) do not seem to have dosage compensation while others do. Additional insights are expected to be developed as these issues are investigated in organisms other than the current model ones [58].

Highlights.

• Advances in single-cell technologies and measurements have been instrumental in elucidating principles for cell size homeostasis in diverse organisms.

• Organisms employ strategies based on regulating timing of cell-cycle events, growth rate, and number of daughters for cell size control.

• Within a population of proliferating animal cells, fitness is maximized at an optimal cell size.

• Concentration of a gene product can become invariant of cell size through size-dependent expression, or scaling of gene dosage with size.