Using a Guided Machine Learning Ensemble Model to Predict Discharge Disposition following Meningioma Resection

Abstract

Objective  Machine learning (ML) algorithms are powerful tools for predicting patient outcomes. This study pilots a novel approach to algorithm selection and model creation using prediction of discharge disposition following meningioma resection as a proof of concept.

Materials and Methods  A diversity of ML algorithms were trained on a single-institution database of meningioma patients to predict discharge disposition. Algorithms were ranked by predictive power and top performers were combined to create an ensemble model. The final ensemble was internally validated on never-before-seen data to demonstrate generalizability. The predictive power of the ensemble was compared with a logistic regression. Further analyses were performed to identify how important variables impact the ensemble.

Results  Our ensemble model predicted disposition significantly better than a logistic regression (area under the curve of 0.78 and 0.71, respectively, p  = 0.01). Tumor size, presentation at the emergency department, body mass index, convexity location, and preoperative motor deficit most strongly influence the model, though the independent impact of individual variables is nuanced.

Conclusion  Using a novel ML technique, we built a guided ML ensemble model that predicts discharge destination following meningioma resection with greater predictive power than a logistic regression, and that provides greater clinical insight than a univariate analysis. These techniques can be extended to predict many other patient outcomes of interest.

Introduction

Discharge disposition is a significant consideration for patients and their families when deciding whether to undergo surgical treatment. Disposition impacts decisions about timing of surgery, time away from employment for patients and caregivers, and choice of a surgeon or hospital. Disposition is also important to providers, who must navigate the logistics of hospital bed availability and work with insurance companies to ensure appropriate coverage for surgical candidates. Efficiently coordinating transitions of care to postacute providers is also important in terms of cost reduction, especially as some payers move toward reimbursement strategies that bundle acute and postacute care into single episodes of care. ¹ Despite these considerations, existing models to predict disposition are rare in all surgical fields ^{2 3 4 5} and nonexistent in neurosurgical literature. In this article, we use a novel machine learning (ML) technique to predict disposition following meningioma resection from preoperative patient and tumor characteristics.

ML is a type of analysis that uses computer algorithms to identify subtle patterns in complicated datasets. ⁶ ML has been used extensively in the fields of cancer ⁷ and genomics ⁸ for applications as varied as classifying tumors from imaging ^{9 10} and predicting transcription factor binding sites. ¹¹ Recently, increasing emphasis has been placed on the potential of ML techniques to revolutionize medical outcomes research, ^{12 13} and ML has been used in other areas of medicine to build patient-focused predictive models that can be studied to glean valuable clinical insight. ^{14 15 16 17 18} We take advantage of ML in an entirely unique way to build a guided ML ensemble that generates predictions that can be used to provide personalized care for meningioma patients. Our approach is distinct in three respects: (1) we use a guided approach to algorithm selection, evaluating and ranking the predictive capabilities of a wide range of ML algorithms; (2) we create an ensemble model, which combines several types of ML algorithms to take advantage of the individual strengths of different model classes; and (3) we train algorithms using holdout datasets and cross-validation, allowing for the inclusion of a large number of predictors without overfitting the final model.

Previous work using ML to predict neurosurgical outcomes has tended to rely on logistic regression for predictive modeling. ¹⁹ This method ignores dozens of other classes of ML algorithms available, each with a unique approach to data analysis. In recent years, researchers have begun to recognize that other classes of ML models have utility in predicting medical outcomes. ^{20 21 22 23} In these studies, however, the alternative class of algorithm is often chosen a priori, with no assurance that the chosen algorithm is the most predictive of the available algorithms. By contrast, we employ a guided approach to algorithm selection by training 34 unique ML algorithms with different preprocessing techniques and ranking them by predictive power to create a “leaderboard.” We then select the best performing algorithms for use in an ensemble model. Ensemble models, which combine several different learning algorithms, frequently produce better predictions than models developed from a single learning algorithm, underscoring the benefit of utilizing multiple approaches when analyzing complicated datasets. ²⁴ Finally, we use a system of data holdouts and cross-validation when training algorithms. By ranking models based on how accurately they predict outcomes on never-before-seen data, we ensure that the models are not overfit to the data on which they were trained. This approach allows us to be aggressive and unbiased in our selection of variables, paving the way for novel clinical insights. Building guided ML ensembles represents a new, powerful approach to modeling neurosurgical outcomes that allows researchers to confidently create the most accurate models for their data and which has countless potential applications.

Methods

Patient Selection

A single-institution, retrospective database of patients was used to train and validate ML models. Patients who underwent resection of intracranial meningioma at our institution between 2001 and 2015 were included in the database. When possible, data were collected on all known operations, including operations at other institutions. Data were collected on a variety of preoperative patient characteristics, including age, race, sex, body mass index (BMI), comorbidities, presenting symptoms, indications for surgery, presence or absence of motor or language deficits, and whether patients presented to the emergency department or the outpatient clinic. Data were also collected on tumor characteristics, including tumor size, and the presence or absence of edema and mass effect/midline shift. In total, 76 different variables were considered (see Supplemental Table S1 for listed variables [online only]). The primary outcome was home versus non-home discharge. For the purpose of training models, each operation was treated separately even if one patient had multiple operations. Institutional Review Board approval for the development of this dataset was obtained. Patient consent was not required and not obtained.

Leaderboard Construction and Model Validation

Before training, 20% of the dataset was randomly selected as the holdout, which was never used in training or validation. The remaining data were divided into five mutually exclusive folds of data, four of which were used together as training, with the final fold used for validation. Each algorithm was evaluated an additional four times by choosing a different fold as the validation data. ²⁵ Receiver-operating characteristic (ROC) curves were calculated for validation (fold 1 used as validation) and cross-validation (the average of each of the five possible validation folds). Scores were reported as the area under the curve (AUC) of the ROC analysis. In this article, only the cross-validation score is reported. The three algorithms with the top cross-validation scores were then selected for use in an ensemble. We use an Elastic Net Classifier to combine the predictions of the three models selected. Following ensemble model creation, validation was performed on the holdout. Model construction was performed using ML software from DataRobot, Inc.

Data Preprocessing

A large number of data preprocessing approaches are represented in the collection of algorithms evaluated in the leaderboard. This section describes the approaches used in the algorithms in the ensemble.

Missing numerical data were dealt with by imputing the median of the column, and creating a new binary column to indicate the imputation took place. Numerical data were standardized in each column by subtracting the mean and dividing by the standard deviation. For linear algorithms (support vector machine and elastic net), categorical data were turned into many binary columns by one-hot encoding. Missing categorical values were treated as their own categorical level and get their own column. For tree-based algorithms, categorical data were encoded with integers. The assignment of category values to integers was done randomly.

Permutation Importance

The relative importance of a feature to the final ensemble was assessed using permutation importance, as described by Breiman. ²⁶ Using the training data only, for each column the ensemble was retrained on data with the values in the column randomly permuted. The difference in performance in AUC between the ensemble models built on the reference data and that of the data with the permuted column was used as a score to rank and compare the relative importance of the features to the ensemble. The variable with the strongest impact on the ensemble is assigned the score of “1.0,” and all subsequent variables are assigned a numerical score relative to 1.0.

Partial Dependence

To understand the response of the ensemble model to changes in a single column, we constructed the partial dependence plots as described by Friedman. ²⁷ A common criticism of newer ML algorithms relative to linear and logistic regression lies in their relative difficulty of interpretation (e.g., their “black boxness”). A partial dependence plot can be understood as a graphical representation of linear or logistic regression model coefficients that extends to arbitrary algorithm types. Partial dependence plots are more dynamic than coefficients alone, however, because variable coefficients can be visualized across a variety of variable values. A subset of the training data was selected. For any column, we made predictions from the ensemble model after having replaced all the values in the column with a constant test value and computing the mean of those predictions. We tested many values to observe how the ensemble model reacts to changes in the column of interest.

Patients were divided into groups according to the variable of interest (e.g., patients without convexity tumors were separated from patients with convexity tumors). The average probability of discharge to home was calculated for each group from the partial dependence predictions. This was charted against the average probability of discharge to home for each group calculated from the raw data alone.

Other Statistical Methods

Traditional statistical analysis was performed on selected patient and tumor characteristics. Continuous variables were compared using the Mann–Whitney U test. Categorical variables were compared using Pearson's chi-square test, and a Yate's correction was employed when expected frequencies were < 1. To assess the significance of differences in performance between the logistic regression and ensemble model, five different validation AUCs were calculated using each of the fivefold of data as the validation set in turn. A p -value was then determined using two-sided t -tests.

Results

Patient Characteristics

A total of 650 individual operations were reviewed for inclusion in the analysis; 39 operations were excluded due to lack of disposition data, leaving a total of 611 operations, representing 552 individual patients, for inclusion in the analysis. Sixty-six percent of patients were female and 35% were male, with a median age at surgery of 55.1 years. Patients who went home after hospital discharge tended to be female ( p  = 0.006), younger (average age 53.4 vs. 61.0 years, p  < 0.001), not have presented at the ED ( p  = 0.003), not have a preoperative motor ( p  < 0.001) or language ( p  = 0.02) deficit, and not have a history of diabetes ( p  < 0.001). They also tended to have smaller tumors (36.4 vs. 49.8 mm, p  < 0.001), and their tumors tended not to demonstrate edema ( p  < 0.001) or mass effect ( p  < 0.001). No significance was noted with respect to patient race, BMI, insurance status, tumor location, or number surgery ( Table 1 ).

Table 1. Patient characteristics for patients Included in machine learning analysis ^a .

Variable	Total	Discharged to home	Not discharged to home	p -Value b
Surgeries, n (%)	611	473 (77)	138 (23)	…
Sex, n (%)	611
Male	215 (35)	153 (71)	62 (29)	0.006
Female	396 (66)	320 (81)	76 (19)
Age at surgery, mean (SD), y	54.6 (14.1)	52.9 (13.6)	60.4 (14.2)	< 0.001
Race, n (%)	611
Caucasian non-Hispanic	521 (85)	403 (77)	118 (23)	0.92
Black	70 (11)	54 (77)	16 (23)
Hispanic	13 (2)	10 (77)	3 (23)
Asian	4 (0.6)	3 (75)	1 (25)
Other	3 (0.4)	3 (100)	0 (0)
BMI, mean (SD)	29.9 (7.5)	29.7 (7.5)	30.1 (7.8)	0.69
Presenting at the ED, n (%)	601
Did present at ED	133 (22)	90 (68)	43 (32)	0.003
Did not present at ED	468 (77)	374 (80)	94 (20)
Missing	10 (1)
Insurance status, n (%)	583
Yes insurance	559 (91)	426 (76)	133 (24)	0.2
No insurance	24 (4)	21 (87)	3 (13)
Missing	28 (5)
Preoperative motor deficit, n (%)	610
Yes deficit	138 (22.6)	76 (55)	62 (45)	< 0.001
No deficit	472 (77.2)	396 (84)	76 (16)
Missing	1 (0.2)
Preoperative language deficit, n (%)	610
Yes deficit	43 (7)	27 (63)	16 (37)	0.02
No deficit	567 (92.8)	445 (78)	122 (22)
Missing	1 (0.2)
Hx of diabetes, n (%)	611
Yes diabetes	129 (21)	81 (63)	48 (37)	< 0.001
No diabetes	482 (79)	392 (81)	90 (19)
Tumor size median (SD), mm	39.7 (18.0)	36.4 (15.8)	49.8 (18.9)	< 0.001
Tumor location, n (%) c	604
Skull base	296 (48)	238 (80)	58 (20)	0.24
Convexity	165 (27)	130 (79)	35 (21)
Other	143 (24)	101 (71)	42 (29)
Missing	7 (1)
Edema, n (%)	585
Present	254 (42)	220 (70)	33 (30)	< 0.001
Not present	332 (54)	231 (87)	101 (13)
Missing	26 (4)
Mass effect, n (%)	588
Present	451 (74)	331 (73)	120 (27)	< 0.001
Not present	137 (22)	122 (89)	15 (11)
Missing	23 (4)
Which surgery, n (%)	611
First surgery	521 (85)	410 (79)	111 (21)	0.07
Not first surgery	90 (15)	63 (70)	27 (30)

Abbreviations: BMI, body mass index; ED, emergency department.

^a Patient comorbidities, presenting symptoms, and indications for operation were not included in this analysis as there were multiple observations per surgery. Mann–Whitney U test and Pearson's chi-square test with Yate's correction were used to check for significant difference between groups.

^bChi-square analyses do not include missing data.

^cExcluding surgeries with multiple tumor locations.

Receiver-Operating Characteristic Curve and Other Classifier Statistics

Using a leaderboard approach, an ensemble model including a Nystroem kernel support vector machine (SVM) classifier, random forest classifier, and elastic net classifier was identified as the model with the highest predictive power. The ensemble model performed significantly better than the logistic regression ( p  = 0.01). The ensemble model had an AUC on the validation set of 0.78 ( Fig. 1 ), while the logistic regression had an AUC of 0.71. Validating on the holdout set resulted in an AUC of 0.81 for the ensemble model and 0.73 for the logistic regression. When optimizing the F1 score, the ensemble model had a specificity of 25%, while the logistic regression had a specificity of only 2.8%. The ensemble model had a positive predictive value (PPV) of 78% and a negative predictive value (NPV) of 83%, while the logistic regression had a PPV of 73% and a NPV of 80%.

Fig. 1.

Receiver-operating characteristic curve for the ensemble model.

Permutation Importance

We performed a permutation importance analysis to determine which variables are most important to the ensemble. This analysis does not, however, demonstrate direction or independent impact of variables on the model. The five variables that most strongly influence the ensemble are, in order: tumor size, presentation at the ED, patient BMI, convexity location, and preoperative motor deficit ( Fig. 2 ).

Fig. 2.

Permutation importance demonstrates the relative importance of the top five most impactful variables for the ensemble model. The most important variable is assigned the value of “1.0” and all other variables are assigned the numerical values based on their importance relative to the most important variable. BMI, body mass index; ED, emergency department.

Partial Dependence

Partial dependence analysis was performed to determine how the five most important variables independently impact the ensemble model. As tumor size increases, there is a steady decline in the probability of discharge to home. There are, however, two sharper downward inflections, one at ∼3.5 cm and other at ∼6.0 cm. Presenting at the ED decreases the probability of discharge to home by ∼3%, while having a preoperative motor deficit decreases the probability by ∼6%. The probability of discharge to home stays roughly the same across all BMIs. Convexity tumor location increased the probability of going home by ∼2% ( Fig. 3 ).

Fig. 3.

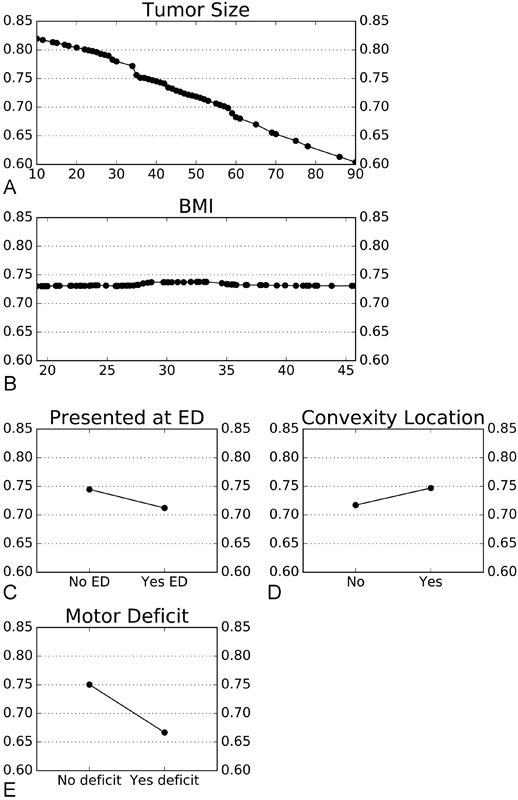
Deeper analysis of each of the five most impactful variables. All X -axes represent probability of discharge to home, with 1 equivalent to 100% likelihood of discharge to home and 0 equivalent to 0% likelihood of discharge to home, and corresponds to lines. Panel (A) tumor size, with tumor size in mm along the Y -axis; Panel (B): BMI, with BMI groupings along the Y -axis; Panel (C) presentation at the ED; Panel (D) convexity tumor location; Panel (E) preoperative motor deficit; and Panel (F) legend. BMI, body mass index; ED, emergency department.

Discussion

Using ML to model medical outcomes holds great promise for improving treatment. ²⁸ However, predictive models are only as useful as they are accurate. Some researchers have argued that algorithms other than logistic regression may be more adept at answering complex clinical questions, ^{17 20} but present no evidence that their chosen algorithm performs better than the dozens of other available ML algorithms. While general recommendations exist for selection of algorithms based on characteristics of a dataset or clinical question, the only way to know with certainty that an algorithm is the most predictive is to directly compare it to other algorithms. ²⁹

Building a guided ML ensemble model allowed us to directly compare the predictive capabilities of a wide range of ML algorithms (including logistic regression), and select the top performing algorithms for inclusion in a final ensemble. This approach, a first in medical literature, allows researchers to be confident that they have built the most predictive models for their data, providing better information for providers and patients when making treatment decisions.

Our guided ML ensemble, which combines a random forest classifier, elastic net classifier, and Nystroem kernel SVM classifier predicts meningioma discharge disposition significantly better than the traditionally employed logistic regression (AUC of 0.78 vs. 0.71; PPV of 78 vs. 73%; NPV of 83 vs. 80%).

Selection of appropriate variables is as important as the selection of appropriate algorithms to the development of an accurate model. In an effort to avoid overfitting, many researchers limit the number of variables in their analysis, relying instead on clinical judgment for variable selection. ^{30 31} This limits the new clinical insights that could have been illuminated had the investigator included variables of unknown importance. ³² As meningioma disposition has never been modeled, we chose to be comprehensive in variable selection. Using our system of data holdout and cross-validation, we were able to include 76 different patient and tumor characteristics in our analysis while still building a generalizable model, evidenced by the fact that the AUC of the holdout predictions was comparable to, if not better than, the AUC of the original cross-validation (0.81 vs. 0.78).

The most exciting potential application of this technology is the development of a point of care guided ML ensemble model that can accept patient information as inputs and provide instantaneous outcome predictions to the physician in the office. This type of model would be able to adapt as more data becomes available or in response to treatment advances, as each new patient acts as an additional data point that can be added to the model's training set. The model can then be retrained, producing predictions that are responsive to new information. A point of care model like this has yet to be described in a neurosurgical setting, but is technically feasible and an important future direction for this type of work.

Until our guided ML ensemble model can be implemented in a point of care setting, it has limited clinical usefulness on its own. Deeper analysis of the model, however, provides clinical insights that are useful to the neurosurgical practitioner right now. Univariate analysis demonstrated that 9 out of the 14 analyzed variables are significantly different in patients who discharged to home versus those who discharged elsewhere. This analysis does not, however, show which variables are most important in determining discharge disposition. Permutation and partial dependence analysis were performed to determine which variables most strongly influence the model, as well as the independent impact of each variable on the model's predictions:

Tumor Size

Permutation analysis demonstrated that tumor size has far and away the greatest impact on likelihood of home discharge. Increasing tumor size shows a more dramatic decrease in the probability of discharge to home, with 80% of patients with tumors 1 cm or smaller predicted to go home compared with 60% of patients with 9 cm or larger tumors. We do not, however, see a perfectly linear correlation between tumor size and likelihood of discharge to home. Rather, there are two subtle negative inflection points at ∼3.5 and 6.0 cm. These inflection points divide tumors into three categories of increasing risk: < 3.5, 3.5 to 6.0, and > 6.0 cm. The identification of risk strata, which is characteristic of tree-based models but challenging with linear models such as logistic regression, elastic net classifiers, and SVM Classifiers, highlights the nuanced insights of the ensemble model.

Presentation at Emergency Department and Preoperative Motor Deficit

Both presentation at the ED and the presence of a preoperative motor deficit decrease the likelihood of home discharge.

Body Mass Index and Convexity Tumor Location

While permutation analysis showed that BMI and convexity tumor location strongly influence the model, partial dependence analysis demonstrated that the probability of discharge to home stays roughly the same across all BMIs and is only slightly improved with convexity tumor location. These data suggest that there exist unknown associations between both BMI and convexity tumor location and other variables that strongly influence the probability of home discharge for a subset of patients. The ability to recognize variables that might only be important for a subset of patients, or that are significant only in combination with other sets of variables, is an advantage of nonlinear models such as random forests. These hidden associations are missed by linear models and in univariate analysis. Further analysis to identify these associations is required to fully describe the impact of BMI and convexity tumor location on disposition following surgery.

It is perhaps surprising that convexity tumor location did not improve the odds of home discharge disposition. Skull base and other tumor location had similarly minimal effects on discharge disposition ( Fig. 4 ). It may be that inferences that practitioners make about patient outcomes based on the location of a tumor are being conveyed to the model by combinations of other variables. For example, the model might recognize the influence of a specific constellation of physical exam and imaging findings associated with skull base tumors rather than the location of the tumor itself. It is also possible that our classification system, which divided tumor location grossly into three categories, is not granular enough to capture the nuances required to accurately differentiate risk based on location. Finally, our dataset represents the practice patterns at a single institution, including patterns of patient selection. For example, patients in our dataset with skull base meningiomas tended to be younger (average age at surgery 53.0 vs. 57.2 years, p  < 0.001) have smaller tumors (average tumor size 35.8 vs. 44.6 mm, p  < 0.001), and were less likely to have preoperative motor deficits (15.9 vs. 25.0%, p  = 0.01) than patients with meningiomas in the convexity. These patterns may not be the representative of the national or global experience.

Fig. 4.

Partial dependence for skull base and other tumor locations. Both X -axes represent probability of discharge to home, with 1 equivalent to 100% likelihood of discharge to home and 0 equivalent to 0% likelihood of discharge to home. Panel (A) skull base tumor location; Panel (B) other tumor location.

Although our approach has many advantages, there are some limitations to this study. Our guided ML ensemble model is trained and validated on the same retrospective, single-institution database. While we demonstrated generalizability of the model to data that was never involved in algorithm training, a stronger validation of the model would be to demonstrate generalizability either to an entirely separate database or prospectively. Our use of data from a single institution may also limit the generalizability of our model, as surgical skills vary from surgeon to surgeon, and outcomes from institution to institution. Repeating this study using data from a large, multi-institution database is an important future direction for this work. It is possible, however, that this disadvantage can be seen as an advantage in terms of providing personalized care. Broadly generalizable models may not capture the nuances of a particular geographic region, institution, or even individual surgeon. Including the “x-factor” of a patient's treatment milieu in predictive analysis could potentially lead to even greater personalization of predictions for patients. Finally, though a powerful modeling tool, ML is unfamiliar to most surgeons, and requires training and expertise to wield appropriately. Our strategy, in particular, is novel and will require further study and validation.

Conclusion

Developing accurate models for predicting patient outcomes paves the way for truly personalized medicine. By training and ranking a diversity of ML models, and by using an ensemble model approach, we built a guided ML ensemble predicts disposition following meningioma resection more accurately than a diversity of alternative ML algorithms (including logistic regression), and that provides greater clinical insight than a univariate analysis. Applying this model in a clinical setting can improve patient counseling and coordination of care, which in turn may reduce costs and excess resource utilization. While these techniques were used to predict disposition following meningioma resection, they can also be extended to allow providers to confidently build the most predictive models for many other patient outcomes of interest.