A method for the quantification of biased signalling at constitutively active receptors

Abstract

Background and Purpose

Biased agonism, the ability of an agonist to differentially activate one of several signal transduction pathways when acting at a given receptor, is an increasingly recognized phenomenon at many receptors. The Black and Leff operational model lacks a way to describe constitutive receptor activity and hence inverse agonism. Thus, it is impossible to analyse the biased signalling of inverse agonists using this model. In this theoretical work, we develop and illustrate methods for the analysis of biased inverse agonism.

Experimental Approach

Methods were derived for quantifying biased signalling in systems that demonstrate constitutive activity using the modified operational model proposed by Slack and Hall. The methods were illustrated using Monte Carlo simulations.

Key Results

The Monte Carlo simulations demonstrated that, with an appropriate experimental design, the model parameters are ‘identifiable’. The method is consistent with methods based on the measurement of intrinsic relative activity (RA _i) (ΔΔlogR or ΔΔlog(τ/K _a)) proposed by Ehlert and Kenakin and their co‐workers but has some advantages. In particular, it allows the quantification of ligand bias independently of ‘system bias’ removing the requirement to normalize to a standard ligand.

Conclusions and Implications

In systems with constitutive activity, the Slack and Hall model provides methods for quantifying the absolute bias of agonists and inverse agonists. This provides an alternative to methods based on RA _i and is complementary to the ΔΔlog(τ/K _a) method of Kenakin et al. in systems where use of that method is inappropriate due to the presence of constitutive activity.

Abbreviations

D₂ receptor

dopamine D₂ receptor

μ receptor

μ‐opioid receptor

Introduction

Biased agonism is a direct consequence of the ability of GPCRs to signal through more than one pathway. Although these receptors were originally called GPCRs because it was thought that they only signalled through G proteins, it was later found that they can also signal through other accessory proteins such as β‐arrestins. In addition, the signalling through G proteins may not be specific, and one receptor may signal through a variety of G proteins. Because various signalling pathways can be used by a receptor, agonists can be either unbiased or biased depending on whether they do or do not activate each of the pathways with the same efficacy, respectively (Costa‐Neto et al., 2016).

Biased agonism introduces an extra level of complexity in receptor functionality. However, this property is currently at the forefront of drug discovery programmes in order to find ligands that induce GPCR signalling in a biased manner (Rankovic et al., 2016). There are many examples of biased agonism with applications on different targets and therapeutic necessities. For simplicity, we will comment on just two: the http://www.guidetopharmacology.org/GRAC/ObjectDisplayForward?objectId=319&familyId=50&familyType=GPCR (μ receptor) and the http://www.guidetopharmacology.org/GRAC/ObjectDisplayForward?objectId=215&familyId=20&familyType=GPCR (D₂ receptor), which are associated with pain and psychiatric disorders respectively.

Opioids, and http://www.guidetopharmacology.org/GRAC/LigandDisplayForward?ligandId=1627 in particular, are typical analgesics for pain. Morphine is a μ receptor agonist, which signals through both G protein and β‐arrestin. It has been shown that the G protein pathway is responsible for pain relief, whereas the β‐arrestin pathway is associated with a number of adverse effects, such as tolerance, nausea, vomiting, sedation, constipation and respiratory depression (Rankovic et al., 2016). This has led to the quest for ligands with biased μ receptor agonism towards the G protein pathway. Drug discovery efforts succeeded in the discovery of http://www.guidetopharmacology.org/GRAC/LigandDisplayForward?ligandId=7334 (DeWire et al., 2013), which is currently in phase 2 clinical trials (Viscusi et al., 2016), and more recently of http://www.guidetopharmacology.org/GRAC/LigandDisplayForward?ligandId=9286 (Manglik et al., 2016).

Typically used antipsychotics act as unbiased D₂ receptor antagonists. Apart from its therapeutically beneficial antipsychotic action, this unbiased D₂ antagonism also has the disadvantage of causing extrapyramidal side effects. Interestingly, drug discovery efforts on structural variations on the low efficacy D₂ agonist, http://www.guidetopharmacology.org/GRAC/LigandDisplayForward?ligandId=34, led to β‐arrestin‐biased D₂ agonists, which conserved the desirable antipsychotic effects of the unbiased antagonists but without the unwanted effects (Rankovic et al., 2016) (see also Urs et al., 2017, for a review).

Thus, biased agonists either by favouring the G protein pathway (μ receptor) or the β‐arrestin pathway (D₂ receptor) allow preservation of the therapeutic advantages of unbiased ligands while avoiding their unwanted side effects. Obviously, accurate pharmacological procedures are needed to provide reliable methods to quantify biased signalling parameters. In an effort towards this goal, a scale based on the operational model of agonism has been proposed (Figueroa et al., 2009; Kenakin et al., 2012).

Quantifying bias by the operational model of agonism

The operational model of agonism (Black and Leff, 1983) is a two‐step model of receptor function. The first step consists of the binding of the ligand to the receptor, while the second step includes all the molecular processes connecting the ligand‐bound receptor with the observed final pharmacological effect. By considering that pharmacological effect is a sigmoid function of the concentration of ligand–receptor complexes, Equation (1) is obtained.

$$E=\frac{E_m{\tau }^n{\left[A\right]}^n}{{\left(K_a+\left[A\right]\right)}^n+{\tau }^n{\left[A\right]}^n},$$ (1)

where E is the pharmacological effect, E _m is the maximum effect of the system, [A] is the concentration of the agonist A, τ is the operational efficacy of A in the receptor system, K _a is the dissociation constant of A for the receptor and n is a parameter related to the slope of the E/[A] curves. A value of n equal to 1 yields rectangular hyperbolic E/[A] curves, whereas values of n greater or less than 1 allow for steeper or flatter curves than the rectangular hyperbola, respectively (Black and Leff, 1983; Black et al., 1985).

The operational efficacy, τ, was defined (Black and Leff, 1983) as τ = [R]_T/K _E, where [R]_T represents the total receptor concentration and K _E the value of the concentration of agonist–receptor complex, [AR], which causes half of the maximum possible effect, E _m. In other words, K _E is inversely proportional to the efficacy of the AR complex. Thus, τ contains both tissue and ligand–receptor efficacy parameters. In addition, K _a is a conditional or functional constant because, although it corresponds to the concentration of ligand that occupies 50% of the overall receptor population, it does not, in general, correspond to the affinity for an individual equilibrium step, for example, the binding of the agonist to the inactive receptor conformation, because it incorporates, in addition, the receptor activation conformational change. Thus, when [A] = K _a, an agonist will occupy more than 50% of the receptors in the active conformation (that is to say, [AR ^*]/([R ^*] + [AR ^*]) > 0.5). Receptor activation will allow the receptor to be bound by an accessory protein, either G protein or β‐arrestin, which, after subsequent activation, will lead to the successful transduction of the initial agonist binding into a functional effect.

The mathematical structure of Equation (1) is weak for fitting purposes. It cannot be used to derive estimates of the affinity and efficacy of an agonist from a single E/[A] curve because there is not a unique set of parameter estimates that provide an optimal fit to the curve. This problem can be solved by generating several curves with different maximal responses without affecting the system functionality at the microscopic molecular level of the receptor. This is known as the irreversible inactivation method, which yields pharmacological systems with different [R]_T values (Furchgott, 1966). When fitting Equation (1) to a set of E/[A] curves (τ varies between those curves bearing different [R]_T values but E _m, K _a and n are shared in all the cases), the components of the pharmacological activation process are distributed into the K _a and τ parameter estimates. As it was shown in Roche et al. (2013b), consideration of agonist‐induced receptor activation (AR ↔ AR ^*) affects the values of K _a and τ operational parameter estimates: a highly efficacious agonist leads to a decrease of K _a (increase of ligand affinity because of agonist binding to active receptor states), whereas a weakly efficacious agonist leads to a decrease of τ. In addition to the agonist‐induced receptor activation conformational change, τ incorporates the binding of either the G protein or β‐arrestin to the AR ^* binary complex (Kenakin and Christopoulos, 2013; Ehlert, 2015) and, indeed, subsequent transduction steps.

A composite parameter (log(τ/K _a)), defined by combining operational efficacy (τ) and functional affinity (K _a) in a single parameter, was identified as a primary index for drug activity (Figueroa et al., 2009; Kenakin et al., 2012). This composite parameter denoted as either LogR (Figueroa et al., 2009) or transduction coefficient (Kenakin et al., 2012) served to define a scale for comparing drugs within a particular pathway (Δlog(τ/K _a)) relative to a reference compound. Finally, biased agonism between two signalling pathways can be quantified by ΔΔlog(τ/K _a). The ΔΔlog(τ/K _a) biased agonism scale was shown to be independent of receptor density ([R]_T) notwithstanding the value of the slope parameter (n) (Kenakin et al., 2012). This property makes this scale appropriate to quantify biased agonism at different cell types.

Despite its proven utility for biased agonism quantification, the ΔΔlog(τ/K _a) scale suffers from a lack inherent to the operational model as it was originally proposed (Black and Leff, 1983). Equation (1) shows that the pharmacological effect is zero in the absence of agonist. Even if a term to account for background effect is included in Equation (1), this cannot account for constitutive receptor activity. For positive E _m, no combination of values of τ and K _a can result in negative values of E whatever the value of [A]. Hence, the response cannot decrease below this background effect. Therefore, the operational model as originally formulated is unable to describe the behaviour of inverse agonists. It follows that a new formulation is needed if we want to encompass the quantification of biased agonism to the whole pharmacological space.

Since the Black and Leff operational model does not consider constitutive receptor activity, it is impossible to use methods based on the Black and Leff operational model to determine whether inverse agonists exhibit biased signalling along different signal transduction pathways. Similarly, it is impossible to quantify the bias of a ligand that acts as an agonist of one signal transduction pathway and an inverse agonist of another. However, Hall (2006) has described a modification of the operational model, which does include constitutive receptor activity. Subsequently, this model was used by Slack and Hall (2012) to demonstrate that, in systems displaying constitutive activity, it is possible to determine the absolute intrinsic efficacy of ligands at that receptor, rather than relative efficacies, if the receptor density can be varied. This model should, therefore, provide a suitable basis for the derivation of a method for determining the bias of ligands that display inverse agonism along some signalling pathways. Ehlert et al. (2011b) have also developed an operational model which includes constitutive activity and demonstrated that it can be used to determine RA _i for inverse agonists and hence ΔΔlogR to quantify ligand bias for this class of ligand; see also Roche et al., 2013a, for a review.

The ΔΔlogR (ΔΔlog(τ/K _a)) method of Ehlert and co‐workers (Ehlert, 2008; Figueroa et al., 2009) has a number of useful properties, which were highlighted in Kenakin et al. (2012). It should be noted here that Kenakin et al. (2012) distinguish between Δlog(τ/K _a) and logRA _i as they used the original definition of intrinsic relative activity (Ehlert et al., 1999) using parameters of a concentration–response curve (RA _i = E_maxAEC_50B/E_maxBEC_50A, where A and B refer to the test and standard ligand, respectively). Firstly, under certain circumstances (full agonists that have concentration–response curves with unit slopes), the reciprocal of the EC₅₀ of an agonist is a good approximation of τ/K _a making it trivial to estimate from a single concentration–response curve. τ/K _a can also be derived straightforwardly for partial agonists when a full agonist can also be characterized since τ is a simple function of the intrinsic activity of a partial agonist whatever the slope of the curve (or can be obtained by simultaneous fitting, e.g. Leff et al., 1990). In this regard, a complementary scale of biased agonism for partial agonists based on τ values has been recently developed (Burgueño et al., 2017). Secondly, normalization to the values of a reference agonist removes the impact of the bias inherent in the different coupling efficiencies of different signalling pathways, which would otherwise form part of an analysis based on the operational model τ parameter. Thirdly, the value of ΔΔlog(τ/K _a) was shown to be independent of the receptor density in the system in which it is measured (for all values of the slope of the transducer function). Finally, there are circumstances in which the same agonist acting at the same receptor does not exhibit the same value of K _a along two different signalling pathways, and the inclusion of the K _a term is claimed to account for this manifestation of the efficacy of the ligand. In any case, K _a will simply cancel if it is the same. Including K _a implicitly in the analysis also avoids the additional error of measuring and using an independent estimate of ligand affinity especially if the conditions of the functional and binding assays are not precisely matched. There is, however, an argument that changes in measured affinity along different pathways may indicate that the system under consideration is not actually adequately described by a Black and Leff operational model (see Appendix) either because at least one of the measurements has not been taken at equilibrium or because other assumptions inherent in an operational model analysis are violated (but see below). This would, of course, invalidate an analysis based on the operational model.

In summary, current approaches for quantification of biased agonism based on operational models may include (Ehlert et al., 2011b) or not (Kenakin et al., 2012; Burgueño et al., 2017) constitutive receptor activity but all require the presence of a reference agonist for within signalling pathway normalization (because they include pathway‐dependent coupling efficiency in the operational efficacy, τ). Thus, there is value in developing a new analytical methodology in this field, which includes constitutive receptor activity but does not require the normalization to the properties of reference ligands.

Methods

Theory

The closest analogue of τ/K _a in the Slack and Hall operational model is εχ/K _a since the Black and Leff operational model is the special case of the Slack and Hall model with χ << 1 and under these conditions εχ ≡ τ (see Appendix and Slack and Hall, 2012). Here, ε is the intrinsic efficacy of the ligand, K _a its apparent equilibrium dissociation constant and χ the ‘coupling efficiency’ of the signal transduction system. However, εχ/K _a suffers from the same dependence on coupling efficiency as τ/K _a. It would be preferable, indeed desirable, to derive a parameter that does not involve coupling efficiency since this eliminates the requirement to normalize to a reference ligand. Since χ quantifies coupling efficiency in the Slack and Hall model, the obvious solution is to determine the value of Δlog(ε/K _a) or even Δlog(ε) (where the single Δ indicates the lack of normalization). It is worth noting at this point that a ternary complex model only approximates an operational model with unit slope under two conditions: [R]_T << [G]_T or [R]_T >> [G]_T, and it is only under that latter condition that such a model also exhibits a receptor reserve (Hall, 2006). Under the former condition, the system is ‘reserveless’ (EC₅₀ = K _a), and hence, the potency of an agonist for any response should be the same under this condition, no matter what signal transduction pathway is engaged (assuming all are reserveless). Only the maximal response can differ under these conditions, and hence, the only indication of bias is a different order of intrinsic activity. Indeed, under this condition, the ratio of ratios of maximal response to basal activity is a measure of absolute bias (see Appendix).

Systems in which [R]_T << [G]_T also have the potential to exhibit different affinities for the same agonist at a given receptor. To achieve this, it is necessary for the signal transduction systems to be partitioned such that they do not compete for the same pool of receptors. The most obvious way to achieve this is when measurements are made in different cell types or lines that only express one of the signal transduction proteins in question. Alternatively, it may be possible for the proteins to be partitioned into distinct cellular domains, which behave independently. Clearly, the latter would require experimental confirmation.

When [R]_T and [G]_T are within an order of magnitude of each other, the binding isotherm is not a sigmoid or linear rational function of ligand concentration, and a standard operational model is not appropriate to analyse the system. There are also issues with identifying a well‐defined transducer function to translate the stimulus (a linear combination of [R], [RG], [AR] and [ARG]) into the response ([RG] + [ARG]) in this case. It is further noteworthy that in this case, the slope of the binding isotherm and that of the activation curve for G cannot be greater than unity (Giraldo et al., 2002). Thus, only in exceptional circumstances can concentration–response curves have unit Hill coefficients under these conditions. Also, as shown in the Appendix, when [R]_T >> [G]_T, the value of K _a should be the same when measured for any response so Δlog(ε/K _a) and Δlog(ε) should be the same (to within experimental error). So, can these parameters be derived? The previous characterization of the Slack and Hall operational model (with arbitrary slope) indicated that it is indeed possible to estimate ε and K _a independently for any ligand if receptor density, and hence signalling in the absence of ligand, can be varied. This would clearly be a rigorous method for estimating the bias. However, for systems that have linear rational binding and transducer functions (i.e. those that generate concentration–response curves with unit slope) and where it is possible to estimate the activity along the signal transduction system which is independent of the receptor under consideration (the ‘background’ activity), it is possible to estimate ε/K _a directly from a single concentration–response curve. Under these conditions, the Slack and Hall model is given by

$$E=\frac{E_{\max }\chi \left(K_a+\epsilon \left[A\right]\right)}{K_a\left(1+\chi \right)+\left[A\right]\left(1+\mathit{\epsilon \chi }\right)}.$$ (2)

Then, when [A] = 0, E _[A]=0 = E _max χ/(1 + χ), when [A] → ∞, E _[A]→∞ = E _max εχ/(1 + εχ), and the potency of the ligand is [A]₅₀ = K _a(1 + χ)/(1 + εχ). Hence,

$$\frac{E_{\left[A\right]\to \infty }}{{\left[A\right]}_{50}{E}_{\left[A\right]=0}}=\frac{E_{\max }\mathit{\epsilon \chi }}{1+\mathit{\epsilon \chi }}÷\left(\frac{K_a\left(1+\chi \right)}{1+\mathit{\epsilon \chi }}\times \frac{E_{\max }\chi }{1+\chi }\right)=\frac{\epsilon }{K_a}.$$ (3)

Thus, ε/K _a is accessible from a single concentration–response curve. We note that the left‐hand side of Equation (3) has previously been shown to be equal to the affinity of a ligand for the active state of the receptor (Ehlert et al., 2011b), and hence, this will also be true of ε/K _a. It is also possible to re‐parameterize Equation (2) in terms of ε/K _a and directly measurable quantities:

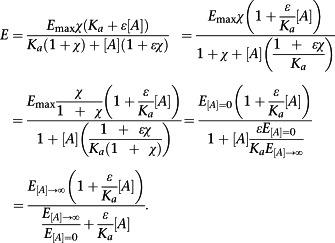(4)

This further underlines the ease with which ε/K _a can be determined in simple experimental systems. From a practical perspective, a more useful form of Equation (4) for curve fitting is Equation (5) below.

$$E=\frac{E_{\left[A\right]\to \infty }\left(1+{10}^Q\left[A\right]\right)}{\frac{E_{\left[A\right]\to \infty }}{E_{\left[A\right]=0}}+{10}^Q\left[A\right]}+\mathit{\text{bkgd}},$$ (5)

where Q = log(ε/K _a). This accounts for the log‐normal distribution of this parameter. The term bkgd has also been added to account for background activity.

An important consideration in the context of ligand bias is to understand how multistate mechanistic models translate into macroscopic operational models since, strictly, it is impossible for a ligand to exhibit biased agonism at a receptor that can only adopt two conformations (‘active’ and ‘inactive’). This is considered in some detail in the Appendix where we show that multistate models are consistent with the Slack and Hall operational model and hence that it is meaningful to estimate bias using Slack and Hall intrinsic efficacy ratios. We also demonstrate that such models define physical limits on the macroscopic intrinsic efficacy of agonists and inverse agonists. This has previously been shown for the two‐state model (Slack and Hall, 2012). Below, we demonstrate the relationship between these parameters and the affinity of the ligand for the active and inactive states of the receptor.

In circumstances where the background activity (i.e. activity in the functional assays that would be present in the absence of the receptor in question) cannot be determined independently or where the transducer function (and hence the concentration–response curves) has a slope which differs from unity, there is no alternative but to vary the coupling efficiency (e.g. by varying the receptor density) in order to estimate intrinsic efficacy and affinity (we demonstrate that there is no re‐parameterization simply in terms of ε/K _a in this case in the Appendix). In this case, the two parameters will be determined separately so it would be possible to determine whether the affinity differed significantly between functional responses. If not, then Δlog(ε) can be estimated as the measure of bias. It should be noted at this point that the expressions for ε and ε/K _a (Equations (A12), (A14), (A19) and (A20)) are independent of [R]_T, and hence, like ΔΔlog(τ/K _a), Δlog(ε) and Δlog(ε/K _a) are independent of the receptor density in the system that they are measured in (barring the requirement for [R]_T to be high enough for there to be constitutive activity).

Finally in this section, we note that, in terms of a two‐state model, it can be shown that ε = α(1 + L)/(1 + αL) (this uses the notation of Hall (2000), where L is the receptor isomerization constant ([R ^*]/[R]) and α is the ratio of the affinities of the ligand for the active and inactive states of the receptor – the definition of intrinsic efficacy in this model). The derivation of this expression is given in the supporting information in Slack and Hall (2012). It is equal to the ratio of the amount of AR ^* at saturating ligand concentrations to that of R ^* in the absence of ligand. This ratio has subsequently been termed R _act by Ehlert (2015) who discussed its use as a measure of pathway activation. Now, when L << 1 (i.e. there is relatively little R ^* in the absence of agonist), the expression for ε above simplifies to ε = α/(1 + αL), and then if α < 1/L (that is the ligand causes less than 50% of the receptor to be in the active state at saturating concentrations), 1 + αL ≈ 1 and ε ≈ α (Slack and Hall, 2012). In other words, for inverse agonists and agonists with no more than moderate intrinsic efficacy (by the criterion 1 < α < 1/L), ε provides a good estimate of the active state selectivity of the ligand. This supports our earlier assertion that measurement of ε provides a rigorous basis for measurement of ligand bias. With the same assumptions, 1/K _a is a good approximation of the affinity constant of the ligand for the inactive state of the receptor (K). Following this logic, ε/K _a is a measure of αK, the affinity constant for the active state and hence a weaker (if more easily measurable) basis for a measure of ligand bias, particularly if estimates of K _a differ among responses, since it does not account for receptor activation. This is clearly also an issue with measures of bias based on RA _i, as noted in Ehlert (2015). Thus, the Slack and Hall model also provides an alternative method to those published by Ehlert and co‐workers (Ehlert et al., 2011a; Ehlert et al., 2011b) for estimating the affinity of ligands for the inactive and active states of the receptor. Similar arguments applied to the multistate model derived in the Appendix (i.e. that ||L|| ≈ ||AL|| ≈ 1) also indicate that, for a receptor with multiple states, ε would represent a weighted average measure of ligand selectivity for the active state(s) responsible for the response under consideration. With the same assumptions, 1/K _a is a measure of the affinity constant for the most abundant state in the absence of ligand, presumably an inactive state.

Nomenclature of targets and ligands

Key protein targets and ligands in this article are hyperlinked to corresponding entries in http://www.guidetopharmacology.org, the common portal for data from the IUPHAR/BPS Guide to PHARMACOLOGY (Harding et al., 2018), and are permanently archived in the Concise Guide to PHARMACOLOGY 2017/18 (Alexander et al., 2017).

Results

Simulations

The two methods discussed above are illustrated using simulated data in Figures 1 and 2. Input parameters and fitted estimates are summarized in Tables 1, 2, 3, 4, 5. For the simulations illustrating analysis using Equation (5), the data were simulated using Equation (2) adding random, normally (E _max, bkgd) or log‐normally distributed errors to the parameters to simulate between‐occasion variability and then adding random, normally distributed error to the individual data points to simulate within‐occasion variability (see figure captions). The data were then analysed using Equation (5) using Microsoft Excel by minimizing the residual sum of squares using the ‘Solver’ Add‐In. A similar approach was taken for simulations based on Equation (A22), but in this case, the simulated data were analysed using Equation (6), below. As can be seen from Tables 3 and 4, the simulations indicate that both methods result in good estimates of the input parameters when sufficiently rich data sets are available. As previously noted, the Slack and Hall (2012) model is only ‘identifiable’ when the receptor density is varied sufficiently for the response in the presence of saturating concentrations of ligand to differ between conditions. This may require more than two different receptor densities to be evaluated. Also, the analysis of a reference agonist alongside an inverse agonist provides a much more robust estimate of E _max (unless the systems demonstrate high levels of constitutive activity). Thus, we have demonstrated that the Slack and Hall operational model, where applicable, provides a method for determining the absolute bias of receptor ligands for different signalling pathways. Since this method can only be applied to systems that demonstrate constitutive activity, it is complementary to the ΔΔlog(τ/K _a) method of Kenakin et al. (2012), which should only be applied to systems that lack measurable constitutive signalling.

$$E=\frac{E_{\max }{\left({10}^X\left({10}^K+{10}^F\left[A\right]\right)\right)}^{{10}^N}}{{\left({10}^K+\left[A\right]\right)}^{{10}^N}+{\left({10}^X\left({10}^K+{10}^F\left[A\right]\right)\right)}^{{10}^N}}+\mathit{\text{bkgd}},$$ (6)

where F = log(ε), K = log(K _a), N = log(n) and X = log(χ).

Figure 1.

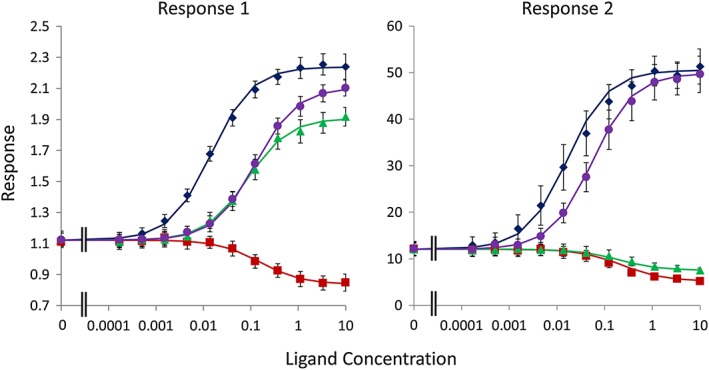
Simulations of analysis using Equation (5). Responses in two systems were simulated with Equation (2) for four ligands (A–D). The seed (true mean) and simulated parameters are summarized in Table 1, and the results of fitting Equation (5) are summarized in Table 3. Points are the mean ± SEM of six simulated data sets, and the curves show the mean of the fitted curves. The values of the system‐related parameters (bkgd, E ₀) were shared for all ligands during fitting. For ‘response 1’, the SD of the normal distribution defining the between‐occasion variability was set to 15% of the mean value of the normally distributed parameters. For the log‐normally distributed parameters, the SD of the log of the parameter was set to 0.15. The SD of the within‐occasion variability was set to 15% of the simulated mean value at each agonist concentration (giving proportional rather than constant errors). For ‘response 2’, the SD of the between‐occasion variability was set to 25% of the mean value of the normally distributed parameters. For the log‐normally distributed parameters, the SD of the log of the parameter was set to 0.25. The SD of the within‐occasion variability was set to 20% of the simulated mean value at each agonist concentration.

Figure 2.

Simulations of analysis using Equation (6). Responses in two systems were simulated with Equation (A22) for four ligands (A–D). The seed (true mean) and simulated parameters are summarized in Table 2, and the results of fitting Equation (6) are summarized in Table 4. Points are the mean ± SEM of six simulated data sets, and the curves show the mean of the fitted curves. The values of the system‐related parameters (bkgd, E _max, χ ₁, χ ₂ and n) were shared for all ligands during fitting. For ‘response 1’, the SD of the normal distribution defining the between‐occasion variability was set to 15% of the mean value of the normally distributed parameters. For the log‐normally distributed parameters except n, the SD of the log of the parameter was set to 0.15. The SD of the within‐occasion variability was set to 15% of the simulated mean value at each agonist concentration (giving proportional rather than constant errors). For ‘response 2’, the SD of the between‐occasion variability was set to 20% of the mean value of the normally distributed parameters. For the log‐normally distributed parameters except n, the SD of the log of the parameter was set to 0.20. The SD of the within‐occasion variability was set to 20% of the simulated mean value at each agonist concentration. In both cases, the SD of n was set to one‐third of that of the other parameters.

Table 1.

Summary of the parameters used in generating the data from Equation (2) for the simulations of analysis by Equation (5)

Parameter	Response 1		Response 2
	True mean	Simulated	True mean	Simulated
E max	1.50	1.49 ± 0.14	50	47.4 ± 8.7
bkgd	0.90	0.80 ± 0.13	5.0	5.2 ± 1.3
logχ	−0.52	−0.55 ± 0.08	−0.70	−0.81 ± 0.24
logε A	2.00	1.97 ± 0.21	2.00	2.12 ± 0.23
logε B	−1.00	−0.96 ± 0.12	−2.00	−2.03 ± 0.23
logε C	1.00	1.06 ± 0.17	−0.52	−0.55 ± 0.11
logε D	1.48	1.47 ± 0.22	2.48	2.15 ± 0.22
pK aA	−0.52	−0.52 ± 0.15	−0.52	−0.51 ± 0.22
pK aB	−1.00	−0.97 ± 0.06	−1.00	−0.94 ± 0.17
pK aC	−0.52	−0.49 ± 0.17	−0.52	−0.62 ± 0.21
pK aD	0.00	0.00 ± 0.14	0.00	0.08 ± 0.28

Values are the mean ± SD of the six simulated sets of parameters. Subscripts A–D refer to the four ligands.

Table 2.

Summary of the parameters used in generating the data from Equation (A22) for the simulations of analysis by Equation (6)

Parameter	Response 1		Response 2
	True mean	Simulated	True mean	Simulated
E max	1.50	1.67 ± 0.17	50	44.0 ± 11.8
bkgd	0.90	0.95 ± 0.10	5.0	5.2 ± 1.2
logχ 1	−0.30	−0.30 ± 0.15	−0.12	−0.06 ± 0.14
logχ 2	−0.90	−0.93 ± 0.20	−0.73	−0.62 ± 0.15
logε A	1.70	1.77 ± 0.12	1.70	1.60 ± 0.18
logε B	−1.00	−0.96 ± 0.11	−2.00	−2.00 ± 0.31
logε C	1.00	0.93 ± 0.16	−0.52	−0.45 ± 0.19
logε D	1.48	1.39 ± 0.10	2.30	2.33 ± 0.24
pK aA	−0.52	−0.56 ± 0.12	−0.52	−0.35 ± 0.26
pK aB	−2.00	−2.07 ± 0.14	−2.00	−1.87 ± 0.23
pK aC	−1.00	−1.04 ± 0.08	−1.00	−0.96 ± 0.19
pK aD	0.00	0.08 ± 0.14	0.00	0.06 ± 0.20
log(n)	0.18	0.16 ± 0.04	−0.10	−0.15 ± 0.09

Values are the mean ± SD of the six simulated sets of parameters. Subscripts A–D refer to the four ligands. Subscripts 1 and 2 refer to the different receptor expression levels.

Table 3.

Comparison of the simulated and fitted parameters for analysis by Equation (5)

Parameter	Response 1		Response 2
	Simulated	Fitted	Simulated	Fitted
bkgd	0.80 ± 0.05	0.79 ± 0.05	5.2 ± 0.1	5.1 ± 0.4
E 0	0.33 ± 0.02	0.33 ± 0.02	6.7 ± 1.4	6.9 ± 1.4
E ∞A	1.44 ± 0.06	1.45 ± 0.06	44.4 ± 3.3	45.5 ± 3.3
E ∞B	0.05 ± 0.01	0.05 ± 0.01	0.07 ± 0.01	0.11 ± 0.04
E ∞C	1.13 ± 0.05	1.12 ± 0.05	2.2 ± 0.5	2.3 ± 0.5
E ∞D	1.32 ± 0.05	1.31 ± 0.05	44.8 ± 3.8	44.7 ± 3.8
logε A/K aA	2.49 ± 0.12	2.47 ± 0.12	2.63 ± 0.15	2.60 ± 0.15
logε B/K aB	0.01 ± 0.05	−0.06 ± 0.11	−1.08 ± 0.13	−1.16 ± 0.20
logε C/K aC	1.55 ± 0.10	1.60 ± 0.10	0.09 ± 0.12	0.23 ± 0.15
logε D/K aD	1.47 ± 0.08	1.51 ± 0.09	2.05 ± 0.09	2.07 ± 0.09

Values are the mean ± SEM of the six simulated sets of parameters. Subscripts A–D refer to the four ligands.

Table 4.

Comparison of the simulated and fitted parameters for analysis by Equation (6)

Parameter	Response 1		Response 2
	Simulated	Fitted	Simulated	Fitted
E max	1.67 ± 0.07	1.68 ± 0.07	44.0 ± 4.8	45.8 ± 5.7
bkgd	0.95 ± 0.04	0.94 ± 0.04	5.20 ± 0.47	4.60 ± 0.83
logχ 1	−0.30 ± 0.06	−0.28 ± 0.05	−0.06 ± 0.06	−0.09 ± 0.06
logχ 2	−0.93 ± 0.08	−0.86 ± 0.08	−0.62 ± 0.06	−0.65 ± 0.09
logε A	1.77 ± 0.05	1.69 ± 0.09	1.60 ± 0.07	1.60 ± 0.12
logε B	−0.96 ± 0.05	−0.93 ± 0.10	−2.00 ± 0.13	−1.94 ± 0.19
logε C	0.93 ± 0.07	0.86 ± 0.08	−0.45 ± 0.08	−0.45 ± 0.09
logε D	1.39 ± 0.04	1.34 ± 0.08	2.33 ± 0.10	2.35 ± 0.23
pK aA	−0.56 ± 0.05	−0.58 ± 0.06	−0.35 ± 0.10	−0.36 ± 0.10
pK aB	−2.07 ± 0.06	−2.07 ± 0.08	−1.87 ± 0.09	−1.86 ± 0.07
pK aC	−1.04 ± 0.03	−1.08 ± 0.03	−0.96 ± 0.08	−0.94 ± 0.10
pK aD	0.08 ± 0.6	0.07 ± 0.05	0.06 ± 0.08	0.07 ± 0.21
log(n)	0.16 ± 0.04	0.19 ± 0.02	−0.15 ± 0.04	−0.16 ± 0.06
log(ε/K a)A	2.33 ± 0.07	2.27 ± 0.09	1.96 ± 0.15	1.96 ± 0.15
log(ε/K a)B	1.11 ± 0.09	1.13 ± 0.12	−0.13 ± 0.14	−0.08 ± 0.17
log(ε/K a)C	1.97 ± 0.07	1.94 ± 0.08	0.51 ± 0.11	0.49 ± 0.13
log(ε/K a)D	1.32 ± 0.07	1.27 ± 0.09	2.27 ± 0.17	2.28 ± 0.15

Values are the mean ± SEM of the six simulated sets of parameters. Subscripts A–D refer to the four ligands. Subscripts 1 and 2 refer to the different receptor expression levels.

Table 5.

Bias factors determined from simulations based on fitting Equations (5) and (6)

Parameter	Equation (5)		Equation (6)
	Simulated	Fitted	Simulated	Fitted
Δlog(ε/K a)A	−0.14 ± 0.17	−0.13 ± 0.16	0.37 ± 0.18	0.31 ± 0.18
Δlog(ε/K a)B	1.10 ± 0.12	1.10 ± 0.21	1.23 ± 0.19	1.21 ± 0.27
Δlog(ε/K a)C	1.46 ± 0.21	1.38 ± 0.18	1.45 ± 0.15	1.45 ± 0.17
Δlog(ε/K a)D	−0.59 ± 0.14	−0.56 ± 0.18	−0.95 ± 0.20	−1.01 ± 0.21
Δlogε A	–	–	0.17 ± 0.09	0.09 ± 0.15
Δlogε B	–	–	1.04 ± 0.15	1.00 ± 0.25
Δlogε C	–	–	1.38 ± 0.09	1.31 ± 0.13
Δlogε D	–	–	−0.94 ± 0.11	−1.01 ± 0.29

Discussion

Concluding remarks

In this report, we have presented novel methods for the analysis of biased signalling in systems with measurable levels of constitutive activity. These methods have some advantages over those that have previously been published, although Δlog(ε/K _a) carries some of the issues associated with methods based on RA _i since it too is a measure of relative affinity for the active state of a receptor not relative intrinsic efficacy. A key issue occurs when estimates of K _a differ between pathways. In this case, it is possible for a ligand to be biased according to its intrinsic efficacy but not according to Δlog(ε/K _a). For example, if for pathway 1 ε ₁ = 0.01 and K _a1 = 10⁻⁶ while for pathway 2 ε ₂ = 1 and K _a2 = 10⁻⁴, the ligand's efficacy is biased (see below for a discussion of how this might be classified) but Δlog(ε/K _a) = 0 indicating no bias. Indeed, it is possible for Δlog(ε) and Δlog(ε/K _a) to be contradictory if K _a1 ≠ K _a2, indicating that some care is required in using the latter method since contributions from differences in affinity and intrinsic efficacy are not distinguished.

There is also an issue with interpreting the direction of a ligand's bias when comparing agonists and inverse agonists. An agonist is more efficacious along pathway 1 compared with pathway 2 when ε ₁ > ε ₂. However, an inverse agonist is more efficacious (causes more inhibition) along pathway 1 when ε ₂ > ε ₁. This interpretation results in, for example, ε ₁/ε ₂ = 10 indicating 10‐fold bias for pathway 1 for an agonist but 10‐fold bias for pathway 2 for an inverse agonist. This also raises a question around how to quantify bias for a ligand that is an agonist of one pathway and inverse agonist of another. The simplest way to resolve these issues is to define bias as the preference to agonize a pathway. In this case, a ligand would be biased towards a given pathway whenever its intrinsic efficacy is numerically greater for that pathway. For an agonist, this is the intuitive definition. It is also intuitively reasonable that a ligand that is an agonist of one pathway and inverse agonist of another is biased towards the pathway it agonizes. By this logic then, an inverse agonist of two pathways is biased towards the pathway it inhibits least, that is, the one for which ε is greater.

Author contributions

J.G. conceived the study. D.A.H. derived the models and performed the simulations. Both J.G. and D.A.H. drafted, reviewed and approved the final manuscript.

Conflict of interest

The authors declare no conflicts of interest.

Declaration of transparency and scientific rigour

This http://onlinelibrary.wiley.com/doi/10.1111/bph.13405/abstract acknowledges that this paper adheres to the principles for transparent reporting and scientific rigour of preclinical research recommended by funding agencies, publishers and other organisations engaged with supporting research.

Appendix

A ternary complex model with competing transducer proteins

Following our previous approach (Hall, 2006), we will derive a ternary complex model with two competing transducer proteins to derive the required operational model under conditions where it exhibits receptor reserve. This will provide a rigorous mathematical demonstration that we may, in fact, neglect the presence of additional transducer proteins when considering bias in systems whose behaviour is consistent with that of an operational model with receptor reserve. We will begin by deriving a system without constitutive activity to support a classical operational model and then derive the model with constitutive activity. From the perspective of GPCR signalling, we have consciously not included the binding of nucleotide to the G protein. This is in part for mathematical simplicity but also because the key conclusions in terms of pathway independence will be the same although, clearly, the precise mathematical expressions will differ. However, Stein and Ehlert demonstrated that an operational model using a simple two‐state model of receptor activation as stimulus (Ehlert et al., 2011b) can accurately describe relevant features of a ternary complex model including nucleotide exchange (Stein and Ehlert, 2015) suggesting that the model described here is unlikely to be misleading.

The first system under consideration is illustrated in the scheme below.

Scheme 1.

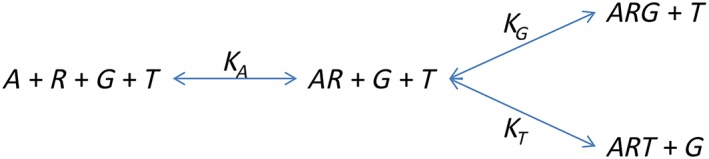
A ternary complex model with competing transducer proteins.

Here, R is the receptor, A the ligand and G and T the two transducer proteins. The conservation equations are as follows:

$$\begin{array}{l}{\left[R\right]}_T=\left[R\right]+\left[\mathit{AR}\right]+\left[\mathit{ARG}\right]+\left[\mathit{ART}\right]\\ {\left[G\right]}_T=\left[G\right]+\left[\mathit{ARG}\right]\\ {\left[T\right]}_T=\left[T\right]+\left[\mathit{ART}\right].\end{array}$$

It will be assumed that [A] is in large excess. The equilibrium dissociation constants are as follows:

$$K_A=\frac{\left[A\right]\left[R\right]}{\left[\mathit{AR}\right]};K_G=\frac{\left[G\right]\left[\mathit{AR}\right]}{\left[\mathit{ARG}\right]};K_T=\frac{\left[T\right]\left[\mathit{AR}\right]}{\left[\mathit{ART}\right]}.$$

We will consider the equilibrium concentration of the ARG complex. By making appropriate substitutions from the definitions of the equilibrium constants, the equation for [R]_T can be expressed in terms of [ARG] as follows:

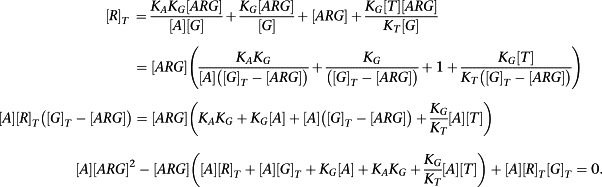To derive an operational model, we now assume (or, indeed, require) that [R]_T >> [G]_T + [T]_T(K _G/K _T). This allows the simplification of the quadratic equation above to

$$\left[A\right]{\left[\mathit{ARG}\right]}^2-\left[\mathit{ARG}\right]\left(\left[A\right]{\left[R\right]}_T+K_G\left[A\right]+K_A{K}_G\right)+\left[A\right]{\left[R\right]}_T{\left[G\right]}_T=0.$$

Note now that [T] no longer appears in these expressions. This assumption renders formation of ARG independent of formation of ART. It is equivalent to assuming that the free concentration of R is not changed by binding to the transducer proteins.

Now, since the same assumption makes ([A][R]_T + K_G[A] + K_AK_G)² >> [A]²[R]_T[G]_T, the physically relevant solution to the quadratic is very well approximated by

$$\left[\mathit{ARG}\right]=\frac{\left[A\right]{\left[R\right]}_T{\left[G\right]}_T}{K_A{K}_G+\left[A\right]\left({\left[R\right]}_T+K_G\right)}.$$

This approximation is detailed in Hall (2013). This can be rearranged to give

$$\left[\mathit{ARG}\right]=\frac{{\left[G\right]}_T\frac{{\left[R\right]}_T}{K_G}\left[A\right]}{K_A+\left[A\right]\left(\frac{{\left[R\right]}_T}{K_G}+1\right)},$$ (A1)

which, taking formation of ARG as the effect of the agonist, is an operational model with E _max = [G]_T and τ = [R]_T/K _G. Thus, under conditions when a pharmacological system can be described by an operational model with receptor reserve, we may treat each signalling cascade independently.

Trivially, it must also be the case that

$$\left[\mathit{ART}\right]=\frac{{\left[T\right]}_T\frac{{\left[R\right]}_T}{K_T}\left[A\right]}{K_A+\left[A\right]\left(\frac{{\left[R\right]}_T}{K_T}+1\right)}.$$ (A2)

Including constitutive activity

The required model is now:

Scheme 2.

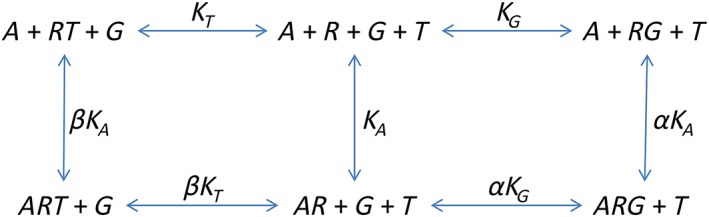
A ternary complex model with competing transducer proteins and constitutive activity.

In this case, the conservation equations are as follows:

$$\begin{array}{l}{\left[R\right]}_T=\left[R\right]+\left[\mathit{RG}\right]+\left[\mathit{RT}\right]+\left[\mathit{AR}\right]+\left[\mathit{ARG}\right]+\left[\mathit{ART}\right]\\ {\left[G\right]}_T=\left[G\right]+\left[\mathit{RG}\right]+\left[\mathit{ARG}\right]\\ {\left[T\right]}_T=\left[T\right]+\left[\mathit{RT}\right]+\left[\mathit{ART}\right].\end{array}$$

The equilibrium constants are as follows:

$$\begin{array}{l}{K}_A=\frac{\left[A\right]\left[R\right]}{\left[\mathit{AR}\right]};\alpha K_A=\frac{\left[A\right]\left[\mathit{RG}\right]}{\left[\mathit{ARG}\right]};\beta K_A=\frac{\left[A\right]\left[\mathit{\text{RT}}\right]}{\left[\mathit{ART}\right]};\\ K_G=\frac{\left[G\right]\left[R\right]}{\left[\mathit{RG}\right]};\alpha K_G=\frac{\left[G\right]\left[\mathit{AR}\right]}{\left[\mathit{ARG}\right]};K_T=\frac{\left[T\right]\left[R\right]}{\left[\mathit{RT}\right]};\beta K_T=\frac{\left[T\right]\left[\mathit{AR}\right]}{\left[\mathit{ART}\right]}.\end{array}$$

Now we must consider the equilibrium concentration of the RG and ARG complex. The derivation is a little more complicated. First, it is necessary to derive an expression for [R].

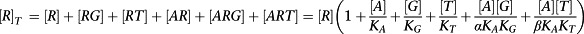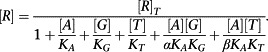(A3)

Now an expression for [G] in terms of [G]_T and other constants is required.

$$\begin{array}{l}{K}_G\left[G\right]\left(1+\frac{\left[A\right]}{K_A}+\frac{\left[G\right]}{K_G}\left(1+\frac{\left[A\right]}{\alpha K_A}\right)+\frac{\left[T\right]}{K_T}\left(1+\frac{\left[A\right]}{\beta K_A}\right)\right)+{\left[R\right]}_T\left[G\right]\left(1+\frac{\left[A\right]}{\alpha K_A}\right)\\ ={\left[G\right]}_T{K}_G\left(1+\frac{\left[A\right]}{K_A}+\frac{\left[G\right]}{K_G}\left(1+\frac{\left[A\right]}{\alpha K_A}\right)+\frac{\left[T\right]}{K_T}\left(1+\frac{\left[A\right]}{\beta K_A}\right)\right)\\ {\left[G\right]}^2\left(1+\frac{\left[A\right]}{\alpha K_A}\right)+\left[G\right]\left(K_G\left(1+\frac{\left[A\right]}{K_A}+\frac{\left[T\right]}{K_T}\left(1+\frac{\left[A\right]}{\beta K_A}\right)\right)+\left({\left[R\right]}_T-{\left[G\right]}_T\right)\left(1+\frac{\left[A\right]}{\alpha K_A}\right)\right)\\ -K_G{\left[G\right]}_T\left(1+\frac{\left[A\right]}{K_A}+\frac{\left[T\right]}{K_T}\left(1+\frac{\left[A\right]}{\beta K_A}\right)\right)=0.\end{array}$$

It is now necessary to assume that

$${\left[R\right]}_T>>{\left[G\right]}_T+sup\left\{{\left[T\right]}_T\frac{K_G}{K_T},{\left[T\right]}_T\frac{{\mathit{aK}}_G}{\beta K_T}\right\}$$

(where ‘sup’ indicates the larger of the two values in the braces), which results in the preceding quadratic simplifying to

$${\left[G\right]}^2\left(1+\frac{\left[A\right]}{\alpha K_A}\right)+\left[G\right]\left(K_G\left(1+\frac{\left[A\right]}{K_A}\right)+{\left[R\right]}_T\left(1+\frac{\left[A\right]}{\alpha K_A}\right)\right)-K_G{\left[G\right]}_T\left(1+\frac{\left[A\right]}{K_A}+\frac{\left[T\right]}{K_T}\left(1+\frac{\left[A\right]}{\beta K_A}\right)\right)=0.$$

Further, since

$${\left(K_G\left(1+\frac{\left[A\right]}{K_A}\right)+{\left[R\right]}_T\left(1+\frac{\left[A\right]}{\alpha K_A}\right)\right)}^2>>K_G{\left[G\right]}_T\left(1+\frac{\left[A\right]}{K_A}+\frac{\left[T\right]}{K_T}\left(1+\frac{\left[A\right]}{\beta K_A}\right)\right)\left(1+\frac{\left[A\right]}{\alpha K_A}\right),$$

the physically meaningful root of the quadratic can beapproximated as

$$\left[G\right]=\frac{K_G{\left[G\right]}_T\left(1+\frac{\left[A\right]}{K_A}+\frac{\left[T\right]}{K_T}\left(1+\frac{\left[A\right]}{\beta K_A}\right)\right)}{K_G\left(1+\frac{\left[A\right]}{K_A}\right)+{\left[R\right]}_T\left(1+\frac{\left[A\right]}{\alpha K_A}\right)}.$$ (A4)

Equations (A3) and (A4) can now be substituted into the expressions for [RG] and [ARG]:

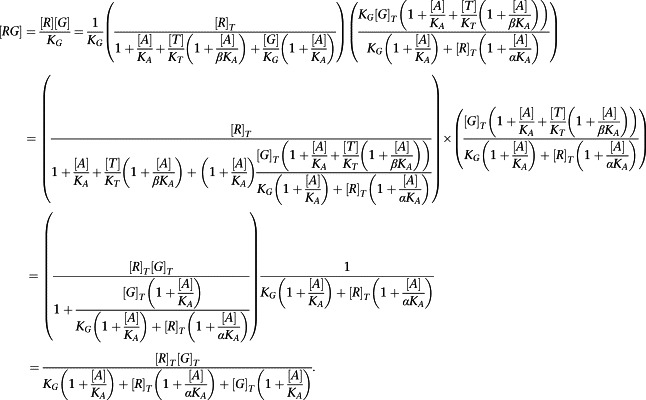But [R]_T >> [G]_T, so

$$\left[\mathit{RG}\right]=\frac{{\left[R\right]}_T{\left[G\right]}_T}{K_G\left(1+\frac{\left[A\right]}{K_A}\right)+{\left[R\right]}_T\left(1+\frac{\left[A\right]}{\alpha K_A}\right)}.$$ (A5)

Also,

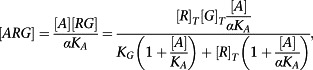(A6)

$$\left[\mathit{RG}\right]+\left[\mathit{ARG}\right]=\frac{{\left[R\right]}_T{\left[G\right]}_T\left(1+\frac{\left[A\right]}{\alpha K_A}\right)}{K_G\left(1+\frac{\left[A\right]}{K_A}\right)+{\left[R\right]}_T\left(1+\frac{\left[A\right]}{\alpha K_A}\right)}=\frac{{\left[G\right]}_T\frac{{\left[R\right]}_T}{K_G}\left(1+\frac{\left[A\right]}{\alpha K_A}\right)}{1+\frac{{\left[R\right]}_T}{K_G}+\frac{\left[A\right]}{K_A}\left(1+\frac{{\left[R\right]}_T}{\alpha K_G}\right)}.$$ (A7)

This is of the form of the model of Slack and Hall (2012) with E _max = [G]_T, K _a = 1/K _A, χ = [R]_T/K _G and ε = 1/α.

Also, note that if Equation (A7) is rearranged to

$$\left[\mathit{RG}\right]+\left[\mathit{ARG}\right]=\frac{{\left[G\right]}_T\frac{{\left[R\right]}_T}{K_G}\left(K_A+\frac{\left[A\right]}{\alpha }\right)}{K_A\left(1+\frac{{\left[R\right]}_T}{K_G}\right)+\left[A\right]\left(1+\frac{{\left[R\right]}_T}{\alpha K_G}\right)},$$

and compared with Equation (A1), it can be seen that Equation (A1) is a special case of Equation (A7) in which [R]_T/K _G << 1, K _A << [A]/α, and we must identify K _G in Equation (A1) with αK _G in Equation (A7). It is then possible to see that with these assumptions τ ≡ εχ = [R]_T/αK _G.

It is also instructive to consider the alternative simplifying condition, [R]_T << [G]_T, [T]_T. In this case

$$\left[\mathit{RG}\right]+\left[\mathit{ARG}\right]=\frac{{\left[R\right]}_T\frac{{\left[G\right]}_T}{K_G}\left(1+\frac{\left[A\right]}{\alpha K_A}\right)}{1+\frac{{\left[G\right]}_T}{K_G}+\frac{{\left[T\right]}_T}{K_T}+\frac{\left[A\right]}{K_A}\left(1+\frac{{\left[G\right]}_T}{\alpha K_G}+\frac{{\left[T\right]}_T}{\beta K_T}\right)}.$$

From this expression, when [A] = 0,

$${\left[\mathit{RG}\right]}_{\left[A\right]=0}=\frac{{\left[R\right]}_T\frac{{\left[G\right]}_T}{K_G}}{1+\frac{{\left[G\right]}_T}{K_G}+\frac{{\left[T\right]}_T}{K_T}}.$$

When [A] >> K _A,

$${\left[\mathit{ARG}\right]}_{\left[A\right]\to \infty }=\frac{{\left[R\right]}_T\frac{{\left[G\right]}_T}{\alpha K_G}}{1+\frac{{\left[G\right]}_T}{\alpha K_G}+\frac{{\left[T\right]}_T}{\beta K_T}}.$$

Also, the midpoint, [A]₅₀, of this expression is

$${\left[A\right]}_{50}=\frac{K_A\left(1+\frac{{\left[G\right]}_T}{K_G}+\frac{{\left[T\right]}_T}{K_T}\right)}{1+\frac{{\left[G\right]}_T}{\alpha K_G}+\frac{{\left[T\right]}_T}{\beta K_T}}.$$

Note then that the expressions when [A] = 0 and when [A] >> K _A are linearly dependent on [R]_T but the expression for [A]₅₀ is independent of [R]_T. In others words, if the receptor density is varied, the EC₅₀ remains constant while the basal and maximal effect will vary in proportion. With this condition, then, the transducer function is of linear rather than linear rational form, and the response is simply proportional to fractional occupancy. This is equivalent to the condition εχ << 1, and since for agonists ε > 1, this must also imply that χ << 1. Also, however, all of these expressions contain terms in [T] as well as [G] so the apparent efficacy under this condition is dependent on activity along and the concentration of the components along the other signalling pathway(s) as well as the one measured.

Now when εχ << 1, the corresponding expressions from the Slack and Hall model are as follows:

$$\begin{array}{l}{E}_{\left[A\right]=0}=\frac{E_{\max }\chi }{1+\chi }\approx E_{\max }\chi \\ E_{\left[A\right]\to 0}=\frac{E_{\max }\mathit{\epsilon \chi }}{1+\mathit{\epsilon \chi }}\approx E_{\max }\mathit{\epsilon \chi }\\ {\left[A\right]}_{50}=\frac{K_a\left(1+\chi \right)}{1+\mathit{\epsilon \chi }}\approx K_a.\end{array}$$

Hence, the ratio of the maximal to the basal response is a measure of intrinsic efficacy. Applying this to the ternary complex model gives

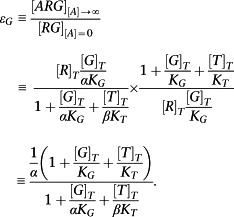The corresponding expression for the T pathway is

$${\epsilon }_T\equiv \frac{\frac{1}{\beta }\left(1+\frac{{\left[G\right]}_T}{K_G}+\frac{{\left[T\right]}_T}{K_T}\right)}{1+\frac{{\left[G\right]}_T}{\alpha K_G}+\frac{{\left[T\right]}_T}{\beta K_T}}.$$

Hence, it is possible to measure bias by taking the ratio of these two values as follows:

$$\frac{{\epsilon }_G}{{\epsilon }_T}=\frac{\beta }{\alpha },$$

which is indeed a well‐defined ratio of intrinsic efficacies.

A multistate model

We begin by considering a system with precisely two receptor conformations and generalize from there. This has the advantage that the system with two states is identical to the cubic ternary complex model (Weiss et al., 1996a; Weiss et al., 1996b; Weiss et al., 1996c) so much of the required algebra has been derived previously (e.g. in notation most similar to that of the current work, Hall, 2006). However, we will assume now that both conformations of the receptor can interact with and activate the G protein, even if extremely weakly (if only one conformation can interact with the G protein the system does not behave like an operational model, Hall, 2013). Based on the discussion above, we also assume that we may neglect the influence of other transducer proteins. The required expression is

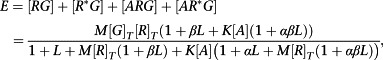(A8)

where the equilibrium constants are now defined (as association constants) as follows.

$$K=\frac{\left[\mathit{AR}\right]}{\left[A\right]\left[R\right]};L=\frac{\left[R^{*}\right]}{\left[R\right]};M=\frac{\left[\mathit{RG}\right]}{\left[G\right]\left[R\right]};\alpha =\frac{\left[{\mathit{AR}}^{*}\right]\left[R\right]}{\left[\mathit{AR}\right]\left[R^{*}\right]}\text{and}\beta =\frac{\left[R^{*}G\right]\left[R\right]}{\left[\mathit{RG}\right]\left[R^{*}\right]}.$$

To generalize to any finite number of states we will again use the notation of vectors and matrices (Hall, 2013) and the concept of the vector norm, specifically the so‐called grid or taxi cab norm, which is simply the sum of the elements of the vector (see below). This results in a remarkably compact expression for the generalization:

$$E=\frac{\mu {\left[G\right]}_T{\left[R\right]}_T\left(‖\mathbf{G\lambda }‖+\kappa \left[A\right]‖\mathbf{AG\lambda }‖\right)}{‖\mathbf{\lambda }‖+\mu {\left[R\right]}_T‖\mathbf{G\lambda }‖+\kappa \left[A\right]\left(‖\mathbf{A\lambda }‖+\mu {\left[R\right]}_T‖\mathbf{AG\lambda }‖\right)}.$$ (A9)

To interpret this expression, we assume that there are n receptor conformations R ¹, R ², ..., R ⁿ and that conformation R ¹ is the most abundant (and hence most stable) in the absence of ligands, including transducer proteins. Note, however, that this restriction is convenient rather than essential since it simply defines the first element of the vectors and matrices as 1. Then κ and μ are the equilibrium association constants for the binding of A and G to R ¹ respectively. λ is a column vector with first element 1 and subsequent elements the isomerization constants (λ ₂ to λ _n) for the transitions of R ¹ into the other n − 1 conformations, that is, λ = [1 λ ₂ ... λ _n]^T. Note that the 1 in the first position is consistent with the isomerization constant definition since it corresponds with conversion of R ¹ to itself. A and G are diagonal matrices whose elements are the ratios of the affinities of A and G for R ¹ and the other receptor conformations:

$$\mathbf{A}=\left[\begin{array}{cccc}1& 0& \dots & 0\\ 0& a_2& \dots & 0\\ ⋮& ⋮& \ddots & 0\\ 0& 0& 0& a_n\end{array}\right],\mathbf{G}=\left[\begin{array}{cccc}1& 0& \dots & 0\\ 0& g_2& \dots & 0\\ ⋮& ⋮& \ddots & 0\\ 0& 0& 0& g_n\end{array}\right].$$

Here, for example, a ₂ is defined as the ratio of κ ₂ = [AR ²]/[A][R ²] and κ = [AR ¹]/[A][R ¹], that is, a ₂ = [AR ²][R ¹]/[AR ¹][R ²]. Similarly, g ₂ = [R ² G][R ¹]/[R ¹ G][R ²] etc. Finally, then, the norms are as follows:

$$‖\mathbf{\lambda }‖=‖\left[\begin{array}{c}1\\ {\lambda }_2\\ ⋮\\ {\lambda }_n\end{array}\right]‖=1+{\lambda }_2+\dots +{\lambda }_n=1+\sum _{i=2}^n{\lambda }_i,$$

$$‖\mathbf{A\lambda }‖=‖\left[\begin{array}{cccc}1& 0& \dots & 0\\ 0& a_2& \dots & 0\\ ⋮& ⋮& \ddots & 0\\ 0& 0& 0& a_n\end{array}\right]\left[\begin{array}{c}1\\ {\lambda }_2\\ ⋮\\ {\lambda }_n\end{array}\right]‖=‖\left[\begin{array}{c}1\\ a_2{\lambda }_2\\ ⋮\\ a_n{\lambda }_n\end{array}\right]‖=1+a_2{\lambda }_2+\dots +a_n{\lambda }_n=1+\sum _{i=2}^n{a}_i{\lambda }_i,$$

$$‖\mathbf{G\lambda }‖=‖\left[\begin{array}{cccc}1& 0& \dots & 0\\ 0& g_2& \dots & 0\\ ⋮& ⋮& \ddots & 0\\ 0& 0& 0& g_n\end{array}\right]\left[\begin{array}{c}1\\ {\lambda }_2\\ ⋮\\ {\lambda }_n\end{array}\right]‖=‖\left[\begin{array}{c}1\\ g_2{\lambda }_2\\ ⋮\\ g_n{\lambda }_n\end{array}\right]‖=1+g_2{\lambda }_2+\dots +g_n{\lambda }_n=1+\sum _{i=2}^n{g}_i{\lambda }_i,$$

Equation (A8), then, is of this form with R equivalent to R ¹ and R ^* equivalent to R ², then κ = K, μ = M, λ = [1 L]^T,

$$\mathbf{A}=\left[\begin{array}{cc}1& 0\\ 0& \alpha \end{array}\right]\text{and}\mathbf{G}=\left[\begin{array}{cc}1& 0\\ 0& \beta \end{array}\right].$$

It is then possible to derive equivalences with Slack and Hall operational model parameters as follows.

First,

$$E=\frac{E_{\max }\chi \left(K_a+\epsilon \left[A\right]\right)}{K_a\left(1+\chi \right)+\left[A\right]\left(1+\mathit{\epsilon \chi }\right)}\equiv \frac{\mu {\left[G\right]}_T{\left[R\right]}_T\left(‖\mathbf{G\lambda }‖+\kappa \left[A\right]‖\mathbf{AG\lambda }‖\right)}{‖\mathbf{\lambda }‖+\mu {\left[R\right]}_T‖\mathbf{G\lambda }‖+\kappa \left[A\right]\left(‖\mathbf{A\lambda }‖+\mu {\left[R\right]}_T‖\mathbf{AG\lambda }‖\right)}.$$

The value of E in the absence of A is

$$\frac{E_{\max }\chi }{1+\chi }\equiv \frac{\mu {\left[G\right]}_T{\left[R\right]}_T‖\mathbf{G\lambda }‖}{‖\mathbf{\lambda }‖+\mu {\left[R\right]}_T‖\mathbf{G\lambda }‖}=\frac{\mu {\left[G\right]}_T{\left[R\right]}_T‖\mathbf{G\lambda }‖/‖\mathbf{\lambda }‖}{1+\mu {\left[R\right]}_T‖\mathbf{G\lambda }‖/‖\mathbf{\lambda }‖}.$$

By inspection then,

$$E_{\max }\equiv {\left[G\right]}_T$$ (A10)

and

$$\chi \equiv \mu {\left[R\right]}_T\Vert \mathbf{G\lambda }\Vert /\Vert \mathbf{\lambda }\Vert .$$ (A11)

The value of E in the presence of a saturating concentration of A is

$$\frac{E_{\max }\mathit{\epsilon \chi }}{1+\mathit{\epsilon \chi }}\equiv \frac{\mu {\left[G\right]}_T{\left[R\right]}_T‖\mathbf{AG\lambda }‖}{‖\mathbf{A\lambda }‖+\mu {\left[R\right]}_T‖\mathbf{AG\lambda }‖}=\frac{\mu {\left[G\right]}_T{\left[R\right]}_T‖\mathbf{AG\lambda }‖/‖\mathbf{A\lambda }‖}{1+\mu {\left[R\right]}_T‖\mathbf{AG\lambda }‖/‖\mathbf{A\lambda }‖}.$$

From this, we see that εχ ≡ μ[R]_T‖AGλ‖/‖Aλ‖. Hence,

$$\epsilon =\frac{\mathit{\epsilon \chi }}{\chi }\equiv \frac{\mu {\left[R\right]}_T‖\mathbf{AG\lambda }‖}{‖\mathbf{A\lambda }‖}÷\frac{\mu {\left[R\right]}_T‖\mathbf{G\lambda }‖}{‖\mathbf{\lambda }‖}=\frac{‖\mathbf{\lambda }‖‖\mathbf{AG\lambda }‖}{‖\mathbf{A\lambda }‖‖\mathbf{G\lambda }‖}.$$ (A12)

The midpoint of the concentration–response curve to A, [A]₅₀, is

$$\frac{K_a\left(1+\chi \right)}{1+\mathit{\epsilon \chi }}\equiv \frac{‖\mathbf{\lambda }‖+\mu {\left[R\right]}_T‖\mathbf{G\lambda }‖}{\kappa \left(‖\mathbf{A\lambda }‖+\mu {\left[R\right]}_T‖\mathbf{AG\lambda }‖\right)}.$$

Taking limits as [R]_T → 0 (and hence χ → 0), this gives

$$K_a\equiv \frac{‖\mathbf{\lambda }‖}{\kappa ‖\mathbf{A\lambda }‖}.$$ (A13)

It is noteworthy that Equation (A13) contains only properties of the free receptor and agonist bound receptors. The transducer protein has no influence on the macroscopic affinity of the agonist according to this model.

Finally then,

$$\frac{\epsilon }{K_a}\equiv \frac{‖\mathbf{\lambda }‖‖\mathbf{AG\lambda }‖}{‖\mathbf{A\lambda }‖‖\mathbf{G\lambda }‖}÷\frac{‖\mathbf{\lambda }‖}{\kappa ‖\mathbf{A\lambda }‖}=\frac{\kappa ‖\mathbf{AG\lambda }‖}{‖\mathbf{G\lambda }‖}.$$ (A14)

For two distinct signalling proteins, G₁ and G₂, it is simply necessary to define the two matrices G ₁ and G ₂ of ratios of affinities of G₁ and G₂ for the conformations of R. Also, since A is a property of the ligand and not of the transducer protein, it remains constant for a given ligand. Hence, from Equation (A12),

$${\epsilon }_1=\frac{‖\mathbf{\lambda }‖‖{\mathbf{AG}}_1\mathbf{\lambda }‖}{‖\mathbf{A\lambda }‖‖{\mathbf{G}}_1\mathbf{\lambda }‖}\text{and}{\epsilon }_2=\frac{‖\mathbf{\lambda }‖‖{\mathbf{AG}}_2\mathbf{\lambda }‖}{‖\mathbf{A\lambda }‖‖{\mathbf{G}}_2\mathbf{\lambda }‖}.$$

So

$$\frac{{\epsilon }_1}{{\epsilon }_2}=\frac{‖\mathbf{\lambda }‖‖{\mathbf{AG}}_1\mathbf{\lambda }‖}{‖\mathbf{A\lambda }‖‖{\mathbf{G}}_1\mathbf{\lambda }‖}÷\frac{‖\mathbf{\lambda }‖‖{\mathbf{AG}}_2\mathbf{\lambda }‖}{‖\mathbf{A\lambda }‖‖{\mathbf{G}}_2\mathbf{\lambda }‖}=\frac{‖{\mathbf{G}}_2\mathbf{\lambda }‖‖{\mathbf{AG}}_1\mathbf{\lambda }‖}{‖{\mathbf{G}}_1\mathbf{\lambda }‖‖{\mathbf{AG}}_2\mathbf{\lambda }‖}.$$

It is noteworthy that this expression is not affected by the coupling efficiency of the signalling pathways concerned and, therefore, by the receptor density.

Now, since K _a ≡ ‖λ‖/κ‖Aλ‖ (Equation (A13)), it is a constant for a given ligand:receptor pair. Then from Equation (A14),

$${\left(\frac{\epsilon }{K_a}\right)}_1=\frac{{\epsilon }_1}{K_a}=\frac{\kappa ‖{\mathbf{AG}}_1\mathbf{\lambda }‖}{‖{\mathbf{G}}_1\mathbf{\lambda }‖}\text{and}{\left(\frac{\epsilon }{K_a}\right)}_2=\frac{{\epsilon }_2}{K_a}=\frac{\kappa ‖{\mathbf{AG}}_2\mathbf{\lambda }‖}{‖{\mathbf{G}}_2\mathbf{\lambda }‖}.$$

Thus,

$${\left(\frac{\epsilon }{K_a}\right)}_1÷{\left(\frac{\epsilon }{K_a}\right)}_2=\frac{\kappa ‖{\mathbf{AG}}_1\mathbf{\lambda }‖}{‖{\mathbf{G}}_1\mathbf{\lambda }‖}÷\frac{\kappa ‖{\mathbf{AG}}_2\mathbf{\lambda }‖}{‖{\mathbf{G}}_2\mathbf{\lambda }‖}=\frac{‖{\mathbf{G}}_2\mathbf{\lambda }‖‖{\mathbf{AG}}_1\mathbf{\lambda }‖}{‖{\mathbf{G}}_1\mathbf{\lambda }‖‖{\mathbf{AG}}_2\mathbf{\lambda }‖}=\frac{{\epsilon }_1}{{\epsilon }_2}.$$

Direct derivation of a multistate operational model

The above ternary complex model motivates the direct derivation of a multistate operational model. Initially, we will consider a two‐state binding model:

Scheme 3.

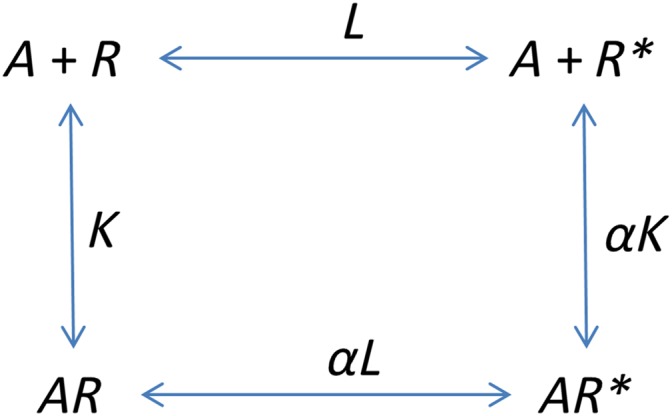
A two‐state model.

In this case,

$$\begin{array}{l}{\left[R\right]}_T=\left[R\right]+\left[R^{*}\right]+\left[\mathit{AR}\right]+\left[{\mathit{AR}}^{*}\right]\\ K=\frac{\left[\mathit{AR}\right]}{\left[A\right]\left[R\right]};L=\frac{\left[R^{*}\right]}{\left[R\right]};\alpha =\frac{\left[R\right]\left[{\mathit{AR}}^{*}\right]}{\left[R^{*}\right]\left[\mathit{AR}\right]}.\end{array}$$

Here, K is an association equilibrium constant rather than a dissociation constant. This results in the following expressions for the concentrations of the receptor species:

$$\begin{array}{l}\left[R\right]=\frac{{\left[R\right]}_T}{1+L+K\left[A\right]+\mathit{\alpha KL}\left[A\right]};\left[R^{*}\right]=\frac{L{\left[R\right]}_T}{1+L+K\left[A\right]+\mathit{\alpha KL}\left[A\right]}\\ \left[\mathit{AR}\right]=\frac{K\left[A\right]{\left[R\right]}_T}{1+L+K\left[A\right]+\mathit{\alpha KL}\left[A\right]};\left[{\mathit{AR}}^{*}\right]=\frac{\mathit{\alpha KL}\left[A\right]{\left[R\right]}_T}{1+L+K\left[A\right]+\mathit{\alpha KL}\left[A\right]}.\end{array}$$

We then define the stimulus, S, as S = [R] + e[R ^*] + [AR] + e[AR ^*]. That is each receptor conformation has a different ability to activate the signal transduction cascade and the impact of an agonist is simply to redistribute those conformations. Here, then, e represents the ratio of the transducer constants for R‐containing and R ^*‐containing species. Now, as ever, define the response, E, as

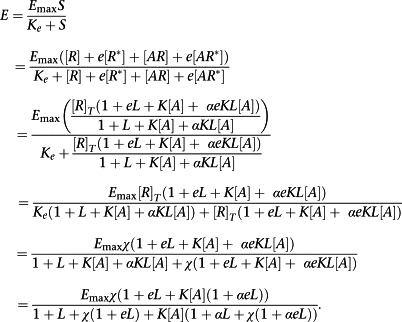(A15)

Where, in the penultimate step, χ = [R]_T/K _e is the coupling efficiency of the R conformation.

It is then straightforward to generalize this model to an arbitrary number of conformations:

$$E=\frac{E_{\max }{\rm X}\left(‖\mathbf{EL}‖+K\left[A\right]‖\mathbf{AEL}‖\right)}{‖\mathbf{L}‖+{\rm X}‖\mathbf{EL}‖+K\left[A\right]\left(‖\mathbf{AL}‖+{\rm X}‖\mathbf{AEL}‖\right)},$$ (A16)

where L = [1 L ₂ ... L _n]^T is again the vector of receptor isomerization constants for the free receptor,

$$\mathbf{A}=\left[\begin{array}{cccc}1& 0& \dots & 0\\ 0& {\alpha }_2& \dots & 0\\ ⋮& ⋮& \ddots & 0\\ 0& 0& 0& {\alpha }_n\end{array}\right],\text{and}\mathbf{E}=\left[\begin{array}{cccc}1& 0& \dots & 0\\ 0& e_2& \dots & 0\\ ⋮& ⋮& \ddots & 0\\ 0& 0& 0& e_n\end{array}\right]$$

are the matrices of changes in isomerization constants in the presence of ligands and of ratios of transducer constants respectively. Finally, Χ is the ratio of the receptor density to the transducer constant for the R ¹ conformation. Hence, for example, e ₂ Χ is the transducer ratio of the R ² state.

Equation (A16) is of identical form to Equation (A9) with E _max = [G]_T, Χ = μ[R]_T, K = κ, L = λ, E = G and A = A. Thus, Equation (A16) is also a Slack–Hall operational model, and we may write the equivalent expressions to Equations (A10)–(A14) as follows:

$$E_{\max }\equiv {\left[G\right]}_T,$$ (A17)

$$\chi \equiv {\rm X}\Vert \mathbf{EL}\Vert /\Vert \mathbf{L}\Vert ,$$ (A18)

$$\epsilon \equiv \frac{‖\mathbf{L}‖‖\mathbf{AEL}‖}{‖\mathbf{AL}‖‖\mathbf{EL}‖},$$ (A19)

$$K_a\equiv \frac{‖\mathbf{L}‖}{K‖\mathbf{AL}‖},$$ (A20)

$$\frac{\epsilon }{K_a}\equiv \frac{K‖\mathbf{AEL}‖}{‖\mathbf{EL}‖}.$$ (A21)

Equation (A16) may be specialized to a classical Black–Leff operation model by requiring that Χ‖EL‖/‖L‖ << 1 to give, after rearrangement,

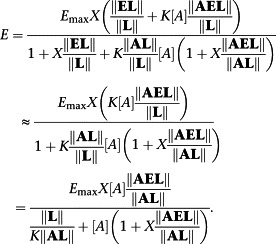Hence, τ ≡ Χ‖AEL‖/‖AL‖ and τ/K _a ≡ KΧ‖AEL‖/‖L‖.

To compare bias along two distinct signalling pathways with matrices of transducer constant ratios E ₁ and E ₂, then gives for the Slack–Hall model:

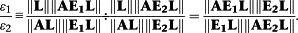Whilst for the classical operational model

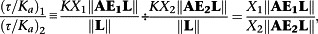the latter being ‘contaminated’ with the relative coupling efficiencies of the two transduction pathways and hence demonstrating the need to normalize this parameter by dividing by that of a standard ligand.

A physical limit to intrinsic efficacy

Equation (A18) (and therefore Equation (A12)) has a further noteworthy property. From the definition of the grid norm,

$$‖\mathbf{AEL}‖=1+\sum _{i=2}^n{a}_i{e}_i{L}_i\text{and}‖\mathbf{AL}‖=1+\sum _{i=2}^n{a}_i{L}_i.$$

Now, if a given agonist strongly and selectively favours a particular receptor conformation, R ^m say, then a _m > > 1 and also a _m > > a _i for i ≠ m. This will result in the terms in a _m dominating in the expressions for ‖AEL‖ and ‖AL‖, and they will simplify to

$$‖\mathbf{AEL}‖\approx a_m{e}_m{L}_m\text{and}‖\mathbf{AL}‖\approx a_m{L}_m.$$

This results in Equation (A19) simplifying as follows:

Thus, the largest and smallest elements of E define the upper and lower limits of the efficacy of a ligand along a given signalling pathway. In the upper‐limit case, this represents the complete conversion of R into conformation R ^m. In the lower‐limit case, it represents the effective elimination of this conformation. Note when a transducer is activated by multiple receptor conformations and a ligand can enrich several of these conformations, then the efficacy of that ligand will be the weighted average of its effect on the abundance of each of those conformations.

Reparameterization of the Slack and Hall operational model when n ≠ 1

The form of the Slack and Hall model when the slope of the transducer function is not unity is

$$E=\frac{E_{\max }{\chi }^n{\left(K_a+\epsilon \left[A\right]\right)}^n}{{\left(K_a+\left[A\right]\right)}^n+{\chi }^n{\left(K_a+\epsilon \left[A\right]\right)}^n}+\mathit{\text{background}}.$$ (A22)

If the background activity can be estimated independently (and therefore subtracted), then in the absence of ligand the response is

$$E_{\left[A\right]=0}=\frac{E_{\max }{\chi }^n}{1+{\chi }^n}.$$

At saturating concentrations of ligand, the response is

$$E_{\left[A\right]\to \infty }=\frac{E_{\max }{\epsilon }^n{\chi }^n}{1+{\epsilon }^n{\chi }^n}.$$

The ratio of these two expressions is

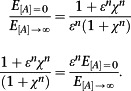The potency of the ligand is

$${\left[A\right]}_{50}=\frac{K_a\left({\left(2{\epsilon }^n{\chi }^n+{\epsilon }^n+1\right)}^{1/n}-{\left({\chi }^n+{\epsilon }^n{\chi }^n+2\right)}^{1/n}\right)}{\epsilon {\left({\chi }^n+{\epsilon }^n{\chi }^n+2\right)}^{1/n}-{\left(2{\epsilon }^n{\chi }^n+{\epsilon }^n+1\right)}^{1/n}}.$$

Rearranging [A]₅₀ gives

$$\begin{array}{l}{\left[A\right]}_{50}=\frac{\left({\left(2{\epsilon }^n{\chi }^n+{\epsilon }^n+1\right)}^{1/n}-{\left({\chi }^n+{\epsilon }^n{\chi }^n+2\right)}^{1/n}\right)}{\frac{\epsilon }{K_a}{\left({\chi }^n+{\epsilon }^n{\chi }^n+2\right)}^{1/n}-\frac{1}{K_a}{\left(2{\epsilon }^n{\chi }^n+{\epsilon }^n+1\right)}^{1/n}}\\ =\frac{\left({\left({\epsilon }^n\left(1+{\chi }^n\right)+1+{\epsilon }^n{\chi }^n\right)}^{1/n}-{\left(1+{\chi }^n+1+{\epsilon }^n{\chi }^n\right)}^{1/n}\right)}{\frac{\epsilon }{K_a}{\left(1+{\chi }^n+1+{\epsilon }^n{\chi }^n\right)}^{1/n}-\frac{1}{K_a}{\left({\epsilon }^n\left(1+{\chi }^n\right)+1+{\epsilon }^n{\chi }^n\right)}^{1/n}}\\ =\frac{\left({\left({\epsilon }^n+\frac{1+{\epsilon }^n{\chi }^n}{1+{\chi }^n}\right)}^{1/n}-{\left(1+\frac{1+{\epsilon }^n{\chi }^n}{1+{\chi }^n}\right)}^{1/n}\right)}{\frac{\epsilon }{K_a}{\left(1+\frac{1+{\epsilon }^n{\chi }^n}{1+{\chi }^n}\right)}^{1/n}-\frac{1}{K_a}{\left({\epsilon }^n+\frac{1+{\epsilon }^n{\chi }^n}{1+{\chi }^n}\right)}^{1/n}}\\ ={\left(\frac{\epsilon }{K_a}\right)}^{-1}\frac{\left(\epsilon {\left(1+\frac{E_{\left[A\right]=0}}{E_{\left[A\right]\to \infty }}\right)}^{1/n}-{\left(1+\frac{{\epsilon }^n{E}_{\left[A\right]=0}}{E_{\left[A\right]\to \infty }}\right)}^{1/n}\right)}{{\left(1+\frac{{\epsilon }^n{E}_{\left[A\right]=0}}{E_{\left[A\right]\to \infty }}\right)}^{1/n}-{\left(1+\frac{E_{\left[A\right]=0}}{E_{\left[A\right]\to \infty }}\right)}^{1/n}}\\ \frac{\epsilon }{K_a}={\left[A\right]}_{50}^{-1}\frac{\left(\epsilon {\left(1+\frac{E_{\left[A\right]=0}}{E_{\left[A\right]\to \infty }}\right)}^{1/n}-{\left(1+\frac{{\epsilon }^n{E}_{\left[A\right]=0}}{E_{\left[A\right]\to \infty }}\right)}^{1/n}\right)}{{\left(1+\frac{{\epsilon }^n{E}_{\left[A\right]=0}}{E_{\left[A\right]\to \infty }}\right)}^{1/n}-{\left(1+\frac{E_{\left[A\right]=0}}{E_{\left[A\right]\to \infty }}\right)}^{1/n}}.\end{array}$$

Thus, it is not possible to factorize these expressions in a way that allows ε/K _a to be determined from the parameters of a curve fit without prior knowledge of one of the individual parameters. There is therefore no alternative but to determine them independently.

Hall, D. A. , and Giraldo, J. (2018) A method for the quantification of biased signalling at constitutively active receptors. British Journal of Pharmacology, 175: 2046–2062. doi: 10.1111/bph.14190.