Development of CHARMM-compatible force-field parameters for cobalamin and related cofactors from quantum mechanical calculations

Abstract

Corrinoid cofactors such as cobalamin are used by many enzymes and are essential for most living organisms. Therefore, there is broad interest in investigating cobalamin-protein interactions with molecular dynamics simulations. Previously developed parameters for cobalamins are based mainly on crystal structure data. Here, we report CHARMM-compatible force field parameters for several corrinoids developed from quantum mechanical calculations. We provide parameters for corrinoids in three oxidation states, Co³⁺, Co²⁺ and Co¹⁺, and with various axial ligands. Lennard-Jones parameters for the cobalt center in the Co(II) and Co(I) states were optimized using a helium atom probe, and partial atomic charges were obtained with a combination of natural population analysis (NPA) and restrained electrostatic potential (RESP) fitting approaches. The Force Field Toolkit was used to optimize all bonded terms. The resulting parameters, determined solely from calculations of cobalamin alone or in water, were then validated by assessing their agreement with DFT geometries and by analyzing molecular dynamics simulation trajectories of several corrinoid proteins for which X-ray crystal structures are available. In each case, we obtained excellent agreement with the reference data. In comparison to previous CHARMM-compatible parameters for cobalamin we observe a better agreement for the fold angle and lower RMSD in the cobalamin binding site. The approach described here is readily adaptable for developing CHARMM-compatible force-field parameters of other corrinoids or large biomolecules.

Graphical abstract

Introduction

Cobalamin, often called vitamin B₁₂, is a biological cofactor that is used by numerous enzymes to catalyze essential reactions in living organisms. Methylcobalamin (MeCbl), 5′-deoxyadenosylcobalamin (AdoCbl) and related corrinoids are used to perform diverse biochemical reactions including methyl transfer, isomerization and dehalogenation.^1,2 Among the most complex biological cofactors known, corrinoids consist of a tetrapyrrolic corrin ring with a central cobalt (Co) cation that can adopt the +1, +2 or +3 oxidation state (Scheme 1A). The corrin ring bears multiple methyl, acetamide and propionamide substituents, with one of the propionamide groups being fused through a propanolamine linkage to a long ribonucleotide tail. Microorganisms incorporate a wide range of compounds at the tail position, including substituted benzimidazoles, purines and phenolics,^3,4 but the most common tail substituent is the nucleotide 5,6-dimethylbenzimidazole (DMB) that is present in cobalamin. Besides the four equatorial N ligands from the corrin ring, Co can also bind up to two additional axial ligands, one each in the α and β positions (see Scheme 1A for the complete structure of cobalamin and Scheme 1B for PDB atom numbering).^1,5–7 The nucleotide tail can serve as an intramolecular ligand at the α position, whereas methyl or adenosyl groups coordinate at the β position to form unique organometallic Co–C bonds. The upper (β)-axial site can also be occupied by hydroxy (HO-), glutathionyl (GS-) or cyano (NC-) ligands.

Scheme 1.

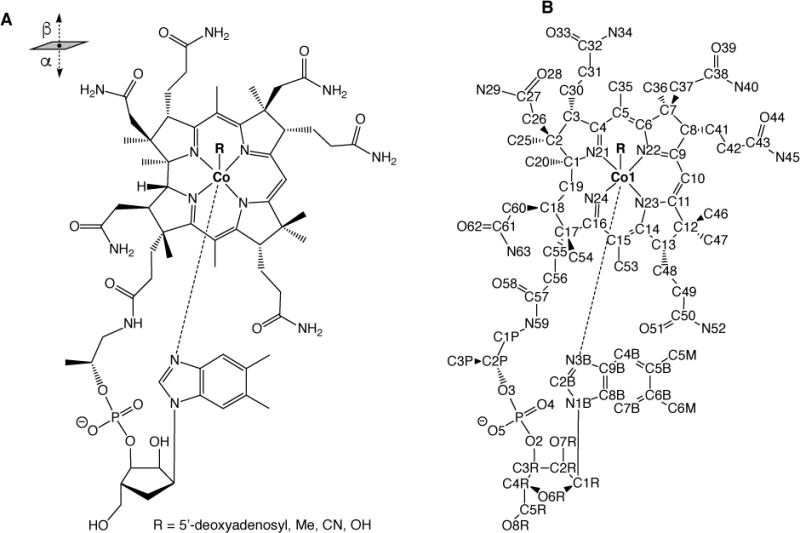
(A) Chemical structure of cobalamin. (B) Standard PDB atom numbering for cobalamin.

Three main cofactor configurations with respect to the α position have been observed in corrinoid proteins. When the nucleotide tail is an intramolecular ligand to Co at the α position, the cofactor is said to be in a “base-on” configuration (or “DMB-on” when the nucleotide is DMB). In some corrinoid proteins, such as the corrinoid iron-sulfur protein (CFeSP) from the Wood-Ljungdahl pathway of acetogenic bacteria, DMB is dissociated from Co and no ligand is present at the α position.^8,9 In this case, the cofactor is said to bind to the protein in a “DMB-off” configuration. In other DMB-off corrinoids, a His residue from the protein serves as the α ligand to Co. This arrangement is referred to as “Hison” coordination and is exemplified by the cobalamin-dependent methionine synthase, MetH.^10,11 Recently, the corrinoid protein HgcA was predicted to bind its corrinoid cofactor in an unprecedented “base-off, Cys-on” configuration.¹²

The oxidation state of Co affects the metal coordination shell, with Co(III) complexes typically being hexacoordinate, Co(II) pentacoordinate and Co(I) tetracoordinate.^1,5 The Co–C bond in MeCbl and AdoCbl can be homolytically cleaved, resulting in a square-pyramidal Co(II) species, although square-planar Co(II) structures have also been reported.^9,13,14 Under strongly reducing conditions, Co(II) can be further reduced to Co(I), leading to the dissociation of the α ligand and a square-planar complex.

Because of their biological importance, numerous studies have been carried out to characterize the structure and function of corrinoids,^1,5,6,15 and several structures of B₁₂-dependent enzymes and cobalamin-binding proteins have been reported.^{10,13,14,16–20} The three major classes of B₁₂-dependent enzymes are the AdoCbl-dependent eliminases and mutases, and the MeCbl-dependent methyltransferases, although corrinoids are also used by enzymes for many other reactions.^5,6,11,15 Recently, X-ray structures of two reductive halogenases have been determined. RdhA from Nitratireductor pacificus uses cobalamin to catalyze the reduction of halogenated phenolic compounds,²¹ while PceA from Sulfurospirillum multivorans uses the corrinoid norpseudo-B12, which has an adenine tail instead of DMB and lacks one of the methyl groups that are present in cobalamin, to catalyzes the reduction of tetrachloroethene and trichloroethene.²² The photoreceptor CarH from Thermus thermophilus uses base-off/His-on AdoCbl to sense light.¹⁰ It has been shown that changes in the oxidation state of Co can induce structural changes in the protein to which it is bound.^13,14,18 However, it is not clear how these changes occur. Detailed knowledge of cobalamin-protein interactions, and how such interactions change under different Co oxidation states, is crucial for a better understanding of cobalamin-dependent enzymes.

Atomistic molecular dynamics (MD) simulations are frequently performed to obtain insight into protein-small-molecule interactions. However, accurate force-field parameters for both the protein and the small molecule are required for reliable results. Current additive force fields, e.g., AMBER²³ and CHARMM,²⁴ are highly accurate for reproducing protein and nucleic acid structures²⁵ and several general force fields such as CGenFF,²⁶ GAFF²⁷ and OPLS²⁸ can be used to describe ligands of interest. Unfortunately, some chemical groups, including metal cations, are typically not covered by general force fields. Thus, parameters must developed from quantum mechanical (QM) calculations, experimental data, or both. For example, parameters for heme,^29,30 photosystem II iron complexes,³¹ chlorophyll ligands,³² several small transition-metal complexes³³ and Zn-containing cofactors (Zinc AMBER Force Field, ZAFF)^34,35 have been developed from QM calculations. Recent software releases can facilitate fitting of force-field parameters from QM data. For example, visual force field derivation toolkit (VFFDT)³⁶ can be used to optimize bond and angle parameters for metal-containing systems, and the Force Field Toolkit (ffTK) plugin in VMD,³⁷ developed in our group, can be used to generate CHARMM-compatible parameters. Automatic optimization of vdW parameters is not presently available in any of the software packages. Instead, these parameters for the metal atom are typically taken from other work^{29,30,32,34,35} or optimized from QM calculations.³³

Several approaches are commonly used to describe ligand coordination to metal cations in atomistic force fields: the bonded model, non-bonded model, cationic dummy atom model and ligand field molecular mechanics (LFMM) model.^38–42 In the bonded model, explicit bond and angle terms are used to describe the interactions between the metal atom and the coordinated ligands. In the non-bonded model, these interactions are described using only Lennard-Jones (LJ) potential and electrostatic terms.³⁸ The cationic dummy model uses fractional charges around the metal center to mimic its valence electrons.⁴² Although the non-bonded model reduces the number of bonded parameters that need to be determined and allows association and dissociation of ligands from the metal center, in practice, the metal often loses its coordination shell during simulations.^41,43 The cationic dummy model improves the stability of metal-ligand coordination compared to the non-bonded model. Non-bonded and cationic dummy models assume that LJ parameters and partial charges do not change significantly during ligand dissociation,^38,41 making them less suited for cases with changing metal oxidation states. Bonded models result in stable metal-ligand complexes, but ligand dissociation cannot be studied with such models.⁴¹ The Ligand Field Molecular Mechanics (LFMM) model adds additional terms to the MM potential between the coordinating ligands and the metal atom that describe the ligand field stabilization energy. This model can be used to simulate ligand dissociation; however, it requires parametrization of the ligand field stabilization energy.⁴⁴ Since the general interest is in studying specific redox states of cobalamin with MD, the bonded model was the most suitable choice for the force-field parameters.

One of the challenges with optimizing force field parameters is that the resulting optimization problem is typically neither consistent nor determined.⁴⁵ Due to inconsistency it is not possible to obtain an exact fit to all of the target experimental and QM data in most cases. For example, fitting of the harmonic terms for bonds and angles (see Eq. 1 in Methods) aims to determine the equilibrium values and the force constants for each bond and angle in the molecule. Yet the MM equilibrium value and distortion energy for each bond or angle will depend not only on its parameters but also on the bonded parameters for adjacent atoms and the non-bonded interactions with other atoms in the molecule. Due to this interdependence it is not possible to exactly reproduce the target equilibrium values and distortion energies of all bonds and angles in the molecule simultaneously. Additionally, the arising optimization problem is often underdetermined with several solutions giving similar agreement with the target data. Because of the issues discussed above additional validation of the force field parameters is desired. Properties that are not used for fitting of the parameters should be used for validation.

Bonded force-field models of Co(III)-cobalamins for the MM2^46,47 and AMBER⁴⁸ force fields have been previously developed by Marques and coworkers. Crystal structures of isolated cobalamins were used to determine the parameters, and these structures were reproduced with high accuracy. Gumbart et al. adapted the AMBER parameters for cyanocobalamin for CHARMM by changing the partial atomic charges to the calculated natural population analysis (NPA) charges.⁴⁹ These parameter sets have been used in simulations of Co(III)-cobalamin in water^50,51 and bound to the protein BtuB.⁴⁹ Al though crystal structures are important for fitting and validating force-field parameters, comparisons to electronic structure calculations are presently lacking for cobalamins. Therefore, we applied the latest tools and procedures to develop CHARMM-compatible force-field parameters for cobalamin based on QM calculations. We used ffTK to construct bonded models of several important forms of cobalamin, including the octahedral adenosyl-, cyano- and methylcob(III)alamin, square-pyramidal cob(II)alamin and square-planar cob(I)alamin. Although previous work only considered cobalamins in the Co³⁺ state, we have re-optimized several parameters for cob(II)alamin and cob(I)alamin to correctly capture the electrostatic and geometric changes caused by the decreased oxidation state of Co. The parameters were carefully validated by showing that they reproduce both DFT and crystal structure geometries. Comparison to simulations with previous CHARMM-compatible cobalamin parameters shows that our parameters increase the conservation of crystal-structure interactions and give better agreement with the cobalamin fold angle in those structures. The approaches described here and in our previous work⁵² can be used to develop CHARMM-compatible force-field parameters for nonstandard corrinoids and other large biomolecules.

Methods

Development of force-field parameters

In the CHARMM force field, the potential energy function consists of bonded (Eq. 1) and non-bonded terms (Eq. 2). The input of the following force-field parameters is required: the force constants K; the equilibrium values of the bonded terms, b₀, θ_o, and φ_o; dihedral phase δ; partial atomic charges q; and LJ parameters ε and σ.²⁴

$$V_{\text{bonded}}={{\displaystyle \sum _{\text{bond}s}{K}_b\left(b-b_o\right)}}^2+{\displaystyle \sum _{\text{angles}}{K}_{\theta }{\left(\theta -{\theta }_o\right)}^2+{\displaystyle \sum _{\text{dihedrals}}{\displaystyle \sum _{n=1}^{n=6}{K}_{\varphi ,\mathrm{n}}}}}\left(1+\cos \left(n\varphi -\delta \right)\right)+{\displaystyle \sum _{\text{impropers}}{K}_{\phi }{\left(\phi -{\phi }_o\right)}^2}$$ (1)

$$V_{\text{nonbonded}}={\displaystyle \sum _{\text{pairs}\text{ij},\text{charges}}\frac{q_i{q}_j}{4\pi {\epsilon }_0{r}_{ij}}}+{\displaystyle \sum _{\text{pairs}\text{ij},\text{Lennard}-\text{Jones}}{\epsilon }_{ij}}\left[{\left(\frac{r_{min,\text{ij}}}{r_{ij}}\right)}^{12}-2{\left(\frac{r_{min,\text{ij}}}{r_{ij}}\right)}^6\right]$$ (2)

Because parameters for several parts of the cobalamin molecule are already present in the CGenFF force field,²⁶ such as the amide and methyl side chains, the nucleotide loop, and the adenosyl axial ligand, parameters were not optimized for these groups. Instead, the corresponding CGenFF charges and atom types were used for these atoms, with the exception of the phosphate group and the ribose sugar of the nucleotide loop, for which CHARMM36 nucleic acid parameters⁵³ were used instead. QM calculations were used to determine the LJ and partial charge parameters for Co, the corrin ring and the Co-bound equatorial and axial ligands, as well as the bond, angle and dihedral terms arising from the side chains on the corrin ring. All LJ parameters were taken by analogy except for Co(II) and Co(I), which were optimized here (see the Supporting Information for the assignment of LJ parameters by analogy). Intially, all improper dihedral parameters for the corrin ring were taken from the previously developed heme parameters for the CHARMM force field.²⁹ The force constants for the impropers were gradually increased to better reproduce experimental corrin fold angles (see Validation and Supporting Information).

To determine the force field parameters for cobalamin, which contains nearly 200 atoms, we adopted a fragment-based approach in which we used representative models for the QM calculations. These models include the unsubstituted corrin ring, Co, and various axial ligands. DMB was replaced with imidazole, and the adenine base was removed from the Ado ligand (Scheme 2A). The smaller models were used to determine the partial atomic charges and the bonded terms for the corrin ring and the axial ligands. Five smaller models were used, one for each state and each β ligand: MeCbl(III), AdoCbl(III), CN-Cbl(III), Cbl(II) and Cbl(I). Additionally, we used two slightly larger model systems, referred to as ExtAD and ExtBC, to determine the bonded parameters resulting from the attachment of the amide side chains and the methyl groups to the smaller model (Scheme 2A). New atom types were introduced for the heavy atoms of the corrin ring, Co, and the carbon in the Co–C bond (see the topology file in the Supporting Information). We aimed to keep the number of new atom types to a minimum, while still correctly reproducing the asymmetry of the corrin ring, which required nine different atom types for the heavy atoms.

Scheme 2.

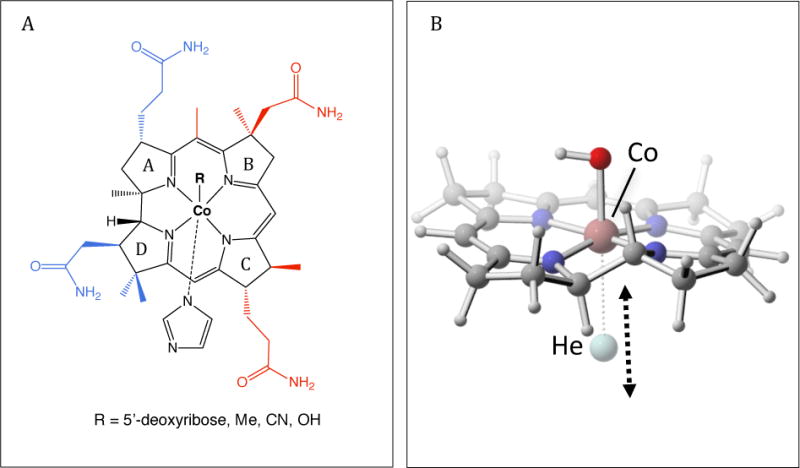
(A) Models used to develop parameters for cobalamin. The smaller models of cobalamin used for fitting most of the force-field parameters are shown in black. Side chains that were added to this model to create the structures ExtAD and ExtBC are shown in blue and red, respectively. (B) Displacement vector of the He probe used to fit the LJ parameters for Co(I) and Co(II).

Quantum mechanical calculations

Single-reference correlated wave function methods such as MP2 are known to perform poorly for describing transition metal-containing systems.⁵⁴ Multireference methods are often highly accurate, but are computationally extremely costly for large systems. Fortunately, density functional theory provides a good balance between accuracy and computational efficiency for these systems. The BP86^55–57 density functional has been shown to reproduce the experimentally observed geometries and various properties of corrinoids accurately.^58–62 Thus, we used the BP86 density functional along with the Def2-SVP basis set^63,64 to optimize the geometries of the model complexes. Recently, however, it was shown that PBE energies (computed at BP86 geometries) provide superior accuracy compared to BP86 and other density functionals for computing reduction potentials, pK_as and Co-ligand binding free energies for aquacobalamin.⁶⁵ Here, we followed a similar approach in which we computed interaction energies with the PBE density functional.

Default convergence criteria were used for the geometry optimizations, and no constraints or restraints were applied during any of the geometry optimizations. All DFT calculations were performed with Gaussian 09.⁶⁶ With the exception of the small AdoCbl(III) model, no imaginary frequencies were found for the optimized geometries. In the AdoCbl(III) model, a single imaginary frequency of −18 cm⁻¹ was found, but it involved several angles of the deoxyribose ring that were not parameterized.

Lennard-Jones parameters

To determine the LJ parameters for Co in the Cbl(I) and Cbl(II) cobalamins, we used the He atom probe approach developed by MacKerell and coworkers.^67,68 Simplified, corrin-based models were used for these calculations. In each case, the total charge of the system was zero. First, the geometry of each complex was optimized without the He probe at the BP86-D3/Def2-SVP level of theory. For the Cbl(II) model, HO-Co(II)-corrin, a He atom was then placed along the Co–O axis on the corrin face opposite the hydroxy group (i.e., He ⋯ Co–O angle = 180). For the Cbl(I) model, Co(I)-corrin, the He atom was placed along a vector normal to the plane defined by atoms in the corrin ring corresponding to C6, N22, C9, C10, C11, N23 and C14 in cobalamin (Scheme 1B). In each case, the He ⋯ Co distance was varied in increments of 0.1 Å and single-point energies were computed with three density functionals: BP86,^55–57 PBE⁶⁹ and B3LYP,^70,71 and three basis sets: Def2-SVP, Def2-TZVP, and Def2-TZVPP.^63,64 D3 dispersion corrections⁷² with Becke-Johnson damping⁷³ were included in all cases. The resolution-of-the-identity (RI) approximation with the corresponding Coulomb density fitting basis sets.⁵⁴ was used to accelerate the evaluation of two-electron integrals. The corresponding non-bonded molecular mechanical (MM) interaction energies were calculated with the NAMDenergy plugin in VMD.⁷⁴

Partial atomic charges

We considered various approaches for determining partial atomic charges. We examined the possibility to fit the charges based on either QM interactions with water molecules²⁶ or the restricted electrostatic potential (RESP method),⁷⁵ which are the standard approaches for the CHARMM and AMBER force fields, respectively.^23,24 Additionally, we looked into assigning charges based on either Mulliken⁷⁶ or natural population analysis (NPA).⁷⁷ Ultimately, we decided to use a combination of NPA and RESP for the assignment of partial charges (see Results). RESP could not be used on all atoms because it is often problematic for buried atoms.^75,78–81 For example, when we used only RESP for the MeCbl(III) model, a physically unrealistic negative partial charge was obtained for Co.

NPA was used to determine the charges for the Co, N21-N24 and N3B atoms. Standard CHARMM charges of +0.09 and +0.015 were used for aliphatic and aromatic hydrogens, respectively, for consistency and compatibility with the CHARMM force field. For the rest of the atoms in the corrin ring, the charges were determined with the RESP approach using AmberTools 14⁸² with the Co and N charges constrained to their NPA values. Twofold symmetry was imposed on the charges along the axis defined by Co and C10 (see Scheme 1B for atom numbering) in all RESP calculations because these two parts of the molecule are nearly identical. For the NPA charges, the average charge of N21 and N24 or N22 and N23 were used to maintain symmetry. When we added the side chains to the small corrin model or the adenosyl group to the MeCbl(III) model, the charges of the hydrogens that had been removed were absorbed into the adjacent carbons, ensuring an integer charge of the new molecule.

Bonded parameters

ffTK was used to optimize all bond, angle and dihedral parameters. QM geometries were used to determine the target bond and angle equilibrium values, and the Hessian in internal coordinates was used to optimize the bond and angle force constants. The Hessian is the matrix of secondary derivatives of the potential energy as a function of the input atom-pair coordinates, and it was used to construct the QM potential energy surface (PES) arising from the displacement of each internal coordinate. The optimized MM geometry and the molecular mechanics (MM) PES were obtained for trial parameters and compared to the corresponding QM ones. The objective function described by Mayne et al.³⁷ was used to measure the quality of the fit of the MM equilibrium bond and angle values and energy changes due to geometric displacements. The fitting procedure consisted of using either the simplex or simulating annealing method, implemented in ffTK, to minimize the objective function. Several refinement runs of this procedure were performed until the objective function stopped decreasing with additional iterations.

Relaxed dihedral scans were used to determine the target QM PES for fitting the dihedral constants. Corrin ring dihedrals were scanned 60° in each direction in 10° increments. The dihedral scan around the Co–N3B bond, which describes the rotation of the imidazole with respect to the corrin ring, was scanned 180° in each direction in 15° increments. All other dihedrals were scanned 90° in each direction in 15° increments. The optimization of the dihedral force constants was done with the simulated annealing protocol developed by Guvench and MacKerell⁸³ and implemented in ffTK.³⁷ The fitting of dihedral terms is often highly undetermined, and several sets of dihedral parameters may fit the same PES.^45,52 Additionally, the optimization problem is ill-conditioned and the algorithm can produce unrealistically high force constants when it attempts to fit a small peak in the PES.⁴⁵ These issues can lead to overfitting and unrealistic high-energy geometries, e.g., nonplanar aromatic structures or eclipsed hydrogen conformations in the methyl groups during MD simulations.⁵² Thus, to avoid overfitting we sought to reduce both the number of fitted dihedrals and the multiplicity of each dihedral. The bonded model of cobalamin results in numerous dihedral terms arising from the creation of five Co–N bonds, which increases the likelihood of overfitting. Hence, the force constants were set to zero for most of these dihedrals (see the Results section for details), and higher multiplicities were only used for a dihedral if they significantly improved the fit to the QM PES. Additionally, dihedrals containing hydrogen atoms were not optimized during the dihedral scans. Instead, they were either set to zero or taken from the CGenFF force field if a good analogue was found. Only QM geometries less than 10 kcal mol⁻¹ above the energy minimum were used for the QM and MM energy comparison.

Molecular dynamics simulations

All MD simulations were performed with NAMD 2.9.⁸⁴ In addition to our optimized cobalamin parameters, we used the CHARMM36 protein,⁸⁵ nucleic acid⁵³ and lipid⁸⁶ force fields and the CHARMM TIP3P model for water.⁸⁷ The temperature and pressure were controlled with the Langevin thermostat and piston, respectively. The target temperature was 310 K and the target pressure was 1 bar. The Langevin piston period was 200 fs and the piston decay was 100 fs. To allow integration of the equations of motion with a 2-fs time step, we used rigid bonds for all covalently bound hydrogens. A 12-Å cutoff was used for the van der Waals interactions and a switching function was applied from 10 to 12 Å to ensure a smooth decay to zero. The particle-mesh Ewald method⁸⁸ was used to calculate long-range electrostatic interactions. We validated our parameters for cobalamin-protein and cobalamin-RNA interactions starting with the corresponding crystal structures, 1N4A, 3GAI, 5C8A, 4GMA and 1NQH. The first four structures were solvated in bulk water, while the 1NQH BtuB structure was embedded in DMPE membrane using CHARMM-GUI.⁸⁹ The Solvate and Autoionize plugins in VMD were used to add bulk water and ions to the systems, respectively. The systems for 1N4A, 3GAI, 5C8A, and 4GMA were ionized with NaCl, while the system for 1NQH was ionized with CaCl₂; a salt concentration of 0.15 M was used in all cases. For all systems, the energy was minimized before the MD simulations, and a two-step equilibration was applied. First, water and ions were equilibrated for 500 ps, after which cobalamin and the protein side chains were equilibrated for an additional 1.5 ns. Additional equilibration steps were added for the membrane system. After equilibrating water and ions, lipid tails and then the whole membrane were equilibrated for 1.5 ns each before proceeding with the equilibration of the protein side chains. All production runs were 10 ns long. Because the positions of multiple adjacent residues were missing in the 4GMA structure, we did not include these residues in the simulations. Instead, we included only those residues that were present in the PDB structure and applied harmonic restraints with a force constant of 10 kcal mol⁻¹ Å⁻² to those residues farther than 15 Å from cobalamin in the crystal structure.

To calculate the corrin fold angle, we first fit two planes to groups of atoms C4 C5 C6 C9 C10 N21 N22 and C10 C11 C14 C15 C16 N23 N24, respectively (Scheme 1B).² To fit the plane, the covariance matrix of each set of atoms with respect to their centroid is first calculated; the normal vector of the fit plane is then the cross product of the first two (largest) eigenvectors of this matrix. Finally, the fold angle is calculated between the two fit planes’ normal vectors.

Results

Lennard-Jones (LJ) parameters

The LJ parameters for Cbl(II) and Cbl(I) were determined using the He probe approach developed by MacKerell and coworkers.^67,68 The non-bonded interactions between He and the cobalamin models were calculated for a range of Co-He distances, using three different DFT functionals: PBE, BP86 and B3LYP. For the small cobalamin models (Scheme 2A) we used a β-hydroxy ligand for the Co²⁺ state and no axial ligands for the Co¹⁺ state. The He probe approach was not used for the hexacoordinated Cbl(III) models because all Co coordination sites are occupied. Hexacoordination of Co greatly limits intermolecular interactions of Co, and the optimization of bonded parameters was expected to correct for any potential intramolecular interaction errors. Therefore, the LJ parameters for all Cbl(III) models were set to zero.

Basis set convergence for the QM interaction energies between a He atom and the cobalamin models Cbl(I) and HO-Cbl(II) was tested in the Supporting Information for the three considered DFT functionals. Figure S1 shows that the energy differences between Def2-TZVP and Def2-TZVPP basis sets are very small for all cases. Figures 1A and 1D display QM interaction energies between a He atom and the two cobalamin models calculated with the three DFT functionals using Def2-TZVPP basis set and D3 correction. We also calculated the corresponding non-bonded molecular mechanical (MM) interaction energies for both cobalamin models with the ε value for Co set to zero (MM Start). The difference between the QM and MM interaction (En_Diff) with this potential was used to determine the LJ parameters. Because it is usually not possible to reproduce the QM PES with the functional form of the LJ potential over all distance ranges,^67,68 we aimed to reproduce the minimum QM interaction energy and distance for the Co–He interaction by adjusting ε and r_min from Eq. 2. The differences between QM energies at different levels of theory and MM Start energies are plotted in Figures 1B and 1E. Improving the agreement between the QM and MM energies requires fitting an LJ potential to these differences. The shape of the LJ potential is determined by ε, which governs the well depth, and r_min, which governs the location of the minimum. All atoms have attractive vdW interactions, so the LJ potential should always have a minimum below zero. As shown in Figures 1B and 1E, the difference in the energy curves between QM and MM Start has a minimum below zero for both Cobl(I) and Cbl(II) states for only the PBE functional. Thus, this level of theory was selected to determine the LJ parameters for Co.

Figure 1.

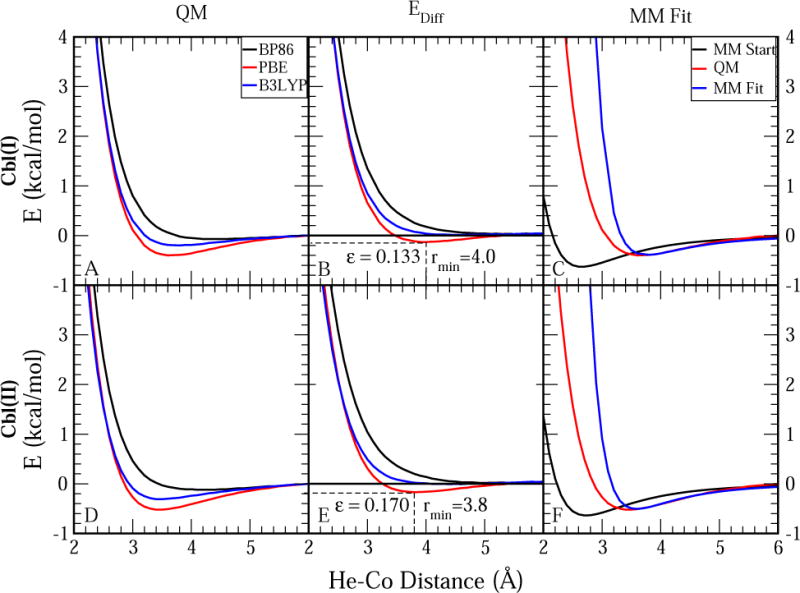
Fitting of LJ parameters for Cbl(II) and Cbl(I) from QM calculations. D3 correction and Def2-TZVPP basis set were used for all QM calculations. See Figures S1 in Supporting Information for QM data at different basis sets. (A) Non-bonded interaction energies between He and Co(I)-cobalamin as a function of the He ⋯ Co distance for three different density functionals. (B) Difference between QM energies from (A) and the corresponding MM energies when the Co LJ potential is set to zero (En_Diff) The colors correspond to the same QM level of theory as in (A). The E = 0 line is shown to illustrate that only the red line (PBE) has a minimum below zero for both Cbl(II) and Cbl(I). (C) Comparison of non-bonded interaction energies between Cbl(I)-cobalamin and helium at BPE level of theory and using MM with (MM Fit) and without (MM Start) LJ potential for the Co atom. (D) Non-bonded interaction energies between He and HO-cob(II)alamin as a function of the He ⋯ Co distance at different levels of theory. (E) Difference between the QM energies from (D) and the corresponding MM energies with the LJ potential for Co set equal to zero. The colors correspond to the same level of theory as in (D). (F) Comparison of non-bonded interaction energies between He and HO-cob(II)alamin calculated at PBE level of theory (QM) and using MM with (MM Fit) and without (MM Start) the LJ potential for Co.

We chose the ε and r_min for the He ⋯ Co LJ potential based on the minimum energy and distance for the calculated En_Diff potential. The Co-specific ε and r_min parameters were then derived from the Lorentz-Berthelot combination rules used in the CHARMM force field²⁴

$${\epsilon }_{\text{Co}}=\frac{{\epsilon }_{\text{He}-\text{Co}}^2}{{\epsilon }_{\text{He}}}\text{and}\frac{r_{min,\text{Co}}}{2}=r_{min,\text{He}-\text{Co}}-\frac{r_{min,\text{He}}}{2}.$$ (3)

Table 1 compares the minimum interaction energies and distances from QM calculations to the corresponding MM values before and after the fit, and shows the final LJ parameters for Co. AMBER-compatible LJ parameters of similar magnitude were previously reported for other Co²⁺-containing complexes.³³ Figures 1C and 1F compare the QM and MM energies at all computed ranges and show that MM Start potential energies were too favorable and the energy minimum distances were too short compared to the corresponding QM energies and distances. The addition of LJ parameters to the Co atom in MM Fit significantly improved the agreement between QM and MM energies, although the new MM potential energies became somewhat too repulsive at distances lower than the QM minimum.

Table 1.

Comparison of the minimum interaction energies and distances for our helium-cobalamin models at the QM and MM levels before and after the fit. The resulting ε and r_min parameters for Co are also shown. The LJ parameters are provided in the standard CHARMM parameter file format as −ε_Co and r_{min, Co}/2.

State	Minimum (kcal mol−1)			Distance (Å)			−εCo (kcal mol−1)	rmin;Co/2 (Å)
	QM	MMinit	MMFit	QM	MMinit	MMFit
Cbl(I)	−0.399	−0.628	−0.390	3.7	2.7	3.8	−0.832	2.52
Cbl(II)	−0.523	−0.637	−0.506	3.5	2.7	3.6	−1.325	2.32

Partial Atomic Charges

Several approaches for determining partial atomic charges were considered. Although optimization of partial atomic charges based on reproducing QM interaction energies with water molecules is recommended for CHARMM-compatible parameters,²⁶ such an approach was not possible for the octahedral cobalamin complex because steric clashes prevent the water molecules from interacting with Co and the nitrogens N21-N24. An alternative approach for determining partial atomic charges is the RESP method, which is used in the AMBER force field and is based on fitting atom-centered charges to the QM electrostatic potential.^23,75 However, this method often struggles with determining accurate charges of buried atoms,^75,78,79,81 such as Co and N21-N24 in cobalamin. We initially used the RESP method to fit all the charges for the MeCbl(III) model (Table S2), but we obtained unrealistic charges for several atoms. Specifically, Co was assigned a negative charge and N21-N24 were assigned positive charges. Although we obtained the expected signs for the charges of these atoms in the Cbl(II) model (positive for Co and negative for the nitrogens), the magnitude of these charges was closer to zero than expected. We concluded that the presence on the axial ligands made the charges of the Co atom and N21-N24 highly underdetermined in the RESP approach.

Mulliken population analysis has also been used to obtain partial atomic charges.⁷⁶ Although Mulliken charges are easily determined even for buried atoms, they are highly sensitive to the chosen basis set.⁷⁶ For example, the Mulliken charges for Co in the MeCbl(III) model calculated at the BP86 level of theory with the Def2-SVP and 6-31G(d) basis sets are 0.22 and 0.87, respectively. Natural population analysis (NPA), which is based on the electron density distribution obtained by transforming molecular orbitals into localized, one-center natural atomic orbitals,⁹⁰ yields more consistent atomic charges with regard to the basis set than Mulliken population analysis.^77,91 The natural atomic charge for atom A in a molecule, Q_A, is obtained by subtracting the sum of the natural populations for that atom, $p_k^{\left(A\right)}$, from its nuclear charge, Z_A, i.e. $Q_A=Z_A-{\displaystyle {\sum }_k{p}_k^{\left(A\right)}}$.

In the present work, we decided to use NPA in combination with the RESP method to determine the partial charges. First, we restrained only the charge of Co to its NPA charge and used RESP for all other heavy atoms, including N21-N24. The resulting charges had the correct sign for Co and N21-N24 (Table S3), but the magnitude of the charges for the nitrogens differed significantly in response to changes in the Co oxidation state. These large differences were not observed for the NPA charges, which suggests that the nitrogens were buried too deeply in the Cbl(II) and Cbl(III) models for a reliable RESP treatment of their charges. Therefore, in all the cobalamin models we used NPA for Co and the nitrogens N21-N24 and N3B; RESP was used for all other heavy atoms in the corrin ring.

The charges were re-optimized for all heavy atoms for Cbl(II) and Cbl(I) models. For the CN-Cbl(III) model we started with the MeCbl(III) charges and re-optimized only the charges on Co, the cyano group and the nitrogens N21-N24 and N3B. Because the NPA charges for Co and N21-N24 in the AdoCbl(III) model were nearly identical to those in the MeCbl(III) model (Table S4), we concluded that no re-optimization of charges was necessary for the analogous atoms in the AdoCbl(III) model. The final charges for Co and the Co-bound nitrogens for all cobalamin models are displayed in Table 2.

Table 2.

Partial atomic charges for Co, the Co-bound nitrogens N21-N34, and N3B for five cobalamin complexes. Partial charges for all atoms are provided in the Supporting Information.

	B12 State
Atom	Me- and AdoCbl(III)	CN-Cbl(III)	Cbl(II)	Cbl(I)
System Charge	+1	+1	+1	0
Co	0.382	0.234	0.613	0.424
N21,N24	−0.403	−0.387	−0.463	−0.479
N23,N22	−0.444	−0.435	−0.496	−0.504
N3B	−0.492	−0.386	−0.509	NA

Bond and angle parameters

Bond and angle parameters were fitted simultaneously as described in the Methods section. To reduce the number of fitted parameters, we initially attempted to impose the same molecular symmetry for the bonds and angles as for the partial atomic charges (see Methods). We refer to this fitting approach as Fit 1. However, Fit 1 did not correctly reproduce the geometric asymmetry of the QM model of MeCbl(III) (Figure S2A). Therefore, we introduced four different atom types (instead of two) for the four corrin ring nitrogens (N21-N24), allowing for differences in bonds and angles parameters between N21 and N24, as well as N22 and N23 (Fit 2). Fit 2 resulted in better agreement with QM geometries (Figure S2A). All target QM bond and angle values were reproduced to within 0.04 Å and 5°, respectively, which is close to the recommended maximum deviations of 0.02 Å and 3° for the CGenFF force field.²⁶

The MeCbl(III) model was used to fit the initial bond and angle parameters. Only the bonds and angles containing Co or N21-N24 were refit for the Cbl(II) and Cbl(I) models. The structural differences between the MeCbl(III) and Cbl(II) QM geometries are concentrated at these atoms (Figure S2B). Although the Cbl(I) model also shows structural differences compared with MeCbl(III) at the edges of the corrin ring (Figure S2B), these differences were addressed by refitting the relevant dihedrals. For the CN-Cbl(III) and AdoCbl(III) models only the parameters involving the two axial ligands and the Co-bound carbon were refitted, respectively. The parameters correctly reproduce the changes in bonds and angles for the three different Co oxidation states (Tables 3 and 4).

Table 3.

Comparison of selected bond lengths for minimized geometries of our MeCbl(III), Cbl(II), and Cbl(I) models. All bond lengths are in Å. NP means that the bond is not present in the model. See the parameter file in the Supporting Information for all optimized bond parameters and 1B for the atom numbering.

	B12 State
	MeCbl(III)		Cbl(II)		Cbl(I)
Bond	QM	MM	QM	MM	QM	MM
Co–N21	1.88	1.87	1.88	1.88	1.84	1.84
Co–N22	1.94	1.98	1.94	1.93	1.91	1.92
Co–N23	1.94	1.97	1.94	1.92	1.91	1.92
Co–N24	1.88	1.86	1.88	1.88	1.84	1.84
Co–N3B	2.17	2.16	2.13	2.12	NP	NP

Table 4.

Comparison of selected angles for minimized geometries of our MeCbl(III), Cbl(II), and Cbl(I) models. All angle values are in deg. NP means that the angle is not present in the model. See the parameter file in the Supporting Information for all optimized angle parameters and 1B for the atom numbering.

	B12 State
	MeCbl(III)		Cbl(II)		Cbl(I)
Angle	QM	MM	QM	MM	QM	MM
N22–Co–N21	91.1	90.7	91.1	90.7	91.3	91.3
N24–Co–N21	82.5	84.0	82.5	82.3	83.5	83.9
N23–Co–N22	95.2	93.9	94.7	95.7	94.5	94.0
N24–Co–N23	91.4	91.8	90.7	91.1	91.3	91.4
N21–Co–N3B	88.4	87.2	92.6	89.1	NP	NP
N22–Co–N3B	90.6	91.3	95.9	95.1	NP	NP
N23–Co–N3B	92.6	87.7	92.2	92.0	NP	NP
N24–Co–N3B	88.7	93.3	98.0	96.6	NP	NP

Selected bond and angle parameters for the different Co states are shown in Tables S5 and S6, respectively. The bond force constants are relatively weak for the bonds between the cobalt atom the corrin ring (ranging from 30 to 70 kcal mol⁻¹ Å⁻²), whereas the bond between Co and the imidazole N (i.e., Co–N3B) is significantly stronger (K_b = 225.8 and 122.7 kcal mol⁻¹ Å⁻² for Cbl(III) and Cbl(II) states, respectively). The force constant for the N23–Co–N3B angle is 222.4 kcal mol⁻¹ Å⁻², while the corresponding force constants for the other three corrin ring nitrogens (N21, N22 and N24) are significantly smaller, ranging from 90 to 98 kcal mol⁻¹ Å⁻² (Table S6). These differences in force constants for chemically similar atoms suggest that some overfitting was introduced due to the use of four atom types for the corrin nitrogens instead of two. Nevertheless, it would not be possible to reproduce the asymmetry of the QM geometry without the introduction of additional atom types. Both bond and angle constants tend to decrease with reduced Co oxidation state, in agreement with previous results by Šebesta et al. for other Co-containing complexes.³³

Dihedral parameters

As discussed in the Methods section, many dihedral terms of the corrin ring were set to zero to avoid overfitting. The following dihedrals were optimized from QM dihedral scans: rotation of the imidazole ligand along the Co–N3B bond and bending of this ligand relative to the plane of the corrin ring (imidazole dihedrals), the dihedrals of the five-membered rings containing N21 and N24 (ring dihedrals), the rotation of the Ado ligand along the Co– C bond (Ado dihedrals) and the dihedrals arising from the connection of the side chains to the corrin ring (connection dihedrals) (Figure S3A). Figures 2, S4 and S5 compare the QM and MM PESs for the dihedral scans and Table 5 shows the root mean-square error (RMSE) for the MM PES. Although the RMSE was relatively high in some cases (> 1 kcal mol⁻¹), the higher deviations from the QM PES were mainly for the high-energy configurations, whereas the low-energy configurations were reproduced to within ~0.5 kcal mol⁻¹, as recommended for the CGenFF force field.²⁶

Figure 2.

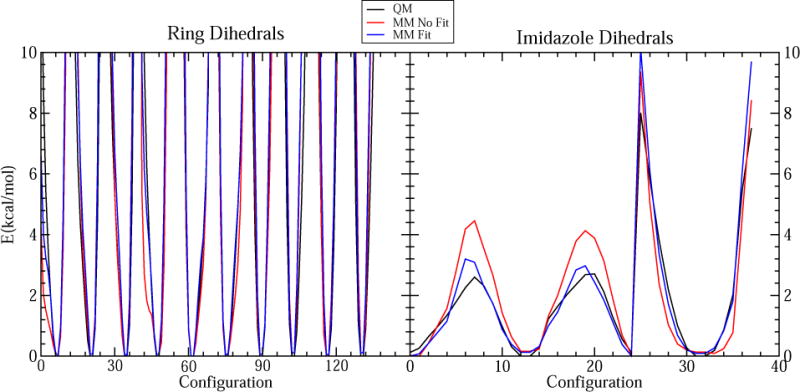
Comparison of the QM PES to the MM PES before (No Fit) and after (Fit) fitting the dihedral constants for ring and imidazole dihedrals.

Table 5.

RMSE of all dihedral constant optimizations performed in this work.

Dihedrals	RMSE (kcal mol−1)
Imidazole	0.56
Ring	2.2
Connection (Con1)	0.22
Connection (Con2)	0.82
Ado	0.40
Cbl(II) refit	1.8
Cbl(I) refit	1.2

There are eight dihedral terms that are centered on the Co–N3B bond. Initially, we fitted all of these dihedral terms, which resulted in a distortion of the planar imidazole ring during MM geometry optimization. Therefore, the number of terms fitted for imidazole dihedrals was reduced to avoid overfitting. We found that fitting only two dihedrals (i.e., N21–Co–N3B–C8B and N22–Co–N3B–C8) using multiplicities of n = 4 and 2, respectively, with the constants for the other six dihedrals set to zero, was sufficient to obtain the desired agreement between the QM and MM PES without distorting the imidazole ring (Figure 2).

To minimize overfitting, we initially did not fit the dihedrals of the corrin ring. However, MD simulations of the MeCbl(III) model in the gas phase showed significant fluctuations for some of these dihedrals, and comparison of the QM and MM PESs for these dihedrals revealed some discrepancies (Figures 2 and S6). Fitting of these dihedrals improved the agreement between the QM and MM PES (Figure 2) and reduced the fluctuations of these dihedrals during MD simulations (Figure S6). Agreement between QM- and MM-optimized geometries also increased. Ring, imidazole, and connection dihedrals were fit using the MeCbl(III) model and were only refitted for other models to improve the agreement with the QM geometries (see Supporting Information). Connection dihedrals were optimized using models ExtAD and ExtBC, and Ado dihedrals were fitted using the AdoCbl(III) model (Figures S4 and S5).

Validation

The overall agreement between optimized MM and QM geometries for the small cobalamin models described in the Methods section was evaluated. Also, the optimized parameters were carefully validated according to two metrics: comparison of corrin fold angles in MD simulations of free and bound cobalamins to the angles reported experimentally⁹² and the stability of bound cobalamins in their binding sites.

Comparison of minimized MM and QM geometries of the small cobalamin models showed that our force-field parameters reproduced the overall shape of the QM geometries very well (Figures 3 and S7). Almost no deviations were found for the Cbl(I) model, while the deviations were very small for the other four models and were not expected to affect the quality of the simulations. The RMSDs between the QM and MM geometries were less than 0.12 Å in all cases (Table 6).

Figure 3.

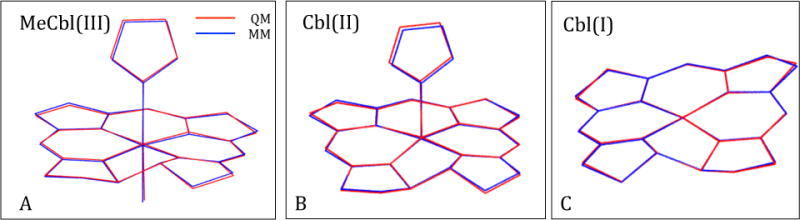
Comparison of QM (red) and MM (blue) geometries for the small (A) MeCbl(III), (B) Cbl(II) and (C) Cbl(I) models. Hydrogens are omitted for clarity. See Figure S5 for a comparison of the CN-Cbl(III) and AdoCbl(III) geometries, and Table 6 for the RMSD between the MM and QM geometries.

Table 6.

RMSD between QM and MM geometries of the five small cobalamin models.

Model	RMSD (Å)
MeCbl(III)	0.070
CN-Cbl(III)	0.117
AdoCbl(III)	0.117
Cbl(II)	0.076
CblI)	0.047

Crystal structures of four proteins and one RNA co-crystallized with cobalamin were selected to validate the force field parameters. These structures included the periplasmic cobalamin-binding protein BtuF from Escherichia coli with base-on CN-Cbl(III) (PDB entry 1N4A),¹⁷ a cobalamin-dependent riboswitch with base-on AdoCbl(III) (PDB entry 4GMA),¹⁹ an adenosyltransferase from Lactobacillus reuteri complexed with Cbl(II) and ATP (PDB entry 3GAI),¹⁴ the B₁₂-dependent photoreceptor CarH from Thermus thermophilus with base-off/His-on (PDB entry 5C8A)¹⁰ and the B₁₂ transporter protein in Escherichia coli BtuB (PDB entry 1NQH).⁹³ Two 10-ns simulations were performed for each crystal structure. Additionally, one 10-ns-long simulation of free, solvated cobalamin was done for each of the five considered states: MeCbl(III), CN-Cbl(III), AdoCbl(III), Cbl(II) and Cbl(I).

Averaged cobalamin fold angles were calculated for simulations of both bound and free cobalamins and compared to values from the initial crystal structures and experiments,⁹² respectively. The corrin fold angle was determined by dividing the conjugated part of the corrin ring in two along the Co-C10 line and calculating the angle between the two resulting planes (see Methods for details). As shown in Tables 7 and 8, the fold angles were too large compared to the target values during the initial MD simulations (MD_In); in several cases, the difference was larger than 10°. Hence, we decided to adjust our parameters to decrease the fold angles. It was found that increasing the force constants for all impropers that involved the nitrogens N21-N24 was an effective way to decrease the fold angle with minimal changes to the minimized MM geometries. Therefore, the force constants for these impropers were gradually increased to obtain the best agreement with target fold angles for free cobalamins (see Supporting Information for details). We used the simulations of cobalamins in water to fit the improper constants to target experimental data in Table 7. Next, the simulations of the crystal structures with the new improper parameters were used to validate the transferability of the parameters to a protein environment. After fitting the improper constants, the fold angles were significantly smaller in MD simulations (MD_Fit) and in better agreement with target values for both aqueous cobalamins and those in protein and RNA environments (see Tables 7 and 8). Some deviations of the fold angle were still observed for simulations of structures 1N4A, 1NQH and 5C8A. For all other cases the angle was within 3° of the experimental value. Adjustments of the improper constants resulted in very small changes to the overall MM geometries and MM bonds and angles. RMSD for the geometries before and after the changes was less than 0.02 Å, while the changes in bonds and angles were less than 0.01 Å and 3°, respectively. The MM-minimized geometries in Figures 3 and S7, as well as MM bonds and angles in Tables S5 and S6, are all after refitting the improper force constants.

Table 7.

Comparison of fold angles (deg) for different cobalamins in aqueous MD simulations before and after fitting the improper force constants (MD_In and MD_Fit) to the experimental fold angles (Exp).⁹²

System	MDIn	MDFit	Exp
MeCbl(III)	18.4	13.5	14.8
CN-Cbl(III)	18.1	12.1	14.1
AdoCbl(III)	15.9	10.6	10.0
Cbl(II)	26.5	14.0	11.5
Cbl(I)	21.1	11.3	NA

Table 8.

Validation of the improper force constants by comparing the corrin fold angles (deg) from MD simulations before and after fitting of improper constants (MD_In and MD_Fit) to the corrin fold angles in the crystal structures (CS). No parameters were altered based on the bound-state simulations. NA indicates that the simulation was not performed.

System	MDIn	MDFit	CS
1N4A	15.5	10.7	3.2
4GMA	15.3	12.7	12.5
3GAI	13.0	8.6	11.2
5C8A(Chain A)	17.1	7.1	2.5
5C8A(Chain B)	15.8	9.3	15.9
1NQH	NA	12.3	4.7

The stability of cobalamin in bound structures was evaluated based on RMSD from the crystal structure position and preservation of important interactions between cobalamin and the protein or RNA. For each system, two key interactions, either within the cobalamin or between it and the protein or RNA bound to it, were chosen and monitored over time (Table 9). For 4GMA and 1NQH, we selected two hydrogen bonds between cobalamin and the RNA or protein. For 1N4A and 3GAI, we selected one hydrogen bond and one vdW interaction. To validate the cobalamin vdW interactions, we monitored the distance between DMB in cobalamin and W63 in 1N4A, which is important for cobalamin binding in BtuF.¹⁷ To assess our Cbl(II) LJ parameters, we monitored the distance between Co and ATP in 3GAI. For 5C8A, we selected one hydrogen bond between the protein and cobalamin and an internal cobalamin hydrogen bond. Only chains A and B from the CarH tetramer in 5C8A were included in the simulation.

Table 9.

Definitions of the distances monitored during each MD simulation. The residue and atom name for the two atoms involved in each distance are specified. Heavy atoms are specified for the hydrogen bond interactions, but the distances were measured between the acceptor atom and the hydrogen bound to the donor atom with the exception of Distance 2 in 1NQH, for which we used the serine hydroxy oxygen due to a switch between a hydrogen bond donor and an acceptor to atoms proximal to B₁₂ C43.

Crystal structure	Distance 1		Distance 2
	Atom 1	Atom 2	Atom 1	Atom2
1N4A	B12, O44	A10, N	B12, C7B	W63, CZ3
4GMA	B12, O39	G49, N2	B12, N34	C75, O2’
3GAI	B12, O44	I113, N	B12, Co	ATP, C5’
5C8A	B12, O51	Q178, N	B12, O65	B12, N59
1NQH	B12, P	S61, OG	B12, C43	S91, OG

The fluctuations of the monitored distances and RMSD are shown in Figures 4 and 5. Overall, the RMSD is low (~ 3 Å or less after alignment of the protein/RNA), and the monitored distances are mostly conserved in all simulations, indicating that cobalamin remained stably bound in its binding site. Only temporary breaking of the monitored hydrogen bonds was observed in most cases, with the exception of distance 2 for 5C8A. This distance is broken and reformed very often for Chain B in both simulations (see Figure S8) and is broken for Chain A in simulation 2 after 4 ns. This interaction may be less stable because only two of the homodimers of the protein tetramer were included in the simulation. The measured distances for the vdW interactions (distance 2 for 1N4A and 3GAI) showed very small fluctuations (~ 1 Å).

Figure 4.

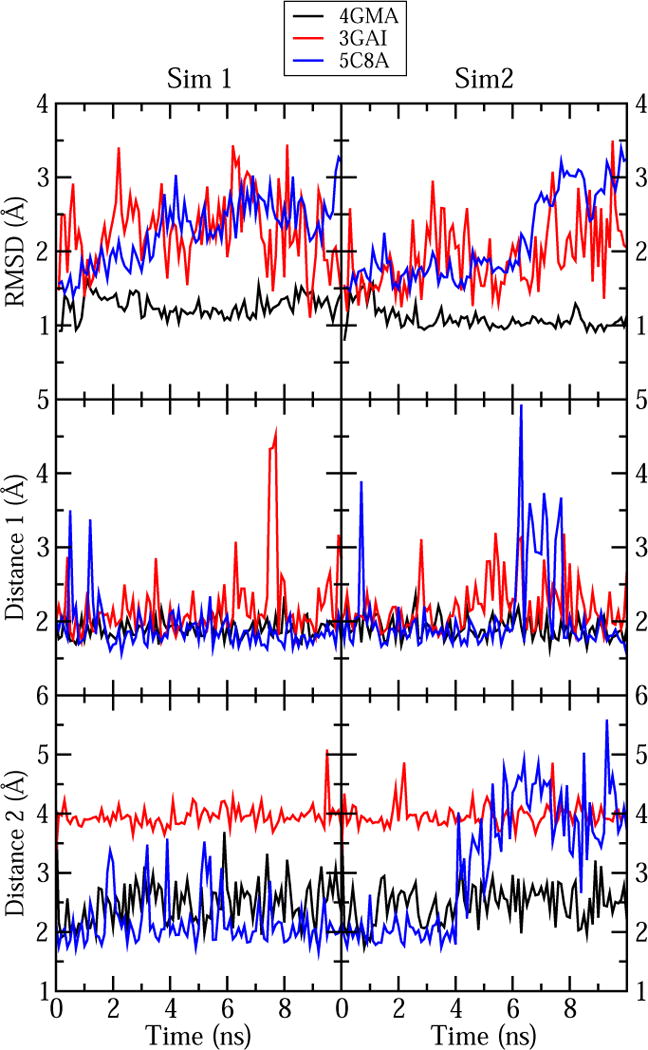
Measurements of the cobalamin RMSD and the two selected distances in our simulations of cobalamin-containing proteins (see Table 9). The results of the first and the second simulation are shown in the left and right graphs, respectively. For 5C8A we only show the distances for chain A; see Figure S8 for the corresponding distances in chain B. Time 0 corresponds to the values in the X-ray crystal structures.

Figure 5.

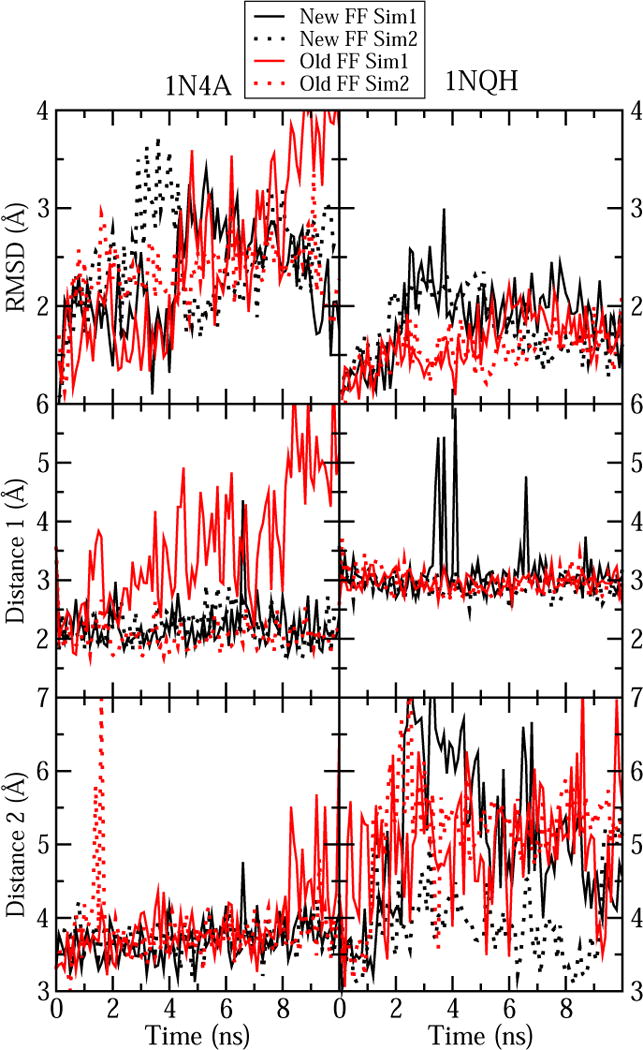
Comparison between our new force field parameters for cobalamin and the previous parameters for simulation of crystal structure 1N4A and 1NQH. Cobalamin RMSD and the two selected distances from Table 9 were monitored for both cases.

Previously, only cobalamin parameters for CN-Cbl(III) have been adapted for simulations with the CHARMM force field.⁴⁹ The two crystal structures containing CN-Cbl(III), 1N4A and 1NQH, were also simulated using these older CHARMM-compatible parameters. Figure 5 compares RMSD and conservation of Distances 1 and 2 between the old and the new force field parameters. For 1N4A one of the two simulations with the old parameters resulted in a high RMSD and significant increases in the monitored distances, suggesting that cobalamin was not stable in its binding site. The other simulation with the old parameters looked very similar those performed with new parameters, yielding low RMSD and conservation of both interactions. Simulations of 1NQH showed less dramatic differences for the two sets of parameters, although fluctuations in Distance 2 were more frequent with the older parameters. The fold angle was also larger and more distinct from the target values for the old parameters than the new ones for both structures. This angle increased from 10.7 to 13.6 (deg.) and from 12.3 to 20.9 (deg.) with the old parameters for 1N4A and 1NQH, respectively.

The validation results show that the optimized cobalamin parameters are suitable for simulations of cobalamin in Cbl(III) and square-pyramidal Cbl(II) states with both base-on and base-off conformations (excluding the states with an extended Co-histidine bond). Comparison to earlier force field parameters for cobalamin reveals that the new parameters lead to smaller RMSD, less frequent fluctuations in interactions with the protein, and smaller deviations of the fold angle compared to the crystal structures. Although it was not possible to validate the Cbl(I) parameters with MD simulations of full cobalamin in a crystal structure, the small Cbl(I) model showed the best agreement with the QM geometry (Figure 3 and Table 6), suggesting that these parameters are also well-suited for MD simulations.

Discussion

We have used DFT calculations and ffTK³⁷ to develop force field parameters for several forms of cobalamin: square-planar Cbl(I), trigonal-bipyramidal Cbl(II) and octahedral Cbl(III), as well as with various axial ligands. The parameters for the amide side chains were taken from the CGenFF force field,²⁶ whereas the parameters for the Co-corrin core and the corrin side chains were fitted explicitly using smaller models of cobalamin (Scheme 2A). In all cases, parameters were optimized from QM data and simulations of cobalamin alone; simulations of cobalamin-binding proteins were only used for subsequent validation.

The He probe approach^67,68 was used to determine the LJ parameters for the Cb(I) and Cbl(II) states. Because noble gases lack dipole moments and are neutral, they simplify the estimation of vdW interactions from QM calculations. Our calculations of the He ⋯ Co interactions suggest that the strength of these interactions may be underestimated without the D3 correction. By fitting the ε and r_min parameters (Table 1), we obtained good agreement between the QM and MM interaction energies for our models.

Cobalamin contains several buried atoms, which makes it difficult to determine the partial atomic charges for these atoms using the standard CHARMM method of computing water interaction energies²⁶ or the RESP method.⁷⁵ Therefore, we used a combination of the NPA⁷⁷ and RESP methods to determine the atomic partial charges. Although NPA charges tend to be more polarized than the corresponding charges from RESP,⁹¹ some over-polarization is desirable to correct for the charges being calculated in gas phase. Usually, over-polarization of partial atomic charges is achieved by computing partial charges at the HF/6-31G(d) level of theory.^23,24,26 However, inclusion of HF exchange is highly detrimental for describing the electronic structure of corrinoids.⁹⁴

The optimized parameters were validated by comparing the MM and QM geometries for the smaller cobalamin models, by examining the corrin fold angles in our simulations, and by evaluating the stability of B₁₂ in the binding site during MD simulation trajectories of several corrinoid proteins. Excellent agreement was found for the geometries (Figures 3 and S7) and the corrin fold angle was reproduced for most cases (Tables 7 and 8) after the adjustment of several improper force constants. Finally, cobalamin remained stably bound in the cofactor binding site in all MD simulations of complexes with protein or RNA (Figure 4). Our parameters reduced the deviations of the cobalamin fold angle, RMSD of cobalamin from its binding-site crystal structure and fluctuations of interactions between cobalamin and the protein when compared to earlier CHARMM-compatible parameters.⁴⁹ Thus, the force field parameters are applicable for MD simulations of these and related systems with the CHARMM force field.

Accurate description of interactions with water molecules is an important aspect of force-field parameters. In the case of cobalamin, the metal center was not accessible for water interactions in any of our protein or RNA systems. Our aqueous simulations showed only limited interaction with water, where hydrogen bonds were formed between the corrin-ring nitrogens and water molecules (see Figure S9).

The parametrization approaches described here and in our previous work on macrolide antibiotics⁵² can be used as a guide to develop force field parameters for other corrinoids or large biomolecules. In particular, our approaches for determining LJ parameters and partial atomic charges for the metal atom in different oxidation states are applicable to other metal cofactors. Similar challenges for both RESP and water interaction approaches for the buried atoms are expected for other octahedral metal complexes. Here, we show that the use of NPA charges provides a good description of electrostatics for cases in which standard methods are inadequate.

Topology and parameter files for cobalamin, as well as instructions for system preparation, are provided in the Supporting Information. The parameters developed here can be used to study cobalamin-protein interactions in B₁₂-dependent enzymes and B₁₂-binding transport proteins for which structures are available. The parameters can also be used to simulate cobalamin redox states for which structures are presently not available, e.g. Cbl(I) and MeCbl(III). However, because the bond between DMB or histidine with the cobalt atom is described by a harmonic spring, it is not possible to simulate ligand dissociation with our force field. Certain forms of corrinoids, such as cobalamin with long Co–N(His) coordination distances, base-off Cbl(II) and Cys-on corrinoids were not parametrized here. However, our molecular topologies allow straightforward modification of the Co oxidation state and the axial ligands, facilitating the investigation of non-standard corrinoids and Co-ligand binding configurations with MD simulations. Additionally, patches for norpseudo-B₁₂ and Factor III_m forms of cobalamin are provided.