Abstract
Objective
To compare the effectiveness of dynamic anemia management strategies by applying the parametric g‐formula to electronic health records.
Data Source/Study Setting
Patients with end‐stage renal disease from the US Renal Data System who had congestive heart failure or ischemic heart disease and were undergoing hemodialysis in outpatient dialysis facilities between 2006 and 2010.
Study Design
We explicitly emulated a target trial of three erythropoietin dosing strategies (aimed at achieving a low, middle, or high hematocrit) and estimated the observational analog of the per‐protocol effect.
Results
Of 156,945 eligible patients, 41,970 died during the 18‐month follow‐up. Compared to the low‐hematocrit strategy, the estimated risk of death was 4.6 (95% CI 4.4–4.9) percentage points higher under the high‐hematocrit strategy and 1.8 (95% CI 1.7–1.9) percentage points higher under the mid‐hematocrit strategy. The corresponding risk differences for a composite outcome of death and myocardial infarction were similar.
Conclusion
An explicit emulation of a target trial using electronic health records, combined with the parametric g‐formula, allowed comparison of real‐world dynamic strategies that have not been compared in randomized trials.
Keywords: Parametric g‐formula, causal inference, target trial, comparative effectiveness research
Comparative effectiveness research evaluates health outcomes in a particular population under two or more different treatment strategies. The strategies that are compared can be baseline interventions, which happen only at a single point in time (e.g., immediate surgery), or strategies that are sustained over time (e.g., take 75 mg of aspirin every day for the rest of your life). Sustained treatment strategies are static when all treatment decisions over the follow‐up period are predetermined at baseline (as in our aspirin example) and dynamic when treatment decisions at each time during the follow‐up depend on time‐evolving patient characteristics. The most common treatment strategies for the care of persons with chronic medical conditions are dynamic. For example, patients on dialysis receive recombinant erythropoietin or epoetin to treat their anemia, with the dose adjusted over time according to both prior epoetin dose and hematocrit or hemoglobin levels (laboratory values which measure the extent of anemia).
In an ideal world, the comparative effectiveness of dynamic treatment strategies would be evaluated in randomized trials. In practice, however, decisions about dynamic strategies must often be based upon observational analyses of existing health care databases. These observational analyses can be viewed as an attempt to emulate a pragmatic clinical trial that we would like to, but cannot or will not, conduct. We refer to this trial as the target trial (Hernán and Robins 2016).
When comparing dynamic treatment strategies in either a target trial or an observational analysis that attempts to emulate one, patients and clinicians are often interested in estimating the effect of following the treatment strategies specified in the protocol of the target trial—the per‐protocol effect (Hernán and Robins 2016). Generally, estimating the per‐protocol effect requires adjustment for pre‐ and postbaseline prognostic factors that affect adherence to the protocol and/or loss to follow‐up (Hernán, Hernández‐Díaz, and Robins 2013; Murray and Hernán 2016).
Conventional statistical methods, however, cannot appropriately adjust for confounding due to postbaseline prognostic factors that affect treatment levels and are, themselves, affected by past treatment, for example, hematocrit when comparing dynamic strategies for epoetin. In contrast, g‐methods (Robins and Hernán 2008; Petersen et al. 2014) were specifically designed to handle time‐varying confounders affected by previous treatment. A g‐method that can be particularly useful for estimating the per‐protocol effect of complex dynamic strategies on continuous treatments (e.g., dose) in either randomized trials with noncompliance (imperfect adherence to the strategies specified in the protocol) or in observational studies is the parametric g‐formula (Robins 1986).
The goal of this study is to provide a step‐by‐step description of the comparison of dynamic strategies using electronic health records. First, we specify the protocol of the target trial, including the statistical analysis plan that can account for postbaseline confounding due to noncompliance and/or loss to follow‐up in estimating the per‐protocol effect. Second, we describe how to emulate the target trial via an application of the parametric g‐formula using electronic health records. As a case study, we compare the effect of dynamic epoetin dosing strategies on the survival of hemodialysis patients with cardiac disease, but the methods described herein can be applied to other comparative effectiveness research questions involving dynamic treatment strategies.
Methods
Our target trial is an updated version of the Normal Hematocrit Study (NHS; Besarab et al. 1998), a randomized controlled trial of patients with cardiac disease who were undergoing hemodialysis and receiving epoetin between 1993 and 1996. The patients were assigned to one of two anemia management strategies: aiming at a normal hematocrit of 42 percent or aiming at a lower‐than‐normal hematocrit of 30 percent. The trial was terminated early because patients who were randomized to the normal hematocrit strategy had increased mortality and myocardial infarction. Subsequent randomized trials among chronic kidney disease patients showed that pursuing normal or near‐normal hematocrit values (39–45 percent) led to worse clinical outcomes than pursuing lower hematocrit values or placebo (Drüeke et al. 2006; Singh et al. 2006; Pfeffer et al. 2009). As a result, the most commonly used strategies in clinical practice aim at hematocrit levels lower than 39 percent. However, these strategies have never been evaluated in randomized trials of hemodialysis patients.
Specifying the Protocol of the Target Trial
In this section, we specify the main components of the protocol of a target trial to compare several dynamic anemia management strategies: eligibility criteria, treatment strategies, outcomes and follow‐up, causal contrasts of interests, and analysis plan.
Eligibility Criteria
Eligible patients are individuals with end‐stage renal disease and congestive heart failure or ischemic heart disease in the previous 2 years who were undergoing hemodialysis in outpatient U.S. dialysis facilities between 2006 and 2010 and had received epoetin therapy in the previous month. The exclusion criteria are similar to those of the NHS study: severe cardiac disability, percutaneous transluminal coronary angioplasty (PTCS), or coronary artery bypass grafting (CABG) in the 3 months before the study baseline; pericardial disease; and cardiac amyloidosis. Additionally, patients are excluded if they were treated with darbepoetin use (an alternative drug with different dosing frequencies) in the previous 3 months or missed dialysis session for an entire month. Study baseline is defined as the first month when all eligibility criteria were met.
Treatment Strategies
We consider three dynamic treatment strategies that are consistent with those widely used in clinical practice, but that have never been compared in randomized trials:
Low hematocrit: At each month, adjust dose of intravenous epoetin alfa (EPO) to try and maintain hematocrit at 30–33 percent,
Mid hematocrit: At each month, adjust dose of EPO to try and maintain hematocrit at 33–36 percent, and
High hematocrit: At each month, adjust dose of EPO to try and maintain hematocrit at 36–39 percent.
To operationalize the implementation of these treatment strategies, we consider the following dosing rule to try and stay within the prespecified hematocrit range: increase monthly EPO dose by exactly 15 percent when hematocrit is below range, decrease the dose by exactly 15 percent when hematocrit is above range, and do not change dose when hematocrit is within range.
In sensitivity analyses, we consider alternative versions of the dosing rule in which monthly EPO dose is increased up to 9,000, 6,000, and 3,000 units when hematocrit is below the range for the high‐, mid‐, and low‐hematocrit group, respectively; decreased to no <6,000, 3,000, and 1,000 units when hematocrit is above the range for the high‐, mid‐, and low‐hematocrit group, respectively; and unchanged when hematocrit is within range.
Outcomes and Follow‐Up
Similar to the NHS trial (Besarab et al. 1998), the endpoints are a composite outcome including death and hospitalization for myocardial infarction and all‐cause mortality. Study subjects are followed from study baseline until the outcome, censoring due to loss to follow‐up, or administrative end of study (18 months after baseline), whichever occurs earlier. A subject is censored upon first occurrence of a data anomaly (e.g., hematocrit value was not reported in the claim but EPO dose was administered), darbepoetin use, or after a 30‐day gap in outpatient dialysis or inpatient claims.
Causal Contrast
The intention‐to‐treat effect is the effect of being assigned to one of the three EPO treatment strategies at baseline regardless of whether the strategies were actually followed. In the presence of nonadherence to the protocol, the intention‐to‐treat effect is less helpful for meaningful results to influence clinical decision making (Hernán and Hernández‐Díaz 2012). We therefore focus our interest on the per‐protocol effect, that is, the effect that would have been observed if all subjects had adhered to their assigned dynamic EPO strategy throughout the 18‐month follow‐up.
Analysis Plan
The parametric g‐formula can be used to estimate the standardized 18‐month risks under full adherence to each treatment strategy in the randomized trial (Robins 1986; Taubman et al. 2009; Lodi et al. 2016). The validity of the method requires that the measured pre‐ and postbaseline covariates are sufficient to control confounding and selection bias due to failure to adhere and loss to follow‐up, and that all models described below are correctly specified. A detailed description of the parametric g‐formula estimation algorithm along with a formal discussion of required assumptions has been previously delineated (Young, Hernán, and Robins 2014). Here, we briefly review the algorithm to estimate the 18‐month death risk by the end of follow‐up under each strategy. The algorithm requires data on the time‐varying treatments, the baseline and time‐varying covariates required to adjust for confounding and selection bias, and the outcome. The steps of the algorithm are as follows.
-
1
Step 1: Fit regression models:
Fit separate regression models for treatment and each covariate at month t as a function of t and past treatment and covariate history, restricted to those who survived and remained uncensored through t. For example, we can summarize covariate history by the baseline covariates and the two most recent values of the time‐varying covariates.
Fit a regression model for the probability of death at month t as a function of t and past treatment and covariate history, restricted to those who survived and remained uncensored through t.
-
2
Step 2: Simulation. For each strategy (denoted g), do the following n times (for a “large” choice of n, possibly the sample size):
t each month t, simulate covariates and treatment using the estimated model coefficients from Step 1a based on previously simulated treatment and covariates under the strategy g through t−1 (values at baseline t = 0 are not simulated but rather sampled from the observed values).
Replace the simulated treatment value at t with the value of treatment that should be assigned according to strategy g based on simulated values of treatment and covariates through t−1.
Compute the discrete‐time hazard of death at t using the estimated regression coefficients from Step 1b for each of the n simulated histories through t consistent with strategy g.
-
3
Step 3: Compute risks. For each of the three strategies g.
For each of the n histories, use the estimated hazards from Step 2c to compute the n history‐specific 18‐month risks by the end of follow‐up under strategy g.
Obtain the 18‐month risk under strategy g in the study population by averaging the n history‐specific risks.
The effect measures (i.e., the 18‐month risk ratios and risk differences) can then be computed directly from the risk estimates under each strategy, and 95% confidence intervals can be obtained by repeating the algorithm in 500 bootstrapped samples.
To evaluate the presence of gross model misspecification, the above algorithm can be easily modified to simulate a population under no intervention on treatment (EPO dose), the so‐called natural course, and compare the distribution of the simulated variables with the ones observed in the actual population (Young et al. 2011).
Emulating the Target Trial Using Observational Data
After specifying the components of the target trial, we then try to emulate them using observational data collected and maintained by the United States Renal Data System (USRDS). This administrative database includes demographics and a detailed longitudinal record of utilization, diagnoses, and procedures for all dialysis patients covered by Medicare (Saran et al. 2015). Patient's history of EPO dose and hematocrit values are recorded in monthly claims submitted by dialysis facilities.
The “Researcher's Guide to the USRDS Database,” available from http://www.usrds.org, describes variables, data sources, collection methods, and validation studies. We used the USRDS standard analytic files as of calendar years 2012 and prior, which were the most recent available data for researchers (as of December 2015). Table 1 delineates how each component of the target trial protocol was emulated as close as possible using the USRDS.
Table 1.
Key Components of the Protocol of a Target Trial of Dynamic EPO Treatment Strategies and Emulation Summary Using the United States Renal Database System (USRDS)
| Component | Target Trial | Emulation Using Observational Dataa |
|---|---|---|
| Eligibility criteria |
|
|
| Treatment strategies |
Patients are randomly assigned to one of the following three dynamic treatment strategies:
Under all strategies, EPO dose (units per administration) is changed according to the following rules: Dose is increased 15%, maintained, or decreased 15% if hematocrit is below, within, or above the target range, respectively. EPO is withheld during the first 4 days of hospitalization and set to the EPO dose received before hospitalization after the first 4 days. The administration of IV iron is left to the discretion of the treating physician, but no use of darbepoetin is allowed. |
To emulate these strategies, we used:
|
| Outcomes |
Primary: all‐cause mortality or nonfatal MI Secondary: mortality alone |
MI date was defined as the date of first inpatient claim during the follow‐up with MI as primary/secondary reason for hospitalization. Death date was identified from USRDS Patients File. |
| Follow‐up | From eligibility and treatment assignment until the earliest of 18 months, death, or loss to follow‐up | Same. Loss to follow‐up was defined as the earlier of (1) data anomaly (e.g., EPO dose >0 even though hematocrit value was not reported in the claim), (2) switch to darbepoetin, and (3) 30‐day gap in outpatient dialysis or inpatient claims. |
| Causal contrasts | Per‐protocol effect | Same. |
| Statistical analysis | Parametric g‐formula to estimate survival curves under each strategy | Same. See Appendix SA2 for SAS code. |
See Table S1 in Appendix SA2 for detailed codes used for identification of inclusion and exclusion criteria using USRDS data.
Implementing the Parametric g‐Formula Using USRDS Data
We estimated the 18‐month risks, risk ratios, and risk differences under each treatment strategy by applying the parametric g‐formula algorithm described above to the USRDS. We arranged the analytical dataset with one record per patient per month, containing hematocrit value at the beginning of the month and average EPO dose per administration in the month (see Text S1 in Appendix SA2 for details on construction of analytical data).
Baseline covariates included age (<50, 50 to <60, 60 to <70, 70 to <80, and ≥80 years), gender, race (black, white, other, or unknown), duration of dialysis (<8, 8 to <27, 27 to <53, 53 to <89, and ≥89 months), cause of renal failure (diabetes, hypertension, glomerulonephritis, and other), hypertension, diabetes mellitus, peripheral vascular disease, cardiac‐related hospitalization for angina pectoris, congestive heart failure, ischemic heart disease, myocardial infarction, coronary artery bypass graft, percutaneous transluminal coronary angioplasty, baseline hematocrit (<27, 27 to <30, 30 to <33, 33 to <36, 36 to <39, and ≥39 percent; measured at beginning of month 0), baseline EPO dose (<1,000, 1,000 to <2,200, 2,200 to <4,400, 4,400 to <8,700, and ≥8,700 units/administration; measured in the month prior to baseline), inpatient days (0, 1 to <7, 7 to <14, 14 to <21, and ≥21 days), U.S. geographic region (Northeast [networks 1–5], Southeast [networks 6–8, 13, 14], Midwest [networks 9–12], West [networks 15–18]), dialysis chain membership (three largest chains, smaller chains, and nonchain facilities), and year of study entry (2006 and 2007–2011).
Time‐varying covariates included inpatient days during the month and the most recent value of hematocrit. Inpatient days was modeled as a categorical variable (three categories: 0 days; 1–4 days; ≥ 5 days) using nested logistic regression models, and hematocrit was modeled using linear regression. Because the hematocrit value is not available for months with zero EPO dose in the USRDS, we only simulated hematocrit when the simulated value of EPO was not zero; otherwise, we carried forward the last simulated value of hematocrit. EPO dose was modeled in two stages: logistic regression for “dose >0” versus “dose = 0” in month t and then a linear regression for the mean of the log EPO dose among those records with dose >0.
All the parametric g‐formula models included an indicator for month of follow‐up, the baseline variables, categorized inpatient days, and restricted cubic splines of the two most recent values of hematocrit (with knots located at 27, 30, 33, 36, and 39 percent) and EPO dose (with knots located at 50, 200, 500, 1,500, 3,000, 4,500, 6,000, 9,000, 12,000, 15,000 U/administration). All analyses were conducted with SAS 9.4 (SAS Institute, Cary, NC, USA) using the GFORMULA SAS macro available with documentation at http://www.hsph.harvard.edu/causal/software.htm. Additional details of implementation and related SAS codes are described in the Appendix SA2.
Results
Figure 1 depicts the selection process for the 156,945 eligible patients. Table 2 summarizes baseline demographics, clinical history, comorbidities, and anemia management. The mean age was 64.7 years, dialysis duration 3.3 years, EPO dose per administration 7,630 units, and hematocrit 35.3 percent; 53 percent were men, 60 percent were white, 96 percent had hypertension, 66 percent had diabetes, and 62 percent had congestive heart failure in the 2 years before baseline.
Figure 1.
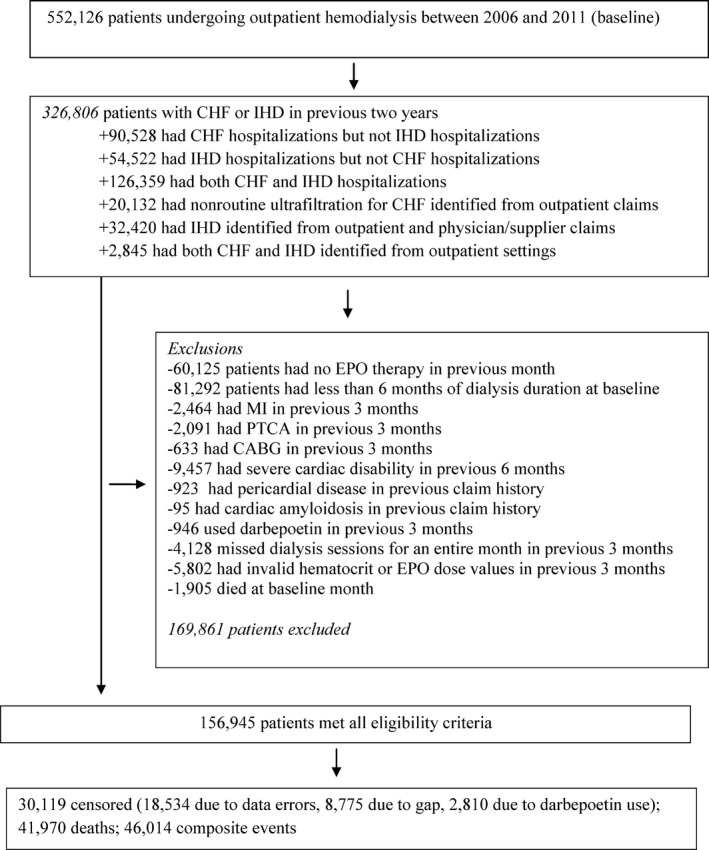
Flowchart of Eligible Patients, United States Renal Data System 2006–2012
Table 2.
Baseline Characteristics of 156,945 Eligible Patients, United States Renal Database System 2006–2012
| Characteristic | Value |
|---|---|
| Patient demographics | |
| Age (year; mean) | 64.7 |
| Male gender (%) | 52.9 |
| Race (%) | |
| White | 59.5 |
| Black | 34.8 |
| Other/unknown | 5.7 |
| Patient clinical history (%) | |
| Primary cause of renal failure | |
| Diabetes | 50.6 |
| Hypertension | 28.6 |
| Glomerulonephritis | 9.4 |
| Other/unknown | 11.4 |
| Duration of dialysis (years) | 3.3 |
| Baseline inpatient days (mean) | 1.3 |
| Hypertension | 96.4 |
| Diabetes | 66.4 |
| Peripheral vascular disease | 38.2 |
| Angina pectoris | 7.3 |
| Congestive heart failure | 62.0 |
| Myocardial infarction | 13.8 |
| Coronary artery bypass graft | 5.8 |
| Percutaneous transluminal coronary angloplasty | 9.6 |
| Anemia management prior to baseline | |
| Hematocrit (%, mean) | 35.3 |
| EPO dose (units/administration, mean) | 7,630 |
| Iron use (%) | 64.1 |
| Facility characteristics (%) | |
| Geographic region | |
| Northeast (Networks 1–5) | 24.3 |
| Southeast (Networks 6–8, 13, 14) | 37.5 |
| Midwest (Networks 9–12) | 21.5 |
| West (Networks 15–18) | 16.7 |
| Dialysis facility chain group | |
| DaVita | 31.3 |
| Fresenius | 32.7 |
| DCI | 4.1 |
| Small chains | 12.9 |
| Nonchain | 19.0 |
During the 18 months of follow‐up (2,069,207 person‐months), there were 41,970 deaths and 30,119 censoring events. The observed 18‐month risk was 30.4 percent for death and 33.3 percent for the composite endpoint. The parametric g‐formula closely replicated these risks (29.9 and 32.9 percent, respectively) and the mean of the covariates under no intervention (Figure S1 in Appendix SA2).
Table 3 shows the 18‐month risks under the three EPO dosing strategies. Compared to the low‐hematocrit strategy, the estimated risk of death was 4.6 (95% CI 4.4–4.9) percentage points higher under the high‐hematocrit strategy and 1.8 (95% CI 1.7–1.9) percentage points higher under the mid‐hematocrit strategy. The corresponding risk differences for the composite endpoint were very similar. The survival curves under the three strategies are shown in Figure 2.
Table 3.
Risks of Death Only and of Death or Myocardial Infarction (MI) Under Low‐Hematocrit (30–33%), Mid‐Hematocrit (33–36%), and High‐Hematocrit (36–39%) Treatment Strategies, United States Renal Database System 2006–2012
| Outcome | Treatment Strategya | 18‐month Risk (%) | Risk Ratio | 95% CI | Risk Difference (%) | 95% CI | ||
|---|---|---|---|---|---|---|---|---|
| Deatha | High hematocrit | 32.1 | 1.17 | 1.16 | 1.18 | 4.63 | 4.42 | 4.91 |
| Mid hematocrit | 29.3 | 1.06 | 1.06 | 1.07 | 1.77 | 1.65 | 1.92 | |
| Low hematocrit | 27.5 | 1 (ref.) | 1 (ref) | |||||
| Death or MIb | High hematocrit | 35.1 | 1.15 | 1.14 | 1.16 | 4.60 | 4.35 | 4.83 |
| Mid hematocrit | 32.3 | 1.06 | 1.05 | 1.06 | 1.76 | 1.62 | 1.89 | |
| Low hematocrit | 30.5 | 1 (ref) | 1 (ref) | |||||
41,970 deaths; 18‐month risk of death: 30.2% (observed), 29.9% (simulated).
46.014 composite events of death and MI: 18‐month risk of death: 33.1% (observed), 32.9% (simulated).
CI, confidence interval.
Figure 2.
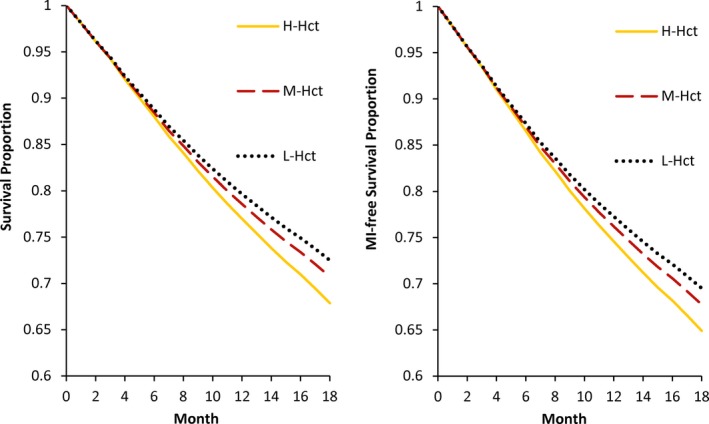
Survival Curves and Myocardial Infarction (MI)‐Free Survival Curves under the Low‐Hematocrit (L‐Hct), Mid‐Hematocrit (M‐Hct), and High‐Hematocrit (H‐Hct) Strategies, United States Renal Database System 2006–2012 [Color figure can be viewed at http://wileyonlinelibrary.com]
The above effect estimates did not materially change when (1) more time‐varying covariates such as iron dose and the number of dialysis sessions were included in the analysis; (2) instead of carrying forward previous hematocrit when hematocrit values were missing, we assumed an increase of 10 percent or a decrease of 10 percent in the hematocrit value compared with the previous reported level; (3) we used one or three lagged measurements (instead of two) to summarize covariate history; (4) we used different regression fitting procedures for the continuous variables EPO dose and hematocrit; (5) we changed number and location of knots for cubic splines; (6) we changed the arbitrary order in the fitting of models in Step 1a (see Text S2 in Appendix SA2); (7) EPO dose per week was modeled instead of dose per administration; and (8) EPO was imputed throughout duration of hospital stay (Zhang et al. 2009).
Discussion
We used observational data from the U.S. Renal Data System to compare three dynamic anemia management strategies that have not been compared in randomized trials. Our g‐formula estimates suggest that targeting a low hematocrit of 30–33 percent reduces the risk of death, compared with targeting higher hematocrits, in individuals with cardiac disease undergoing hemodialysis.
Our findings support current FDA recommendations that the lowest possible EPO dose should be used to achieve a hematocrit of 30–33 percent for dialysis patients. They are also consistent with randomized trials in non‐ESDR patients, which have consistently shown that patients assigned to higher hematocrit levels (by receiving more EPO) did not have better outcomes, or had worse outcomes, than those assigned to lower hematocrit levels.
In contrast, several observational studies (Ma et al. 1999; Collins et al. 2001) found that higher hematocrit values were associated with better patient outcomes, which were used as evidence for erstwhile EPO treatment guidelines (NKF‐k 2001). However, these associations may simply indicate that patients with higher hematocrit values are healthier in ways not adequately adjusted for in the analysis. Our observational study adjusts for baseline and postbaseline confounders using the parametric g‐formula and explicitly describes the protocol of a target trial so that, unlike previous observational studies, we compare EPO dosing rules rather than observed hematocrit levels.
The parametric g‐formula has been previously applied to compare dynamic treatment strategies, including lifestyle interventions (Taubman et al. 2009; Danaei et al. 2013; Garcia‐Aymerich et al. 2014; Lajous et al. 2013) and clinical interventions (Young et al. 2011; Edwards et al. 2015; Lodi et al. 2015). However, none of these applications of the parametric g‐formula were based on a database of health claims. Our study demonstrates the opportunities afforded by a large ESRD claims database to compare dynamic treatment strategies that are unlikely to be included in randomized trials. However, a valid application of the parametric g‐formula to these datasets requires two critical assumptions.
First, the validity of the estimates relies on the assumption that the available covariates are sufficient to control for confounding and selection bias (Hernán and Robins 2006; Robins and Hernán 2008; Daniel et al. 2013). We believe that this assumption approximately holds in our analysis because the USRD includes longitudinal data on hematocrit value, which is the driving factor of EPO dosing. In general, researchers considering a database for comparative effectiveness research need to carefully evaluate whether longitudinal data on treatment, confounders, and outcome are adequately recorded. Second, the validity of the estimates relies on the assumption that models for the outcome, treatment, and confounders are correctly specified at each follow‐up time. We conducted several sensitivity analyses and found our results generally robust to changes in modeling assumptions.
To increase robustness of analysis, when possible, we also recommend conducting analyses that rely on a different g‐method. For example, we previously used inverse probability (IP) weighting (Cain et al. 2010; Zhang et al. 2014) to compare dynamic EPO dosing strategies. Compared with the parametric g‐formula, IP weighting relies on fewer modeling assumptions and is not subject to the so‐called g‐null paradox, which may lead to rejection of the null hypothesis of no treatment effect even when the null hypothesis is true (Robins and Wasserman 1997). The g‐null paradox is not an important concern for our study because previous experimental studies suggest that there are indeed differences between EPO dosing strategies (Besarab et al. 1998; Singh et al. 2006; Pfeffer et al. 2009).
Yet the parametric g‐formula has several advantages over IP weighting for the comparison of dynamic treatment strategies. First, the parametric g‐formula offers more flexibility to compare clinically relevant strategies. Our previous IP‐weighted analysis (Zhang et al. 2014) compared EPO dosing strategies under which EPO dose is increased somewhere between 10 and 25 percent when the hematocrit is below range, decreased somewhere between 10 and 25 percent when the hematocrit is above range, and changed somewhere between a 10 percent decrease and 10 percent increase when the hematocrit is in range. IP‐weighted estimates from this analysis can be interpreted as effects of random dynamic strategies (Taubman et al. 2008), that is, strategies under which individuals receive a dose value randomly drawn from a distribution. Random assignment rules are not natural for clinical practice. In contrast, our current g‐formula estimates can be interpreted as effects of deterministic dynamic strategies, that is, strategies under which individuals receive a fixed dose (Taubman et al. 2008). This reflects what a physician will realistically do in practice (Young, Hernán, and Robins 2014). Second, IP‐weighted estimates may be unstable when treatment is continuous or certain treatment values are rare (Robins and Hernán 2008).
The trade‐off for the greater clinical relevance and stability of the parametric g‐formula estimates is a heavier reliance on modeling assumptions, as discussed above. Doubly robust g‐methods (e.g., targeted maximum‐likelihood estimation [Petersen et al. 2014]) that, in theory, combine the strengths of IP weighting and the g‐formula are currently under development.
In conclusion, we described how to specify, emulate, and analyze a target trial to compare dynamic dosing strategies via an application of the parametric g‐formula to a large health care database. Our study can help guide decision making by patients, clinicians, and policy makers, as well the design of future randomized trials.
Supporting information
Appendix SA1: Author Matrix.
Appendix SA2:
Table S1: ICD‐9‐CM Diagnosis and Procedure Codes Used in the Study.
Text S1: Construction of Analytical Dataset.
Text S2: A description of the GFORMULA Macro.
Table S2: Covariates Used in the g‐Formula Analysis to Compare the Outcomes of Hemodialysis Patients Who Had Cardiac Disease and Were Treated with EPO: USRDS 2006–2012.
Text S3: SAS Codes.
Table S3: Risks Death Only and Composite Endpoints under Low (30–33 percent), Mid (33–36 percent), and High (36–39 percent) Hematocrit Treatment Strategies, USRDS 2006‐2012.
Figure S1: Comparison of Observed Means of All Time‐Varying Variables and Model‐Based Predicted Means under No Intervention, USRDS 2006–2012.
Acknowledgments
Joint Acknowledgment/Disclosure Statement: This research was supported through a Patient‐Centered Outcomes Research Institute (PCORI) Pilot Project Award (Title: Comparison of Dynamic Treatment Strategies for Patient‐Centered Outcomes Research).
All statements in this report, including its findings and conclusions, are solely those of the authors and do not necessarily represent the views of the Patient‐Centered Outcomes Research Institute (PCORI), its Board of Governors, or Methodology Committee.
The data reported herein have been supplied by the US Renal Data System. The interpretation and reporting of these data are the responsibility of the authors and in no way should be seen as the official policy or interpretation of the US government.
Disclosures: None.
Disclaimer: None.
References
- Besarab, A. , Bolton W. K., Browne J. K., Egrie J. C., Nissenson A. R., Okamoto D. M., Schwab S. J., and Goodkin D. A.. 1998. “The Effects of Normal as Compared with Low Hematocrit Values in Patients with Cardiac Disease Who Are Receiving Hemodialysis and Epoetin.” New England Journal of Medicine 339 (9): 584–90. [DOI] [PubMed] [Google Scholar]
- Cain, L. E. , Robins J. M., Lanoy E., Logan R., Costagliola D., and Hernán M. A.. 2010. “When to Start Treatment? A Systematic Approach to the Comparison of Dynamic Regimes Using Observational Data.” International Journal of Biostatistics 6 (2). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collins, A. J. , Li S., Peter W. S., Ebben J., Roberts T., Ma J. Z., and Manning W.. 2001. “Death, Hospitalization, and Economic Associations among Incident Hemodialysis Patients with Hematocrit Values of 36 to 39%.” Journal of the American Society of Nephrology 12 (11): 2465–73. [DOI] [PubMed] [Google Scholar]
- Danaei, G. , Pan A., Hu F. B., and Hernán M. A.. 2013. “Hypothetical Mid‐Life Interventions in Women and Risk of Type 2 Diabetes.” Epidemiology 24 (1): 122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daniel, R. , Cousens S., De Stavola B., Kenward M., and Sterne J.. 2013. “Methods for Dealing with Time‐Dependent Confounding.” Statistics in Medicine 32 (9): 1584–618. [DOI] [PubMed] [Google Scholar]
- Drüeke, T. B. , Locatelli F., Clyne N., Eckardt K.‐U., Macdougall I. C., Tsakiris D., Burger H.‐U., and Scherhag A.. 2006. “Normalization of Hemoglobin Level in Patients with Chronic Kidney Disease and Anemia.” New England Journal of Medicine 355 (20): 2071–84. [DOI] [PubMed] [Google Scholar]
- Edwards, J. K. , Cole S. R., Westreich D., Mugavero M. J., Eron J. J., Moore R. D., Mathews W. C., Hunt P., and Williams C.. 2015. “Age at Entry into Care, Timing of Antiretroviral Therapy Initiation, and 10‐Year Mortality among HIV‐Seropositive Adults in the United States.” Clinical Infectious Diseases 61 (7): 1189–95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garcia‐Aymerich, J. , Varraso R., Danaei G., Camargo C. A., and Hernán M. A.. 2014. “Incidence of Adult‐Onset Asthma after Hypothetical Interventions on Body Mass Index and Physical Activity: An Application of the Parametric g‐Formula.” American Journal of Epidemiology 179 (1): 20–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hernán, M. A. , and Hernández‐Díaz S.. 2012. “Beyond the Intention‐to‐Treat in Comparative Effectiveness Research.” Clinical Trials 9 (1): 48–55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hernán, M. A. , Hernández‐Díaz S., and Robins J. M.. 2013. “Randomized Trials Analyzed as Observational Studies.” Annals of Internal Medicine 159 (8): 560–2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hernán, M. A. , and Robins J. M.. 2006. “Estimating Causal Effects from Epidemiological Data.” Journal of Epidemiology and Community Health 60 (7): 578–86. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hernán, M. A. Robins J. M.. 2016. “Using Big Data to Emulate a Target Trial When a Randomized Trial Is Not Available.” American Journal of Epidemiology 183 (8): 758–64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lajous, M. , Willett W. C., Robins J., Young J. G., Rimm E., Mozaffarian D., and Hernán M. A.. 2013. “Changes in Fish Consumption in Midlife and the Risk of Coronary Heart Disease in Men and Women.” American Journal of Epidemiology 178 (3): 382–91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lodi, S. , Phillips A., Logan R., Olson A., Costagliola D., Abgrall S., van Sighem A., Reiss P., Miró J. M., and Ferrer E.. 2015. “Comparative Effectiveness of Immediate Antiretroviral Therapy Versus CD4‐Based Initiation in HIV‐Positive Individuals in High‐Income Countries: Observational Cohort Study.” Lancet HIV 2 (8): e335–43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lodi, S. , Sharma S., Lundgren J. D., Phillips A. N., Cole S. R., Logan R., Agan B. K., Babiker A., Klinker H., and Chu H.. 2016. “The Per‐Protocol Effect of Immediate Versus Deferred Antiretroviral Therapy Initiation.” AIDS 30 (17): 2659–63. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma, J. Z. , Ebben J., Xia H., and Collins A. J.. 1999. “Hematocrit Level and Associated Mortality in Hemodialysis Patients.” Journal of the American Society of Nephrology 10 (3): 610–9. [DOI] [PubMed] [Google Scholar]
- Murray, E. J. , and Hernán M. A.. 2016. “Adherence Adjustment in the Coronary Drug Project: A Call for Better Per‐Protocol Effect Estimates in Randomized Trials.” Clinical Trials 13 (4): 372–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- NKF‐k . 2001. “DOQI Clinical Practice Guidelines for Anemia of Chronic Kidney Disease: Update 2000.” American Journal of Kidney Diseases 37 (1 suppl 1): S182–238. [DOI] [PubMed] [Google Scholar]
- Petersen, M. , Schwab J., Gruber S., Blaser N., Schomaker M., and van der Laan M.. 2014. “Targeted Maximum Likelihood Estimation for Dynamic and Static Longitudinal Marginal Structural Working Models.” Journal of Causal Inference 2 (2): 147–85. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pfeffer, M. A. , Burdmann E. A., Chen C.‐Y., Cooper M. E., de Zeeuw D., Eckardt K.‐U., Feyzi J. M., Ivanovich P., Kewalramani R., and Levey A. S.. 2009. “A Trial of Darbepoetin Alfa in Type 2 Diabetes and Chronic Kidney Disease.” New England Journal of Medicine 361 (21): 2019–32. [DOI] [PubMed] [Google Scholar]
- Robins, J. 1986. “A New Approach to Causal Inference in Mortality Studies with a Sustained Exposure Period—Application to Control of the Healthy Worker Survivor Effect.” Mathematical Modelling 7 (9): 1393–512. [Google Scholar]
- Robins, J. , and Hernan M.. 2008. “Estimation of the Causal Effects of Time‐Varying Exposures” In Longitudinal Data Analysis, pp. 553–99. London: Chapman and Hall/CRC. [Google Scholar]
- Robins, J. M. , and Wasserman L.. 1997. “Estimation of Effects of Sequential Treatments by Reparameterizing Directed Acyclic Graphs” In Proceedings of the Thirteenth conference on Uncertainty in artificial intelligence, pp. 409–20. San Francisco: Morgan Kaufmann. [Google Scholar]
- Saran, R. , Li Y., Robinson B., Ayanian J., Balkrishnan R., Bragg‐Gresham J., Chen J. T., Cope E., Gipson D., and He K.. 2015. “US Renal Data System 2014 Annual Data Report.” American Journal of Kidney Diseases 66 (1): Svii. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Singh, A. K. , Szczech L., Tang K. L., Barnhart H., Sapp S., Wolfson M., and Reddan D.. 2006. “Correction of Anemia with Epoetin Alfa in Chronic Kidney Disease.” New England Journal of Medicine 355 (20): 2085–98. [DOI] [PubMed] [Google Scholar]
- Taubman, S. , Robins J., Mittleman M., and Hernán M.. 2008. “Alternative Approaches to Estimating the Effects of Hypothetical Interventions.” JSM Proceedings, Health Policy Statistics Section: 4422–6. [Google Scholar]
- Taubman, S. L. , Robins J. M., Mittleman M. A., and Hernán M. A.. 2009. “Intervening on Risk Factors for Coronary Heart Disease: An Application of the Parametric g‐Formula.” International Journal of Epidemiology 38 (6): 1599–611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Young, J. G. , Hernán M. A., and Robins J. M.. 2014. “Identification, Estimation and Approximation of Risk under Interventions That Depend on the Natural Value of Treatment Using Observational Data.” Epidemiologic Methods 3 (1): 1–19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Young, J. G. , Cain L. E., Robins J. M., O'Reilly E. J., and Hernán M. A.. 2011. “Comparative Effectiveness of Dynamic Treatment Regimes: An Application of the Parametric g‐Formula.” Statistics in Biosciences 3 (1): 119–43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang, Y. , Thamer M., Cotter D., Kaufman J., and Hernán M. A.. 2009. “Estimated Effect of Epoetin Dosage on Survival among Elderly Hemodialysis Patients in the United States.” Clinical Journal of the American Society of Nephrology 4 (3): 638–44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang, Y. , Thamer M., Kaufman J., Cotter D., and Hernán M.. 2014. “Comparative Effectiveness of Two Anemia Management Strategies for Complex Elderly Dialysis Patients.” Medical Care 52 (03): S132. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix SA1: Author Matrix.
Appendix SA2:
Table S1: ICD‐9‐CM Diagnosis and Procedure Codes Used in the Study.
Text S1: Construction of Analytical Dataset.
Text S2: A description of the GFORMULA Macro.
Table S2: Covariates Used in the g‐Formula Analysis to Compare the Outcomes of Hemodialysis Patients Who Had Cardiac Disease and Were Treated with EPO: USRDS 2006–2012.
Text S3: SAS Codes.
Table S3: Risks Death Only and Composite Endpoints under Low (30–33 percent), Mid (33–36 percent), and High (36–39 percent) Hematocrit Treatment Strategies, USRDS 2006‐2012.
Figure S1: Comparison of Observed Means of All Time‐Varying Variables and Model‐Based Predicted Means under No Intervention, USRDS 2006–2012.


