To grow is not enough: impact of noise on cell environmental response and fitness

Abstract

Quantitative single cell measurements have shown that cell cycle duration (the time between cell divisions) for diverse cell types is a noisy variable. The underlying distribution is mean scalable with a universal shape for many cell types in a variety of environments. Here we explore through both experiment and theory the response of these distributions to large environmental perturbations. In particular, we discuss how the stochasticity of the ensemble may be related to the response. Our findings show that slow growing, noisy populations are more adaptive than those which are fast growing. We suggest that even non-cooperative cells in exponential growth phase may not optimize fitness through growth rate alone, but also optimize adaptability to changing conditions. In this work, we wish to emphasize that in a manner similar to genetic evolution, noise in biochemical processes may be important to allow for cells to adapt to rapid to environmental changes.

I. Introduction

The concept of biological fitness is a starting point of discussion in many questions in evolutionary biology.¹ At the most basic level, fitness is still often defined to be the “birth-rate” or the rate at which new individuals are added to the population. Cooperative and mutlicellular systems may require a more complicated definition; but often even these phenomena are shown to derive from the maximization of total sustainable single-cell number.^2–5 In the case of non-cooperative, single-cell species (e.g. bacteria at low cell density), fitness as birth-rate is accepted. For such a population during exponential growth, the number of cells in an ensemble can be well described as a function of time if we know the initial number N₀, and the cell cycle duration τ, yielding N(t) = N₀ exp(ln(2)t/τ). In this way the constant r = ln(2)/τ, often labeled the “growth-rate”, is used to measure fitness – the larger r and the faster an organism grows, the fitter it is.

However, the growth rate for a single cell is often hard to define. Experiments conducted in constant environments maintained in microfluidic devices (so called “Mother Machines”) show that the cell cycle duration⁶ is stochastic and exhibits large variations for both prokaryotes and eukaryotes.⁷ Thus one should consider a statistical distribution of cell cycle durations P(τ), where τ is the time between 2 successive cell divisions (septum formations). Owing to the fact that synthesis of new proteins and replication of DNA require finite time, there is perhaps a physical lower limit for the cell cycle duration, τ^* (dependent on the environment), below which no intact cells can divide. From an evolutionary perspective, we quickly see that to optimize fast growth, P(τ) should be a narrow distribution centered as close to τ^* as possible; however, the measured distribution for E. coli stands in stark opposition to this idea^6,7 (Fig. 1), exhibiting a significant variance in τ. Quite strikingly, P(τ) is mean scaleable:^8,9 the coefficient of variation $\text{CV}=\sqrt{\langle \delta {\tau }^2\rangle }/\langle \tau \rangle$ where δτ = τ − 〈τ〉 and

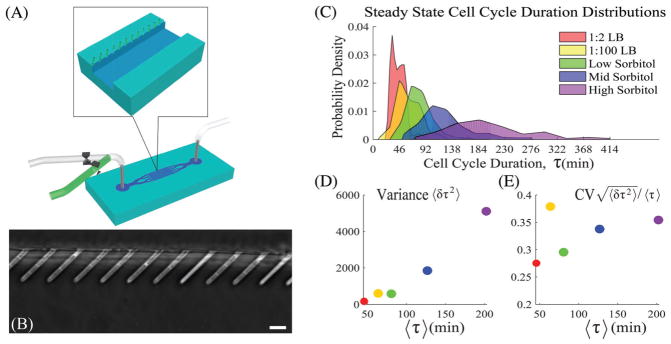
Fig. 1.

(A) Cartoon of the mother machine. (B) An image displaying E. coli cells in the microchannels. The scale bar is 5 microns. (C) E. coli cell cycle duration distributions (CCDDs) measured at constant nutrient conditions. See the Section III (ESI^†) for more details. (D) Measured variance of the cell cycle duration. (E) Coefficient of variation (CV) of the cell cycle duration: CV is roughly constant across all conditions. Please see Fig. S1 (ESI^†) panel B for a direct overlay of the distributions displayed in (C) and scaled by the respective mean values.

$$\langle \tau \rangle =\int \mathrm{d}\tau \tau P(\tau )$$ (1)

is generally a constant across a wide variety of conditions, with shape conservation spanning cell types from E. coli to human dermal fibroblast cells.⁷ In Fig. 1 we display the distributions and corresponding statistics for the ensembles investigated in this work and verify that they reflect the features discussed here.

These observations, in conjunction with established cell cycle models^10,11 and more recent experimental results for protein synthesis and volume regulation, have given rise to the present discussion about whether a cell is best described as regulating its time until division, a “timer” mechanism; volume at division, a “sizer” mechanism; or mass added over a single generation, a “constant adder” mechanism.^12–14

Nevertheless, stochasticity in the cell cycle dynamics and heterogeneity in cell growth rate seems universal, which begs the question “Why is this important?” Specifically, we wish to probe the effects of programmed non-genetic heterogeneity apparent in this trend: that slow growing cultures exhibit greater variability in their cell cycle regulation. Perhaps, the costs/benefits of this noise may be better understood in a non-constant environment: we show below that slower growing cultures under stressed conditions are able to return to a fast growth state when introduced to rich media at a greater rate than faster growing, less-stressed cultures. Perhaps fitness, even for exponentially growing cultures, should take adaptability to environmental variability into consideration as well. The question we will focus on for this investigation is, “does increasing the noise in the mechanisms regulating the cell cycle correlate with decreased cell fitness?” We would like to note here that we will talk about adaptation to environmental shock throughout the paper and before we continue want to state we will use this definition for “adaptabl”: a culture is considered to be adaptable if it is able to maintain the highest growth rate possible for as long as possible.

II. Methods

A. Experimental design

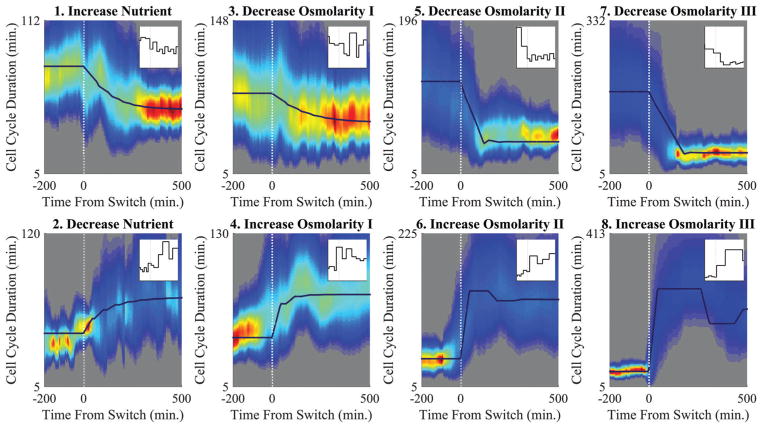
We grew E. coli in the mother machine and collected single cell cycle duration data. We grew cells in five different types of media, performed step changes in the growth medium, and measured how cells responded to these sudden environmental changes (see Section III, ESI^†). Fig. 3 shows how the CCDDs changed over time. For each experiment, the distribution is initially constant and stable before the sudden environmental change. After the change, the distribution shifted over time, and eventually reached the new stable distribution for the new environment. We find that the cell cycle duration trajectories for individual cells follow a similar trend but include significant noise (Fig. 3 insets).

Fig. 3.

Eight step environmental change experiments. The experimental distributions (here fitted to Gamma distributions and smoothed; see Fig. S5 (ESI^†) for a direct comparison with the raw data) are displayed using colors with highest probability in red and lowest probability in blue. The black lines are the model predictions for the average. The insets are representable single cell trajectories. The magnitude of the environmental shock increases from left to right across the figure in both rows. The difference in the mean stationary CCDD from the start of the experiment to the finish is approximately: for experiments 1 & 2 20 min, 3 & 4 40 min, 5 & 6 80 min, and 7 & 8 150 min. Please see Section IV (ESI^†) for more details.

We observed the response of CCDDs ρ(τ,n) in a series of step change experiments where for time t < 0 cells were exposed to a constant environment, and at t = 0 the environment was altered in such a way that the new mean cell cycle duration was measurably different (see Section III, ESI^†). The results are for E. coli in a mother machine, but we also conducted a series of bulk temperature shift experiments to compare with the micro-fluidic results (see Section V, ESI^†). Fig. 3 shows the results of the eight environmental shift experiments conducted. The top row contains relaxation experiments where the cells were grown in suboptimal conditions including one nutrient limited and three hypertonic solutions (where the osmolarity was increased with the addition of Sorbitol) before shifting the media to the optimal environment (in diluted LB medium) for fast growth. The bottom row are the reverse, stress experiments.

To compare the efficiency of response across all experiments, we proposed to examine the quantity, Δ,

$$\mathit{\Delta }=\langle \frac{1}{\lambda }{\int }_0^{\lambda }\tau (t)\mathrm{d}t\rangle -max({\mu }_{\mathrm{i}},{\mu }_{\mathrm{f}})$$ (2)

where the environment step change occurred at t = 0, λ = 500 min is the minimum period for all eight experiments to complete the response to their new environments, and the average 〈 〉 is taken over all cells. (Note that the trends observed are maintained over a wide range of λ see Section IV, ESI.^†) μ_i,f is the steady state average cell cycle duration before and after the step change, respectively. When Δ is large and positive, the cells respond so inefficiently that during response they grow even slower than in the stressed condition. When Δ is large and negative, the cells are able to remain or enter in the fast growth state for the majority of the response period.

B. Model derivation

Here we present a short derivation of the generational transition probability, M, with minimal context. The biological assumptions used to motivate the form of M are contained in Results. For an integrated treatment, please see Section II (ESI^†). For a collection of mother cells, we consider a sequence of cell cycle times (τ₁, τ₂,…) and the corresponding cell cycle duration distributions indexed by generation, ρ(τ,n). In general, ρ(τ,n) can vary between generations, and the generational dynamics can be described by a Markovian stochastic model for ρ(τ,n), which describes the change of this distribution in terms of a transition probability, M,

$$\rho ({\tau }^{\prime },n+1)=\int \mathrm{d}\tau M(\tau \to {\tau }^{\prime };\varphi )\rho (\tau ,n)$$ (3)

where M depends on the current environment described by ϕ. M describes the probability of a daughter cell to divide after duration τ′ given that the mother cell divided after duration τ. Note for a constant environment, the Markovian dynamics at long times will arrive a steady distribution, which is what we have called P(τ) in the Introduction. Eqn (13) is simply a statement of probability conservation; and by developing a model for M, we can predict how cells can respond to environmental changes over time.

We take into account two sources of regulation for cell cycle duration – optimization of protein synthesis rates to the current environment (instantaneous information), and the maintenance of proteome similarity to the mother cell (inherited information). Our form of the transition probability consists of one gaussian term to handle inheritance and another to handle instantaneous optimization with respect to the current environment. This form was assumed to admit an analytic solution, and also is consistent with experimental measurements of this transition probability from our data. To include inheritance, we consider the cycle duration τ′ (of the daughter cell) to be normally distributed with mean τ (the cycle duration of the mother cell) and some unknown variance σ₂²:

$$M_2(\tau \to {\tau }^{\prime })=Aexp\left[-\frac{1}{2{{\sigma }_2}^2}{({\tau }^{\prime }-\tau )}^2\right]$$ (4)

This term suggests that the daughter cell cycle remains close to that of the mother cell due to inheritance. To include the optimization of DNA/protein synthesis with respect to the current environment, the transition probability takes the form

$$M_1({\tau }^{\prime })\equiv \frac{1}{\sqrt{2\pi }{\sigma }_1}exp\left[-\frac{1}{2{{\sigma }_1}^2}{({\tau }^{\prime }-\mu (\varphi ))}^2\right]$$ (5)

where μ(ϕ) is the average cell cycle duration of a cell in environment ϕ at steady state. The total transition probability from τ of the mother cell to τ′ of the daughter cell should balance the inherited information with the process of protein/DNA synthesis. Therefore we expect

$$M(\tau \to {\tau }^{\prime })~M_1({\tau }^{\prime })M_2(\tau \to {\tau }^{\prime })$$ (6)

There is a problem with this construction, however, because taking a look at the product of our two transition probabilities (where the normalization is absorbed into the constant A):

$$M(\tau \to {\tau }^{\prime })=Aexp\left[-\frac{1}{2{{\sigma }_1}^2}{(\tau -\mu )}^2\right]exp\left[-\frac{1}{2{{\sigma }_2}^2}{({\tau }^{\prime }-\tau )}^2\right]$$ (7)

we can see that the most probable state for τ′ is always between τ and μ regardless of the value of σ₁ or σ₂. In general, there may be a negative correlation between adjacent generations at steady state and in order to construct the most general form for the transition probability that can reproduce these dynamics, we will also include some current state (τ) dependence in the term representing instantaneous information:

$$M_1(\tau \to {\tau }^{\prime })\approx Aexp\left[\frac{1}{2{{\sigma }_1}^2}{({\tau }^{\prime }+\alpha \tau -(1+\alpha )\mu )}^2\right]$$ (8)

The biological motivations behind this is discussed further in the Results section and the ESI.^† Putting together both terms (instantaneous and inherited information), we arrive at our desired transition probability:

$$M(\tau \to {\tau }^{\prime })\propto exp\left[-\frac{{({\tau }^{\prime }+\alpha \tau -(1+\alpha )\mu (\varphi ))}^2}{2{\sigma }_1{(\varphi )}^2}\right]\times exp\left[-\frac{{({\tau }^{\prime }-\tau )}^2}{2{\sigma }_2{(\varphi )}^2}\right]$$ (9)

where σ₁, σ₂ are positive constants describing the noise, and μ is the mean cell cycle duration for a given condition ϕ. σ₁, σ₂ and μ all depend on the current environmental variable ϕ. α is a constant between 0 and 1, representing the fraction of the cell cycle after DNA replication has terminated and before septum formation see Section II (ESI^†) for more details. The first term represents adaptability – increasing its weight (decreasing σ₁) is equivalent to boosting the amount of information a cell may obtain about its environment. Conversely, the second term represents stability and increasing its weight (decreasing σ₂) is equivalent to increasing the similarity between mother and daughter cells. When the environment is constant, dynamics generated by M must produce the steady state CCDD, P(τ). Therefore, (σ₁,σ₂,μ) are determined by the environment and their corresponding steady state distributions. Indeed, for constant environmental conditions, the model predicts that the correlation of cell cycle duration is,

$$C(n)=\langle \delta \tau (0)\delta \tau (n)\rangle /\langle \delta {\tau }^2(0)\rangle ={\left[\frac{1/{{\sigma }_2}^2-\alpha /{{\sigma }_1}^2}{1/{{\sigma }_2}^2+1/{{\sigma }_1}^2}\right]}^n$$ (10)

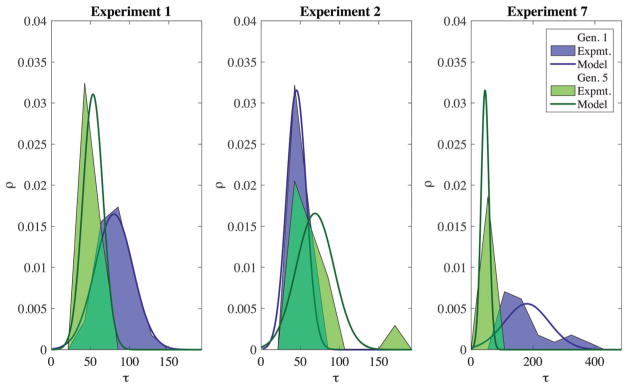
Since (σ₁,σ₂) depend on environmental conditions, this result is a way to use steady state cell cycle correlations to obtain M. In addition, it is possible to explicitly obtain transition probabilities from the experimental data. Fig. 4 shows an overlay of our model M and the data collected for the initial and final distributions of three representative experiments. For a more complete comparison see Fig. S1 (Section II B), and Fig. S6 and S7 (Section IV C) (ESI^†).

Fig. 4.

Comparisons between model and experiment of the initial (generation 0) and final distributions (first generation at which the population is equilibrated to the final state) from three representative experiments. The x-axis is τ (min): the cell cycle duration and the y axis is ρ (1/min): the probability density. The three experiments displayed are, from left to right: Experiment one, nutrient increase; Experiment two, nutrient decrease; and Experiment seven, the removal of the highest osmotic stress tested.

III. Results

A. Growth rate is inversely correlated with CCDD variance

We first sought to determine how the variance of the cell cycle duration distribution (CCDD) correlates with the mean ensemble growth rate. The duration distribution is best described as a shifted gamma distribution: $\frac{1}{\mathit{\Gamma }(K){\theta }^K}{(\tau -{\tau }^{\ast })}^{K-1}{\mathrm{e}}^{-\frac{\tau }{\theta }}$, where θ and K are parameters. The mean growth rate r of the population is obtained by solving⁷

$$\tau \ast r+Kln(1+r/\theta )=ln2$$ (11)

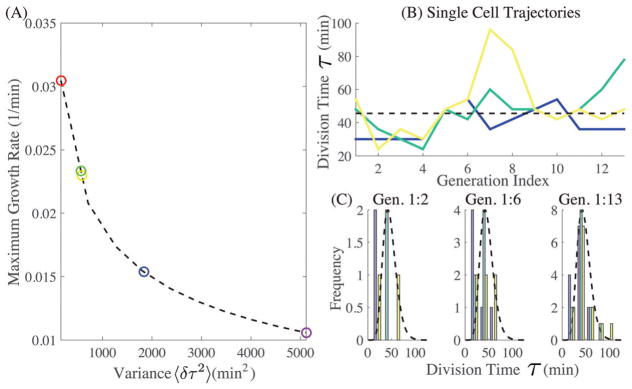
P(τ) is bounded on the left due to the finite time required to construct a new cell as discussed above. Given this minimum time τ^*, one may calculate the maximum growth rate for a given variance 〈δτ²〉 by changing parameters (K,θ). In Fig. 2, we set τ^* to be length of the shortest observed cell cycle and numerically calculated the maximum growth rate for variances ranging over experimentally observed values. Over this range, the maximum growth rate diminished by a factor of three as we increased 〈δτ²〉. Clearly, for this case of fixed τ^*, increased noise in the regulation of the cell cycle correlates with a lower growth rate. It is also important to note that cell division dynamics in E. coli appears to be ergodic: each individual mother cell explores the entire distribution and if data from a single cell is collected over a long period of time, the resultant distribution appears to match that of a collection of many cells at a single time, shown in Fig. 2. This suggests that there are no “persistor cells” that grow very slowly at all times to benefit the collective culture when subjected to harsh environments. More generally, it can be shown that given any CCDD with finite width, there exists a narrower one which attains the same growth-rate or greater (Section I, ESI^†). We note that the existence of “persistor cells” has been confirmed^15–18 in specialized cases and that these cells play an important role in culture survivability. From our analysis of division phenotypes in the mother machine, however, they do not contribute significantly to the measured CCDD.

Fig. 2.

(A) The maximum ensemble growth rate, r, where r is solved according to τ^*r + K ln(1 + r/θ) = ln 2, when τ^* = 12 min (the shortest division recorded) and K and θ are allowed to vary, as a function of variance (experimentally observed values are circles). (B) Single cell cycle duration trajectories (from 3 separate cells in the mother machine). The dotted line is the average duration. (C) The CCDD histogramed from single mother cells over different generation intervals (dotted line is the full distribution corresponding to the CCDD collected from the entire ensemble).

Thus, if an environmentally dependent τ^* is assumed, the population growth-rate is not improved by increasing the noise in the cell cycle duration distribution and from the usual definition of fitness, this would suggest cells should narrow this distribution to maximize the mean growth rate. However, there is an alternative hypothesis recently presented.^19,20 Suppose that the minimum time for a single cell cycle is not governed by some lower bound τ^*, but instead that the mean cell cycle time, 〈τ〉 is environmentally limited. In the case where the cell cycle distribution is not mean scaled, and the CV varies (it has been shown^19,20 that in some environments the CV is more variable than in the conditions we tested); the growth rate is positively correlated with the CV. In fact one may explicitly express, using the von Foerster equation when ρ(τ) is gamma distributed and unbiased (i.e. M(τ → τ′) = ρ(τ′)), the growthrate as a function of the mean and $\text{CV}:r=\frac{1}{\langle \tau \rangle {\text{CV}}^2}\left(2^{{\text{CV}}^2}-1\right)$. It is clear from this formulation that the growthrate is positively correlated with the CV. This phenomenon has been investigated in both bacterial systems without the consideration of epigenetic inheritance¹⁹ and in yeast including epigenetic inheritance²⁰ which seems to magnify the effect. We focus on the case where the CV is roughly constant and without the consideration of epigenetic inheritance; but for cases where the CCDD are poorly mean scaled, epigenetics make a big impact, or the mean cycle duration is limited while τ^* is effectively zero, we want to make it clear to the reader that the results of this paper are incomplete and wish to direct them to the work referenced above.^19,20

Alternatively this noise may be intrinsic to underlying molecular mechanisms; and stochasticity is prevalent in gene expression,^21,22 polymerase activity,²³ and chemotaxis.^24,25 Cells might require higher energy consumption (sacrificing energy efficiency which carries its own evolutionary importance²⁶), or an increase of τ^* (increasing minimum duration) to minimize noise. Here we probe the potential costs for the observed programmed non-genetic heterogeneity assuming an environmentally dependent τ^*.

B. Cell response rate is inversely correlated to mean growth rate and positively correlated to noise

We observed the response of CCDDs ρ(τ,n) in a series of step change experiments where for time t < 0 cells were exposed to a constant environment, and at t = 0 the environment was altered in such a way that the new mean cell cycle duration was measurably different (see Section III, ESI^†). The results are for E. coli in a mother machine, but we also conducted a series of bulk temperature shift experiments to compare with the micro-fluidic results (see Section V, ESI^†). Fig. 3 shows the results of the eight environmental shift experiments conducted. The top row contains relaxation experiments where the cells were grown in suboptimal conditions including one nutrient limited and three hypertonic solutions (where the osmolarity was increased with the addition of Sorbitol) before shifting the media to the optimal environment (in diluted LB medium) for fast growth. The bottom row are the reverse, stress experiments. The model is able to predict the time course of cell response, including the overshoots observed in severe stress conditions (Fig. 3)

The trend across the top row in Fig. 3 is clear: as the magnitude of the shift increases (left to right), the response speed (change in the mean divided by the time over which the change occurred) increases as well. A complementary trend may be observed on the bottom row: as the severity of the stress increases (left to right), the response speed also increases (see Fig. 5A). However, while for the relaxation experiments (top row) response speed directly correlates with adaptability, for the stress experiments (bottom row) this is not the case. We consider an adaptable cell to be one which responds “efficiently” to environmental changes in terms of its growth rate alone. (Here we observe negligible filamentation rates and cellular aging is not an issue as cells were only followed for fewer than fifty generations.) Thus an efficient response is considered to be one where the growth rate is as high as possible for as long as possible. In the case of the relaxation experiments (top row), the faster the response speed, the greater the adaptability as a greater response speed allows the cell to spend more time in a fast growth state. For the stress experiments (bottom row) the reverse is true: the greater the response speed, the less time the cell is able to remain in the fast growing state. In fact, we have observed that for severe environmental stresses, cells respond so inefficiently that they attain a growth rate during the period of response which is even lower than that of the final stable growth rate (e.g. Fig. 3 last panel). Thus, to compare the efficiency of response across all experiments, we proposed to use a new quantity, Δ,

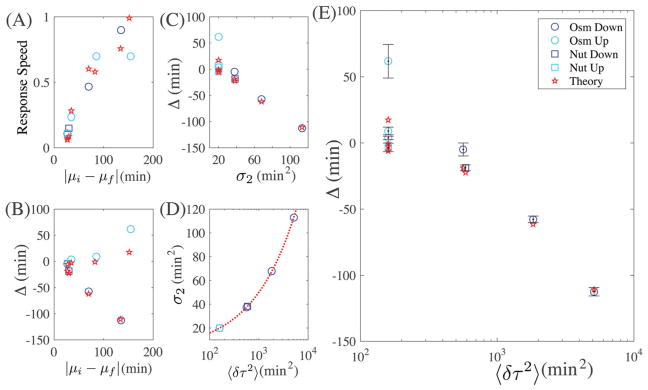
Fig. 5.

(A) Average cell response speed vs. shock severity: |μ_f − μ_i|. (B) Δ vs. shock severity |μ_f − μ_i|. (C) Δ vs. σ₂ for the initial ensemble before the step change. (D) σ₂ vs. variance of the cell cycle duration 〈δτ²〉 derived from the autocorrelation function before the step change. (E) Δ vs. variance (bars denote standard deviation). As the variance of the initial CCDD before the environment change increases, Δ decreases, and thus the response efficiency improves. Theory results are displayed as red lines or stars.

$$\mathit{\Delta }=\langle \frac{1}{\lambda }{\int }_0^{\lambda }\tau (t)\mathrm{d}t\rangle -max({\mu }_{\mathrm{i}},{\mu }_{\mathrm{f}})$$ (12)

where the environment step change occurred at t = 0, λ = 500 min is the minimum period for all eight experiments to complete the response to their new environments, and the average 〈 〉 is taken over all cells. (Note that the trends observed are maintained over a wide range of λ. See Section IV, ESI.^†) μ_i,f is the steady state average cell cycle duration before and after the step change, respectively. When Δ is large and positive, the cells respond so inefficiently that during response they grow even slower than in the stationary state corresponding to the stressed condition. When Δ is large and negative, the cells are able to remain or enter in the fast growth state for the majority of the response period. We analyze these results in the context of a phenomenological model introduced below.

C. Phenomenological cell cycle state model

As introduced in the Methods section, we consider a sequence of cell cycles (τ₁, τ₂,…) and the change of the cell cycle distribution over generations, ρ(τ,n) where n is the index of generation. For a constant environment at long times, cells are at steady state in the mother machine, and ρ(τ,n) ≡ P(τ) shown in Fig. 1. For a changing environment, we consider a Markovian stochastic model for ρ(τ,n), which describes the change of this distribution from one generation to the next as

$$\rho ({\tau }^{\prime },n+1)=\int \mathrm{d}\tau M(\tau \to {\tau }^{\prime };\varphi )\rho (\tau ,n)$$ (13)

where M is the transition probability, which depends on the current environment described by ϕ.

In constructing M, we considered the following: organismal survival depends on two broad qualities – stability and adaptability. Stability is a measure of short-term fitness, how precisely a system can maintain conditions optimized for a constant environment. Adaptability is a measure of long-term fitness, how quickly a system is able to achieve optimized conditions when introduced to a new environment. For example, in the context of genetic evolution, a more mutable genome offers an organism less stability but improved adaptability over many generations both through simply allowing for greater genetic diversity at any given time^27,28 and high mutation rates.^29,30

Motivated by these ideas in conjunction with the “constant-adder model”^12–14 and older foundational work,³¹ we propose the following approximate Gaussian model for the cell cycle dynamics.

We take into account two sources of regulation for cell cycle duration – optimization of protein synthesis rates to the current environment (instantaneous information), and the maintenance of proteome similarity to the mother cell (inherited information). Let us begin with the shorter argument – the comparison of proteome composition between mother and daughter cells. We assume that the greater number of proteins shared between the mother and daughter cell, the smaller the difference between their cycle durations. As proteome inheritance is roughly normally distributed, we approximate the cycle duration τ′ (of the daughter cell) to be normally distributed with mean τ (the cycle duration of the mother cell) and some unknown variance σ₂². At the beginning of a cell cycle, a cell’s proteome is entirely inherited from proteins present in the mother cell. One source of noise inherited from the mother is due to protein partitioning. The probability of inheriting m proteins from a mother cell containing N proteins is given by the symmetric binomial distribution $P(m)=\frac{N!}{m!(N-m)!}\frac{1}{2^N}$. For N very large, this distribution is well approximated by a Gaussian distribution of mean $\frac{N}{2}$ and variance $\frac{N}{4}$. These inherited proteins constitute roughly half of the cell’s final proteome (or the proteome of the cell at the time of its division) though this fraction differs based on the number of proteins inherited and degradation rates. Taking these considerations into account, we expect the term representing the regulation of proteome similarity between mother and daughter cells to take the form:

$$M_2(\tau \to {\tau }^{\prime })=Aexp\left[-\frac{1}{2{{\sigma }_2}^2}{({\tau }^{\prime }-\tau )}^2\right]$$ (14)

It is unclear if this partition noise bears significant weight on the CCDD, but it may be noted that if it does, it is likely there will be an anticorrelation between sister cell cycle durations.

Now we will handle the optimization of protein synthesis. Let us begin by describing the simplest construction of the constant-adder model: let us define a mean protein/DNA synthesis rate of k proteins/DNA per minute, and say that the cell must synthesize additional N proteins/DNA during its cell cycle. From a uni-directional stochastic mass accumulation model we get a gamma distribution for the probability of reaching size N at time t (for N ≥ 1):

$$\pi (N,t)=\frac{k^{N+1}}{\mathit{\Gamma }(N+1)}{t}^N{\mathrm{e}}^{-kt}$$ (15)

with a mean of $\mu =\frac{N+1}{k}$ and variance ${{\sigma }_1}^2=\frac{N+1}{k^2}$ (see Section II, ESI^†). Since k depends on the environmental condition ϕ, both μ and σ₁ depend on ϕ. As long as N ≫ 1, this distribution is suitably symmetric, and we may well approximate the transition probability with a Gaussian function (in terms of t ≡ τ′) with the given mean and variance:

$$\pi (N,t)\approx M_1({\tau }^{\prime })\equiv \frac{1}{\sqrt{2\pi }{\sigma }_1}exp\left[-\frac{1}{2{{\sigma }_1}^2}{({\tau }^{\prime }-\mu )}^2\right]$$ (16)

As mentioned in the Methods section, we maintain some current state dependence in the adaptive term so that we may allow for a negative correlation between adjacent generations at steady state, as predicted by the constant adder model. Work has shown^6,12 subsequent cell cycle durations to be anticorrelated (i.e. if τ is above the mean, the most probable state for τ′ is below the mean). The biological motivation for our implementation of the current state (τ) dependence is described below.

In what follows we will describe what may be the original “sizer”, or mass-accumulation, model described by Bremer and Chuang in 1981.³¹ We do not wish to imply that we believe the “sizer” model to be a good substitute for the “constant adder” that has proven so robust in recent studies,^12,13 but merely that when interpreted as a product of two weighted regulatory tendencies (mass-accumulation and proteome maintenance), the “constant adder” can be even more widely applied to cell populations experiencing variable environmental conditions. We begin by breaking down the cell cycle into three smaller stages. Consider the cell cycle to be composed of three periods τ^A, before the initiation of DNA replication, τ^B, during replication, and τ^C after replication:

$$\tau ={\tau }^A+{\tau }^B+{\tau }^C$$ (17)

Bremer and Chuang found that the time between associated points in replication from generation to generation (e.g. the time between the initiation of replication in the mother cell and daughter cell or termination of replication between cells) were highly conserved. (We would like to note that there were other studies conducted which focused on similar issues around the same time³² though, to our knowledge, recent interest in the topic has depreciated. Nonetheless, there has been more modern work³³ focusing on the tight regulation of the DNA replication time in cyanobacteria partly aimed to probe where this regulation breaks down.) This implies (where generation n is denoted τ_n):

$${\tau }^B=\text{constant}\equiv B$$ (18)

and furthermore:

$${\tau }_{n-1}^C+{\tau }_n^A=\text{constant}\equiv D$$ (19)

So we can write down an expression for the nth division time in terms of the preceding n −1 division time:

$${\tau }_n={\tau }_n^A+{\tau }_n^B+{\tau }_n^C=(D-{\tau }_{n-1}^C)+B+{\tau }_n^C=(D+B)+{\tau }_n^C-{\tau }_{n-1}^C$$ (20)

Now, D + B is simply the mean the total cycle time (relabeling it μ). With this we have:

$${\tau }_n=\mu +{\tau }_n^C-{\tau }_{n-1}^C$$ (21)

Continuing, we know ${\tau }_n^C$ is just some fraction α₁ of the total mean and similarly ${\tau }_{n-1}^C$ is some fraction α₂ of the total division time τ_n−1:

$${\tau }_n=\mu +{\alpha }_1\mu -{\alpha }_2{\tau }_{n-1}$$ (22)

Approximating the fraction of the cell cycle accounted for by region C as constant across each generation, i.e. α₁ = α₂ ≡ α yields:

$${\tau }_n=\mu +\alpha \mu -\alpha {\tau }_{n-1}=\mu +\alpha (\mu -{\tau }_{n-1})$$ (23)

We note that this may be a very poor approximation under certain conditions. We merely make this assumption to reduce the complexity of the model and provide an analytical solution. Therefore, on average, we have

$$\langle {\tau }_n\rangle =\langle \mu +\alpha \mu -\alpha {\tau }_{n-1}\rangle =\mu +\alpha (\mu -\langle {\tau }_{n-1}\rangle )$$ (24)

Similarly, we want an expression for the variance:

$${\sigma }^2({\tau }_n)={\sigma }^2(\mu +{\tau }_n^C-{\tau }_{n-1}^C)={\sigma }^2(\mu -{\tau }_{n-1}^C)+{\sigma }^2({\tau }_n^C)={\sigma }^2({\tau }_n^C)\equiv {{\sigma }_1}^2$$ (25)

Applying the stochastic protein synthesis argument above restricted to period C yields:

$$M_1({\tau }_{n-1}\to {\tau }_n)\approx Aexp\left[\frac{1}{2{{\sigma }_1}^2}{({\tau }_n+\alpha {\tau }_{n-1}-(1+\alpha )\mu )}^2\right]$$ (26)

We have provided physiological motivation for a weighted averaging of the current state and the mean of the total distribution; however, as we are primarily interested in a generalizable phenomenological model and are unable to retrieve the value for α from experiment, we will use the symmetric average α = 1 during data fitting for simplicity. Though this parameter selection loses physiological significance, the trends observed do not meaningfully change when a smaller alpha value is used. The total transition probability from τ of the mother cell to τ′ of the daughter cell should balance the inherited information with the process of protein/DNA synthesis. Therefore we expect:

$$M(\tau \to {\tau }^{\prime })\propto \text{exp}\left[-\frac{{({\tau }^{\prime }+\alpha \tau -(1+\alpha )\mu (\varphi ))}^2}{2{\sigma }_1{(\varphi )}^2}\right]\times exp\left[-\frac{{({\tau }^{\prime }-\tau )}^2}{2{\sigma }_2{(\varphi )}^2}\right]$$ (27)

where σ₁, σ₂ are positive constants describing the noise, and μ is the mean cell cycle duration for a given condition ϕ. σ₁, σ₂ and μ all depend on the current environmental variable ϕ. α is a constant between 0 and 1, representing the fraction of the cell cycle after DNA replication has terminated and before septum formation see Section II (ESI^†) for more details.

D. Model and experiment comparison

Our model has four parameters, α, μ, σ₁, and σ₂. As mentioned above, because we are unable to retrieve the value of α from experimental data, we assume α = 1 for all experiments. μ is always set to be the mean of the CCDD corresponding to the stationary distribution. The values selected for σ₁ and σ₂ are at the heart of our discussion since the adaptability of the culture depends on the relative weight of these terms. We may express σ₁ and σ₂ given only μ for the stationary distribution, CV for stationary distribution, and a third quantity Π: ${\sigma }_1=\sqrt{2(1+\mathit{\Pi })}\text{CV}\mu ,{\sigma }_2=\sqrt{2(1-\mathit{\Pi })}\text{CV}\mu$. Π is retrieved from the steady state autocorrelation function C(n) = Πⁿ, or directly from the experimental response curve, 〈τ_n〉 = 〈τ_n−1〉Π, where the index is taken to be over generations succeeding the switch i.e. n = 0 corresponds to the generation over which the environmental switch occurs. Please see Section IV (ESI^†) for more details regarding the fitting. We compare both fits in Section IV C Fig. S6 and S7 (ESI^†).

When we fit directly to the experimental response curve, since the experiment is a step change, we use the mean and CV of the final stationary distribution. It may be noted that in Fig. 3 we show the result corresponding to the case where Π is fit directly to the experimental response curve. Fig. 4 shows an overlay of our model M and the data collected for the initial and final distributions of three representative experiments. For a more complete comparison see Fig. S1 (Section II B, ESI^†). The model is able to well fit and replicate, quantitatively, the response curve for both the mean and variance of the CCDD. It may be noted that while the model does recapture the nonmonotonic responses associated with strong osmotic shock from rich to stressed conditions (experiments 6 and 8), it does not lend itself to a clear interpretation regarding the mechanism behind this behavior. We interpret the overshoot of the final mean cycle duration to be attributable to the cell slowing division in order to restructure its proteome to fit the new condition (perhaps the synthesis of more active pumps to remove the osmolite); however, we cannot provide a more detailed explanation.

Our experiments show, the response speed increases with increasing environmental shock severity over all trials which implies two things: firstly, the stronger the osmotic shock, or nutrient depletion, the faster the culture leaves the fast-growth state (which may be unsurprising). Secondly, this means that when stressed cells are introduced to a rich environment, the slower they are growing before the environmental switch, the faster the rate of response. On the other hand, we find that Δ for the shock and relaxation experiments display two opposing trends: as the severity of the environmental change, measured as |μ_i − μ_f| increases, Δ decreases for the relaxation experiments and increases for the stress experiments (see Fig. 5B). Clearly the response efficiency cannot be predicted from the severity of the environmental change alone. If non-genetic heterogeneity plays a role in cell adaptation, there is a parameter that should be well correlated with response efficiency, σ₂. As σ₂ (calculated from the initial state) increases, the similarity between mother and daughter cells decreases –which should make the cell more adaptable. We find that this agrees with experiment: as σ₂ increases, Δ decreases (Fig. 5C). σ₂ is not the ideal parameter for comparison, however, since it cannot be directly measured experimentally. It would be better if the same trend could be observed for the total variance, 〈δτ²〉, of the cycle duration distribution. Here we may utilize a result from the constant-adder model, which predicts that the autocorrelation function is conserved across different environmental conditions.¹² Given the autocorrelation function we can derive σ₂ with the variance of the ensemble. As the variance increases, σ₂ increases (Fig. 5D). Thus we know if σ₂ must be large for an efficient response, the variance must also be large for an efficient response. We find that this well agrees with experiment: as the variance of the initial CCDD increases, Δ decreases (Fig. 5E).

IV. Discussion

We may now return to answer our original question, “does increasing the noise in the mechanisms regulating the cell cycle correlate with decreased cell fitness?” We have discussed how increased non-genetic heterogeneity does indeed decrease the mean ensemble growth rate, and thus correlates with decreased cell fitness in this way; however, this noise does not seem to impair cell adaptability. Perhaps most strikingly, we see that cell response rate from a stressed condition to rich media is inversely correlated to the mean ensemble growth rate before the switch and positively correlated to the noise before the switch. Thus increasing the variance of the CCDD, attributable to increasing non-genetic heterogeneity of the culture, actually correlates with improved adaptability of the cell to environmental changes. In this way increasing the noise may actually correlate with improved cell fitness. This may be because with increased noise, cells can explore a wider range of phenotypes and some are already well suited for a new environment before it is introduced.

This idea falls into a rich discussion which seems to be gaining momentum: that even the simplest biological systems with minimal cooperativity exhibit mechanisms which limit growth for single cells at short times to boost long term growth. This is observed in budding yeast² where cells which cluster due to gravity selection exhibit an increased death rate. Clearly increasing the death rate for an individual cell lineage is deleterious for the growth of that lineage; however, it turns out that this phenomenon leads to a higher overall cell density and longer term growth rate due to the intrinsic geometric confinement of the yeast budding pattern. Similar spatial patterning is observed in slime molds³ where cells will actually synchronize their cycles which does not confer any clear single-cellular benefit though it does contribute to pseudo-multicellular phenomena. These cooperative phenomena are observed in bacteria as well. Recent investigation has probed what situations give rise to the emergence of a decoupling between the fitness of a collective and its constituent individuals.⁴ In a similar vein, it has been shown that bacteria will sometimes select to signal for slow growth while still at low density so that metabolism homeostasis may preserved for a longer period of time entering stationary phase at high densities.⁵ We think the phenomena described in this work are interesting in part because they do not appear to rely on cell–cell communication (growth in the mother-machine has limited signalling due to the low occupation of each microchannel and the high flow rate through the main channel hindering signalling between channels); yet they still fall into this class of ideas: long term bulk growth rate is improved through mechanisms which hinder short term single cell growth (in our interpretation, due to noise).

In other stochastic systems, the fluctuation dissipation theorem (FDT) expresses a similar concept. However, we have not proved this connection conclusively, since in E. coli, 〈δτ²〉 is positively correlated with the mean division time and one could also argue that a slower dividing cell responds efficiently. Alternatively, it could be due to the difference in the magnitude of the shift: larger environmental shocks result in faster response due to improved sensing. Though we interpret this improvement to be due to the noise, even if this effect is a product of the mean cell cycle duration or the magnitude of the environmental shift, we hope our presentation of this phenomenon will motivate further investigation. The conclusive proof that this phenomenon is due to noise alone requires comparison between strains that divide with the same mean, but different 〈δτ²〉. Such a construct is currently not available to us.

On much shorter time scales, noise in protein expression³⁴ has proven to be important for cellular robustness³⁵ and displayed clinical relevance: increasing the stochasticity of protein expression can help combat dormant pathogens such as HIV.³⁶ Here we showed that these short term fluctuations in the biochemical regulation of the cell cycle are correlated with the ability of a cell to adapt to a changing environment, analogous to the long term genetic adaptations³⁷ and complementary to long term memory of a periodic, fluctuating environment.^38,39 Our results here provide some motivation for the mean-scaling (or fixed CV) of CCDDs and their universal shape: when growing fast, cells may benefit most from stability where a greater gain may be achieved from optimizing growth for the current and immediate environment; however when growing slowly, cells might benefit more from improving their adaptability so that when superior growth conditions are presented they may respond efficiently to best utilize the new environmental conditions. When the mean cell cycle duration is large, it most benefits the population to be heterogeneous. When the mean is small it is best for the population to be homogenous.

Insight, innovation, integration.

Identifying mechanisms that govern cell cycle regulation is one of the fundamental questions in biology. In this paper, using a combination of modeling and microfluidic experiments in the test system of E. coli, we find that increased noise in the cell cycle time, while negatively impacting the overall cell growth rate, correlates to improved adaptability of the cell to changing environments. This suggests that stochastic noise in the cell cycle has an evolutionary role: a more variable cell cycle allows the cell to respond more efficiently to environmental changes.