A Cognitive Psychometric Model for Assessment of Picture Naming Abilities in Aphasia

Abstract

Picture naming impairments are a typical feature of stroke-induced aphasia. Overall accuracy and rates of different error types are used to make inferences about the severity and nature of damage to the brain’s language network. Currently available assessment tools for picture naming accuracy treat it as a unidimensional measure, while assessment tools for error types treat items homogenously, contrary to findings from psycholinguistic investigations of word production. We created and tested a new cognitive psychometric model for assessment of picture naming responses, using cognitive theory to specify latent processing decisions during the production of a naming attempt, and using item response theory to separate the effects of item difficulty and participant ability on these internal processing decisions. The model enables multidimensional assessment of latent picture naming abilities on a common scale, with a relatively large cohort for normative reference. We present the results of four experiments testing our interpretation of the model’s parameters, as they apply to picture naming predictions, lexical properties of the items, statistical properties of the lexicon, and participants’ scores on other tests. We also created a website for researchers and clinicians to analyze item-level data using our model, providing estimates of latent abilities and percentile scores, as well as credible intervals to help gauge the reliability of the estimated model parameters and identify meaningful changes. To the extent that the model is successful, the estimated parameter values may aid in treatment decisions and progress monitoring, or they may help elucidate the functional properties of brain networks.

Impaired picture naming (anomia) is common in most cases of aphasia and is assessed as part of most comprehensive aphasia test batteries. Picture naming has played an important role in aphasia assessment, due to its strong constraints of having well-defined targets and its engagement of the full complement of systems required to transform intentional meaning into speech sounds. Although picture naming accuracy is a relatively easily obtained and reliable test score (Walker & Schwartz (2012) report test-retest reliability of r(24) = .99), it is generally recognized as being influenced by multiple dissociable component processes (e.g., vision, attention, grammar, semantics, lexical access, morphology, phonology, syllabification, articulation, etc.). The types of errors that are committed can provide useful information for diagnosis and specific targeting of these component processes in treatment. In the context of aphasia assessment, naming errors are typically categorized with respect to their lexical status, semantic relationship to the target, and/or phonological relationship to the target. The relative frequencies of different response types may be informative on their own; for example, a high proportion of semantic errors suggests a deficit at the conceptual level of processing (Schwartz et al., 2009; Walker et al., 2011). Additionally, complex cognitive models have been used to make inferences about the integrity of theoretical components of a speech production system, given a distribution of response types (Foygel & Dell, 2000; Walker & Hickok, 2016). While these approaches are able to address the multifaceted nature of the task, they tend to neglect the differences among test items, despite a rich literature on how psycholinguistic properties of targets influence error rates (Harley & MacAndrew, 2001; Martin, Weisberg, & Saffran, 1989; Nickels & Howard, 1995, 1999, 2004; Swan & Goswami, 1997; Vitkovitch, Humphreys, & Lloyd-Jones, 1993). In the cases where item-level effects have been addressed (e.g., Gordon & Dell, 2001; Nozari, Kittredge, Dell, & Schwartz, 2010), a small number of parameter manipulations were implemented to demonstrate a plausible relationship between specific model components and item-level effects, rather than comprehensively incorporating item-level effects into the model on the basis of a full theory with the aim of assessment. On the other hand, the simple psychometric models that have been used to disentangle the effects of item difficulty and participant ability on picture naming responses usually treat accuracy as a unidimensional measure (Fergadiotis, Kellough, & Hula, 2015). We believe that if the picture naming task can be formalized at the proper level of description, the benefits of these approaches can be combined, providing an opportunity to improve the utility of picture naming performance for diagnostic and treatment outcome assessment as well as for informing mechanistic (i.e., neurocomputational) models of speech production.

Multinomial Processing Trees

A multinomial processing tree (MPT) model describes the information-processing steps that lead to responses in an experimental paradigm that has discrete categorical outcomes on each trial (Batchelder, 1998; Batchelder & Riefer, 1999). These internal processing steps can be formalized as a binary branching tree, where each bifurcation is associated with a parameter representing the probability of successful processing at that step, and each leaf node is associated with a response type. The probability of each response type is easily calculated as a product of the branches leading from the root node to the leaf node(s) of interest, and summing these products if there are multiple leaf nodes of the same type. MPT models have been constructed to explain performance on a wide variety of psychological tests (for a review, see Erdfelder, Auer, Hilbig, Aßfalg, Moshagen, & Nadarevic, 2009). The most similar MPT modeling work to that presented here is a study by Reiter (2000), which analyzed picture naming responses on the Boston Naming Test (Kaplan, Goodglass, & Weintraub, 1983) from individuals with cerebrovascular or Alzheimer’s dementia. MPT models are designed for specific testing paradigms, however, so the use of different test items, scoring protocols, and populations of interest precludes a direct extension to our data. Furthermore, while Reiter (2000) had the explicit aim of categorizing individuals by diagnosis, our goal was to create an interpretable measurement scale for picture naming abilities in the context of aphasia, that is, providing quantitative assessments of the computational integrity of the various processing stages involved in picture naming. Ideally, these quantitative assessments will be useful for clinical treatment decisions and progress monitoring, as well as characterizing functional brain circuits using neuroimaging techniques.

Building a model with parameters that are probabilities of successful processing (as opposed to network connectivity matrices, neuronal firing rates, neuroimaging signals, vocal tract configurations, acoustic spectrograms, etc.) has advantages and disadvantages; while the mechanistic propositions are intentionally vague, the statistical applications are well-understood. As Batchelder (1998, p. 332) proposes, “What is needed to transfer our knowledge of information processing into serviceable assessment tools is to develop simple, approximate models … Such models capture the fundamental information-processing events in a testing paradigm; however, they are pragmatic in the sense that they trade theoretical completeness for statistical serviceability.” While the serviceability of MPT models for assessment of individual participants has been demonstrated across many experimental paradigms, these models often assume homogeneity of test items. Because the MPT parameters can be conceptualized as probabilities of success, however, they are potentially compatible with formalizations from item response theory (see Supplementary Material for further discussion).

The picture naming task for aphasia assessment is a testing paradigm that can benefit from analysis with an MPT model that accounts for item and participant heterogeneity (Batchelder, 2010; Matzke, Dolam, Batchelder, & Wagenmakers, 2015). In the remaining sections, first we describe the participants and the picture naming data that were utilized for model development; next we turn to the details of the MPT model and the parameter estimation procedure; then we present the results of four experiments testing our interpretations of the model’s parameters. We conclude with a description of an online model fitting tool, along with a discussion of the model’s limitations and potential applications for research and clinical purposes. Our intended audience is both the clinician or researcher who may find immediate uses for this particular assessment tool, as well as the mathematical psychologist who may find opportunities to adapt or improve the framework presented here. To that end, we try to take a pragmatic approach by generally focusing on the utility of the model in the main text, and we provide model code and further rationale for our modeling decisions that we consider extraneous to the model’s essential use and interpretation in Supplementary Material.

Evaluating Anomia in People with Aphasia

Participants

We analyzed archived behavioral data from 365 participants with a single-event, left-hemisphere ischemic stroke and aphasia, from two different research institutions in different geographical regions of the United States. Two hundred seventy-five participants were examined at the Moss Rehabilitation Research Institute (MRRI) in Philadelphia, PA; their data were available from a public archive called the MAPPD database (Mirman et al., 2010; www.mappd.org). Ninety participants were examined at the University of South Carolina in Columbia, SC; they were recruited as part of a larger study of ischemic stroke, and represent a subsample of the 98 participants who were included in the examination of structural MRI and aphasia classification by Yourganov, Smith, Fridriksson, and Rorden (2015) and who also performed picture naming. Table 1 provides clinical and demographic characteristics for the two cohorts, separately and combined. The demographic data, clinical data, participant-level picture naming data, and participant-level parameter estimates used in this paper are available from: http://www.cogsci.uci.edu/~alns/MPTfit.php.

Table 1.

Demographic and clinical characteristics of the participants.

	MRRI	SC	Combined		MRRI	SC	Combined
N				Aphasia type*a
Participants	275	90	365	Anomic	118 (43%)	34 (38%)	152 (42%)
				Broca’s	62 (23%)	32 (36%)	94 (26%)
Gender				Conduction	48 (17%)	10 (11%)	58 (16%)
Female	118 (43%)	36 (40%)	154 (42%)	Wernicke’s	38 (14%)	6 (7%)	44 (12%)
Male	157 (57%)	54 (60%)	211 (58%)	Global	1 (0.4%)	7 (8%)	8 (2%)
				Transcortical Sensory	5 (2%)	0 (0%)	5 (1%)
Ethnicity*				Transcortical Motor	3 (1%)	0 (0%)	3 (0.8%)
White	145 (53%)	78 (87%)	223 (61%)	Missing	0 (0%)	1 (1%)	1 (0.3%)
African American	112 (41%)	11 (12%)	123 (34%)
Hispanic	3 (1%)	0 (0%)	3 (0.8%)	WAB AQ*a
Asian	1 (0.4%)	1 (1%)	2 (0.5%)	M	72.7	62.9	69.5
Missing	14 (5%)	0 (0%)	14 (4%)	SD	18.0	25.7	21.2
				min	25.2	15.8	15.8
Age (years)				median	76.5	68.4	74.5
M	58.8	59.9	59.1	max	97.9	96.5	97.9
SD	13.1	11.8	12.8	Missing	33%	2%	25%
min	22	36	22
median	59	62	59.5	Apraxia of Speech*b
max	86	83	86	Present	54 (20%)	36 (40%)	90 (25%)
Missing	5%	1%	5%	Absent	221 (80%)	54 (60%)	275 (75%)
Months post aphasia onset				PNT (% correct)*
M	29.9	37.0	31.6	M	60%	43%	56%
SD	46.3	46.2	46.3	SD	28%	33%	30%
min	1	6	1	min	1%	0%	0%
median	11	22	13.5	median	69%	42%	62%
max	381	276	381	max	98%	96%	98%
Missing	5%	1%	5%

Measures marked with an asterisk (*) exhibit significantly different (p < .05) proportions or means between the MRRI and SC cohorts, according to two-tailed Fisher’s exact tests for 2 categorical variables, Chi-squared tests of independence for more than 2 categorical variables, and unpaired two-tailed t-tests for continuous variables.

^aKertesz, 2007

^bClinical impression by speech-language pathologist

The participant cohorts exhibited clear statistical differences with respect to clinical measures (indicated in Table 1), with the SC cohort tending to present with more severe aphasia. The target populations for recruitment were similar for both projects, however, with hospital in-patients being approached as well as members of local stroke survivor groups. The prevailing assumption is that the differences in the cohorts’ clinical characteristics were due to the offer of treatment during recruitment for SC studies along with a cautious optimism for improvement, while MRRI’s recruiters had to clearly communicate that participants were not expected to benefit from enrollment in their studies. Despite these differences in sampling methods, the underlying population of people with aphasia was theoretically the same, and we therefore combined the data to obtain broader coverage of the ability spectrum.

Picture Naming Data

Picture naming data were collected using the Philadelphia Naming Test (PNT; Roach, Schwartz, Martin, Grewal, & Brecher, 1996), a confrontation naming task consisting of 175 drawings of common nouns with high familiarity and name agreement. All participants were presented with all test items, yielding a total of 63,875 total naming trials for analysis. Each response was classified into one of eight categories, based on lexical status, semantic relatedness, and phonological relatedness (see Table 2). Lenient scoring to correct for articulatory motor impairment was not applied, to be commensurate with other naming measures (e.g., Fergadiotis et al., 2015; Kaplan et al., 1983; Kertesz, 2007). The psycholinguistic properties of the PNT items (frequency, length, and phonological density) and item-level model parameter estimates used in this paper are also available from: http://www.cogsci.uci.edu/~alns/MPTfit.php.

Table 2.

Picture naming response categories. A more complete description of the scoring rationale is provided by Roach et al. (1996).

Response Category	Code	Description	Example Target: cat
Correct	C	The response matches the target.	cat
Semantic	S	The response is a word with only a semantic relation to the target. Semantically related responses are judged by the scorer as having a taxonomic or associative relation to the target.	dog
Formal	F	The response is a word with only a phonological relation to the target. Phonologically related responses share the initial or final phoneme with the target, or a single phoneme in the same word position aligned from center to center, or two phonemes in any word position.	hat
Mixed	M	The response is a word with both a semantic and phonological relation the target.	rat
Unrelated	U	The response is a word with neither a semantic nor a phonological relation to the target.	fog
Neologism	N	The response is not a word, but it has a phonological relation to the target.	cag
Abstruse Neologism	AN	The response is not a word, nor does it have a phonological relation to the target.	rog
Non-naming Attempt	NA	All other responses, including omissions, descriptions, non-nouns, picture parts, and fragments are considered non-naming attempts.	I don't know

Preliminary analyses revealed significant variance in the response type rates across both participants and items. Under an assumption of homogeneity, responses should be interchangeable without disrupting the observed distributions and by randomly permuting the responses across participants or items, we can observe whether this is truly the case. Monte Carlo statistical tests (Smith & Batchelder, 2008) detected both participant and item heterogeneity in response type distributions (n = 10,000; both p < .0001). Similarly, one-way ANOVAs examining each of the response type rates across participants and items were significant (all p < .05), except for abstruse neologism rates across items. These results mean that the sample includes participants who tend to produce different response types and the picture naming test includes items that tend to elicit different response types. There is enough variance in the data to warrant an account of the statistical effects of items on naming response types.

A Cognitive Psychometric Model for Picture Naming

Model Architecture

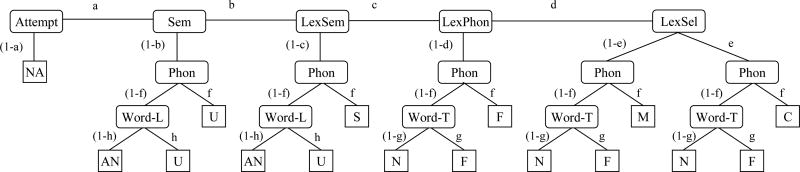
We created an MPT model that specifies a set of possible internal errors that lead to the various possible response types during a picture naming trial. The model’s architecture is informed by the interactive two-step theory of lexical access (Dell, Schwartz, Martin, Saffran, & Gagnon, 1997; Foygel & Dell, 2000), in particular, the two-step assumption; the MPT model remains agnostic with respect to interactivity among representations (see Supplementary Material for further discussion). The fundamental two-step assumption is that substitution errors during production can occur either at the whole word (lexical) level or the segment (phonological) level. We will use the terms word, lexeme, or lexical to refer to the former type of representations, and string, phonemes, or phonological to refer to the latter. Some error types are unambiguous with respect to their level of origin; semantic errors result from lexical substitutions and neologism errors result from phonological substitutions. Real word responses that are phonologically related to the target can arise from substitutions at either level, however, and a statistical model that considers the frequencies of different error types as well as test item properties can help identify the most likely origin. Figure 1 depicts the MPT model in a manner that emphasizes the two levels of linguistic representation which are assumed to be essential for word production: lexical and phonological representations. In order to name a picture, a participant must decide which word matches the picture, and which speech sounds express that word. The model has 5 probabilities that govern lexical selection processes, illustrated along the horizontal top level of the tree diagram, and the model has 3 probabilities that govern phonological processing after lexical selection, illustrated as descending branches from the second level of the tree diagram. Descriptions of the probabilities are provided in Table 3. Beside the separation of lexical and phonological processing levels, the MPT model adopts several more processing assumptions from cognitive theory about picture naming.

1. Errors of omission and commission result from separable (i.e., conditionally independent) processes. Therefore, non-naming attempts are the only responses that depend on a single parameter. This is a simplifying assumption that sifts lexical access errors from failures that may have occurred in peripheral systems (Dell, Lawler, Harris, & Gordon, 2004; but see Bormann, Kulke, Wallesch, & Blanken, 2008).

2. Some lexical errors require more correct processing than others (Schwartz, Dell, Martin, Gahl, & Sobel, 2006). A semantic error reveals at least partial retrieval of the pictured concept’s features. Additionally, a hallmark of the interactive theory of lexical retrieval (Dell et al., 1996) is that initial success during lexical selection may be undermined by feedback from concurrently activated phonological neighbors. Thus, a formal error at the lexical level reveals at least partial retrieval of the target word.¹ In the final stage of lexical processing, strong competitors that are both semantically and phonologically related must be rejected; mixed errors reveal this close proximity to the target. The MPT model’s architecture thus establishes a conditional gradient of correct processing over the possible lexical errors, from non-naming attempts to correct responses. The effect of this conditional gradient is that when we evaluate a probability of a particular lexical selection error, we are only considering “downstream” lexical selections as possible alternatives; the probabilities of “upstream” selections are already accounted for by other parameters.

   It is worth noting that this structure is one of many possible trees that can fit the data equally well with the same number of parameters. For example, lexical selection could be represented with 6 branches emerging from the root node, 1 for No Attempt and 1 for each of the 5 lexical selection possibilities, or the nodes at the lexical level of our binary branching tree could be reordered. The statistical properties of these models in terms of fit would be nearly identical to our binary branching model, although the values and interpretations of the parameters would be different (Batchelder & Riefer, 1999). We therefore do not view the conditional gradient in our binary branching model as a strong theoretical claim about serial processing stages at the lexical level; rather, it is a mathematically convenient and theoretically motivated way to describe the possible outcomes of lexical selection. This formalism deviates from the typical parallel processing approach, which, for example, usually treats Semantic and Mixed errors as arising from similar mechanisms and, thus, similar parameters. It is important to remember that the parameters in an MPT model are probabilities of success, and therefore a similar mechanistic source may be reflected in similar probabilities of successfully avoiding those errors (see Supplementary Material for further discussion), which is indeed the case for the LexSem and LexSel abilities in our sample. Somewhat side-stepping the issue of finding the best-fitting tree structure, we believe that experiments validating our interpretation of the model’s parameters, using data external to the model fitting procedure, are a more convincing demonstration of the model’s utility than fit statistics alone.

3. The probability that a phonological error results in a real word depends on the statistical structure of the lexicon and the generative rules for production (Dell, 1986). A phonological error is operationalized as a single phoneme addition, deletion, or substitution; the probability of a resulting real word depends on how many phonologically similar neighbors the original word has. This probability can be estimated for a specific lexeme or a random lexeme, depending on whether the phonological neighborhood of the selected lexeme can be assumed to be the same as the target, or is otherwise unknown. For example, if the target were cat, the probability of responses such as “rat” or “zat” is likely different than the probability of responses such as “umbrella” or “flurp”; in the former case, the probability of a real word is influenced by the target’s phonological neighborhood, while in the latter case, the probability of a real word depends on the lexicon as a whole. This difference becomes manifest in the MPT model through the use of the item-dependent Word-T parameter that describes the phonological density of the target lexeme, and the global Word-L parameter that describes the phonological density of the entire lexicon.

4. A probability on any given trial is determined by the participant only, the item only, the participant and the item, or a global constant that applies to all trials. The probability of identifying the correct semantic neighborhood of the picture (i.e., picture recognition) is assumed to depend on the participant only; the pictures themselves are assumed to be of approximately equal quality, with familiar targets. The probability of a phoneme change in the target word creating a real word is assumed to depend on the item only, while the probability of a phoneme change in a random word creating a real word is assumed to be the same on all trials. All other probabilities in the MPT model are assumed to depend on both the participant and the item, according to a Rasch model.

Figure 1.

The MPT model architecture. Nodes with rounded corners represent latent processing decisions, and leaf nodes with square corners represent response types. C = Correct, S = Semantic, F = Formal, M = Mixed, U = Unrelated, N = Neologism, AN = Abstruse Neologism, NA = Non-naming Attempt. Each branch is associated with a probability indicated by the letters a–h.

Table 3.

The MPT model parameters.

Parameter	Symbol	Description	Scope
Attempt	a	Probability of initiating an attempt	P&I
Sem	b	Probability of identifying the correct semantic neighborhood of the picture	P
LexSem	c	Probability of retrieving correct lexical-semantic information	P&I
LexPhon	d	Probability of retrieving correct lexical-phonological information	P&I
LexSel	e	Probability of selecting a target lexeme over competitors	P&I
Phon	f	Probability of retrieving correct phonemes	P&I
Word-T	g	Probability of a phoneme change in the target word creating a real word	I
Word-L	h	Probability of a phoneme change in a random word creating a real word	G

Scope abbreviations: G = globally independent of trial; P = participant dependent; I = item dependent; P&I = participant and item dependent.

Bayesian Estimation of Model Parameters

All analyses in this article were performed using MATLAB functions or custom scripts. We used Gibbs sampling to construct posterior distributions of the model parameters given the data with the JAGS software package (Plummer, 2003) and the MATJAGS interface (available from http://psiexp.ss.uci.edu/research/programs_data/jags/). Essentially, we begin with assumptions about the possible values of each parameter (prior distributions), and then randomly sample these values, keeping or rejecting them based on the how likely the data are to occur under those specified values. The resulting chain of samples approximates the most likely distribution of parameter values that generated the data (posterior distributions).

Prior distributions for ability and difficulty parameters were standard normal distributions, while prior distributions for probability parameters were standard uniform distributions. The model had 2,190 participant parameters (365 participants × 6 parameters), 1,050 item parameters (175 items × 6 parameters), and 1 global parameter, for a total of 3,241 parameters. The data were the 63,875 categorical naming response vectors, in the form of seven 0s and a 1 indicating the response category. Posterior predictive distributions were also generated; for each sample of parameter values, a prediction was made for the response type on each trial, and the most frequently predicted response type (the mode) was assumed to be the most likely response type.

Because the fitting procedure is stochastic, multiple sampling chains are randomly initialized and run in parallel to check for consistency in the resulting estimates. We ran 4 chains of 1,000 samples. Visual inspection of the chains showed rapid convergence and good mixing, indicating successful sampling of the posterior distribution (Lee & Wagenmakers, 2014). Agreement between the modes of the posterior predictive distributions and the observed data was 67.7%.

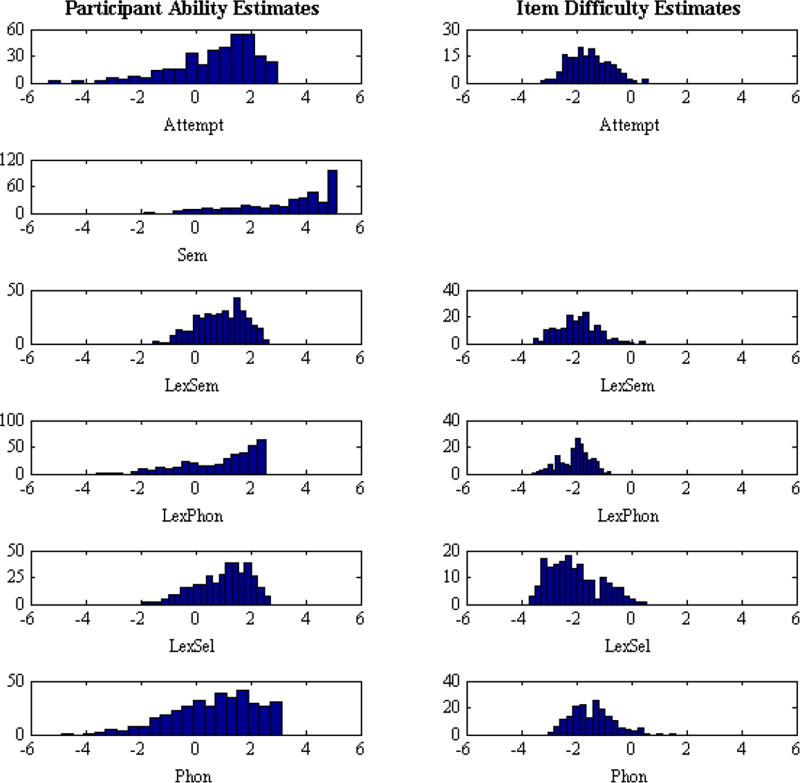
The means of the posterior distributions were taken as point estimates of the model’s parameters after observing the data. These represent our best guesses for the individual parameter values, which sit on a logit scale centered at 0 and range from approximately −6 to 6. The frequency distributions of the ability and difficulty parameter point estimates are shown in Figure 2. (Estimates for the Word-T and Word-L parameters, relating to the statistical structure of the lexicon, are discussed further in Experiment 3.) Consistent with our preliminary analyses, there appears to be plenty of variance among the estimated participant abilities and item difficulties. Under our prior assumptions, there would only be a single bar stacked at 0 for each of the parameters. The means of the posterior distributions have clearly been influenced by the data.

Figure 2.

Frequency distributions of posterior means for the MPT model’s ability and difficulty parameters. Although Sem is a probability, it was converted to a logit scale for consistency with the other parameters.

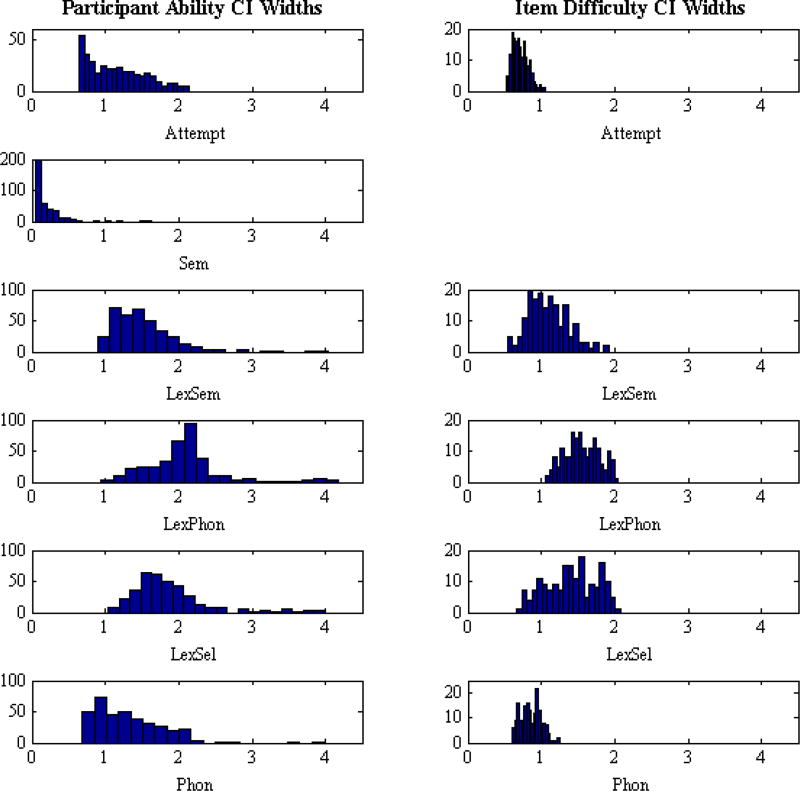
The Bayesian estimation procedure also provides an interval estimate for the parameters, a range of credible values; the width of the interval indicates how confident we can be in our point estimates. The frequency distributions of 95% credible interval (CI) widths are shown in Figure 3. A 95% CI for a parameter on the logit scale would have a width of approximately 4 under our prior distribution (i.e., 0 plus or minus 2 standard deviations); after observing data, a CI width of 1 would mean that we have eliminated approximately 75% of the prior credible parameter values. One notable result is that the LexPhon ability estimates carry the most uncertainty (largest CI widths), which is caused by the shared explanatory duty for Formal responses with the Phon parameter, combined with a higher position in the tree hierarchy. The takeaway point here is that the source of phonological errors is inherently more difficult to identify than other lexical errors by design of the model, and the Bayesian approach to parameter estimation captures this uncertainty. The most straightforward way to further reduce uncertainty in parameter estimates is to gather more data, perhaps by combining multiple baseline administrations of the PNT. Another notable result is that some participants have large CI widths due to many Non-Naming Attempts, which do not allow for further refinement of lexical access ability estimates. In these cases, the point estimates of ability are dominated by the means of the prior distributions, i.e., 0, which, given the task and multiplicative model structure, we view as an appropriately low estimate. We therefore include all ability estimates in further analyses; excluding participants based on CI widths does not substantially alter the results.

Figure 3.

Frequency distributions of posterior 95% credible interval (CI) widths for the MPT model’s ability and difficulty parameters. Although Sem is a probability, it was converted to a logit scale for consistency with the other parameters.

The distributions of the log likelihoods of the data under the fitted model for participants and items are shown in Figure S1. The log likelihood of the data is calculated using the log-transformed proportion of the posterior predictive samples that were attributed to the observed category on each trial, summed over participants or items. Although the absolute magnitude of a log likelihood can be difficult to evaluate on its own, the approximately normal shape of the distributions and lack of outliers indicate that the model’s estimates are not obviously favoring or neglecting specific participants or items. We demonstrate in Experiment 1 that the model still extracts useful information even for the worst-fit participant and item, those for which the model assigns the lowest probability to the observed data.

Validation of Parameter Interpretations

After estimating the parameter values that best fit the picture naming data, we examined two broad questions. (a) Does the model make reasonable predictions about picture naming data? A model of picture naming that makes wild, unfulfilled predictions is not a useful model; on the other hand, successful picture naming predictions provide evidence that the model’s parameters are working as intended (Experiment 1). Perhaps more importantly, (b) do the model’s parameters measure the intended constructs? Because the model is motivated by cognitive theory, the model’s components should apply to phenomena beyond the picture naming data used for model fitting. Item difficulties should relate to lexical properties of the items (Experiment 2), probabilities of phonological real word errors should relate to the statistical properties of the lexicon (Experiment 3), and participant abilities should relate to other behavioral tasks (Experiment 4).

Experiment 1

To evaluate the MPT model’s item-level picture naming predictions, we compared them with predictions from several other, purely statistical (i.e., data-driven), pattern recognition models. The goal was to determine whether the MPT model’s assumptions about the data-generating processes improve predictions, beyond what is available in the data, prima facie.

Method

This study did not receive research ethics committee approval, because it did not qualify as human subjects research; all data were pre-existing and de-identified. We used the picture naming data to create a guessing game, and we evaluated the accuracy of guesses that were informed by different models. Parameters are just a set of variables that can each take a value, a list of numbers, and a model is a set of rules that maps a set of data values into a set of parameter values, and vice versa. We have already described how the MPT model maps between its parameters and picture naming data, using the modes of the posterior predictive distributions. Although we use the term “prediction” here, the method is more akin to lossy compression; rather than withholding a small set of testing data, all of the data are used to obtain parameter values, which are subsequently used to reconstruct the data. We use the term “prediction accuracy” to refer to the fidelity of this reconstruction, i.e., the percent of items where the response category can be accurately recovered from the parameters.

We also provide an intuitive measure of prediction quality that we call “net profit.” Imagine that we set fair payouts for our game using the relative frequencies of response types in the entire data set,

$$P_k=\frac{{\sum }_{k=1}^K{X}_k}{X_k},$$

where P_k is the payout multiplier for a wager on response category k, X_k is the total number of responses in category k, and K is the number of response categories, so that recovering a less frequent response category is worth more. We bet 1 dollar per datum, wagering the entire dollar on a single response category. We can then calculate the expected net profit when using each model as our guessing strategy.

Alternatively, since the model generates probabilities, we could distribute 100 cents over the response categories in proportion to our expectations, but this would yield suboptimal gains. Consider a weighted coin that is known to result in Heads 60% of the time, so a fair payout multiplier is set, {H=1.667, T=2.5}. The payout multiplier is fair if the probabilities of the outcomes are common knowledge; whether we bet the entire dollar on Heads or Tails or split the wager 60/40, the expected net profit is 0. But if we learn that the person flipping the coin does it in such a way that results in Heads 70% of the time, making the original payout multiplier no longer fair, always betting on Heads gives better returns than splitting the bet 70/30. For example, making 10 bets with each strategy would result in expected net profits:

$${\mathit{\text{NP}}}_1=7\times (1.00\times 1.667)+3\times (0.00\times 2.5)-10.00=1.669$$

$${\mathit{\text{NP}}}_2=7\times (0.70\times 1.667)+3\times (0.30\times 2.5)-10.00=0.418$$

Our models are like informants that review the data and gather as much information as possible, then give us their best estimate of how the “real” odds on a naming trial deviate from the “fair” odds. Better information leads to better bets and more profit. Whether the gathered information (the fitted model) is useful outside of this context is a matter that we set aside for further validation experiments. Other popular model selection criteria, sometimes known as goodness-of-fit statistics, such as the Akaike information criterion (AIC), Bayesian information criterion (BIC), or deviance information criterion (DIC), make strong assumptions about the inherent value (or cost) of additional parameters, in order to address a concern that a model’s predictive value is driven by additional complexity, per se, rather than the intended theoretical constructs and thus may not generalize (Pitt & Myung, 2002). Here, we are explicitly interested in the raw predictive value of the MPT model, intentional or otherwise, and we compare it with other statistical models that have no theoretical constructs nor any expectations to generalize. The net profit metric allows us to directly evaluate the contribution of adding parameters or changing rules to the predictive value of a model in a pragmatic and familiar context, i.e., monetary value. We examined several comparison models along with a baseline and a ceiling model.

1. Uniform Random Model - Each prediction was randomly selected from the 8 possible categories with equal probability. This model was presented as a baseline for comparison, and the values are assumed to follow directly from probability theory. We use the expected value of the hypergeometric distribution to determine the number of accurate predictions for each response type. This model had 0 parameters.

2. Population Probability Matching Model - Each prediction was based on the relative frequencies of response types in the entire data set. For example, because 55.8% of all responses were correct, there was a .558 probability of predicting a correct response on each trial. This model had 7 parameters, one for each response type rate except one, which is determined by the parameters summing to 1.

3. Individual Probability Matching Model – Each prediction was based on the relative frequencies of response types for each individual participant. For example, if a participant had 95.0% correct responses, there was a .950 probability of predicting a correct response on each of the trials for that participant. Describing a participant’s naming profile in terms of the relative frequencies of responses is the same approach taken by models that assume homogeneity of items. This model had 2,555 parameters, which included 7 response type rates (with 1 determined rate) for each of the 365 participants.

4. Modal Model - Each prediction was based on the most frequently observed response type (i.e., the mode) for each participant. For example, if a participant has a plurality of responses that are neologisms, then all responses are predicted to be neologisms. This is an optimal guessing strategy when item-level information is unavailable. This model had 365 parameters, one for each participant.

5. Modal+Correction(badfit) Model - Each prediction was based on the mode for each participant, and for a limited number of responses that deviate from the mode, a 2-tuple of parameters rectified the prediction error; 1 parameter indexed the divergent datum and 1 parameter indexed the response category that was actually observed. Because the MPT model had 3,241 parameters, and the modal model only had 365 parameters, this model used the remaining 2,876 parameters to rectify 1,438 prediction errors. The choice of which predictions to rectify does not influence the total prediction accuracy, but it does influence the net profit depending on the relative frequency of the errors which are rectified. For this model, errors are corrected in order of the participants who have the most prediction errors under the modal model. This model had 3,241 parameters, the same as the MPT model.

6. Modal+Correction(Mix) Model – This model is the same as above, but corrections are made in order of the relative frequency of the response types. Because Mixed errors are the least frequent responses, they have the greatest impact on net profit. This model corrects 1,438 of the 1,587 Mixed responses in the data, in order to maximize the net profit.

7. Feedforward Neural Network Model - Each prediction was based on the output layer of a feedforward neural network model. The model was constructed using the MATLAB neural network pattern recognition tool, and 10 randomly initialized versions of the model were trained on the full data set using the default backpropagation method. Because this is a stochastic gradient descent method, different instantiations of the model can identify different local minima of prediction error. All units used the default sigmoid transfer function. The model architecture is illustrated in Figure S2. The model had 2 input layers, each a vector of 0s with a 1 indicating an item or a participant. Each input layer was connected to its own hidden layer, and these hidden layers were then connected to a common hidden layer leading to the output layer. The size of the hidden layers determined the number of connections in the model ((365 × N1) + (175 × N2) + ((N1 + N2) × N3) + (N3 × 8)), and thus the number of parameters. The model had 6 units in the hidden layer for participants, 5 units in the hidden layer for items, and 10 units in the common hidden layer. The model had 3,255 parameters.

8. Full Model - Each prediction is based on the full data set; the model is simply a list of the response types that were observed on each trial, so the predictions are perfectly accurate. This model is presented as a ceiling² for comparison. The model has 63,875 parameters.

Results & Discussion

The picture naming prediction results are presented in Table 4, and there are several noteworthy findings. As expected, randomly guessing is a poor strategy, even when the population frequencies are taken into account. When the participant-level frequencies are accounted for, performance dramatically improves, but total accuracy still remains worse than strategies that use the frequency mode or consider the individual item when making predictions. Three of the neural networks solely predicted correct responses, the mode for the full data set, and none of them predicted any lexical errors (semantic, formal, mixed, or unrelated). Perhaps the most striking result is that the MPT model had the highest total accuracy and correctly predicted every type of response. The results indicate that the MPT model’s predictions are at least as good as several different classes of data-driven, pattern recognition models; its cognitive assumptions are useful for explaining this type of data.

Table 4.

Item-level predictions and accuracy. The number of times each model predicted each type of response is given in the corresponding cell, with the accuracy percentage in parentheses. The total accuracy is the percentage of all trials that were accurately recovered by the model. The net profit is the expected return if the model were used as a betting strategy.

Model	# of parameters	Predictions								Total Accuracy	Net Profit
		Corr	Sem	Form	Mix	Unrel	Neolog	AbNeo	NonNam
Uniform (Random)	0	7,985 (55.83)	7,984 (1.37)	7,984 (1.95)	7,984 (0.49)	7,984 (1.04)	7,984 (7.18)	7,984 (0.65)	7,984 (16.69)	10.649	−30,363.30
ProbMatch (Pop.)	7	35,662 (55.831)	2,634 (4.12)	3,161 (4.95)	1,587 (2.48)	2,303 (3.61)	6,049 (9.47)	1,821 (2.85)	10,658 (16.686)	35.538	−15.93
ProbMatch (Ind.)	2,555	35,662 (72.091)	2,634 (5.28)	3,161 (10.25)	1,587 (1.89)	2,303 (14.20)	6,049 (20.76)	1,821 (18.73)	10,658 (42.072)	51.053	54,465.23
NNet-01	3,255	63,875 (55.831)	0 (0)	0 (0)	0 (0)	0 (0)	0 (0)	0 (0)	0 (0)	55.831	0.00
NNet-02	3,255	63,875 (55.831)	0 (0)	0 (0)	0 (0)	0 (0)	0 (0)	0 (0)	0 (0)	55.831	0.00
NNet-03	3,255	63,875 (55.831)	0 (0)	0 (0)	0 (0)	0 (0)	0 (0)	0 (0)	0 (0)	55.831	0.00
NNet-04	3,255	62,415 (56.589)	0 (0)	0 (0)	0 (0)	0 (0)	730 (33.7)	0 (0)	730 (37.8)	56.113	3,639.21
NNet-05	3,255	61,320 (57.014)	0 (0)	0 (0)	0 (0)	0 (0)	0 (0)	0 (0)	2,555 (36.44)	56.191	4,324.05
NNet-06	3,255	55,915 (62.146)	0 (0)	0 (0)	0 (0)	0 (0)	0 (0)	0 (0)	7,960 (47.88)	60.368	21,204.60
NNet-07	3,255	54,600 (63.081)	0 (0)	0 (0)	0 (0)	0 (0)	2,450 (35.84)	0 (0)	6,825 (54.29)	61.096	29,290.78
NNet-08	3,255	50,225 (67.624)	0 (0)	0 (0)	0 (0)	0 (0)	4,200 (31.76)	1,225 (36.16)	8,225 (56.24)	63.197	54,308.55
NNet-09	3,255	50,050 (68.248)	0 (0)	0 (0)	0 (0)	0 (0)	3,150 (29.90)	0 (0)	10,675 (49.977)	63.303	39,226.75
NNet-10	3,255	50,050 (67.968)	0 (0)	0 (0)	0 (0)	0 (0)	0 (0)	0 (0)	13,825 (46.944)	63.418	35,950.94
Modal	365	48,300 (69.892)	0 (0)	175 (25.7)	0 (0)	1,050 (30.57)	3,150 (39.71)	700 (50.7)	10,500 (54.752)	64.938	66,519.11
Modal+Correction(badfit)	3,241	48,074 (70.591)	80 (100)	274 (100)	43 (100)	1,141 (48.12)	3,281 (46.42)	934 (63.1)	10,048 (58.947)	67.189	93,582.82
Modal+Correction(Mix)	3,241	46,862 (72.037)	0 (0)	175 (25.7)	1,438 (100)	1,050 (30.57)	3,150 (39.71)	700 (50.7)	10,500 (54.752)	67.189	124,397.02
MPT	3,241	45,404 (74.016)	240 (33.3)	514 (32.1)	35 (26)	1,419 (29.88)	4,043 (49.00)	991 (42.8)	11,229 (58.180)	67.667	88,658.19
Full	63,875	35,662 (100)	2,634 (100)	3,161 (100)	1,587 (100)	2,303 (100)	6,049 (100)	1,821 (100)	10,658 (100)	100	447,125.00

It is worth considering the items and participants for which the MPT model made the worst predictions. The MPT model extracted profitable information even for the participant and item with the lowest posterior log likelihoods (and thus the lowest prediction accuracies): For the participant whose responses had the lowest predictability (24.6%) - a female participant with Wernicke’s aphasia who produced 3.4% Correct responses, 13.7% Non-Naming Attempts, and 27.4% Unrelated responses - the model’s net profit over the 175 items was $869.88. For the item that elicited responses with the lowest predictability (47.4%) - slippers, which prompted 33% Correct responses and 29% Semantic or Mixed errors - the model’s net profit over the 365 participants was $762.49. There was only a single participant for whom the MPT model’s predictions yielded a net cost ($-12.12) with 45.1% accuracy over the 175 items: a female participant with Broca’s aphasia who produced 45.1% Correct responses, 13.1% Non-naming Attempts, and 10.9% Neologism errors. Although the MPT model’s predictions yielded a slight loss of net profit for this participant, the prediction accuracy was no worse than guessing the mode (i.e., Correct) for each trial. The model’s predictions were profitable for each of the items over the 365 participants; the item with the minimum net profit, baby, prompted 78% Correct responses and yielded a net profit of $262.37. The MPT model offers predictive value for all participants and items in our sample, even in the worst cases.

If our objective were to maximize the efficiency of our model by balancing prediction accuracy with model complexity, then the modal model would be the winner. But identifying an individual participant as “mostly [response type]” reveals little else about their underlying pathology and their behavior in other contexts. Similarly, the modal models with correction maximize the net profit in a guessing game based on this specific dataset, but this is not our goal either. The main strength of the theory-driven MPT model is that its components are interpretable and should generalize to any data that rely on the same theoretical constructs. Future comparisons of the MPT model against other theoretically motivated models of picture naming should also benefit from investigations that go beyond goodness-of-fit statistics.

Experiment 2

A primary function of the extended MPT model is that it sorts test items by different types of difficulty. Some items are more prone to eliciting errors than other items, making them more difficult, but they may be difficult in different ways by challenging different naming abilities. Table 5 lists the top and bottom ranked items for each type of difficulty. Items like skull or plant are difficult because they have strong lexical competitors, like skeleton or flowers, respectively; items such as binoculars or stethoscope do not have strong lexical competitors, but they have strong phonemic sequencing and articulation demands. Easy items, on the other hand, are unlikely to elicit errors of a certain type. The Word-T parameter does not apply to a psychological ability, but rather describes each item’s phonological neighborhood, i.e., the probability that a phonological slip results in another real word. Items such as eye or pie have many similar sounding words that could result from slight aberrations, while items such as octopus or volcano do not.

Table 5.

The top and bottom ranked items for each type of difficulty (1 = easy or high probability, 175 = difficult or low probability).

Rank	Attempt	LexSem	LexPhon	LexSel	Phon	Word-T
1	cat	pen	eye	eye	man	eye
2	book	balloon	dog	bed	cat	pie
3	pen	well	ear	key	baby	nail
4	key	book	baby	hand	dog	hat
5	shoe	typewriter	apple	tree	cow	man
:	:	:	:	:	:	:
171	dinosaur	bowl	slippers	celery	volcano	thermometer
172	cheerleaders	glass	rake	helicopter	thermometer	stethoscope
173	stethoscope	slippers	microscope	slippers	microscope	ambulance
174	microscope	wig	broom	skull	binoculars	octopus
175	garage	van	crutches	plant	stethoscope	volcano

Previous research has demonstrated that lexical properties of words influence the types of responses that participants make when they try to produce them. Properties such as frequency, familiarity, age of acquisition, length, phonological density, and phonotactic complexity have all been identified as potentially important contributors to error opportunities. We tested whether some of these known lexical influences were observable in the item difficulty parameter estimates. The goal was to test a small number of psycholinguistic measures that we believed would exhibit clear relationships with the two major processing levels in the MPT model, lexical and phonological, rather than an extensive investigation of psycholinguistic properties of the items.

Method

This study did not receive research ethics committee approval, because it did not qualify as human subjects research; all data were pre-existing and de-identified. We obtained 3 psycholinguistic measures for each of the 175 target words on the PNT, from the Irvine Phonotactic Online Dictionary (www.iphod.com). We chose this database because it includes psycholinguistic measures for an ostensibly complete lexicon of American English, including pronunciation variants. In the current study, for words with multiple pronunciations, the most common one for American English was selected. None of the measures disambiguate different word senses. The 3 measures we chose were:

1. Lexical frequency (LexFreq) - The log transformed number of times the target word appeared in American television and movie transcripts. These data originate from the SUBTLEXus database (www.subtlexus.lexique.org), but are available from the IPHOD database as well.

2. Phonological length (PhonLeng) - The number of phonemes in the target word.

3. Phonological density (PhonDens) - The log transformed number of phonological neighbors, i.e., the number of words that are related to the target by adding, changing, or deleting a single phoneme.

We used ascending stepwise multiple linear regression to identify the significant unique contributions of these psycholinguistic measures to each of the item difficulty parameters and the Word-T probability parameter. (Word-L applies to the entire lexicon and does not vary across trials by item; we investigate this parameter further in Experiment 3.) We began with no predictors in the model, and then used a criterion (p < .05) for inclusion or exclusion of predictors. We expected lexical frequency would be associated with lexical selection difficulties, and we expected phonological length and density would be associated with phonological processing difficulty.

Results & Discussion

The results are presented in Table 6, with each row corresponding to a regression model, and the psycholinguistic measure with the strongest simple linear correlation is shaded. The sign of the coefficient is easier to interpret than the magnitude; positive coefficients mean that items become more difficult as the lexical measure increases, while negative coefficients mean that items become easier as the lexical measure increases. All of the item difficulties had at least one lexical property as a significant linear predictor. Higher lexical frequency reduced difficulty at all processing steps, including LexSem, consistent with previous studies (Kittredge, Dell, Verkuilen, & Schwartz, 2008). Word length influenced naming during later processing stages, with longer targets increasing difficulty during selection of the correct lexeme and corresponding phonemes. Phonological density had a facilitative effect on speech production, indicated by the negative coefficients in Table 6, again, consistent with previous studies (Gordon, 2002). We observed a general trend of more psycholinguistic variables predicting processing difficulty at progressively later stages, conforming with the notion of a cascading hierarchical processing system. Finally, phonological density was also the best predictor of the Word-T probability, in accordance with our expectations. The MPT model’s estimates of item difficulty have clear and sensible relationships with the lexical properties of the items and provide additional converging evidence for a multistep model of naming. The item difficulty parameters provide a new way to quantify the psycholinguistic processing demands of words in the English lexicon directly from aphasic picture naming responses.

Table 6.

Multiple linear regression models predicting item difficulty parameters from lexical properties. The linear coefficient associated with each predictor in each of the regression models is given in the corresponding cell. The strongest simple linear predictor is shaded. Item difficulty parameters are measured on a logit scale; the Word-T parameter is measured as a probability.

		Intercept	Lexical Property			Model fit
			LexFreq	PhonLeng	PhonDens	df	rmse	simple R2
Item Difficulty	Attempt	−0.04	−0.15		−0.24	172	.59	.29
	LexSem	−1.03	−0.14			173	.74	.05
	LexPhon	−0.49	−0.24			173	.47	.29
	LexSel	−2.04	−0.17	+1.03		172	.79	.28
	Phon	−0.26	−0.19	+0.42	−0.32	171	.41	.66
	Word−T	0.01			+0.10	173	.13	.47

Experiment 3

The probability of a phonological error producing a real word should depend on the distribution of phonological neighborhood densities in the lexicon, and this was confirmed in the previous section. Words with many phonological neighbors, such as cat, are more likely to create other real words through random phonological perturbations than words, such as helicopter, which have very few similar sounding words. These probabilities can be estimated directly through simulation methods by randomly replacing phonemes in a word to create a legal string and observing the frequency of real word outcomes. Because classical test theory assumes item homogeneity, previous investigations only addressed the average probability of a phonological real word error over the entire lexicon, corresponding to the MPT model’s Word-L parameter. Using sets of items from speech error corpora and picture naming studies, Dell and Reich (1981) and Best (1996) estimated that this probability ranged from .20 to .45 for the English lexicon. Dell et al. (1997) estimated that the average probability of a phonological real word error, for the PNT items specifically, was .26. Here, we use updated simulation methods to generate similar probability estimates, and then compare them to the MPT model estimates we obtained using actual picture naming responses.

Method

This study did not receive research ethics committee approval, because it did not qualify as human subjects research; all data were pre-existing and de-identified. We estimated the probability of a phonological error creating a real word by sampling from a model lexicon. Simulations and analyses were performed using custom MATLAB scripts. The lexicon included the 39,698 common entries from 3 different collections of American English words: the SIL word list collected from a university message board, the CMU pronunciation dictionary collected from several machine-readable dictionaries and open source submissions, and the SUBTLEXus database collected from television and movie transcripts. A phonological error was simulated by first selecting a word from the lexicon based on its relative frequency in the SUBTLEXus database, then selecting one of the phoneme positions randomly, and replacing vowels or consonants with phonemes of the same type based on the relative frequency of phonemes in the lexicon. If the replacement led to two of the same consecutive phonemes, one of them was deleted. If the resulting string existed in the lexicon, it was considered to be a real word. We calculated the rate of real word outcomes for 1,000 sets of 175 phonological errors. We found an average real word outcome rate of .21, with rates ranging from .15 to .27. This represents our prediction interval for the Word-L parameter and the average of the Word-T parameters. While this probability of real word outcomes may seem high to experts familiar with phonological errors in aphasia, it is important to remember that this is the probability of a single phonemic error resulting in a real word; in practice, multiple phonemic errors may occur during production, further reducing the chance of observing a real word outcome.

Results & Discussion

The mean of the posterior distribution for the Word-L parameter was .15, with a 95% credible interval ranging from .12 to .18. The estimate for the Word-L parameter is on the low end of our prediction range, and this may be due to the simulation procedure biasing estimates toward real word outcomes by starting with real words, or it may be due to human scorers biasing the data toward nonword outcomes by failing to recognize real words during a lexical decision task, or a combination of these. In any case, the results are still quite consistent with our simulation estimates. The average of the posterior means for the Word-T parameter, that is, the average expected phonological word error rate for the PNT items specifically, was .23. Again, these results are in good agreement with our simulation estimates. In striking contrast to the assumption of item homogeneity held by many previous models, however, the Word-T posterior means had a positively skewed distribution (Figure S3), ranging from .01 to .80. The MPT model is sensitive to these item-level statistics, using them to sort out potential sources of phonological relationships between targets and responses.

Experiment 4

Picture naming accuracy has been shown to correlate strongly with other measures of aphasia severity, and a data-driven analysis of a large test battery suggested that these relationships can be deconstructed further. Mirman, Zhang, Wang, Coslett, & Schwartz (2015) used principal components analysis to investigate the covariance between 17 behavioral measures, including PNT accuracy, from 99 participants with aphasia. PNT accuracy mostly loaded onto the first two principal components. The first principal component explained approximately 36% of the variance in PNT accuracy along with approximately 50% to 90% of the variance in tasks that required decisions about the meanings of pictures and words (Camel and Cactus Test, Pyramid and Palm Trees Test, Synonymy Triplets, Semantic Category Probe Test, Peabody Picture Vocabulary Test, and Semantic Category Discrimination). The second principal component explained approximately 38% of the variance in PNT accuracy along with approximately 42% to 72% of variance in tasks that required speech production (Philadelphia Repetition Test, Nonword Repetition Test, and Immediate Serial Recall Span). The Mirman et al. (2015) principal components analysis used data from all of the tasks to identify the orthogonal dimensions which account for the most variance in the full data set. Here, we adopted a theory-driven approach and used the MPT model parameters, estimated from the picture naming task alone, to predict performance on the same tasks that shared principal components with picture naming accuracy. The goal was to investigate whether the shared variance across behavioral measures can be explained in terms of our model’s assumptions about the processing abilities required for picture naming.

Method

This study did not receive research ethics committee approval, because it did not qualify as human subjects research; all data were pre-existing and de-identified. We examined scores on additional behavioral tests from all participants in the MAPPD database who had them available (n = 127), including the 99 participants from the Mirman et al. (2015) study. Synonymy triplets (SYN; word-word matching), Peabody Picture Vocabulary Test (PPVT; word-picture matching), and Camel and Cactus Test (CCT; picture-picture matching) represented measures requiring semantic decisions, while the Philadelphia Repetition Test (PRT), Nonword Repetition Test (NWR), and Immediate Serial Recall Span (ISR) represented measures requiring overt speech production. The same measures that we obtained for the MR cohort were not available for the SC cohort. Instead, for this group, the Pyramids and Palm Trees Test (PPT) represented a task requiring semantic decisions, and the repetition section from the Western Aphasia Battery (WAB-rep) represented a task requiring speech production. 76 participants were administered the Pyramids and Palm Trees Test. This test is a picture-picture matching test based on thematic co-occurrence, just like the Camel and Cactus Test, but it only has two alternatives per trial instead of four. The PPT measure therefore leads to a higher chance of success by guessing, pushing scores toward ceiling and reducing the overall variance. While this makes it a less ideal measure than the CCT, it should still depend on similar processes. One participant in the SC cohort was missing WAB data, leaving 89 for analysis. It is worth noting that the repetition section of the WAB involves repetition of words, phrases, and sentences of varying length, making it more like the multi-word ISR task than the single-word PRT task. We used ascending stepwise multiple linear regression to identify the significant unique contributions of the participant abilities to each of the behavioral measures. We began with no predictors in the model, and then used a criterion (p < .05) for inclusion or exclusion of predictors.

Results & Discussion

The results are presented in Table 7, with each row corresponding to a regression model, and the participant ability with the strongest simple linear correlation is shaded. All coefficients are positive, meaning that test scores increase as abilities increase. All behavioral measures had at least one naming ability as a significant linear predictor. Tasks requiring semantic decisions about words were best predicted by the LexSel ability, while the Phon ability explained tasks requiring speech production. The PPT measure is predicted by the Attempt ability, consistent with this parameter’s role in general processing external to the lexical system. The ISR and WAB repetition tasks require multiple words to be remembered and produced; the LexPhon ability governs interference and substitutions of whole words rather than segments, and is therefore a logical predictor for these tasks. While these tasks engaged the abilities required for production of multiple words, they still did not depend on the LexSem or LexSel abilities.

Table 7.

Multiple linear regression models predicting behavioral test scores from naming abilities. The linear coefficient associated with each predictor in each of the regression models is given in the corresponding cell. The strongest simple linear predictor is shaded. Test scores are measured as percentages; the ISR span is measured as a list length.

		Intercept			Participant Ability				Model fit
			Attempt	Sem	LexSem	LexPhon	LexSel	Phon	df	rmse	simple R2
Semantic Decision	SYN	63.3	3.84		4.14		4.70		123	11.3	.51
	PPVT	41.3		25.9			10.6		124	13.8	.47
	CCT	61.3	2.69				7.58		124	11.1	.47
	PPT	88.6	2.92						74	7.6	.36
Speech Production	PRT	58.6		25.2				5.94	124	11.9	.41
	NWR	37.7						11.8	125	19.0	.44
	ISR	2.1	0.20			0.24		0.27	124	0.77	.48
	WAB-rep	25.3	6.87	29.1		6.55		5.50	84	14.8	.62

Because we are attempting to measure latent psychological traits that cannot be observed directly, we do not believe that there are single, perfect test scores that will measure them definitively. Instead, theoretical constructs are abstractly defined in statistical terms by all possible measurements that depend upon them. The labels that we attach to these constructs are somewhat arbitrary. For example, Mirman et al. (2015) refer to their first principal component as a “semantic recognition” factor, while we prefer to identify the tasks that primarily load onto this component as measuring a “semantic decision” trait (or even a “symbolic association” ability); the point is that we are talking about a set of measurements that we believe depend upon the same latent psychological construct to a first approximation. We expect some discrepancies among these measurements due to inherent noise, data collection errors, broadly-defined constructs, or complex test score dependencies, and we therefore evaluate and discuss correlations among the measurements. The simple linear correlations between naming abilities and other test scores were stronger than those between any of the individual naming response types, except ISR and correct responses, and they were of the same approximate magnitude as the correlations between test scores of the same type. Correlations among semantic decision test scores (SYN, PPVT, CCT) ranged from .69 to .76, while correlations between the LexSel ability and these test scores ranged .69 to .71. Correlations among speech production test scores (PRT, NWR, ISR) ranged from .63 to .73, while correlations between the Phon or LexPhon ability and these test scores ranged from .64 to .69. If there is enough shared variance between the test scores to claim that they measure the same latent trait, as suggested by Mirman et al. (2015), then the MPT ability estimates seem to provide an equally good measure. While approximately 36% to 62% of the variance in other test scores can be explained by picture naming abilities, the point is not to replace these tests, but rather to supplement them with an independent measure of the same theoretical constructs. The sensible relationships that exist between picture naming abilities and other behavioral measures suggest that the MPT model’s parameters are indeed measuring useful theoretical constructs.

General Discussion

Naming impairments following stroke vary with respect to the frequency and types of errors that are committed. Responses might bear semantic and/or phonological relations to the target, and these response patterns can indicate damage at different levels of the mental processing hierarchy. During word production, it is assumed that substitution errors can occur either at the whole word or the segment level (Dell, 1986). A statistical model of the picture naming process can help to interpret picture naming responses in terms of latent selection probabilities and identify the most likely source of the errors. Furthermore, the picture naming targets vary with respect to the lexical properties that challenge these different processing levels, and modeling these effects can improve estimates of participant abilities, while also providing information about the specific difficulties associated with the items.

We created an MPT model that formalized the latent selection probabilities involved during word production, separating the effects of participants and items, and we used a Bayesian approach to estimate the model parameters that best fit a sample of 63,875 picture naming trials collected from 365 participants with stroke-induced aphasia. In Experiment 1, we compared the MPT model’s picture naming predictions with those from other pattern-recognition models that did not have any psychologically motivated components. We found that the MPT model’s predictions were more accurate and better distributed over the possible response types than the purely data-driven models. The MPT model extracted useful information for predicting picture naming responses from all participants, and to all items, in the sample. In Experiment 2, we investigated the relationship between lexical properties of the targets and the targets’ estimated difficulties. We found significant linear relationships between lexical properties and all item difficulties. Lexical frequency made a unique contribution to all of the latent processing decisions, while phonological length and density made unique contributions to the final selection and production of the phonological string. In Experiment 3, we investigated the relationship between the statistical structure of the lexicon and the estimated probability of a phoneme change resulting in a real word. Estimated probabilities were consistent with simulations of phonological substitution errors using a model English lexicon, and their distribution highlights a contrast with models that assume this probability is the same for all items. Factoring these item differences into model estimates can help to refine the localization of errors within the processing hierarchy. In Experiment 4, we investigated the relationship between estimated participant abilities and other test scores that depend on the same psychological constructs. Test scores that required semantic decisions (word-to-word, word-to-picture, and picture-to-picture matching) had a significant, unique contribution from the LexSel ability, but not the Phon or LexPhon abilities. Test scores that required spoken production of single words (word and pseudoword repetition) were best predicted by the Phon ability, which governs substitutions at the segment level, while test scores that required spoken production of multiple words (list, phrase, and sentence repetition) were best predicted by the LexPhon ability, which governs substitutions of similar sounding lexemes at the whole word level, though these test scores also had a significant, unique contribution from the Phon ability; none of the repetition test scores had significant, unique contributions from the LexSem or LexSel abilities. Taken together, our experiments provide substantial support for our interpretations of the model’s parameter values.

Potential Applications

The PNT and our accompanying MPT model were designed particularly with research purposes in mind, but we hope that clinicians may also find it to be a useful tool. We have shown that the ability estimates provided by the model relate to psychological constructs of interest better than the individual response type frequencies, opening the possibility for novel investigations into behavioral and anatomical relationships. Lesion-symptom mapping studies may benefit from improved quantitative assessments of the symptoms, and functional neuroimaging studies may find uses for item difficulty estimates in experiments designed to manipulate brain activity. The localization of error sources within different levels of a mental processing hierarchy may aid clinicians in making therapy decisions, by choosing to focus on the identified problem areas during treatment, and could provide useful metrics for evaluating recovery progress.

The credible intervals for parameter estimates have a natural application to longitudinal studies of treatment effects, by providing a way to approximate the likelihood of an observed change in ability. The less that the posterior distributions from independent test administrations overlap, the more likely it is that a change occurred in the latent ability. By considering the distribution of response types and different kinds of naming abilities, treatment effects may be observable that would not otherwise be detectable in the overall accuracy score. Future work may seek to incorporate items from other popular naming tests by placing them on the same difficulty scales as the PNT, which could enable comparison across a much wider range of measures.

Model Fitting Online

We created a website, available at http://www.cogsci.uci.edu/~alns/MPTfit.php, that provides picture naming ability estimates for a given set of item-level PNT data. We have provided examples of formatted data on the website to help users familiarize themselves with the model’s inputs and outputs. After scoring a PNT, item-level data are often entered into a spreadsheet; if the rows are sorted alphabetically by target, then a column of data representing an individual participant’s responses can be copied and pasted into the form on the website.

The online fitting procedure assumes fixed item difficulties for computational simplicity, meaning that it uses a point estimate for each item’s difficulty instead of considering a distribution of possible difficulty values, adopting the posterior means that were obtained from fitting the model to the large data set presented in this article. The website employs a simple Metropolis-Hastings sampling algorithm programmed in PHP, rather than installing JAGS on the server to implement Gibbs sampling. The sampler runs 2 chains with 5,000 samples using a normal jump distribution with a standard deviation of 0.1, and discards the first 2,500 samples as burn-in. The sample average (i.e., the posterior mean) is used as a point estimate of ability. Correlations between the ability point estimates obtained with the different sampling methods, Gibbs and Metropolis-Hastings, ranged from .94 to .98. Percentile scores for abilities are calculated relative to the posterior means of the full cohort of 365 participants. The 95% credible intervals for ability estimates are constructed using the posterior means plus or minus two posterior standard deviations. Although the sampling algorithm uses the logit scale for parameter estimation, results are converted to a probability scale centered at the mean of the difficulty estimates for the PNT items and displayed as a percentage, which may have a more natural interpretation. These ability estimates can be interpreted as the probability of successful processing on a PNT item of average difficulty. Conveniently, the expected percentage of correct naming attempts on the PNT can be roughly approximated by multiplying these 6 abilities. Percentile scores can be interpreted as the percentage of our participant sample who had a lower ability.

Limitations

The limitations of the model fall into two broad categories relating either to the model’s assumptions or to the data and procedures used for model fitting. With respect to the model’s assumptions, we take the position of statistician George Box (1979, p. 202), who claimed, “All models are wrong but some are useful.” Insofar as we have demonstrated the MPT model’s usefulness, we view its “wrong” assumptions as opportunities for improvement. One inherent limitation is that the use of probabilities does not shed much light on the mechanistic implementation of the underlying processing system. Instead, they provide constraints on the quality or efficiency of these mechanisms, and can aid in deciding between possible mechanistic descriptions. In this way, models aimed at different levels of Marr’s computational hierarchy can inform one another. Other simplifying assumptions are ripe for elaboration however, such as the treatment of non-naming responses. Previous research suggests that, in some cases, there are clear relationships between lexical processing and non-naming responses, via internal error detection and suppression. This generic response category also could be subdivided into further informative response types, like descriptions or grammatical category errors. Other response type definitions might be reconsidered as well, phonological errors, in particular. Post-lexical processing and articulation errors could be identified and incorporated into an MPT framework. More complex models of phonological production could extend the model to new types of data, for instance, governing a sequence of phonological outputs instead of a dichotomous score. Additionally, the choice of item response functions could be more nuanced; the simple Rasch model makes some strong assumptions, such as all items having the same discriminability with respect to a latent trait. Despite these limitations, or perhaps because of them, the MPT model presented here can hopefully serve as a baseline model for continued development and improvement.

With respect to the data collection and fitting procedures, we are constrained by the same burdens that encumber aphasia research and computational modeling generally. Recruitment of participants typically results in a sample of convenience, rather than a true random sample of the population. This is an important point for interpreting the percentile scores provided by the model fitting website. The value of a normative comparison between an individual and a group depends critically on their similarity along relevant characteristics. Future versions of the website may include functionality for stratifying normative cohorts by clinical or demographic characteristics; all clinical and demographic data used in this paper are available on the website, enabling manual construction of comparison groups. While the analysis presented here includes one of the largest PNT data sets ever collected, the cohort size pales in comparison to normative samples for widely-adopted assessment tools collected by organizations like the Educational Testing Service or Mayo Clinic that number in the thousands. Administering the PNT, transcribing and scoring responses, and entering scores into a database requires a significant investment of time by trained professionals, at present. With the advent of adequately automated procedures, the statistical framework presented here may aid in the development of shorter, computer adaptive tests, similar to ones that have already been developed for assessing PNT accuracy (Hula, Kellough, & Fergadiotis, 2015).

The expansion of our databases and models also presents as a double-edged sword, because the sampling procedures for fitting the full model demand considerable computational resources that increase rapidly as models and datasets grow in size and complexity. Although the simplified model and sampler used by the website improve fitting times, it still requires approximately 6 seconds per individual. To fit the full model with JAGS, running chains in parallel on a Marquis C734-GSR workstation with a 2.6 GHz Intel Xeon E5-2650 v2 8-core processor required approximately 60 GB of RAM and 5.4 hours to generate a 508 MB matrix file containing the posterior samples. Customizing parameter estimation procedures may increase efficiency, and there are demonstrated opportunities for GPU acceleration of Gibbs sampling for IRT models with large data sets (Sheng, Welling, & Zhu, 2014). The MPT model in its current form can therefore continue to benefit from large scale research projects that collect PNT data.

Finally, validation is an ongoing process, and although we have presented evidence that the MPT parameter values can be meaningfully interpreted, we have not yet investigated any clinical applications of the model or website. The interval estimates of abilities provide a sense of the reliability of point estimates; however, a more complete investigation of test-retest reliability will require multiple administrations of the PNT. This information will be important for interpreting any observed changes between test administrations. Further work will be needed to establish cutoff scores to identify impairments and to assess whether the model’s parameters are useful for making therapy decisions and monitoring recovery progress in comparison with available standards. The mathematical framework and tools presented here will hopefully aid in these future developments.

Public Significance.

Successful picture naming requires multiple cognitive abilities. Assessment of picture naming abilities in stroke patients can be improved by considering the target items’ influences on rates of different error types.