Lattice Models of Bacterial Nucleoids

Abstract

Mesoscale molecular modeling is providing a new window on the inner workings of living cells. Modeling of genomes, however, remains a technical challenge, due to their large size and complexity. We describe a lattice method for rapid generation of bacterial nucleoid models that integrates experimental data from a variety of biophysical techniques and provides a starting point for simulation and hypothesis generation. The current method builds models of a circular bacterial genome with supercoiled plectonemes, packed within the small space of the bacterial cell. Lattice models are generated for Mycoplasma genitalium and Escherichia coli nucleoids, and used to simulate interaction data. The method is rapid enough to allow generation of multiple models when analyzing structure/function relationships, and we demonstrate use of the lattice models in creation of an all-atom representation of an entire cell.

Graphical Abstract

INTRODUCTION

Through the confluence of new experimental approaches and advances in computer technology and methods, it is now becoming possible to create data-driven models of entire cells at the molecular, or even atomic, scale¹. Effective methods have been developed for modeling the soluble compartments of cells and have been used to study the effects of diffusion, crowding and confinement on cellular function^2,3. Methods are also available for modeling of biological membranes at the cellular level⁴. These methods, however, rely largely on the fact that cytoplasmic and membrane features are most often homogeneous across the space that is modeled, so a self-avoiding random distribution through space or within a surface is sufficient to create the model. However, modeling of cell structures with large-scale structural coherence, such as entire cellular genomes, remains an area of active research.

Currently, bacterial nucleoids are particularly amenable for this type of mesoscale approach: diverse experimental data is being gathered on all aspects of their structure and function, and the size of bacterial nucleoids is just within the limits of current computational abilities. Experimental studies have revealed a general model of circular bacterial nucleoids^5,6,7. Supercoiling induces the formation of a collection of superhelical plectonemes that help compact the DNA within the confined and crowded environment of the cell. Some interpretations also propose an additional hierarchical structure of larger globular domains. Fluorescence data show that the overall circular form of the DNA is reflected in the ultrastructure of the nucleoid, with opposite sides of the circular genome generally located near opposite poles of the cell.

Computational work on bacterial nucleoids is being performed at many levels of scale. For example, a coarse-grain model of the Escherichia coli chromosome, using 4047 beads to represent the 4.6 million base pairs (bp), was used to explore the role of entropy in the segregation of daughter chromosomes during replication⁸. Similar coarse-grain models at various levels of granularity are being used to interpret data from methods that provide contact maps, such as Hi-C, from organisms such as Caulobacter crescentus⁹ and Mycoplasma pneumonia¹⁰. Lattice models have been used to explore the overall ultrastructure of the C. crescentus nucleoid, underscoring the role of local domains and self-avoidance in achieving the observed ultrastructure¹¹. Most recently, a ground-breaking atomic level model of an entire E. coli nucleoid was created by a progressive multiscale approach, with structural domains specified by ChIP data on areas of active transcription¹².

We have implemented a lattice model of bacterial nucleoids, for use in our mesoscale modeling pipeline^13,14. The method is rapid enough to allow generation of hundreds of models, allowing exploration of hypotheses about the effect of local DNA properties on the overall nucleoid ultrastructure, while still producing a model sufficiently detailed to be used for generation of atomic level representations.

METHODS

Summary of Approach

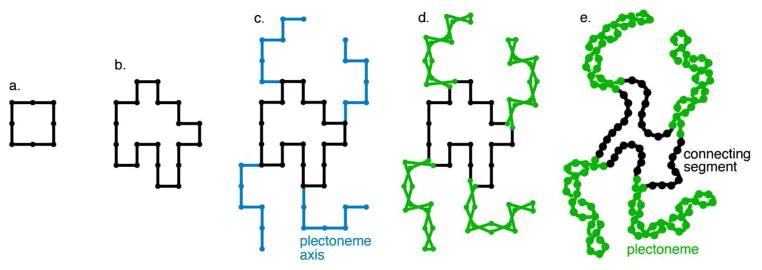
The current method models idealized nucleoids that are representative of the observed properties of model organisms. We model a single DNA circle, partitioned into a collection of equal plectonemes separated by a uniform-length connecting segment. Each plectoneme is an unbranched hairpin loop with a user-defined superhelicity. The overall method is shown in Figure 1: a lattice-based model is generated first (Figure 1a–d), then it is relaxed to yield the final model (Figure 1e).

Figure 1.

Summary of the method. A small square of points (a) is enlarged and migrated on lattice points (b). Helix axes (blue) are added for plectonemes (c). Each point of the helix axis is split into two to form the superhelical hairpin (d). Additional points are added between each lattice point, and the structure is relaxed off the lattice (e).

Lattice Model

Three-dimensional lattice models are generated in several steps: first generating the connecting segments, then defining the axis of the plectoneme, and finally creating the superhelical hairpin of the plectoneme. In most models we use a lattice spacing that represents 20 bp.

To generate the connecting segments, we start with a small square/rectangle at the center of the cell volume, and then build out additional lattice points to give the desired summed length of all the segments. Two types of changes are employed: points are migrated in places where two neighboring lattice edges are orthogonal, so the central lattice point may be moved to the opposite side of the square, and the model is grown to the appropriate size by adding two new lattice points adjacent to two existing points. The connecting segments are built in a series of cycles, adding two new points at a random location, then performing a series of migration steps at random locations. In this stage, a coarser user-defined lattice spacing is used, to ensure that there is sufficient unoccupied space to connect plectoneme axes in the following step. In the current study, we used a lattice spacing of 60 bp to create the linked connecting segments, then converted them to the 20 bp lattice by scaling the whole structure to the finer lattice and adding additional points along lattice edges.

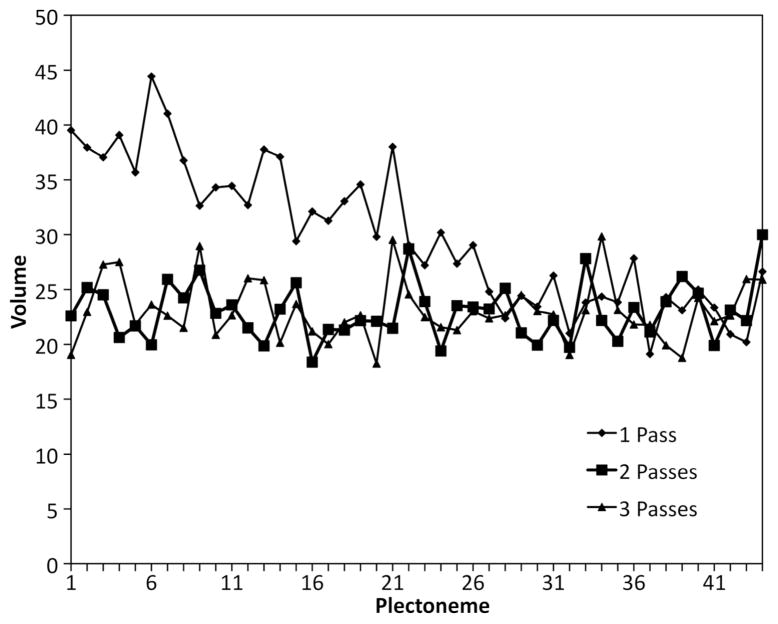
The plectonemes are then added using a random walk, rooted at appropriate locations in the ring of connecting segments. Each step chooses randomly from the unoccupied neighboring points and a “bias” parameter allows users to preferentially choose the point in the straight direction with a given probability. If the random walk reaches an impasse, the process is started again from the root point. The plectonemes are added sequentially around the genome. To minimize artifacts from differences in crowding at the different stages, the entire process is then repeated in one or more additional passes, removing each plectoneme in turn and rebuilding it in the presence of all of the other plectonemes. Figure 2 shows that one repeat of this process is sufficient to give consistent properties across all plectonemes. For the 2 and 3 pass experiments, average and standard deviation values for the plectoneme volume (described in more detail below) were 22.95 (5.40) and 23.07 (5.12). Similar behavior was seen when looking at persistence length (data not shown).

Figure 2.

Volume of plectonemes in three lattice generation protocols, building each plectoneme in one pass, or adding additional passes where plectonemes are rebuilt. Volumes are an approximation of the convex hull encompassing the plectoneme (described below), and values are given as the ratio of number of lattice points in the plectoneme volume relative to the number of lattice points defining the plectoneme. Models are for a mycoplasma nucleoid with a cell diameter of 380 nm, calculated with a bias value of 95%.

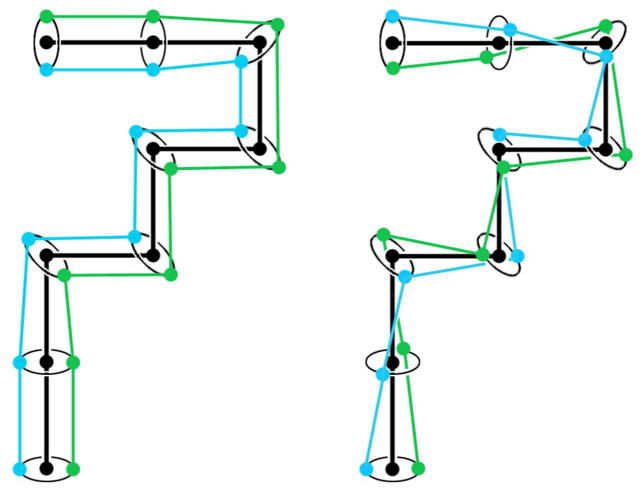
Finally, lattice points in the plectoneme are split, creating two points to represent the two local DNA double helical strands of the superhelix (Figure 3). These points are placed orthogonal to the local tangent to the path of the plectoneme, and are successively rotated around this tangent axis to correspond to the user-defined value of the superhelical density.

Figure 3.

Each point in the plectoneme axis is split into two points (left), and then rotated to generate the user-defined superhelicity (right).

Off-lattice Local Optimization

Lattice models are then relaxed to yield a coarse-grain bead model that is not constrained to the lattice. In this refinement process, the model resolution is reduced from 20 bp per bead to 10 bp per bead by adding an additional bead centered between each lattice point. The current method uses a simple optimization algorithm, performing small steps sequentially on each bead to relax small deviations from ideal geometry. Three constraints are currently implemented: 1) The distance between linked beads is constrained to lie within a given range centered on the optimum by moves along the vector connecting the two beads; 2) The angle between three successive beads is constrained to lie between 120 and 180 degrees by moves on the central bead to open or close the angle; 3) Close contacts between segments that are not directly linked are resolved with small moves that drive each bead away from the closest non-neighbor bead in the chain. A small random move is also applied at each step. In tests with mycoplasma models, this method relaxes models to lie within the constraints in 10,000 steps (data not shown).

Analysis Tools

Persistence lengths (σ) were estimated using the familiar equation:

$$<cos\mathrm{\theta }>=exp(-\mathrm{L}/\mathrm{\sigma })$$

where the angle between tangents to the chain (θ) is evaluated for lengths (L) of ~2 to 50 beads in the relaxed chain. The local superhelical radius is calculated for a particular plectoneme point by scanning all points on the opposite strand in the hairpin and using the minimum separation.

Plectoneme volumes are calculated using a lattice approximation of the convex hull. For each position in the lattice space, a 3X3X3 cube surrounding the position is used to define 26 directions in space. Lattice points of the plectoneme are then scanned and assigned to the closest of the 26 directions. Positions that amass a sum of 16 or greater directions are designated as inside the volume. Overlap values are calculated with a modification of the Polarization Index¹⁵:

$$\text{Overlap}=\text{sqrt}({\mathrm{V}}_{\mathrm{S}}/{\mathrm{V}}_{\mathrm{A}}\ast {\mathrm{V}}_{\mathrm{S}}/{\mathrm{V}}_{\mathrm{B}})$$

Where V_A and V_B are the volumes of the two plectonemes and V_S is the volume of their intersection. This gives a value of 1 for complete intersection of the volumes, and 0 if they do not intersect.

Experimental Design

We use average values from Hi-C and EM studies to model two organisms. Mycoplasmas are spherical or elongated cells with volumes that correspond to spherical cell diameters in the range of about 215 to 430 nm¹⁶. For most work, we chose an intermediate value of 380 nm, within a spherical cell envelope. The Escherichia coli model is based on an ideal capsular shape with a length of 1.78 um and width of 0.78 um¹². In all experiments, average values were obtained over 10 separate models with a particular set of parameters. Hi-C data has been used to identify the distribution and size of plectonemes in these organisms. Based on this data, we create an idealized description of the genome structure with equal-size and evenly-spaced plectonemes (Table 1).

Table 1.

Plectoneme Parameters

	Number	Hairpin	Connecting Segment
Mycoplasma pneumoniae
~800 kbp
Experiment10	44	15–33 kbp
Model	44	17 kbp	1 kbp
Escherichia coli
~4,600 kbp
Experiment17	169	2–66 kbp
Model	169	11 kbp	16 kbp

RESULTS AND DISCUSSION

The current method generates idealized models of bacterial nucleoids. Several simplifying assumptions are made: the plectonemes are treated as unbranched superhelical hairpins, with consistent length and spaced equally around the circular genome, and the cell envelope is an ideal spherical or capsular shape. Natural extensions to all of these simplifications will be possible in future work, allowing the modeling of more realistic topologies based on DNA contact data and cell morphology from microscopy. In addition, the supercoiling of the DNA helix is not treated explicitly: rather, the expected number of superhelices are modeled based on the defined superhelical density.

A typical model of the mycoplasma nucleoid is shown in Figure 4. The length of each plectoneme, if extended, would be about 7 times the diameter of the cell, so they are extensively folded and crumpled into the cell volume. In the current scheme, generation of the initial ring of connecting segments begins at the center of the cell, thus most models show them towards the center of the cell. This limitation may be lifted by initiating growth of the connecting segments at a particular location in the cell, for instance, if the origin of replication is tethered to the cell surface or if a particular locus of transcription/translation is identified.

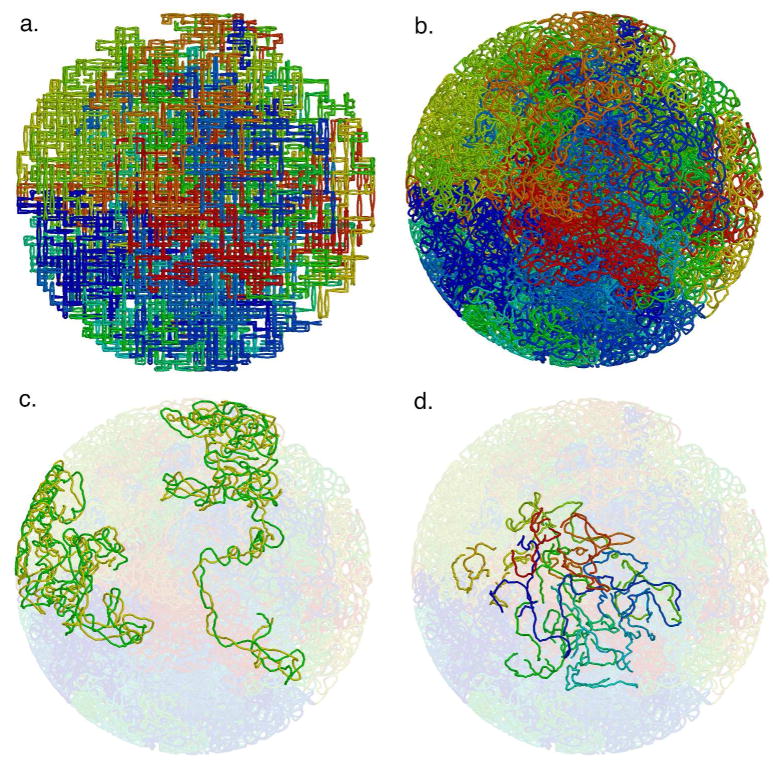
Figure 4.

Mycoplasma nucleoid lattice model. Lattice model (a) and relaxed model (b) for a bias value of 50%. The tube has a radius of 1 nm, corresponding approximately to a DNA double helix. The 44 plectonemes are colored sequentially around the circular genome from blue to red. (c) The two plectonemes with the smallest and largest volume, colored with one side of the superhelix in yellow and the other in green. (d) The short connecting segments between superhelical hairpins.

The method is rapid enough to allow generation of multiple models for each experiment. With the current unoptimized working code, the models in Figure 4 required 1.3 seconds for generation of the lattice model and 9.7 minutes for off-lattice optimization on a single cpu of an iMac with a 3.5 GHz Intel Core i5.

Bias, Persistence Length and Overlap

Experimental studies on the stiffness of the DNA helix yield a variety of results. DNA when free in solution shows a long persistence length of about 50 nm (about 150 bp)¹⁸, but observations of contact distances of DNA within cells shows far more flexibility. For instance, study of looping by lac repressor in supercoiled plasmids estimated persistence lengths of 6.4 nm (about 20 bp)¹⁹. Assumptions about the persistence length can lead to models with different global characteristics. In our model, we use a “bias” parameter, which selectively favors random walk growth towards straight trajectories, to tune the local persistence length. Table 2 shows nucleoid characteristics for models across the range of possible bias values. At a bias value of 5% (close to being a random walk), each plectoneme is contorted and localized, with a persistence length of about 38 bp and a small volume. At the other extreme, a bias value of 95% (with straight moves whenever possible), plectonemes are extended with larger volume and longer persistence length. These values are consistent with other recent work, which found apparent persistence lengths of 25–43 bp over entire E. coli genome model¹².

Table 2.

Properties of Models

Bias	Persistence Length (bp)	Volume per Base Pair (nm3)
5%	38.2 (1.7)	87.6 (18.4)
25%	41.8 (2.0)	108.6 (24.2)
50%	45.8 (2.4)	145.7 (34.5)
75%	52.4 (3.3)	220.0 (51.3)
95%	67.7 (6.0)	350.1 (73.2)

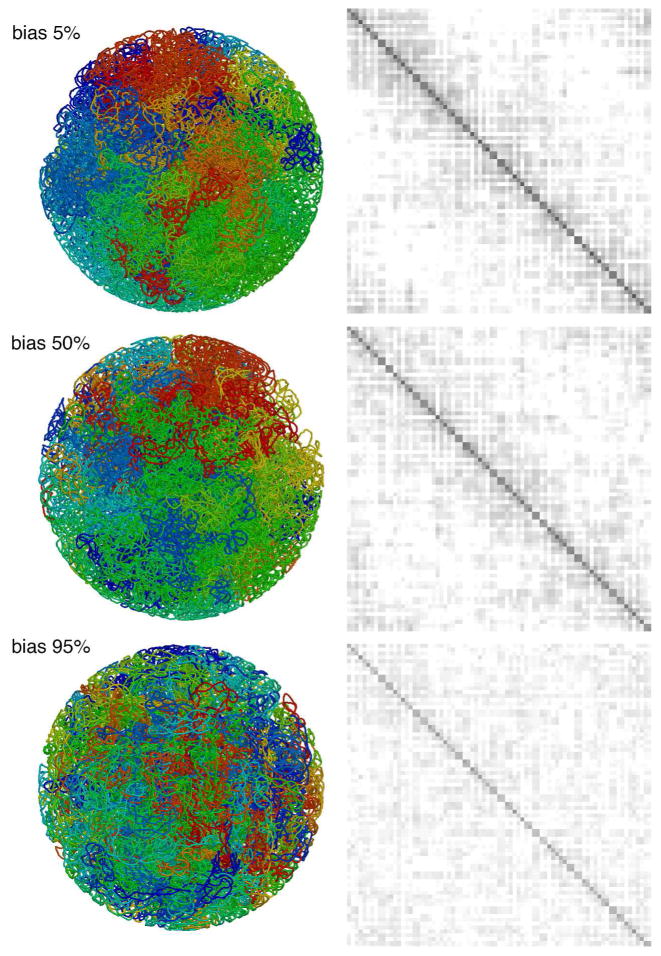
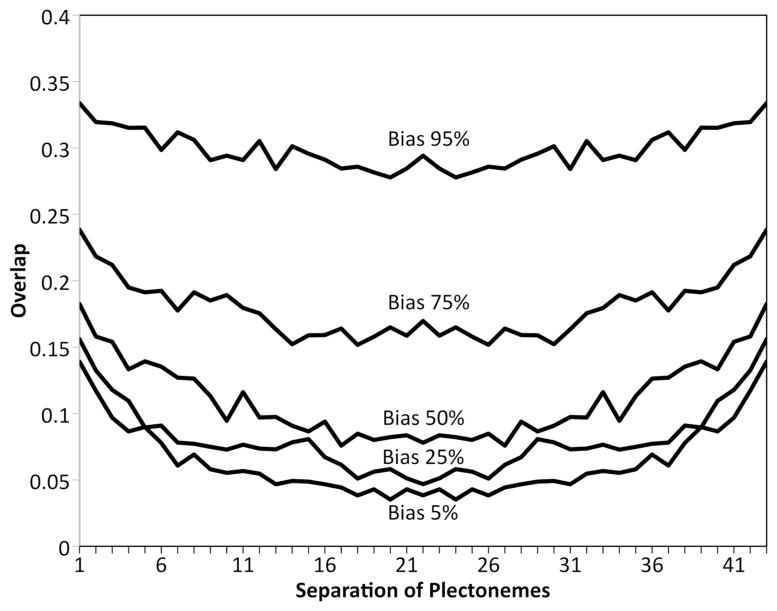
For the models with lower values of the bias parameter, computed distance maps (Figure 5) show the characteristic pattern observed in HiC studies. All of the maps show the pattern of close-contact diamonds along the diagonal, which correspond to interactions within the plectoneme. The two lower values of bias also show the characteristic blank region corresponding to interactions of plectonemes with others spaced halfway around the circular genome. The 95% bias model does not show this feature, since all of the plectonemes are extensively interdigitated, as seen in the representative model shown in the figure. To quantify this relationship, we averaged plectoneme overlap values based on their intergenomic distance (Figure 6), revealing a relatively flat profile for the 95% bias model, and the expected dip for cross-genome interactions in the low-bias models. In the remaining studies, we chose a bias value of 50% as a compromise between achieving a larger persistence length but retaining the characteristic features of the experimental contact data.

Figure 5.

Distance maps for three values of the bias parameter used in generation of the plectoneme helix axis. The entire genome is arrayed on the horizontal and vertical axes with a resolution of 10 kbp, and average distances are shown with a linear ramp from black at 0 nm to white at 200 nm and above. Representative models are shown on the left.

Figure 6.

Overlap of plectonemes relative to their separation around the circular genome.

Cell Size

Mycoplasma cells present a highly confined environment for the nucleoid, as shown in Table 3. Using a very conservative radius of 1 nm for the DNA double helix to calculate the volume of DNA (V_dna) relative to the volume of the cell (V_cell), a single DNA circle would occupy roughly 15% of the volume in the smallest mycoplasma cells, and roughly 3% in the average-sized cells modeled above. This poses a challenge for modeling these small cells. The number of lattice points needed to model the genome (N_dna) is often a significant fraction of the number of points available in the whole cell volume (N_cell). In fact, the 20 bp lattice has fewer than half the required points to model a self-avoiding random chain for the smallest mycoplasma cells. We have modified the method in two ways to model these small, crowded cells.

Table 3.

Volume Relationships in Nucleoid Lattice Models

Cell Radius (nm)	Ndna/Ncell		Vdna/Vcell
	20bp spacing	10bp spacing
110.	2.256	0.564	0.153
150.	0.890	0.222	0.060
190.	0.438	0.109	0.030
230.	0.247	0.062	0.017
E. coli model	0.101	0.025	0.007

In the first approach, we retain the 20 bp lattice, but allow additional interleaved lattices that do not occlude one another. These lattices are centered along the body diagonal of the original lattice, ensuring that no lattice edges will intersect between the interleaved lattices. Using this approach, we need three interleaved lattices to model the radius 110 nm cell. In the second approach, we use a 10 bp lattice, which provides a sufficient number of lattice points to build the model.

As we might expect, the two methods give quite different results, using the same 50% value for the bias as used for the larger cell models (Figure 7). Since the different layers do not see one another, the interleaved approach yields a model with many interdigitated plectonemes with high volume per base pair, 98.6 (19.0) nm3, and a high level of overlap, 0.419 (0.180). The 10 bp lattice spacing yields a model with more compact and separated plectonemes, with volume per base pair of 49.4 (11.1) nm3 and overlap of 0.195 (0.181), but has a very contorted path. The persistence length for both methods is somewhat smaller than the comparable radius 190 nm cell, at 32.8 (3.7) bp for the interdigitated models and 20.1 (1.0) bp for the 10 bp lattice models. Presumably this is a consequence of the higher probability of running into the cell membrane in the smaller cell, requiring more frequent changes of direction, and in the 10 bp lattice model, the ability to make many small sharp turns on the finer lattice. These results underscore the need for additional work on highly crowded models to explore the balance between the localization of plectonemes and the degree of local deformation of the helix.

Figure 7.

Two methods for generating nucleoids for small (radius 110 nm) mycoplasma cells: interleaved 20 bp lattices and a finer 10 bp lattice. An average cell (radius 190 nm) is shown at the bottom.

Superhelical Density

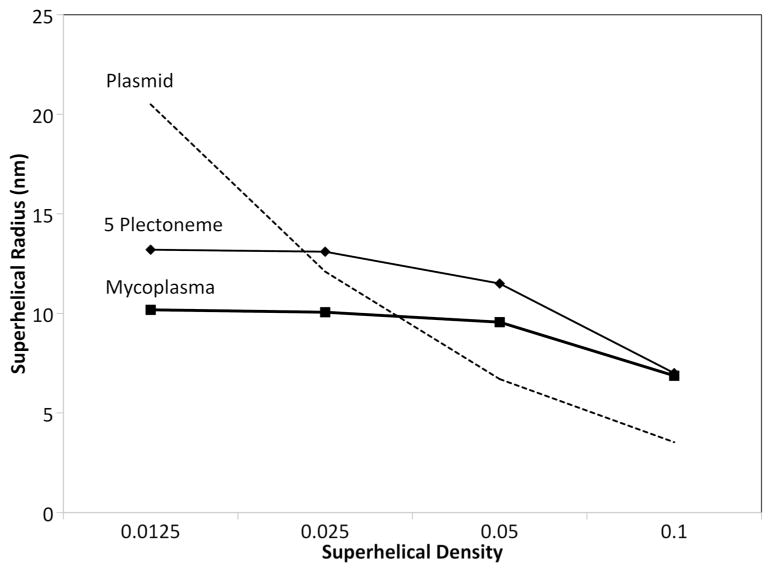
We also explored the effect of superhelical density on the characteristics of the model. EM experiments with plasmids show that the radius of the superhelix is a function of the superhelical density, with tightly wound DNA leading to tight superhelices²⁰. Models of the mycoplasma nucleoid show a similar behavior (Figure 8), although not as marked as in the plasmid study. In the models, the radius reaches a maximum of about 10 nm at low superhelical densities. We also did a study with models that include only 5 plectonemes in a 300 nm radius space, to probe the role of crowding on this behavior. Superhelical radii for the 5 plectoneme models also level out, but at a higher value, indicating that crowding is playing a role in keeping the two strands of the superhelix close to one another in the mycoplasma model. We did not, however, see the exponential increase in radius at lower superhelical densities in the relatively uncrowded 5 plectoneme model, as seen in the EM study. This is most likely a consequence of the local nature of the relaxation method. Experiments using very long relaxation protocols do lead to more open structures (data not shown), but unfortunately also lead to progressive unwinding of the superhelix, since there are no supercoiling constraints on the individual DNA helices in our model. The comparison is encouraging, however, since the superhelical radius is of a similar magnitude as in the plasmid study, and based on this similarity, the persistence length of the modeled DNA is consistent with the observed conformation of the plasmids.

Figure 8.

Superhelical radius for mycoplasma nucleoid models with different superhelical density.

Escherichia coli

The lattice method scales naturally to larger genomes, such as that of Escherichia coli. Figure 9 presents results for a cell with a single copy of the genome, constrained within a capsule-shaped volume. As observed in micrographic analyses, the nucleoid adopts a distinctive domain structure, with neighboring plectonemes forming larger globular domains, arranged overall in a compressed circle. A computed distance plot shows the characteristic strong diagonal structure for these individual domains, showing contacts within the plectoneme and clustering of neighboring plectonemes. It also shows the weaker cross-diagonal that corresponds to interactions between plectonemes at opposite sides of the circular genome. These cross diagonals are indicative of a circular genome structure that is confined within an oval space, allowing contacts between, for instance, the regions colored red and blue in Figure 9 with regions colored green.

Figure 9.

Distance map for the Escherichia coli nucleoid model at 10 kbp resolution. The image at the left shows one of the ten relaxed models, rendered with an expanded DNA radius of 2 nm for clarity.

Lattice Models in Mesoscale Modeling

One of our major goals is to use these models as part of a pipeline to build full mesoscale models of entire cells. The general concept is to begin by creating models of large, complex structures like bacterial nucleoids or eukaryotic cytoskeletons, then construct the soluble and membrane components around this model, locally relaxing the nucleoid or cytoskeleton if necessary. The entire model may then be used as a starting point for additional simulation and for interpretation of experimental results. For example, experimental contact maps provide information on average properties of populations of cells, and simulated models provide a way to disambiguate this information, quantifying the diversity of properties in individuals that lead to the observed overall properties.

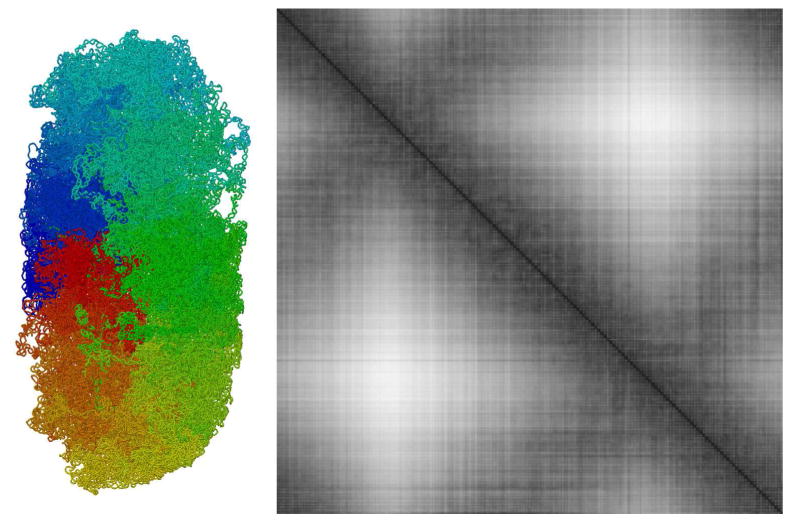
The model in Figure 10 was created using our “Instant Packing” method¹⁴ for interactive placement of molecules. Membranes are created with an approach similar to LipidWrapper⁴ for rapid placement without noticeable periodicity, and soluble molecules are placed using a voxelized representation of the available space. Then, the model is locally optimized to resolve clashes. The model is created using a draft recipe of molecular structures, locations, interactions and abundances (manuscript in preparation) based on the Mycoplasma pneumoniae proteome (taken from the MyMpn Database, http://mympn.crg.eu) and manually curated to identify structural entries from the Protein Data Bank (http://www.rcsb.org).

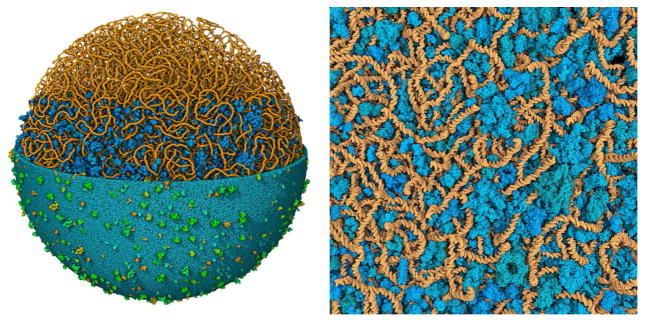
Figure 10.

Lattice-generated model of a mycoplasma nucleoid integrated into an atomic mesoscale model of the entire bacterium. All macromolecules are shown. On the left, the entire nucleoid (orange) is shown, soluble molecules (blue) are included in the lower three-quarters of the image, and the membrane (cyan and green) is shown in the lower half. An enlarged detail is shown at right.

CONCLUSIONS

This study demonstrates the feasibility of using rapid lattice methods for mesoscale-level modeling of bacterial nucleoids. The method is rapid enough to enable exploration of a variety of hypotheses, and provides models that are consistent with the available in vivo contact data. Future work will include extension of the current idealized method to include a more realistic description of plectonemes, including experimentally-determined length and distribution, and branched topologies. Modeling of cell shape based on 3D descriptions from cryo-electron microscopy will also be straight-forward. Finally, integration of the the method into our mesoscale modeling suite will streamline the addition and analysis of molecules directly interacting with the DNA, such as co-transcriptional polysomes and proteins involved in DNA architecture, repair, and regulation.