MR fingerprinting Deep RecOnstruction NEtwork (DRONE)

Abstract

PURPOSE

Demonstrate a novel fast method for reconstruction of multi-dimensional MR Fingerprinting (MRF) data using Deep Learning methods.

METHODS

A neural network (NN) is defined using the TensorFlow framework and trained on simulated MRF data computed with the Extended Phase Graph formalism. The NN reconstruction accuracy for noiseless and noisy data is compared to conventional MRF template matching as a function of training data size, and quantified in simulated numerical brain phantom data and ISMRM/NIST phantom data measured on 1.5T and 3T scanners with an optimized MRF EPI and MRF FISP sequences with spiral readout. The utility of the method is demonstrated in a healthy subject in vivo at 1.5 T.

RESULTS

Network training required 10 to 74 minutes and once trained, data reconstruction required approximately 10 ms for the MRF EPI and 76 ms for the MRF FISP sequence. Reconstruction of simulated, noiseless brain data using the NN resulted in a root-mean-square error (RMSE) of 2.6 ms for T₁ and 1.9 ms for T₂. The reconstruction error in the presence of noise was less than 10% for both T₁ and T₂ for signal-to-noise greater than 25 dB. Phantom measurements yielded good agreement (R²=0.99/0.99 for MRF EPI T₁/T₂ and 0.94/0.98 for MRF FISP T₁/T₂) between the T₁ and T₂ estimated by the NN and reference values from the ISMRM/NIST phantom.

CONCLUSION

Reconstruction of MRF data with a NN is accurate, 300–5000 fold faster and more robust to noise and undersampling than conventional MRF dictionary matching.

Introduction

Magnetic Resonance Fingerprinting (MRF) (1) is an acquisition strategy that uses a variable schedule of RF excitations and delays to induce differential signal evolution in tissue of differing types. Quantitative tissue parameter maps are then obtained by matching the acquired signal to a pre-computed dictionary consisting of the time-evolution of the magnetization for different values of the set of tissue parameters. Multiple quantitative tissue parameter maps can be simultaneously obtained from a single experiment, significantly reducing the total scan time.

To avoid errors in the reconstructed tissue maps, the reconstruction dictionary is typically computed with fine granularity over the entire range of possible tissue values. Dictionary size, however, grows exponentially as the number of tissue parameters (i.e the dictionary dimension) is increased which can quickly result in prohibitively large dictionaries that require extensive computational resources to process (2). This increased memory, storage and computational burden is a limiting factor for clinical adoption of MRF methods and is particularly pernicious in innovative high dimensional applications of MRF (3,4). Reducing the dictionary density is a poor solution for this problem since it limits the a priori accuracy of the reconstruction even before experimental factors are accounted for.

Existing methods address aspects of this problem but important challenges remain. Dictionary compression (5,6) uses the compressibility of the fingerprints to reduce the dimensionality of the dictionary leading to faster post-processing. Unfortunately, to create the compressed dictionary the full fine-grained dictionary must first be generated prior to decomposition with the singular value decomposition (SVD), itself a computationally expensive operation. Recent work by Yang et al (7) used a randomized SVD with an iterative polynomial fit to reduce the memory requirements though at the cost of increased processing time. Additionally, when optimized acquisition schedules are used (8,9), the compressibility of the dictionary may be significantly reduced rendering these methods less effective. Optimizing the acquisition schedule can indeed reduce the number of image frames needed for accurate reconstruction but the reduction is smaller than the exponential growth of the dictionary with increasing dimensions.

In recent years, the availability of inexpensive graphical processing units (GPU) has led to significant advances in neural networks (NN) and Deep Learning (DL) algorithms used to train these networks (10). Mathematical work in NN theory has shown that any Borel measurable function can be represented by a NN with a finite number of neurons (11) which can therefore offer a compact representation of complicated functions. In this paper we exploit this property and describe a novel method that reframes the MRF reconstruction problem as learning an optimal function that maps the acquired signal magnitudes to their corresponding tissue parameter values, trained on a sparse set of dictionary entries (12). The trained neural network reconstruction function is remarkably compact (~20 times smaller than typical MRF dictionaries) and reconstruction is nearly instantaneous (~300–5000 fold faster than conventional dictionary matching techniques) due to its rapid feedforward processing. We call our method the MRF Deep RecOnstruction NEtwork (DRONE) and we validate it by numerical simulations and phantom experiments at 2 different magnetic field strengths and demonstrate its utility in the brain of a healthy subject scanned at 1.5T.

Methods

Neural Network

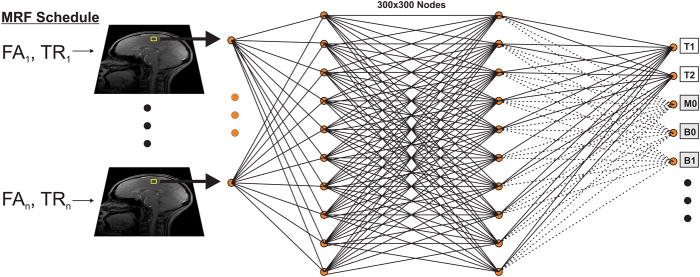
A four layer fully-connected NN composed of input and output layers and two hidden layers was defined using the TensorFlow framework (13) as shown in Fig. 1. The input layer consisted of 25 or 50 nodes to correspond to the magnitude images acquired with our schedule optimized echo-planar imaging (EPI) MRF sequence (8) or 571 nodes to correspond to images acquired with a conventional MRF sequence with sliding-window filtering (14,15). Complex-valued images can also be processed by this network topology by splitting the real and imaginary channels, or through the use of a complex-valued network (16). In this proof-of-concept study only T₁ and T₂ were considered so the output layer consisted of two nodes; reconstruction of additional parameters would require a larger output layer. Each of the two hidden layers had 300 nodes. The network size was empirically selected to ensure accurate functional mapping while avoiding the risk of overfitting. The chosen size represented a good compromise between the required training time, storage space and accuracy of the resultant reconstructions. The network was trained by the ADAM stochastic gradient descent algorithm (17) with the learning rate set to 0.001 and the loss function (cost) defined as the mean squared error:

$$LF=\frac{1}{n}\sum _{k=1}^n{(P_{\mathit{training}}^k-P_{\mathit{recon}}^k)}^2,$$ (1)

where k ranges over the n training samples and P is the training or reconstructed tissue parameter of interest (T₁ or T₂ in this study). Two different activation functions were defined. A hyperbolic tangent (tanh) function was used for the hidden layers with a sigmoid function used for the output layer. In total, the NN required storage of 300×300=90,000 coefficients.

Fig. 1.

Schematic of the reconstruction approach used in this study. MRI data acquired with the optimized MRF EPI sequence is fed voxelwise to a four layer neural network containing two 300×300 hidden layers. The network is trained by a dictionary generated with the Extended Phase Graph algorithm with the tanh and sigmoid functions used as activation functions of the first and last hidden layers respectively. The network then outputs the underlying tissue parameters T₁ and T₂. Additional tissue parameters including M₀, B₀, B₁ etc… (gray boxes) can similarly be obtained by training the network with a suitable dictionary.

Pulse Sequence

Numerical simulations, phantom and in vivo experiments in this study used a modified gradient-echo EPI MRF pulse sequence with Cartesian sampling whose flip angles (FA) and repetition times (TR) were set according to an optimized measurement schedule, shown in Supporting Fig. S1, as previously described (8,18,19). To illustrate the flexibility of the proposed reconstruction a conventional MRF FISP pulse sequence (20–23) with a variable density spiral readout and 600 time-points (571 after sliding-window filtering) was also used (14,15) for the phantom experiments.

Network Training

Numerical simulations and phantom experiments were carried out using a training dictionary of ~69000 entries consisting of T₁ and T₂ in the range 1–2500 ms in increments of 2 ms between 1–300 ms and increments of 10 ms between 300–2500 ms, excluding entries where T₁ < T₂. An additional set was also defined consisting of T₁ and T₂ values absent from the training dictionary to test the network’s ability to reconstruct tissue parameters values outside its training set. The same range and increments of T₁ and T₂ values were used for the test set but with a different starting point to ensure that there was no overlap with the training dictionary. Reconstruction of the test set data was used to verify the efficacy of training by comparing the resultant values to the true values. A larger range dictionary was used for the in vivo experiments which consisted of T₁ in the range 1–5000 ms in increments of 5 ms between 1–300 ms, increments of 10 between 300–1500 ms and increments of 50 ms between 1500–5000 ms. The same set of increments was used for T₂ but only up to 3000 ms. The magnetization due to each (T_1, T₂) pair was calculated using the Extended Phase Graph formalism (20,24). Gaussian noise with 1% standard deviation and zero mean was added to the training dictionary to promote robust learning, as previously exhibited with denoising autoencoders (25). This dictionary was used to train the network to convergence, requiring approximately 10 to 74 mins on an Nvidia K80 GPU with 2 GB of memory. The size of the dictionary required approximately 13 MB of storage for the MRF EPI sequence and 313 MB for the MRF FISP sequence.

Numerical Simulations

The performance of the network in reconstruction of realistic brain T₁ and T₂ values was assessed using the Brainweb digital brain phantom (26). An MRF EPI acquisition was simulated as described above, and the resulting signal used as an input to the network.

Signal-to-noise (SNR) vs reconstruction error

Monte Carlo simulations were used to test the network reconstruction of noisy data. Complex Gaussian random noise was added to the data for variable levels of SNR. The SNR was defined as 20log₁₀(S/N) where S is the average white matter signal intensity in the acquisition and N is the noise standard deviation. The SNR was varied from 10 to 40 dB in increments of 5 dB and the noisy data reconstructed with the proposed network. This was repeated 100 times for each SNR level. The resulting T₁ and T₂ maps were compared to their ground truth values according to the formula: Error = 100 × |True – Measured|/True and the mean and standard deviation of the percent error calculated.

Training dictionary density vs reconstruction error

The effect of the training dictionary density on the resulting reconstruction error was measured by sub-sampling the initial dictionary variously from 2 to 60 fold. The network was then trained with each sub-sampled dictionary and used to reconstruct the initial, fully sampled dictionary whose entries were corrupted by zero mean Gaussian noise with standard deviation of either 0 (i.e. noiseless) or 1%. No noise was injected into the training dictionary for reconstruction of the noiseless data. This was repeated 5 times for each undersampling factor and the the root-mean-square error (RMSE) calculated for each repetition. The NN reconstruction was also compared to a conventional MRF dictionary matching reconstruction by matching the initial, fully sampled dictionary to each sub-sampled dictionary and calculating the resultant error. The mean and standard deviation of the RMSEs, across the 5 repetitions, of the reconstructed T₁ and T₂ maps of each reconstruction method were then calculated as a function of the dictionary sub-sampling factor.

MRI

All experiments with the optimized MRF EPI sequence were conducted on a 1.5 T whole-body scanner (Avanto, Siemens Healthineers, Erlangen, Germany). The manufacturer’s body coil was used for transmit and a 32-channel head coil array used for receive. The TI/TE/BW was set to 19 ms/13 ms/2009 Hz/pixel. The slice thickness was set to 5 mm and the in-plane resolution set to 2×2 mm² with a matrix of 128×128 and an acceleration factor R=2 for a total scan time of ~3 seconds for the 25 frames acquired with the optimized schedule. A higher in-plane resolution could be obtained by increasing the number of phase encoding steps hence the echo time or, alternatively, by increasing the acceleration factor at the cost of decreased signal-to-noise (SNR). To ensure sufficient SNR in the in vivo experiments, the same acquisition parameters were used but with a slightly longer (~5 seconds) acquisition. The images were reconstructed online using the GRAPPA (27) method.

The MRF FISP experiments were conducted on a 3 T whole-body scanner (Prisma, Siemens Healthineers, Erlangen, Germany) with 2-channel parallel transmit and 20-channel parallel receive array. The TI/TE/BW was 20 ms/2.5 ms/261 Hz/pixel with a 5 mm slice thickness, an in-plane resolution of 1.2×1.2 mm² and a matrix size of 200×200. A 30 point sliding-window filter was applied to the 600 time-points to yield the 571 images used in the DRONE reconstruction as described in Ref. (14). The total acquisition time was ~7.5 seconds for the 600 frames acquired.

Phantom

The accuracy and precision of the NN reconstruction was assessed using the International Society for Magnetic Resonance in Medicine (ISMRM)/National Institute of Standards and Technology (NIST) multi-compartment phantom with calibrated T₁ and T₂ values similar to those of the human brain (28). The phantom was scanned at the two magnetic field strengths with the pulse sequences described above and the images reconstructed with both the proposed NN as well as conventional dictionary matching. The resulting T₁/T₂ maps were compared to the true phantom values which were characterized by NIST for each magnetic field strength and calculated using gold-standard NMR spectroscopy IR and CPMG sequences (28,29).

In Vivo Human

A healthy 35-year-old male subject was recruited for this study and provided informed consent prior to the experiment in accordance with our Institution Human Research Committee. Following DRONE reconstruction of the measured data, regions-of-interest (ROIs) of 10 pixels were defined corresponding to grey matter, white matter and cerebrospinal fluid (CSF). The mean±standard deviation of the T₁/T₂ values within those ROIs was calculated and compared to values from the literature.

Results

Network Training

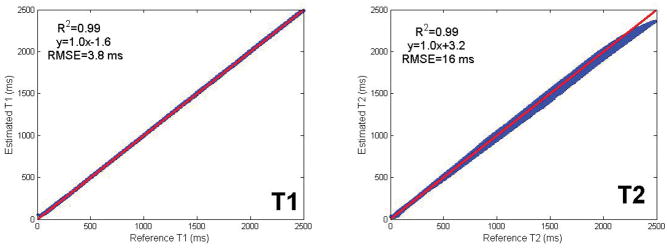
The reconstructed test data is shown in Fig. 2 in comparison to the true values. Excellent agreement was obtained between the true and reconstructed T₁ and T₂ values yielding a correlation coefficient of R²=0.99 for both T₁ and T₂ with a negligible bias of 1.6 ms for T₁ and 3.2 ms for T₂ and an RMSE of 3.8 ms for T₁ and 16 ms for T₂. T₁ and T₂ values at the edge of the training dictionary range showed increased deviation from the true values, likely due to the vanishing gradient of the activation function in these regions (30) as described in the Discussion section below.

Fig. 2.

Shown is a comparison between the true T₁ and T₂ and those reconstructed by a network trained on a distinct dictionary. The red line indicates the least-squares fit curve. The reconstructed T₁ and T₂ values showed excellent agreement (R²=0.99) with the true values with a negligible bias in T₁ and T₂ of 1.6 and 3.2 ms respectively, validating the feasibility of the proposed approach. Very short and very long T₁ and T₂ values showed increased deviation from the true values due to vanishing gradient of the activation function used for those ranges.

Numerical Simulation

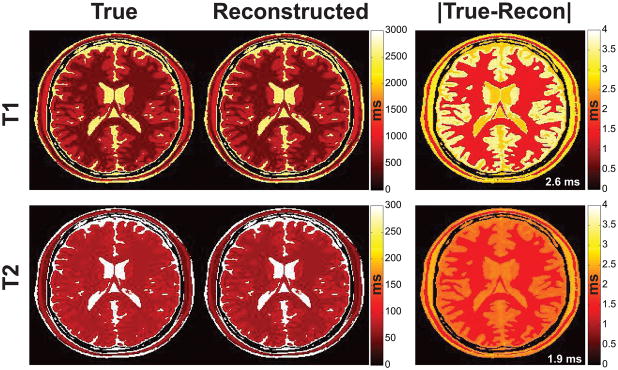
The true and reconstructed T₁ and T₂ maps of the noiseless numerical brain phantom are shown in Fig. 3 along with the associated error map calculated as the absolute value, i.e. Error=|True-Reconstructed|. The RMSE for each map was 2.6 and 1.9 ms for T₁ and T₂ respectively. The largest error in the brain was less than 0.5% in T₁ and less than 3% in T₂.

Fig. 3.

True and reconstructed T₁/T₂ images from the numerical brain phantom shown on a common ms scale and the associated absolute error map. The true phantom values approximate those of the in vivo brain, e.g. white matter T₂ > 70 ms. Note the close agreement between the reconstructed and true maps. The T₁ and T₂ RMSEs of 2.6 and 1.9 ms respectively are shown inset in white in the error map for this noiseless acquisition.

SNR vs reconstruction error

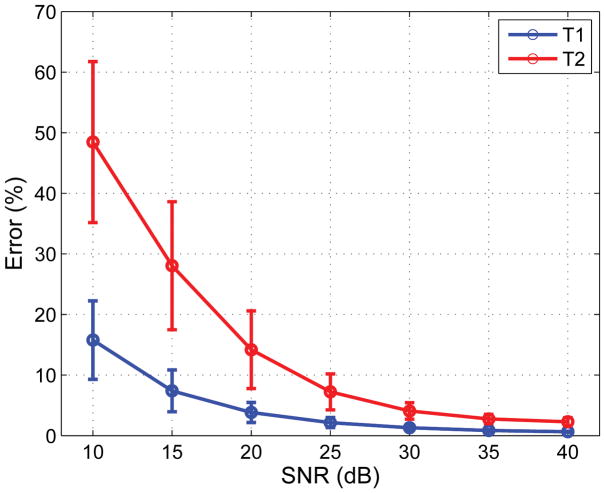
The mean T₁ and T₂ error as a function of SNR is shown in Fig. 4. The error was relatively large (~15% and ~48% for T₁ and T₂) at the lowest SNRs but dropped rapidly with increasing SNR, reaching less than 2% for the highest SNR levels tested.

Fig. 4.

The T₁ and T₂ reconstruction error in percent as a function of the SNR. The mean (circles) and standard deviation (whiskers) were calculated across the 100 Monte Carlo iterations. Reconstructions at the lowest SNR level showed significant error that nevertheless dropped rapidly with increasing SNR and was less than 2% for T₁ and T₂ at the highest SNR level tested.

Training dictionary density vs reconstruction error

The mean T₁ and T₂ RMSEs across the five repetitions are shown as a function of the dictionary undersampling factor in Supporting Fig. S6 for the different noise levels tested. For a noiseless acquisition with small dictionary undersampling, the error was similar for both the NN and MRF dictionary matching reconstructions. The error increased with increasing undersampling factors for both methods but at a significantly higher rate for the dictionary matching. Indeed, at the largest undersampling factor tested (×60), the error in the NN reconstruction was 2 fold smaller than the dictionary matching for T₁ and 4 fold smaller for T₂ (Supporting Figs. S2,S3,S6). Moreover, the dictionary matching performance degraded rapidly in the presence of noise. In particular, dictionary matching of short (< 11 ms) T₂ tissues resulted in large errors that dominated the total RMSE (Supporting Figs. S4,S5). Such T₂ values were not estimable by conventional dictionary matching (but were estimable by DRONE reconstruction) and were therefore not included in the RMSE calculations shown in Supporting Fig. S6, unlike the DRONE reconstruction which included all tissues. Despite the smaller set of tissues used in calculation of the dictionary matching error, the DRONE reconstruction error was still 7–44% smaller for T₁ and 2–8% smaller for T₂ in the presence of noise.

Phantom

The DRONE reconstruction accuracy was evaluated by estimating T₁ and T₂ values in the well-characterized calibrated ISMRM/NIST phantom. The measured T₁ and T₂ values were derived from the mean T₁ and T₂ values estimated within each compartment.

MRF EPI

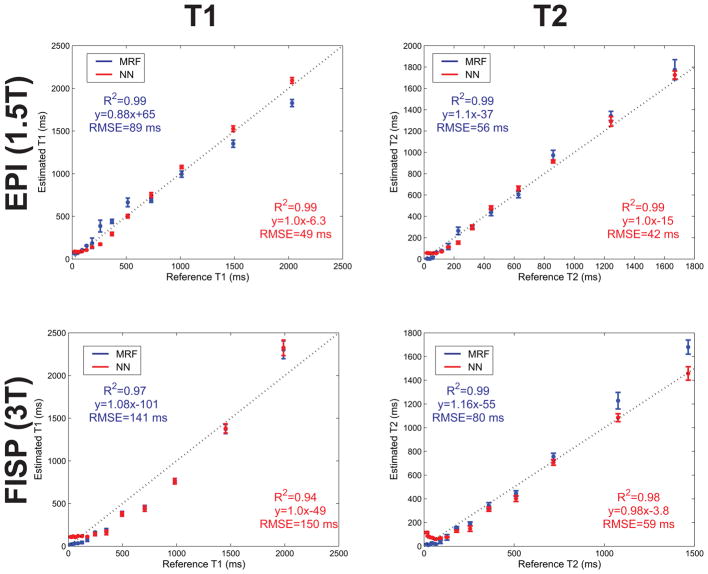
The estimated T₁ and T₂ values from all compartments (Fig. 5) showed good agreement to the true phantom values (R²=0.99) and a small estimation bias of 6.3 ms for T₁ and 15 ms for T₂. The calculated T₁ and T₂ RMSEs were 49 and 42 ms respectively. In contrast, conventional dictionary matching yielded higher RMSEs (89 and 56 ms for T₁ and T₂). The reconstruction of the 128×128 T₁ and T₂ maps required ~10 ms with the NN which was ~300 fold faster than the ~3s required with conventional dictionary matching using a ~69000 entries dictionary.

Fig. 5.

NN and MRF dictionary matching reconstructions of the ISMRM/NIST phantom for the sequences tested. Shown is a comparison between the reference and measured compartment T₁ and T₂ values for data acquired with the optimized MRF EPI sequence at 1.5T (top) and with the MRF FISP sequence at 3T (bottom). The reference values were calculated by NIST using spectroscopic inversion-recovery and spin-echo sequences. The dashed line is the identity line and the error bars represent the standard deviation of the measured T₁ and T₂ values within each compartment. The uncorrected larger B₁ inhomogeneity at 3T may have contributed to the larger T₁ RMSE with the MRF FISP sequence.

MRF FISP

The T₁ and T₂ values estimated with the MRF FISP sequence also showed good agreement to the true phantom values (R²=0.94 for T₁ and 0.98 for T₂) with an estimation bias of 49 ms for T₁ and 3.8 ms for T₂. The T₂ RMSE was similar to that of the MRF EPI acquisition at 59 ms but the T₁ RMSE (150 ms) was larger. Although B₁ correction was not applied to either sequence, the B₁ inhomogeneity is greater at 3 T which likely contributed to the larger error in the MRF FISP sequence. The larger number of time-points in the MRF FISP sequence naturally required a longer time for reconstruction (76 ms) compared to the MRF EPI acquisition. Remarkably, despite the nearly 23 fold increase in the number of time-points, the increase in reconstruction time was only ~7 fold. Conventional dictionary matching with the same size dictionary yielded RMSEs of 141 and 80 ms for T₁ and T₂ and required ~380 seconds or 5000 times longer.

In Vivo Human Brain

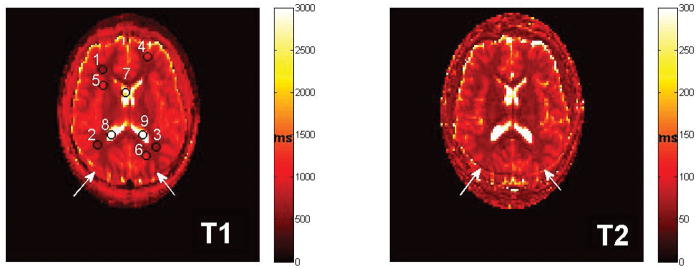
The T₁ and T₂ maps reconstructed by DRONE are shown in Fig. 6 along with the ROIs chosen. The mean±standard deviation T₁ and T₂ for each tissue compartment are listed in Table 1 and are similar to values obtained from the literature (1,31).

Fig. 6.

In vivo quantitative T₁ and T₂ maps from the brain of a healthy subject reconstructed with the proposed NN. Because no fat suppression was applied, a mild chemical shift artifact is visible in the images (white arrows). The numbered black circles indicate the locations of the grey matter, white matter and CSF ROIs used to calculate the mean T₁ and T₂ values shown in Table 1.

Table 1.

Mean±standard deviation T₁s and T₂s values of the ROIs selected.

ROI	T1 (ms)	T2 (ms)
White Matter
1	608±9	62±3
2	642±12	67±4
3	633±9	66±3
Average	627±10	65±3
Grey Matter
4	895±153	92±14
5	1182±65	102±10
6	1241±187	120±17
Average	1106±135	105±14
CSF
7	3292±515	1475±118
8	3665±413	1710±332
9	4026±123	1544±147
Average	3815±424	1576±199

Discussion

MRF enables quantitative tissue mapping in a short acquisition time at the cost of increased complexity in the reconstruction. While computational resources are typically cheaper and more accessible than scanner time, the large dictionaries required for MRF applications can overburden even the most advanced hardware. To avoid this problem multi-parametric MRF dictionaries are by necessity undersampled in some dimensions entailing an a priori reduction in accuracy. Instead, in this work, a four layer NN capable of modeling the history-dependent Bloch equations used in MRF sequences was demonstrated. Unlike conventional dictionary matching where the acquired signals can only be matched to the discrete entries computed in the dictionary, the proposed method relies on the functional representation of the NN which yields continuous-valued parameter outputs. This is a notable advantage of the NN reconstruction since the reconstruction accuracy is no longer strictly limited by the dictionary density. Moreover, the network training process results in a signal-to-parameter mapping that is more robust to noise than a conventional dictionary matching approach (Fig. 4 and Supporting Fig. S6) because the mapping is forced to be expressed in low-dimensional space and is thus insensitive to small corruptive input perturbations. This mapping need not result a loss of accuracy provided that the salient features of the signal are adequately preserved by the NN, in analogy with truncation of small singular values in the singular value decomposition (32). Because conventional MRF dictionaries are generated from combinations of tissue parameters, each T₁ and T₂ value can be repeated multiple times in the dictionary. Despite this natural redundancy, the error in the NN reconstruction was still smaller for increasing dictionary undersampling than with conventional dictionary matching.

Conventional dictionary matching does not learn a functional mapping, relying instead on the similarity between the normalized measured data and the corresponding normalized dictionary entry. An unfortunate side-effect of the normalization is that noisy signals, arising from tissues with short T₂ for example, are amplified and then matched to some dictionary entry leading to increased reconstruction errors (Supporting Fig. S4). The dictionary matching was greatly influenced by the low SNR of the short T₂ values rendering them nonestimable. Those values, corresponding to T₂s smaller than 11 ms, were excluded from the calculations of the dictionary matching error but were included in those of the NN reconstruction. It should be noted that as the noise is increased, the smallest detectable T₂ value will get correspondingly larger. Because the NN was trained on noisy signals it yielded smaller error for both T₁ and T₂ (Fig. 4 and Supporting Figs S4,S5,S6).

The in vivo MRF EPI T₁ and T₂ maps reconstructed by DRONE (Fig. 6) correspond well to the known anatomy and the average values of the associated ROIs are similar, for grey and white matter, to those reported by Ma et al and references therein (1). The average CSF value obtained in our study (~1600 ms for T₂) was similar to other studies (33,34) but significantly larger than the 550 ms reported by Ma et al. Susceptibility of the MRF FISP sequence to out-of-plane flow, as proposed in that paper, may explain the discrepancy though recent work by Daoust et al (34) suggests that flow only has a small effect on the T₂ of CSF at 1.5T.

A successful application of deep learning networks requires large and high quality training data. In a clinical context, large, high quality datasets may be difficult to obtain and expensive to generate. Training the network on simulated dictionary data eliminates this concern and permits generating arbitrarily large training sets. Our results (Figs. 5,6) show that networks trained on simulated data can accurately reconstruct measured data despite the presence of inevitable noise and other sources of errors in the measurements.

The compact size of the NN solves many of the problems inherent to conventional dictionary matching. Specifically, DRONE required merely ~5% of the storage and memory needed for storing even the small training dictionary used - larger dictionaries would reduce this fraction further. Because of its feedforward structure, reconstruction with the network was 300-fold faster than conventional dot product dictionary matching of the optimized MRF EPI data and up to 5000-fold faster for the larger MRF FISP data. Accelerated matching techniques such as that reported by Cauley et al (5) still necessitated 2 seconds per slice for reconstruction which was ~16 fold longer than what would be required with a NN reconstruction of an equivalent number of time-points. While the dictionary used in that study was larger than the one used in this work, the number of entries in the NN training dictionary has no effect on the final reconstruction time once the network is fully trained. Because the network topology is fixed, additional training entries simply modify the weights/biases of the network but do not increase the reconstruction time. Similarly, because the architecture of our network (300×300 fully-connected hidden layers) theoretically allows up to 600² degrees of freedom (one weight and one bias per node), the inclusion of additional parameters in the reconstruction would only require increasing the size of the training dictionary which would not affect the post-training reconstruction time. In theory, a larger network can better represent complicated functional mappings albeit at the cost of increased reconstruction time and increased risk of overfitting the data. The relatively simple network architecture used in this study provided accurate reconstructions at near instantaneous processing time.

This work represents an initial proof-of-concept for MRF reconstruction by a NN and can be optimized to further improve the results. For instance, although the training time for the network used in this study was relatively small (~10–74 minutes), alternative methods may yield faster training. The size of the network and the small number of images used with the optimized MRF EPI schedule contributed to the short training time but conventional MRF sequences that require a greater number of acquisitions (10–100 fold higher) will require a longer training time as will simultaneous reconstruction of additional tissue parameters given the larger training dictionary needed. The sigmoid and tanh activation functions used in this study are a common choice for NN training (35) but skew the accuracy of the network towards the middle of the training dictionary range (Fig. 2) where the gradient is largest and the back-propagation algorithm is thus most effective. This problem is well known in the machine-learning literature with a number of techniques available for addressing it (36). Alternative training strategies and activation functions such as Softmax and ReLu are beyond the scope of this work and will be examined in future studies.

Conclusion

We have demonstrated the feasibility of using deep learning networks for reconstruction of MRF data. The proposed approach yields fast and accurate reconstruction with a limited storage requirement despite training on sparse dictionaries and can therefore resolve the technical issues inherent to the exponential growth of multi-dimensional dictionaries.

Supplementary Material

Supp info

Supporting Fig. S1. Schedule of FAs and TRs used for the optimized MRF EPI and the MRF FISP sequences.

Supporting Fig. S2. MRF dictionary matching reconstruction of the noiseless T₁ and T₂ values tested in comparison to the true values for the lightly undersampled (X2) and 60-fold undersampled (X60) training dictionaries.

Supporting Fig. S3. NN reconstruction of the noiseless T₁ and T₂ values tested in comparison to the true values for the lightly undersampled (X2) and 60-fold undersampled (X60) training dictionaries.

Supporting Fig. S4. MRF dictionary matching reconstruction of the T₁ and T₂ values corrupted by 1% Gaussian noise in comparison to the true values for the lightly undersampled (X2) and 60-fold undersampled (X60) training dictionaries. The dictionary matching of noisy data was particularly susceptible to short (<11 ms) T₂ values for the noise level tested resulting in large errors.

Supporting Fig. S5. NN reconstruction of the T₁ and T₂ values corrupted by 1% Gaussian noise in comparison to the true values for the lightly undersampled (X2) and 60-fold undersampled (X60) training dictionaries. Because the NN reconstruction was trained on noisy data it was more robust to the effects of noise.

Supporting Fig. S6. RMSE of the MRF dictionary matching (open circles) and NN reconstruction (closed circles) for the different undersampling factors and noise levels tested. For the noiseless acquisition (blue curves) the error in the NN reconstruction was 2 fold smaller for T₁ and 4 fold smaller for T₂ at the largest undersampling factor tested. For the noisy acquisition (red curves) only tissues with T₂s > 11 ms were included in the error calculation for the MRF dictionary matching whereas all tissues were included in the NN reconstruction error. Nevertheless, the NN reconstruction error was still smaller or equal to the MRF error for all undersampling factors tested.