Testing Cross-Phenotype Effects of Rare Variants in Longitudinal Studies of Complex Traits

Abstract

Many gene mapping studies of complex traits have identified genes or variants that influence multiple phenotypes. With the advent of next-generation sequencing technology, there has been substantial interest in identifying rare variants in genes that possess cross-phenotype effects. In the presence of such effects, modeling both the phenotypes and rare variants collectively using multivariate models can achieve higher statistical power compared to univariate methods that either model each phenotype separately or perform separate tests for each variant. Several studies collect phenotypic data over time and using such longitudinal data can further increase the power to detect genetic associations. While rare-variant approaches exist for testing cross-phenotype effects at a single time point, there is no analogous method for performing such analyses using longitudinal outcomes. In order to fill this important gap, we propose an extension of Gene Association with Multiple Traits (GAMuT) test, a method for cross-phenotype analysis of rare variants using a framework based on the distance covariance. The approach allows for both binary and continuous phenotypes and can also adjust for covariates. Our simple adjustment to the GAMuT test allows it to handle longitudinal data and to gain power by exploiting temporal correlation. The approach is computationally efficient and applicable on a genome-wide scale due to the use of a closed-form test whose significance can be evaluated analytically. We use simulated data to demonstrate that our method has favorable power over competing approaches and also apply our approach to exome chip data from the Genetic Epidemiology Network of Arteriopathy.

1 Introduction

Pleiotropy refers to the phenomenon of one genetic variant influencing more than one distinct trait. Several studies in recent years suggest the existence of many genetic variants that influence multiple phenotypes (Lees, Barrett, Parkes, & Satsangi, 2011; Liu et al., 2012). In the presence of such cross-phenotypic effects, joint genetic analysis of multiple phenotypes can be more accurate for phenotype prediction and statistically more powerful for gene mapping than univariate methods that model each phenotype separately (Maier et al., 2015; Galesloot, Van Steen, Kiemeney, Janss, & Vermeulen, 2014; Allison et al., 1998). Genetic pleiotropy induces phenotypic correlation which is more readily detectable through cross-phenotype analyses using the extra information provided by the correlation among the phenotypes. Although several tests of pleiotropy for common variants exist, they are usually less powerful for rare variants (Schaid et al., 2016). A recent method called ‘Gene Association with Multiple Traits (GAMuT)’ (Broadaway et al., 2016) was proposed to fill this gap for rare variants. The authors also argued that performing cross-phenotypic tests for rare variants might be more important than performing the same types of analyses for common variants since population-genetic models suggest rare variants are likely to be pleiotropic in nature under the model of infintesimal genetic architecture (Broadaway et al., 2016).

In many studies related to genetic epidemiology, such as the Genetic Epidemiology Network of Arteriopathy (GENOA) study (Daniels et al., 2004), observations at multiple time points are available for each subject. More accurate inference can be drawn by exploiting the temporal correlation in these measurements. However, most of the researchers tend to use existing single time point methodologies on such data after collapsing the repeated measurements into a single value (e.g. average across time points). Such a simple approach fails to take advantage of the extra information provided by repeated measurements and can be less powerful as a result.

A rare-variant statistical approach for cross-phenotype analysis of longitudinal outcomes requires a framework that can handle multiple phenotypes observed over multiple time points and furthermore can simultaneously handle information from multiple rare variants within a gene, since gene-based testing can be more powerful than testing of individual variants (Morris & Zeggini, 2010; He et al., 2016; M. C. Wu et al., 2011; Kwee, Liu, Lin, Ghosh, & Epstein, 2008). Such an approach currently does not exist in the statistical or genetics literature. There exist methods for longitudinal analysis of genetic data (Fan et al., 2012; Furlotte, Eskin, & Eyheramendy, 2012) based on random effects models (Fitzmaurice, Laird, & Ware, 2012) or generalized estimating equations (GEE) (Zeger & Liang, 1986). However, such models cannot be applied to test the association of the longitudinal phenotype data with an entire gene or thousands of markers taken together in a flexible manner. A recent method based on the longitudinal genetic random field model allows longitudinal analysis of multiple genetic variants simultaneously (He et al., 2016), but no extension of the method is available for cross-phenotypic effects. Finally, there are other multi-marker approaches such as sequence kernel association test (SKAT) (M. C. Wu et al., 2011) and similarity regression (SIMreg) (Tzeng, Zhang, Chang, Thomas, & Davidian, 2009) that are used for gene mapping, but such approaches do not directly apply to multi-phenotype data or longitudinal data. There has been some recent work on multivariate extensions to SKAT (B. Wu & Pankow, 2016; Sun et al., 2016). However, like GAMuT (Broadaway et al., 2016), these methods do not apply to longitudinal data. Another method using multivariate functional linear models (MFLM) (Wang et al., 2015) uses multi-phenotype data, but does not apply to longitudinal data. MFLM has also been shown to have much inferior power compared to GAMuT and SKAT in the single phenotype case (Broadaway et al., 2016). Moreover, the above tests require continuous phenotypes and therefore cannot be applied to important categorical phenotypes like presence or absence of a disease, which is not ideal for a test of pleiotropy.

In this article, we propose an extension of the GAMuT method for longitudinal data using some simple adjustments. The approach utilizes the correlation across time since it does not collapse the repeated measures, and also uses the correlation across phenotypes. Therefore it is appropriate for testing the genetic association for cross-phenotype longitudinal data and is especially powerful for rare variants. We demonstrate its power and control of type-I error through simulations and also apply the method to perform exome-chip analysis of multivariate repeated measures of cardiovascular-related phenotypes from the GENOA study (Daniels et al., 2004).

2 Methods

The GAMuT test (Broadaway et al., 2016) relies on a machine-learning framework called kernel distance-covariance (KDC) (Gretton et al., 2007; Hua & Ghosh, 2015; Székely, Rizzo, Bakirov, et al., 2007) and provides a non-parametric test for independence between a set of phenotypes and a set of genetic variants within a gene of interest. The framework is based on comparing pairwise phenotypic similarity between samples with genotypic similarity between samples. It allows for arbitrary number of genotypes and phenotypes, and therefore it is ideal for testing rare variants. It also allows for covariates and is computationally efficient due to its ability to provide analytic p-values using Davies’ (Davies, 1980) method.

Let us start with a single time point. Suppose a sample of N subjects has data on L phenotypes. The phenotype vector for the j^th subject (j = 1,2,…,N) is P_j = (P_j1,P_j1,…,P_jL). Each phenotype can be either continuous or categorical. Let $P=\left(P_1^T,P_2^T,\dots ,P_N^T\right)$ be the phenotype matrix for all samples. Similarly, the genotype vector for sample j at V rare-variant sites in the gene of interest, G_j = (G_j1,G_j2,…,G_jV), and the genotype matrix $G=\left(G_1^T,G_2^T\dots ,G_N^T\right)$ for all samples can be defined. Here G_jv (j = 1,2,…,N;v = 1,2,…,V) is the number of copies of the minor allele that the subject possesses at variant v. P is an N × L matrix and G is an N × V matrix, and kernel similarity measure between these two matrices is used by GAMuT to test the independence between the set of rare variants and the set of phenotypes.

To apply the GAMuT test, an N × N phenotypic similarity matrix Y and N × N genotypic similarity matrix X are first defined. Different kernels can be used to define the similarity matrices. For example, Y can be modeled using a projection matrix (Schork & Zapala, 2012), such that Y = P(P^T P)⁻¹P^T. A linear, quadratic or Gaussian kernel can also be used. Let the kernel function y(P_i,P_j) denote the similarity between phenotype vectors of subject i and subject j. For linear kernel, $y\left(P_i,P_j\right)={\displaystyle {\sum }_{l=1}^L{P}_{il}{P}_{jl}}$; for quadratic kernel, $y\left(P_i,P_j\right)={\left(1+{\displaystyle {\sum }_{l=1}^L{P}_{il}{P}_{jl}}\right)}^2$; and for Gaussian kernel, $y\left(P_i,P_j\right)=exp\left(-{{\displaystyle {\sum }_{l=1}^L\left(P_{il}-P_{jl}\right)}}^2\right)$ (M. C. Wu et al., 2011; Kwee et al., 2008; Schaid, 2010). Similar kernels can be used for the genotypes.

Once the similarity matrices X and Y are defined, they are centered as X_c = HXH and Y_c = HYH, where $H=I-1_N{1}_N^T/N$ is the centering matrix, I being the identity matrix of dimension N, and 1_N being the N × 1 vector with each element equal to 1. The GAMuT test statistic is then defined as

$$T_{\mathit{GAMuT}}=\frac{1}{N}\mathit{trace}\left(Y_c{X}_c\right)$$ (1)

Under the null hypothesis that the genotypes and the phenotypes are independent, the test statistic has the same asymptotic distribution as $\frac{1}{N}{\displaystyle {\sum }_{i,j=1}^N{\mathrm{\lambda }}_{Xi}{\mathrm{\lambda }}_{Yi}{z}_{ij}^2}$, where λ_Xi and λ_Yi are the ith ordered nonzero eigenvalue of X_c and Yc, respectively, and $z_{ij}^2$ are independent and identically-distributed ${\mathrm{\chi }}_1^2$ random variables. Davies’ method can then be used to compute the p-value (Davies, 1980).

When phenotype data are available at multiple time points, the phenotypes for j^th subject at time point t can be defined as $P_j^{\left(t\right)}=\left(P_{j1}^{\left(t\right)},P_{j2}^{\left(t\right)},\dots ,P_{jL}^{\left(t\right)}\right)$. If we combine all samples and time points, it will result in a three-dimensional array, for which it is harder to apply a kernel method. Instead, we concatenate the $P_j^{\left(t\right)}$ s for t = 1,2,…,T and define the phenotype vector for jth sample as

$$P_j=\left(P_j^{\left(1\right)},P_j^{\left(2\right)},\dots ,P_j^{\left(T\right)}\right)$$

which now has dimension 1 × LT. Subsequently the N × LT phenotype matrix P and the genotype matrix G are defined similar to the single time point case. GAMuT (or any other multi-phenotype rare variant model) can be applied using these matrices in the usual manner. For our analysis we applied a weighted linear kernel for modeling the genotypes. A projection matrix or a linear kernel was used for modeling the phenotypes. The weighting scheme for modeling the genotypes, following (M. C. Wu et al., 2011), is based on the minor allele frequency (MAF) of each variant. The observed GAMuT test statistic is then compared with the appropriate mixture of chi-square distribution and p-values are obtained using Davies’ method.

We note that the concatenated phenotype vector differs from the normal case since it can impose an unusual correlation structure. The correlation structure among phenotypes at the same time point (within time point correlation) may not be similar to the correlation of the same phenotype across time (between time point correlation). Methods that inherently assume exchangeability of the phenotypes in some sense may perform poorly on such concatenated data. However, we have performed extensive simulation studies to verify that in most cases, the performance of the longitudinal version of GAMuT is better than other methods considered here (See 3). We applied GAMuT using both a projection matrix and a linear kernel for measuring phenotypic similarity. These two versions of GAMuT were compared against competing methods.

2.1 Simulations

Various simulations were done to verify that longitudinal GAMuT controls the type-I error at the desired level and to compare its statistical power with that of other methods. The model to generate longitudinal phenotype data is simple yet realistic. For each sample j, first we generated phenotype vectors for each time point t independently. Let us denote the independently generated phenotype vector at time t for subject j as $P_j^{\left(t\right)\ast }$. The model used to generate the $P_j^{\left(t\right)\ast }$ s is the same model used in the original GAMuT paper (Broadaway et al., 2016) which considers different biological factors to simulate realistic datasets. A coalescent model was used to simulate the genotype data, while a multivariate normal distribution was used to simulate the phenotype data. See the supplementary materials for a more detailed description of the simulation procedure.

To obtain the final phenotype vectors $P_j^{\left(t\right)\ast }$ s, a fixed effect of time and an error across time is then added to these values according to the following model:

$$P_j^{\left(t\right)}=P_j^{\left(t\right)\ast }+{\mathrm{\beta }}_{\mathit{time}}t+{\mathrm{\epsilon }}_{tj},$$ (2)

where ε_tj = (ε_tj1,ε_tj2,…,ε_tjL). We assume (ε_1ji,ε_2ji,…,ε_Tji) are iid from N(0,Γ) for all i = 1,2,…,L. The variance covariance matrix Γ is assumed to have a first order autoregression (AR(1)) or a compound symmetry (CS) structure. The variances of $P_j^{\left(t\right)\ast }$ and ε_tj are both assumed to be 1. We used several choices of the parameter ρ corresponding to the AR(1) or CS structure. This model ensures that the correlation between $P_{jl1}^{\left(t\right)}$ and $P_{jl2}^{\left(t\right)}$ is driven by the single time point simulation scheme and the correlation between $P_j^{\left(t1\right)}$ and $P_j^{\left(t2\right)}$ is driven by Γ. The final correlation between observations across time is half the value of the correlations in the matrix Γ, since the final variance of the observations is 2. We carried out the simulations in such a way (See Supplementary Materials Section 1) that the final correlation between phenotypes within a time point are between 0 and 0.3 (0.3 and 0.4 for high correlation). The coefficients corresponding to effect of time β_time were simulated using a U (0,1) distribution.

We also simulated cases where the additive fixed effect of time is not linear. However, at the model fitting stage, the effect of time is regressed away using a linear regression (Hua & Ghosh, 2015). Such simulation frameworks illustrate the performance of our approach under model misspecification. Situations with a quadratic and a sinusoidal time effect are considered. One important advantage of GAMuT is that it is also applicable to categorical data. We simulated a binary phenotype data using a probit model from the already simulated continuous data, we coded the phenotype as 1 when it is greater than some fixed value c and 0 when it is less than c. We chose c to be the arithmetic mean of the phenotype. We used a linear effect of time when simulating binary data. Only GAMuT and univariate SKAT allow for binary data, therefore we compared only these two for the binary data simulations. We used linear regression to adjust for the effect of time even in case of binary phenotypes. Adjustment using a logistic regression was also compared and had very similar results (results not shown).

A feature of longitudinal data is potential dropout over time, resulting in missing data. We applied our approach on the case where 20% observation are missing (completely at random) and the effect of time is linear. kNN imputation (Torgo & Torgo, 2011; Kowarik & Templ, 2016) was used to impute the missing data before applying the association tests.

For each simulated dataset, we used 1000 samples, 10 correlated phenotypes and 3 time points (6 time points in one scenario). The correlation between the phenotypes within a time point was either low (between 0 and 0.3) or high (between 0.3 and 0.4). The number of associated phenotypes varied between 0 (null case), 2, 4, 6, and 8. We used 10⁶ for type-I error simulations and 10000 replications for power simulations.

For the simulated datasets, we compared the performance of the longitudinal version of GAMuT (using either projection matrix or linear kernel for phenotypes) with variations of other existing approaches. In particular, we considered competitors MFLM and multivariate SKAT (MSKAT) (B. Wu & Pankow, 2016), which can be applied on the concatenated data in a manner similar to GAMuT. The parameters in the MFLM method were used as suggested by the authors (Wang et al., 2015) and the Q-statistic was used for implementing MSKAT. We also comapared univariate SKAT for which the phenotypes are first collapsed into single time point using arithmetic mean and then tested individually. To adjust for the multiple testing due to testing each phenotype individually, we used a 98% principal component approach similar to the original GAMuT paper (Broadaway et al., 2016). The approach finds the effective number of independent tests by computing the number of principal components needed to explain 98% variability. The effective number of tests is then used to adjust the p-values in a way similar to Bonferroni adjustment. Similarly, an approach combining the single time-point GAMuT p-values is also included in the simulation study. The approach computes the GAMuT p-value (Broadaway et al., 2016) for each time point and combines them using a Bonferroni adjustment. This method is referred to as ’GAMuT (Multi)’. A second method GAMuT (Meta) to combine the individual GAMuT p-values is also used in one simulation scenario (see Supplementary Materials Section 2 for details). GAMuT (Meta) performs meta-analysis using the estimate of the correlation structure across the time points, which was only possible in simulations. Therefore, it is unusable in practice and was included only to demonstrate the power gain by the joint analysis compared to the meta-analysis approach.

2.2 Analysis of GENOA data

High body mass index (BMI), low high-density lipoprotein (HDL), and high blood pressure are related phenotypes that are known to be associated with high risk of cardiovascular diseases, stroke and diabetes. These phenotypes are moderately heritable (Vattikuti, Guo, & Chow, 2012; Zarkesh et al., 2012; Hottenga et al., 2005) and understanding their genetic basis is clinically important. The GENOA study (Daniels et al., 2004) seeks to identify genetic variants that influence risk for hypertension and arteriosclerotic complications of hypertension (Lange et al., 2002). It includes a cohort of African American sibships from Jackson, Mississippi, that were genotyped for a large collection of rare variants using the Illumina Human Exome Beadchip. Over two different time points, data were collected on several phenotypes including BMI, HDL, systolic blood pressure (SBP) and diastolic blood pressure (DBP). We selected these four phenotypes for our analysis.

Following Broadaway et al. (2016), we randomly sampled 1 sibling from each sibling pair and performed standard data cleaning on this resulting dataset of independent subjects. After further data cleaning, our sample consisted of 539 subjects. For each subject, we included data from both time points and the samples having missing data at one time point (116 samples) were not dropped. The missing data were subsequently imputed using k nearest neighbors. The data also included covariates such as gender, age, and smoking status (ever smoked at least 100 cigarettes) and use of anti-hypertension or lipid-lowering medication. Following Broadaway et al. (2016), we also calculated the top ten genetic principal components using ancestry informative markers included on the Illumina array. The final imputed phenotype data along with the covariate data were analyzed using longitudinal GAMuT (both projection matrix and linear kernel), univariate SKAT, multivariate SKAT and MFLM. The use of the methods, including the choice of kernels and tuning parameters, was similar to the application to the simulated datasets.

3 Results

3.1 Type-I error simulations

In the main text, we present simulation results for datasets generated under an AR(1) correlation structure across time. Results for simulated datasets generated assuming a compound symmetry structure across time have very similar results and are provided in the Supplementary Materials. Figures 1 and 2 show the quantile-quantile (QQ) plots for the longitudinal version of GAMuT, using linear kernel and projection matrix, respectively, on simulated null datasets. The plots are provided for both linear and binary cases with no missing data. QQ plots for datsets generated with missing data as well as those for high correlation among phenotypes are shown in the Supplementary Materials and they show similar patterns to those in Figures 1 and 2. Table 1 shows the type-I errors for different methods under various simulation set up. It is evident that GAMuT controls the type-I error for almost all the simulation models considered. For tests with small level of significance (10⁻⁵), GAMuT (and SKAT) shows a slight inflation in type-I error in a few cases (Supplementary Table 1). However, the inflation is not significant and can be due to unstable estimation of Type-I error for the very small threshold. The only methods that show significant size inflation in some cases are GAMuT (Multi) and MFLM.

Figure 1.

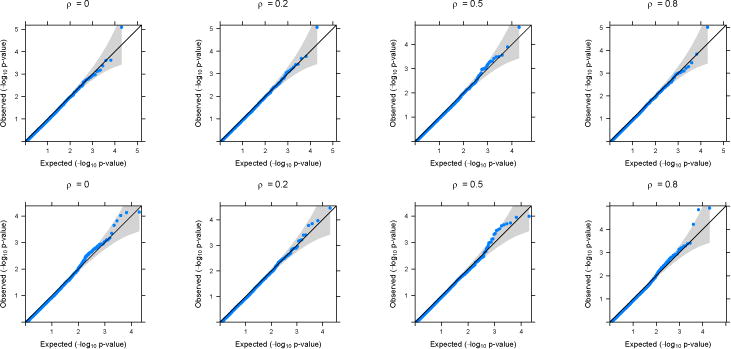
QQ-plots based on application of GAMuT (Linear) on simulated null datasets. Top row shows the plots for continuous phenotypes and the bottom row shows the plots for binary phenotypes (linear time effect). The correlation structure across time is considered to be AR(1) with parameter ρ.

Figure 2.

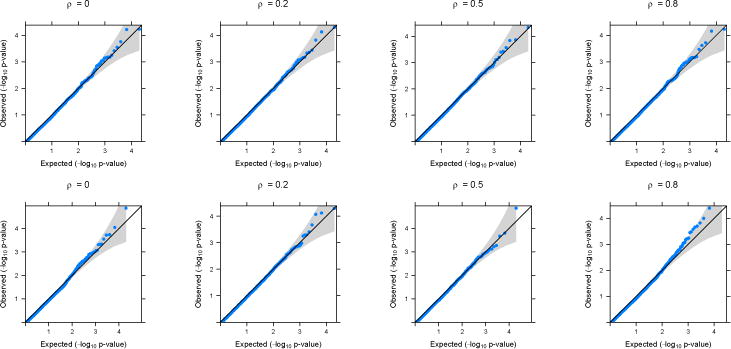
QQ-plots based on application of GAMuT (Projection) on simulated null datasets. Top row shows the plots for continuous phenotypes and the bottom row shows the plots for binary phenotypes (linear time effect). The correlation structure across time is considered to be AR(1) with parameter ρ.

Table 1.

Type-I error of different methods under various simulations, target α = 0.01. The correlation structure across time is considered to he AR(1) with parameter ρ.

	GAMuT (Projection)				GAMuT (Linear)				GAMuT (Multi)
	ρ = 0	ρ = 0.2	ρ =0.5	ρ = 0.8	ρ = 0	ρ = 0.2	ρ =0.5	ρ = 0.8	ρ = 0	ρ = 0.2	ρ =0.5	ρ = 0.8
Linear	0.010	0.009	0.009	0.009	0.009	0.009	0.009	0.009	0.009	0.009	0.008	0.008
Linear(high correlation)	0.009	0.009	0.008	0.009	0.010	0.010	0.010	0.011	0.009	0.010	0.009	0.009
Linear (6 time points)	0.006	0.006	0.006	0.007	0.007	0.007	0.006	0.008	0.008	0.008	0.007	0.007
Quadratic	0.010	0.009	0.009	0.009	0.009	0.009	0.009	0.009	0.009	0.009	0.008	0.009
Sine	0.010	0.008	0.010	0.009	0.010	0.009	0.009	0.009	0.009	0.008	0.008	0.009
Binary	0.010	0.010	0.009	0.010	0.010	0.009	0.009	0.010	0.012	0.012	0.011	0.013
Missing	0.008	0.008	0.007	0.007	0.008	0.008	0.007	0.008	0.008	0.008	0.007	0.009
	SKAT				MSKAT				MFLM
	ρ = 0	ρ = 0.2	ρ =0.5	ρ = 0.8	ρ = 0	ρ = 0.2	ρ =0.5	ρ = 0.8	ρ = 0	ρ = 0.2	ρ = 0.5	ρ = 0.8
Linear	0.008	0.008	0.008	0.008	0.010	0.009	0.009	0.009	0.007	0.008	0.009	0.007
Linear (high correlation)	0.007	0.007	0.007	0.007	0.009	0.009	0.008	0.009	0.007	0.007	0.008	0.009
Linear (6 time points)	0.007	0.008	0.007	0.007	0.006	0.006	0.006	0.007	0.007	0.008	0.007	0.007
Quadratic	0.008	0.008	0.008	0.007	0.010	0.009	0.009	0.009	0.007	0.008	0.009	0.007
Sine	0.008	0.008	0.008	0.007	0.010	0.008	0.010	0.009	0.008	0.008	0.009	0.007
Binary	0.007	0.007	0.008	0.006	0.010	0.010	0.009	0.010	0.010	0.009	0.008	0.009
Missing	0.008	0.009	0.008	0.009	0.008	0.008	0.007	0.007	0.008	0.009	0.008	0.009

3.2 Power simulations

Next we compared the statistical power of the longitudinal GAMuT against univariate SKAT (which uses the mean of each phenotype across phenotypes), multivariate SKAT, MFLM and GAMuT (Multi). All results reported correspond to an AR(1) correlation structure across time and a genomewide p-value threshold of 5×10⁻⁶. However, we also performed simulations for CS type correlation structure and less stringent p-value thresholds. They are reported in the Supplementary Materials. Figure 3 shows the power comparison when a linear effect of time was assumed to simulate the data (See Supplementary Materials for quadratic and sinusoidal time effects). Figure 4 shows the case of binary phenotypes and Figure 5 shows the missing data scenario. Simulations to compare the statistical power of the methods for a larger number of time points (T = 6) was also done and the results are shown in Supplementary Figure 4. The performance of the methods are similar across all the simulations with low correlation. GAMuT (Linear) has the highest power in all situations except the case when only two phenotypes have genetic association and the correlation across time is 0, which is unlikely in practice. The power of GAMuT (Linear) increases rapidly compared to other methods with the increase in number of associated phenotypes, illustrating its usefulness under pleiotropy. Also, GAMuT (Linear) has much increased power compared to other methods as the correlation of phenotypes across time increases. The power curves for GAMuT (Projection) are not shown since it had very similar performance as MSKAT. Univariate SKAT is the second most powerful method when the number of associated phenotypes is small, but MSKAT (and GAMuT(Projection)) and GAMuT (Multi) have improved power over SKAT as the number of associated phenotypes continues to increase.

Figure 3.

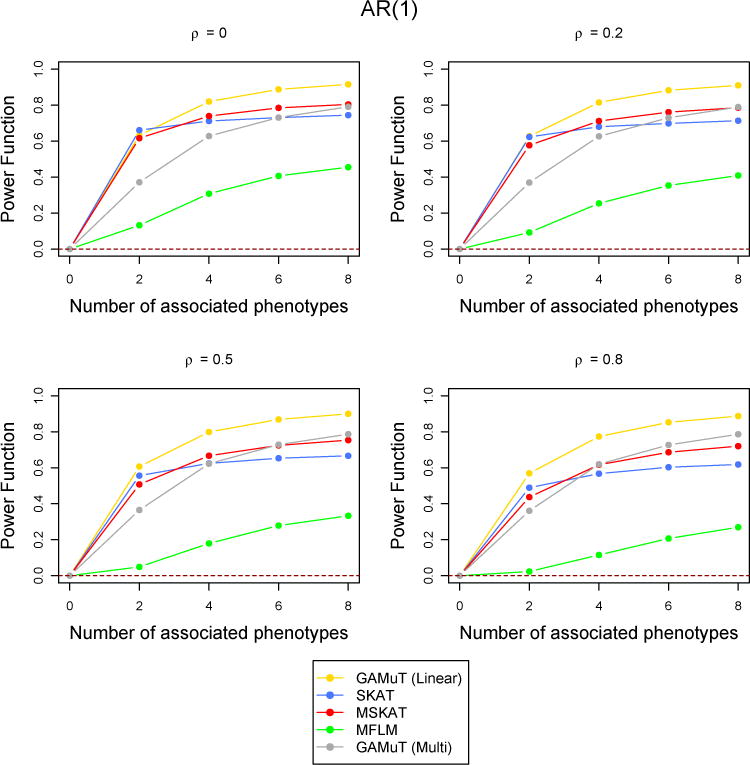
Comparison of power curves for different methods in the linear time effect set up. The correlation structure across time is considered to be AR(1) with parameter ρ and the tests are done at the p-value threshold 5 × 10⁻⁶. The value of the power function corresponding to 0 associated phenotypes shows the type-I error and the horizontal dotted line indicates the level of the test.

Figure 4.

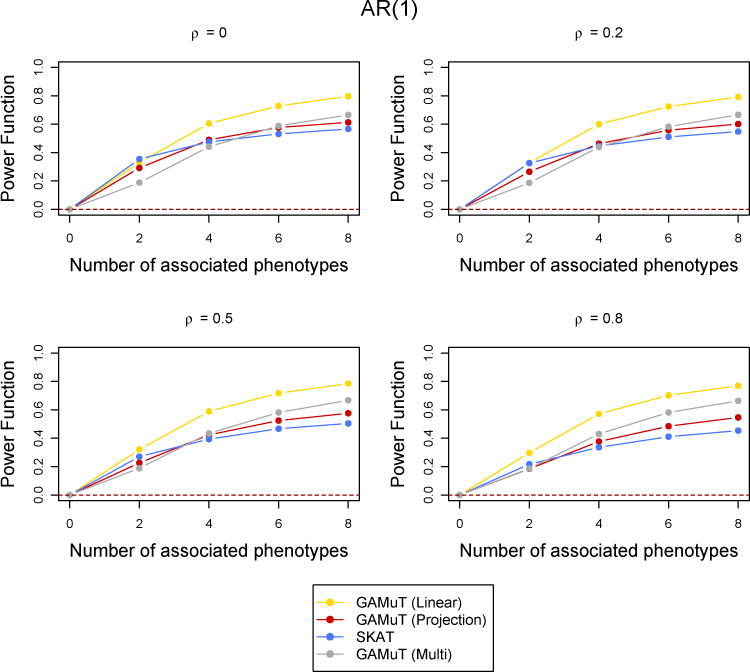
Comparison of power curves for different methods in the binary phenotypes case. The correlation structure across time is considered to be AR(1) with parameter ρ and the tests are done at the p-value threshold 5 × 10⁻⁶. The value of the power function corresponding to 0 associated phenotypes shows the type-I error and the horizontal dotted line indicates the level of the test.

Figure 5.

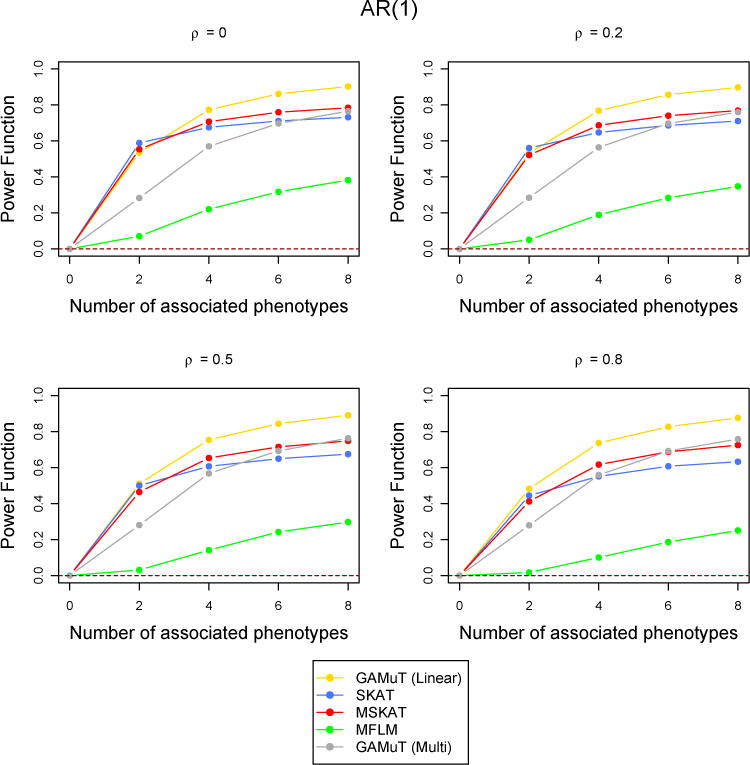
Comparison of power curves for different methods in the missing data scenario. The correlation structure across time is considered to be AR(1) with parameter ρ and the tests are done at the p-value threshold 5 × 10⁻⁶. The value of the power function corresponding to 0 associated phenotypes shows the type-I error and the horizontal dotted line indicates the level of the test.

However, when the correlation among the phenotypes are high, MSKAT and GAMuT (Projection) performes better than GAMuT (Linear) for low temporal correlation and/or small number of associated phenotypes (Figure 6). Similar results are observed for other simulation scenarios with high correlation (results not shown). MFLM has inferior power compared to the other fours methods in every simulation set up. As discussed in Broadaway et al. (2016), the performance of MFLM is sensitive to departure from very specific type of data they simulated (Wang et al., 2015). If data are simulated using the approach of (Wang et al., 2015), the performance of MFLM is comparatively better, but GAMuT had very similar performance and still outperforms all other approaches. Therefore we have not reported any result using their simulation approach.

Figure 6.

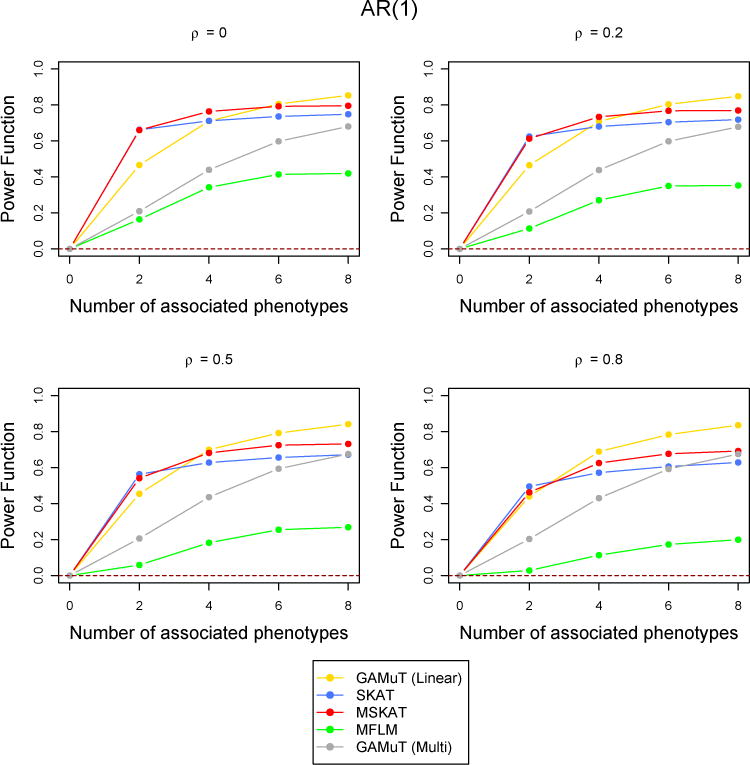
Comparison of power curves for different methods in the linear time effect set up when the correlations between phenotypes were higher. The correlation structure across time is considered to be AR(1) with parameter ρ and the tests are done at the p-value threshold 5 × 10⁻⁶. The value of the power function corresponding to 0 associated phenotypes shows the type-I error and the horizontal dotted line indicates the level of the test.

3.3 Analysis of GENOA data

We applied longitudinal GAMuT and the competing methods to the four phenotypes BMI, HDL, SBP and DBP from the GENOA exome-chip study. Prior to the analysis, covariate adjustment were made for gender, age, smoking status, use of anti-hypertension medication, use of lipid lowering medication, and ancestry on the 539 unrelated subjects. We applied longitudinal GAMuT using both projection matrix and linear kernel to the information collected at two time points. We also applied MSKAT and MFLM to this same dataset. We also applied univariate SKAT on the collapsed data using the average value of phenotypes across time. For GAMuT and SKAT, we applied a weighted linear kernel to quantify pairwise genotypic similarity, where weights were a function of minor-allele frequency and was of the same form to that typically utilized in SKAT (M. C. Wu et al., 2011).

We used a study-wise significance threshold of 1.5 × 10⁻⁵, which corresponds to a Bonferroni correction based on the number of genes tested (3278). P-values less than 10⁻³ were considered as suggestive.

Figure 7 shows the QQ-plot for different methods. MFLM shows sizeable inflation of p-values which could not be resolved by transformations. The MFLM method was subsequently dropped from the analysis of GENOA data. The other four approaches did not show such large p-value inflation.

Figure 7.

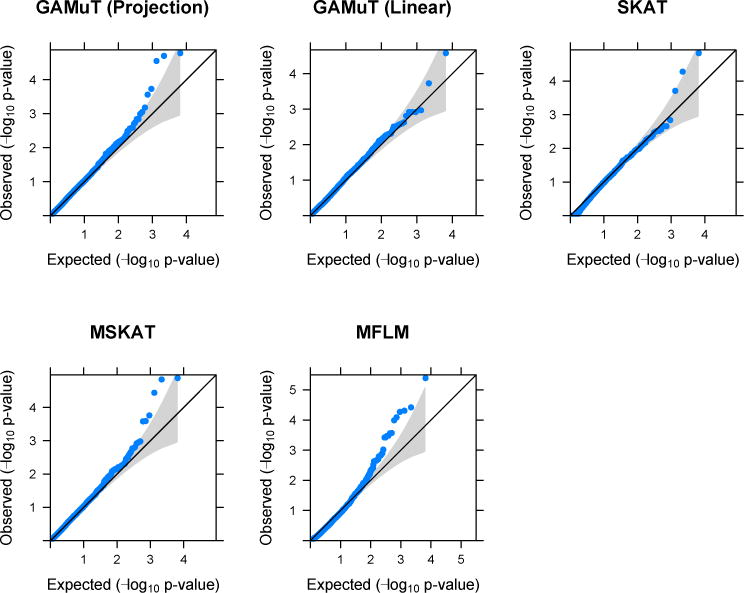
QQ-plots based on application of different methods on GENOA data.

Figure 8 shows the genome-wide results using different methods on the GENOA data. All the genes passing the suggestive or genomewide threshold by at least one method are reported in Table 2. Consistent with our simulation findings, we observed that GAMuT with a projection phenotype matrix yielded quite similar findings to MSKAT in the GENOA analyses. The top two genes identified by these two methods were EFCAB7 and COL9A3, with the results from MSKAT being genomewide significant while the result from GAMuT (projection) being borderline significant. No variants in EFCAB7 or COL9A3 have been reported to be associated with any traits in genome wide studies. EFCAB7 (EF-hand calcium binding domain 7) may play a physiological role in cardiac development based on a study of patients with Ellis-van Creveld syndrome (Nguyen et al., 2016). COL9A3 (collagen type 9 alpha 3) is associated with intervertebral disc disease, a disease frequent among older individuals (Martirosyan et al., 2016).

Figure 8.

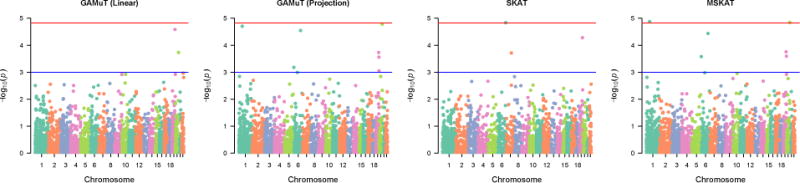
Manhattan plots based on application of different methods on GENOA data.

Table 2.

Genomewide results based on the application of different methods on GENOA data.

Chromosome	Gene Name	OMIM Number	Number of Variants	GAMuT (Projection)	GAMuT (Linear)	SKAT	MSKAT
1	EFCAB7	–	6	1.98E-05	0.010	0.325	1.33E-05
6	ENPP3	602182	6	2.84E-05	0.009	0.431	3.66E-05
6	NQO2	160998	5	0.001	0.007	0.061	2.63E-04
6	FNDC1	609991	10	0.006	0.003	1.46E-05	0.005
7	ZNF655	–	5	0.009	0.006	1.94E-04	0.009
19	CD33	159590	5	1.85E-04	2.61E-05	5.25E-05	1.75E-04
19	ZNF551	–	5	0.001	0.001	0.033	0.001
19	ZNF667	611024	5	2.75E-04	0.008	0.005	2.55E-04
20	COL9A3	120270	5	1.66E-05	1.85E-04	0.031	1.43E-05

ZNF667 (zinc finger protein 667) and ENPP3 (ectonucleotide pyrophosphatasep/phosphodiesterase 3) were genomewide suggestive with GAMuT with a projection phenotype matrix. No ZNF667 variants have been reported to be associated with any traits in genome wide studies. The ZNF667 protein, however, may play a role in neuroprotection by acting as a transcriptional repressor (Yuan, Huang, Yuan, Zhao, & Jiang, 2013). A variant in ENPP3 was associated with response of circulating adiponection in response to fenofibrate treatment (Aslibekyan et al., 2013). Adiponectin, a protein secreted by adipose tissue, is associated with improved insulin sensitivity, suppressed development of atherosclerosis, and altered inflammation. Fenofibrate targets circulating adiponectin levels to prevent the onset and progression of cardiovascular disease.

The top gene identified by longitudinal GAMuT with a linear kernel was CD33, which also was borderline significant. CD33 (sialic acid-binding immunoglobulin-like lectin 3) is an established gene for Alzheimers disease (Lambert et al., 2013). Recently this gene was associated with cognitive decline (Nettiksimmons, Tranah, Evans, Yokoyama, & Yaffe, 2016). Mid-life hypertension is associated with cognitive decline (Gottesman et al., 2014).

Univariate SKAT analysis identified a different gene, FNDC1 (fibronectin type III domain containing 1), which was genomewide significant. Interestingly, none of the methods that directly model cross-phenotype effects showed a strong signal for FNDC1, suggesting perhaps that this gene is associated only with a single phenotype rather than the multiple phenotypes that were considered. In a case-control study, several variants in FNDC1 showed suggestive association with coronary artery disease (Wild et al., 2011). Several suggestive genes were identified by each method. However, only MSKAT found two genes just passing the genomewide significance threshold. All the genes passing the suggestive or genomewide threshold by at least one method are reported in Table 2. We performed a non-parametric bootstrap analysis (with 1000 bootstraps) for each gene to confirm that the results are stable and not extra-sensitive to sampling fluctuations. The bootstrap confidence interval of the p-values are narrow in most cases indicating the stability of the methods. (Supplementary Table 2).

4 Discussion

There is increasing evidence that genetic variants can exhibit cross-phenotypic effects and the statistical power to find such cross-phenotypic effects can be enhanced by utilizing longitudinal phenotype data collected over time. We propose a simple extension of GAMuT for longitudinal data which can be applied on both continuous and binary phenotypes and can adjust for covariates. It is computationally efficient due to the use of Davies’ exact method for p-value computation and becomes usable at the genome-wide scale (Software will be made available for public use and will be made available on GitHub pages).

Instead of defining a kernel on the complicated three dimensional data (Phenotypes × Subjects × Time), we considered a concatenated data and have shown in simulation studies that such adjustment results in high statistical power and achieves proper control of the type-I error. The longitudinal extension of GAMuT was also shown to have higher power compared to other competing methods, similarly adjusted for longitudinal data.

The concatenated data may result in a completely different correlation structure among the columns of the phenotype matrix compared to what is usually observed for a single time point phenotype matrix. We performed extensive simulation studies to verify that GAMuT preserves its advantages of being highly powerful and being able to control type-I error at the desired level for such data. The construction of a projection matrix may be harder for longitudinal data and our results indicate that the linear kernel for measuring the phenotypic similarity has favorable statistical power over projection matrix. For low correlation among phenotypes, GAMuT with linear kernel dominated every other competing methods in almost every situation that were considered. However, GAMuT (Projection) had higher power for scenarios with low temporal correlation and/or small number of associated phenotypes.

Additionally, the longitudinal extension of GAMuT was also applied on the GENOA data collected at two time points. Every gene passing the suggestive threshold using any of the competing methods were also detected by at least one of the two GAMuT methods. GAMuT (Projection) was able to identify more genes passing the suggestive threshold. It is not surprising since the phenotypes in this study had high correlations and only 4 phenotypes were used. In general, we suggest to use GAMuT (Projection) for longitudinal data when the correlation among the phenotypes is high and/or the correlation across time is very small. However, GAMuT (linear) may be the better choice if many phenotypes are expected to be associated.

In the age of information explosion, more and more data are collected and often data are available on many phenotypes and over several time points. Our extension of GAMuT for longitudinal data can scale efficiently to handle an arbitrary number of phenotypes and time points, and enables the statistical analysis of cross-phenotypic effect of rare variants by taking advantage of such data to enhance statistical power and helps to develop a better understanding of the genetic background of important complex traits.