Diffusion tensor imaging using multiple coils for mouse brain connectomics

SUMMARY

The correlation between brain connectivity and psychiatric or neurologic diseases has intensified efforts to develop brain connectivity mapping techniques on mouse models of human disease. The neural architecture of mouse brain specimens can be shown non-destructively and three-dimensionally by diffusion tensor imaging, which enables tractography, the establishment of a connectivity matrix, and connectomics. However, experiments on cohorts of animals can be prohibitively long.

To improve throughput in a 7T preclinical scanner, we present a novel two-coil system where each coil is shielded, placed off-isocenter along the axis of the magnet, and connected to a receiver circuit of the scanner. Preserving the quality factor of each coil is essential to SNR performance and throughput, because mouse brain specimen imaging at 7T takes place in the coil-dominated noise regime. In that regime, we show a shielding configuration causing no SNR degradation in the two-coil system.

To acquire data from several coils simultaneously, the coils are placed in the magnet bore, around isocenter, where gradient field distortions can bias diffusion tensor imaging metrics, affect tractography and contaminate measurements of the connectivity matrix. We quantified experimental alterations in fractional anisotropy and eigenvector direction occurring in each coil. We showed that when the coils were placed 12 mm away from isocenter, measurements of the brain connectivity matrix appeared minimally altered by gradient field distortions.

Simultaneous measurements on two mouse brain specimens demonstrated a full doubling of the diffusion tensor imaging throughput in practice. Each coil produced images devoid of shading or artifact. To further improve the throughput of mouse brain connectomics, we suggested a future expansion of the system to four coils.

To better understand acceptable trade-offs between imaging throughput and connectivity matrix integrity, studies may seek to clarify how measurement variability, post-processing techniques, and biological variability impact mouse brain connectomics.

Graphical Abstract

When using a two-coil system to accelerate mouse brain connectomics, the connectivity matrix is affected by gradient field distortions off isocenter. On a 7T preclinical scanner, selecting a 12 mm coil offset-to-isocenter minimally alters the connectivity matrix. The doubling of the DTI throughput is fully achieved in practice in our system.

INTRODUCTION

The correlation between changes in brain connectivity and psychiatric or neurologic diseases^1–4 has intensified efforts to develop brain connectivity mapping techniques on mouse models of human disease. Oh et al.⁵ provided the most definitive connectome of the mouse brain using fluorescent markers to map axonal projections. This connectome, based on optical microscopy, used nearly 1300 animals and was acquired over several years. Calabrese et al. ⁶ demonstrated similar results using diffusion-tensor-imaging (DTI) connectomics, and showed concurrence with the optical methods in much of the brain. While the two methods provide overlapping insight into brain connectivity, they are different. DTI^7–12 shows the complex neural architecture of the brain indirectly, non-destructive and three-dimensionally, and it is potentially extensible to a large number of animals and disease models.

DTI requires the acquisition of one reference scan without diffusion-sensitization and a minimum of six additional scans, each diffusion-sensitized along a different axis. As a result, DTI acquisitions times are typically long. DTI studies have been applied to fixed specimens of rodent brain as well. Because lengthy acquisition times are acceptable ex vivo, the brain cytoarchitecture can be studied in great detail. But, the challenges of high spatial resolution, combined with the need to repeat diffusion sensitization multiple times, frequently result in scan times greater than a dozen hours^13,14 per mouse brain.

Diffusion tensor imaging has also enabled the use of tractography^15–17, which delineates fiber tracks^18,19 linking different regions of the brain. However, the use of a single diffusion tensor to determine fiber tracks breaks down in the presence of complex fiber crossings within a single voxel²⁰. To overcome that limitation, DTI methods have been expanded: diffusion spectrum imaging²¹, spherical deconvolution techniques²², and Q-ball imaging²³ rely on many gradient directions or b-values to resolve multiple fiber populations oriented differently within one voxel. In turn, the acquisition time increases significantly and may become an important experimental consideration^24–26. Calabrese et al.⁶ acquired diffusion data from 120 diffusion directions in an experiment lasting nearly 10 days.

As a compounded challenge, the total acquisition time required to create population-based atlases of mouse brain connectivity, or to compare different cohorts of animals, is multiplied by the number of specimens included in the study and can amount to several weeks of magnet time.

To make those statistically powerful experiments possible, several approaches have been proposed. Cryogenic probes^27–31 can shorten the acquisition time of diffusion imaging experiments limited by signal-to-noise ratio. However, ex vivo diffusion imaging of gadolinium-perfused mouse brain specimens is likely bound by gradient duty cycle. In that case, the higher SNR realized by a cryogenic receiver does not translate into a shorter repetition time and leaves the imaging throughput unchanged.

One of the most straightforward methods to increase DTI throughput is the use of multiple coils³² simultaneously. But, multiple coils increase throughput by a factor equal to the number of coils only if no SNR penalty is incurred³³. At 7T, SNR is tightly bound to the quality factor of the coil, because imaging of mouse brain specimens takes place in the coil-dominated noise regime^34,35. In that regime, SNR and throughput deteriorate even with small degradations of the coil quality factor. Hence, to harvest the most benefit in imaging throughput, a multiple-coil system should preserve the quality factor of each coil. In particular, if shielding is used to isolate each coil from the other, the RF dissipation caused by the shield should remain insignificant. Moreover, to achieve the high b-values required, DTI measurements are typically made within relatively small inner-diameter gradient sets. As several coils are loaded with brain specimens and placed around the magnet isocenter, even a relatively small offset to isocenter can cause significant gradient inhomogeneity^36–39, bias DTI metrics, affect tractography and ultimately alter measurements of the connectivity matrix.

In this manuscript, we assess how experimental throughput and mouse brain connectomics are affected by a two-coil system, first by measuring each effect separately, and finally by making measurements on two mouse brains simultaneously in a two-coil system.

METHODS

A two-coil system was developed for our 7T horizontal bore scanner (BioSpec 70/20 Advance III with Paravision 6.0.1, Bruker, Billerica, MA), equipped with a 12-cm inner-diameter gradient set (model BGA-12S2) capable of 440 mT/m and a slew rate of 4570 T/m/s. The scanner features a single transmitter channel, connected through an adapter (model T12325, Bruker, Ettlingen, Germany) to a two-way power divider (model NMC002–300, Novamedical, Wilmington, MA, USA). After splitting, the RF transmit signal is routed through a T/R switch (model NSMW-003A TR, Novamedical) to each radiofrequency coil of the two-coil system. Conversely, signal received by each coil is routed through an external preamplifier (model NSMW-003A TR, Novamedical) to a dedicated receiver circuit of the scanner. During lengthy acquisitions, the temperature within the bore is kept constant by a vigorous airflow of 12 l/min, temperature-regulated to a few degrees above room temperature, which remains independent of gradient set temperature. Coil tuning and matching are carried out after all RF components have reached their equilibrium temperature.

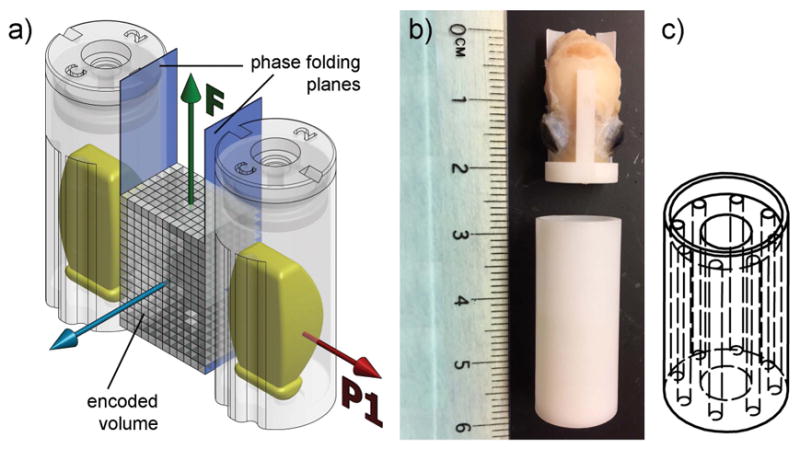
The two-coil system features two floating, split shields, cubic-shaped (an edge is 70 mm long), made out of electrolytic tough pitch copper (20 mm wide, 0.002-in thick). Each copper piece overlaps adjacent pieces by 5 mm. Interleaved between overlapping sheets of copper, a piece of thin, non-conducting-adhesive polyimide tape (0.75-in wide, 0.0025-in thick) provides electrical isolation, while limiting RF leakage. The two cubical shields are aligned with each other and tightly held together by a frame, which centers the shields around the axis of the bore, and places the magnet isocenter at the center of the wall shared between both shields (figure 1a). Each shield can be opened to load the RF coil with a mouse brain specimen. In-between experiments, the location of each coil inside the shield can be adjusted, closer or further away from the shared surface of the shields where most RF dissipation occurs. In turn, when the two-coil system sits in place inside the magnet, that adjustment changes the coil offset to isocenter. This allows one to study the effect of the shield on the coil quality factor, SNR and throughput on one hand, and the effect of the coil offset to isocenter and gradient field distortion on DTI metrics and connectomics on the other hand.

Figure 1.

a) The multiple-coil system includes two shielded coils. Each coil can be moved within its shield to adjust its offset to isocenter. b) Finite-element, three-dimensional radiofrequency simulation of our coil resonating at 300.5 MHz, loaded by a conductive mouse brain, and centered in our cubic shield. The software integrates the amount of power dissipated in the coil (54%), in the mouse brain (46%), and all the other electrical components including the shield (<0.1%).

We studied six different coil positions away from isocenter: 12 mm, 18 mm, and 24 mm, in each direction along the magnet axis. Those coil offsets include the distinct locations where SNR deterioration, or DTI degradation, is most pronounced. At the minimal coil offset to isocenter achievable in practice (12 mm), SNR is most profoundly degraded by the proximity of one dissipating surface of the shield, while the recorded DTI metrics are minimally altered by relatively small gradient field distortions. Conversely, at a larger coil offset of 24 mm, the measurement of DTI metrics deteriorates significantly due to relatively large distortions of the gradient field, while SNR is minimally impacted (the coil sits almost at the center of the shield, far away from RF-dissipating surfaces).

The DTI sequence encoded a 3D volume containing the magnet isocenter (figure 2a). The frequency direction was located along the long axis of the brain, and the first phase encode direction followed the axis of the magnet bore. Because of phase back-folding, a 12-mm wide encoding volume, sufficient to include a mouse brain, could be mirrored in such a fashion as to center the field-of-view on the axis of each coil.

Figure 2.

a) During DTI acquisition, a 3D imaging sequence encodes a volume including the magnet isocenter. The frequency axis F is parallel to the long axis of the brain specimens. The first phase-encode axis P1 is set along the magnet axis. The effective field-of-view is mirrored onto each coil by phase back-folding. b) A mouse brain specimen and its container. c) The homogenous phantom contains 0.4 ml of water doped with CuSO₄ 100mM, and loads the coil identically to a mouse brain.

To provide the DTI ground truth, and an SNR benchmark enabling throughput comparison, a single coil was constructed, identical to those in use in the two-coil system, but devoid of shielding and consequently free of shield-induced RF dissipation. Previous experience, confirmed by measurements shown further in the manuscript, demonstrate that insignificant amounts of extraneous noise couples to the unshielded coil inside the bore. That reference coil was placed on magnet isocenter to record almost unbiased DTI metrics, reported throughout the manuscript as “ground truth”. Similarly, the SNR performance and throughput of the unshielded reference coil on isocenter defined the benchmark used consistently throughout the text.

Shielding Effects on SNR

To assess the theoretical impact of the two-coil system on SNR and throughput, a three-dimensional finite-element radiofrequency simulation of the shielded radiofrequency coil was carried out using HFSS (version 16, Ansys, Canonsburg, PA). The amount of power dissipated in the coils, shields, and specimens was calculated numerically.

To validate the model experimentally, we fabricated a homogeneous phantom exhibiting the same electrical load and properties as a mouse brain (figure 2b and c). The homogeneous phantom enables precise, reproducible SNR measurements in the same noise regime as mouse brain imaging. First, the amount of water contained in the phantom (0.4 ml) was empirically chosen so that the frequency drop during coil loading is identical to a mouse brain. Second, the water in the phantom was doped with copper sulfate at a 100 mM concentration, corresponding to the same electrical load as a mouse brain (Table 1). We loaded the homogeneous phantom into the coil sitting on the positive axis of the bore, after adjusting the coil position within the shield +12 mm, +18 mm, or +24 mm away from the shared surface of both shields. We inserted the two-coil system into the magnet, and moved it along the bore axis until the homogeneous phantom was centered on magnet isocenter, in order to measure the impact of the shield on SNR independently from effects due to off-isocenter imaging. A 3D spin-echo image volume was acquired 6 times at each coil location, using the following parameters: TR 200 ms, TE 5.4 ms, FOV 25.6 × 12.8 × 12.8 mm, BW 100 kHz, voxel 200 μm isotropic. To estimate signal-to-noise ratio precisely, we used histograms of the image volumes and fitted Rician distributions to the noise and signal peaks. The mode and standard deviation of each distribution were calculated from the fitting parameters, and the signal-to-noise ratio was computed by dividing the signal mode by the noise standard deviation.

Table 1.

The resonant frequency and quality factor of the reference coil are altered the same way by loading a mouse brain or the homogeneous phantom into the coil, indicating that SNR measurements on the homogenous phantom are representative of mouse brain imaging.

	Resonant Frequency (MHz)
	Unloaded	Loaded with Brain	Loaded with Phantom
Reference Coil	300.36	299.41	299.55
	Quality Factor
	Unloaded	Loaded with Brain	Loaded with Phantom
Reference Coil (Unshielded)	720	380	395
Coil 1 (Shielded)	705	370	385
Coil 2 (Shielded)	710	380	380

Also, the quality factor of each shielded coil in the two-coil system remains similar to the unshielded reference coil, demonstrating that the shield causes negligible RF losses, and that all three coils are almost identical.

Shimming Effects on SNR

When using several coils simultaneously, it is no longer possible to shim the magnet on each mouse brain individually. Shim values over a volume encompassing all the coils must be used. We placed on magnet isocenter a centrifuge tube (diameter 28 mm, length 80 mm) containing water and 5 mM CuSO₄, centered within a 72-mm inner-diameter birdcage coil (model T10720V3, Bruker). We defined a small, intermediate, and large shimming volume, which would enclose both coils of the two-coil system with a coil offset to isocenter of ±12 mm, ±18 mm, and ±24 mm respectively. Using the centrifuge tube, we recorded the shimming currents minimizing B₀ inhomogeneity within each of the three volumes. After activating the shimming currents corresponding to the largest volume, we placed the reference coil loaded with the homogeneous phantom at position +24 mm along the magnet axis, and recorded SNR. We then moved the coil to position −24 mm and repeated the measurement. Similarly, we used the currents associated with the intermediate shimming volume to make SNR measurements at a coil offset of ±18 mm, and the currents shimming the small volume for SNR acquired at position ±12 mm.

Gradient Field Distortion Effects on DTI metrics

A two-coil system requires off-isocenter imaging. To evaluate the impact of off-isocenter imaging on diffusion imaging metrics and tractography, we selected a single mouse brain specimen, fixed and gadolinium-perfused, as described elsewhere⁴⁰. Briefly, the mouse was transcardially perfused during sacrifice with a mixture of saline and ProHance (Bracco, Princeton, NJ) followed by a solution of formalin and ProHance, in accordance with protocols approved by the Duke Institutional Animal Care and Use Committee. The skull was removed from the body, leaving the mouse brain intact inside the cranial cavity. A mouse brain specimen prepared in such a fashion exhibits a T₁ at 7 T ranging from 100 to 120 ms, much shorter than in vivo tissue. Before imaging, the skull was inserted into a small container filled with a perfluoropolyether fluid (Galden, Solvay, Brussels, Belgium) to limit changes in magnetic susceptibility at the tissue surface.

The brain was inserted into the unshielded reference coil, and ground truth DTI data were recorded on magnet isocenter. Subsequently, to estimate the alteration of DTI metrics due to off-isocenter imaging independently of other causes of variability, the reference coil was moved to a ±12 mm, ±18 mm and ±24 mm offset to isocenter, where comparable DTI data from the same brain was acquired. A 3D Stejskal-Tanner spin echo sequence was run with 21 different angles of diffusion sensitization at a b-value of 1500 s/mm², using the parameters: TR 100 ms, TE 20 ms, FOV 25.6 × 12.8 × 12.8 mm, BW 100 kHz, voxel 100 μm isotropic, ∂ = 4.5 ms, Δ = 10 ms. The 21 gradient directions were uniformly distributed to guarantee rotational invariance⁴¹, based on a model of electrostatic charge repulsion⁴². Four baseline images (b₀) were also acquired without diffusion-sensitization gradient lobes. The total acquisition time for a complete DTI data set was 11 hours. To evaluate the reproducibility of the DTI measurements, the acquisition on isocenter was repeated 6 times. Similarly, 6 datasets were acquired at a ±12 mm coil offset to isocenter. Other data were recorded once only, from the reference coil positioned at −24 mm, −18 mm, +18 mm and +24 mm along the magnet axis.

Even though great care was taken to align the mouse brain in an identical fashion during different acquisitions, small variations in specimen positioning are unavoidable. To compare the DTI metrics at different coil locations, each data set was registered to a common atlas, Waxholm Space⁴³. The registration did not require the interpolation of the eigenvectors, to guarantee the accuracy of DTI metrics. More specifically, each of the diffusion-sensitized volumes (21 sets) was registered to the average of the four b₀ images to correct for eddy-current-induced image distortion, using an affine registration (ANTS, University of Pennsylvania⁴⁴), which defined the first image transform. The resulting 25 co-registered volumes were averaged to generate a diffusion-weighted image, which was registered onto the reference mouse brain atlas within Waxholm Space, using an affine transformation (which defined a second transform) followed by a diffeomorphic transform (defining a third transform). At that point, registration into Waxholm Space of the original 4 b₀ sets was possible by using the second and third transforms; similarly, the original 21 diffusion-attenuated sets could be registered into Waxholm Space by using the first, second, and third transforms. In addition, it was possible to rotate the 21 diffusion-directions using the angular components of the second affine transform. As a final step, the 25 volumes registered to Waxholm Space, accompanied by the rotated 21 gradient directions, were processed in a pipeline using Diffusion Toolkit (www.trackvis.org, Massachusetts General Hospital, Boston, MA) to compute the final sets of registered diffusion metrics, including a fractional anisotropy (FA) map, a diffusion-weighted image set, maps of the eigenvalues, and sets of the three eigenvectors. Regardless of the original experimental position of the mouse brain, the resulting volumes are registered with each other and can be compared on a voxel-by-voxel basis. In addition, Waxholm Space contains 166 brain regions segmented individually, enabling a regional analysis of diffusion metrics (figure 3).

Figure 3.

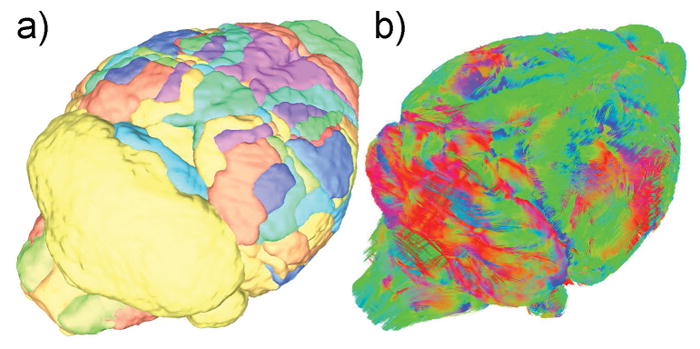
a) The 166 brain region available in Waxholm Space, each segmented individually, can be used for regional analysis of DTI metrics and to create connectivity matrices between regions. b) Color-coded rendering of fiber tracks, used to generate a connectivity matrix between brain regions (red: left-right, green: rostral-caudal, blue: ventral-dorsal)

For each of the 166 brain regions, an average fractional anisotropy was calculated on isocenter, as well as ±12, ±18 and ±24 mm away from isocenter. The dot product was calculated between the eigenvectors on isocenter, and the eigenvectors of each set acquired off-isocenter. For each voxel, the dot product was converted into an angular deviation. For each region, we reported its median angular deviation.

Gradient Field Distortion Effects on the Connectivity Matrix

For each of the sets acquired at a different offset along the magnet axis, we computed tractography maps using DSI Studio’s (http://dsi-studio.labsolver.org/) deterministic fiber tracking algorithm⁴⁵, using an anisotropy threshold of 0.1, a 45° angular threshold, a step size of 0.02 mm, and bounds constraining the length of the fiber track between 0.5 and 40 mm. The whole brain was randomly seeded to reveal two-million tracks, with sub-voxel seeding and tri-linear directional interpolation. A connectivity matrix of the 166 brain regions was generated for each dataset.

Combined Effects of Simultaneous Measurements in the Two-Coil System

Finally, combining together the effects due to shielding, shimming, off-isocenter imaging, RF coil and shield variability, we acquired simultaneously a DTI dataset from two different brain specimens prepared as described earlier (called “brain A” and “brain B”) using the two-coil system (comprised of “Coil 1” and “Coil 2”). The coils were placed at the minimum offset to isocenter of ±12 mm. First, we acquired simultaneously DTI data from brain A in coil 1, and brain B in coil 2. Then we swapped the brains, and acquired DTI data from brain A in coil 2, and brain B in coil 1. To exclude biological variability from ground truth comparisons, we acquired DTI data from brain A in the reference coil on magnet isocenter, where the same measurement was repeated for brain B. For each brain, we registered the DTI metrics acquired in the two-coil system to the ground truth data acquired on isocenter.

Also, to compare the RF performance of each coil during transmission, we measured the power required to achieve a 90° flip angle in a 5-mm thick slab centered on the horizontal plane of the magnet, using a 1-ms hard pulse, for each coil individually loaded with each brain in turn.

RESULTS

SNR Deterioration Due to Shielding and Shimming

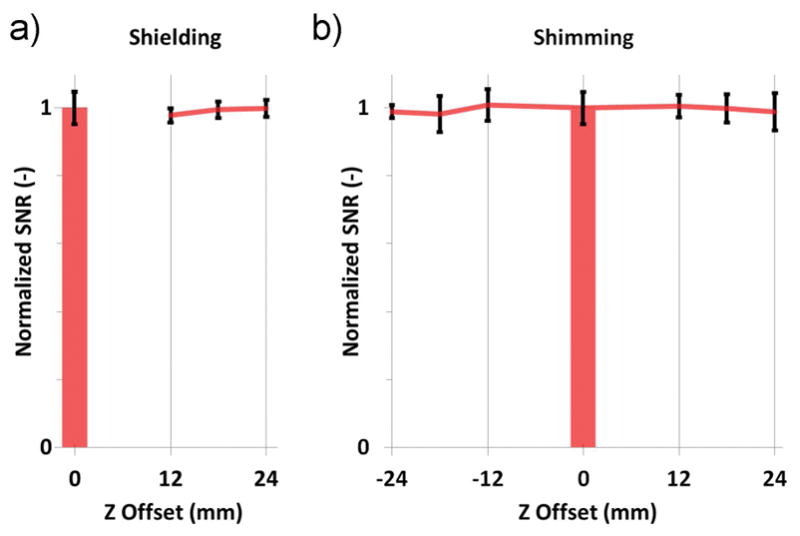
The finite-element, electromagnetic simulation of the two-coil system showed that the acquisition takes place in the coil-dominated noise regime, and that the 70-mm cubic-shaped shields are large enough to cause small-to-negligible radiofrequency losses (figure 1b). We investigated one of the two identically-designed shields experimentally, and could confirm that the SNR acquired from the homogeneous phantom is left largely unchanged by the position of the coil within the shield or the proximity of one dissipating surface. Also, shimming over a wider volume, to include both coils of the two-coil system, revealed an insignificant SNR penalty (figure 4).

Figure 4.

a) Compared to the benchmark SNR provided by the unshielded reference coil on isocenter (bar), the signal-to-noise ratio acquired by a shielded coil of our system remains stable, even when the coils sits in close proximity to one dissipating surface of the shield (12 mm coil offset to isocenter). b) Shimming is carried out on a volume encompassing both coils, and does not degrade SNR.

Alteration of DTI Metrics Due to Gradient Field Distortions

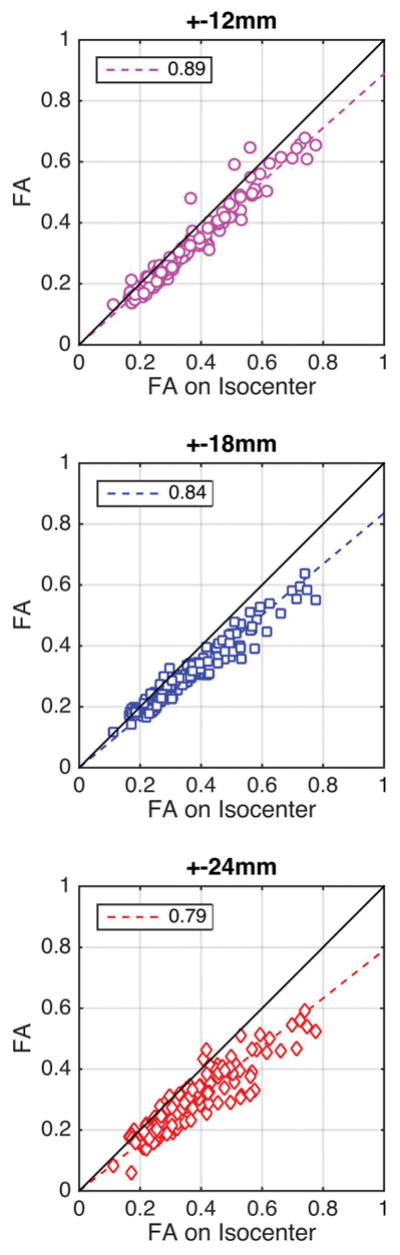
Figure 5 shows how fractional anisotropy is affected by gradient field distortion off-isocenter: each brain region is represented as an ordered pair showing the ground truth FA measured by the reference coil on isocenter (as abscissa), and its average FA measured off-isocenter (as ordinate). When the coil is located 12 mm away from isocenter, fractional anisotropy is underestimated by approximately −11%. At larger coil offsets to isocenter, the underestimation of FA increases in severity.

Figure 5.

Each marker represents a brain region. When the coil is located 12mm away from isocenter (top), FA is under-estimated by approximately 11% in most brain regions. The under-estimation of FA becomes more pronounced (−16%) at a 18 mm coil offset to isocenter (middle). When the coil is furthest away from isocenter, at a 24 mm offset, FA is underestimated by 21% (bottom).

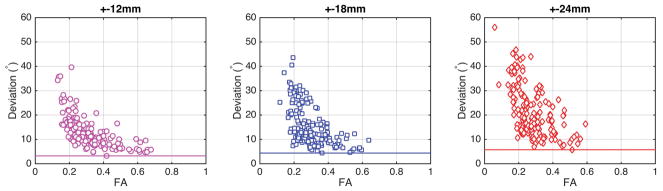
Figure 6 shows a graph of angular deviation vs. fractional anisotropy recorded experimentally, for each of the 166 brain regions. When the measurement was made in a coil 12 mm away from isocenter, the main eigenvector of half the voxels within a brain region deviated by more than 3.2° from the ground truth. The deviation remained smaller than 11° in the regions with the highest fractional anisotropy. In more isotropic regions, the measurement of the eigenvector direction deviated by as much as 40° from the direction of the eigenvector measured on isocenter. When the measurement was made from a coil located further away from isocenter, the deviation of the main eigenvector became more pronounced. The minimum deviation within one brain region was 3.2° when the coil was placed 12 mm away from isocenter, 4.4° when the coil was located 18 mm away, and 5.7° when the coil sat 24 mm away from the center of the magnet. At those respective coil offsets, the maximum deviation within one brain region reached to 40°, 44°, and 56°.

Figure 6.

Each marker corresponds to a brain region. When the coil is located 12 mm away from isocenter (left), the deviation of the main eigenvector of all brain regions is comprised between 3° and 11° degrees for highly isotropic regions. At a coil offset to isocenter of 18 mm (center), the eigenvector deviation is larger than at a 12 mm offset. Also, FA is more severely underestimated. When the coil is located at a 24 mm offset to isocenter (right), the deviation of the main eigenvector, as well as the underestimation of FA, are more severe.

Changes in the Connectivity Matrix Due to Gradient Field Distortions

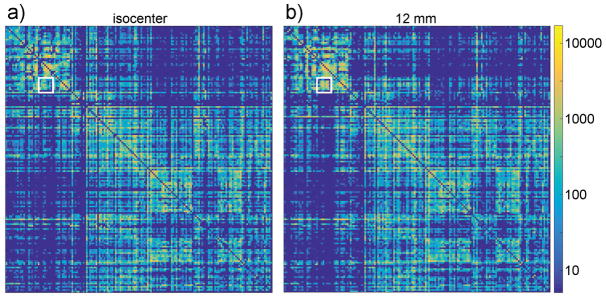
The connectivity matrix acquired on isocenter was qualitatively similar to the matrix acquired off-isocenter, at a small coil offset of 12 mm (figure 7). Visually, off-isocenter imaging at a 12-mm offset does not appear to drastically alter highly-connected region pairs, although minor differences are apparent. On isocenter, the brain regions showing the strongest connection are the cerebellar cortex to the cerebellar white matter, with a connection including 11,948 fiber tracks. Most of region pairs showing a strong connection (>1000 tracks) are visible regardless of coil offset to isocenter. More specifically, in the ground truth dataset acquired on isocenter, 39 regions included a connection at least 1,000-track strong. From those 39 regions, when the coil was placed 12 mm away from isocenter, 3 regions failed to show a connection 1000-track strong. At a coil offset of 18 mm, 4 regions failed to show a connection at least 1000-track strong. Finally, at 24 mm offset to isocenter, 9 regions no longer showed a connection 1000-track strong.

Figure 7.

The connectivity matrix were acquired from the same specimen, in a coil on isocenter (left), and in a coil 12 mm away from isocenter (right). Both matrices are similar, although some differences are apparent, as indicated by the white square. The scale on the right shows the number of tracks connecting region-pairs.

We calculated region-by-region the Spearman rank correlation⁴⁶ ρ between any combination pair of the 6 connectivity matrices acquired in the reference coil on isocenter, to assess the variability of matrices stemming from repeated measurements of the same brain on isocenter. We obtained ρ_isocenter = 0.75 ± 0.06. Similarly, a comparison between the matrices acquired by the coil located ±12 mm away from isocenter gave ρ_{12 mm} = 0.74 ± 0.07.

To estimate the effect of imaging off-isocenter, we compared any pair of matrices including one measurement made on isocenter and one measurement acquired ±12 mm away from isocenter and found ρ_{iso-to-12 mm} = 0.66 ± 0.02.

Combined Changes Due to Simultaneous Measurements in the Two-Coil System

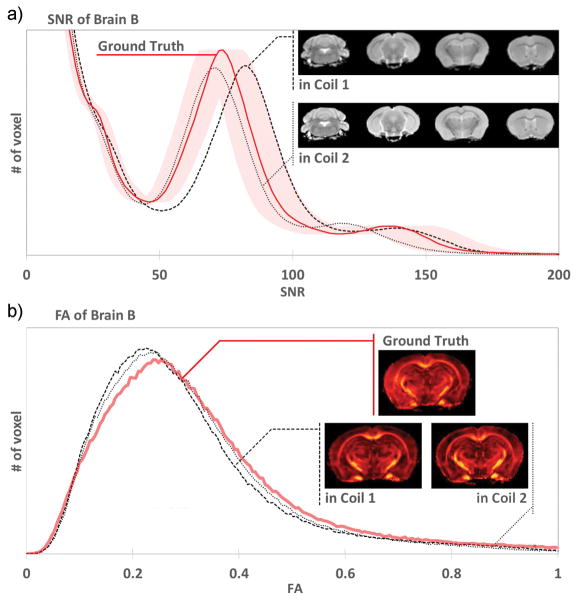
Figure 8 shows histograms of the fractional anisotropy and SNR of brain B, acquired as ground truth on isocenter by the reference coil, and compared to measurements on brain B as well, inside each coil of the two-coil system (while brain A was scanned in the other coil). The fractional anisotropy was underestimated in the two-coil system as compared to ground truth. The SNR of brain B was similar in both coils of the two-coil system, and remained within 10% of the benchmark SNR of the reference coil. Similar data from brain A is not shown.

Figure 8.

a) Comparing histograms of the B₀ scans, each coil of the two-coil system provided SNR within 10% of the ground truth (shaded area). The insert shows several slices acquired by each coil: no shading or artifacts were apparent in either coil. b) As expected, histograms of the fractional anisotropy show that FA was underestimated in the two-coil system. The insert shows FA maps at the same slice position, acquired as ground truth in the reference coil, and acquired in each of the two coils.

Finally, during transmit, coil 1 loaded with brain A required a power of 3.56 mW to achieve a 90° flip angle using a 1-ms hard pulse. Comparatively, coil 2 loaded with the same brain A requires 3.72 mW to achieve the same flip angle, a relatively small difference of 0.19 dB, or 4.5 %. Using the other brain, coil 1 loaded with brain B requires slightly more power to achieve the 90° flip angle: 3.65 mW. On the same brain, coil 2 loaded with brain B consumes 3.78 mW (0.15 dB, or 3.7% more power than coil 1). From brain A and B, the power required to achieve a 90° flip angle in each coil varied by less than 0.2 dB.

DISCUSSION

When the coils are 12-mm away from isocenter, the conducting surface of each coil is closest to the wall shared by the shields, a few millimeters away. At that coil position, SNR was found to decrease very slightly by 3%; however, the variation remains within the measurement error. This demonstrates that it is possible, in the coil-dominated noise regime, to shield a high-quality factor coil, loaded lightly by a conductive specimen, without significantly degrading its SNR performance. However, the shields are relatively large in size (a cube 70 mm in size). If the size of each shield decreases, for example to carry out DTI measurements in a smaller inner-diameter gradient set or using more coils simultaneously, the RF dissipation caused by each shield may grow to a point where SNR is measurably degraded.

Shimming over a larger volume, as required by several coils used simultaneously within a single set of shim coils, does not affect SNR significantly on our scanner, regardless of the coil position. Consequently, the full throughput gain of a factor of 2 was achieved by our two-coil system.

The homogeneous phantom enabled reproducible SNR measurements, more precisely than a fixed mouse brain: first, a fixed brain held in our perfluoropolyether fluid noticeably dehydrates with time, which affects SNR. Secondly, the brain specimen comprises several types of tissue, each with different SNR characteristics (as shown in figure 8), which complicates SNR estimation, and may introduce variability in identifying landmarks or region-of-interests.

Within a gradient set, several types of imperfections exist which may alter DTI metrics ^36–39. Imperfect calibration of the gradient set, as well as gradient non-linearity, cause errors in diffusivity measurements. In addition, a gradient field includes concomitant field components in the plane transverse to the gradient direction, which distorts the direction of diffusion-sensitization. In our gradient set, images of a homogeneous phantom containing a polymer grid revealed no discernable image warping within 25 mm of isocenter (the 100-um-isotropic-resolution, three-dimensional image volumes are not shown), indicating that the region encompassing both coils of the two-coil system suffers from gradient miscalibration and non-linearity smaller than 0.4% (the manufacturer specifies linearity errors smaller than 1%). However, a more thorough measurement and recalibration procedure ^47,48, or a full correction of gradient non-linearity³⁷ may reduce the error recorded by the two-coil system. The Stejskal-Tanner sequence used in our experiments is immune to errors stemming from concomitant gradient field terms ³⁸. Homogeneous phantoms^49–52 enable the quantification of DTI measurement errors and their spatial variation. They may indicate regions within the gradient set where a coil can be located, and guarantee that errors fall within an acceptable range. That permissible error range, in our connectomics application, depends on the DTI acquisition scheme and the method used to compare connectivity matrices, as well as normal and pathological variability of mouse brain connectivity. Further research should clarify the permissible range of DTI measurement errors and their impact on mouse brain connectomics.

Bammer et al. ³⁷ show the spatial distortion of a gradient field within the magnet bore. For a two-coil system, the direction of the gradient field is least distorted if both coils are located along the z-axis of the magnet (we chose that configuration). In the future, since 4 receive channels are available on our scanner, it may be desirable to increase the number of coils to 4. In order to minimize the deviations in gradient direction, the coils could be located in the transverse plane with no z-axis offset, on the positive or negative x-axis, or on the positive or negative y-axis. However, the distortion of the gradient field at the location of the four coils should be investigated to determine if it can be ignored in practice, or if a correction or recalibration is necessary to generate a connectivity matrix suitable to connectomics. Such correction methods may allow each coil to be placed further away from magnet isocenter, in any position, and may be beneficial to any multiple-coil system requiring off-isocenter imaging.

Eigenvector deviation alters fiber track trajectories, cause false-positive connections between regions, reduce true connectivity and changes the connectivity matrix. Quantification of this effect is not straightforward: the connectivity between regions close to each other is less likely to be altered than the connectivity between regions distant from each other. The measurement error of the eigenvector direction, when the coil is placed 12-mm coil away from isocenter, remains small in highly anisotropic regions (<11°), and smaller than 40° for any brain region. It remains smaller than the threshold angle forcing track termination (45°). Therefore, eigenvector deviation is unlikely to cause the false termination of track. Visually, at a 12-mm offset to isocenter, the effect on the connectivity matrix appears small. Quantitatively, of all the region pairs showing a strong connection, only 8% of the region-pairs no longer showed a strong connection when the coils were placed 12-mm away from isocenter, while up to 23% of the region-pairs no longer appeared strongly connected when the coil offset to isocenter reached 24 mm.

Imperfect registration has an effect —which has not yet been assessed— of the entire analysis, relying on a voxel-to-voxel comparison between ground truth data acquired on isocenter, and data from the same brain acquired off-isocenter. In case of misregistration, the connectivity between regions anatomically connected appears diminished, while false connectivity between regions increases. We can infer that the effect of misregistration is small: the Spearman rank correlation coefficient applied to the 6 datasets that we acquired repeatedly on isocenter is consistent with previous literature reports⁶. The Spearman rank correlation coefficient includes all causes of variability, including registration.

To assess the feasibility of a two-coil system for connectomics, we used a deterministic fiber-tracking algorithm and 100 μm isotropic resolution voxels. More elaborate methods may reveal more subtle effects. For example, Calabrese et al. ⁶ reported that at a higher spatial resolution of 43 μm, 72% of mouse brain voxels were found to have 2 or more fiber populations, and suggested that accounting for different populations is important in establishing the connectivity matrix.

Finally, the simultaneous measurements of two different brains loaded into our two-coil system aggregate all the confounding effects presented earlier, compounded with supplementary challenges^32,53,54. Images from each coil within our system were similar, devoid of shading, unusual artifacts, and appeared unaffected by phase or steady state effects, the latter likely mitigated by the short T₁ of our fixed brain specimens.

Each of the two coils exhibited similar RF characteristics. To limit geometric variability, the coils were constructed around identically 3D-printed supports. The overlapping copper construction of each shield was identical. Also, the coils required no manual soldering, which may introduce variability in RF performance. During power transmission, the small, 0.2 dB imbalance in the power required by each coil obviated the need for adjustable attenuation downstream the power splitter. In addition, we speculate that temperature-regulation of the bore and the thorough tuning and matching of each coil may have helped achieve more consistent results.

Images of the same mouse brain, acquired with each coil within the system, exhibit slightly different amounts of SNR, varying by less than 10% of the ground truth SNR. The small differences may be attributed to variations of the flip angle achieved in each coil, or to some degree of electronic coupling between the different receiver channels of the scanner. Similarly, SNR and contrast variations may be attributed to changes in gadolinium chelate concentration due to the diffusion of contrast agent across fixed tissue, or to alterations in proton density due to specimen dehydration.

CONCLUSION

In this work, we quantified some of the trade-offs between SNR performance and DTI measurement integrity in a two-coil system relying on radiofrequency shielding and off-isocenter imaging. We presented a configuration, where each coil sits 12 mm away from isocenter inside a 70-mm cubic shield, in which SNR was unaffected by shielding, and where the connectivity matrix of mouse brain specimens appeared mostly preserved despite gradient field distortions off-isocenter. Simultaneous measurements of two brains in the system demonstrated that the doubling of DTI throughput could be achieved in practice. The results presented here may guide an expansion of the system to four coils. In addition, and independently of the technique used to apply connectomics to large cohorts of animals, future studies may seek to clarify how measurement variability, post-processing techniques, and biological variability impact mouse brain connectomics. In turn, those studies may help define robust research protocols balancing throughput considerations with reproducible, meaningful results.

List of Abbreviations

DTI

diffusion tensor imaging

SNR

signal-to-noise ratio

TR

Repetition Time

TE

Echo Time

FOV

Field-of-view

BW

Bandwidth

FA

Fractional Anisotropy

3D

Three-dimensional