Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2018 May 2;140(21):6582–6590. doi: 10.1021/jacs.8b01347

The Role of Dopant Ions on Charge Injection and Transport in Electrochemically Doped Quantum Dot Films

Solrun Gudjonsdottir †, Ward van der Stam †, Nicholas Kirkwood †, Wiel H Evers †,‡, Arjan J Houtepen †,*
PMCID: PMC5981292  PMID: 29718666

Abstract

graphic file with name ja-2018-01347f_0007.jpg

Control over the charge density is very important for implementation of colloidal semiconductor nanocrystals into various optoelectronic applications. A promising approach to dope nanocrystal assemblies is charge injection by electrochemistry, in which the charge compensating electrolyte ions can be regarded as external dopant ions. To gain insight into the doping mechanism and the role of the external dopant ions, we investigate charge injection in ZnO nanocrystal assemblies for a large series of charge compensating electrolyte ions with spectroelectrochemical and electrochemical transistor measurements. We show that charge injection is limited by the diffusion of cations in the nanocrystal films as their diffusion coefficient are found to be ∼7 orders of magnitude lower than those of electrons. We further show that the rate of charge injection depends strongly on the cation size and cation concentration. Strikingly, the onset of electron injection varies up to 0.4 V, depending on the size of the electrolyte cation. For the small ions Li+ and Na+ the onset is at significantly less negative potentials. For larger ions (K+, quaternary ammonium ions) the onset is always at the same, more negative potential, suggesting that intercalation may take place for Li+ and Na+. Finally, we show that the nature of the charge compensating cation does not affect the source-drain electronic conductivity and mobility, indicating that shallow donor levels from intercalating ions fully hybridize with the quantum confined energy levels and that the reorganization energy due to intercalating ions does not strongly affect electron transport in these nanocrystal assemblies.

Introduction

Quantum dots (QDs) are known for their tunable optoelectronics properties, processability, and cheap and facile solution-based synthesis.1 For these reasons they are promising for optoelectronic applications such as displays,2 solar cells,1c,3 and LEDs.1c,4 To optimize the potential of QDs for such applications, control over electronic doping is essential.5 Traditionally, doping of semiconductors is achieved by introducing impurity atoms into the crystal that act as electron donors and acceptors. For QDs there have been many attempts to dope them in a similar manner.6 However, due to charge compensation by localized counter charges on the surface of the nanocrystals, introduced impurities rarely contribute excess carriers in conduction or valence states.6b Additionally, significant distortion of the QD crystal structure even at one dopant per QD6a can make this approach difficult. In practice, it still remains a challenge to fully and reversibly control the charge carrier density.6b A less invasive and potentially more controllable approach is to use external dopants that reside outside the QD but still dope it electronically. Chemical redox doping has been used for this purpose.7 More recently, photochemical doping8 has also been shown to be efficient in tuning the charge carrier density.

However, arguably the most controllable method to dope QD films is by electrochemical doping. In this approach, electrons or holes are injected via an electrode, and their charge is compensated by electrolyte ions that diffuse into the QD film.9 Ideally, the charge compensation by electrolyte ions is uniform due to the porous nature of QD films, resulting in a uniform charge density and absence of band bending. This method enables reversible carrier density tuning in a wide range and allows the Fermi-level to be set on demand by controlling the potential with a potentiostat. Furthermore, electrochemical and spectroelectrochemical methods have been used to examine many different properties of QDs such as the band gap energies, QDs trap states, QDs valence, and conduction band energy levels and the effect of charge injection on blinking of the QDs.9b,10 The versatility of electrochemical methods to dope QDs is demonstrated by the wide range of QD compositions studied, such as CdSe, CdTe, core–shell quantum dots (CdSe-ZnS and CdSe-CdS-ZnS),10b,11 PbSe quantum dot superstructures,12 Cu2S,13 HgTe,6b and ZnO.14 For electrochemical charge injection, the charge compensating electrolyte ions can be regarded as external dopants. It is to be expected that the nature of these dopant ions affects the rate and energetics of charge injection and may also influence electron transport in these films. However, the role of the electrolyte ions has not been studied in detail before.

Here, we investigate the role of the electrolyte cation in electron injection into QD films. ZnO QD films were selected as they exhibit very stable and reversible charge injection, allowing in-depth electrochemical investigations, including performing many different experiments on the same ZnO QD film.7a By using differential capacitance and source-drain electronic conductance measurements combined with spectroelectrochemical measurements, both the mobility of electrons moving perpendicular through the film (out-of-plane) during charge injection and the mobility of electrons moving parallel to the substrate (in-plane) in a source-drain configuration can be determined. The out-of-plane electron mobility is shown to be 7 orders of magnitude lower than the in-plane mobility. By performing cyclic voltammetry (CV) at different scan rates, it is shown that the concentration and the size of the electrolyte cation affects the electron injection rate. We conclude that ion diffusion limits charge injection, and we determine the diffusion coefficients for different cations. Interestingly, cyclic voltammograms show a lower onset of electron injection into the ZnO QDs by up to 0.4 V for smaller ions (Li+ and Na+), suggesting that they may intercalate into the ZnO lattice. Finally, it is shown that the size of the cation does not affect the in-plane conductivity or mobility of the electrons. This shows that the electrons tunnel between QDs independent of the positive counterions. The implications of this are discussed.

Experimental Section

Materials

Zinc acetate dihydrate (Zn(CH3COO)2·2H2O reagent grade), potassium hydroxide (KOH pellets), lithium perchlorate (LiClO4, 99.99%), tetramethylammonium hexafluororphosphate ((CH3)4N(PF6), ≥98%), tetrabutylammonium perchlorate ((CH3(CH2)3)4N(ClO4), ≥99%), tetraoctylammonium tetrafluoroborate ((CH3(CH2)7)4N(BF4), ≥97%), anhydrous methanol, ethanol, and toluene were purchased from Sigma-Aldrich. Anhydrous acetonitrile was purchased from Alfa Aesar. Acetonitrile was dried before use in an Innovative Technology PureSolv Micro column. All other chemicals were used as received.

ZnO QD Synthesis

ZnO QDs were synthesized in air by a modification of two known procedures.15 Typically, 3.425 mmol of zinc acetate dihydrate and 50 mL of ethanol were added to a flask and heated to 60 °C. In a separate flask, 6.25 mmol of KOH and 5 mL of methanol were combined and stirred at room temperature. When both reagents had dissolved, the potassium hydroxide mixture was dropwise added to the stirred zinc acetate dihydrate mixture. The solution was stirred for 1 min more before the heat source was removed. The QDs were purified by adding toluene until the solution became turbid. The flocculates were isolated by centrifugation at 2000 rpm for 1 min and redissolved in ethanol. The QD dispersion was stored at −20 °C to avoid further growth by Ostwald ripening.

ZnO QD Film Preparation

QD films were drop-cast on two different types of working electrodes and annealed at 60 °C for 1 h in air. The typical film thickness was approximately 700 nm. One type of working electrode was indium-doped tin oxide (ITO) on glass, while the second one was a home-built interdigitated electrode (IDE). The IDE is a glass substrate coated with four separate gold working electrodes prepared in house via optical lithography. These four working electrodes provide five source-drain gaps of different sensitivities; that is, it is possible to choose between four different gap lengths: 8.825 mm, 6.8 cm, 0.3403 m, and 0.8548 m. An image of the IDE is shown in the Supporting Information, Figure S1.

Electrochemical Measurements

All electrochemical measurements were performed according to a procedure performed previously with an Autolab PGSTAT128N potentiostat including an additional dual-mode bipotentiostat BA module in a nitrogen glovebox to ensure oxygen- and water-free conditions.13,16 The QD film deposited on the WE is immersed in a container containing 0.1 M LiClO4 acetonitrile electrolyte solution unless stated otherwise. The container furthermore contained an Ag wire pseudoreference electrode and Pt sheet counter electrode. The Ag wire pseudoreference electrode was calibrated multiple times throughout the course of the experiments with a ferrocene/ferrocinium couple,17 and its potential was found to be constant at −4.79 eV vs vacuum.

Spectroelectrochemical Measurements

All spectrolectrochemical measurements were performed with an ITO working electrode. In the measurements, the absorption changes were measured with a fiber based UV–vis spectrometer, Ocean Optics USB2000 using an Ocean Optics DH 2000 lamp as a light source.

Differential Capacitance Measurements

The differential capacitance was measured as described elsewhere.9a The ZnO QD film deposited on IDE serves as the WE. The same electrochemical cell as described above was used. Potential steps of 35 mV were applied, and after each potential step the electrochemical charging current was measured for 5 s. The initial peak current decays quickly in about 1 s to a constant current which is attributed to a background current of the electrolyte. This background current was subtracted to obtain the charging current of the film. To obtain the differential capacitance (in C/V), the charging current was integrated and divided by the potential step. By multiplying the differential capacitance (units of C/V) with the potential (in V) the total injected charge is obtained (units of C).

Source-Drain Electronic Conductance Measurements

The electronic conductance measurements were performed on ZnO QD films on the IDE with a gold source-drain geometry. The width of the source-drain gap was 25 μm while the gap length was 6.8 cm. These measurements were performed in each potential step in the differential capacitance measurements after equilibrium was reached. When equilibrium was reached, the potential of WE1 was scanned in a CV manner around the fixed potential of WE2. The change in potential for WE1 was ±10 mV compared to the potential of WE2. The slope of the current versus the potential gives the in-plane (or parallel) conductance, G∥, of the film. From the conductance, it is possible to calculate the in-plane source-drain electron conductivity, σ∥:

graphic file with name ja-2018-01347f_m001.jpg 1

where w is the source-drain gap width, l is the gap length, and h is the height of the film. The in-plane mobility, μ∥, can then be calculated with eq 2:

graphic file with name ja-2018-01347f_m002.jpg 2

where n is the charge carrier density and e is the elemental charge.

Results and Discussion

Flow of Electrons in the ZnO Film

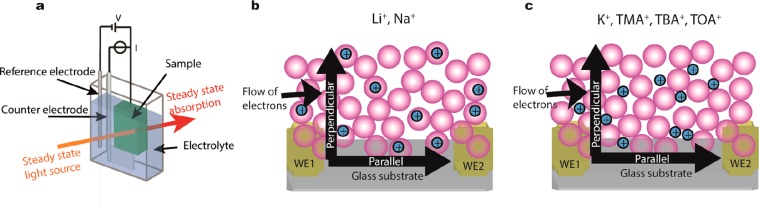
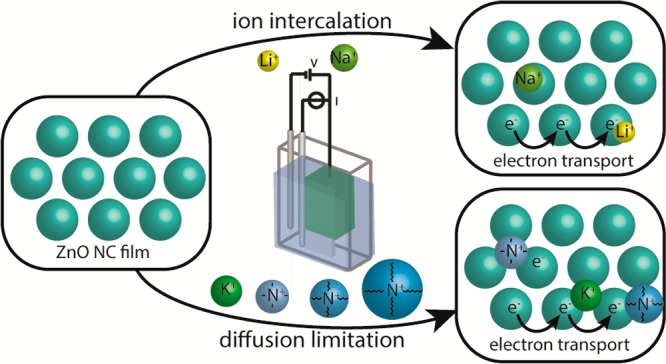
Figure 1a shows the experimental approach as previously described by Boehme et al.9c,18 (Spectro)electrochemical and conductivity measurements are done in an electrochemical cell with three electrodes (for CV and for differential capacitance measurements) or four electrodes (source-drain conductivity measurements) with a home-built interdigitated electrode (IDE, see Experimental Section). Two types of electron currents are monitored (Figure 1b,c): perpendicular (out-of-plane) to the electrode during charge injection or parallel (in-plane) to the electrode during source-drain conductivity measurements. We find that there is a great difference between the parallel and perpendicular conductivities.

Figure 1.

Figure 1

Open in a new tab

Schematic representation of the (a) three electrode (spectro)electrochemical setup. The cell contains a Ag wire pseudoreference electrode, Pt sheet counter electrode, and the sample on a working electrode. The solution is typically a 0.1 M LiClO4 acetonitrile electrolyte solution. The steady state absorption can be measured during the electrochemical measurements. (b) The ZnO film on the IDE with Li+ or Na+ as an electrolyte cation. The ions have intercalated into the ZnO QDs upon electron injection. The schematic includes the parallel (in-plane) and perpendicular (out-of-plane) flow of electrons. (c) The ZnO film on the IDE with K+, TMA+, TBA+, or TOA+ as an electrolyte ion. The ions occupy the voids of the film. The schematic includes parallel and perpendicular flow of electrons.

In the electrochemical experiment, charge is injected into the QDs. To compensate for the charge, cations flow into the voids of the film. Here, we inject electrons into ZnO QDs film in six different electrolyte solutions of different concentrations. From the results it is possible to separate the different electrolyte cations into two groups (Figure 1b,c). The former one includes the smaller electrolyte cations, Li+ and Na+. For these ions, electron injection occurs at more positive potential than for the larger ions, which might be due to intercalation. The second group includes the larger electrolyte cations K+, TMA+, TBA+, and TOA+. They are able to diffuse into the voids of the ZnO QDs, but their size hinders intercalation.

General Properties of Electron Injection

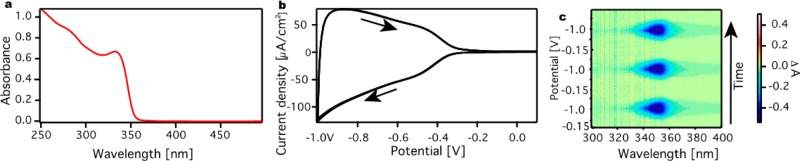
The ZnO QDs were synthesized as outlined in the Experimental Section. Figure 2a shows the absorption spectrum of the ZnO QDs in ethanol, with the first absorbance peak around 350 nm. By using an empirical correlation from Meulenkamp et al.19 the diameter of the ZnO QD was calculated to be 3.8 nm. Figure 2b shows the cyclic voltammogram for a ZnO QD film on an ITO electrode in a 0.1 M LiClO4 in acetonitrile electrolyte solution, where the potential was scanned from 0.1 V vs the Ag pseudoreference electrode in negative direction to −1.0 V at 25 mV/s and back to 0.1 V. The scan was repeated three times and is completely reproducible. From the voltammogram it can be seen that the current density starts to increase around −0.4 V and keeps increasing until the potential is reversed. This current density corresponds to electron injection into the ZnO QDs.9b The symmetry and the reproducibility of these cyclic voltammetry (CV) measurements show that the electron injection is reversible and stable. Figure 2c shows the change in absorption during CV for a ZnO QD film over time for three scans. Time runs from bottom to top, and the scan starts at −0.15 V. Around −0.5 V, a change in absorption around 350 nm can be seen which corresponds to a bleach of the band edge absorption due to the injection of electrons in the 1Se conduction level of the ZnO QDs (see the Supporting Information, Figure S2).20 Like the CV measurements, the spectroelectrochemical measurements are highly reversible and stable. We note that this is due to the rigorous water and oxygen free conditions of the experiments.

Figure 2.

Figure 2

Open in a new tab

Spectroelectrochemical measurements for a ZnO QD film. (a) Absorption spectrum of a ZnO QDs suspension in ethanol. (b) Cyclic voltammogram for a ZnO QD film on ITO in 0.1 M LiClO4 acetonitrile electrolyte solution. The scan was started at 0.1 V, which is in the band gap of the ZnO QD, and arrows indicate the scan direction. The scan speed was 25 mV/s, and the scan is repeated three times. (c) The differential absorption during CV scans. As electrons are injected in the conduction band of the ZnO QDs (around −0.4 V), a negative differential absorbance of the 1Se conduction level is measured (blue area).

In-Plane versus Out-of-Plane Electron Current

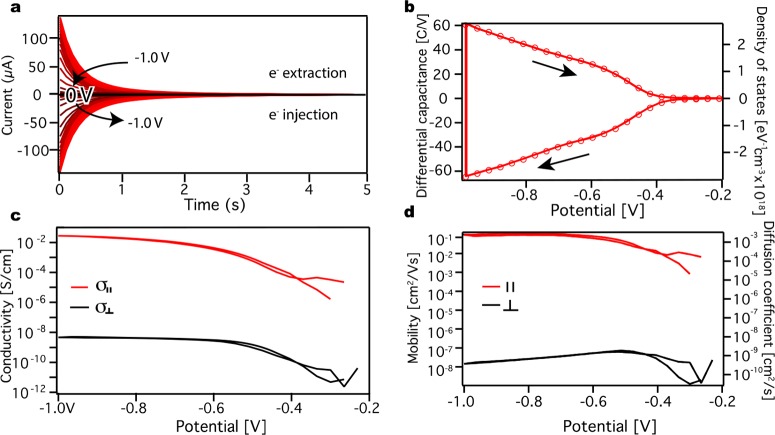
We now compare the electron current in the parallel (in-plane) and perpendicular (out-of-plane) directions with respect to the WE surface. Figure 3a shows the results of differential capacitance measurements (see the Experimental Section), which we use to calculate the total charge injected into the ZnO QD film. The measurements were performed with a potential step of 35 mV from 0 to −1.0 to 0 V again, on a gold IDE. In the bandgap of the ZnO QD the current is low; however, when electron injection occurs (∼–0.4 V, represented by red curves), an initial peak current is seen that decays in ∼0.5 s. From Figure 3a the differential capacitance can be determined after each potential step as described in the Experimental Section. The outcome is depicted in Figure 3b in units of C/V and corrected for background currents. At potentials more negative than −0.4 V, electrons are injected into the QD film (negative currents in Figure 3a). The amount of injected charge increases until the scan is reversed (at −1.0 V). When the scan is reversed, the number of withdrawn electrons (positive currents in Figure 3a) is very close to the number of injected electrons. This again shows the ability of ZnO to receive and release electrons reversibly. The right axis in Figure 3b shows the density of states, calculated from the differential capacitance, ΔQ/ΔV, and the film volume, Vfilm, according to eq 3:

graphic file with name ja-2018-01347f_m003.jpg 3

Figure 3.

Figure 3

Open in a new tab

Differential capacitance and electronic source-drain conductance measurements. (a) Differential capacitance measurements performed on a ZnO QD film on an IDE in 0.1 M LiClO4 acetonitrile electrolyte solution. Potential steps of 35 mV were taken, and the current was measured for 5 s until equilibrium was reached. The potential was stepped from 0 to −1.0 V and then reversed to 0 V. (b) The differential capacitance of the QD film with units of C/V is on the left axis, while the density of states is shown on the right axis. Arrows indicate the scan direction. (c) Calculated parallel source-drain electron conductivity (red line) compared to the perpendicular electron conductivity (black line). (d) Difference in parallel source-drain electron mobility (red) and the perpendicular mobility (black) on the left axis and the parallel (red) and perpendicular (black) diffusion coefficients on the right axis.

From Figure 3a it is also possible to calculate the resistance of the film. If the film acts as a capacitor, the current response of a step potential is given by21

graphic file with name ja-2018-01347f_m004.jpg 4

where E is the potential step, R⊥ is the out-of-plane film resistance, τ⊥ is the relaxation time, also known as the RC-time, and C is the film capacitance. We note that the charging currents in Figure 3a are not perfectly exponential (see the Supporting Information, Figure S3). For simplicity we therefore determine τ⊥ as the time where the current has dropped to 1/e of the maximum.

As the capacitance C is known directly from integrating the current (Figure 3b) we determine R⊥ and relate it to the film conductivity,σ⊥, by eq 5:

graphic file with name ja-2018-01347f_m005.jpg 5

where hfilm is the height of the film and Afilm is the area of the film. The resulting out-of-plane conductivity, σ⊥, is plotted as a function of applied potential for both the forward and the backward scan (black line in Figure 3c).

For the same film, source-drain electronic conductance measurements were performed after each differential capacitance measurement (see the Experimental Section). The corresponding source-drain currents can be seen in the Supporting Information, Figure S4. The conductivity can be calculated as shown in the Experimental Section. The resulting in-plane conductivity, σ∥, is plotted as a function of applied potential as well for both the forward and the backward scan (red line in Figure 3c). When the two conductivities are compared, we find that the out-of-plane electronic conductivity is 7 orders of magnitude lower than the in-plane electronic conductivity (10–9 vs 10–2 S/cm). As both σ⊥ and σ∥ are determined on the same film during the same potential scan, the charge carrier density, n, is necessarily the same, showing that the mobility (given by 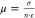Inline graphic) also differs by 7 orders of magnitude. The charge carrier density (Supporting Information, Figure S5) is derived by dividing the total injected charge obtained from Figure 3b (see the Experimental Section) by the film volume (1.4 × 10–10 m3). The in-plane mobility, μ∥ is plotted as a red line, and the out-of-plane mobility μ⊥ is plotted as a black line in Figure 3d.

The great difference in conductivities and mobilities can be explained by the role of the electrolyte cations in the electronic doping of the QD film. In the out-of-plane conductivity electrons are injected into the film, to compensate for the negative injected charge in the film, the electrolyte cations diffuse into the pores of the film. Therefore, the out-of-plane conductivity of the electrons is limited by the diffusion of the cations. This is not seen in the in-plane source-drain conductivity as the electrons have already been injected into the film, and no additional charging takes place. These experiments are performed under steady state conditions where the electron density (and hence also the ion density) is constant and hence diffusion of ions is not required. The in-plane mobility varies over several orders of magnitude with potential or equivalently with charge density. This is expected for electron transport in a disordered semiconductor system.22 The maximum value of the in-plane mobility (10–1 cm2/(V s)) is found to be similar to previous experimental values of the source-drain mobility (10–2 cm2/(V s)).20 The out-of-plane mobility is orders of magnitude lower (10–8 cm2/(V s)).

The diffusion coefficient, D, of an ordered system can be calculated with the Einstein relation:

graphic file with name ja-2018-01347f_m007.jpg 6

where kb is the Boltzmann constant, T is the temperature, and e is the elemental charge. We note that the Einstein relation may not strictly be valid in the case of strongly interacting or highly disordered systems.22b However, for reasons of simplicity and given the 7-orders of magnitude difference between in-plane and out-of-plane mobilities we are interested in here, we will disregard this effect. The calculated diffusion coefficients are shown in Figure 3d, right axis. We find that D⊥ is ∼10–9 cm2/s. This value is lower than for diffusion of ions in solvents. However, such low values are not uncommon for ion diffusion in porous solids.23 Hence, we conclude that charge injection, and the corresponding out-of-plane conductivity, is limited by diffusion of charge compensating cations through the porous NC film.

Effects of the Cation on Charge Injection

To investigate the diffusion of the counterions in more detail, we performed scan-rate dependent cyclic voltammetry measurements. The diffusion coefficient of the electrolyte cations can be determined by the Randles-Sevcik equation which states that for diffusion limited currents the peak current (ip) can be connected to the scan rate (v) according to

graphic file with name ja-2018-01347f_m008.jpg 7

where n is the number of electrons, F is the Faradaic constant, A is the area of the working electrode, C* is the concentration of the electrolyte, and D is the diffusion coefficient. The Randles–Sevcik equation assumes diffusion of a reactant from a bulk solution to a smooth electrode surface. Although a QD film is nanoporous and not a smooth surface, this formalism is also often used for porous electrodes,24 and we do the same. In the Supporting Information we argue that the Randles–Sevcik equation also holds in the porous QD film investigated here.

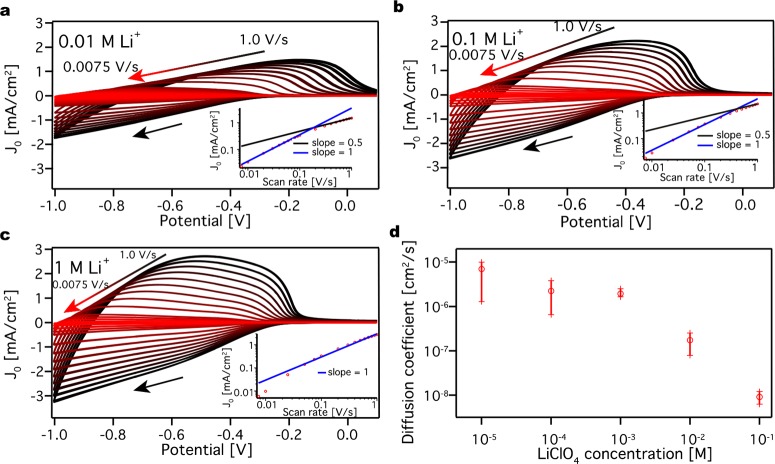
To see the effect of the cation concentration on electron injection, a ZnO QD film was immersed in solutions of LiClO4 in acetonitrile with three different concentrations: 0.01, 0.1, and 1 M. CV measurements were performed with scan rates between 0.0075 and 1.0 V/s, and the peak current density (JP) was plotted against the scan rate (Figure 4). For increasing Li+ concentration the current density (J0) increases and the CVs become more symmetric. Furthermore, the log–log plot of the peak current density versus the scan rate for 0.01 M LiClO4 shows that the peak current density is linearly dependent on the scan rates at low scan rates (<0.2 V/s) but at higher scan rates (>0.2 V/s) it scales with √v. This behavior clearly shows that at low scan rates charging is limited by the capacitance of the film, while at higher scan rates the current is limited by counterion diffusion. This diffusion limitation becomes apparent around 0.18 V/s.

Figure 4.

Figure 4

Open in a new tab

Determination of diffusion coefficients in LiClO4 acetonitrile electrolyte solution. Cyclic voltammograms at different scan rates for a ZnO QD film in (a) 0.01 M LiClO4 acetonitrile electrolyte solution, (b) 0.1 M LiClO4 acetonitrile electrolyte solution, and (c) 1 M LiClO4 acetonitrile electrolyte solution. J0 stands for the current density. The panels include a peak current density versus scan rate plot on a log–log scale. The slope is given by 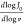Inline graphic, where v stands for the scan rate. The scans have negative direction, indicated by a black arrow. By increasing the electrolyte concentration, the current and the symmetry increases. (d) Average diffusion coefficient and the standard deviation obtained from three different measurements for different concentration of LiClO4 acetonitrile electrolyte solution.

By increasing the concentration of LiClO4, the diffusion limitations appear at higher scan rates, that is at around 0.4 V/s for 0.1 M LiClO4 and >1 V/s for 1 M LiClO4. This shows that, at low concentrations of the cation, the diffusion current of the cations inside the pores of the QD film is lower. By using the Randles–Sevcik equation, the diffusion coefficients were determined to be 7.9 × 10–8 and 6.3 × 10–9 cm2/s at 0.01 and 0.1 M, respectively. For the 1 M electrolyte solution, the peak current density does not depend on the square root of the scan rates within the investigated range; therefore, it is not possible to calculate a diffusion coefficient. By increasing the concentration of the cation, the diffusion coefficient decreases, which shows that something is slowing the process down such as “jamming” of cations in the pores of the film. If this is the case, one would expect the diffusion coefficient to become constant at lower Li+ concentrations. Figure 4d shows such measurements for a concentration range from 10 μM to 0.1 M. Figure 4d shows the average obtained diffusion coefficient and the standard deviation obtained from 3 measurements. Below 1 mM concentration, a concentration independent diffusion coefficient of ∼10–5 cm2/s is obtained.

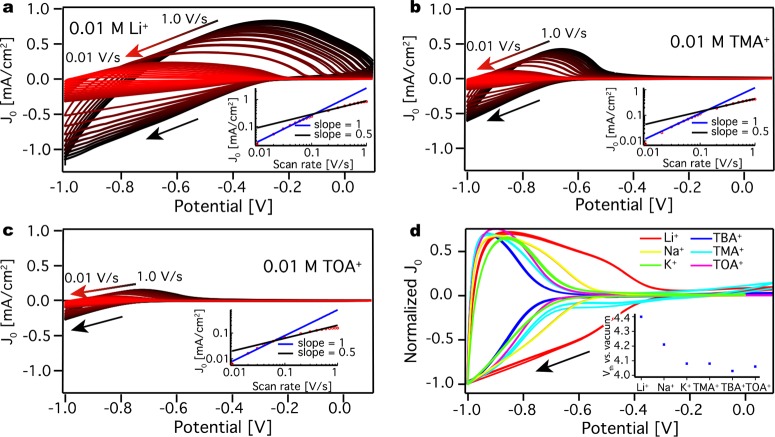
In addition to the ion concentration, we investigate the type and size of the cation and its effect on electron injection. In previous studies on Cu2S13 and CdSe9c our group has showed a strong effect of the size of the charge compensating ions on the reduction of nanocrystals. Furthermore, it has been shown by Brozek et al.25 that the charge compensating cation can affect both the injected electron stability and the chemical reduction of ZnO nanocrystals greatly. Therefore, a ZnO QD film was subsequently immersed in four different electrolyte solutions, containing different cations: lithium (Li+), tetramethylammonium (TMA+), tetrabutylammonium (TBA+), and tetraoctylammonium (TOA+). Furthermore, three different concentrations were investigated: 0.01, 0.1, and 0.5 M. (The solubility of tetraalkyammonium salts in acetonitrile does not permit experiments at 1 M). All experiments were done on the same ZnO QD film starting from the largest cation (TOA+) to the smallest one (Li+). Figure 5a–c shows the cyclic voltammograms for the ZnO QD film in 0.01 M Li+, TMA+, and TOA+ acetonitrile electrolyte solution. For simplicity, the CVs are plotted on the same scale, which allows for direct comparison of the current density between the different counterions (magnifications of the CVs including the one for TBA+ are shown in the Supporting Information, Figure S7). As can be seen in Figure 5a–c, increasing the size of the cation dramatically decreases the peak current density by 1 order of magnitude. By using the Randles–Sevcik equation, the diffusion coefficient was determined for the different cations in 0.01 and 0.1 M acetonitrile electrolyte solutions (Table 1). As before, at the highest concentration charge injection is not diffusion limited in the range of scan rates investigated, and hence, it is not possible to calculate a diffusion coefficient. Table 1 shows that, by increasing the size of the ion, the diffusion coefficient decreases. This trend can be seen for both concentrations. As for Li+ the diffusion coefficient for the different ions decreases with higher concentration.

Figure 5.

Figure 5

Open in a new tab

Cyclic voltammograms for a ZnO QD film. (a) CVs at different scan rates in 0.01 M LiClO4 acetonitrile electrolyte solution. The panel includes a peak current density versus scan rate plot on a log–log scale. (b) CVs at different scan rates in 0.01 M TMAPF6 acetonitrile electrolyte solution. The panel includes a peak current density versus scan rate plot on a log–log scale. (c) CVs at different scan rates in 0.01 M TOABF4 acetonitrile electrolyte solution. The panel includes a peak current density versus scan rate plot on a log–log scale. (d) CVs measured at 0.1 V/s for different electrolyte cations in a 0.1 M acetonitrile electrolyte solution. The panel includes a plot of the threshold potential versus vacuum for the different ions. By increasing the size of the electrolyte cation, charge injection occurs at lower potentials. The scans have negative direction, indicated by a black arrow, and are repeated three times for every scan rate. The slope from the insets is given by 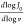Inline graphic, where v stands for the scan rate and J0 stands for current density.

Table 1. Calculated Diffusion Coefficients in cm2/s for the Four Different Cations in 0.01 and 0.1 M Concentrations.

  Li+ TMA+ TBA+ TOA+
0.01 M 7.90 × 10–8 1.89 × 10–8 9.18 × 10–9 2.14 × 10–9
0.1 M 6.30 × 10–9 1.24 × 10–9 7.70 × 10–10 4.61 × 10–10
Open in a new tab

Furthermore, Figure 5a–c shows that the onset for charge injection is around −0.4 V for Li+ while it is around −0.8 V for the other ions. The same difference in current and onset potential for Li+ compared to the other cations (TMA+, TBA+, and TOA+) can be seen at concentrations of 0.1 and 0.5 M in acetonitrile electrolyte solution (Supporting Information, Figures S8 and S9). To examine the difference in the onset of charge injection for the different electrolyte cations in more detail, two additional measurements were performed with Na+ (r+ = 116 pm) and K+ (r+ = 150 pm), which have ionic radii in between Li+ (r+ = 90 pm) and TMA+ (r+ = 320 pm). Figure 5d shows CV scans at 0.1 V/s for the six different ions (Li+, Na+, K+, TMA+, TBA+, and TOA+). To make the onset of the electron injection clearer, the current density was normalized. An injection threshold potential Vth (vs vacuum) is determined for every ion by identifying the first minimum in the second derivative of the first forward scan and is shown in Figure 5d. For K+, TMA+, TBA+, and TOA+ the threshold potentials are very similar (∼4.06 V vs vacuum) while for Na+ (4.21 V vs vacuum) and for Li+ (4.4 V vs vacuum) it is more positive.

We can rule out that mass transfer effects cause a different onset of charge injection, since the CVs are fully reversible at the low scan rates used in Figure 5d. Further, source-drain conductance measurements, which are performed at steady state for the different ions, show the same offset in potential (Supporting Information, Figure S10). Therefore, the difference in potential cannot be explained by faster diffusion of the smaller Li+ and Na+ ions. Since the differential capacitance and total injected charge (see also below where this is discussed in more detail) are indistinguishable for the different ions, we can rule out that there exist differences in the portion of the film that gets charged, due to smaller ions penetrating deeper into the QD film. We conclude that the differences in the onset of charge injection must reflect a true thermodynamic free energy difference.

We believe that the observed differences with Li+ and Na+ are due to intercalation of these ions into the ZnO QDs, while the other ions are too large to intercalate into the ZnO QDs. Li+ is a known interstitial donor in bulk ZnO.26 Moreover, both Li+ and Na+ have been reported to occupy interstitial sites and form shallow donors in ZnO QDs26b and the syntheses of intentionally Li+ and Na+ doped ZnO nanocrystals have previously been reported.27 In fact, ZnO and ZnO nanostructures are considered as anode material in Li ion batteries that rely on Li intercalation, albeit at more negative electrochemical potentials.28 Kushima et al. have proven Li+ intercalation in ZnO nanowires under large electrochemical bias by the use of in situ transmission electron microscopy.29 Additionally, Hupp et al.30 saw a similar trend in electrochemical charging of TiO2 where the electron injection onset was ∼0.8 V more negative when using TBA+ compared to either Li+ or Na+. By using a combination of reflectance and electrochemical quartz crystal microbalance, they observed that both Na+ and Li+ intercalated into the TiO2 while TBA+ did not due to steric hindrance. A similar shift of the onset potential for charging with cation size was reported by Boehme et al.9c for CdSe QD films and was explained by the increased proximity of the charge on the cation and the electrons. Recently Puntambekar et al.31 have claimed Li + intercalation in CdSe QDs upon electrochemical charge injection.

Taken together, our experimental results and the discussed literature reports strongly suggest that Li+ and Na+ intercalate into the ZnO lattice resulting in a less negative onset potential for electron injection. In any case it is clear from the above experiments that the type, size, and concentration of the electrolyte cation affect the electron injection rate and energy greatly.

Effect of the cation on the Source-Drain Conductivity

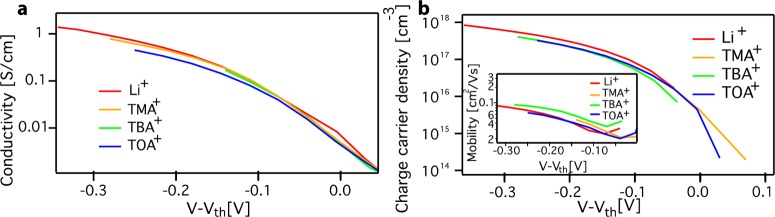
The presence of dopant ions is known to strongly affect charge transport. To investigate if this is the case, we compare the in-plane conductivity and mobility for the different cations. Figure 6a shows the source-drain conductivity for a ZnO QD film immersed in a 0.1 M acetonitrile electrolyte solution for four different ions: Li+, TMA+, TBA+, and TOA+. All of the measurements were performed with the same film starting with the largest dopant ion TOA+. As the onset for charge injection is different for each ion (Supporting Information, Figure S10) a threshold potential Vth for charge injection was determined for every ion by finding the minimum residual between the in-plane conductivity of Li+ and the other ions (see the Supporting Information). Figure 6a shows the conductivity and mobility vs V – Vth. The source-drain conductivities for all cations are very similar. Figure 6b shows the charge carrier density of the film for the four different ions. Similar to the in-plane conductivity, the charge carrier density is very similar for the different ions. Consequently, the electron mobility for the different ions, shown as the inset in Figure 6b, is also very similar. Alternatively, the conductivity can be plotted against the charge carrier density for the different ions, eliminating the need to determine a threshold potential, see the Supporting Information Figure S11. Also in this case the conductivities are almost identical. We argue that any differences observed are within the experimental error and that the type, size, and location of the dopant ion (intercalating or occupying voids between QDs) do not significantly affect the electron mobility.

Figure 6.

Figure 6

Open in a new tab

Source-drain measurements for a ZnO QD film for four different cations. (a) The source-drain conductivity for a ZnO QD film on an IDE immersed in acetonitrile electrolyte solution for four different ions: Li+, TMA+, TBA+, and TOA+ concentration of 0.1 M. A threshold potential was subtracted from the original potential. (b) Charge carrier density of the ZnO QD film as a function of potential for Li+, TMA+, TBA+, and TOA+ electrolyte solutions (concentration 0.1 M). The panel includes the parallel mobility for the film for the four different ions.

This observation is remarkable if one considers that there are various ways the cationic dopants could influence electron transport. In bulk semiconductors, the dominant effect is ionized impurity scattering.32 However, charge transport in nanocrystal films typically takes place via tunneling between NCs and not via band-like transport, with concomitant lower mobilities and much shorter mean free paths. It is unlikely that ionized impurity scattering will be the limiting factor for charge transport in such systems.

Alternatively, intercalating ions could add energy levels close to the conduction band (shallow donor levels) that may take part in electron transport. Interstitial hydrogen shallow donor levels have for instance recently been shown to strongly affect electron transport in nanoporous TiO2.33 Hydrogen is also known to form an interstitial donor in bulk ZnO with a shallow donor level 58 meV below the conduction band.34 Similarly, Li+ and Na+ have been shown to form shallow donors in ZnO.26b However, the similarity of the electron mobilities shown in Figure 6b shows that intercalated Li+ and Na+ donor ions do not significantly affect electron transport in this ZnO QD film.

This can be understood by realizing that in quantum-confined crystals the shallow donor level merges with the 1Se electron level. One can see this quickly by looking at the equation for the exciton Bohr radius aB

graphic file with name ja-2018-01347f_m009.jpg 8

where μ is the reduced effective mass of the exciton, me* and mh are the relative electron and hole effective masses respectively, εr is the relative dielectric constant of the material, and a0 = 0.53 Å is the Bohr radius of atomic hydrogen. For an interstitial shallow donor, the Bohr radius is determined by the same equation, except that the hole effective mass is the ion mass and hence falls out of the equation. However, since the hole effective mass in ZnO is much larger than the electron mass (me* ≈ 0.24 and mh ≈ 0.8)35 the shallow donor and exciton Bohr radii are very similar. This implies that, if ZnO is quantum confined, the shallow donor state will also be quantum confined. As the 1Se electron level and the shallow donor are delocalized over the nanocrystal it is in fact a single state, as also concluded previously based on DFT calculations,36 which is simply the solution to the Schrodinger equation of a particle in a box with a positive point charge. The energy of this state is lower than without the presence of the positive point charge, as reflected in the lower onset of electrochemical charging for intercalating Li+ or Na+ compared to nonintercalating ions.

Charge transport will in both of the cases of intercalating and nonintercalating ions take place via electron tunneling between NCs. The moderate variation in energy levels between intercalating and nonintercalating ions apparently does not affect the tunneling rate significantly. For the case of larger crystals that are not quantum confined intercalating ions add additional energy levels below the conduction band (the shallow donor level) that may strongly affect transport, as reported for electron transport in bulk-like TiO2 nanocrystal films.33

Finally, it is conceivable that polarization of cations after an electron transfer event leads to a significant reorganization energy that may depend on the nature of the cation. In a Marcus-type electron transport picture this can strongly affect the electron transfer rate and hence also the electron mobility. The fact that this is not observed suggests that there are no significant differences in reorganization energy for the different electrolyte ions or that the reorganization energy due to these ions is small in all cases.

Conclusions

In summary, we have shown that the electrolyte cations play an important role in electrochemical charging of QD films. Charge injection is limited by cation diffusion, inducing a 7-fold difference between the in plane (steady state) and out of plane (charging) conductivity. The size of the electrolyte cations is shown to dramatically affect the rate of electron injection, by changing the diffusion coefficients of the cations. When the electrolyte concentration is increased, the diffusion coefficient of the electrolyte ions decreases, as a result of jamming of the cations inside the pores of the film. Interestingly, for the smaller cations, Li+ and Na+, the electron injection onset occurs at higher potentials in the CV scans. This points to intercalation of the Li+ and Na+ ions into the ZnO QDs while the steric hindrance of the larger ions hinders the intercalation. Finally, it was shown that electronic conductivity in source-drain measurements is not affected by the type, size, or location of the dopant ion. This observation indicates that shallow donor levels from intercalating ions fully hybridize with the quantum confined energy levels and that the reorganization energy due to ions does not strongly affect electron transport in these nanocrystal assemblies. These findings shed light on the role of the electrolyte ions as external dopants and will help to achieve rational design of doped semiconductor NC films of various compositions. For instance, it is clear that the energy of charge injection, and thereby the conduction band edge, can be adjusted by the choice of the electrolyte cation, without affecting charge transport properties of the doped films.

Acknowledgments

A.J.H. acknowledges support from the European Research Council Horizon 2020 ERC Grant Agreement No. 678004 (Doping on Demand). The authors thank Ivan Infante for valuable discussions regarding ion intercalation in QDs.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/jacs.8b01347.

  • Home-built interdigitated electrode, change in absorbance during CV for ZnO QD film, exponential fits for charging currents, source-drain electronic conduction measurements, charge carrier density, Randles–Sevcik equation for porous materials, magnification of CVs, CVs for 0.1 M acetonitrile solution containing different electrolytes, CVs for 0.5 M acetonitrile solution containing different electrolytes, source-drain electron conduction measurements for different electrolyte ions, and determination of the threshold potential. (PDF)

The authors declare no competing financial interest.

Supplementary Material

ja8b01347_si_001.pdf (1.5MB, pdf)

References

  1. a Bailey R. E.; Nie S. Alloyed semiconductor quantum dots: Tuning the optical properties without changing the particle size. J. Am. Chem. Soc. 2003, 125 (23), 7100–7106. 10.1021/ja035000o. [DOI] [PubMed] [Google Scholar]; b Wang X.; Zhuang J.; Peng Q.; Li Y. A general strategy for nanocrystal synthesis. Nature 2005, 437 (7055), 121–4. 10.1038/nature03968. [DOI] [PubMed] [Google Scholar]; c Talapin D. V.; Lee J.-S.; Kovalenko M. V.; Shevchenko E. V. Prospects of colloidal nanocrystals for electronic and optoelectronic applications. Chem. Rev. 2010, 110 (1), 389–458. 10.1021/cr900137k. [DOI] [PubMed] [Google Scholar]
  2. a Zhang F.; Zhong H.; Chen C.; Wu X.-g.; Hu X.; Huang H.; Han J.; Zou B.; Dong Y. Brightly Luminescent and Color-Tunable Colloidal CH3NH3PbX3 (X = Br, I, Cl) Quantum Dots: Potential Alternatives for Display Technology. ACS Nano 2015, 9 (4), 4533–4542. 10.1021/acsnano.5b01154. [DOI] [PubMed] [Google Scholar]; b Kovalenko M. V.; Manna L.; Cabot A.; Hens Z.; Talapin D. V.; Kagan C. R.; Klimov V. I.; Rogach A. L.; Reiss P.; Milliron D. J.; Guyot-Sionnnest P.; Konstantatos G.; Parak W. J.; Hyeon T.; Korgel B. A.; Murray C. B.; Heiss W. Prospects of nanoscience with nanocrystals. ACS Nano 2015, 9 (2), 1012–1057. 10.1021/nn506223h. [DOI] [PubMed] [Google Scholar]; c Bourzac K. Quantum dots go on display: adoption by TV makers could expand the market for light-emitting nanocrystals. Nature 2013, 493 (7432), 283. 10.1038/493283a. [DOI] [PubMed] [Google Scholar]
  3. a Carey G. H.; Abdelhady A. L.; Ning Z.; Thon S. M.; Bakr O. M.; Sargent E. H. Colloidal Quantum Dot Solar Cells. Chem. Rev. 2015, 115 (23), 12732–63. 10.1021/acs.chemrev.5b00063. [DOI] [PubMed] [Google Scholar]; b Lan X.; Voznyy O.; Garcia de Arquer F. P.; Liu M.; Xu J.; Proppe A. H.; Walters G.; Fan F.; Tan H.; Liu M.; Yang Z.; Hoogland S.; Sargent E. H. 10.6% Certified Colloidal Quantum Dot Solar Cells via Solvent-Polarity-Engineered Halide Passivation. Nano Lett. 2016, 16 (7), 4630–4. 10.1021/acs.nanolett.6b01957. [DOI] [PubMed] [Google Scholar]
  4. a Sun Q.; Wang Y. A.; Li L. S.; Wang D.; Zhu T.; Xu J.; Yang C.; Li Y. Bright, multicoloured light-emitting diodes based on quantum dots. Nat. Photonics 2007, 1 (12), 717–722. 10.1038/nphoton.2007.226. [DOI] [Google Scholar]; b Shirasaki Y.; Supran G. J.; Bawendi M. G.; Bulović V. Emergence of colloidal quantum-dot light-emitting technologies. Nat. Photonics 2013, 7 (1), 13–23. 10.1038/nphoton.2012.328. [DOI] [Google Scholar]
  5. Shim M.; Wang C.; Norris D. J.; Guyot-Sionnest P. Doping and Charging in Colloidal Semiconductor Nanocrystals. MRS Bull. 2001, 26 (12), 1005–1008. 10.1557/mrs2001.257. [DOI] [Google Scholar]
  6. a Mocatta D.; Cohen G.; Schattner J.; Millo O.; Rabani E.; Banin U. Heavily Doped Semiconductor Nanocrystal Quantum Dots. Science 2011, 332, 77–81. 10.1126/science.1196321. [DOI] [PubMed] [Google Scholar]; b Schimpf A. M.; Knowles K. E.; Carroll G. M.; Gamelin D. R. Electronic doping and redox-potential tuning in colloidal semiconductor nanocrystals. Acc. Chem. Res. 2015, 48 (7), 1929–37. 10.1021/acs.accounts.5b00181. [DOI] [PubMed] [Google Scholar]; c Sahu A.; Kang M. S.; Kompch A.; Notthoff C.; Wills A. W.; Deng D.; Winterer M.; Frisbie C. D.; Norris D. J. Electronic impurity doping in CdSe nanocrystals. Nano Lett. 2012, 12 (5), 2587–94. 10.1021/nl300880g. [DOI] [PubMed] [Google Scholar]
  7. a Shim M.; Guyot-Sionnest P. n-type colloidal semiconductor nanocrystals. Nature 2000, 407, 981–983. 10.1038/35039577. [DOI] [PubMed] [Google Scholar]; b Koh W. K.; Koposov A. Y.; Stewart J. T.; Pal B. N.; Robel I.; Pietryga J. M.; Klimov V. I. Heavily doped n-type PbSe and PbS nanocrystals using ground-state charge transfer from cobaltocene. Sci. Rep. 2013, 3, 2004. 10.1038/srep02004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. a Schimpf A. M.; Gunthardt C. E.; Rinehart J. D.; Mayer J. M.; Gamelin D. R. Controlling carrier densities in photochemically reduced colloidal ZnO nanocrystals: size dependence and role of the hole quencher. J. Am. Chem. Soc. 2013, 135 (44), 16569–77. 10.1021/ja408030u. [DOI] [PubMed] [Google Scholar]; b Rinehart J. D.; Schimpf A. M.; Weaver A. L.; Cohn A. W.; Gamelin D. R. Photochemical electronic doping of colloidal CdSe nanocrystals. J. Am. Chem. Soc. 2013, 135 (50), 18782–5. 10.1021/ja410825c. [DOI] [PubMed] [Google Scholar]
  9. a Vanmaekelbergh D.; Houtepen A. J.; Kelly J. J. Electrochemical gating: A method to tune and monitor the (opto)electronic properties of functional materials. Electrochim. Acta 2007, 53 (3), 1140–1149. 10.1016/j.electacta.2007.02.045. [DOI] [Google Scholar]; b Guyot-Sionnest P. Charging colloidal quantum dots by electrochemistry. Microchim. Acta 2008, 160 (3), 309–314. 10.1007/s00604-007-0787-y. [DOI] [Google Scholar]; c Boehme S. C.; Wang H.; Siebbeles L. D. A.; Vanmaekelbergh D.; Houtepen A. J. Electrochemical charging of CdSe quantum dot films: Dependence on voids size and counterion proximity. ACS Nano 2013, 7 (3), 2500–2508. 10.1021/nn3058455. [DOI] [PubMed] [Google Scholar]
  10. a Boehme S. C.; Azpiroz J. M.; Aulin Y. V.; Grozema F. C.; Vanmaekelbergh D.; Siebbeles L. D.; Infante I.; Houtepen A. J. Density of Trap States and Auger-mediated Electron Trapping in CdTe Quantum-Dot Solids. Nano Lett. 2015, 15 (5), 3056–66. 10.1021/acs.nanolett.5b00050. [DOI] [PubMed] [Google Scholar]; b Amelia M.; Lincheneau C.; Silvi S.; Credi A. Electrochemical properties of CdSe and CdTe quantum dots. Chem. Soc. Rev. 2012, 41 (17), 5728–43. 10.1039/c2cs35117j. [DOI] [PubMed] [Google Scholar]
  11. Gooding A. K.; Gómez D. E.; Mulvaney P. The Effects of Electron and Hole Injection on the Photoluminescence of CdSe:CdS:ZnS Nanocrystal Monolayers. ACS Nano 2008, 2 (4), 669–676. 10.1021/nn7003469. [DOI] [PubMed] [Google Scholar]
  12. Alimoradi Jazi M.; Janssen V.; Evers W. H.; Tadjine A.; Delerue C.; Siebbeles L. D. A.; van der Zant H. S. J.; Houtepen A. J.; Vanmaekelbergh D. Transport Properties of a Two-Dimensional PbSe Square Superstructure in an Electrolyte-Gated Transistor. Nano Lett. 2017, 17 (9), 5238–5243. 10.1021/acs.nanolett.7b01348. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. van der Stam W.; Gudjonsdottir S.; Evers W. H.; Houtepen A. J. Switching between Plasmonic and Fluorescent Copper Sulfide Nanocrystals. J. Am. Chem. Soc. 2017, 139 (37), 13208–13217. 10.1021/jacs.7b07788. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Hoyer P.; Eichberger R.; Weller H. Spectroelectrochemical Investigations of Nanocrystalline ZnO Films. Ber. Bunsenges. Phys. Chem. 1993, 97, 630–635. 10.1002/bbpc.19930970416. [DOI] [Google Scholar]
  15. a Wood A.; Giersig M.; Hilgendorff M.; Vilas-Campos A.; Liz-Marzan L. M.; Mulvaney P. Size effect in ZnO. The cluster to quantum dot transition. Aust. J. Chem. 2003, 56, 1051–1057. 10.1071/CH03120. [DOI] [Google Scholar]; b Mashford B. S.; Stevenson M.; Popovic Z.; Hamilton C.; Zhou Z.; Breen C.; Steckel J.; Bulovic V.; Bawendi M.; Coe-Sullivan S.; Kazlas P. T. High-efficiency quantum-dot light-emitting devices with enhanced charge injection. Nat. Photonics 2013, 7 (5), 407–412. 10.1038/nphoton.2013.70. [DOI] [Google Scholar]
  16. Boehme S. C.; Vanmaekelbergh D.; Evers W. H.; Siebbeles L. D. A.; Houtepen A. J. In Situ Spectroelectrochemical Determination of Energy Levels and Energy Level Offsets in Quantum-Dot Heterojunctions. J. Phys. Chem. C 2016, 120 (9), 5164–5173. 10.1021/acs.jpcc.5b12016. [DOI] [Google Scholar]
  17. Ruch P. W.; Cericola D.; Hahn M.; Kötz R.; Wokaun A. On the use of activated carbon as a quasi-reference electrode in non-aqueous electrolyte solutions. J. Electroanal. Chem. 2009, 636 (1–2), 128–131. 10.1016/j.jelechem.2009.09.007. [DOI] [Google Scholar]
  18. Boehme S. C.; Vanmaekelbergh D.; Evers W. H.; Siebbeles L. D. A.; Houtepen A. J. In Situ Spectroelectrochemical Determination of Energy Levels and Energy Level Offsets in Quantum -Dot Heterojunctions. J. Phys. Chem. C 2016, 120 (9), 5164–5173. 10.1021/acs.jpcc.5b12016. [DOI] [Google Scholar]
  19. Meulenkamp E. A. Synthesis and Growth of ZnO Nanoparticles. J. Phys. Chem. B 1998, 102 (29), 5566–5572. 10.1021/jp980730h. [DOI] [Google Scholar]
  20. Roest A. L.; Kelly J. J.; Vanmaekelbergh D.; Meulenkamp E. A. Staircase in the electron mobility of a ZnO quantum dot assembly due to shell filling. Phys. Rev. Lett. 2002, 89 (3), 036801. 10.1103/PhysRevLett.89.036801. [DOI] [PubMed] [Google Scholar]
  21. Bard A. J.; Faulkner L. R.. Electrochemical methods. Fundamentals and applications, 2nd ed.; John Wiley & Sons, Inc.: New York, 2001. [Google Scholar]
  22. a Chandler R. E.; Houtepen A. J.; Nelson J.; Vanmaekelbergh D. Electron transport in quantum dot solids: Monte Carlo simulations of the effects of shell filling, Coulomb repulsions, and site disorder. Phys. Rev. B: Condens. Matter Mater. Phys. 2007, 75 (8), 085325. 10.1103/PhysRevB.75.085325. [DOI] [Google Scholar]; b van de Lagemaat J. Einstein relation for electron diffusion on arrays of weakly coupled quantum dots. Phys. Rev. B: Condens. Matter Mater. Phys. 2005, 72 (23), 235319. 10.1103/PhysRevB.72.235319. [DOI] [Google Scholar]
  23. Page C. L.; Short N. R.; El Tarras A. Diffusion of chloride ions in hardened cement pastes. Cem. Concr. Res. 1981, 11 (3), 395–406. 10.1016/0008-8846(81)90111-3. [DOI] [Google Scholar]
  24. a Laoire C. O.; Mukerjee S.; Abraham K. M. Elucidating the Mechanism of Oxygen Reduction for Lithium-Air Battery Applications. J. Phys. Chem. C 2009, 113 (46), 20127–20134. 10.1021/jp908090s. [DOI] [Google Scholar]; b Shen J.; Wang H.; Zhou Y.; Ye N.; Li G.; Wang L. Anatase/rutile TiO2 nanocomposite microspheres with hierarchically porous structures for high-performance lithium-ion batteries. RSC Adv. 2012, 2, 9173–9178. 10.1039/c2ra20962d. [DOI] [Google Scholar]
  25. Brozek C. K.; Hartstein K. H.; Gamelin D. R. Potentiometric Titrations for Measuring the Capacitance of Colloidal Photodoped ZnO Nanocrystals. J. Am. Chem. Soc. 2016, 138 (33), 10605–10. 10.1021/jacs.6b05848. [DOI] [PubMed] [Google Scholar]
  26. a Özgür Ü.; Alivov Y. I.; Liu C.; Teke A.; Reshchikov M. A.; Doğan S.; Avrutin V.; Cho S. J.; Morkoç H. A comprehensive review of ZnO materials and devices. J. Appl. Phys. 2005, 98 (4), 041301. 10.1063/1.1992666. [DOI] [Google Scholar]; b Orlinskii S. B.; Schmidt J.; Baranov P. G.; Hofmann D. M.; de Mello Donega C.; Meijerink A. Probing the wave function of shallow Li and Na donors in ZnO nanoparticles. Phys. Rev. Lett. 2004, 92 (4), 047603. 10.1103/PhysRevLett.92.047603. [DOI] [PubMed] [Google Scholar]
  27. a Joshi A. G.; Sahai S.; Gandhi N.; Krishna Y. G. R.; Haranath D. Valence band and core-level analysis of highly luminescent ZnO nanocrystals for designing ultrafast optical sensors. Appl. Phys. Lett. 2010, 96 (12), 123102. 10.1063/1.3354025. [DOI] [Google Scholar]; b Saáedi A.; Yousefi R.; Jamali-Sheini F.; Zak A. K.; Cheraghizade M.; Mahmoudian M. R.; Baghchesara M. A.; Dezaki A. S. XPS studies and photocurrent applications of alkali-metals-doped ZnO nanoparticles under visible illumination conditions. Phys. E 2016, 79, 113–118. 10.1016/j.physe.2015.12.002. [DOI] [Google Scholar]
  28. Zhang J.; Gu P.; Xu J.; Xue H.; Pang H. High performance of electrochemical lithium storage batteries: ZnO-based nanomaterials for lithium-ion and lithium-sulfur batteries. Nanoscale 2016, 8 (44), 18578–18595. 10.1039/C6NR07207K. [DOI] [PubMed] [Google Scholar]
  29. Kushima A.; Liu X. H.; Zhu G.; Wang Z. L.; Huang J. Y.; Li J. Leapfrog Cracking and Nanoamorphization of ZnO Nanowires during In Situ Electrochemical Lithiation. Nano Lett. 2011, 11 (11), 4535–4541. 10.1021/nl201376j. [DOI] [PubMed] [Google Scholar]
  30. Lyon L. A.; Hupp J. T. Energetics of Semiconductor ElectroddSolution Interfaces- EQCM Evidence for Charge-Compensating Cation Adsorption and Intercalation during Accumulation Layer Formation in the Titanium DioxiddAcetonitrile System. J. Phys. Chem. 1995, 99, 15718–15720. 10.1021/j100043a005. [DOI] [Google Scholar]
  31. Puntambekar A.; Wang Q.; Miller L.; Smieszek N.; Chakrapani V. Electrochemical Charging of CdSe Quantum Dots: Effects of Adsorption versus Intercalation. ACS Nano 2016, 10 (12), 10988–10999. 10.1021/acsnano.6b05779. [DOI] [PubMed] [Google Scholar]
  32. Neamen D. A.Semiconductor physics and devices: Basic principles, 4th ed.; McGraw-Hill Education: New York, 2012. [Google Scholar]
  33. Halverson A. F.; Zhu K.; Erslev P. T.; Kim J. Y.; Neale N. R.; Frank A. J. Perturbation of the electron transport mechanism by proton intercalation in nanoporous TiO2 films. Nano Lett. 2012, 12 (4), 2112–6. 10.1021/nl300399w. [DOI] [PubMed] [Google Scholar]
  34. a Cox S. F.; Davis E. A.; Cottrell S. P.; King P. J.; Lord J. S.; Gil J. M.; Alberto H. V.; Vilao R. C.; Piroto Duarte J.; Ayres de Campos N.; Weidinger A.; Lichti R. L.; Irvine S. J. Experimental confirmation of the predicted shallow donor hydrogen state in zinc oxide. Phys. Rev. Lett. 2001, 86 (12), 2601–4. 10.1103/PhysRevLett.86.2601. [DOI] [PubMed] [Google Scholar]; b Gil J. M.; Alberto H. V.; Vilão R. C.; Piroto Duarte J.; Ayres de Campos N.; Weidinger A.; Krauser J.; Davis E. A.; Cottrell S. P.; Cox S. F. J. Shallow donor muonium states in II-VI semiconductor compounds. Phys. Rev. B: Condens. Matter Mater. Phys. 2001, 64 (7), 075205. 10.1103/PhysRevB.64.075205. [DOI] [Google Scholar]
  35. Enright B.; Fitzmaurice D. Spectroscopic Determination of Electron and Hole Effective Masses in a Nanocrystalline Semiconductor Film. J. Phys. Chem. 1996, 100, 1027–1035. 10.1021/jp951142w. [DOI] [Google Scholar]
  36. Goings J. J.; Schimpf A. M.; May J. W.; Johns R. W.; Gamelin D. R.; Li X. Theoretical Characterization of Conduction-Band Electrons in Photodoped and Aluminum-Doped Zinc Oxide (AZO) Quantum Dots. J. Phys. Chem. C 2014, 118 (46), 26584–26590. 10.1021/jp5090229. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ja8b01347_si_001.pdf (1.5MB, pdf)

Articles from Journal of the American Chemical Society are provided here courtesy of American Chemical Society

RESOURCES