Morphological properties of atmospheric aerosol aggregates

Abstract

Ultrafine particles (smaller than about 0.1 μm) are often emitted from combustion and other high-temperature processes in the form of fractal-like aggregates composed of solid nanoparticles. Results of a study of atmospheric aggregates are reported. Particles were collected on transmission electron microscope grids fitted on the last two stages of a single-jet eight-stage low-pressure impactor for periods of a few minutes. Photomicrographs of transmission electron microscope grids from the impactor stages were analyzed to obtain the fractal dimension (D_f) and prefactor (A) for aggregates. D_f increased from near 1 to above 2 as the number of primary particles making up the aggregates increased from 10 to 180. Total particle concentrations in size ranges roughly equivalent to the low-pressure impactor stages were measured with a mobility analyzer and condensation particle counter. In one set of measurements, the fraction of the particles present as aggregates was about 60% for particles with aerodynamic diameters between 50 and 75 nm and 34% for the range 75 to 120 nm. The total aggregate concentration in the 50- to 120-nm size range was about 400 ml⁻¹. The primary particles that make up atmospheric aggregates are more polydisperse than soot aggregates generated from a single laboratory source, an ethane/oxygen flame. Most measurements were made in the Los Angeles area, where the aggregates may represent a signature for diesel emissions. Rural aggregate concentrations in the size range 50 to 120 nm were less than 1% of the concentrations at urban sites. The data will permit better estimates of atmospheric aggregate residence times, transport, and deposition in the lung, optical extinction, and heterogenous nucleation.

The ultrafine particle size range (d_p < 0.1 μm) of the atmospheric aerosol is composed of both primary and secondary particulate matter. The primary component, emitted directly from sources, often includes aggregates of smaller particles. (Note that the term “primary” in this context differs from its use to designate the individual particles that compose aerosol aggregate structures.) The secondary component is composed of particulate matter formed in the atmosphere, including sulfuric acid and sulfates, and organic reaction products of low volatility. Particles that form in the atmosphere tend to evaporate in the electron microscope, the principal observational method used in this study.

This paper describes a systematic study of the morphology of atmospheric ultrafine aggregates; most of the measurements were made in the Los Angeles area. For comparison purposes, a few measurements were made at San Jacinto, CA (a nearby rural site), Research Triangle Park, NC, and of a laboratory-generated soot. Sources of ultrafine aggregates at the locations where our measurements were made include diesel emissions, soot from incomplete combustion (for example, home fireplaces, cooking fires, etc.), and welding fumes. Diesel emissions are probably the largest single source of atmospheric “black carbon” in the U.S., accounting for 0.15 terragrams/yr (1). Gray et al. (2) report that in the Los Angeles area, primary particulate carbon emissions were the principal contributor to fine particle mass loading. Martins et al. (3) found that high mass fractions of black carbon (in the form of aggregates) and the degree of particle nonsphericity are associated with high optical absorption efficiency. Measurements of the type described in this paper may make it possible to track the effects of controlling diesel emissions and other combustion processes on air quality.

The fractal dimension can often be used to characterize aggregate morphology through the expression (4–9)

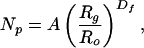1

where D_f is the fractal dimension, N_p is the number of primary particles in the aggregate, A is a dimensionless prefactor, R_o is the primary particle radius, and R_g is the characteristic radius of the aggregate, which we take to be the radius of gyration. Eq. 1 is a result of the power law dependence of the density–density correlation function for the primary particles in an aggregate on distance from a selected reference point (5, 8). If Eq. 1 holds to distances of order of the primary particle diameter, R_g → R_o, and there is no particle overlap, then A = 1. Values of A are usually of order unity but may fall significantly above or below one, as discussed below.

Values of D_f reported for laboratory-generated soot aggregates vary widely, ranging from 1.5 to 3.0 (Table 1). Values of D_f shown in the table are averaged over the aerosol cloud, except for the electron microscope study (7), which was based on measurements of individual aggregates. The ranges of D_f of the individual particles may be higher than the values shown. Few data, however, have been reported for fractal-like atmospheric particles. Katrinak et al. (12) determined values of D_f for 38 carbonaceous aggregates sampled in Phoenix, AZ. The particles were collected by impaction and analyzed by electron microscopy. They were divided into three groups: (i) fractal-like aggregates with 1.35 < D_f < 1.89; (ii) possibly nonfractal particles with D_f > 2; and (iii) particles of mixed morphology. Aggregates coated with what were believed to be nitrates and sulfates were also observed. Neither the type of impactor used nor the efficiency of particle collection as a function of particle size was reported.

Table 1.

Average values of D_f for soot aggregates from laboratory sources

Source	Df	Method of analysis	Reference
Acetylene flame	1.5–1.6	Electron microscopy	7
Butane flame	1.87–2.19	Light scattering	10
Diesel engine	2.1–2.9	Mobility analyzer	11
Spark ignition engine	2.2–3.0	Mobility analyzer	11

Scope of Study

The morphology of atmospheric aggregates influences their effects on public health (13), water vapor nucleation (14), and absorption and scattering of light (15). For example, aggregate transport rates determine their atmospheric residence time and patterns of deposition in the lung. Rates of diffusional transport of individual aggregates depend on values of N_p, D_f, and A (16–18). As we will show, aggregates are distributed with respect to size (N_p) and mixed with nonaggregated particles in the atmosphere. We report measurements of the fraction of the particles in a given size range that possess aggregate structures and the frequency distribution of aggregates with respect to N_p. Mathematical models of aggregate transport and light scattering are usually based on the assumption that the primary particles that compose the aggregates are monodisperse. Our measurements of primary particle size distribution show that this is not the case. Although this is a detailed study, the measurements are limited geographically; many more measurements will be needed to characterize these aggregates sufficiently to permit reliable estimates of the large-scale effects of atmospheric aggregates.

Experimental Methods

Sampling Sites.

Most measurements were made at a sampling site located at the University of California, Los Angeles (UCLA), on the fifth floor, between two buildings, Engineering IV and Boelter Hall, about 1 mile east of the 405 Freeway. Cars, delivery trucks, and diesel vehicles pass at ground level on the street and driveway below the sampling point. Measurements were also made at San Jacinto, CA (a rural sampling site in the Los Angeles area), on the pier in Santa Monica, CA, at the Veterans Administration near UCLA, and at Research Triangle Park, NC.

Measurement of Particle Size Distributions.

An eight-stage low-pressure impactor (LPI) was used to sample particles according to their aerodynamic diameters. The LPI is a single jet impactor equipped with a critical orifice that maintains a flow rate of 1 liter/min (19, 20). The impaction velocity ranged from 3.5 to 300 m/s for stages 1–8. The stages have 50% aerodynamic diameter cutoffs of 4.0, 2.0, 1.0, 0.5, 0.26, 0.12, 0.075, and 0.05 μm, for stages 1–8, respectively. The particles were collected on 400 mesh transmission electron microscope (TEM) nickel grids with carbon backing (Ted Pella, Redding, CA). To minimize the effects of particle bounce, only one stage at a time had a TEM grid attached for sampling; this grid was secured at the center of a 25-mm-diameter glass stage, whereas the other stages were coated with Apiezon grease. The sampling time was 5 min for stages 7 and 8. A similar measurement was made for stage 4 to compare the ultrafine and accumulation mode morphologies. The total time needed to sample all of the stages was about half an hour.

A differential mobility analyzer (DMA) (TSI, St. Paul, model 3070) and condensation particle counter (CPC) (TSI model 3010) were used to measure mobility diameter (including both aggregated and nonaggregated particles). The DMA operates by introducing polydisperse charged particles into a stream of clean air that flows in the annular space between two concentric tubes with an adjustable voltage between them. The trajectory of the particle depends on the flow, voltage difference, and particle electrical mobility (21). Particles of a narrow electrical mobility range are removed through a slit located toward the end of the inner tube. This stream of monodisperse aerosol of known mobility diameter is counted by the CPC. The size distribution is found by stepping through 39 voltage differences. Each size distribution scan takes about 10 min to cover a mobility diameter range from 10 to 320 nm.

Measurement of Aggregate Structure.

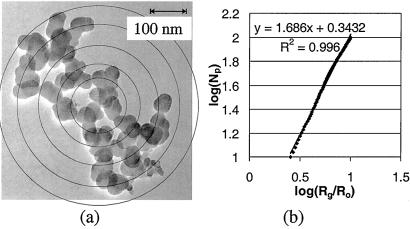
Image analysis is an established method for determining D_f. A review of image analysis methods used to study particles can be found in Brasil et al. (22). In our study, the aggregates collected on the TEM grids were studied by using a JEOL 100CX TEM. At a magnification of ×200,000, the viewable area is about 0.12 μm². The pictures were taken at ×50,000–250,000. The film was developed and scanned into tagged image format files by using a Microtek Scanmaker E6 (Redondo Beach, CA). The files were imported into corel draw, and circles were drawn around the primary particles (Fig. 1a). A visual basic program (Microsoft) was executed to determine the size and position of the primary particles. The analysis of a single aggregate took 10–30 min, depending on the number of primary particles. These data were used to determine D_f, N_p, A, and primary particle size distribution.

Figure 1.

Fractal analysis of an aggregate for stage 7. (a) An electron micrograph of an aggregate imported into corel draw. The concentric circles correspond to different r_i. (b) The fractal dimension (D_f) was determined from the slope of the log–log plot of the normalized radius of gyration and number of primary particles. The normalizing radius R_o is based on a volume average, and A is determined from the Y intercept.

Measurement of the Fraction of Aggregates in Ultrafine Range.

A DMA-CPC system was used to obtain the total particle concentration (including aggregates and droplets) in mobility diameter ranges equivalent to the LPI size cuts (Table 2). Samples were collected on August 4, 2000, outside Boelter Hall. About 10 min was required for measurements with the DMA-CPC system. Hence the LPI, used to determine the aggregate concentration, was operated intermittently over the DMA sampling period. The particles collected with the LPI were counted along perpendicular axes, and the number counts were fitted with a Gaussian distribution. A three-dimensional Gaussian curve was obtained by combining the two Gaussian distributions. The volume under the curve is proportional to the total concentration, which was calculated from the flow rate and sampling time.

Table 2.

Comparison of aggregate size ranges, nm, for LPI and DMA-CPC

LPI	DMA-CPC
50–75 (stage 8)	51–71
75–120 (stage 7)	71–100

Our method of determining particle concentration in the LPI by using the Gaussian curve extrapolation was checked by using 0.36-μm polystyrene latex particles (PSL) (Duke Scientific, Palo Alto, CA) and an optical particle counter (PMS, Boulder, CO, model LAS-X). The number count determined by the Gaussian curve fitting technique was 7,700 particles/ml, which agreed very well with the count (7,800 particles/ml) for the corresponding particle diameter range measured by the optical particle counter. The agreement between the LPI and optical particle counter is expected because both instruments were calibrated with PSL particles.

Laboratory-Generated Soot Aggregates.

To compare with the atmospheric aggregates, we also sampled soot particles from a laboratory source. A premixed flame with a 1.5-volume equivalence ethane/oxygen ratio was used to produce soot, and samples were collected 60 mm above the flame. A pneumatic probe with a TEM grid was used to sample soot particles by thermophoresis (23). The flame was surrounded by a Plexiglas cylinder to minimize air entrainment and steady the flame.

Results and Discussion

Morphology of Atmospheric Particles.

Atmospheric particles can be classified as coarse (d_p > 2.5 μm), accumulation mode (0.1 μm < d_p < 2.5 μm), and ultrafine (d_p < 0.1 μm) (24). Particles were collected with the eight-stage impactor, for which the coarse range corresponds approximately to stages 1 and 2 and the accumulation mode to stages 3–6. The ultrafine range corresponds approximately to stages 7 and 8. The physical characteristics of the aerosol observed at the UCLA site were as follows:

2 < d_p < 10 μm: droplets with a core of solid matter and irregularly shaped solid particles (nonaggregates).

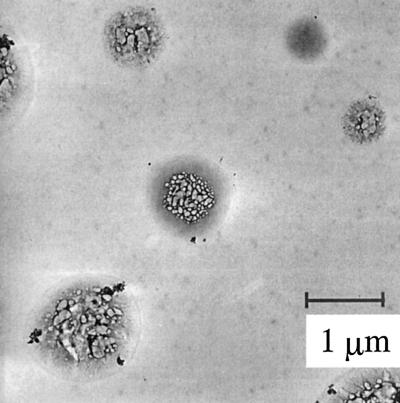
0.26 < d_p < 2.0 μm: mostly droplets, irregularly shaped solid particles (nonaggregates), and large aggregates (Fig. 2).

Figure 2.

Particles from LPI stage 4. Most of the particles are probably droplets that evaporated in the electron microscope. Note the soot-like aggregates that have been incorporated into the droplet. The sample was taken on May 20, 1997, on the fifth floor bridge way between Boelter Hall and Engineering IV at UCLA.

<0.26 μm: aggregates of primary particles (Fig. 3) and halos of evaporated droplets.

Figure 3.

Chain aggregates of ultrafine particles from stage 7. a shows a short chain with low D_f and b a longer chain with high D_f. The sample was taken on Feb 20, 2001, at the San Jacinto Air Quality Management District (AQMD) site.

Our study focused on the particles collected on stages 7 and 8, corresponding to aerodynamic diameters less than 0.12 μm. These particles tended to be either spherical droplets or free aggregates. Qualitative elemental analysis by the electron dispersive x-ray method and structural analysis by selected area diffraction indicated that the primary particles are amorphous and mostly carbonaceous.

Fractal Dimension and N_p.

Values of D_f were determined from an analysis of aggregate photomicrographs. Taking the logarithm of both sides of Eq. 1 gives: log N_p = log A + D_f log R_g − D_f log R_o [2]

where R_g is the radius of gyration = [(1/M)Σ(m_ir_i)]^1/2, m_i is the mass of the ith primary particle, M is the total aggregate mass = Σm_i, and r_i is the distance of the ith primary particle from the center of mass. Fig. 1 is a photomicrograph of an aggregate from stage 7; primary particles were drawn in corel draw, with r_i represented by concentric circles. The value of R_g was calculated from the aggregate image and the measured diameters of the polydisperse primary particles. The corresponding log–log plot of N_p versus the normalized radius of gyration is also shown in Fig. 1. According to Eq. 2, D_f is the slope of the log–log plot, and the log of A is the Y intercept (25); the value of D_f does not depend on the value of R_o so long as the linear relationship between N_p and R_g holds. Linear fits to the data usually showed Pearson correlation coefficients greater than 0.995. A few aggregates, which could not be represented by good linear fits, were not included in the overall analysis. Also excluded were a few aggregates with fractal dimensions that varied over 0.3 fractal units when the nested circles did not center on the center of mass.

Aggregates with chain-like structures are formed by collisions of smaller chains described by certain collision algorithms that lead to values of D_f between 1.5 and 2.0 (26–28). Fig. 4a, based on the analysis of 102 particles collected in the Los Angeles area, shows that D_f increased from near 1 to more than 2 as the number of primary particles making up the aggregates increased from 10 to 180. The two-dimensional analysis of photomicrographs should result in values of D_f between 1 and 2, although values somewhat higher than 2 can be estimated. Values of D_f > 2 may result from the polydispersity of the primary particles composing the atmospheric aggregates.

Figure 4.

(a) D_f tends to increase with N_p for particles collected over a 4-year period, 1997–2001, at five different sites: Boelter Hall–Engineering IV bridge at UCLA, Santa Monica Pier, and the Veterans Administration Hospital San Jacinto Air Quality Management District site. The average D_f is 1.63. Particles were also collected at rural areas in (b) Research Triangle Park, NC, and (c) San Jacinto, CA. The aggregates collected in North Carolina and San Jacinto had averages D_f of 1.73 and 1.80, respectively. Data for these sites did not show the same trend as the urban sites.

It is of interest to compare our results for D_f with those of other investigators. In the absence of a sufficient database for atmospheric aggregates, data for aggregates emitted by different sources are shown in Table 1. These data are limited to ranges in values of D_f averaged over N_p. For example, the mobility and light scattering techniques cited in the table intrinsically generate D_f values averaged over N_p; measurements using electron microscopy were reported as averages. Thus we could not compare the trend that we observed (Fig. 4a) with the data for sources.

Although the two-dimensional image analysis used in our studies is limited to aggregates with D_f <2, Fig. 4a shows that aggregates with D_f > 2 were probably present; points with the higher values shown are less accurate than those for D_f < 2. According to Table 1, values of D_f approaching 3 have been reported for diesel and spark ignition engines (11). These values are higher than the values we observed, probably because droplets were included by the investigators.

The increase in D_f with N_p for the Los Angeles sites (Fig. 4a) can be explained by the aggregation of short chains with low D_f values to form larger aggregates with higher D_f. Such an increase has been observed in computer simulations of the aggregation of an aerosol cloud of unitary particles in a fixed volume of gas (“box” model) (27). Aggregation can take place in the atmosphere and/or at an important source type, e.g., diesel engines.

Values of D_f at the rural sites (Fig. 4 b and c) showed no trend with N_p. Most of the data scattered in the range 1.5–2 expected for cluster–cluster aggregation. This may result from the absence of fresh sources of aggregates containing short chains. Thus we can draw inferences concerning atmospheric aggregation dynamics from measurements of aggregate fractal properties, but simulations of aggregate dynamics should take into account the distribution of D_f as well as aggregate size.

Prefactor.

Like D_f, the prefactor A is important in calculations of the dynamics of aggregation processes (28). In the absence of measured values, A is usually assumed to be unity. However, experimental values of A may vary significantly around unity (29). For polydisperse primary particles, it is necessary to choose a suitable average value of R_o to maintain a one-parameter model. In our calculations, values of R_o were set equal to the volume averaged particle radius. Values of A determined in this way therefore depend on the type of average radius that is selected for R_o. The distribution of A was nearly lognormal, with a count mean average (CMA) value of 2.9, and ranged from 0.6 to 8.0. An important difference between the methods based on the mobility diameter and the radius of gyration is that the latter analyzes each aggregate individually; the value of A from the mobility diameter method is averaged over a large number of aggregates that may vary in shape. Taking this difference into consideration, our CMA value of 2.9, based on the radius of gyration method, is in agreement with the prefactors determined in previous experiments based on mobility diameter. Previous studies using the radius of gyration to analyze simulated aggregates in the free molecular regime (29) reported prefactors that ranged from 0.48 to 1.59, which are much smaller than those found in our study.

Fraction of Ultrafine Particles That Are Aggregates.

The ultrafine size range includes secondary aerosol formed in the atmosphere by gas-to-particle conversion in addition to directly emitted aggregates. The secondary particles tend to be hygroscopic and are probably spherical. The fraction of the ultrafine particles present as aggregates was measured by TEM for stages 7 and 8 at the Boelter Hall sampling site on August 4, 2000. The total number of particles corresponding to each stage was measured with the DMA-CPC. (Table 2 compares aggregate size ranges for the LPI stages and DMA-CPC bins.) The total particle number density measured with the CPC was 1.2 × 10⁴ ml⁻¹. The DMA-CPC counted 266 particles/ml for mobility diameters corresponding to stage 8 and 96 for stage 7. Counts for aggregates on stage 8 were determined by TEM by using the Gaussian fitting technique discussed above. The aggregate concentration for stage 8 was 160 particles/ml, which accounted for 60% of the concentration counted by the DMA-CPC.

Counts of stage 7 using the Gaussian fitting method gave an aggregate concentration of 36 particles/ml; another fitting was performed for the total concentration (aggregates and droplets). The total concentration calculated in this fashion for stage 7 was 102 particles/ml, about 6% higher than the concentration measured with the DMA-CPC. The stage 8 count was much smaller than the DMA-CPC count for the same size range, probably because the small droplets evaporated by the time the TEM was focused. Smaller droplets evaporate faster, leaving less evidence of their presence. For example, the halos (evaporated droplets) on stage 8 are smaller and do not provide as much contrast to the carbon background as those on stage 7. Fewer aggregates were observed on stage 7 at the San Jacinto and Research Triangle Park sites, making up less than 1 and 10%, respectively of the numbers observed at the UCLA sites.

Various uncertainties are associated with our determinations of the aggregate fractions. The LPI measurements were based on the assumption that the 50% aerodynamic cutoff diameter of the LPI is a step-function, above which the collection efficiency is 100%. It was further assumed that the aerodynamic cutoff diameter is equivalent to the electrical mobility diameter, which on theoretical grounds is not expected to be true for aggregates. However, the assumption is supported by the close agreement between the total counts (aggregates and droplets) on stage 7 of the LPI and the equivalent size range for the DMA-CPC (Table 2). Thus the assumption of equivalence of the aerodynamic and mobility diameters was extended to stage 8 to estimate the total particle concentration.

Additionally, there is a small uncertainty in the concentration measured with the DMA-CPC, associated with the adjustments for charging inefficiencies and sampling losses. It is also possible that aggregates break up in the impactor, giving a high count compared with the atmospheric concentration. This probably did not occur for impactor stages 7 and 8, because the aggregates were not surrounded by smaller aggregates. A comparison of particles collected with the LPI with those collected with a thermal precipitator showed no significant affect of impaction on the morphology.

Size Distributions of Primary Particles in Atmospheric and Laboratory Generated Aggregates.

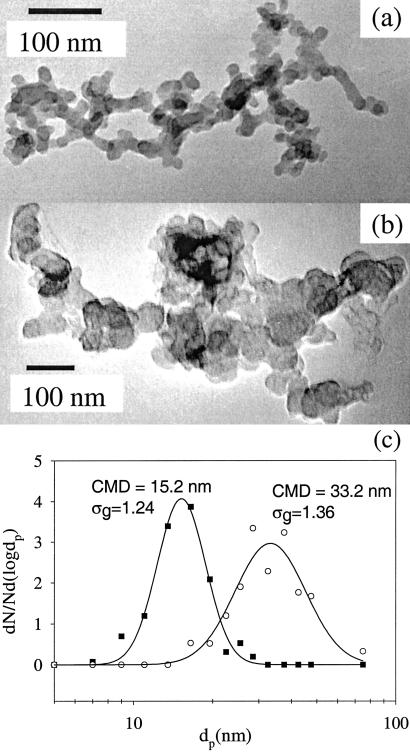
Aggregates sampled from the ethane flame were compared with atmospheric aggregates. The ethane soot had an average value for the prefactor A of 2.8 with a range of 1.1–6.2. The average D_f was 1.73 and ranged from 1.20 to 2.37. The average D_f for the soot from the ethane flame falls between values for acetylene and butane reported earlier (Table 1). The values of D_f for ethane soot are consistent with formation by cluster–cluster aggregation (27). The primary particles in the aggregates were more uniform and smaller than those in the atmosphere (Fig. 5c). The primary particle size of atmospheric aggregates ranged from 6 to 100 nm. The broad polydispersity and wide range may have resulted because the atmospheric aggregates came from a variety of sources with different primary particle sizes (Fig. 5 a and b). Another possibility is that sources not sampled in our study (such as diesel emissions) may have a broader primary particle distribution than the soot generated from an ethane flame. For example, Shi et al. (30) found that the primary particles in diesel aggregates ranged from 10 to 40 nm, but they did not report the primary particle size distribution.

Figure 5.

(a) Soot from an ethane/oxygen flame and (b) atmospheric aggregates shows similar fractal structures but has different primary particle sizes and distributions. (c) Primary particle size distributions for a and b. The atmospheric aggregate has a broader distribution of primary particles either because it is composed of particles from multiple sources that aggregate in the atmosphere or because of polydisperse sources such as diesel emissions.

Aggregate Surface Areas.

The average surface area of the atmospheric aggregates was estimated by summing the surface area of the primary particles composing the aggregates and dividing by the number of aggregates. For aggregates on stage 8, the average surface area was 0.188 μm² and for stage 7, 0.417 μm². A sphere of unity density that deposited on stage 8 would have a surface area of 0.031 μm² and on stage 7, 0.071 μm², both based on the aerodynamic diameter. Thus the area of a spherical particle of equivalent aerodynamic diameter would underestimate the aggregate surface area by a factor of about 6 on average. For the largest aggregate on stage 8, the value of the surface area was 26 times that of the value corresponding to the aerodynamic diameter. The high surface area of aggregates provides adsorption sites for substances such as polycyclic aromatic hydrocarbons (PAH), consistent with studies that reported that particle phase PAH peaked in the size range 0.05–0.12 μm (31).

Aggregate Size Distributions.

Distributions of aggregates with respect to N_p for stages 7 and 8 are shown in Fig. 6. The aggregates from stage 7 were selected at random from a traverse of the grid. All aggregates were analyzed for stage 8. The count-mean N_p for aggregates deposited on stage 8 was 60 primary particles and for stage 7, N_p was 120. Aggregates deposited on stage 8 (50–75 nm) were composed of fewer but larger primary particles than those deposited on stage 7 (75–120 nm). This result is consistent with laboratory studies, which showed that aggregates composed of smaller primary particles grow more rapidly than larger ones, given the same volumetric concentration (32).

Figure 6.

Size distribution with respect to N_p of 46 and 55 aggregates for stages 7 and 8, respectively. (a) Stage 8 has a count mean N_p of 60, whereas (b) stage 7 has 120.

Summary and Conclusion

Much of the elemental carbon in the atmosphere is emitted in the form of aggregates. Atmospheric aggregates can be tracked as a separate component of the atmospheric aerosol and may represent a useful category for epidemiological studies and air quality. Both aggregate characterization and dynamics are of interest. Characterization refers to properties such as concentration and fractal dimension. Near our laboratory, where most of the measurements were made, aggregate concentrations were of the order of 400 particles/ml in the size range 50–120 nm. Concentrations at a rural site outside Los Angeles were about 1% of the urban count. Fractal dimensions for urban aggregates ranged from near one for small aggregates (10 primary particles) to more than two for aggregates of 180. In one set of measurements, about 60% of the total number of particles in the size range 50–75 nm and 34% in the range 75–120 nm were aggregates. Aggregate surface areas based on the primary particles that compose the aggregate are much greater than values calculated from the nominal aerodynamic diameter.

Dynamic parameters such as atmospheric residence times, rates of transport, and deposition in the lung and aggregation in the atmosphere can be estimated from our measurements. However, our data provide only snapshots for a few sites (as well as guidelines for the kinds of measurements required). Much more data will be needed to characterize atmospheric aggregates sufficiently to permit reliable estimates of their large-scale effects.

Abbreviations

LPI

low-pressure impactor

DMA

differential mobility analyzer

CPC

condensation particle counter

TEM

transmission electron microscope

UCLA

University of California, Los Angeles