Understanding Cerebellum Granular Layer Network Computations through Mathematical Reconstructions of Evoked Local Field Potentials

Abstract

Background

The cerebellar granular layer input stage of cerebellum receives information from tactile and sensory regions of the body. The somatosensory activity in the cerebellar granular layer corresponds to sensory and tactile input has been observed by recording Local Field Potential (LFP) from the Crus-IIa regions of cerebellum in brain slices and in anesthetized animals.

Purpose

In this paper, a detailed biophysical model of Wistar rat cerebellum granular layer network model and LFP modelling schemas were used to simulate circuit's evoked response.

Methods

Point Source Approximation and Line Source Approximation were used to reconstruct the network LFP. The LFP mechanism in in vitro was validated in network model and generated the in vivo LFP using the same mechanism.

Results

The network simulations distinctly displayed the Trigeminal and Cortical (TC) wave components generated by 2 independent bursts implicating the generation of TC waves by 2 independent granule neuron populations. Induced plasticity was simulated to estimate granule neuron activation related population responses. As a prediction, cerebellar dysfunction (ataxia) was also studied using the model. Dysfunction at individual neurons in the network was affected by the population response.

Conclusion

Our present study utilizes available knowledge on known mechanisms in a single cell and associates network function to population responses.

Introduction

Cerebellum, which forms a critical part of the hind brain, has been known to perform and be involved in several functions such as cognition, attention and emotional responses in addition to motor coordination and learning [1, 2]. Major sensory information reach cerebellum through MF s (MFs) through excitatory connections to granule neurons and inhibitory connection to Golgi neurons by the formation of glomeruli in the granular layer. Primary information processing on incoming spike trains are expansion recoded at the granular layer, passed to Purkinje neurons and then to deep cerebellar nuclei for consolidation of motor memory [3].

Spatio-temporal operations at the granular layer are crucial to understand the cerebellar motor coordination and learning roles [4]. Cerebellum granular layer population activity during somatosensory function has been studied by recording the Local Field Potential (LFP) from cerebellar Crus-IIa [5, 6, 7]. An extracellular microelectrode or “LFP electrode” records voltage fluctuations (LFP) from the extracellular medium generated by spatially inhomogeneous transmembrane currents related to neuronal processes. Typical activity in acute brain slices has been observed as single spike inputs to granule cells (GrCs) although some short bursts can be artificially observed through electrical stimulation. In vitro LFP activity in granular layer has been observed as negative N_2a and N_2b waves, attributed to MF stimulation with single pulses at a frequency of 0.1 Hz [6]. In vivo LFP activity in granular layer was characterized by Trigeminal (T) and Cortical (C) waves produced by trigeminal and cortical pathways resulting from whisker-pad air puff stimuli, often seen as bursts inputs to granule neurons. The T wave corresponds to trigeminal afferents and the C wave corresponds to the cerebral cortex and pontine nuclei [7].

Electrophysiological studies on animal models have significantly helped in the understanding of molecular and cellular mechanisms of cerebellar functions and dysfunctions at single neuron and circuit levels [6, 7, 8, 9]. Electrophysiological recordings have been translated to detailed biophysical models of neuronal cells [10, 11] to develop biologically realistic mathematical models of microcircuit and to study the molecular and cellular mechanisms underlying cerebellar function [12]. Reconstructions also assist in elaborating animal models for the study of several neurological disorders [9]. Modelling somatosensory pathway, which activates Crus IIa of cerebellum, is crucial for understanding granule neuron computation in incoming MF spike trains.

LFP are population signals composed of several components, including action potentials, synaptic transmembrane currents, sodium currents, calcium spikes and ephaptic leaks [13]. Recording LFP is a useful technique to study network function because of the consequential biophysical understanding of the generation of this ensemble response. LFPs are a class of important signals also known to connect hand movement patterns to underlying neuronal mechanisms, assisting in the development of neuroprosthetic devices [14].

A number of neurologic and psychiatric conditions such as autism, attention disorder, mood disorders, schizophrenia and ataxia have been associated with cerebellar dysfunction [15]. Many of these conditions are caused by cerebellar lesions, direct injury to the cerebellum, genetic mutation and the presence of toxins in the cerebellum [16]. Cerebellar ataxia is attributed to a group of disease conditions that affect spatial accuracy and temporal coordination of movement [16]. Channel dysfunction has been known to cause a number of neurological diseases [17, 18]. An earlier study [9] showed that mutations in Fibroblast Growth Factor Homologous Factors (FHFs) 1 and 4 present in cerebellum GrCs cause motor learning defects like ataxia in mice.

In this study, granular layer circuit activity during somatosensory function was studied by reconstructing the granular layer evoked post-synaptic LFP. LFP during in vitro, in vivo and induced plasticity conditions was reconstructed to know how granule neuron cluster activation implicates variations in cerebellar input layer response.

Methods

Single Neuron and Synapse Models

A detailed model of cerebellar granule neuron [10] including a soma, four dendrites and an axon implemented using compartmental cable theory was employed. Ion channel localization is described elsewhere [10, 19]. Excitatory and inhibitory synapses with dynamics of AMPA and NMDA receptors and GABA receptors were used to represent synaptic dynamics [20].

Cerebellar Golgi neurons are the inhibitory, spontaneous spiking, interneurons regulating timing in the input layer [3, 21]. The biophysical model consisting of cerebellar Golgi neuron consisted of a soma, 3 dendrites and an axon with ion channels mechanisms was used [11]. Synaptic information processing was modelled through AMPA, NMDA and GABA receptor mechanisms implemented as described in [12].

Cerebellar Granular Layer Network

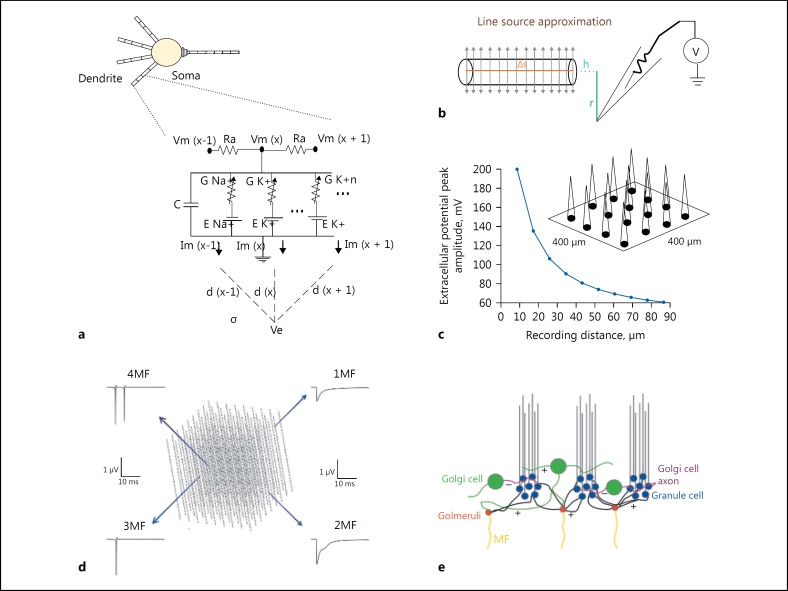
A computational model of Wistar rat Crus-IIa granular layer consisted of granule and Golgi neurons models, synapse models, spatial arrangement and their connections. In our study, a biophysical rat cerebellar granular layer circuit model was adapted from the previously published model [12, 22]. The granule neuron model was employed (Fig. 1a) to empirically study spatio-temporal properties of granular layer. In the circuit model, an MF excited a glomerulus, constituting dendritic terminals from 53 unique GrCs and 3 or 4 Golgi cells (GoC). As in experiments, in the model, a GrC was activated by 4–8 different MFs (excitatory) and a single GoC axon connected to 600 GrCs (inhibitory). This convergence and divergence ratio of granular layer circuitry was reproduced as in [12]. A 100 μm cubic model consisted of 4,096 GrCs (blue circles), 27 GoCs (green circles), 315 glomeruli (red circles) and more than 40,000 synapses (Fig. 1d, e).

Fig. 1.

Modeling local field potential from single neuronal compartment and neuronal ensembles. a Electrical equivalent circuit of GrC model with calculation of extracellular potential from dendrite compartments. b Schematic of Line Source Approximation (LSA). c Schematic of Multi Electrode LFP electrode recording from granular layer ensemble. d Cerebellar granular layer network, 100 μm cubic model. e Schematic of granular layer network connectivity, colors indicated as, GrCs (in blue), GoCs (in green), Glomeruli (in red) and MF indicated as yellow lines.

Modelling Local Field Potential

To model glomerular activation of granule cell clusters, the ratio of GoC to GrC was maintained at 1: 500 [23, 24] and 3: 50 for the surface area [25, 26]. Estimates suggest that granule neuron yield a 30 times larger electrogenic surface compared to Golgi neurons in the circuit and most of the Golgi neurons are silent [27]. Field potential generated is known to be significantly contributed by transmembrane currents from granule neurons [28, 29]. Granule neuron transmembrane currents were linearly summed contribution of ionic and capacitive currents (Fig. 1a for compartment circuit representation). The transmembrane current changes were retained as constant throughout the compartment due to small size and ohmic nature of electrical potential assumed throughout the compartment [30, 31].

LFP was reconstructed from a 100 μm³ circuit model. Forward modelling technique [32, 33] was used to calculate extracellular potential from individual granule neuron compartments. The computational schema mainly involved 2 steps: (1) Estimation of transmembrane ionic current from granule neuron model. (2) Calculation of field potential from estimated transmembrane currents using the Line Source Approximation technique [32, 34].

Cerebellar granular layer is densely packed with granule neurons [35] and high extracellular resistance was assumed for the neuropil, modelled as isotropic volume conductor, since there was no capacitive effect in the medium in the range 0–3,000 Hz [36]. From a neurite modelled as a point source, the Laplace equation was used to calculate electric potential in the extracellular medium [37].

Modelling Rat Somatosensory Pathway and Its Response in Granular Layer by Reconstructing in vitro and in vivo Behaviour

In the circuit model, neighboring GrC clusters were stimulated to mathematically reconstruct the cerebellum LFP's Trigeminal (T) and Cortical (C) waves [7, 28, 38]. Individual clusters of granule neurons were known to be excited by glomeruli within 30 μm of diameter as observed in granular layer slices [4, 39] and cluster activation matched with granular layer functional units reported by [40]. MF – GrC input jitter or synaptic delay [41] was set to 3+/–0.5 ms, based on contribution from different cuneate cells in response to tactile receptor stimulation [42] and MF branching and spatial distribution of glomeruli rosette causing a time delay in activating glomeruli. In simulations, the MF conduction velocity was set to 200 μm/ms, estimated from MEA recordings from 12 slices and 236 electrodes, reported in supplementary material [6]. Jitter values were also matched with previous simulation study on single-granule neuron [28]. Single neuron-based LFP reconstruction was a reconstruction of activity in brain slices (in vitro) and in anaesthetized animals (in vivo). Typical activity in acute brain slices have been through single spikes or EPSPs, although some short duration bursts can be artificially observed through electrical stimulation. Spike burst inputs as observed in anesthetized animals were also configured as in vivo stimulus patterns. Synaptic input to generate T and C waves was given through the MFs. The input synaptic stimuli pattern for T-wave set at 320th ms, a burst (4 spikes) and the input stimuli pattern for C-wave set at 340th ms with another burst (4 spikes; Fig. 3c). Time between MF bursts was set to 20 ms to construct LFP C wave as a continuation of the T wave. Background noise in the network was generated by a random spike pattern in MFs at 2–8 Hz [43, 44]. In simulations, stimuli were applied after 300 ms to get the numerical stability, given multiple circuit elements and stable baseline LFP reflective of any background noise incorporated. Optimal values for input spike pattern were selected for corresponding LFP output responses that provided a good fit to LFP traces recorded in the experiments [6, 7]. Simulations were performed to reconstruct the LFP waves by exploring the parameter space by varying the number of spikes and frequency of inputs.

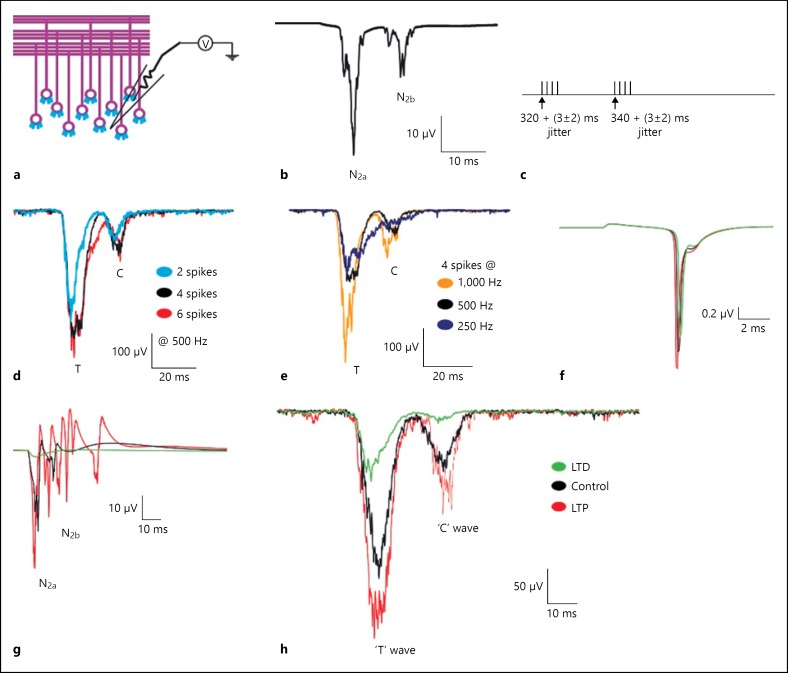
Fig. 3.

Computed evoked in vitro and in vivo waves of cerebellum granular layer in control and plasticity conditions. a Schematic of cerebellar granular layer. b Simulated in vitro LFP generated using detailed network model, negative waves corresponding to the first spike (N_2a) and doublet (N_2b). c Reconstructed sensory stimuli corresponds to T and C wave input. d Simulated in vivo LFP wave showing T and C waves for various number of input spikes (2-blue, 4-black and 6-red) at 500 Hz. e Simulated T and C waves for various input stimuli frequency (1,000 Hz-orange, 500 Hz-grey and 250 Hz-blue). f, g Comparison of single-cell and population responses under in vitro and plasticity conditions respectively. LTP (red trace), LTD (green trace) and control (black trace). h TC waves reconstructed from detailed network model.

Validating Circuit Model by Simulating Plasticity Condition

MF – GrC plasticity showed long-term changes and bidirectionality involving induced LTP and LTD [45]. Low-frequency short burst and poor membrane depolarization favored LTD and strong depolarization, and high-frequency long burst favored LTP. Both LTD and LTP phenomena depended on ­changes in synaptic release probability. Granular layer LTP is also accompanied by changes in intrinsic electroresponsiveness of granule neuron, which enhanced the firing rate and reduction of spike threshold [20, 46]. To predict how induced plasticity modified population responses, MF – GrC plasticity was modelled by modifying intrinsic excitability of sodium channel and release probability of AMPA and NMDA synapses [20].

Modelling Spatial Reach of Granular Layer LFP

Unlike other parts of the brain, cerebellar granular layer is densely packed with tiny granule neurons [35]. This close compactness of neurons in the extracellular space could influence the spatial reach of LFP wave forms of cerebellum. To explore the attenuation in cerebellar granular layer, the spatial reach of T and C waves was simulated on an 800 × 800 × 300 μm network. Glomerulis within 350 μm diameter were stimulated with in vivo T- and C-wave input (method 2.5). The LFP at different spatial scales was calculated (method 2.3) within the range from 20 to 350 μm. The half width of T and C waves was calculated as a measure of displacement in time. The amplitude of the T and C wave was calculated as the difference in magnitude of the wave from its baseline LFP.

Simulating MEA LFP

Computational reconstruction of multiple LFP electrodes was performed to predict neuronal activity at the network level [4, 6, 47, 48]. Multi-electrode LFP was modelled by spatially arranging virtual recording points “electrodes” in a square matrix (Fig. 1c). Each electrode in the array was distanced 100 μm from neighboring electrodes; neuronal ensemble activity from 800 × 800 μm area was estimated from these electrodes. LFP at each recording point was calculated using the formula given below:

$$V_e(x,y,z)=\frac{1}{4\pi \sigma s}log\frac{\sqrt{h^2+r^2}-h}{\sqrt{l^2+r^2}-l}$$

x, y, z are the coordinates in the three-dimensional space corresponding to where the electrode is set in network model to record the neuronal activity. Changing x and y coordinates gave various electrode positions in the x-y plane with a fixed z- axis. “Δs” represented the length of the single line source; l = Δs + ℎ represented the distance from the start of the line, “r” represented the radial distance from the line, “h” represented the longitudinal distance from the end of the line and “σ” represented the conductivity of the extracellular medium (Fig. 2b).

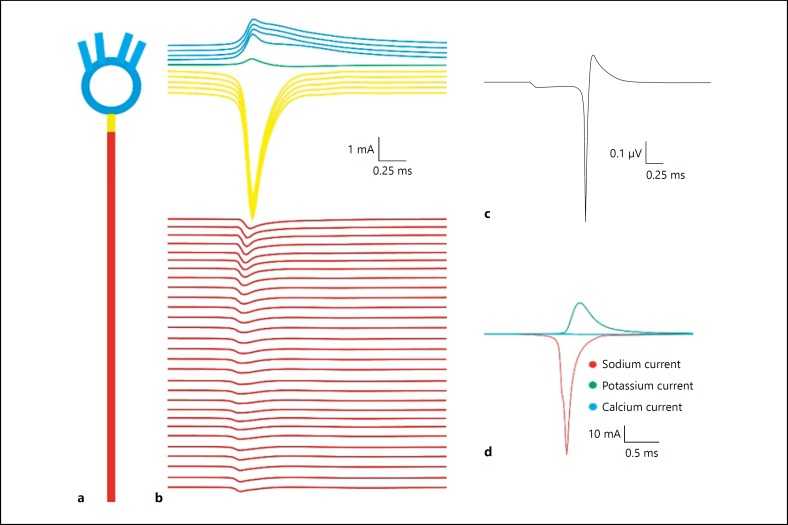
Fig. 2.

Sink-source dynamics of single-granule neuron. a Cartoon of single-granule neuron. b Individual compartmental ionic currents generated using a granule-neuron model. Compartment-wise summation of extracellular components generating single-neuron LFP. c Estimated single-neuron LFP. d Individual ionic current contribution to extracellular current.

Modelling Cerebellar Dysfunction

Experimental data have reported that Fhf^1–/– Fhf^4–/– mutant mice showed severe ataxia and other neuronal deficit [9]. In the network model, the granule neuron voltage-gated sodium channel model was adapted from [10], based on [49, 50, 51] to reproduce the Fhf^1–/–Fhf^4–/– mutant mice GrC behaviour. The C_on and O_on values were increased 10 times and C_off value decreased to 40% of its default value [9]. The “diseased” network model was provided with in vitro and in vivo input patterns described in section 2.4.

Implementation and LFP Simulation

LFP modelling schema was implemented using MPI on the NEURON simulation environment [52, 53]. An embarrassingly parallel method was computationally relevant to simulate the model due to a majority of granule neurons compared to morphologically complex Purkinje (PK) cells [54]. Field potential generated by granule neurons was calculated in each computational node. The total LFP was calculated as linear sum of individual node LFPs. On-the-fly implementation of LFP modelling schema effectively reduced the storage space [37]. All LFP traces were averaged traces from 15 simulation runs.

Results

Transmembrane Ionic Currents Majorly Contributed to the Extracellular Field Potential Generated by Granule Neurons

A detailed granule neuron model was used to study the compartmental contribution of transmembrane ionic currents to generate extracellular potential. Axonal initial segment showed significantly higher contribution to the single-neuron LFP (yellow trace in Fig. 2b) due to its high density of fast sodium and delayed rectifier potassium channels. Time delays seen due to the opening of sodium and potassium channels were evident in single-neuron reconstructions (Fig. 2b).

Cerebellar granule neuron axonal Na⁺ channels generated electric dipoles (source-sink) during spiking [10]. The extracellular potential generated from a neuronal compartment was calculated as the sum of total transmembrane ionic currents from that compartment (Fig. 2c, d, 3a). The sink-source effect in somato-dendritic and axonal current was observed in the generated extracellular potential and color-map plot (Fig. 2b). Extracellular currents showed a delay in return to the resting level after the conduction of an action potential (Fig. 2b). A time delay in K+ ionic currents was also observed in the extracellular potential.

Validating Granular Layer Model by Reconstructing Cerebellar Granular Layer Evoked Post-Synaptic LFPs in Control and Plasticity Conditions

A few glomeruli at the center of the network were stimulated with in vitro like input to generate the LFP waves (Fig. 3b). The LFP waves, N_2a and N_2b, correspond to the first and second (doublet) spike of the granule neuron respectively. The network simulation reproduced the in vitro LFP observed in experimental condition [6]. Input from inhibitory GABAergic synapses resulted in suppression of the doublet (N_2b wave) as observed in a single neuron based LFP reconstruction (Fig. 3f, g).

Tactile stimulation [7] generates the in vivo evoked LFP in rat, which was reconstructed in the simulation. Two subsequent bursts along MF terminals [43, 55, 56] generated the waves. The T wave in our models was generated by a short burst (4 spikes at 320th ms) along the MFs and the C wave by another short burst (4 spikes at 340th ms) that came after 20 ms of the T-wave (Fig. 3d) [7]. The assumption was that 2 separate clusters of GrCs generated the T and C waves [7].

As a parameter exploration with the model, the input stimuli pattern for sensory response was examined generating a single in vivo LFP wave at a time (Fig. 4). TC wave was simulated by activating a number of glomeruli (referred as spot) with a time jitter of about 3ms [6]. LFP simulation with TC wave input 4 spikes at 320 and 340 ms, frequency = 250 Hz and 1,000 Hz showed distorted TC waves with time delays, half width and amplitude not comparable to experimental data (Fig. 3e) [7]. When inter-spike interval was increased (at 250 Hz), the width of T wave increased and the amplitude decreased; the C wave was not reliably reproduced (Fig. 3e blue trace). Simulation with input frequency 1,000 Hz showed more prolonged waves (Fig. 3e orange trace). Simulation with 4 spikes at 320 and 340 ms at frequency 500 Hz showed the TC wave with a close match to the profile of the LFP waves reported in the experiments [7]. Simulation with 2 spikes at 500 Hz showed a smaller T wave and a C wave that were more positive and had less lag. Six spikes at 500 Hz produced a wider T wave and the wave overlapped with the C wave (Fig. 3d). The optimal parameters were 4 spikes of 500 Hz frequency at 320 and 340th ms to reconstruct the TC waves from network model.

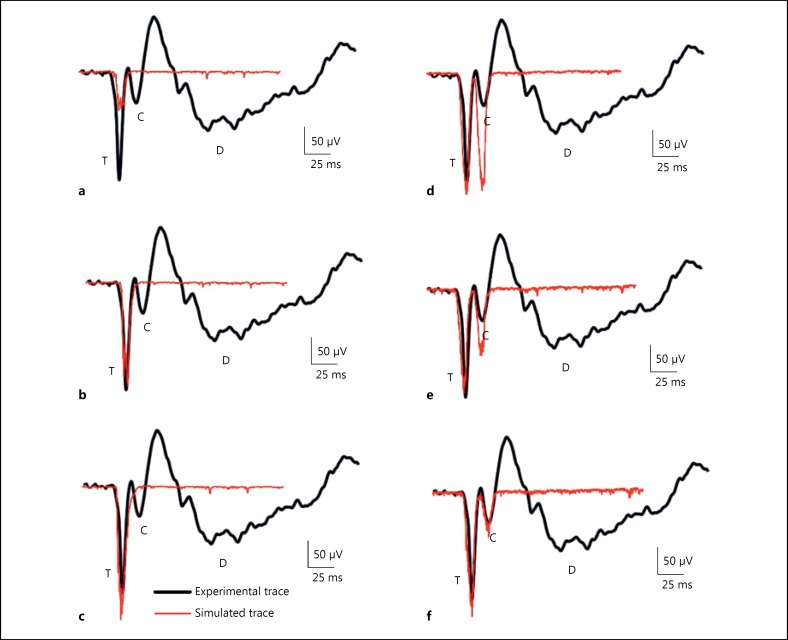
Fig. 4.

Glomerular activation shapes the trigeminal (T) and cortical (C) waves. a–c Represent the simulated traces of the T wave and (d–f) represents the simulated traces of the C wave; (a) 10 glomeruli, (b) 20 glomeruli, (c) 30 glomeruli, (d) 25 glomeruli, (e) 12 glomeruli, (f) 6 glomeruli. Red traces were the simulated LFP from network model. Black traces were the in vivo LFP wave from experiments of [7].

Spatiotemporal properties of granular layer were studied by simulating the plasticity in network model. The changes in molecular mechanisms such as intrinsic excitability and release probability affected the LFP waves in terms of amplitude and delay. With LTP, an increase in peak amplitude and a decrease in delay were observed when compared to the control (Fig. 3d, e, f). On the contrary, a decrease in amplitude and increase in delay were observed with LTD (Fig. 3d, e, f). Furthermore, coupling neuroreceptor parameters in models such as AMPA and NMDA with a detailed reconstruction of GrC intrinsic excitability [10, 19], allowed modeling evoked LFP responses and its variations.

The model allowed dissecting the effect of presynaptic changes in a single-granule neuron firing and electro responsiveness on the evoked LFP response. As observed with single-granule neurons, the increase in release probability or a change in g_max of the synaptic conductance could affect the evoked LFP response in population.

Glomerular Activation Shapes the Trigeminal (T) and Cortical (C) Waves

In the circuit model, 2 independent granule neuron clusters were activated to generate T and C waves. Around 25 glomeruli were excited with Mf patterns to reconstruct the T wave and 6 glomeruli to generate the C wave to match the behaviour of these waves with the reported experimental traces [7]. During simulations, 50% of cells were found to be spiking and the remaining 50% were non-spiking. The glomerular activation for each of these waves also corresponded with the synaptic activation parameters suggested by ReCONV [28]. Glomeruli activation pattern and the corresponding TC wave are shown in Figure 4.

In the T-wave-related GrC cluster, an increasing number of glomeruli (10, 20, and 30) was stimulated to study the role of glomerular activation in shaping the LFP wave (Fig. 4a, b, c). T-wave amplitude and width were doubled in response to the activation of 12 glomeruli when compared to 6. Activating 25 glomeruli with MF inputs was optimal to generate the T-wave (Fig. 4c) as done in experiments.

The C wave was obtained by activating 25, 12 and 6 glomeruli (Fig. 4d, e, f). When the number of activated glomeruli was decreased from 25 to 12, the amplitude and width of the C wave also reduced by half. A cluster with around 6 glomerular activations was found to be optimal in generating the C-wave behaviour (in terms of amplitude and width) as in experiments [7] (also see Fig. 4f).

Predicting the Spatial Reach of Granular Layer LFP

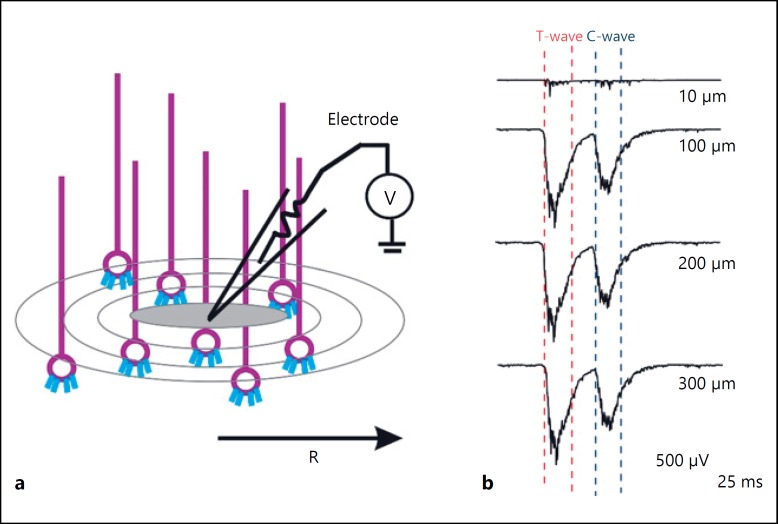
To study the spatial properties of the cerebellar granular layer LFP, the spatial reach of TC waves was simulated on an 800 × 800 μm³ network model. Glomeruli within the spatial radius (from 20 to 350 μm) was stimulated to generate the LFP waves (Fig. 5a, b). A gradual increase in the amplitude and width of TC wave was observed when the spatial reach was increased (Fig. 5b). These 2 waves (TC) approached each other in response to an increased number of glomerular activation (Fig. 5b). An associated increase in half-wave width and amplitude of TC wave was also observed with increase in spatial range (Fig. 5b). Spatial reach simulation indicated that there were no significant changes in the amplitude or width of TC waves beyond 100 μm of spatial radius (Fig. 5b).

Fig. 5.

Spatial reach of TC wave. a Schematic of LFP electrode recording at various spatial radius. b Simulated traces of in vivo LFP at different spatial reach. c, d Half-width and amplitude of LFP waves correspond to different spatial radius. The data points correspond to the T wave (red) and C wave (blue).

Multiple Electrode LFP Simulations Revealed Spatial Attenuation In Granular Layer

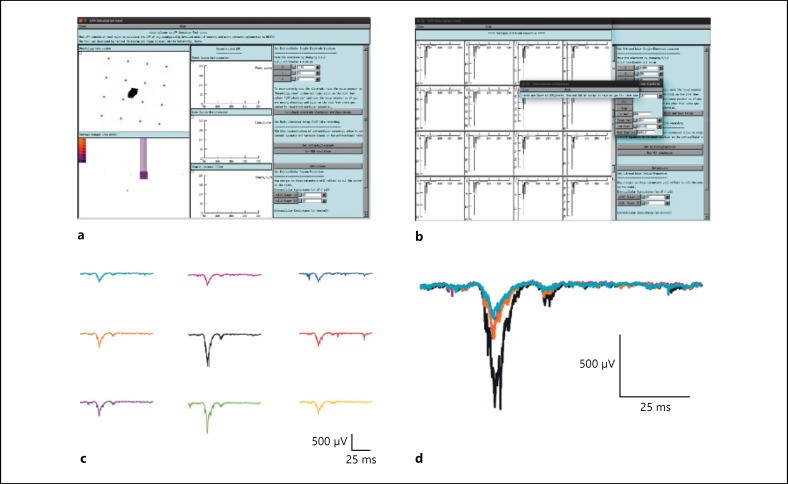
To assess the attenuation property of the cerebellar granular layer, multiple electrode LFP was simulated on the 800 × 800 × 300 μm³ network model. A virtual Multi-Electrode Array LFP of cerebellar granular layer circuit recording during somatosensory function [6, 7] was reproduced in the simulation. Few glomeruli at the center were stimulated to generate N_2a, N_2b and TC waves.

Multiple electrode LFP simulations showed that the attenuation of LFP traces were more at the periphery compared to the center. This attenuation affected only the amplitude and width of the TC wave and not the time lag (Fig. 6b, f). The comparisons of LFPs at different electrodes were plotted in Figure 6b. The varying behaviour obtained in these traces represents underlying neuronal activity in the area closer to the electrodes (Fig. 6b, c). LFP traces from center of the electrode showed larger LFP waves compare to the LFP from the surrounding electrodes. Spatial attenuation of LFP waves during network activity was reconstructed. The lateral inhibition of GoCs was more evident in reconstructed LFP wave forms (Fig. 6c).

Fig. 6.

Simulating multiple electrode LFP. a Screenshot of LFPsim simulating granular layer multiple electrode LFP. b Simulated granular layer evoked LFP under in vitro condition. c The reconstructed in vivo multiple electrode LFP. d Electrode traces from (3 × 3) electrode array at the center was shown in different colors.

Granule Neuron Dysfunction in Single Neuron Affects Population Response

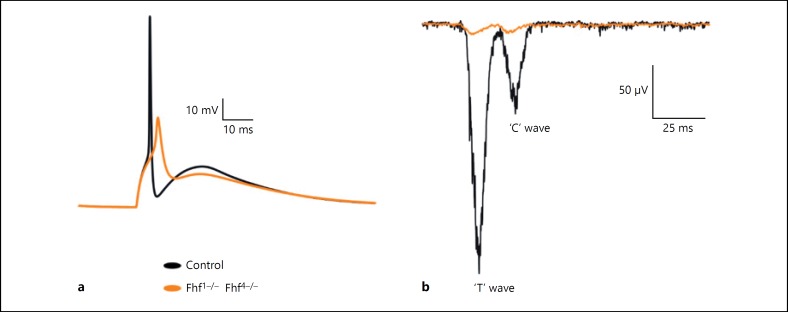
Ataxia-like condition was simulated in the reconstructed network to understand the effect of dysfunction in circuit computation. In single-neuron simulation, the sodium channel with FHF1^–/– and FHF4^–/– mutation modelled by changing the gating dynamics resulted in the failure of the granule neuron model to generate action potential during subsequent firing [9].

The first spike latency was significantly delayed in ataxia-like condition (orange) compared to control (black; Fig. 7a). Extracellular potential generated from the granule neuron model with dysfunction failed to generate extracellular current in response to the MF input. Dysfunction in the individual neurons of the network significantly affects the population response (Fig. 7b). Simulation of network model with dysfunction showed significantly reduced LFP waves (Fig. 7b) compared to those of the control.

Fig. 7.

Simulating ataxia-like condition in the granular layer model. a Single-granule neuron response to MF input. b Simulated in vivo LFP in ataxia-like condition when compared to control. Granule neuron response in control (black) and ataxia-like condition (orange).

Discussion

In the present study, the molecular and cellular bases for generation of cerebellar LFP was studied by modelling the LFP using biophysically realistic model of granular layer. A detailed granule neuron model was implemented to study spatio-temporal properties of the network along with cerebellar function. Granular layer LFP was biophysically modelled using the forward modelling schema [32]. Axonal and dendritic compartment was approximated to a line source and somatic compartment to a point source. Because of close compactness of granular layer, the conductivity of the medium assumed as constant throughout the extracellular media.

Cable compartmental contribution of ionic currents to electric potential generated by a single-granule neuron was studied using the multi-compartmental model. During the action potential, the hillock compartments acted as sink and somato-dendritic compartments acted as source relating the sink-source effect to relevantly affect LFP. The fast peak shoot noticed in the extracellular action potential (Fig. 2b) was due to the highly clustered sodium channel in the axon-hillock region and the slow steep down was due to the slow inactivation of the highly clustered K⁺ channels at the dendrites (Fig. 2b) [9, 19, 20]. A time delay in individual ionic currents was also observed because of the opening and closing of sodium and potassium channels during depolarization and hyperpolarization. These observations strongly suggest that individual ionic currents, especially the sodium and potassium currents, are the key players in generating the granular layer field potential. The simulations suggest that the sink-source dynamics of granule neuron may also have a direct correlation to the back-propagation of action potential from axon to dendrite [10, 57].

A single MF excitation generated 1–2 spikes in granule neurons with feed-forward inhibition from GoCs occurring after a time window of approximately 4 ms [58]. Studies have reported that the inhibitory loops present in the granular layer play a significant role in regulating granular layer oscillations [12, 59, 60]. In the model, the GoC-GrC inhibition started after 4 ms time window. LFP simulations revealed that time window reflect through properties of evoked LFP waves (see [28] for single-neuron-based study) in setting the temporal geometry of post-synaptic responses in granular layer. GoC-GrC inhibitory connection and time window has a major role in granular layer computation.

Evoked LFP response during in vitro and in vivo studies was effectively reproduced using the network model. The relationship of the underlying spiking behaviour of granule neuron to the in vitro population response N_2a and N_2b waves was studied using single-neuron simulation [6]. Simulations indicated that the activation of approximately 20 glomeruli can generate the N_2a N_2b LFP waves in the granular layer.

Network simulations accurately reproduced the LFP profile of TC waves that was observed earlier [7]. The major prediction observed during the reconstruction of in vivo evoked response was that separate clusters of GrCs could independently generate LFP waves, which were reflected in both single neuron and network models. In vitro, in vivo LFP generated using a multi-compartmental neuron approach reconstructed the behaviour of N_2a, N_2b and TC waves as observed in experimental conditions.

Cerebellum has an important role in procedural learning; at present, the cerebellum has 16 forms of plasticity, distributed across the different modules in cerebellar cortex and cerebellar nuclei. Among those, granular layer LTP and LTD at MF – GrC synapse is important for the spatio temporal plasticity and in input-related learning [61]. The modulatory effect of plasticity is more evident in evoked LFP through intracellular mechanisms. Reconstructed evoked LFP observed after the induction of LTP showed larger amplitude and width of TC waves, while LTD showed relatively lesser amplitude and width. This observation suggests that LFP reflects the overall properties and mechanisms of spiking/non-spiking in both single neuron and neuronal populations. Simulations also suggest that specific receptive fields may activate specific clusters of granule neurons (as seen in T and C waves) that are regulated by GoC inhibition.

Individual glomerular units excited 50 granule neurons in the network model. A gradual increase in glomeruli stimulation showed an increase in amplitude and width of both N_2a N_2b (in vitro) as well as TC (in vivo) waveforms. Around 20 glomeruli were activated to generate N_2a N_2b waves, 25 glomeruli for T wave and 6 glomeruli for C wave. These measurements suggest that the neuronal activity from approximately 4,000 granule neurons (packed into 100 μm³ slice) could contribute to the generation of in vivo LFP. However, a subset of this neuronal population was required for generating in vitro LFP.

In the network model, MFs stimulated with background activity reconstructed the TC waves for a lesser number of input spikes compared to the single neuron-based reconstruction reported previously [28]. This observation suggests the role of background activity in the network during evoked stimuli that generated the LFP waves. Simulations also suggest that the optimal parameters relate to the amplitude and delay properties of response to burst patterns and stimulus time [7].

The in vivo LFP simulations revealed the importance of synaptic weight distribution [28] and glomerular activation in determining the profile of granular layer LFP waves. Simulations suggested that the behaviour of granular layer LFP mainly depended on the activation of several glomeruli in the T and C clusters. These results also indicate that the reduced amplitude and width of C wave observed in the experiments may be due to a lesser number of glomeruli getting activated during the activation of the C cluster.

In this study, we considered only the evoked post-synaptic LFP contribution from the granular layer. The MF electrical stimulation evokes N₁-N₂-P₂ wave complexes in the granular layer. The N₁ and N₂ waves correspond to the granular layer presynaptic and postsynaptic activity respectively. The P₂ (positive bound) corresponded to the currents generated from the molecular layer [62, 63] and were not modelled. Similarly, LFP recorded during somatosensory stimulation was characterized by T-C-D waves generated by granule neuron activity in response to trigeminal, cortical and pontine nuclei afferents [7]. The positive-bound after C wave, not modelled here, may be contributed by the activity from the molecular layer.

Single extracellular electrode recorded field potential difference generated by ionic currents during depolarization of neurons [13] and the network behaviour was studied using Multiple Electrode Array recordings. Recently, more advanced high density arrays were used to study the network activity [48, 64]. Network variabilities during circuit functions were studied using multiple-electrode array recordings [13]. The attenuation property of cerebellar granular LFP was studied by reconstructing multiple-electrode LFP during the network function. The LFP wave generated from the slice model (800 × 800 × 300 μm³) of cerebellar granular layer reproduced the MEA wave activity observed in experimental studies [6, 7].

As suggested by experiments, the simulated LFP waves reconstructed from peripheral electrodes showed attenuation compared to traces from electrodes at the center of the network [4]. Simulations suggest that the attenuation was mainly contributed by the impendence nature of granular layer extracellular medium because of the presence of tightly packed granule neurons as well as lateral inhibition from Golgi neurons around the synaptic field.

The spatial reach of granular layer LFP was simulated at various electrode distance measurements (spatial reach varied from 20 to 350 μm radius). The optimal spatial reach (spatial radius) of granular layer LFP was estimated using spatial reach simulations. The amplitude and width of the LFP wave was observed to be saturated at a spatial radius greater than 100 μm. The results suggest that the neuronal activity beyond 100–120 μm spatial radius may not contribute to the generation of granular layer LFP. The observed spatial radius value was found to be lesser in the cortex when compared to the previously reported value [65]. This reduction in magnitude could be due to a larger number of current sources, which were densely packed in the granular layer as well as the lateral inhibition from GoCs around the synaptic field.

Simulating ion channels mutations in individual neurons affected population responses [17, 18]. Sodium channel mutation in granule neuron has been known to cause motor learning disorders in mice [9]. Ataxia-like dysfunction has been shown to affect granule neuron repeated firing by inactivating sodium channels. Extracellular potential generated from a granule neuron with dysfunction showed failed and delayed response. LFP reconstructed from the circuit model with dysfunction showed distorted TC waves, attributing ionic currents to the generation of LFP [29, 37] and suggest that dysfunction at individual neurons in the network reflected in the population response. The study also revealed the effect of dysfunction at single neuron in population code attributing observations on circuit behaviour. Theoretical modelling of such cerebellar microcircuit can help to understand the neuronal basis for cerebellum-related dysfunctions. The progress in computational reconstruction of such detailed models will also help in developing animal models of such disorders.

Conclusion

The study focused on modelling evoked population responses of the granular layer for somatosensory stimuli. The local field potential generated by a granular layer depended on surface area of source-sink dipoles in the granular layer. Simulations reconstructed the granular layer in vitro and in vivo LFP using the biophysically detailed models of neurons. The LFP modelling may provide insight into the generation of granular layer behaviour and will aid in constraining detailed large-scale biophysical network models. The main findings and implications of this work are described below:

The sink-source effect of granule neuron is mediated by the Na⁺ and K⁺ ion channels clustered at the soma, hillock and axon regions. Simulation suggests that the flow of Na⁺ and K⁺ currents mediated the generation of evoked granular layer extracellular field potentials recorded in the experiments [6, 7].

The vertical organization of GrC-PK layer tactile projections and patch-like activation of PK cells [66] suggest that independent granule neuron cluster activation generated the trigeminal and cortical waves in the simulation as observed in the in vivo experiments [7]. Glomerular activation and estimated LFP spatial-radius propose that GrC-PK layer tactile projections may have a spread of 30–100 μm. The network model can be further used to study aspects of cerebellar functions including beam hypothesis [3].

Simulations with ataxia model suggest that the dysfunction at a single neuron can lead to population code malformations in circuit computations. Further progress in the computational reconstruction of such disease models will also assist in developing animal models of similar disorders.

Disclosure Statement

The manuscript complies with ICMJE.

Funding Source

SR/CSRI/60/2013, Indo-Italy POC 2012–14 from DST, BT/PR/5142/MED/30/764/2012, DBT/CTEP/02/201500213 from DBT, Sir Visvesvaraya Faculty Fellowship from MeitY, Govt. of India and partially by Embracing The World. H.P. was supported by CSIR grant (9/942(0012)2K15-EMR-I).

Author Contribution

H.P. implemented the model and performed all the simulations in this manuscript. H.P., S.D., B.N., G.N., and E.D. contributed in the interpretation of simulations. H.P., S.D., B.N., G.N., and E.D. contributed to conception and design of the work and in developing the manuscript.