Abstract
Copper–oxide-based high-temperature superconductors have complex phase diagrams with multiple ordered phases. It even appears that the highest superconducting transition temperatures for certain cuprates are found in samples that display simultaneous onset of magnetism and superconductivity. We show here how the thermodynamics of fluid mixtures—a touchstone for chemistry as well as hard and soft condensed matter physics—accounts for this startling observation, as well as many other properties of the cuprates in the vicinity of the instability toward “striped” magnetism.
The phase diagrams of conventional superconductors are usually simple, with no ordered phases competing with the superconducting state. By contrast, high-temperature superconductors have a number of competing phases that appear as the temperature is lowered. One of the most astonishing manifestations of this competition occurs in the LaCuO family of materials, where coexisting magnetism and high-temperature superconductivity (1–15) have been reported. In La1.6−xNd0.4SrxCuO4, long-period magnetic (“stripe”) order (as detected by neutron diffraction) sets in at a higher temperature than the superconducting Tc [and indeed, charge “stripe” order appears at a still higher temperature (1, 4)]. In La2CuO4.12 and La1.88Sr0.12CuO4, superconductivity and long-period magnetism appear to have the same onset temperature in the same bulk crystal! However, although muon spin relaxation data tell a grossly similar story (5–8), in La1.6−xNd0.4SrxCuO4, the corresponding data (12) for La2CuO4.12 show that the magnetism is peculiar in that it resides in only a fraction of the sample, and its temperature evolution is due to the growth of the magnetic fraction rather than an increase in the order within the magnetic fraction. We show how these observations can be understood from the classical thermodynamics of two-phase mixtures, which is applicable because of the well-documented tendency of antiferromagnets to expel holes (16–22). Related thermodynamic signatures of competing orders are observed in other transition metal oxides (see ref. 23).
Phase Diagrams with Competing Orders.
The interplay between “stripe” magnetism and superconductivity can be understood most simply by treating the liquids of mobile charge carriers in high-temperature superconductors as fluids with a variety of ground states. As for other complex fluids, such as liquid crystals, the coupling between the order parameters for the various ground states can lead to phases with mesoscopic density modulations as well as diverse combinations of the order parameters themselves. To make this phenomenon explicit, we follow a standard paradigm of statistical physics and consider (24–29) the simplest Landau free energy, F, for two coupled order parameters, S⃗ and Δ, which represent the long period antiferromagnet and the superconducting order parameters, respectively. Spin rotation invariance and gauge invariance (Δ is a complex number whose phase cannot influence the free energy) imply that F is a function of |S⃗.S⃗| and |Δ|2:
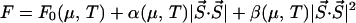 |
1 |
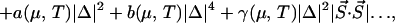 |
where T is the temperature, μ is the chemical potential for doped holes, … represents higher-order terms in powers of the ordering fields, and the various coefficients embody the effects of all of short-distance physics. The phase diagram is then determined (at mean-field level) by minimizing F with respect to S⃗ and Δ. Although such a mean-field description ignores important fluctuations, especially given the fact that high-temperature superconductors are quasi-two-dimensional, it provides a valid zeroth order way to examine the global structure of the phase diagram.
From the macroscopic viewpoint adopted in the present paper, the parameters that enter the Landau free energy in Eq. 1 are purely phenomenological. However, some insight concerning the microscopic physics can be inferred from the behavior of these parameters. In particular, if g > 0, superconductivity and long-period magnetism compete, whereas if g < 0, they enhance each other. Indeed, Ichikawa et al. (4) have concluded that static magnetism and superconductivity compete, and this is certainly intuitively sensible. Recent experiments on the behavior of vortex cores (30) and on superconductivity-induced changes in the magnetic susceptibility (31) of optimally doped La2−xSrxCuO4 confirm that g > 0, in agreement with these arguments. One main purpose of this paper is to show how, even if g > 0, magnetism and superconductivity can set in at the same temperature in a single sample.
An important subtlety arises from the fact that, as in many experiments on classical fluids, it is the total number of constituents of the fluid rather than the chemical potential that is fixed. For the cuprates, the constituents are the charge carriers (doped holes), and their number is fixed by the chemical composition of the compound under study (e.g., the x in La2−xSrxCuO4). Therefore, μ must be determined from the implicit relation
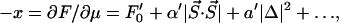 |
2 |
where x is the concentration of doped holes, ′ denotes differentiation with respect to μ, and S⃗ and Δ are the equilibrium values of the ordering fields as a function of T and μ. However, where two-phase coexistence occurs in the phase diagram, there are values of μ at which ∂F/∂μ has a discontinuity. In this case, Eq. 2 has solutions for fixed μ at two different values of x, x1, and x2, but has no solutions for x1 < x < x2. The equilibrium state for fixed x in this range consists of a two-phase mixture, with the volume fractions of the hole-rich (x = x2) and hole-poor (x = x1) phases determined by the classical lever rule, f1 = (x2 − x)/(x2 − x1), and f2 = 1 − f1. Otherwise, in those ranges of x for which the equilibrium state is single phase, it is possible, if desired, to perform a Legendre transform, so that the coefficients in the Landau free energy (α, β, etc.) are expressed as functions of x and T.
Generally, broken symmetry phases occur only at lower temperatures, so it is reasonable to expect α and a to change sign at bare transition temperatures defined according to α(x, T) ≡ α0(x, T)[T − Ts(x)] and a(x, T) ≡ a0(x, T)[T −TΔ(x)], where α0, a0 > 0. (Here, we use the same symbol for the original and Legendre transformed coefficients in the Landau theory.) On both theoretical and empirical grounds, we expect the native magnetic ordering temperature Ts(x) to be a generally decreasing function of x, reflecting the frustration of hole motion in the magnetically ordered state. However, a peak in Ts(x) at a special “commensurate” value of x can occur when the period of the stripe order is a small integer times the underlying crystalline lattice constant; such a commensurability effect gives rise (1, 4) to the anomalous stability of the long period magnetism at x = 1/8, as shown schematically in Fig. 1. TΔ(x) is known empirically to be a nonmonotonic function of x, reaching a peak around an optimal value of x ≈ 0.15 and dropping slowly as x is increased or decreased.
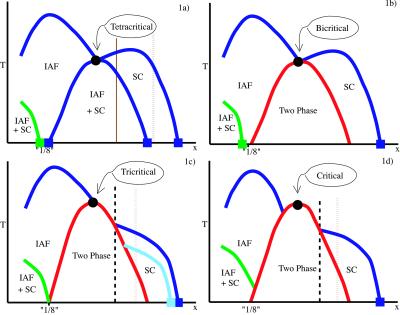
Figure 1.
Schematic phase diagrams derived from the Landau free energy under the various conditions described in the text. IAF and SC indicate incommensurate (striped) antiferromagnetic and superconducting order, respectively. The circles represent classical critical or multicritical points and the squares quantum critical points. The various vertical lines represent trajectories through the phase diagram discussed in the text. The pale blue phase boundary in c represents the effect of an applied magnetic field on the phase diagram.
Several generic phase diagrams are derivable from such a Landau free energy. Most simply, a tetracritical point can occur at (T, μ) = (T*, μ*), which leads to a phase diagram of the type shown in Fig. 1a. Here, in addition to the phases with either magnetic or superconducting order, there is a homogeneous intermediate phase with bulk coexistence of the two orders. We have included in this and all subsequent frames of Fig. 1 a second superconducting phase (which is permitted but not required in the simplest Landau theory) at hole concentrations x < 1/8. This is motivated by the observation that many high-temperature superconductors exhibit multiple humps in the superconducting transition temperature plotted against hole concentration, most notably the Yba2Cu3O7-δ [especially when lightly Zn doped (32)] and La2−xSrxCuO4 related compounds. As mentioned above, we have also indicated a peak in the magnetic ordering temperature at x = 1/8. The corresponding anomalous suppression of the superconducting transition temperature at this point shown in Fig. 1 is a consequence (4) of the peak in the magnetic ordering under the assumption that g > 0, even if TΔ(x) is monotonic in this range of x.
The tetracritical point obtains as long as solutions exist to the simultaneous equations α(μ*, T*) = 0 and a(μ*, T*) = 0, which at the same time satisfy the inequalities β(μ*, T*) > 0, b(μ*, T*) > 0, and β(μ*, T*) b(μ*, T*) > 4 γ(μ*, T*)2. If, on the other hand, the last of these inequalities is violated, i.e., if 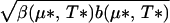 < 2γ(μ*, T*), the tetracritical point is replaced by a bicritical point. Not only does that mean that there is no phase with bulk coexistence of the two orders; it also means that below the bicritical point, there is a region of two-phase coexistence, where a hole-poor magnetically ordered and a hole-rich superconducting state coexist, as shown in Fig. 1b. In reality, this coexistence must not be taken literally. Because of the long-range Coulomb interaction between holes, macroscopic phase separation is thermodynamically forbidden. Where macroscopic phase coexistence would occur in a neutral system, a form of Coulomb frustrated phase separation (21, 22) is expected, leading to a state that is inhomogeneous on an intermediate length scale. This also means that the two coexisting phases are in microscopic proximity to each other, and hence that a modicum of superconducting order will be induced in the magnetic regions, via the proximity effect and conversely (ref. 33; and J. C. Davis, personal communication). Such competition is a recurring theme in this problem; there are empirical and theoretical reasons to believe (34, 35, 36) that the long antiferromagnetic stripe order itself is at least in part a consequence of Coulomb frustrated electronic phase separation on a smaller length scale.
< 2γ(μ*, T*), the tetracritical point is replaced by a bicritical point. Not only does that mean that there is no phase with bulk coexistence of the two orders; it also means that below the bicritical point, there is a region of two-phase coexistence, where a hole-poor magnetically ordered and a hole-rich superconducting state coexist, as shown in Fig. 1b. In reality, this coexistence must not be taken literally. Because of the long-range Coulomb interaction between holes, macroscopic phase separation is thermodynamically forbidden. Where macroscopic phase coexistence would occur in a neutral system, a form of Coulomb frustrated phase separation (21, 22) is expected, leading to a state that is inhomogeneous on an intermediate length scale. This also means that the two coexisting phases are in microscopic proximity to each other, and hence that a modicum of superconducting order will be induced in the magnetic regions, via the proximity effect and conversely (ref. 33; and J. C. Davis, personal communication). Such competition is a recurring theme in this problem; there are empirical and theoretical reasons to believe (34, 35, 36) that the long antiferromagnetic stripe order itself is at least in part a consequence of Coulomb frustrated electronic phase separation on a smaller length scale.
A third possibility shown in Fig. 1c occurs if there is a tricritical point where α(μ*, T*) = β(μ*, T*) = 0, while all of the other coefficients (including certain higher order terms, not discussed explicitly) remain positive. This leads to a phase diagram of the sort shown in Fig. 1c. Here, superconductivity, if it appears at all, manifests itself below a phase boundary that terminates on the edge of the two-phase region in a critical end point.
For completeness, we present a fourth possible phase diagram topology, shown in Fig. 1d, for which a more thorough analysis of the free energy function is necessary. Here, instead of a multicritical point, we consider the occurrence of a simple critical point, below which phase separation occurs into hole-rich and hole-poor phases, neither of which is ordered. In this case, both the antiferromagnetic and the superconducting phase boundaries terminate at critical end points.
Relation to Experiment in La2CuO4+δ.
The thermal evolution of a given material should be associated with a trajectory in one of the generic phase diagrams in Fig. 1. In particular, we propose associating with La2CuO4+δ with the vertical dashed line in Fig. 1 c or d. It is a special trajectory, in the sense that it is tuned to pass close to the critical end point, but this requires fine tuning of only one parameter. Below Tc, the system forms an inhomogeneous mixture of a high-density superconducting and a low-density antiferromagnetic phase. At Tc, the sample is a single-phase superconductor, with a superconducting volume fraction fSC(T) = 1 − fMag(T) that shrinks at the expense of the antiferromagnet as T is reduced through the two-phase region. Because there are no critical effects on the shape of the phase boundary associated with a critical end point, just below Tc, fMag = A(Tc − T) + … … where A is determined by the slope of the phase boundary. Because the magnetic ordering of the hole-poor phase would set in at a temperature well above Tc, the ordered moment M(T) in the antiferromagnetic fraction is immediately large and essentially temperature independent! The growth of the magnetism is associated more with the growth of the hole-poor fraction rather than with the rise of the order parameter within the hole-poor regions.
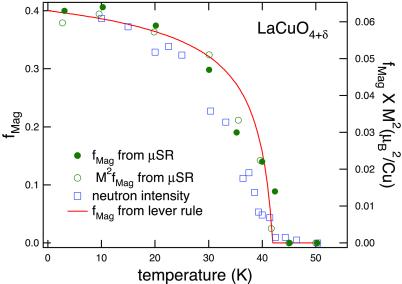
Not only is this scenario consistent with the simultaneous onset of superconductivity and magnetism, but it also reconciles the neutron scattering and μ-SR data, which we reproduce in Fig. 2. Specifically, in a two-phase mixture in which only one phase is magnetic, the intensity I of the Bragg scattering measured by neutrons is related to fMag and M, measured in μ-SR, according to the relation
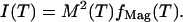 |
3 |
That the absolute neutron intensity (15) at low temperature is 0.022 μ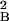 , which is 40% of that anticipated from the muon experiments according to Eq. 3, suggests that either the sample interior penetrated by the neutrons is different from the surface region probed by the muons, or that the integration of the magnetic signal in the neutron experiment could be incomplete. (We look forward to future muon and neutron experiments on the same samples to resolve the origin of the current discrepancies.) In Fig. 2, we have scaled the neutron data so that it matches the inferred intensity from μ-SR data at T = 0; the (scaled) neutron data still falls somewhat short of M2(T)fMag(T) immediately below Tc, probably because the neutron data are peak intensities rather than integrals over the three-dimensional (in reciprocal space) structures containing the net spectral weight responsible for the muon data. More specifically, if there is any broadening in the peaks as Tc is approached, the peak intensity will be reduced relative to the integral. The red line in the figure corresponds to the lever rule prediction for an average hole density (15) x̄ = 0.15 and assuming the simplest possible parabolic form for the bounding curve of the two-phase region Tc(x) = 4T0 (x2 − x)(x − x1)/(x2 − x1)2. To have no free parameters in determining the theoretical curve, we have taken x1 = 1/8, reflecting the special stability of the striped phases at x ≈ 1/8. The remaining parameters can be deduced directly from f0 ≡ fMag (0) = 0.4 and the condition that antiferromagnetism and superconductivity onset at the same temperature, T2(x̄) = Tc = 42K, according to To = Tc/[4f0(1 − f0)] and x2 = x1 + (x̄ − x1)/f0. It turns out that the theoretical curves are very sensitive to the exact value of f0. For instance, the quality of the fit can be improved if we take f0 = 0.35, which is somewhat smaller than the reported value, although possibly within experimental uncertainty.
, which is 40% of that anticipated from the muon experiments according to Eq. 3, suggests that either the sample interior penetrated by the neutrons is different from the surface region probed by the muons, or that the integration of the magnetic signal in the neutron experiment could be incomplete. (We look forward to future muon and neutron experiments on the same samples to resolve the origin of the current discrepancies.) In Fig. 2, we have scaled the neutron data so that it matches the inferred intensity from μ-SR data at T = 0; the (scaled) neutron data still falls somewhat short of M2(T)fMag(T) immediately below Tc, probably because the neutron data are peak intensities rather than integrals over the three-dimensional (in reciprocal space) structures containing the net spectral weight responsible for the muon data. More specifically, if there is any broadening in the peaks as Tc is approached, the peak intensity will be reduced relative to the integral. The red line in the figure corresponds to the lever rule prediction for an average hole density (15) x̄ = 0.15 and assuming the simplest possible parabolic form for the bounding curve of the two-phase region Tc(x) = 4T0 (x2 − x)(x − x1)/(x2 − x1)2. To have no free parameters in determining the theoretical curve, we have taken x1 = 1/8, reflecting the special stability of the striped phases at x ≈ 1/8. The remaining parameters can be deduced directly from f0 ≡ fMag (0) = 0.4 and the condition that antiferromagnetism and superconductivity onset at the same temperature, T2(x̄) = Tc = 42K, according to To = Tc/[4f0(1 − f0)] and x2 = x1 + (x̄ − x1)/f0. It turns out that the theoretical curves are very sensitive to the exact value of f0. For instance, the quality of the fit can be improved if we take f0 = 0.35, which is somewhat smaller than the reported value, although possibly within experimental uncertainty.
Figure 2.
Interplay between magnetic and superconducting order in La2CuO4+δ. The open and closed circles represent, respectively, the antiferromagnetic fraction, fMag(T), and the product M2(T) fMag(T) from the μ-SR data in ref. 7. The open squares represent the neutron intensity I(T) from ref. 9, scaled by a factor of 2.7. The solid line is a theoretical prediction for fMag(T), using the lever rule, for the vertical dashed trajectory in the tricitical phase diagram in Fig. 1c,assuming the two-phase region is bounded by the curve T2 = 4T0(x1 − x)(x − x2)/(x2 − x1)2 with parameters (discussed in the text) T0 = 43.7K, x1 = 0.125, x2 = 0.188, and with a mean hole density X̄ = 0.15, representative (15) of stage IV La2CuO4+δ.
In the discussion above, we have ignored nonelectronic physics. The most obvious possibility here is that motion of excess oxygen results in an inhomogeneous distribution of oxygen, which in turn would lead to inhomogeneous hole-density and electronic properties. The final outcome would be an inhomogeneous distribution of magnetism and superconductivity, even while charge neutrality would obviously be satisfied on a local scale. Nonetheless, our sense is that this explanation of the data is improbable. First, the onsets of superconductivity and magnetism coincide (13, 14) in La2−xSrxCuO4 as well as La2CuO4+δ in the same range of average hole density. Second, the findings of Lee et al. (15) provide an important clue concerning how charge neutrality is preserved at long length scales without substantial oxygen motion; they report magnetic order with a remarkably long correlation length (greater than 125 Å) in the basal plane, but with interplanar correlations extending only over two to three planes. Charge neutrality can therefore be preserved over distances of order 10–15 Å, even while the system breaks up into thin magnetic and superconducting layers—“pancakes” parallel to the basal planes. Finally, NMR studies (T. Imai and Y. S. Lee, personal communication) suggest that the material is electronically single-phase at temperatures above Tc, implying that the observed inhomogeneities are induced by the onset of order.
La2−xSrxCuO4, La1.6−XNd0.4 Sr2CuO4, etc.
The phase diagrams in Fig. 1 provide a framework for understanding many other properties of the lanthanum cuprate family. To begin with, a miscibility gap leading to coexistence of superconducting and nonsuperconducting phases readily accounts for the finding of optimal Meissner fractions for La2−xSrxCuO4 only near special hole densities (37). In addition, as for the superoxygenated La2CuO4+δ discussed above, the ordered magnetic moments deduced from neutron diffraction (13, 14) are less than the frozen local moments deduced from muon spin relaxation (5–7) and much less than that seen for ordinary insulating two-dimensional antiferromagnets, implying also that the magnetic order resides in only a part of the sample. The appropriate phase diagram for La2−xSrxCuO4 might then look like a disorder broadened (glassy) image of Fig. 1b. On the other hand, as Nd is inserted, the magnetism (as detected in neutron diffraction) becomes stronger (1–4) and seems to appear throughout the sample volumes (8), even while superconductivity survives. There is also remarkable evidence for a nonmonotonic temperature dependence of the superfluid density (38), which implies that on cooling, La1.55Nd0.3Sr0.15CuO4 first undergoes a transition to a uniform superconducting state and then to a state with coexistence of magnetism and superconductivity. Thus, the tetracritical diagram, Fig. 1a might be more appropriate for La1.6−xNd0.4Sr2CuO4, with a microscopic coexistence of magnetic and superconducting order; La1.55Nd0.3Sr0.15CuO4 might then be represented by the solid brown trajectory in that figure. Finally, La1−xBaxCuO4 exhibits two separated superconducting “domes,” with an intervening magnetic regime (at x = 1/8) that is magnetic and not superconducting (39–42). The corresponding phase diagram could therefore be that shown in Fig. 1 a or b. Of course, any real material exists not on a one-dimensional axis representing the doping, but rather in a multidimensional space spanned by the parameters required to shift from diagram to diagram in Fig. 1. The outcome is then that, as demonstrated by inelastic neutron scattering from La1.86Sr0.14CuO4 (43), optimally doped La2−xSrxCuO4, described by the dotted trajectory in Fig. 1a, can show behavior associated with the quantum critical point where magnetism disappears in the tetratcritical diagram.
Additional Details.
With the exception of La2CuO4+δ, all of the materials discussed have intrinsic disorder due to the random arrangement of the dopant atoms; any stripe ordering transition is thus expected (44–47) and observed (48) to be intrinsically glassy, with the ordered phase being a “stripe glass.” It should also be clear that the interplay between magnetism and superconductivity, which accounts for so many key observations, omits other features (49–52) expected or observed, of the actual phase diagrams. Within the magnetic regime there can be a variety of phases, which we have not indicated: the long period magnetic order can be commensurate with the underlying lattice or incommensurate, and the stripes can point along the copper oxide bonds (“horizontal”) or (53, 54) at 45° to them (“diagonal”). Finally, we have not shown the transitions involving charge order although certainly, at least for La1.6−xNd0.4Sr2CuO4, there is a separate transition (1, 4) at which unidirectional charge density wave (“charge stripe”) order appears at a temperature above the magnetic and superconducting transitions.
Prospects.
A miscibility gap in the phase diagram not only resolves old puzzles, but also provides a framework for understanding current and future experiments. Particularly important are measurements of magnetic field-dependent effects, as they permit a continuous variation of the parameters in the Landau free energy. Many predictions follow readily from the simple analysis presented here. For example, if La2CuO4+δ, in zero field happens to lie on a trajectory that passes through a critical end point, as we have supposed, then in a magnetic field, which will suppress the superconducting Tc, magnetic Bragg scattering, originating from a small magnetic fraction, will still appear at a temperature roughly equal to the zero field Tc. This is illustrated in Fig. 1c, where the field shrinks the superconducting region of the phase diagram from the solid to the lighter blue line. However, as we pointed out above, the vortex state is complicated—it is clear that physics beyond the simple Landau theory needs to be invoked (55) to understand the dramatic magnetic field-induced increases in the antiferromagnetic Bragg intensities, which are not anticipated from simply applying the lever rule (which would make them field-independent). This physics is clearly beyond the scope of the present work, but may relate to early theory indicating that vortices in superconductors derived from Mott–Hubbard insulators are insulating nano-antiferromagnets, with a different charge density than the surrounding superconductor (56, 57). Magnetoresistance data (58, 59) indicate enhanced insulating tendencies in La2−xSrxCuO4 for x near 1/8, i.e., fields above Hc2 uncover the behavior also seen when superconductivity is suppressed by chemical pressure. Furthermore, neutron diffraction reveals field-induced magnetic Bragg scattering, which sets in near the zero-field critical temperature for superconductivity (60). Even for samples beyond the miscibility gap, because type II superconductors below Hc2 are heterogeneous mixtures of “normal” vortices and superconducting material, the vortices can exhibit—on a finite length scale—the magnetism one might have expected if superconductivity had not intervened (assuming g > 0). Recent inelastic neutron scattering experiments (30) on optimally doped La2−xSrxCuO4 are in agreement with this expectation—the vortices are found to behave as nanomagnets with growing “stripe” order with decreasing temperature.
Acknowledgments
We acknowledge important conversations with S. Brown, S. Chakravarty, L. Gorkov, Z. Fisk, T. Imai, A. Kapitulnik, C. Renner, Y. J. Uemura, and J. Tranquada, and technical assistance from S. Brown. This work was initiated while two of us (S.A.K. and G.A.) were participants in the High Tc Program at Institute for Theoretical Physics–University of California, Santa Barbara. S.A.K. was supported, in part, by National Science Foundation Grant DMR98–08685 at the University of California, Los Angeles.
References
- 1.Tranquada J, Sternlieb B J, Axe J D, Nakamura Y, Uchida S. Nature (London) 1995;375:561–563. [Google Scholar]
- 2.Tranquada J M, Axe J D, Ichikawa N, Moodenbaugh A R, Nakamura Y, Uchida S. Phys Rev Lett. 1997;78:338–341. [Google Scholar]
- 3.Ostenson J E, Budko S, Breitwisch M, Finnemore D K, Ichikawa N, Uchida S. Phys Rev B Condens Matter. 1997;56:2820–2823. [Google Scholar]
- 4.Ichikawa N, Uchida S, Tranquada J M, Niemoller T, Gehring P M, Lee S-H, Schneider J R. Phys Rev Lett. 2000;85:1738–1741. doi: 10.1103/PhysRevLett.85.1738. [DOI] [PubMed] [Google Scholar]
- 5.Niedermayer Ch, Bernhard C, Blasius T, Golnik A, Moodenbaugh A, Budnick J I. Phys Rev Lett. 1998;80:3843–3846. [Google Scholar]
- 6.Panagopoulos, Rainford, B. D., Cooper, J. R., Scott, C. A. & Xiang, B. T. (2001) Preprint (cond-mat/0007158).
- 7.Weidinger A, Niedermayer Ch, Golnik A, Simon R, Recknagel E, Budnick J I, Chamberland B, Baines C. Phys Rev Lett. 1989;62:102–105. doi: 10.1103/PhysRevLett.62.102. [DOI] [PubMed] [Google Scholar]
- 8.Nachumi B, Fudamoto Y, Keren A, Kojima K M, Larkin M, Luke G M, Merrin J, Tchernyshyov O, Uemura Y J, Ichikawa N, et al. Phys Rev B Condens Matter. 1998;58:8760–8772. [Google Scholar]
- 9.Hunt A W, Singer P M, Thurber K R, Imai T. Phys Rev Lett. 1999;82:4300–4303. [Google Scholar]
- 10.Julien M-H, Campana A, Rigamonti A, Carretta P, Borsa F, Kuhns P, Reyes A P, Moulton W G, Horvatic M, Berthier C, et al. Phys Rev B Condens Matter. 2001;63:144508–144518. [Google Scholar]
- 11.Curro N J, Hammel P C, Suh B J, Hucker M, Buchner B, Ammerahl U, Revcolevschi A. Phys Rev Lett. 2000;85:642–645. doi: 10.1103/PhysRevLett.85.642. [DOI] [PubMed] [Google Scholar]
- 12.Savici A T, Fudamoto Y, Gat I M, Larkin M I, Uemura Y J, Luke G M, Kojima K M, Lee Y S, Kastner M A, Birgenau R J. Phys. Rev. 2000. 289–290, 338. [Google Scholar]
- 13.Yamada K, Lee C H, Kurahashi K, Wada J, Wakimoto S, Ueki S, Kimura H, Endoh Y, Hosoya S, Shirane G, et al. Phys Rev B Condens Matter. 1998;57:6165–6172. [Google Scholar]
- 14.Suzuki T, Goto T, Chiba K, Shinoda T, Fukase T, Kimura H, Yamada K, Ohashi M, Yamaguchi Y. Phys Rev B Condens Matter. 1998;57:R3229–R3232. [Google Scholar]
- 15.Lee Y S, Birgeneau R J, Kastner M A, Endoh Y, Wakimoto S, Yamada K, Erwin R W, Lee S-H, Shirane G. Phys Rev B Condens Matter. 1999;60:3643–3654. [Google Scholar]
- 16.Nagaev E L. Sov Phys JETP Letters (Pis'ma v Zh Eksp Teoret Fiz) 1972;16:558–561. [Google Scholar]
- 17.Visscher P B. Phys Rev B Condens Matter. 1974;10:943–945. [Google Scholar]
- 18.Gorkov L P, Sokol A V. J Phys. 1989;50:2823–2828. [Google Scholar]
- 19.Emery V J, Kivelson S A, Lin H-Q. Phys Rev Lett. 1990;64:475–478. doi: 10.1103/PhysRevLett.64.475. [DOI] [PubMed] [Google Scholar]
- 20.Hellberg C S, Manousakis E. Phys Rev Lett. 1999;83:132–135. doi: 10.1103/PhysRevLett.84.3022. [DOI] [PubMed] [Google Scholar]
- 21.Emery V J, Kivelson S A. Physica C. 1993;209:597–621. [Google Scholar]
- 22.Kivelson S A, Emery V J. In: Strongly Correlated Electronic Materials: The Los Alamos Symposium 1993. Bedell K S, Wang Z, Meltzer B E, Balatsky A V, Abrahams E, editors. Redwood City, CA: Addison–Wesley; 1994. pp. 610–656. [Google Scholar]
- 23.Dagotto, E., Hotta, T. & Moreo, A. (2001) Phys. Rep., in press (preprint: cond-mat/0012117).
- 24.Blount E I, Varma C M, Aeppli G. Phys Rev Lett. 1990;64:3074–3077. doi: 10.1103/PhysRevLett.64.3074. [DOI] [PubMed] [Google Scholar]
- 25.Joynt R. Supercond Sci Technol. 1988;1:210–214. [Google Scholar]
- 26.Hess D W, Tokoyasu T, Sauls J A. J Phys Cond Matt. 1989;1:8135–8141. [Google Scholar]
- 27.Machida K, Ozaki M, Ohmi T. J Phys Soc Jpn. 1989;58:2244–2252. [Google Scholar]
- 28.Machida K, Ozaki M, Ohmi T. J Phys Soc Jpn. 1989;58:4116–4122. [Google Scholar]
- 29.Zhang S-C. Science. 1997;275:1089–1096. doi: 10.1126/science.275.5303.1089. [DOI] [PubMed] [Google Scholar]
- 30.Lake B, Aeppli G, Clausen K N, McMorrow D F, Lefmann K, Hussey N E, Mangkorntong N, Nohara M, Takagi H, Mason T E, Schröder A. Science. 2001;291:1759–1762. doi: 10.1126/science.1056986. [DOI] [PubMed] [Google Scholar]
- 31.Lake B, Ronnow H M, Christensen N B, Aeppli G, Lefmann K, McMorrow D F, Vorderwisch P, Smeibidl P, Mangkorntong N, Sasagawa T, et al. Nature (London) 1999;400:43–46. [Google Scholar]
- 32.Koike Y, Akoshima M, Aoyama M, Nishimaki K, Kawamata T, Adachi T, Noji T, Watanabe I, Ohira S, Higemoto W, Nagamine K. Int J Mod Phys. 2000;14:3312–3315. [Google Scholar]
- 33.Howald C, Fournier P, Kapitulnik A. Preprint (cond-mat/0101251). 2001. [Google Scholar]
- 34.Emery V J, Kivelson S A, Tranquada J. Proc Natl Acad Sci USA. 1999;96:8814–8817. doi: 10.1073/pnas.96.16.8814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Zaanen J, Gunnarson O. Phys Rev B Condens Matter. 1989;40:7391–7399. doi: 10.1103/physrevb.40.7391. [DOI] [PubMed] [Google Scholar]
- 36.Zaanen J, Osman O Y, Kruis H V, Nussinov Z, Tworzydlo J. Preprint (cond-mat/0102103). 2001. [Google Scholar]
- 37.Harshman D R, Aeppli G, Batlogg B, Espinosa G A, Cava R J, Cooper A S, Rupp L W, Ansaldo E J, Williams D Ll. Phys Rev Lett. 1989;63:1187–1190. doi: 10.1103/PhysRevLett.63.1187. [DOI] [PubMed] [Google Scholar]
- 38.Tajima S, Noda T, Eisaki H, Uchida S. Phys Rev Lett. 2001;86:500–504. doi: 10.1103/PhysRevLett.86.500. [DOI] [PubMed] [Google Scholar]
- 39.Moodenbaugh A R, Xu Y, Suenaga M, Folkerts T J, Shelton R N. Phys Rev B Condens Matter. 1988;38:4596–4600. doi: 10.1103/physrevb.38.4596. [DOI] [PubMed] [Google Scholar]
- 40.Axe J D, Moudden A H, Hohlwein D, Cox D E, Mohanty K M, Moodenbaugh A R, Xu Y. Phys Rev Lett. 1989;62:2751–2754. doi: 10.1103/PhysRevLett.62.2751. [DOI] [PubMed] [Google Scholar]
- 41.Luke G M, Le L P, Sternlieb B, Wu W D, Uemura Y J, Brewer J H, Riseman T M, Ishibashi S, Uchida S. Physica C. 1991;185:185–189. [Google Scholar]
- 42.Kumagai K, Kawanao K, Watanabe I, Nishiyama K, Nagamine K. Hyperfine Interact. 1994;86:473–475. [Google Scholar]
- 43.Aeppli G, Mason T E, Hayden S M, Mook H A, Kulda J. Science. 1997;278:1432–1435. doi: 10.1126/science.278.5342.1432. [DOI] [PubMed] [Google Scholar]
- 44.Hirota K, Yamada K, Tanaka I, Kojima H. Physica B. 1998;241:817. [Google Scholar]
- 45.Larkin A I. Zh Eksp Teoret Fiz. 1970;58:1466–1469. [Google Scholar]
- 46.Kivelson S A, Emery V J. In: Stripes and Related Phenomena. Bianconi A, Saini N L, editors. New York: Kluwer; 2000. pp. 91–100. [Google Scholar]
- 47.Zachar O. Phys Rev B Condens Matter. 2000;62:13836–13839. [Google Scholar]
- 48.Tranquada J M, Ichikawa N, Uchida S. Phys Rev B Condens Matter. 1999;59:14712–14722. doi: 10.1103/physrevb.54.7489. [DOI] [PubMed] [Google Scholar]
- 49.Kivelson S A, Fradkin E, Emery V J. Nature (London) 1998;393:550–553. [Google Scholar]
- 50.Chakravarty S, Laughlin R B, Morr D, Nayak C. Phys Rev B Condens Matter. 2001;63:94503–94512. [Google Scholar]
- 51.Varma C. Phys Rev B Condens Matter. 1997;55:14554–14580. [Google Scholar]
- 52.Vojta M, Sachdev S. Phys Rev Lett. 1999;83:3916–3919. [Google Scholar]
- 53.Wakimoto S, Birgineau R J, Kastner M A, Lee Y S, Erwin R, Gehring P M, Lee S-H, Fujita M, Yamada K, Endoh Y, et al. Phys Rev B Condens Matter. 2000;61:3699–3706. [Google Scholar]
- 54.Wakimoto S, Tranquada J M, Ono T, Kojima K M, Uchida S, Lee S-H, Gehring P M, Birgineau R J. Preprint (cond-mat/0103135). 2001. [Google Scholar]
- 55.Demler E, Sachdev S, Zhang Y. Phys Rev Lett. 2001;87:67202–67205. doi: 10.1103/PhysRevLett.87.067202. [DOI] [PubMed] [Google Scholar]
- 56.Arovas D P, Berlinsky A J, Kallin C, Zhang S C. Phys Rev Lett. 1997;79:2871–2874. [Google Scholar]
- 57.Han J H, Lee D-H. Phys Rev Lett. 2000;85:1100–1103. doi: 10.1103/PhysRevLett.85.1100. [DOI] [PubMed] [Google Scholar]
- 58.Ando Y, Boebinger G S, Passner A, Kimura T, Kishio K. Phys Rev Lett. 1995;75:4662–4665. doi: 10.1103/PhysRevLett.75.4662. [DOI] [PubMed] [Google Scholar]
- 59.Ono S, Ando Y, Murayama T, Balakirev F F, Betts J B, Boebinger G S. Phys Rev Lett. 2000;85:638–641. doi: 10.1103/PhysRevLett.85.638. [DOI] [PubMed] [Google Scholar]
- 60.Lake B, Ronnow H M, Christensen N B, Aeppli G, Lefmann K, McMorrow D F, Vorderwisch P, Smeibidl P, Mangkorntong N, Sasagawa T, et al. Preprint (cond-mat/0104026). 2001. [DOI] [PubMed] [Google Scholar]