Greater tibial bone strength in male tennis players than controls in the absence of greater muscle output

Summary

Background/Objective

The greatest forces experienced by bones result from muscular contractions—muscles produce most force in high-velocity eccentric contractions. Bouncing movements, e.g., sprinting or hopping—where such contractions occur—are highly beneficial for lower limb bones. However, there is a growing body of evidence that torsional stresses are highly osteogenic. Sports in which frequent quick turning occurs—hence large torsional stresses can be expected—e.g., tennis, may also improve bone strength even in the absence of large ground reaction and muscle forces.

Methods

To investigate the relative effects of bouncing and turning movements on bones, we recruited 47 older men (mean age 62.4 ± 12.9 years). They were competitive sprinters (representing exposure to bouncing movement), competitive tennis players (turning movements), and inactive controls. Peripheral quantitative computed tomography scans of tibial diaphysis at 66% distal–proximal length were taken; muscle sizes from peripheral quantitative computed tomography and countermovement jump performance were also examined.

Results

Bone strength of tennis players was clearly greater than that of controls (23% greater bone mass; p < 0.001) and similar to that in sprinters. Tennis players' jump relative power and height were 15% and 25% lower than those of sprinters (p < 0.05) and similar to control values, being 2% greater and 6% lower, respectively (p > 0.5). Material eccentricity analysis suggests that torsional stresses may be a significant adaptive stimulus to tibial bone.

Conclusion

Results suggest that sports with quick turning movements are highly osteogenic, even in the absence of greater muscular output. This may be related to the large torsional stresses produced during turning movements.

Introduction

There is good reason to assume that the effects of exercise on bone strength are mainly the result of mechanical signals [1], [2]. Moreover, it is now well recognised that the largest forces on bones involve regional muscle contractions [3]. Accordingly, it is assumed that bouncing movements such as running and hopping are particularly beneficial for bones due to the large eccentric muscle forces produced in order to negotiate mass inertia during ground contact. In support of this are results of exercise studies based on bouncing activities in children [4], [5] and older adults [6], which have resulted in some of the most impressive exercise effects on bones observed in interventional models. Similarly, athletes in sports involving running or bouncing movements have greater bone strength than those in other sports [7], [8]. In particular, master sprinters have 14–23% greater tibial bone mass than age-matched controls [9]. That this difference is comparable to the largest group differences in lower limb bone strength observed between young athletes and controls [8] is particularly impressive, considering that exercise benefits for bones are negatively associated with age [10], [11]. Jumpers display large interlimb asymmetries in ground reaction force (GRF), with peak GRFs being much larger than those experienced by sprinters [12], [13]. However, side-to-side differences in jumpers are impressively small, amounting to a few percent between jumping and control leg [14]. This suggests that the greater GRFs in jumping do not result in any marked benefits in bones above those accrued through sprinting. In addition, sprinters have far greater muscle strength and power than sedentary controls [15], with values similar to those of Olympic weightlifters [16]. Hence, they can be considered a model of optimal lower limb musculoskeletal health.

However, the discourse has, to date, largely neglected the possibility that different types of deformations could differ in their effectiveness at stimulating bone anabolic responses. This is despite the pioneering study by Rubin et al. [17] in which torsional loading has already been demonstrated as a more potent stimulus to prevent disuse-related bone loss than axial loading. The largest effects so far observed as a result of exercise in humans are found in sports that involve torsional arm bone loading—namely tennis [18] and baseball [19]. Indeed, in a recent study upper limb bones were found to be more than proportionally strong against torsional strain as the moment arm for torsional muscle stress (bone width) increased [18].

Different kinds of exercises involve different amounts of compressive, torsional or bending deformation as shown for the human tibia in a recent study [20]. Bouncing steps—where the tibia is loaded by mass inertia, and mostly over the forefoot—are rare in tennis. In contrast, these are the dominant activities in sprint running, with no sharp turns or changes of direction. While the tibia experiences substantial strain in torsional and both bending axes during linear locomotion at different speeds, the main effect of increasing walking and running speed is in concurrent rise of anterior–posterior bending [20]. Hence, torsional strains are not the likely source of observed greater bone mass in sprinters compared with distance runners, walkers, and controls [9]. Turning movements are highly prevalent in tennis, representing over 50% of movement events, with each player completing several hundred turns during a typical high-level match [21]. These quick turns, both for baseline work and for attack and defence, must be expected to involve particularly large torsional strains in the tibia even in the absence of large reaction and muscle forces. This is supported by the findings of much larger peak knee and ankle torques (likely to cause tibial torsion) in turning movements compared with straight-line locomotion [22], [23]. Animal studies have reported greater bone strength in mice whose environment was altered to encourage turning movements, compared with those where linear locomotion was favoured [24]. Existing studies investigating the effects of regular tennis play on lower limb bone [25], [26], [27], [28], muscle size [26], [27], [28], and muscular output [26], [29], [30] have produced conflicting findings. However, these differences may be, at least in part, attributable to methodological issues such as use of dual-energy X-ray absorptiometry for bone assessment, different methods of muscle assessment, and study of players with different levels of ability. Comparisons of the bone strength of sprint runners and tennis players would be an ideal way of discerning the relative importance of bouncing versus turning movements in tibial bone strength.

Hence, to examine the relative effects of these two movement types on bone strength, a study of veteran tennis players and sprinters was conducted. For the first time in tennis players, lower limb peripheral quantitative computed tomography (pQCT) scans were taken for analysis of bone geometry. Jumping mechanography was used to measure muscular performance. This technique is highly repeatable and sensitive compared with other common neuromuscular and locomotory tests, such as maximum gait speed and chair-rise tests [31]. It can be successfully applied even in very old and frail individuals incapable of performing other tests, and assesses the effects of both athletic type [32] and age [33]. Old age is associated with a significant loss of lower limb force, particularly power [34] as well as bone strength [35]; therefore, the effects of exercise in older age are particularly important. In order to assess the potential of tennis to improve and maintain lower limb musculoskeletal health at an older age, elite master tennis players and sprinters (i.e., those who have a high training volume and compete regularly at national/international level) were recruited. Comparisons with age-matched inactive individuals would allow examination of the effects of regular tennis play on different aspects of musculoskeletal health. It was hypothesised that, compared with controls, tennis players would have a bone benefit that could not be explained on grounds of muscle force or power. In addition, despite the lack of large GRFs and associated muscle forces, the bone strength of tennis players would be comparable with that of sprinters.

Materials and methods

Participants

Forty-seven older adult men—inactive controls, sprinters, or tennis players, mean age 62.4 ± 12.9 years—were recruited into the study. The osteogenic potential of exercise appears to be lower in older women than in older men [11], likely due to the effects of oestrogen on bone mechanosensitivity [36]. Hence, only men were selected in order to maximise the ability to detect group differences. Control participants and sprinters formed a subset of a group for whom pQCT data had previously been published [9], [10]. Participants selected for this study were males for whom both pQCT and jumping mechanography data had been collected; pQCT data were taken only from the scanner used to examine tennis players, to prevent the need for cross-calibration. Control participants were employees of Manchester Metropolitan University or members of the local University of the Third Age. Inclusion criteria have been described previously [9]—briefly, participants had to be mentally active (evidenced by their continued employment at Manchester Metropolitan University or educational participation at University of the Third Age) but not highly physically active, i.e., they were involved in <2 hours of endurance-type exercise per week, and no regular resistive or exhaustive exercise. Conversely, athletes and tennis players were recruited when they reported to compete regularly at national or international competitions in their sport, and they trained for 3 or more hours per week in their chosen discipline. Master sprint athletes (as dictated by their self-rated best discipline) were recruited by distributing flyers and through personal communication at World and European Master Athletics Championships between 2005 and 2009. Master tennis players were recruited at the British Veterans' Clay Court Championships in Bournemouth in July 2012. Upper limb bone and muscle measures in these players had previously been reported as part of a larger cohort [11]. This study was approved by Manchester Metropolitan University's Local Ethics Committee and conformed to Declaration of Helsinki guidelines. Details of current training volume (number of hours per week dedicated to sprint- or tennis-specific training), and age at which sprinters and tennis players began to train and compete regularly in their sport were recorded using questionnaires.

All participants' height, body mass, and age were recorded. In all groups, participants were excluded if they had any musculoskeletal disorder known to affect the bones or they had suffered a fracture within the preceding 24 months.

Peripheral quantitative computed tomography scanning

For all participants, a pQCT scan (XCT 2000; Stratec Medizintechnik GmbH, Pforzheim, Germany) of the preferred hopping leg at 66% distal–proximal tibia length (measured from the medial malleolus to the palpated medial knee joint cleft) was taken. As the main aim of a larger study [11] was investigation of asymmetries in the upper limbs, only diaphyseal bone was examined to minimise radiation exposure. Scans were analysed using version 6.00 of the software supplied with the machine. To determine the outer contour of a bone, a peeling threshold of 650 mg/mm³ (shown previously to accurately determine diaphyseal bone geometry [37]) with peeling mode 1 was used. The same threshold was used to separate cortical bone, and a correction was applied to cortical bone mineral density (BMD) values to account for the partial volume effect [38].

From the output resulting from the Automated Analysis function of the software, total bone mineral content (mg/mm), total bone cross-sectional area (mm²), cortical bone area (Ar.ct, mm²), and cortical BMD (mg/mm³) were recorded. Values for cortical thickness (mm), periosteal circumference (mm), and endocortical circumference (mm) obtained from a ring model were also recorded, as were both axial and polar moments of inertia (I_x, I_y, and I_p, mm⁴). The XCT software gives both “true” moment of inertia values (calculated pixel by pixel) and a moment of inertia calculated from a ring model. A perfect circle would have a minimal polar moment of inertia; therefore, the ratio of “true” polar moment of inertia to the ring model value was examined—the closer the ratio was to 1, the more circular the bone. In addition, a region of interest was hand drawn around the muscle area and separated using a threshold of 35 mg/mm³ to determine gross calf muscle cross-sectional area (mm²). Reproducibility of these measurements within our laboratory using the same scanner had been reported previously [39], [40]; short-term error is up to 0.5% for total bone mineral content, total bone cross-sectional area, and Ar.ct; 1.2% for calf muscle cross-sectional area; and <5% for derived measures. In order to examine bone adaptation to bending and torsional moments, material eccentricity (ME) analysis was performed as described previously [18], [39]. Axial and polar moments of resistance (R_x, R_y, and R_p, mm³) indicate strength in bending and torsion. Dividing them by Ar.ct (as a surrogate for bone strength in compression) gives ME—an indication of the relative bending/torsion and compressive strength of the bone. The moment arms for bending and torsional moments are bone length and width, respectively; therefore, relationships between ME and the respective moment arm length were examined.

Jumping mechanography

Two countermovement jumps were performed on a GRF plate (Leonardo; Novotec Medical, Pforzheim, Germany) by each participant. Participants were instructed to jump as high as possible, and the jump with the greatest peak power was analysed. Peak force (F_Max, kN), peak mass-adjusted force (F_MaxRel, N/kg), peak power (P_Max, kW), peak mass-adjusted power (P_MaxRel, W/kg), and peak jump height (H_Max, cm) were recorded. Participants were allowed to move their arms to maintain balance, but instructed to keep the arms below shoulder height.

Statistical analysis

Data were analysed using the R statistical environment (version 2.14.0, www.r-project.org). Shapiro–Wilk testing revealed that all data were normally distributed (p > 0.05). Group comparisons of age, mass, and height were examined using one-way analysis of variance, with the Bonferroni post hoc test used to detect group differences. Training start age and training volume in sprinters and tennis players were examined using unpaired T tests. Group differences in bone, muscle, and jump parameters were examined using linear models, with relevant bone, muscle, or jump as a dependent variable and group (control, sprinter, and tennis player) as a fixed factor. Although groups were age, mass, and height matched, the standard deviations of age and mass were quite large. Given strong associations between age/mass and muscle and bone, these two factors were included as covariates in the analysis. Sport start age and training years differed between sprinters and tennis players, but sport start age was not available for nonsporting controls. However, as start age, current age, and training years are inter-related, inclusion of any two of these factors would be mathematically equivalent to the inclusion of all three. Therefore, in addition to current age, years of training was included as a covariate in the main analysis. A second analysis was also completed using only sprinter and tennis player data, with athletic group as a fixed factor and age, mass, sport start age, and training years as covariates. Both analyses started with a full model including all factors; a parsimonious model was created by backward selection of nonsignificant factors on the basis of highest p value until a model containing only significant predictors was created. Given that differences between sprinters and controls had been previously examined (and was not the aim of this study), when a significant effect of group was found in the primary analysis, preplanned treatment contrasts were used to examine differences between tennis players and controls, and tennis players and sprinters only. As two comparisons (contrasts) were made, Bonferroni correction was applied to resultant p values. Data are presented as mean (standard deviation); statistical effects were considered significant at p < 0.05.

Results

Cohort characteristics

There were no group differences in age, mass height, or regular training volume (Table 1). Sprinters had started their sport later than tennis players and had less years of training (both p < 0.001), although all sprinters and players had trained for at least 6 years.

Table 1.

Cohort characteristics [as mean(SD)] and group comparisons.

Parameter	Group values			Group effect p value
	Control	Sprinter	Tennis
N	17	15	15	—
Age (y)	62.2 (9.8)	62.0 (16.7)	61.8 (12.9)	0.99
Mass (kg)	76.7 (9.2)	75.7 (10.4)	78.6 (9.2)	0.69
Tibia length (mm)	381 (26)	384 (17)	391 (17)	0.38
Height (m)	1.75 (0.06)	1.76 (0.06)	1.77 (0.06)	0.79
Current sport start age (y)	—	39.0 (19.0)	15.5 (11.1)	<0.001
Training years	—	23.3 (15.2)	46.9 (14.6)	<0.001
Training volume (h/wk)	—	9.1 (6.2)	9.6 (5.6)	0.81

SD = standard deviation.

Bone measures

Significant main effects of athletic group on total bone mineral content, cortical area, cortical thickness (all p < 0.001), and both axial moments of inertia and polar moment of inertia (all p < 0.01) were found (Table 2). There was no group effect on total bone area, cortical BMD, and periosteal or endocortical circumference. Contrasts revealed that total bone mineral content, cortical area, cortical thickness (all p < 0.001), and anterior–posterior axial moment of inertia and polar moment of inertia (both p < 0.05) were greater in tennis players than in controls. There were no significant differences in any bone parameter between tennis players and sprinters. Body mass was positively associated with total bone mineral content, total and cortical cross-sectional area (CSA), periosteal and endocortical circumferences, and both axial and polar moments of inertia (all p < 0.001). There were no significant effects of age or training years on any bone parameter. A secondary analysis found that inclusion of training years and sport start age as covariates did not result in any group differences between sprinters and tennis players.

Table 2.

Bone parameters separated by group, main effects of athletic group and mass, and subsequent contrast results where applicable.

Variable	Group values			Multiple linear model
	C	S	T	Intercept			Athlete								Mass				Full model
							Main effect		Contrastsa						Main effect				p	Adjusted R2
									T versus Sb			T versus Cb
				b	SE	p	p	η2p	b	SE	pb	b	SE	pb	b	SE	p	η2p
vBMC.tot (mg/mm)	417.4 (46)	503 (67.3)	514.2 (58.5)	277.8	63.8	***	***	0.45	−2.3	18.5	>0.99	−91.0	17.9	***	3.0	0.8	***	0.25	***	0.51
Ar.tot (mm2)	710.4 (118.8)	743.2 (82.9)	745.3 (100)	275.3	104.1	*									5.9	1.3	***	0.31	***	0.28
Ar.ct (mm2)	330.4 (35.6)	415.3 (52)	412.2 (48.7)	235.9	51.6	***	***	0.51	9.7	15.0	>0.99	−77.50	14.50	***	2.2	0.6	**	0.22	***	0.54
vBMD.ct (mg/mm3)	1185 (36)	1168 (47)	1196 (33)
Ct.Thder (mm)	4.13 (0.71)	5.19 (0.64)	5.18 (0.76)	5.17	0.18	***	***	0.36	0.02	0.26	>0.99	−1.05	0.25	***					***	0.33
PsC (mm)	94.2 (7.8)	96.5 (5.5)	96.6 (6.5)	66.1	6.8	***									0.4	0.1	***	0.30	***	0.28
EcC (mm)	68.3 (11)	63.9 (6.5)	64.1 (9.3)	40.5	10.7	***									0.3	0.1	*	0.11	***	0.09
Ix (mm4)	41,533 (10,779)	50,955 (11,797)	52,202 (12,131)	−9,076	11,337	0.43	**	0.23	1068	3290	>0.99	−9149	3177	*	780	141	***	0.41	***	0.47
Iy (mm4)	23,912 (6029)	32,253 (9522)	28,390 (6922)	−1,912	8,492	0.82	**	0.24	5008	2464	0.10	−3726	2380	0.24	386	106	***	0.24	***	0.33
Ip (mm4)	65,445 (16,209)	83,208 (18,093)	80,591 (18,254)	−10,987	17,321	0.53	**	0.27	6076	5026	0.47	−12,875	4855	*	1165	216	***	0.40	***	0.48
Circularity	1.14 (0.03)	1.17 (0.05)	1.14 (0.04)

When a significant effect of group was found, preplanned treatment contrasts were used to examine differences between tennis players and controls, and tennis players and sprinters only. Although age and training years were initially included as factors, they were not found to be significant for any variable hence they are not shown.

For vBMD.ct and circularity no significant predictors were found.

*p < 0.05.

**p < 0.01.

***p < 0.001.

Ar.ct = cortical bone area; Ar.tot = total bone cross-sectional area; b = model coefficient; C = control; Ct.Th_der = cortical thickness; EcC = endocortical circumference; η²_p = partial eta-squared; PsC = periosteal circumference; S = sprinter; SE = standard error of the coefficient; T = tennis; vBMD.ct = cortical bone mineral density; vBMC.tot = total bone mineral content.

^aPositive model coefficients represent greater values in tennis players.

^bBonferroni correction applied due to multiple comparisons.

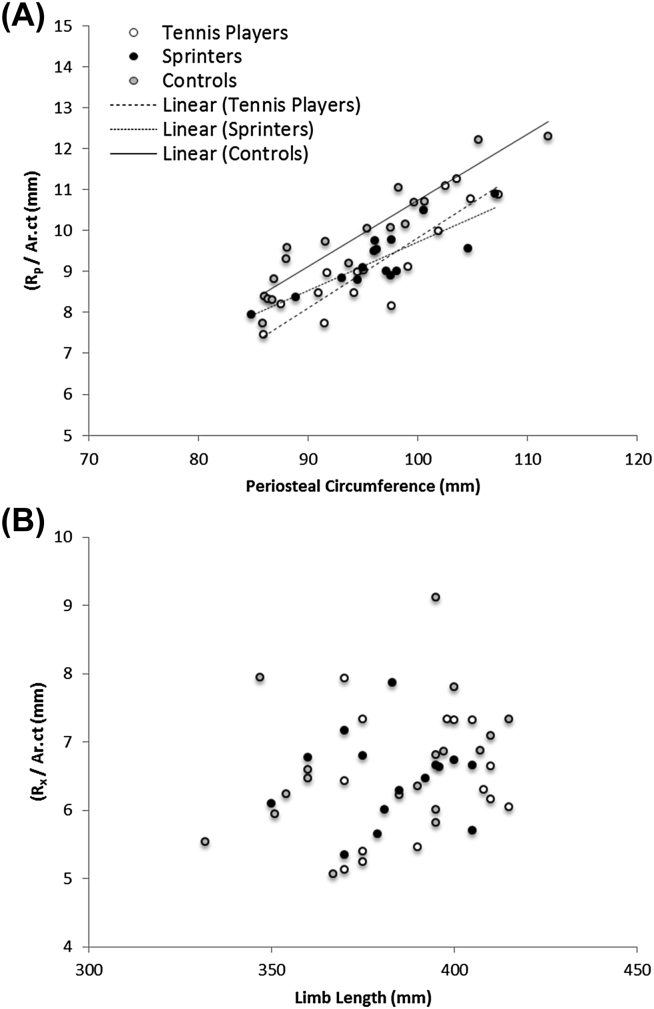
There was a highly significant relationship between torsional ME (R_p/Ar.ct) and periosteal circumference (p < 0.001, group R² values = 0.71–0.89, Fig. 1). Tennis players had a lower torsional ME than controls when periosteal circumference was considered (p < 0.001), but there was no difference between tennis players and sprinters (p = 0.70). In contrast, there was no significant association between anterior–posterior or mediolateral axial ME value and bone length (p = 0.13 and p = 0.83, respectively) or athletic group (p = 0.43 and p = 0.13, respectively).

Figure 1.

Relationships between (A) torsional material eccentricity and periosteal circumference and (B) anterior–posterior material eccentricity and bone length. All regressions in Figure 1A are significant at p < 0.001; R² values for groups are 0.71–0.89. Ar.ct = cortical bone area.

Muscle and force measures

There was a significant effect of athletic group on maximal relative power (p < 0.01), maximal power, jump height, and muscle size (p < 0.01) (Table 3). Post hoc contrasts revealed no significant differences in muscle and force measures between controls and tennis players (Bonferroni-corrected p = 1, except muscle size where p = 0.07). In contrast, maximal power, relative power, and jump height were greater in sprinters than in tennis players. Age was significantly negatively associated with all jump variables (p < 0.001) but not with muscle size. Body mass was positively associated with muscle size, maximal force (both p < 0.001), and maximal and relative power (both p < 0.05). There was no significant effect of training years on muscle or force parameters. When start age and training years were included in secondary analysis, differences in maximal power between sprinters and tennis players were no longer significant (p = 0.14).

Table 3.

Muscle cross-sectional area and counter-movement jump parameters separated by group, and main effect of group.

Variable	Group values			Intercept			Athlete								Age				Mass				Full model
	C	S	T				Main effect		Contrastsa						Main effect				Main effect				p	Adjusted R2
									T versus Sb			T versus Cb
				b	SE	p	p	η2p	b	SE	p	b	SE	p	b	SE	p	η2p	b	SE	p	η2p
MuscA (mm2)	8990 (1078)	9399 (1337)	9534 (999)	4472	1135	***	*	0.12	−100	329	1.00	−689	318	0.07					66	14	***	0.34	***	0.36
PMax (kW/kg)	2.82 (0.71)	3.44 (1.32)	3.00 (0.78)	4.41	0.81	***	*	0.21	0.53	0.21	*	−0.12	0.20	>0.99	−0.06	0.01	***	0.65	0.03	0.01	**	0.18	***	0.66
PMaxRel (W/kg)	37.4 (11.1)	45.6 (15.8)	38.2 (9.5)	105.0	10.1	***	**	0.21	6.7	2.6	*	−1.20	2.50	>0.99	−0.7	0.1	***	0.67	−0.3	0.1	*	0.12	***	0.69
FMax (kN)	1.82 (0.32)	1.96 (0.44)	1.84 (0.4)	1.18	0.37	***									−0.01	0.00	***	0.33	0.02	0.00	***	0.35	***	0.48
FMaxRel (N/kg)	23.8 (3.9)	25.9 (4.2)	23.5 (4.4)	35.96	2.49	***									−0.19	0.04	***	0.34					***	0.32
HMax (m)	0.34 (0.1)	0.40 (0.15)	0.32 (0.10)	0.67	0.06	***	*	0.17	0.08	0.03	*	0.02	0.03	>0.99	−0.01	0.00	***	0.47					***	0.49

Although training years were initially included as a factor, it was not found to be significant for any variable; hence, it is not shown.

*p < 0.05.

**p < 0.01.

***p < 0.001.

b = model coefficient; C = control; η²_p = partial eta-squared; MuscA = calf muscle cross-sectional area; S = sprinter; SE = standard error of the coefficient; T = tennis.

^aPositive model coefficients represent greater values in tennis players.

^bBonferroni correction was applied due to multiple comparisons.

Discussion

The aim of this study was to investigate the relative effects of regular turning and bouncing movements—experienced by tennis players and sprinters, respectively—on lower limb bone strength. The main findings are that the tibial bone strength in tennis players is similar to that observed in sprint runners and much greater than that observed in controls. This is despite tennis players having lower muscle power than sprinters and no significant advantage in muscle size or strength over controls.

Ankle and knee extensor moments, i.e., those resulting from muscular contractions likely to stress the tibia, during sprinting are large (>300 N m) [41]. Therefore, even in low-speed sprinting, large tibial diaphysis strains (∼1000∈ compressive, ∼1600∈ shear), which are three times greater than walking strains, are observed [42]. Similarly, high strain rates—required for bone mechanoadaptation [43]—occur during sprinting, likely related to the high rate of force development [12]. Locomotory speed is positively associated with anterior–posterior bending, with little effect on torsional strain [20]. Little is known about lower limb kinetics in tennis; however, turning movements—highly prevalent in tennis but not in sprinting—engender substantial ankle and knee torsions that are likely to impose large torsional tibia stresses [22], [23].

Bouncing movements (such as sprinting) are highly osteogenic [4], [6], [8], [44]. However, while there is evidence for a strong osteogenic effect of torsional stresses [17], [18], [19], [45] and turning movements resulting in greater bone strength in mice compared with linear locomotion [24], the effects of torsional and turning movements on human bone strength are unexplored. Greater tibial shaft bone mass in tennis players and sprinters was a result of a greater cortical area, although it was unclear whether this was a result of periosteal apposition or endocortical contraction/retention. In contrast, a significantly greater periosteal circumference in master athletes has been observed previously [9]. However, periosteal growth velocity [46] and expansion due to exercise [47] decrease markedly around 13–15 years of age. The mean start age for both athlete groups was greater than these ages, likely preventing substantial periosteal apposition through exercise. While advantages in periosteal circumference following exercise during youth persist decades after cessation of activity [48], improvements in bone mass and cortical area diminish. Therefore, group differences in bone mass and cortical area reflect the current level of habitual strain experienced by athletes and controls.

It could be expected that torsional movements would result in increases in tibial circularity. The tibial diaphysis in athletes participating in odd-impact sports have a more rounded shape than in runners [49], [50], likely due to the predominance of anterior–posterior bending stress in running. Similarly, mice encouraged to perform turning movements had rounder diaphyses than free-roaming mice and those where linear locomotion was favoured [51]. Sprinters' bones were found to be less round than those of tennis players and controls in this study, which suggests that torsional influences on bones were less in the former group. Indeed, higher-speed running is primarily associated with large anterior–posterior strains [20]. However, there were no differences in circularity between controls and tennis players. Substantial torsional strain occurs in the tibia during walking and running [20], where one might expect substantial anterior–posterior bending. In fact, torsional strains are evident even at low walking speeds where limited bending strains occur. This suggests that even nonsporting controls are subject to substantial torsional tibia strains; therefore, muscular forces in bouncing and turning motions may not be easy to interpret without kinetic and kinematic studies. That tennis players had bone strength similar to sprinters and far greater than controls—while having no advantage in muscle strength—is supportive of a good osteogenic potential of turning/torsional movements even in the absence of large muscle forces.

Bone strength is a product of bone size and geometry—the same bone mass distributed into a wider-diameter, thinner-walled shaft will be stronger in bending and torsion. ME analysis involves normalisation of bone's torsional/bending strength for bone size. This gives a measure of a bone's geometrical shape—greater ME indicates greater torsional/bending resistance relative to compressive resistance. ME analysis revealed that controls' tibiae were more than proportionally adapted to torsional stress compared with those of tennis players and sprinters, with values in the latter two groups being similar. This appears counterintuitive, but may be related to the late sport start age of tennis players and controls. As athletes were unable to increase bone size via exercise in adulthood, the additional bone mass required to increase strength must be deposited on the endocortical surface, which is mechanically less advantageous in bending and torsion. ME analysis also revealed that tibiae were more than proportionally adapted to torsional stress as the moment arm for torsion (bone width) increased, suggesting a key role of torsion in bone adaptation. The same relationship was not observed in bending strength in either axis, contrary to previous observations [39]. However, variability in limb length (predictor variable) was smaller in the current study, which may have influenced the ability to detect associations.

This is the first study to examine lower limb bone strength in tennis players using pQCT. While regular tennis play is associated with greater racquet arm bone strength, muscle size, and grip strength in children, and young and older adults [1], [18], [52], studies investigating lower limb bone [25], [26], [27], [28], muscle size/lean mass [26], [27], [28], and muscular output [26], [29], [30] have produced conflicting results. Methodological considerations may, at least in part, explain these results. Previous studies of bone employed dual-energy X-ray absorptiometry scanning. Unlike pQCT, dual-energy X-ray absorptiometry is unable to distinguish between trabecular and cortical bones or directly examine cross-sectional bone geometry—all influenced differently by physical activity [18], [52], [53]. Some studies reported only BMD group differences—BMD is affected differently by exercise dependent on site [9], [18], [53]; therefore, whole limb BMD measurements may not detect site-specific adaptations. Finally, these studies have recruited players of different abilities and ages, ranging from professional male adult players and prepubescent males to recreational postmenopausal players.

Calf muscle CSA in tennis players was no greater than that in controls, similar to previous observations in older male tennis players [27]. However, this is contrary to previous findings of greater lower limb lean mass in recreational prepubescent and elite young adult players [26], [28]. In all cases, muscle volume assessed by magnetic resonance imaging (the “gold standard” of muscle size assessment) was not used, and future magnetic resonance imaging-based studies may elicit more conclusive findings. Jump performance in sprinters was greater than that in controls (as observed previously [16]) and tennis players, particularly 15–25% higher maximal power and jump height. Jump performance of tennis players was very similar to that of controls (p > 0.5 prior to Bonferroni correction). All group differences were nonsignificant and—with the exception of maximal jump height, which was greater in controls—within the short-term error of the measurement technique. Therefore, it is extremely unlikely that the lack of observed tennis player–control differences in muscular output is a result of cohort size.

Jump performance has previously been examined only in prepubescent male tennis players [26], and found to be greater than in controls. However, in that study, control participants had 14% greater total mass and 58% greater fat mass than tennis players but similar (within 1%) lean mass, which may explain the differences in group jump performance. Isokinetic and isometric force testing found no greater strength in elite male players [30], but greater strength in a mixed group of old and young male and female players [29] compared with controls, although in the latter study, controls also had 12.5% greater fat mass. Previous research has also shown 17–24% lower isokinetic knee extension power (dependent on movement angular velocity) in tennis players compared with track athletes [54]—similar to the 19% greater mass-adjusted power in this study. Therefore, at present, there is no clear evidence of improved lower limb muscular output in tennis players, although in comparison there is substantial evidence of an advantage in sprint runners. Why tennis players should not have a greater muscular output than controls is unclear, and the lack of biomechanical studies involving the lower limb of tennis players prevents further examination. Fibre-type distribution may have affected results—tennis players have a similar lower limb fibre-type distribution to endurance athletes (i.e., Type I dominant) [55]. In contrast, sprinters have a greater proportion of Type II fibres with a pattern similar to inactive controls.

There are several limitations to this study, the most important being the possibility of a self-selection bias influencing results. It may be that people with bigger, stronger muscles, fast muscle fibre-type dominance etc., may self-select to participate in sports as they have a performance benefit. Therefore, observed group differences may have a genetic component, rather than being entirely attributable to the effects of regular exercise. While the muscle and bone advantages observed in the sprinters are easy to reconcile with this idea, it is difficult to understand how increased bone strength in the absence of greater muscular output would be advantageous in tennis players. Nutritional intake was not measured; however, the effects of vitamin D and calcium are modest compared with observed group differences [56], and could not explain a large portion of group variance. The lack of childhood activity data is also a limitation, as are the greatly different start ages of the two athletic groups. However, the main osteogenic influence of exercise in youth on diaphyseal bone is on periosteal circumference [57], [58], and these advantages persist with age [48]. Therefore, the similar total bone area and periosteal circumference in the three groups in our study suggests that physical activity during their childhood was similar and that start age may not have greatly influenced the results. A recent study showed greater exercise benefits in epiphyseal trabecular BMD and diaphyseal endocortical circumference in adult starters compared with that in athletes who had trained since childhood [11], showing that bone mass can still be substantially increased in adulthood without periosteal expansion. In fact, start age was not significantly associated with any bone strength parameter in athletes (p > 0.3, except I_y where p = 0.07), nor did the inclusion of start age as a covariate substantially influence observed group differences. Similarly, tennis players had participated in their sport for much longer than sprinters. However, according to the negative feedback-based system proposed in the mechanostat theory, bones will habituate to a new loading environment over time. Indeed, even in the extreme case of spinal cord injury, we see that bone parameters reach a new, lower steady-state after 3–8 years [59]. All sprinters and tennis players had trained and competed in their sport for at least 6 years; therefore, we could expect that bones had adapted to the increased loading. This is supported by the lack of a significant effect of training years on bone parameters. While training volume was recorded; the volume of dedicated conditioning work (e.g., resistance training or endurance exercise) was not assessed. However, a bone is thought to adapt to habitual peak strains [60], and it is unlikely that conditioning work represented the greatest habitual tibial strains in these athletes. This is supported by the concurrent increase in GRFs [61] and tibial deformation [20], [42] with walking/running speed. In addition, compared with the observed 20–25% group differences in bone strength in this study, the effects of other conditioning exercise are minor, for example, 1–2% hip BMD increase following resistance-exercise intervention [62] and no significant differences in bone strength between regular cyclists or swimmers and controls. Only male players were studied; therefore, the authors are unable to generalise these results across both sexes.

In conclusion, bone strength in tennis players was far greater than that in controls, and similar to that in sprinters. Analysis of bone geometry provided evidence of torsional stresses as a primary adaptive influence on tibial bone. While sprint runners have greater muscle power and jump performance than tennis players and controls, tennis players have no advantage in muscular output over inactive peers. These results are supportive of a large osteogenic potential of movements resulting in large torsional stresses, independent of improvements in muscle output. Therefore, in addition to its exciting potential to improve bone strength in the upper limbs, regular tennis play may also be effective in improving lower limb bone strength. Randomised controlled trials of regular tennis play (or activities mimicking these actions) would be a valuable progression from current cross-sectional evidence.

Conflicts of interest

All authors declare that they have no conflicts of interest.