Cosolutes, Crowding, and Protein Folding Kinetics

Abstract

Long accepted as the most important interaction, recent work shows that steric repulsions alone cannot explain the effects of macromolecular cosolutes on the equilibrium thermodynamics of protein stability. Instead, chemical interactions have been shown to modulate, and even dominate, crowding-induced steric repulsions. Here, we use¹⁹F NMR to examine the effects of small and large cosolutes on the kinetics of protein folding and unfolding using the metastable 7 kDa N-terminal SH3 domain of the Drosophila signaling protein drk (SH3), which folds by a two-state mechanism. The small cosolutes consist of trimethylamine N-oxide and sucrose, which increase equilibrium protein stability, and urea, which destabilizes proteins. The macromolecules comprise the stabilizing sucrose polymer, Ficoll, and the destabilizing globular protein, lysozyme. We assessed the effects of these cosolutes on the differences in free energy between the folded state and the transition state and between the unfolded ensemble and the transition state. We then examined the temperature dependence to assess changes in activation enthalpy and entropy. The enthalpically mediated effects are more complicated than suggested by equilibrium measurements. We also observed enthalpic effects with the supposedly inert sucrose polymer, Ficoll, that arise from its macromolecular nature. Assessment of activation entropies shows important contributions from solvent and cosolute, in addition to the configurational entropy of the protein that, again, cannot be gleaned from equilibrium data. Comparing the effects of Ficoll to those of the more physiologically relevant cosolute lysozyme reveals that synthetic polymers are not appropriate models for understanding the kinetics of protein folding in cells.

Graphical abstract

INTRODUCTION

Historically, descriptions of how the complex, crowded cellular environment affects proteins predicted enhanced folding and diminished unfolding via excluded volume effects resulting from hard core repulsions between the protein and crowding molecules.^1–3 In these descriptions, protein and crowder are treated as inert particles that interact solely through steric repulsions, with no “chemical” contribution. We test this idea by studying the effects of several small and macromolecular cosolutes on the folding and unfolding kinetics of the metastable 7 kDa N-terminal SH3 domain of the Drosophila signaling protein drk (SH3), which exists in a two-state equilibrium between a folded (F) state and the unfolded (U) ensemble.⁴ Fluorine labeling of its sole tryptophan results in two 19F resonances, one for each state.⁵ The transition occurs in seconds, allowing quantification of folding (k_U→U‡) and unfolding (k_F→U‡) rates using two-dimensional 19F homonuclear exchange spectroscopy-based NMR experiments.^6,7

The equilibrium modified standard-state unfolding-free energy $(\mathrm{\Delta }{G}_{\mathrm{u}}^{\circ }\prime )$, -enthalpy $(\mathrm{\Delta }{H}_{\mathrm{u}}^{\circ }\prime )$, -entropy $(\mathrm{\Delta }{S}_{\mathrm{u}}^{\circ }\prime )$, and -heat capacity $(\mathrm{\Delta }{C}_{\text{p,u}}^{\circ }\prime )$ of SH3⁷ and other proteins^8–13 have been determined in buffer, in solutions of small and large cosolutes, and in cells. The results reveal that the equilibrium entropic effects of hard-core steric repulsions are balanced, or even dominated, by enthalpic (chemical) interactions, although there are reports of pure entropic effects.^14,15 Surprisingly, supposedly “inert” synthetic polymers such as Ficoll, dextran, and their monomers, sucrose and glucose, also exhibit enthalpic contributions.^11,12 Senske et al. even observed a positive $\mathrm{\Delta }\mathrm{\Delta }{S}_{\mathrm{U}}^{\circ }\prime$ for ubiquitin in dextran and glucose solutions, the opposite of what is predicted from a purely excluded-volume point of view.¹¹

Equilibrium measurements, however, only provide information about transitions between F and U. The effects involving the transition state (U^‡) remain ill-defined. These poorly populated states determine whether a protein folds or aggregates, and therefore are key to understanding aggregation-related diseases.^16–18 It has been stated that protein folding and unfolding needs to be studied under crowded conditions,¹⁹ but most such studies use synthetic polymers. Our goal is to characterize how small and large cosolutes alter the barriers that define SH3 folding (U → U^‡) and unfolding (F → U^‡) to define conditions useful for understanding the kinetics of protein folding and misfolding in cells. The free energies required to reach the transition state from the unfolded ensemble, $\mathrm{\Delta }{G}_{\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$ and the folded state, $\mathrm{\Delta }{G}_{\mathrm{F}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$, are determined by the Eyring–Polanyi equation^20–22

$$\mathrm{\Delta }{G}_{\mathrm{F},\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}=-RT\ln \left(\frac{kh}{k_{B}T}\right)$$ (1)

where $\mathrm{\Delta }{G}_{\mathrm{F},\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$ is the modified standard-state activation free energy for folding or unfolding at absolute temperature T, R is the gas constant, k is the folding, k_U→U‡, or unfolding, k_F→U‡, rate at T, h is Planck’s constant, and k_B is the Boltzmann constant. Together, $\mathrm{\Delta }{G}_{\mathrm{F}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$ and $\mathrm{\Delta }{G}_{\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$ describe the equilibrium between the thermodynamic states and the transition state

$$\mathrm{\Delta }{G}_{\mathrm{U}}^{{\circ }^{\prime }}=\mathrm{\Delta }{G}_{\mathrm{F}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}-\mathrm{\Delta }{G}_{\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$$ (2)

To determine the enthalpic and entropic barriers to transition state formation, we measured the folding and unfolding activation enthalpies $(\mathrm{\Delta }{H}_{\mathrm{F},\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}})$, entropies $(\mathrm{\Delta }{S}_{\mathrm{F},\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}})$, and heat capacities $(\mathrm{\Delta }{C}_{p,\mathrm{F},\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}})$ from the temperature dependence of k_U→U‡ and k_F→U‡. Two fitting methods were used. The first method, which we call the three-parameter fit (eq 3), modified the strategy used by Fersht and co-workers²³

$$\begin{array}{l}\ln (k_{\text{F,U}\to \mathrm{U}\mathrm{‡}})=[\ln \left(\frac{k_{\mathrm{B}}}{h}T\right)+\frac{\mathrm{\Delta }{S}_{\mathrm{F},\mathrm{U}\to \mathrm{U}\mathrm{‡},T_{\mathrm{o}}}^{{\circ }^{\prime }\mathrm{‡}}}{R}\\ -\frac{\mathrm{\Delta }{H}_{\mathrm{F},\mathrm{U}\to \mathrm{U}\mathrm{‡},T_{\mathrm{o}}}^{{\circ }^{\prime }\mathrm{‡}}}{RT}-\frac{\mathrm{\Delta }{C}_{p,\mathrm{F},\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}(T-T_{\mathrm{o}})}{RT}\\ +\frac{\mathrm{\Delta }{C}_{p,\mathrm{F},\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}}{R}\ln \left(\frac{T}{T_{\mathrm{o}}}\right)]\end{array}$$ (3)

where T_o is the reference temperature for the activation enthalpy and entropy. In the second method, which we call the “two-parameter fit,” $\mathrm{\Delta }{G}_{p,\mathrm{F},\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$ is set to zero, and there are only two parameters, the assumed temperature-independent activation entropy, $\mathrm{\Delta }{S}_{\mathrm{F},\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$, and the assumed temperature-independent activation enthalpy, $\mathrm{\Delta }{H}_{\mathrm{F},\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$.

Activation parameters are analyzed by whether they raise or lower the barriers to folding or unfolding. A decreased folding rate in cosolute results from a positive change in the activation free energy of folding, $\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$, indicating that the cosolute makes folding more difficult by raising the barrier, and vice versa. The sign convention for the enthalpic $(\mathrm{\Delta }{H}_{\mathrm{F},\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}})$ and entropic $(-T\mathrm{\Delta }{S}_{\mathrm{F},\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}})$ contributions is the same as that for the changes in free energy. $\mathrm{\Delta }{H}_{\mathrm{F},\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$ and $-T\mathrm{\Delta }{S}_{\mathrm{F},\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$ values under a particular set of conditions are often statistically indistinguishable. That is, $\mathrm{\Delta }{G}_{\mathrm{F},\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$ is a small difference between larger and nearly equal values of $\mathrm{\Delta }{H}_{\mathrm{F},\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$ and $-T\mathrm{\Delta }{S}_{\mathrm{F},\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$. In these instances, the sign of each contribution is compared to $\mathrm{\Delta }{G}_{\mathrm{F},\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$ to determine whether the entropy or enthalpy change dominates the free energy barrier.

The metastability of SH3 allowed us to use heat alone as a perturbant. Several groups have reported activation parameters for folding and unfolding from studies that extrapolate the effect of denaturants to the effect of buffer alone. Examples include variation of pH,^23,24 urea,^25–30 and guanidinium chloride.^27,31,32 Other studies using only heat include that of Ai et al., who used 15N relaxation dispersion to assess the folding and unfolding of an apocytochrome b₅₆₂ variant in 85 g/L PEG 20K,³³ and that of the Gruebele group,^34,35 who used FRET to measure the temperature dependence of phosphoglycerate kinase folding in buffer and in individual cells. We provide a comprehensive analysis of cosolute effects on folding and unfolding by using¹⁹F labeling, a technique pioneered by the Frieden lab.^36–38 19F NMR reduces experiment time, allowing the exploration of large and small, stabilizing and destabilizing cosolutes, which is complemented by using¹⁵N enrichment to assess cosolute effects on the structures of the folded state and the unfolded ensemble.

EXPERIMENTAL METHODS

Protein Expression and Purification

19F-labeled SH3 was expressed and purified as described previously.³⁹ Briefly, the purification consisted of three steps: anion exchange chromatography and size exclusion chromatography to isolate SH3, followed by hydrophobic interaction chromatography to remove a truncated SH3 contaminant. Sample purity and stability were verified by ESI mass spectrometry (Thermo LTQ-FTR-ICR-MS, 7T) and 1D¹⁹F NMR experiments.

NMR

Purified, fluorine-labeled protein (1 mg) was resuspended in 450 μL of NMR buffer (50 mM acetic acid/ sodium acetate, HEPES, bis-Tris propane, pH 7.2 ± 0.1, 5% vol/vol D₂O)⁴⁰ with the stated amount of cosolute. The concentration of lysozyme (ε₂₈₀ = 36 mM⁻¹ cm⁻¹) was verified by UV–visible spectrophotometry (NanoDrop ND-1000). Polymers, sugars, and urea were weighed (Ohaus PA64). After the protein was resuspended in buffer, the pH was adjusted with small volumes (<1 μL) of 3 M HCl. Fluorine experiments were performed at 15, 20, 25, 30, 35, 40, and 45 °C with a Bruker Avance III HD spectrometer operating at a¹⁹F Larmor frequency of 470 MHz running Topspin 3.2 and equipped with a Bruker QCI cryoprobe.

Spin–lattice relaxation rates (R₁) for each condition were measured using an inversion recovery sequence [t_mix = 0, 0.05, 0.1 (×3), 0.25, 0.5, 0.8, 1.0, 1.5 s]. Sixteen transients were used for buffer, 32 for 100 g/L urea, 64 transients for 200 g/L Ficoll and 100 g/L lysozyme, and 64 and 128 transients for 200 g/L sucrose. The acquisition time was 2 s, with a relaxation delay of 4 s, while the sweep width was 70 ppm.

A modified version of the Bruker NOESY library experiment, a pseudo-3D experiment in which the t₁ increments for each mixing time [t_mix = 1.5, 70, 140 (×3), 210, 300, 500, and 800 ms] were interleaved, was used to measure the folding and unfolding rates. Sweep widths were 70 ppm in both dimensions, with 1024 complex points collected during t₂ with 75 or 100 complex points in t₁ for each t_mix. Sixteen transients were acquired per increment, and a 2 s relaxation delay was used. Data for relaxation and folding experiments were processed using Topspin 3.2 as described previously.⁷ Representative one- and two-dimensional¹⁹F spectra are shown in Figure S1.

Fluorine-labeled and 15N-enriched protein samples were prepared identically, and 4-,4-dimethyl-4-silapentane-1-sulfonic acid (DSS) was added to a final concentration of 0.1% (v/v). Two-dimensional¹⁵N–¹H HSQC experiments were performed at 15, 20, 25, 30, and 35 °C on a Bruker Ascend spectrometer operating at an ¹H Larmor frequency of 850 MHz and an¹⁵N Larmor frequency of 86 MHz running Topspin 3.2 and equipped with a Bruker QCI cryoprobe. A sensitivity-enhanced HSQC Bruker Library pulse sequence was used. The sweep widths were 38 ppm (3275 Hz) for F1 and 16 ppm (13587 Hz) for F2. A total of 256 points was collected in t₁ and 2048 in t₂. Eight transients were acquired per increment. The temperature dependence of the ¹HN chemical shifts was determined from the change in the upfield ¹H^N chemical shifts with increasing temperature.⁴¹ Data were processed using Topspin 3.2. The temperature coefficients,⁴¹ in ppb/K, and their uncertainties were determined from plots of the ¹HN chemical shifts versus temperature, using a linear regression.⁴²

Assignments for one- and two-dimensional ¹⁹F experiments were taken from the data of Evanics et al.⁵ The addition of fluorine causes minor ¹H and ¹⁵N chemical shift perturbations relative to the unlabeled protein.⁵ The chemical shifts of the fluorinated protein were inferred from previous assignments determined at a pH of 7.2⁴³ and by overlaying an HSQC spectrum of wild-type SH3 on a spectrum of the 5-fluorotryptophan-labeled protein.⁵

Selection of Fits for Temperature Dependence in Cosolutes

Four fitting schemes were tested: (1) a three-parameter fit for folding and unfolding, (2) a two-parameter fit with $\mathrm{\Delta }{C}_{p,\mathrm{F},\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}=0$, (3) a two-parameter fit with $\mathrm{\Delta }{C}_{p,\mathrm{F},\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}=\text{buffer}$, and (4) a two-parameter fit with $\mathrm{\Delta }{C}_{p,\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$ set equal to the value in buffer and $\mathrm{\Delta }{C}_{p,\mathrm{F}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}=0$. Scheme 2 was eliminated because of the obvious curvature in the data. Scheme 1 was ruled out, because the limited number of points restricted the ability to determine the extra parameter $(\mathrm{\Delta }{C}_p^{{\circ }^{\prime }\mathrm{‡}})$. The large r values and the low P_r values indicate that setting $\mathrm{\Delta }{C}_p^{{\circ }^{\prime }\mathrm{‡}}$ to zero for unfolding is appropriate, ruling out Scheme 3. Scheme 4 was chosen because crowding has only a small effect on the equilibrium heat capacity of SH3 unfolding⁷ and because the linear fit was determined suitable for the unfolding reaction.

Analysis of Uncertainty

For determination of relaxation rates, one mixing time was acquired three times. The sample standard deviation (SD) was used to drive a Monte Carlo analysis (n = 1000) to determine R₁.

For folding rates, one mixing time was repeated three times. The sample SD was used to drive a Monte Carlo analysis (n = 1000), and data were fit as described.⁶ R₁ was set to values determined by inversion recovery experiments.

For the three-parameter analysis, the folding rate SDs were used to drive another Monte Carlo analysis in which 10,000 randomly generated data sets were fit to eq 3 to obtain $\mathrm{\Delta }{H}_{\mathrm{F},\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$, $-T\mathrm{\Delta }{S}_{\mathrm{F},\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$, and $\mathrm{\Delta }{C}_{p,\mathrm{F},\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$ and their SDs. ΔG°′^‡ (303 K) were calculated from the folding and unfolding rates at 303 K using eq 1.

For the two-parameter analysis, the $\mathrm{\Delta }{H}_{\mathrm{F},\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$ and $T\mathrm{\Delta }{S}_{\mathrm{F},\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$ were determined from weighted linear regression of the sample folding rates and their SD.⁴² The probability of the values arising from uncorrelated data (P_r) was determined using the correlation coefficient, r.⁴²

Viscosity Measurements

The viscosities of water, 100 g/ L urea, 50 g/L trimethylamine-N-oxide (TMAO), and 200 g/L sucrose were measured in triplicate at 10, 20, 30, and 40 °C using a Viscolite 700 (Hydramotion, York, U.K.). For each condition, the viscosity as a function of T was fit to an exponential function, which was used to extrapolate the viscosities at 15, 25, and 35 °C. Viscosity-adjusted folding rates were determined from the viscosity of the solution relative to water at 30 °C.

RESULTS

Cosolutes and SH3 Structure

Amide proton temperature coefficients (the slope of a plot of ¹HN upfield shift against increasing temperature) can be used as indicators of intra-protein hydrogen bonding. Cierpicki and Otlewski analyzed coefficients from a database of 14 proteins of known structure⁴¹ and found that 85% of amide protons participating in an intraprotein hydrogen bond have coefficients greater than −4.6 ppb/K.⁴¹ Amides with coefficients between −7 and −5 ppb/K have a 20–70% probability of being hydrogen bonded, while amide protons with coefficients more negative than −7.0 ppb/ K have a less than 20% probability of intraprotein hydrogen bond participation.⁴¹ Temperature coefficients for the folded and unfolded states of SH3 were determined in buffer and in cosolutes (Figure 1, Table S1). Although 300 g/L Ficoll was used for structural studies, 200 g/L Ficoll was used for determination of activation parameters, because concentrations higher than 200 g/L sucrose are too stabilizing to measure folding (vide infra).

Figure 1.

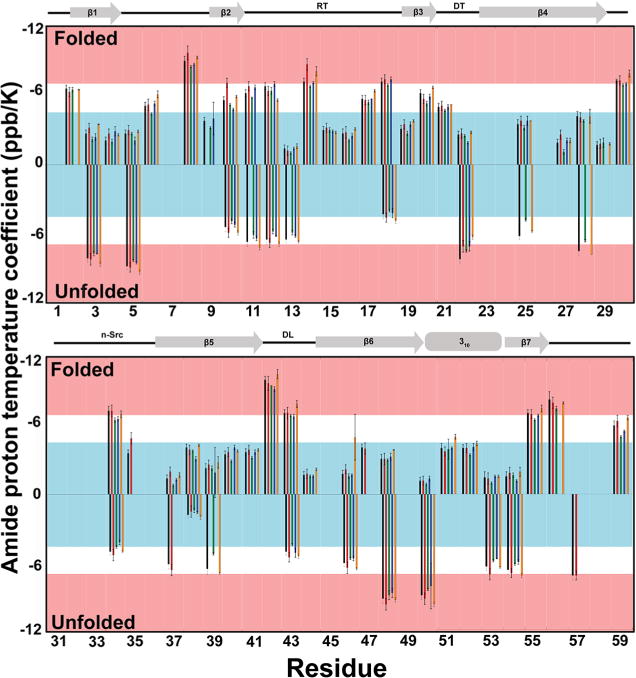
Amide proton temperature coefficients. Buffer, black; 100 g/L urea, red; 200 g/L sucrose, green; 300 g/L Ficoll, blue; 100 g/L lysozyme, orange; no bar means no data. RT, reverse turn; DT, diverging turn; n-Src loop; DF, distal loop. Bars ending in the blue box have a ≥85% probability of participating in an intramolecular hydrogen bond. Bars ending in a pink box have a ≤20% probability of participating in an intramolecular hydrogen bond.⁴¹ Values were determined using a linear least-squares fit of ¹H–N chemical shifts from 288 to 308 K in 5 K increments at pH 7.2. Uncertainties represent one standard deviation.

Of the 46 coefficients determined for the folded state in buffer, 36 agree with the NMR structure (pdb 2A36⁴⁴). Of the 10 outliers, coefficients for three hydrogen-bonded residues (K4, L17, and K21) fell between −6 and −5 ppb/K, where probability drops from around 70 to 30%. Three nonconforming coefficients come from non-hydrogen-bonded residues with coefficients greater than −4.5 ppb/K (N35, N51, Y52). These residues are, or are adjacent to, aromatic residues, which deshield nearby amide protons to give more positive coefficients.⁴¹ Four residues (T12, A13, N35, G43) are located in flexible loops, which can experience abnormal gradients.⁴⁵ Some of the discrepancies may also arise because the fluorine at position 36 is absent from the structure. We conclude that temperature coefficients are a good measure of hydrogen bonding in folded SH3.

Cosolutes altered the coefficients of several residues in the folded state (Figure 1). In urea, 8 of 45 coefficients were more negative compared to buffer, and in lysozyme, 12 out of 45 were more negative; however, 20 of 44 coefficients were less negative in sucrose than in buffer. Ficoll gave mixed results; gradients for three residues of 46 residues were less negative and eight were more negative. For all conditions, however, fewer than half of the coefficients were significantly altered, and none shifted from the 85% cutoff for participation in a hydrogen bond (Figure 1, blue box) to the 20% cutoff for hydrogen bonding (Figure 1, pink box), or vice versa. Taken together, there is no compelling reason to conclude that these cosolutes result in large changes to the folded state.

Coefficients for the unfolded state were quantified for 23 residues. Interpretation for the unfolded state must be especially parsimonious, because temperature gradients are poor predictors of hydrogen bonding in unstructured peptides and in proteins undergoing conformational exchange,⁴⁵ both of which apply to unfolded SH3.^46,47 For urea, only 1 residue out of 15 was altered, suggesting no change. Slopes were made more positive for 13 out of 19 residues in sucrose and 5 out of 11 residues in Ficoll, while 10 of 19 residues were more negative in lysozyme. For both states in cosolute solutions (except for unfolded lysozyme), less than half of the changes in the amide proton coefficients were significant (as determined by comparing the differences to the uncertainties, Table S1). There was no pattern to the significant changes, and adding stabilizing or destabilizing cosolutes does not shift coefficients above or below the 85% cutoff of −4.6 ppb/K. The small magnitude of the changes and the lack of a pattern favor the null hypothesis; i.e., hydrogen bonding in the folded state and the unfolded ensemble is largely unaffected by cosolutes.

We also measured composite chemical shift perturbations, Δδ_comp, caused by the cosolutes:⁴⁸

$$\begin{gathered} \mathrm{\Delta }{\delta }_{\text{comp}}=\left[{\left({\mathrm{\Delta }}^1{\mathrm{H}}_{\text{consolute}-\text{buffer}},\text{ppm}\right)}^2 \\ +{\left({\mathrm{\Delta }}^{15}{\mathrm{N}}_{\text{consolute}-\text{buffer}},\text{ppm}\cdot \mathrm{0}.154\right)}^2\right] \end{gathered}$$ (4)

The data are compiled in Table S2. The locations of the changes show no obvious pattern with respect to the structure of the folded state (Figures S2 and S3). Perturbations in sucrose and Ficoll range between 0.01 and 0.11 ppm, indicative of weak cosolute–protein interactions and consistent with observations for another polymer, polyvinylpyrrolidone.⁴⁹ In urea, the maximum perturbation is slightly larger, 0.14 ppm, while the average perturbation in lysozyme (0.08 ppm for both states) was larger than that for other cosolutes, with an upper limit of 0.19 ppm, consistent with observations for SOD1 in 50 g/L lysozyme.⁵⁰ The average perturbation across all cosolutes ranges from 0.02 to 0.05 ppm (Table S3). Furthermore, the differences in Δδ_comp values between the folded and unfolded states are insignificant (i.e., <0.02 ppm⁴⁹). Ultimately, analysis of both amide proton temperature coefficients and the Δδ_comp indicates that the cosolutes do not dramatically affect the structure of either state.

Activation Parameters in Buffer

Folding and unfolding rates were determined from 19F homonuclear exchange spectroscopy data, as described in the Experimental Methods. Equation 1 was used to determine $\mathrm{\Delta }{G}_{\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$ and $\mathrm{\Delta }{G}_{\mathrm{F}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$, while rates from 288 to 313 K were used to determine $\mathrm{\Delta }{H}_{\mathrm{F},\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$, $-T\mathrm{\Delta }{S}_{\mathrm{F},\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$, and $\mathrm{\Delta }{C}_{p,\mathrm{F},\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$ (Figure 2, Table S1). Two- and three-parameter fits were tested. The standard deviations of the rates were used to drive a Monte Carlo analysis of uncertainties for the three-parameter fit, and a weighted linear regression was used for the two-parameter fit (Experimental Methods).

Figure 2.

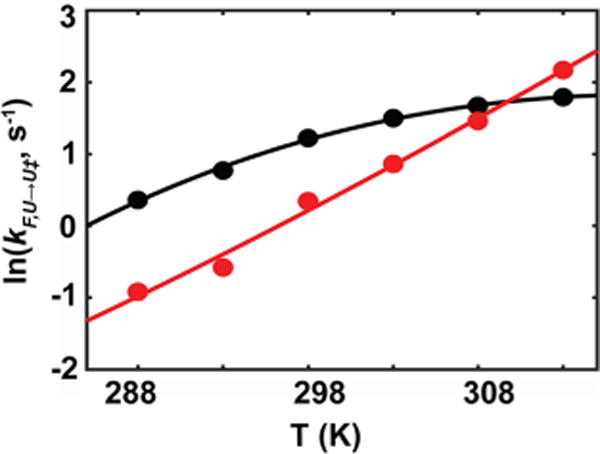
Temperature dependence of folding rates (black) and unfolding rates (red) for SH3 in buffer. Data were fit with eq 3, incorporating $\mathrm{\Delta }{C}_{p,\mathrm{F},\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$. The uncertainties (one standard deviation) are smaller than the points, and are listed in the Supporting Information (Table S4).

Analysis of the residuals from the two- and three-parameter fits was used to assess each model. The idea is that an appropriate model will result in random residuals. The concavity of the residuals for the folding data fitted with the two parameters (Figure S4) and the random residuals from the three-parameter fit suggest that inclusion of the third parameter, $\mathrm{\Delta }{C}_{p,\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$, is appropriate for folding. For unfolding, however, both fits give random-looking residuals, perhaps favoring a two-parameter fit, and consistent with the observation that either fit is appropriate for chymotrypsin inhibitor 2 (CI2) unfolding.²³ The key point is that $\mathrm{\Delta }{C}_{p,\mathrm{F}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$ is smaller than $\mathrm{\Delta }{C}_{p,\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$ because more surface area is buried from the unfolded state to the transition state than from the transition state to the folded state.²³

$\mathrm{\Delta }{G}_{\mathrm{F},\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$, $\mathrm{\Delta }{H}_{\mathrm{F},\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$, $-T\mathrm{\Delta }{S}_{\mathrm{F},\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$, and $\mathrm{\Delta }{C}_{p,\mathrm{F},\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$ in buffer determined from the three- and two-parameter fits are compiled in Table 1. Even though the $\mathrm{\Delta }{H}_{\mathrm{F},\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$ (and $-T\mathrm{\Delta }{S}_{\mathrm{F},\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$) values from the two procedures are not always within the uncertainties of the measurements, the large r and low P_r values indicate that it is reasonable to set $\mathrm{\Delta }{C}_p^{{\circ }^{\prime }\mathrm{‡}}=0$ for unfolding.

Table 1.

Activation Parameters for Folding (U → U^‡) and Unfolding (F → U^‡) at 303 K

conditiona	reaction	ΔG°′‡ (kcal/mol)	ΔH°′‡ (kcal/mol)	−TΔS°′‡ (kcal/mol)	rb	Prc
buffer	U → U‡ d	16.85 ± 0.01e	8.1 ± 0.2e	8.7 ± 0.2e	NAf
	U → U‡ g	16.85 ± 0.01e	9.0 ± 0.2	7.9 ± 0.2	0.94	1.4
	F → U‡ h	17.24 ± 0.01	22.8 ± 0.2e	−5.5 ± 0.2e	NAf
	F → U‡ g	17.24 ± 0.01	22.1 ± 0.2	−4.9 ± 0.3	0.99	1.4
100 g/L urea	U → U‡ d	17.85 ± 0.01	6 ± 2e	12 ± 2e	NAf
	F → U‡ g	16.95 ± 0.01	16.7 ± 0.9	−0.3 ± 0.9	0.96	10
50 g/L TMAO	U → U‡ d	16.48 ± 0.04	6 ± 1e	10.3 ± 0.9e	NAf
	F → U‡ g	17.73 ± 0.04	28 ± 1	−10.0 ± 0.9	0.99	10
200 g/L sucrose	U → U‡ d	16.71 ± 0.03	8.5 ± 0.9e	8.2 ± 0.6e	NAf
	F → U‡ g	17.71 ± 0.03	25.3 ± 0.5	−6.9 ± 0.6	0.99	10
200 g/L Ficoll	U → U‡ d	16.76 ± 0.02	6.4 ± 0.5e	10.3 ± 0.7e	NAf
	F → U‡ g	17.52 ± 0.04	26.2 ± 0.5	−8.8 ± 0.6	0.99	3.7
100 g/L lysozyme	U → U‡ d	17.70 ± 0.02	9.8 ± 0.9e	7.9 ± 0.9e	NAf
	F → U‡ g	17.32 ± 0.03	23.4 ± 0.8	−6.1 ± 0.9	0.99	10

^aAll at pH 7.2 ± 0.1.

^br, Pearson correlation coefficient.

^cP_r, percent probability that r arises from uncorrelated data.⁴²

^d $\mathrm{\Delta }{C}_p^{{\circ }^{\prime }\mathrm{‡}}=-0.59$ kcal/mol.

^eTemperature-dependent with a reference temperature of 303 K.

^fNA, not applicable; not a linear fit.

^g $\mathrm{\Delta }{C}_p^{{\circ }^{\prime }\mathrm{‡}}=0$.

^h $\mathrm{\Delta }{C}_p^{{\circ }^{\prime }\mathrm{‡}}=0.3$ kcal/mol K.

Activation Parameters in Cosolutes

The temperature dependence of folding and unfolding rates in buffer and cosolutes (Figure 3, Table S4) was used to determine the activation parameters (Table 1). The cosolute concentrations and temperatures were selected which allowed quantification of kinetics. These ranges are limited by the equilibrium stability of the protein. That is, low signal prevents rate quantification when the population of the folded or unfolded state is less than 10%. These limiting conditions restrict the ability to assess curvature and hence the ability to quantify $\mathrm{\Delta }{C}_p^{{\circ }^{\prime }\mathrm{‡}}$. Since crowding has only a small effect on the equilibrium heat capacity of SH3 unfolding,⁷ we set $\mathrm{\Delta }{C}_{p,\mathrm{F},\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$ to the buffer value for folding, while the large r values and the low P_r values indicated that setting $\mathrm{\Delta }{C}_p^{{\circ }^{\prime }\mathrm{‡}}$ to zero for unfolding is appropriate (Experimental Methods). The changes in the activation parameters compared to buffer are given in Table S5. The equilibrium values calculated from the kinetic data are given in Table S6.

Figure 3.

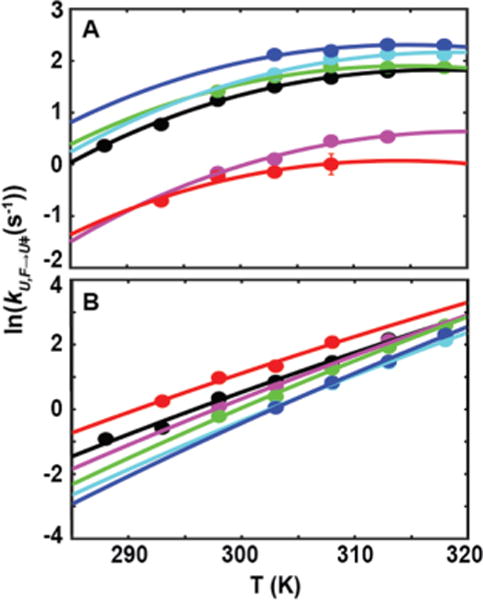
Temperature dependence of folding (A) and unfolding (B) of SH3 in buffer and cosolutes. Buffer, black; 100 g/L urea, red; 50 g/L TMAO, blue; 200 g/L sucrose, cyan; 200 g/L Ficoll, green; 100 g/L lysozyme, magenta. Folding rates in panel A are fit with $\mathrm{\Delta }{C}_{p,\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}=-0.59$ kcal/mol K, while unfolding rates in panel B are fit with $\mathrm{\Delta }{C}_{p,\mathrm{F}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}=0$. The uncertainties are smaller than the points, and are listed in Table S4.

Viscosity Correction

A potential shortcoming of Eyring analysis is that the protein is treated as a small molecule in the gas phase. Kramers’ rate theory accounts for diffusion as the protein crosses the reaction barrier.⁵¹ According to the Stokes–Einstein relationship, viscosity is proportional to diffusion^52,53 and, therefore, contributes to the rate

$$k=\frac{A}{\eta {(T)}^{\beta }}{\mathrm{e}}^{-\mathrm{\Delta }{G}^{\mathrm{‡}}/k_{\mathrm{B}}T}$$ (5)

where k is the rate, A is a temperature- and viscosity-independent prefactor, and η(T)^β is the temperature dependence of the viscosity. The Stokes–Einstein relationship predicts a β of unity and therefore a linear dependence of rate on viscosity, but β values between 0 and 1 and even deviations from linearity have been observed.⁵⁴ Tollinger et al. demonstrated a linear decrease of the SH3 folding rate with increasing viscosity in glycerol.⁵⁵ Therefore, we assumed a β of unity for the small cosolutes and adjusted the folding rates accordingly

$$k_{\mathrm{o}}=k\frac{{\eta }_{\mathrm{c}}}{{\eta }_{\text{buffer},303\mathrm{K}}}=k{\eta }_{\text{rel}}$$ (6)

where k₀ is the viscosity-adjusted rate, η_c is the viscosity, η_buffer,303K is the viscosity of water at 303 K (0.8 cP), and η_rel is the viscosity adjusted to buffer at 303 K. Wong et al.²⁵ and Perl et al.²⁷ used similar analyses.

Diffusion of CI2 in Ficoll and lysozyme deviates from Stokes–Einstein behavior because the macroviscosity of the solution does not match the microviscosity felt by the protein.^56–58 Therefore, we chose to not interpret the Ficoll data and only considered the viscosity effects for TMAO, urea, and sucrose. The adjusted rates are listed in Table S4, and the temperature dependence of the adjusted rates was determined as described above. The adjustment lowers the values of $\mathrm{\Delta }{H}_{\mathrm{F},\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$and $-T\mathrm{\Delta }{S}_{\mathrm{F},\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$, but the signs of $\mathrm{\Delta }\mathrm{\Delta }{H}_{\mathrm{F},\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$ and $-T\mathrm{\Delta }\mathrm{\Delta }{S}_{\mathrm{F},\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$ (Supporting Information, Table S5) in crowded solutions are unchanged. Therefore, our interpretations are unaffected and we concentrate the Discussion on the results from the unadjusted Eyring analysis.

DISCUSSION

Activation Parameters in Buffer Alone

We first sought to determine if SH3 is a representative protein for studies of folding and unfolding. $\mathrm{\Delta }{H}_{\mathrm{U}\to \mathrm{U}\mathrm{‡},303\mathrm{K}}^{{\circ }^{\prime }\mathrm{‡}}$ is positive (Table 1), suggesting that the cost of breaking water–protein bonds in the unfolded ensemble outweighs the benefit of forming intra-protein interactions in the transition state. $\mathrm{\Delta }{H}_{\mathrm{F}\to \mathrm{U}\mathrm{‡},303\mathrm{K}}^{{\circ }^{\prime }\mathrm{‡}}$ is also positive (Table 1), indicating the cost of breaking native intraprotein interactions is greater than the benefit of forming water–protein interactions in the newly exposed surface of the transition state. These suggestions are consistent with data for CI2,²³ protein L,³² hisactophilin,²⁵ and NTL9.³¹

$-T\mathrm{\Delta }{S}_{\mathrm{U}\to \mathrm{U}\mathrm{‡},303\mathrm{K}}^{{\circ }^{\prime }\mathrm{‡}}$ is positive, meaning that the transition state has a lower entropy than the unfolded state. This observation suggests the lower configurational entropy of the transition state compared to the unfolded ensemble overcomes the increase in entropy as solvent is released upon burial of hydrophobic area. $-T\mathrm{\Delta }{S}_{\mathrm{F}\to \mathrm{U}\mathrm{‡},303\mathrm{K}}^{{\circ }^{\prime }\mathrm{‡}}$ is negative (Table 1), indicating that the transition state is higher in entropy than the folded state. This observation is consistent with CI2²³ and CspB,^27,28 suggesting that, like folding, the increase in conformational entropy dominates the solvent-ordering effects from exposing hydrophobic surface.

Whether the enthalpy or entropy contributes more to the pathway can be determined by comparing the signs of $\mathrm{\Delta }{H}_{\mathrm{F},\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$ and $-T\mathrm{\Delta }{S}_{\mathrm{F},\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$ to that of $\mathrm{\Delta }{G}_{\mathrm{F},\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$ (Table 1). Sign analysis shows that, at 303 K, the entropic contribution to folding slightly outweighs the enthalpic contribution, but the enthalpic contribution dominates the free energy barrier to unfolding.

$\mathrm{\Delta }{C}_{p,\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$ is negative in buffer, indicating a decrease of solvent exposure as the unfolded state forms the transition state. $\mathrm{\Delta }{C}_{p,\mathrm{F}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$ is positive but small, indicating a small increase in surface area on unfolding. The data indicate that the solvent exposure of the transition state lies between the unfolded and folded states but more closely resembles the folded state. This observation is consistent with other data indicating that only 25% of the SH3 surface exposed in the unfolded state is also exposed in the transition state.⁵⁵ The signs of $\mathrm{\Delta }{C}_p^{{\circ }^{\prime }\mathrm{‡}}$ for folding and unfolding agree with observations for other proteins.^{23,28,29,31,32} Finally, the sign of the measured equilibrium heat capacity change for SH3 unfolding, $\mathrm{\Delta }{C}_p^{{\circ }^{\prime }}$, matches the prediction from the difference of activation values $[\mathrm{\Delta }{C}_{p,\mathrm{F}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}-\mathrm{\Delta }{C}_{p,\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}]$.⁷ In summary, our activation parameters indicate the folding and unfolding of SH3 resembles that of other small proteins.

Cosolutes and SH3 Structure

Next, we considered the feasibility of assigning cosolute effects to the folded state or the unfolded ensemble by adapting ideas from Φ-value analysis.⁵⁹ To determine if an interaction is present in the transition state, Φ-value analysis compares the change in activation free energy for folding and unfolding to the change in the equilibrium stability of a wild-type protein caused by an amino acid substitution that deletes the potential interaction.⁵⁹ Interpreting Φ-values is simplified if the free energy of either the folded or unfolded state can be aligned for the two proteins. The analysis can be expanded to activation enthalpies, entropies, and heat capacities. The free energy of the unfolded ensemble is often aligned, under the assumption that substitutions only affect the folded state.⁶⁰ A similar approach can be applied to crowding effects, where the perturbation is a cosolute, rather than a mutation. Although such comparisons of activation parameters are useful for characterizing the transition state,^59,61 it is important to bear in mind that cosolutes may affect structure, and therefore complicate analysis.

For experiments performed in cosolutes, it is tempting to align the folded state, because classical theories assume that stabilizing cosolutes, both large and small, affect only the unfolded ensemble. However, cosolute-induced structural effects differ between proteins and between protein states. Some investigations report cosolute-induced structural changes via unfolded state compaction,^62,63 structural rearrangements,⁶⁴ and increased secondary structure content,^65,66 while others report no increase in secondary structure.^67,68

Unlike most protein systems, we can observe both the folded state and unfolded ensemble of SH3 in a single experiment, and we tested ideas about structural effects on both states by using amide proton temperature coefficients (Figure 1, Table S1)⁴¹ and chemical shift changes (Tables S2 and S3 and Figures S2 and S3).^49,69 Although we know that cosolutes interact with the SH3 unfolded ensemble,⁷ the cosolute-induced changes in chemical shift perturbations and changes between the folded and unfolded states in the presence of each cosolute are insignificant. Our analysis supports the null hypothesis: neither the structure of the folded state nor the unfolded ensemble is greatly changed by the cosolutes we studied. Therefore, we cannot align either end state.

One might also align the states based on solvation free energy,^70–72 but this approach poses a similar problem, because we cannot know absolute free energies. Although we understand that repulsive interactions between SH3 and the cosolute drive up the chemical potential and that attractive interactions drive down the potential, we can only measure differences. In summary, we cannot align either end state using either structural or solvation arguments, and we are forced to interpret cosolute-induced changes only as changes in the barriers to folding and unfolding.

Activation Parameters for Cosolutes Compared to Buffer

We quantified the cosolute-induced changes in the activation parameters compared to buffer along with their uncertainties (Figure 4, Table S5) as well as the equilibrium thermodynamic values calculated from the activation parameters (Table S6). Positive cosolute-induced changes (Figure 4, Table S5) represent increases in the barriers to folding and unfolding, while negative values represent decreases.

Figure 4.

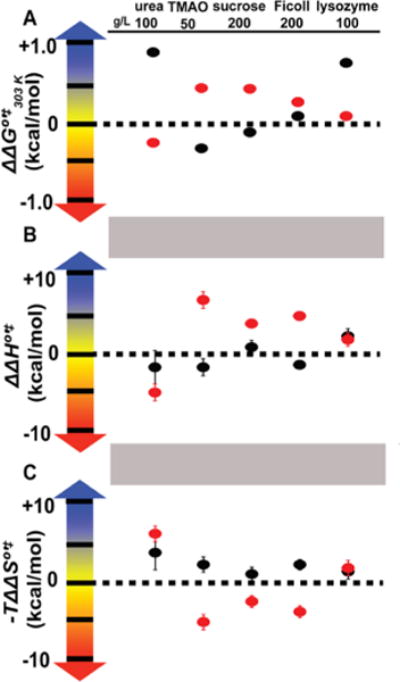
Changes in the activation free energy (A), enthalpy (B), and entropic component (C) in cosolutes. Folding, black; unfolding, red. Changes in the activation free energy were determined at 303 K. Changes in activation enthalpy and entropy were determined at 303 K for folding, and without a reference temperature for unfolding, as described in the text. Uncertainties (one standard deviation) in panel A are smaller than the points. Changes in entropy were multiplied by 303 K. All values and uncertainties are listed in Table S5.

Urea

To provide a benchmark, we started with urea, because its effects on equilibrium stability and folding kinetics are well-known.^{7,11,13,26,28,73} Makhatadze and Privalov used calorimetry to determine that the urea-induced equilibrium thermodynamic destabilization of RNase A, lysozyme, and cytochrome c arises from a positive, stabilizing $-T\mathrm{\Delta }\mathrm{\Delta }{S}_{\mathrm{U}}^{{\circ }^{\prime }}$ that is overpowered by a negative, destabilizing $\mathrm{\Delta }\mathrm{\Delta }{H}_{\mathrm{U}}^{{\circ }^{\prime }}$.⁷³ The negative $\mathrm{\Delta }\mathrm{\Delta }{H}_{\mathrm{U}}^{{\circ }^{\prime }}$ may arise from favorable hydrogen bonding between urea and the protein backbone,^73,74 while the positive $-T\mathrm{\Delta }\mathrm{\Delta }{S}_{\mathrm{U}}^{{\circ }^{\prime }}$, counterintuitive for a system where the equilibrium stability indicates formation of a disordered unfolded state, arises either from the ordering of solvent around newly exposed protein or from the restriction of protein motion upon hydrogen bonding.²⁶ This early calorimetric work revealed the entropy of the cosolute, urea, and solvent may influence protein equilibrium thermodynamic stability.

Urea lowers $\mathrm{\Delta }{G}_{\mathrm{F}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$ and raises $\mathrm{\Delta }{G}_{\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$ (Figure 4A), consistent with previous studies of SH3⁵⁵ and tryptophan synthase.²⁶ The $\mathrm{\Delta }{G}_{\mathrm{U}}^{{\circ }^{\prime }}$ calculated from these values is negative, in agreement with observations that urea destabilizes proteins.⁷³

Urea also lowers $\mathrm{\Delta }{H}_{\mathrm{F}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$, consistent with observations for tryptophan synthase,²⁶ but its effect on $\mathrm{\Delta }{H}_{\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$ cannot be resolved (Figure 4B). For unfolding, the decrease makes intuitive sense because urea interacts favorably with the backbone,⁷³ and more backbone is exposed and available to interact in the transition state than in the folded state. The derived $\mathrm{\Delta }\mathrm{\Delta }{H}_{\mathrm{U}}^{{\circ }^{\prime }}$ is also negative, in agreement with previous studies.^7,73

Entropically, urea raises both $-T\mathrm{\Delta }{S}_{\mathrm{F}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$ and $-T\mathrm{\Delta }{S}_{\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$ (Figure 3C, Table S5), as was seen for Bacillus subtilis²⁸ CspB in urea and B. caldolyticus CspB²⁷ and human fibroblast growth factor⁷⁵ in guanidinium chloride. A more positive $-T\mathrm{\Delta }{S}_{\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$ suggests that the loss of entropy from the conformational ordering of SH3 on its way from the unfolded ensemble to the transition state outweighs the concomitant disordering of urea molecules as they escape. The entropic hindrance to unfolding likely arises because the unfavorable ordering of urea on the increased urea-attracting surface of the transition state outweighs the gain in conformational entropy of the protein.

Analysis of the relative contributions indicates that, for unfolding, $\mathrm{\Delta }\mathrm{\Delta }{H}_{\mathrm{F}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$ dominates, while, for folding, $-T\mathrm{\Delta }\mathrm{\Delta }{S}_{\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$ is more important. The good agreement between the effects of urea on SH3 activation parameters and the effect of urea on other proteins indicates that SH3 is a reasonable model, and that our method is valid for evaluating the effects of other cosolutes. As observed for equilibrium and kinetic measurements of protein folding in urea, both protein–urea interactions and cosolute and solvent entropy influence SH3 folding barriers.

TMAO and Sucrose

Lee and Timasheff’s work showed that sucrose⁷⁶ and other stabilizing osmolytes^77–79 are preferentially excluded from the protein surface, resulting in preferential hydration of the protein.⁸⁰ Osmolytes like trimethylamine N-oxide (TMAO) and sucrose are more strongly excluded from the unfolded state than the folded state, leading to stabilization, a conclusion compatible with entropically driven stabilization.⁸¹

Bolen pioneered the idea of an osmophobic effect⁸² attributed to unfavorable interactions between osmolytes and the protein backbone.^71,83–86 The osmophobic effect was subsequently revealed to be dominated by a stabilizing enthalpic contribution balanced by a destabilizing entropic contribution,^87,88 directly contradicting entropically driven stabilization, though entropic stabilization mechanisms have been proposed.^{14,15,89–91} The origin of the enthalpic contribution is not well understood, although Rose and colleagues suggest that stabilization is inversely related to the fractional polar surface area of the osmolyte.⁹² In terms of equilibrium thermodynamics, stabilizing osmolytes appear to use a mechanism opposite to that of destabilizing osmolytes.¹³ Assessing changes in activation parameters, however, will elucidate whether the mechanisms are truly opposite, or point to other effects undetected at equilibrium. Recent studies indicate stabilization mechanisms may vary between stabilizing osmolytes, emphasizing the need for a kinetic investigation.^93,94

Our equilibrium-from-kinetics values for osmolytes (Table S6) agree with observations of enthalpic-mediated stabilization,^11,87,95 and are the opposite of what is observed for urea. TMAO and sucrose increase $\mathrm{\Delta }{G}_{\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$ (Figure 4A) and decrease $\mathrm{\Delta }{G}_{\mathrm{F}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$, consistent with other findings^95–99 and support an “anti-urea” mechanism for stabilizing osmolytes.

We observe that TMAO decreases $\mathrm{\Delta }{H}_{\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$ and increases $\mathrm{\Delta }{H}_{\mathrm{F}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$ (Figure 4B). These trends are consistent with the idea of unfavorable enthalpic interactions between these cosolutes and the protein backbone. Folding is likely enthalpically favored because it minimizes unfavorable protein–osmolyte interactions relative to the more exposed unfolded and transition states. The derived $\mathrm{\Delta }\mathrm{\Delta }{H}_{\mathrm{U}\to \text{TMAO}}^{{\circ }^{\prime }}$ is stabilizing (Table S5), agreeing with previous observations in TMAO and other stabilizing osmolytes.^11–13,95

Entropically, TMAO hinders folding and promotes unfolding (Figure 4C), the opposite of predictions based exclusively on hard-core repulsions. Therefore, compaction of the unfolded ensemble cannot be the sole driving force. We suggest that, analogous to the ordering of urea molecules around unfolded SH3, the entropic effect of TMAO may arise from the increased entropy of the cosolute as it is excluded from the larger unfolded surface, or if the protein is compacted, from water release. The derived change in equilibrium entropy is destabilizing (Table S6), consistent with a preferential hydration mechanism.^87,88

Sucrose uses a mechanism like TMAO for unfolding, but the activation parameters could not be resolved for folding. At concentrations greater than 0.3 M, sucrose has been shown to switch from preferential hydration to preferential folded-state accumulation, with more protein adhering to the folded state relative to the unfolded ensemble.⁹³ Preferential folded state accumulation has also been observed for RNase A in sorbitol^77,79 and trehalose.⁷⁸ In preferential accumulation, the folded state is promoted through the entropically favorable release of water from the surface.⁷⁹ We suspect the effects of preferential hydration in TMAO are counteracted by preferential folded-state accumulation of sucrose.

Sign analysis shows that $\mathrm{\Delta }\mathrm{\Delta }{H}_{\mathrm{U}\to \mathrm{U}\mathrm{‡}\text{TMAO}}^{{\circ }^{\prime }\mathrm{‡}},\mathrm{\Delta }\mathrm{\Delta }{H}_{\mathrm{F}\to \mathrm{U}\mathrm{‡},\text{TMAO}}^{{\circ }^{\prime }\mathrm{‡}}$, and $\mathrm{\Delta }\mathrm{\Delta }{H}_{\mathrm{F}\to \mathrm{U}\mathrm{‡},\text{sucrose}}^{{\circ }^{\prime }\mathrm{‡}}$ dominate $\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathrm{F},\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$. In agreement with an “anti-urea” mechanism for stabilizing osmolytes, $\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathrm{F}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$, $\mathrm{\Delta }\mathrm{\Delta }{H}_{\mathrm{F}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$, and $-T\mathrm{\Delta }\mathrm{\Delta }{S}_{\mathrm{F}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$ in TMAO and sucrose have an effect opposite to that observed in urea. However, $-T\mathrm{\Delta }\mathrm{\Delta }{S}_{\mathrm{U}\to \mathrm{U}\mathrm{‡},\text{TMAO}}^{{\circ }^{\prime }\mathrm{‡}}$ and $-T\mathrm{\Delta }\mathrm{\Delta }{S}_{\mathrm{U}\to \mathrm{U}\mathrm{‡},\text{urea}}^{{\circ }^{\prime }\mathrm{‡}}$ have the same sign, weakening the “anti-urea” hypothesis. This observation suggests that, although stabilizing and destabilizing osmolytes have opposing affinities for proteins, the contributions are weighted differently. Finally, although stabilizing osmolytes enthalpically promote folded-state repulsion, likely through avoidance of unfavorable interactions, the entropic contributions may arise from increases in cosolute and solvent entropy.

Ficoll

This branched sucrose polymer, and other synthetic polymers, are predicted to interact with proteins in two ways, both of which are stabilizing: entropically driven excluded volume effects^100,101 and preferential hydration.^11,12 Although data from equilibrium stability studies of SH3 could not be resolved into changes in enthalpy and entropy,⁷ Benton et al.¹² showed that sucrose and Ficoll increase $\mathrm{\Delta }{H}_{\mathrm{U}}^{{\circ }^{\prime }}$ for CI2, supporting a preferential hydration model. Senske et al.¹¹ also observed a positive ΔΔH_u for ubiquitin in a similar polymer, dextran. Although these studies suggest that preferential hydration is the stabilization mechanism of synthetic polymers such as Ficoll, the relative contributions of preferential hydration and steric repulsions remain unclear. Comparing the activation parameters obtained in Ficoll to those obtained in sucrose and TMAO can help unravel the relative contributions.

The effects of Ficoll on the activation free energy of folding and unfolding vary with the protein. For instance, Ficoll has been shown to both decrease^65,102 and increase^68,103 $\mathrm{\Delta }{G}_{\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$, while increasing^62,65,103 or having no effect on⁶⁵ $\mathrm{\Delta }{G}_{\mathrm{F}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$ relative to buffer. Another study hinted at more complicated effects, where Ficoll lowers $\mathrm{\Delta }{G}_{\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$ for a fast-folding step but lowers $\mathrm{\Delta }{G}_{\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$ for a slow folding step.¹⁰⁴ We observe that Ficoll increases the equilibrium stability, i.e., $\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathrm{U}}^{{\circ }^{\prime }}$, of SH3 via a larger $\mathrm{\Delta }{G}_{\mathrm{F}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$ (Figure 4A). The effects mirror those observed for TMAO and sucrose.

The signs of the enthalpy and entropy changes in Ficoll compared to buffer are the same as those for TMAO for both folding and unfolding. The signs are also the same for unfolding in sucrose, but for folding in sucrose, the values are within uncertainty of zero. In Ficoll, folding is enthalpically favored, while unfolding is enthalpically hindered, while the opposite is observed for the entropic effects, indicating that the preferential hydration mechanism proposed for TMAO also applies to Ficoll. As suggested by Record’s group,⁷² the appearance of a negative $\mathrm{\Delta }\mathrm{\Delta }{H}_{\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$ in Ficoll not observed in sucrose may arise from the shielding of sucrose monomers in this branched polymer. This restriction may prevent preferential binding of sucrose monomers to the native state, resulting in the dominance of preferential hydration effects also seen in TMAO.

For TMAO, sucrose, and Ficoll, the trends in $\mathrm{\Delta }\mathrm{\Delta }{H}_{\mathrm{F},\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$ and $-T\mathrm{\Delta }\mathrm{\Delta }{S}_{\mathrm{F},\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$ conflict with traditional crowding theory in three ways. First, the presence, let alone the dominance, of an enthalpic contribution contradicts the model based solely on hard-core repulsive entropic effects.¹⁰¹ As stated above, the enthalpic contributions point to preferential hydration.^11,12 Second, the entropic effects conflict with stabilization of the folded state predicted by pure steric repulsions;^90,101 instead of promoting folding and hindering unfolding, the entropic changes promote unfolding and hinder folding. This contradiction underscores the importance of cosolute and solvent entropy. Third, excluded volume theory predicts that larger molecules should be stronger stabilizers because they exclude more volume, but equilibrium data have shown that smaller molecules are more stabilizing.^7,105 Our $\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathrm{F},\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$ data for TMAO, sucrose, and Ficoll show that this trend also applies to the transition state.

Lysozyme

Lysozyme destabilizes CI2¹⁰⁶ and SH3,⁷ but its effect on the equilibrium enthalpy and entropy changes has not been elucidated. Line width and tumbling-time data⁷ indicate that protein destabilization arises, at least in part, from lysozyme–SH3 interactions with the unfolded ensemble. Lysozyme also forms nonspecific, destabilizing interactions with CI2.^58,106 Since lysozyme interacts favorably with proteins, analysis of kinetic data can determine whether lysozyme acts like urea or other contributions, such as excluded volume, come into play. If lysozyme is merely a giant urea molecule, the changes in activation parameters should resemble those induced by urea.

Like urea, lysozyme decreases $\mathrm{\Delta }{G}_{\mathrm{U}}^{{\circ }^{\prime }\mathrm{‡}}$ (Table S6) and raises $\mathrm{\Delta }{G}_{\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$ (Figure 4A, Table S5). However, the similarity diverges for unfolding; urea decreases $\mathrm{\Delta }{G}_{\mathrm{F}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$, but lysozyme slightly increases this energy (Figure 4A). Also unlike urea, for which $\mathrm{\Delta }\mathrm{\Delta }{H}_{\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$ is within the uncertainty of zero, lysozyme increases $\mathrm{\Delta }{H}_{\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$ as well as $\mathrm{\Delta }{H}_{\mathrm{F}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$. Although the contributions to the unfolding reaction resemble osmolytes and Ficoll, $\mathrm{\Delta }\mathrm{\Delta }{H}_{\mathrm{U}\to \mathrm{U}\mathrm{‡}}^{{\circ }^{\prime }\mathrm{‡}}$ is of the opposite sign. These data show that neither the preferential binding model of urea^73,74 nor the preferential hydration model of TMAO and Ficoll^11,12 adequately explain SH3–lysozyme interactions. We suspect that, in addition to transient chemical interactions, lysozyme exhibits a macromolecular effect. Nevertheless, these effects are diametrically opposed to the macromolecular effect expected from simple theories, which predicts purely entropic stabilization of the native state with no enthalpic contribution.

A large portion of our data as well as data from other groups can be explained using recent ideas from the Harries group.^107–110 These new ideas involve an effective interaction between cosolute and protein. For stabilizing cosolutes, in addition to a hard-core steric component, one must invoke enthalpically repulsive and entropically attractive cosolute–protein interaction. More specifically, this concept can explain much of our TMAO and sucrose data and the differences between the effects of Ficoll, sucrose, and TMAO, including the observation that small cosolutes can have a larger effect than macromolecular cosolutes.

CONCLUSIONS

Our work provides kinetic evidence for a preferential hydration mechanism of stabilization by osmolytes. However, the results reveal nuances that are not detected at equilibrium for stabilizing versus destabilizing osmolytes, and even among stabilizing osmolytes themselves. The kinetic resemblance of Ficoll to TMAO suggests a preferential hydration mechanism, while the presence of an enthalpic effect lacking in sucrose may indicate a macromolecular effect, because the polymeric nature of Ficoll hinders folded state formation. For the stabilizing osmolytes and Ficoll, the entropy changes are opposite those predicted for a pure steric-repulsion-based, excluded volume mechanism, suggesting the entropy of the solvent and cosolute, rather than the configurational entropy of the protein, dominates entropic effects. Finally, neither the preferential interaction model of urea nor the preferential hydration model of osmolytes fully explain the mechanism of the biologically relevant crowder, lysozyme. Although crowding agents are used in reductionism-based efforts to assess the crowding phenomena that occur in cells, the underlying mechanisms are complex and these polymers do not act like globular protein crowders. Thus, not only should protein folding and misfolding be studied under crowded conditions, but also the crowding agents themselves should be physiologically relevant.¹⁹