Abstract
Forbes, Wright, Markon, and Krueger (2017) make a compelling case for proceeding cautiously with respect to the overinterpretation and dissemination of results using the increasingly popular approach of creating “networks” from co-occurrences of psychopathology symptoms. We commend the authors on their initial investigation and their utilization of cross-validation techniques in an effort to capture the stability of a variety of network estimation methods. Such techniques get at the heart of establishing “reproducibility”, an increasing focus of concern in both psychology (e.g., Pashler & Wegenmakers, 2012) and science more generally (e.g., Baker, 2016). However, as we will show, the problem is likely worse (or at least more complicated) than they initially indicated. Specifically, for multivariate binary data, the marginal distributions enforce a large degree of structure on the data. We show that some expected measurements – such as commonly used centrality statistics – can have substantially higher values than what would usually be expected. As such, we propose a nonparametric approach to generate confidence intervals through Monte Carlo simulation. We apply the proposed methodology to the National Comorbidity Survey - Replication, provided by Forbes et al, finding that the many of the results are indistinguishable from what would be expected by chance. Further, we discuss the problem of multiple testing and potential issues of applying methods developed for one-mode networks (e.g., ties within a single set of observations) to two-mode networks (e.g., ties between two distinct sets of entities). When taken together, these issues indicate that the psychometric network models should be employed with extreme caution and interpreted guardedly.
Introduction
We commend the authors – Forbes, Wright, Markon, and Krueger (2017) – for bringing to light one of the issues that has arisen recently when attempting to make inferences about the structure of so-called psychopathology networks1 Specifically, Forbes et al. note that there are emerging regarding our ability to determine the extent that network structures obtained from two (or more) samples are similar or different in key respects. That is, do they replicate? Judging the similarity of various symptom network solutions can be challenging for a number of reasons, not the least of which is the number of parameters modeled including the number of edges (paths) connecting nodes (symptoms) and various measures that are derived from these, perhaps most critically, centrality measures that speak to the relative importance of individual symptoms vis a vis the total network. Depending upon the specific measures of centrality under consideration, such centrality measures could represent a powerful way to identify symptoms that are more fundamental (as opposed to accessory) to a given syndrome, bridge distinct symptom networks, or strongly related to other symptoms.
However, to have confidence in the results of any single network estimation procedure, it is important to be able to demonstrate its replicability, that is how similar are the estimated edge weights and centrality parameters across two different samples. Problems in establishing “reproducibility” is an increasing focus of concern in both psychology (e.g., Pashler & Wagenmakers, 2012) and science more generally (e.g., Baker, 2016). As noted above, the sheer number of parameters estimated make establishing the similarity of two more networks challenging and traditional approaches such as intuitive “eye balling” of the magnitude of various measures of agreement, concordance, or replicability (for instance, the Pearson correlation coefficient, the intraclass correlation) – many of which will not be appropriate – fails to provide a framework for making strong inferential statements regarding replicability of network parameterizations. Moreover, for technical reasons, measures of association based on binary data provide special challenges owing to their sensitivity to base rates (i.e., marginal frequencies) which may differ across samples either by design or sampling effects. Having a methodology for assessing network similarity that adequately addresses this challenge would make it possible for researchers to validly judge reproducibility and replicability.
In this commentary, we describe a simple, yet effective method for generating empirical confidence intervals for whatever statistic is desired for inspection and demonstrate its use on a sample data set under the conditions described by Forbes et al. (in press). We then go on to provide some general comments regarding its application.
More specifically, we first review the notion of empirically creating appropriate null distributions for quantities of interest. We then discuss the application of such approaches to traditional one-mode networks where one set of nodes that are similar to each other or the same type (e.g., individuals). Following this, we provide an overview of the structure of two-mode matrices as commonly thought of in terms of network structure or graph theory, where there are two different types of nodes (e.g., symptoms and people). After that, we introduce the proposed hypothesis testing for two-mode binary networks and explicate the method by reanalyzing one of the data sets from Forbes et al. (2017) to obtain confidence intervals under an appropriate null distribution for edges and centrality statistics. This allows us to conduct, subsequent statistical tests can be performed by determining whether the statistic of interest lies within the null confidence interval. If it does, then we conclude that the observed network statistic is performing the same as it would under a random two-mode network; if it does not, then a process of potential interest is likely driving the observed value for the tested statistic.
Background for Proposed Test
In multivariate statistics, it is often difficult to derive the exact sampling distribution for many quantities of interest. A standard practice is to generate random data with appropriate constraints, fit the hypothesized model to these generated data, and then compare the quantity of interest when computed under random data with that in the observed network. If they are very similar, then we cannot conclude that the observed data are any different than random data. Such an approach is often employed in other areas of multivariate statistics (e.g., use of parallel analysis in factor analysis, Horn, 1965).
In parallel analysis, the eigenvalues obtained from the covariance (or correlation) matrix derived from the sample data are compared to the eigenvalues obtained from covariance (or correlation) matrices arising from completely random data2. The central idea behind of parallel analysis is that if a set of measured variables arises from a common factor model with f factors, then the f largest eigenvalues as computed from the data set should exceed that of the expected (e.g., average) eigenvalues of random data. One critical factor in making this comparison is how the random data are generated. Specifically, the constraints that are placed on each of the data sets in the comparison population are critical. If the eigen-decomposition is on the correlation matrix, a common constraint is the generated data should have the same sample size (e.g., the same number of observations) and the same number of variables. If the eigen-decomposition is on the covariance matrix, an additional constraint for consideration would be to ensure that the randomly generated variables had the same variances.
Similarly, corresponding procedures for comparing observed fit statistics to fit statistics derived from random data has been implemented in the domain of cluster analysis. Specifically, Steinley (2006, 2007, 2008) and Steinley and Brusco (2011) generated distributions based on random data to test the quality of a cluster solution and to determine whether the correct number of clusters had been chosen, respectively. Using this general approach, Steinley (2004) developed a method for sampling cluster agreement-matrices to approximate the statistic’s sampling distribution3. While used extensively in multivariate statistics, such approaches have also seen use in traditional network analyses – as explained in the following section.
One-mode Networks
For one-mode networks (e.g., the rows and the columns of the adjacency matrix describe the same entities, such as a friendship network) statistical inference has long been an active area of research and methodological development due to the fact that the standard inferential techniques relying on independence of observations does not apply. As a solution, it has been argued that the testing network statistics of interest can be obtained by generating a null distribution from a population of networks that have an appropriate structure that the researcher wishes to control. Generally, these networks are generated uniformly (e.g., each network has an equal chance of being selected and included in the population. Anderson, Butts, and Carley (1999) described an approach to conduct hypothesis testing on network level statistics when controlling for the number of observations (e.g., the number of actors or nodes) and the overall density (e.g., the number of links). Additional constraints can be added to the generation process, such as controlling for the number of mutual, asymmetric, and null ties. Furthermore, for one-mode networks, the notion of generating networks with specific properties has flourished with recent developments in exponential random graph modeling (see Hunter & Handcock, 2006).
Two-mode Matrices
Two-mode data binary data has long been of interest in the psychological sciences (Arabie & Hubert, 1990; Arabie, Hubert, & Schleutermann, 1990; Brusco & Steinley, 2006, 2007a, 2007b, 2009, 2011; Brusco, Shireman, & Steinley, in press; Rosenberg, Van Mechelen, & De Boeck, 1996). In terms of networks and graph theory, two-mode binary data can be thought of as a bipartite graph and represented in a standard data matrix with n rows and p columns (where, often, rows represent the subjects and columns represent the variables). In the network literature, these are often deemed affiliation matrices. Until recently, there has been a dearth of methods for generating binary affiliation matrices with fixed margins, with the ones being used somewhat cumbersome and inefficient and too slow for application to large networks (Admiraal & Handcock, 2008; Chen, Diaconis, Holmes, & Liu, 2005). However, within the last few years, a pair of papers have appeared (Harrison & Miller, 2013; Miller & Harrison, 2013) that provide a computationally efficient method for generating affiliation matrices with fixed margins.
Interestingly, the motivating example for this work arises out of ecology to test cohabitation of species in biogeographical data, where the data are often of the form species×habitat. As a bit of background, original work by Diamond (1975) made extensive claims about “species assembly rules” that aimed to explain the interaction between specific species and their chosen habitats – indeed, some of the relationships between species and habitats were quite strong. However, Connor and Simberloff (1979) argued that, if one controlled for the base rates of the different species and the different habitats, then many of these so-called “strong” associations could have arisen by random chance. According to Miller and Harrison (2013), this set off years of argument about the nature of null hypothesis testing and whether to control for the marginal distributions or not. Owing to the fact that the effect disappears when the marginal distributions are controlled for, the current guidelines recommend that the marginal distributions are fixed such that observed effects are not due to the base rates of the rows and columns alone.
If the two-mode matrix is viewed as a contingency table, then fixing both marginal distributions corresponds to Fisher’s exact test, with the following assumptions:
Each observation is classified into one and only one category of the row variable and into one and only one category of the column variable.
The N observations come from a random sample such that each observation has the same probability of being classified into the ith row and the jth column as any other observation.
The null hypothesis is: The event of an observation being in a particular row is independent of that same observation being in a particular column.
This framework will serve to generate the random matrices for our test, as described below.
Proposed Test
The goal of this commentary is to present such a test based on generating a set(s) of matrices from pre-specified marginal distributions. The desire is to provide a statistical context for evaluating the magnitude some measures of correspondence with respect to the expected parameter estimates generated from random processes with known base rates. Further, much like the ecology literature, we argue that in the psychopathology literature it is imperative to compare observed results to null distributions that have the same prevalences of the symptoms themselves and the same distributions of severity across the individuals. This is a necessary condition to begin making precise, generalizable statements about specific symptoms by guaranteeing that any observed/interpreted relationships between the variables is due to their co-occurrence within the same individuals are not an artifact imposed by the marginal distributions.
Holding the within-person marginal distributions constant is necessary because the goal of network analysis in some ways is much more lofty that that of the common cause models, such as factor analysis. In the latter, it is often assumed that all items loading onto the same factor should be (theoretically) exchangeable; however, in network analysis the goal is to discover the explicit connections between individual items – as such, the items themselves take on a much more pronounced role in the modeling process. Specifically, for factor models, knowing that a subject endorsed 3 out of 5 items on a disorder is often enough, in fact, that is what much of the diagnostic literature is predicated on; conversely, for network models, the specific 3 items are much more important because the goal is to make causal (or pseudo-causal) connections between specific items. The bar is much higher. Likewise, holding the within-item prevalences constant is extremely important as well. Specifically, it can easily be shown that items that have a higher prevalence of occurring are more likely to have observed edges in the network model. Consequently, it is important to model random items with the same rates of occurrence to ensure that observed network edges are not merely a byproduct of items that have been endorsed more than other items. Without such a reference, researchers will remain in the dark about what their findings indicate with these newer network models. The following two subsections describe how the the procedure works, with a more mathematical explanation provided in the Appendix.
Algorithm for Within Network Importance
The ingredients for testing so-called “within” network importance are fairly straight-forward. Namely, all that is required is the original data matrix Xn×p with n rows and p columns as well as the estimated network statistic of interest, say θ̂. The goal is then to obtain the sampling distribution for θ under the null distribution that the location of the ones (i.e., the presence of the symptom, say) in the binary matrix X are random, subject to the observed marginal distributions for both the rows and columns.
Procedurally, the process is fairly simple. First, the user must choose the number of random data matrices to generate. After this is chosen, each random matrix is generated such that it has identical column totals (e.g., each item prevalence is the same in the random matrices as in the observed matrix) and row totals (e.g., the severity profiles of the observations in the random matrices are the same as in the observed matrix). However, in the random generation process, the elements in the random matrices are generated such that the rows and columns are independent of each other conditional on the row totals and column totals (e.g., the marginal distributions) being the same. After all of the random matrices are generated, the statistic of interest (e.g., edge weights, centrality parameters, etc.) is computed on each of the random matrices. Finally, the statistic for the observed data is compared to the reference distribution derived from the random matrices, allowing for the calculation of a percentile score. If this score is between the 2.5 percntile and the 97.5 percentile, we can say that the observed data are providing results that are consistent with what we would expect to see in random data. That is, the p-values associated with the estimates do not exceed a nominal level of .05.
Algorithm for Between Importance
The first algorithm discusses determining whether the observed data deviates from the what would be observed via random chance and concerns network elements that are internal to one data set (hence, the moniker of “within”). However, it is also possible to compute the correspondence or stability of network statistics across different data sets, which we will term as “between”. To compute the correspondence between two networks, in additional data set, Yn2×p, is required (note that while the number of variables must be the same, the two data sets may have different numbers of observations). Network structures are then derived from both X and Y, and a measure of correspondence is computed. Then, pairs of random matrices are generated, with one corresponding to X and one corresponding to Y, and the respective marginal distributions are fixed to those of the observed matrices. The same measure of correspondence is computed for each pair for random matrices, allowing for the generation of sampling distribution under random chance to be obtained. The computation of percentile scores than proceeds in the same fashion as described for the within network importance.
Relationship to Bootstrapping
Recently, Epskamp, Boorsboom, and Fried (in press) have introduced methods for applying bootstrap techniques to psychological networks. These methods are designed to (i) assess the accuracy of estimated network connections, (ii) investigate the stability of centrality indices, and (iii) test whether network connections and centrality estimates for different variables differ from each other. The primary difference between the methodology proposed above and bootstrapping approach is that the former is assessing whether the observed effects are different than what we would expect from random chance while the latter assess stability and accuracy of coefficient estimation.
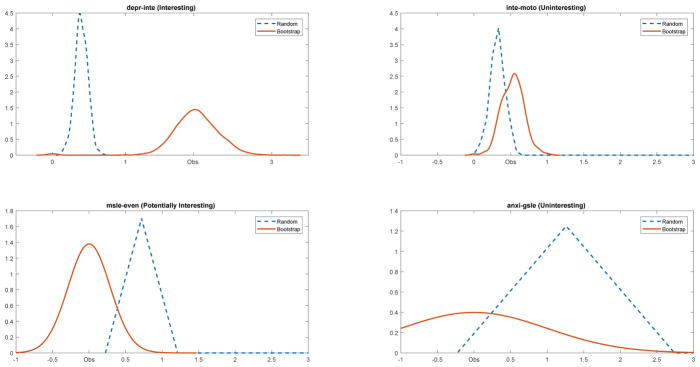
As such, it is possible, and as we see in the examples below, perhaps expected (due to the constraints placed on the network space due to the marginal distributions) that estimated network effects can be both simultaneously stable and not different than random chance. Additionally, a confidence interval around the either the connections between variables or the centrality estimates, as derived from the bootstrap approach, can not include zero and still overlap with (or even fall within) the confidence interval indicating what we would expect by chance alone. In that instance, the estimate would be stable, but not particulary interesting/informative – and, in such a scenario we would caution against interpreting the estimate because, while the effect is shown to exist, it is not different than what would be expected by chance alone. We summarize the four possible outcomes derived from the outcomes of the two testing procedures in Table 1.
Table 1.
Four Potential Outcomes Between Bootstrap Procedure and Random Chance
| Random Chance | |||
|---|---|---|---|
| v̂ ≠ vrc | v̂ = vrc | ||
|
| |||
| Bootstrap | v̂ ≠ v0 | Interesting | Uninteresting |
|
|
|||
| v̂ = v0 | Potentially Interesting | Uninteresting | |
|
|
|||
In Table 1, we provide the more general possibility of testing hypotheses (or constructing confidence interval) concerned with comparing the effects with a pre-specified null value, v04. Likewise, we can construct, from the procedure outlined above, the expected value of the effect under random chance, vrc. Then, the combined information of whether the estimate (v̂) is different than the hypothesized value (v0) and/or the value under random chance (vrc) is useful for determining the interestingness/importance of an effect 5. Obviously, the most interesting effect will be situations where it is shown that the estimate is both different from the hypothesized value and what is expected under random chance. Conversely, if effects are not different from what is expected under random chance, the information derived from the bootstrap method is uninteresting regardless of the degree of stability, accuracy, or difference from the hypothesized value. Lastly, when the effects are different from chance but not different from the hypothesized value, the result could be potentially interesting. In terms of the network diagram, this would correspond to unobserved links between pairs of variables. As such, each observed link can be interesting (different from zero, different from random chance) or uninteresting (not different from random chance); likewise, each unobserved link could be uninteresting (not different from zero, not different from random chance) or potentially interesting (not different from zero, different from random chance). We use “potentially” interesting because relationships (e.g., presence of links) and conditional independence (e.g., absence of links) are both inferred when the network diagram is visually inspected.
Example
The goal of these analyses is to infer the true underlying causal relationships between psychological symptoms, thus, a significant result would be one that informs us of relations above and beyond what their prevalence rates tell us. Given the length constraints of the commentary, we focus on demonstrating the within-network evaluation6 algorithm for the NCS-R data7 as fit with the Ising model. Specifically, we will demonstrate the construction of confidence intervals around the estimated edge weights and centrality statistics as estimated using the qgraph package in the R statistical computing environment. To begin with, we need the marginal distributions of the NCS-R data. The frequency of each symptom is provided in Table 2, while the severity frequency (e.g., the number of symptoms endorsed by each subject, ranging from 0–18) is provided in Figure 1. From these data, we can immediately see the issue with only fixing one of the distributions. For instance, if we only fixed the prevalence of each symptom, then they would be distributed equally across the subjects, resulting in the average subject being assigned 3.75 symptoms. This would completely ignore the role of the severity continuum and its distribution in forming the network structure. Likewise, if we fixed only the severity marginals, we would see equally distributed counts over all of the symptoms, resulting in each having the same expected prevalence; consequently, differing prevalence rates alone could potentially define the “network” structure.
Table 2.
Frequency of Symptoms in the NCS-R Data
| Major Depressive Episode Symptom | Frequency | Generalized Anxiety Disorder Symptom | Frequency |
|---|---|---|---|
| Depressed Mood | 2253 | Chronic Anxiety | 4778 |
| Loss of Interest | 1929 | Anxiety about > 1 Event | 3732 |
| Weight Problems | 1898 | No Control Over Anxiety | 2461 |
| Sleep Problems | 2047 | Feeling On Edge | 1639 |
| Psychomotor Disturbances | 1117 | Fatigue | 1270 |
| Fatigue | 1899 | Concentration Problems | 1490 |
| Self-reproach | 954 | Irritability | 1458 |
| Concentration Problems | 1978 | Muscle Tensions | 972 |
| Suicidal Ideation | 1539 | Sleep Problems | 1415 |
Figure 1.
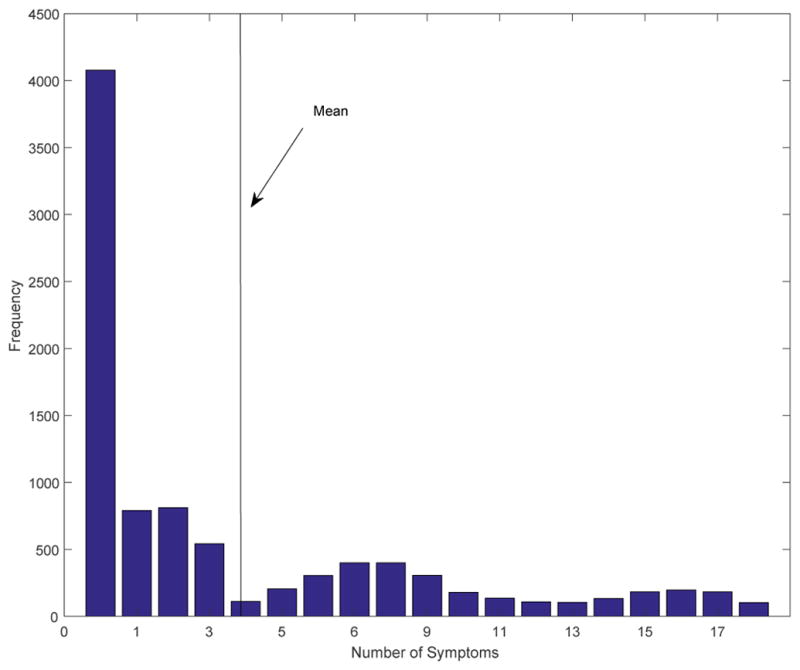
Frequency Distribution of Number of Symptoms in NCS-R Data Showing the Number of Individuals with Different Numbers of Symptoms
Centrality Statistics
We implemented the algorithm as described above. For this small example, we generated 1000 matrices with marginals fixed to the values indicated in Table 2 and Figure 1. For each parameter of interest, we sorted the 1000 values from highest to lowest and created an empirical 99% confidence interval by taking the 5th and 995th ordered value. While we provide 99% confidence intervals here, more discussion is provided at the end of this section regarding choosing appropriate confidence levels. The confidence intervals for the centrality statistics are displayed in Table 3. From Table 3, we see that there are some variables that have significant centrality statistics when compared to what would be expected from chance. Significant values of centrality statistics are noted with an asterisk. For betweennness, we see that not all non-zero centrality statistics are significant, the most egregious being the betweenness score for “Anxiety about > 1 Event” is 38; however, we find that is not significantly different than would be expected by chance. This indicates that the magnitude of the centrality statistics does not necessarily indicate its relevance. We see similar results for closeness centrality, where 33% of the statistics are significant; unfortunately, without a formal test, it is impossible to determine which are different than chance as all of the estimates are within .017 of each other and magnitude alone does not confer significance. For strength, about two-thirds of the centrality statistics are significant.
Table 3.
Confidence Intervals for Centrality Statistics
| Variable | Betweenness | Closeness | Strength | |||
|---|---|---|---|---|---|---|
| Estimate | 99% C.I. | Estimate | 99% C.I. | Estimate | 99% C.I. | |
| Depressed Mood | 69 | [0,11]* | .055 | [.031, .046]* | 22.262 | [7.139, 8.015]* |
| Loss of Interest | 0 | [0,9] | .038 | [.028, .047] | 7.719 | [6.691, 7.612] |
| Weight Problems | 0 | [0,9] | .042 | [.028, .046] | 7.240 | [6.700, 7.537] |
| Sleep Problems | 6 | [0,11] | .047 | [.029, .047] | 9.550 | [6.834, 7.704]* |
| Psychomotor Disturbances | 0 | [0,8] | .038 | [.019, .046] | 6.370 | [5.002, 6.998] |
| Fatigue | 40 | [0,9]* | .053 | [.029, .047]* | 8.828 | [6.683, 7.557]* |
| Self-reproach | 0 | [0,6] | .037 | [.019, .046] | 6.084 | [4.831, 7.061] |
| Concentration Problems | 14 | [0,9]* | .049 | [.029, .047]* | 9.569 | [6.771, 7.666]* |
| Suicidal Ideation | 0 | [0,9] | .043 | [.021, .044] | 6.281 | [5.586, 7.189] |
| Chronic Anxiety | 0 | [82,136]* | .043 | [.045, .084]* | 8.046 | [15.447, 25.429]* |
| Anxiety about > 1 Event | 38 | [0,38] | .047 | [.037, .054] | 23.079 | [8.969, 11.526]* |
| No Control Over Anxiety | 0 | [0,11] | .042 | [.032, .047] | 10.251 | [7.386, 8.447]* |
| Feeling On Edge | 2 | [0,10] | .040 | [.023, .046] | 9.921 | [5.859, 7.234]* |
| Fatigue | 42 | [0,7]* | .052 | [.020, .046]* | 9.016 | [5.265, 7.037]* |
| Concentration Problems | 0 | [0,8] | .040 | [.021, .045] | 8.759 | [5.554, 7.113]* |
| Irritability | 12 | [0,8]* | .046 | [.021, .045]* | 9.220 | [5.473, 7.088]* |
| Muscle Tensions | 0 | [0,7] | .033 | [.019, .046] | 4.673 | [4.802, 6.946]* |
| Sleep Problems | 5 | [0,8] | .044 | [.020, .045] | 8.859 | [5.404, 7.065]* |
Note:
’s are used to indicate confidence intervals where the estimate does not fall within the confidence interval.
Finally, it is important to note that sometimes the centrality statistics are significantly less than would be expected by chance. This is true for “Chronic Anxiety” for betweenness and closeness, as well as “Muscle Tensions” for strength. This complicates the evaluation of this type of output because it is unknown whether observed results are significantly greater than chance, significantly less than chance, or no different than chance. Once again, the necessity for a formal test is highlighted.
Edge Weights
The difficulty is exacerbated for evaluating the edgeweights as displayed in Table 4. In Table 4, a “+” in the lower-triangle indicates the estimated edgeweight is significantly greater than chance, a “−” indicates the estimated edgeweight is less than chance, and a blank indicates that the value fell within the 99% confidence interval. One of the first things to notice is the prevalence of minus signs in Table 4. This indicates the absence of a link is just as important as the presence of a link. Out of the 153 possible links, only 99 were significantly different than chance (65%), indicating that approximately one-third of the estimated network is functioning equivalently to what we would expect by chance. Furthermore, with the three possible classifications of any individual edgeweight being (a) significantly greater than expected by chance, (b) significantly less than expected by chance, and (c) no different than expected by chance, the edgeweights are classified into those categories at the almost equal rates of 30%, 35%, and 35%, respectively. This uniform distribution of edgeweights to the three possible outcomes indicates that evaluating the results from these models by mere inspection of the edgeweights themselves is noninformative.
Table 4.
Estimates and Significance for Edge Weights
| depr | inte | weig | mSle | moto | mFat | repr | mCon | suic | anxi | even | ctrl | edge | gFat | gCon | irri | muse | gSle | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| depr | 1.93 | 3.01 | 3.51 | 1.83 | 2.92 | 1.84 | 3.03 | 3.52 | 0.52 | 0 | 0.16 | 0 | 0 | 0 | 0 | 0 | 0 | |
| inte | + | 0.76 | 0.69 | 0.52 | 1.18 | 0.88 | 0.97 | 0.63 | 0 | 0 | 0.16 | 0 | 0 | 0 | 0 | 0 | 0 | |
| weig | + | 1.39 | 0.76 | 0.21 | 0.15 | 0.66 | 0.29 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| mSle | + | + | + | 0.66 | 1.10 | 0.19 | 0.79 | 0.45 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | .77 | |
| moto | + | + | + | 0 | .37 | 1.35 | 0 | 0.09 | 0 | 0 | 0 | −.35 | .11 | .17 | .16 | 0 | ||
| mFat | + | + | + | .49 | 1.17 | 0 | 0 | 0 | 0 | 0 | 1.38 | .11 | .17 | .16 | 0 | |||
| repr | + | + | 0.31 | 0.94 | 0.26 | 0 | 0.11 | 0 | 0.21 | 0 | 0.09 | 0.24 | 0 | |||||
| mCon | + | + | + | + | + | 0.31 | 0 | 0 | 0 | 0 | 0 | 0 | 0.97 | 0 | 0 | |||
| suic | + | + | − | − | + | 0.14 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||
| anxi | − | − | − | − | 7.02 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||||
| even | − | − | − | − | − | − | + | 5.90 | 1.96 | 1.67 | 2.43 | 1.89 | 0 | 2.23 | ||||
| ctrl | − | − | − | − | − | − | − | − | + | 1.06 | 0.66 | 0.58 | 0.54 | 0.49 | 0.58 | |||
| edge | − | − | − | − | − | − | − | + | + | 0.74 | 2.02 | 1.60 | 0.93 | 1.61 | ||||
| gFat | − | − | − | − | + | − | − | + | + | 1.22 | 0.82 | 1.23 | 0.75 | |||||
| gCon | − | − | − | − | − | − | − | + | + | + | 1.41 | 0.34 | 0.64 | |||||
| irri | − | − | − | − | + | − | + | + | + | + | 0.36 | 1.19 | ||||||
| muse | − | + | + | 0.92 | ||||||||||||||
| gSle | − | − | − | + | − | − | − | − | − | + | + | + | + | + | + |
Note: A “+” in the lower triangle indicates the corresponding edgeweight in the upper triangle is significantly greater than chance; a “−” indicates it is significantly less than chance, and a blank indicates it is no different than chance.
Once again, however, the specific edgeweights that are significant cannot be deduced by any pattern of edgeweights or their raw magnitude. For instance, the probability of an edgeweight being no different than chance if the observed edgeweight is greater than zero is 44% – so an observed edgeweight greater than zero is almost as equally as likely to be due to chance as not. To make it more salient, that would mean that nearly half of the edges depicted on the left side of Figure 3 in the Forbes et al. article are due to chance alone. Additionally, some of the zeros are included in the confidence intervals and some are not. Specifically, the probability of an edgeweight being significantly worse than chance given the observed edgeweight is less than or equal to zero is 28%. In terms of the graphical representation, that would mean that nearly 3 out of 10 of the lines that are absent on the left hand side of Figure 3 are absent due to chance. Such variability in the confidence of the fidelity of observed edges in the figure renders these types of depictions of networks almost useless. This calls for an implementation of a formal testing procedure to assess the relevance of reported edgeweights or their absence.
Figure 2 illustrates the four possible outcomes as described in Table 1. The upper-left panel indicates an “interesting” finding between depressed mood and loss of interest. The edgeweight (1.93) falls above the distribution for random chance, and the bootstrap confidence interval around the edgeweight does not include zero. The lower-left panel indicates a “potentially interesting” connection between sleep problems (depression) and anxiety about more than one event. Specifically, the estimated value of zero is non-significant by both the eLasso and the bootstrap confidence interval around the estimate (0.00); however, the distribution based on random chance alone would expect this connection to be greater than what was observed. The final two panels on the right indicate two different “uninteresting” scenarios. The lower right panel shows the distribution for the edgeweight between chronic anxiety and sleep problems from anxiety – both distributions encompass the observed estimate of zero. The upper-right panel indicates a situation, in this case the relationship between loss of interest and psychomotor disturbances. The bootstrap test indicates that the edgeweight is significantly different than zero; however, the distribution derived from random matrices indicates that the observed value of 0.52 is not unexpected.
Figure 2.
Examples of Bootstrap Compared to Random Distribution
Confidence Levels
Above, we used a 99% confidence level to help control for multiple tests and illustrate the general notion of the differences between generating confidence intervals that reflect accuracy and stability through a bootstrap procedure versus the types of confidence intervals that aid in determining if effects are different than would be expected by random chance alone. However, it is imperative to realize that even a more stringent confidence interval level will not aid in overcoming the threat of Type I error rates in the context of so many tests. Generally, there are different tests for edgeweights and 3p tests for centrality measures (e.g., one for each variable on strength, closeness, and betweenness). In Table 4, there are unique effects – for an α = .05, there would be (.05)153 = 7.65 significant effects based on chance alone, with the more stringent α = .01, (.01)(153) = 1.53 significant effects are expected to be due to chance alone.
In situations that rely on multiple testing, it is common to correct each individual test’s alpha to obtain an overall familywise α that corresponds to the prespecified value. The most conservative adjustment is the Bonferroni correction, which divides the familywise α by the total number of tests to obtain an appropriate level of α for each individual test – in this case, the adjusted α is (.05)/153 = .0003. As Epskamp, Borsboom, and Fried (in press) indicate, this type of correction can be overly burdensome and lead to the possibility of not finding any of the true effects (e.g., Type II errors). Beyond the inherent inverse relationship between Type I and Type II error, the computational burden to generate the requisite number of bootstrap samples for such small values of α can result in the procedure not being used in practice. For instance, generating enough samples to be able to obtain a 99.97% confidence interval would require around 10,000 samples; however, somewhere in the neighborhood of 50,000 – 10,000 would be preferable. As such, in their recommendations, Epskamp et al. (in press) indicate that corrections for chance will be relegated to future research, and in the interim, it is appropriate to proceed with uncorrected tests for the edgeweights.
While the sentiment to proceed with testing each test at α = .05 (the default setting in the Espkamp et al. bootstrapping software) is understandable, cautions, nonetheless, are called for. First, the probability of committing at least one Type I error when conducting multiple tests is 1–(1–α)T, where T is the number of tests being conducted. For instance, if you conduct two tests and do not correct for α the probability of committing at least one Type I error is 1 – (.95)2 = .0975; however, for the example above, the probability of making at least one Type I error is 1–(.95)153 = .9997 – an almost certainty. Furthermore, it is well known that the magnitude of p-values cannot be compared to determine which effects are more likely to be significant and which are more likely to be either insignificant or a potentially a Type I error. The inability to do such a ranking is readily seen if one considers alternative correction methods beyond the Bonferroni correction. Specifically, the Holm-Bonferroni method (Holm, 1979) is uniformly more powerful than the Bonferroni correction; however, it proceeds by comparing the lowest p-value to the strictest criterion, and then, as p-values increase, the comparison criteria becomes less stringent. A similar test that is more powerful, but require assumptions regarding the joint distribution of the test statistics is Hochberg’s step-up procedure (Hochberg, 1988); likewise, one could consider Hommel’s (1988) stagewise rejective multiple test procedure. Unfortunately, each of these procedures would require in increase in the number of bootstrap samples – which would lead to the potential relaxation of the requirement to control for the familywise error rate.
Beyond the potential to incorrectly assume that effects are significant when they are not, the inattention to appropriately control for multiple testing has the potential to call into question all prior research in an area. This can be seen best with the application of multiple testing in fMRI research, another area that relies on a large number of tests and constructs substantive theory from patterns of significance. Recently, Eklund, Nichols, and Knuttson (2016) demonstrated that somewhere in the neighborhood of 40,000 fMRI studies may be invalid due to the inability to control for Type I error rates appropriately. Furthermore, in their conclusion the authors make a particularly relevant statement: “Although we note that metaanalysis can play an important role in teasing apart false-positive findings from consistent results, that does not mitigate the need for accurate inferential tools that give valid results for each and every study”. Since we are in the early stages of developing psychological networks, the most prudent course of action is also establishing appropriate inferential tools immediately and prevent the need to potentially correct hundreds or even thousands of published studies 5, 10, or 20 years from now. This view of tightening the reins for publication is further supported by the recommendation of a group of statisticians who recently weighed in on the reproducibility of psychological science (Johnson et al., 2017): “The results of this reanalysis provide a compelling argument for both increasing the threshold required for declaring scientific discoveries and for adopting statistical summaries of evidence that account for the high proportion of tested hypotheses that are false”. In fact, they suspect that potentially 90% (!!!) of of tests performed in psychology experiments are testing negligible effects.
Fidelity of Data
Lastly, we note that there are several decisions made at the data analytic level that can affect and alter the results of any given network model. Some examples would include how the data are collected or how the responses are coded. For instance, it is possible that specific criteria could be coded differently depending on the interview employed to collect the data. Another example would be the so-called “skip out” issue that can occur in epidemiological questionnaires. For “skip out” items, there are gateway items that are assessed first – if the response to the gateway item is negative, then the remainder of the items are not asked; whereas, if the response to the gateway item is affirmative, then all subsequent related items are asked. A question arises on how to handle the subsequent items if they were not assessed. A common approach is to assume that if the gateway item is not endorsed, then all subsequent sub-items are not endorsed either – this is akin to a logical data imputation. Whether this is appropriate or not will depend on the specific set of questions and criteria being assessed. If it is inappropriate, the estimated effects will be biased; however, that being said, these biases will not effect the validity of the testing approach described above, nor does it mitigate the issues with not controlling for multiple testing.
Discussion
Replicability
From these findings, we see that the results of many network analyses, as conducted on binary data, might be overstating their findings. While space limitations only allowed for a modest analysis of the performance the Isingfit model on one data set, current work is expanding the investigation to a broader class of binary matrices as well as extending to the three other types of network models mentioned by Forbes et al. (2017). Preliminary results indicate that the findings will be similar to what was observed for the Isingfit model. In short, we second the conclusion of Forbes et al. and offer the addendum that discovering believable results, at the specific symptom level (whether that is the relationship between pairs of symptoms) or variable level statistics (e.g,. centrality statistics), will likely be much more difficult than previously envisioned. As shown above, this is due to the fact that empirical findings are difficult to distinguish from random chance, and we do not believe that it would be too strong of a suggestion that previously published findings using this methodology should be reevaluated using the above testing procedure. Without this additional testing, future research based on existing findings will likely lead to a significant degree of non-replicability as the findings are potentially no difference than chance. While the network approach represents an important alternative view of diagnostic systems that could provide new insights into both the basic structure of psychopathology and identify promising targets for intervention by virtue of their centrality, existing methods must be considered unproven. Research practitioners must appreciate the limitations of the existing state-of-the-art and develop and refine approaches likely to provide more robust and interpretable solutions.
Are Psychopathology “Networks” Actually Networks?
In the first footnote, we note that much of the terminology in recent psychopathology network analysis has been borrowed from the traditional network analysis literature – much of which is rooted in psychology and sociology (see Wasserman & Faust, 1994). To determine whether the transferability of methods in traditional network analysis to psychopathology networks is warranted (or should be taken at face value), it is worth highlighting the differences between the two. Generally, there are two types of networks that can be considered: (1) networks that directly assess the relationships between the same set of observations (e.g., one-mode matrices as described above), and (2) affiliation networks where the connections are assessed between two sets of observations (two-mode matrices as described above). Clearly, psychopathology networks fall into the class of affiliation matrices where the connections are measured between observation and diagnostic criteria. The relationships between the criteria are then then derived by transforming the two-mode affiliation matrix to a one-mode so-called “overlap/similarity” matrix between the criteria, where traditional network methods are applied to this overlap/similarity matrix. Faust (1997) indicated that potential pitfalls arise when applying standard centrality measures to networks derived from affiliation matrices: “In going from the affiliation relation to either the actor co-membership relation or the event overlap relation, one loses information about the patterns of affiliation between actors and events. Thus, one needs to be cautious when interpreting centralities for these one-mode relations” (pp. 189). The concerns of Faust (1997) are related directly to the concerns raised in the introduction where the methods developed for one-mode networks are applied to the two-mode networks (e.g., affiliation network or bipartite graph).
Conclusion
As Johnson et al. (2017) argue, the editorial policies (and funding priorities) must be compelled to adapt to higher standards prior to putting their stamp of approval on results. Given the nature of problems that confront psychometric network modeling, including (but not limited to): (1) the possibility of observing “significant” effects that are not different than random chance, (2) the difficulties induced by conducting numerous significant tests, which is not controlled for via bootstrapping, and (3) the uncertainty regarding applying traditional methodology developed for one-mode networks to two-mode networks, we wholeheartedly agree with the recommendation by Forbes and company to turn a skeptical eye towards these models. Additionally, given the results from the example above and the theoretical issues that surround multiple testing and appropriate reference distributions, we do not agree with Epskamp, Boorsboom, and Fried (in press) that it is reasonable to continue conducting tests at the α = .05 while we wait for methodologists to develop procedures that address the shortcomings. Rather, it is the other way around: wait until methodologists develop the appropriate fixes then proceed with fitting these models. Not following such an approach runs the very real risk of creating a series of publications that contain results that are not reproducible and likely no different than what is expected under one of the most basic models of chance in all of categorical data analysis.
While we have provided numerous caveats and cautions to employing psychometric network models, we do believe that they are opening a potentially important area of research for us to consider. Specifically, the moving more to a causal structure model, as opposed to a common cause (such as latent variable) model holds great appeal as the parallelism to traditional medical models of diseases is enhanced. In our view, it is likely that the true model (or at least the best fitting models) will be a hybrid of network models and latent variable models. Further, while we provide extreme caution in using these methods to motivate theory, we do believe that such techniques can be a useful tool in the arsenal of the researcher when used to supplement a rich, substantive knowledge regarding the psychopathology being studied. Additionally, we note that by using correlations (or functions thereof) the network models have wed themselves closely to traditional latent variable models in terms of how the relationships between variables are conceptualized. However, there is a rich history in assessing the similarity between binary items in general and elements within a bipartite graph specifically. Broadening approaches beyond the logistic regression framework encapsulated by the Isingfit approach (and perhaps even abandoning the notion of correlation as the foundational measure of association) could open the entire field of psychometric networks to entirely new horizons. Finally, many of the concerns raised in this commentary could be alleviated if we move from the current state of exploratory psychometric networks to confirmatory psychometric networks, allowing a priori specified effects to be tested rather being hamstrung out of the gate by the need to correct for multiple testing.
Acknowledgments
The first author was partially supported by National Institute of Health Grant #R01AA023248-01.
Appendix
Algorithm for Within Replicability
The ingredients for testing so-called “within” replicability are fairly straightforward. Namely, all that is required is the original data matrix Xn×p with n rows and p columns as well as the network statistic of interest, say θ̂. The goal is then to obtain the sampling distribution for θ under the null distribution that the location of the ones in the binary matrix X are random subject to the observed marginal distributions for both the rows and columns.
The algorithm proceeds as follows:
Compute θ̂ from X; compute rX and cX (the marginal distributions for the rows and columns, respectively, which in this case are just sums across the columns and rows).
Choose the number of random data matrices, R, to generate.
Generate the ith random matrix, Mi, such that rMi = rX and cMi = cX (e.g., the marginal distributions of the random matrices will be equivalent to those of the observed matrix, X).
Compute θi for i = 1, . . . , R. Order the θ’s from smallest to largest, letting the ordered vector of θ be denoted as θ(o).
Create a confidence interval under the null distribution of random association as .
If the observed test statistic, θ̂, falls within the interval in Step 5 then we cannot reject the null. Consequently, we conclude the observed value could have arisen by random chance alone.
Algorithm for Between Replicability
The algorithm for testing so-called “between” replicability is almost identical. All that is required is a second data matrix, Yn2×p, with which we want to compare the original data matrix Xn1×p. The process proceeds as follows
Compute θ̂XY from f(X,Y), where f(·) is a function of correspondence between the two structures uncovered from X and Y (for instance, the function could be the correlation of the edge weights between the two network structures). Additionally, compute rX and cX from X; compute from Y, rY and cY from Y.
Choose the number of pairs of random data matrices, R, to generate.
Generate the ith pair of random matrices (Mi,Ni), such that rMi = rX and cMi = cX and rNi = rY and cNi = cY.
Compute θi for i = 1, . . . , R. Order the θ’s from smallest to largest, letting the ordered vector of θ be denoted as θ(o).
Create a confidence interval under the null distribution of random association as .
If the observed test statistic, θ̂, falls within the interval in Step 5 then we cannot reject the null. Consequently, we conclude the observed value could have arisen by random chance alone.
Footnotes
We note that there is a a good deal of appropriation of terminology from the social network analysis literature used in these analyses; we would caution too much transference as the psychopathology networks are induced from bipartite graphs versus being observed directly.
The eigenvalues from the completely random data are obtained by averaging over several – usually one thousand or more – sets of eigenvalues that have been obtained from independently generated random data.
Such an approach has been superceded by the derivation of a closed-form solution for comparing the equivalence of two partitions (Steinley, Brusco, & Hubert, 2016), but the basic logic still applies.
We note that most of the time v0 = 0.
Note: Under many situations, the expected value of the effect is often zero (e.g., no effect). For instance, in the simple case of a t-test or a linear regression model, generating data from random distributions – accomplished by randomly assigning group labels for the t-test or randomly generating predictors uncorrelated with the dependent variable for regression – we would expect mean differences of zero and slopes of zero. The deviation from no effect for these psychological networks is due to the restriction of the range of the sample space of potential networks that is induced from the observed marginal distributions.
The between network importance algorithm would be implemented in a similar fashion, but due to space constraints we have not included an example here
The data set was provided to us by the first author, Miriam Forbes, of the target article
Contributor Information
Douglas Steinley, University of Missouri.
Michaela Hoffman, University of Missouri.
Michael J. Brusco, Florida State University
Kenneth J. Sher, University of Missouri
References
- Admiraal R, Handcock MS. networksis: A package to simulate bipartite graphs with fixed marginals through sequential sampling. Journal of Statistical Software. 2008;24:1–21. doi: 10.18637/jss.v024.i08. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson BS, Butts C, Carley K. The interaction of size and density with graph-level indices. Social Networks. 1999;21:239–267. [Google Scholar]
- Arabie P, Hubert LJ. The bond energy algorithm revisited. IEEE Transactions on Systems, Man, and Cybernetics. 1990;20:268–274. [Google Scholar]
- Arabie P, Hubert L, Schleutermann S. Blockmodels from the bond energy algorithm. Social Networks. 1990;12:99–126. [Google Scholar]
- Baker M. Is there a reproducibility crisis? A Nature survey lifts the lid on how researchers view the crisis rocking science and what they think will help. Nature. 2016;533:452–455. [Google Scholar]
- Brusco MJ, Shireman E, Steinley D. A comparison of latent class, K-means, and K-median method for clustering dichotomous data. Psychological Methods. doi: 10.1037/met0000095. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brusco MJ, Steinley D. Inducing a blockmodel structure on two-mode data using seriation procedures. Journal of Mathematical Psychology. 2006;50:468–477. [Google Scholar]
- Brusco MJ, Steinley D. Exact and approximate algorithms for part-machine clustering based on a relationship between interval graphs and Robinson matrices. IIE Transactions. 2007a;39:925–935. [Google Scholar]
- Brusco MJ, Steinley D. An evaluation of a variable-neighborhood search method for blockmodeling of two-mode binary matrices based on structural equivalence. Journal of Mathematical Psychology. 2007b;51:325–338. doi: 10.1016/j.jmp.2009.08.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brusco MJ, Steinley D. Integer programs for one- and two-mode blockmodeling based on presepecified image matrices for structural and regular equivalence. Journal of Mathematical Psychology. 2009;53:577–585. doi: 10.1016/j.jmp.2009.08.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brusco MJ, Steinley D. A tabu search heuristic for deterministic two-mode blockmodeling of binary network matrices. Psychometrika. 2011;76:612–633. doi: 10.1007/s11336-011-9221-9. [DOI] [PubMed] [Google Scholar]
- Chen Y, Diaconis P, Holmes SP, Liu JS. Sequential Monte Carlo methods for statistical analysis of tables. Journal of the American Statistical Association. 2005;100:109–120. [Google Scholar]
- Connor EF, Simberloff D. The assembly of species communities: Chance or competition? Ecology. 1979;60:1132–1140. [Google Scholar]
- Diamond JM. Ecology and evolution of communities. Harvard University Press; Cambridge, MA: 1975. Assembly of species communities; pp. 342–444. [Google Scholar]
- Eklund A, Nichols TE, Knutsson H. Cluster failure: Why fMRI inferences for spatial extent have inflated false-positive rates. Proceedings of the National Academy of Science. 2016;113:7900–7905. doi: 10.1073/pnas.1602413113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Epskamp S, Borsboom D, Fried EI. Estimating psychological networks and their accuracy: A tutorial paper. Behavior Research Methods. doi: 10.3758/s13428-017-0862-1. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Forbes MK, Wright AGC, Markon KE, Krueger RF. Evidence that psychopathology symptom networks have limited replicability. Journal of Abnormal Psychology. 2017 doi: 10.1037/abn0000276. this issue. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harrison MT, Miller JW. Importance sampling for weighted binary random matrices with specified margins. 2013 arXiv:1301.3928 [stat.CO] [Google Scholar]
- Holm S. A simple sequentially rejective multiple test procedure. Scandinavian Journal of Statistics. 1979;6:65–70. [Google Scholar]
- Hommel G. A stagewise rejective multiple test procedure based on a modified Bonferroni test. Biometrika. 1988;75:383–386. [Google Scholar]
- Horn JL. A rationale and technique for eistimating the number of factors in factor analysis. Psychometrika. 1965;30:179–185. doi: 10.1007/BF02289447. [DOI] [PubMed] [Google Scholar]
- Hunter DR, Handcock MS. Inference in curved exponential family models for networks. Journal of Computational and Graphical Statistics. 2006;3:565–583. [Google Scholar]
- Johnson VE, Payne RD, Wang T, Asher A, Mandal S. On the reproducibility of psychological science. Journal of the American Statistical Association. 2017;112:1–10. doi: 10.1080/01621459.2016.1240079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller JW, Harrison MT. Exact sampling and counting for fixed-margin matrices. The Annals of Statistics. 2013;41:1569–1592. [Google Scholar]
- Pashler H, Wagenmakers EJ. Editors’ introduction to the special section on the replicability in psychological science: A crisis of confidence? Perspectives on Psychological Science. 2012;7:528–530. doi: 10.1177/1745691612465253. [DOI] [PubMed] [Google Scholar]
- Rosenberg S, Van Mechelen I, De Boeck P. A hierarchical classes model: Theory and method with applications in psychology and psychopathology. In: Arabie P, Hubert LJ, De Soete G, editors. Clustering and classification. River Edge, NJ: World Scientific; 1996. pp. 123–155. [Google Scholar]
- Steinley D. Properties of the Hubert-Arabie adjusted Rand index. Psychological Methods. 2004;9:386–396. doi: 10.1037/1082-989X.9.3.386. [DOI] [PubMed] [Google Scholar]
- Steinley D. Profiling local optima in K-means clustering: Developing a diagnostic technique. Psychological Methods. 2006;11:178–192. doi: 10.1037/1082-989X.11.2.178. [DOI] [PubMed] [Google Scholar]
- Steinley D. Validating clusters with the lower bound for sum of squares error. Psychometrika. 2007;72:93–106. [Google Scholar]
- Steinley D. Stability analysis in K-means clustering. British Journal of Mathematical and Statistical Psychology. 2008;61:255–273. doi: 10.1348/000711007X184849. [DOI] [PubMed] [Google Scholar]
- Steinley D, Brusco MJ. Testing for validity and choosing the number of clusters in K-means clustering. Psychological Methods. 2011;16:285–297. doi: 10.1037/a0023346. [DOI] [PubMed] [Google Scholar]
- Steinley D, Brusco MJ, Hubert L. The variance of the adjusted Rand index. Psychological Methods. 2016;21:261–272. doi: 10.1037/met0000049. [DOI] [PubMed] [Google Scholar]