Principal cluster axes: A projection pursuit index for the preservation of cluster structures in the presence of data reduction

Abstract

A measure of “clusterability” serves as the basis of a new methodology designed to preserve cluster structure in a reduced dimensional space. Similar to principal component analysis, which finds the direction of maximal variance in multivariate space, principal cluster axes finds the direction of maximum clusterability in multivariate space. Furthermore, the principal clustering approach falls into the class of projection pursuit techniques. Comparisons are made with existing methodologies, both in a simulation study and analysis of real-world datasets. Furthermore, a demonstration of how to interpret the results of the principal cluster axes is provided on the analysis of Supreme Court voting data and similarities between the interpretation of competing procedures (e.g., factor analysis and principal component analysis) is provided. In addition to the Supreme Court analysis, we also analyze several datasets often used to test cluster analysis procedures, including Fisher's Iris Data, Agresti's Crab Data, and a data set on glass fragments. Finally, discussion is provided to help determine when the proposed procedure will be the most beneficial to the researcher.

Introduction

Finding clusters in multidimensional space can be quite difficult for a variety of reasons. For instance, when there are a large number of variables (i.e., dimensions) present, Milligan (1980) showed that a few meaningless dimensions (i.e., variables that did not contribute to the cluster structure and were considered to be random noise) can degrade the capability of even the best algorithms of finding the underlying cluster structure. In general, there are three basic approaches to addressing this problem: (a) appropriately selecting the correct variables to include or exclude from the analysis, (b) appropriately weighting each variable's contribution to the objective function used in the clustering procedure, and (c) clustering observations that have been projected into a lower dimensional space.

Steinley and Brusco (2008a) compared eight variable selection techniques that were based on a wide range of techniques and models. Regardless of whether the procedure was driven by “classic” clustering procedures (i.e., hierarchical or non-hierarchical cluster analysis) or the more statistically formal mixture models, Steinley and Brusco found that all procedures were subject to the problem induced by “noisy” variables. Furthermore, the procedures with higher rates of cluster recovery were more capable of excluding the noisy variables. Milligan and Cooper (1988) and Steinley and Brusco (2008b) also indicated that appropriately weighting variables prior to conducting the cluster analysis can have a marked influence on the recovery of the underlying cluster structure.

One potential drawback of many variable selection and weighting techniques is that each variable is evaluated univariately and its inclusion into the final cluster analysis routine is predicated on an individual display of clusterability; however, when working in a multivariate setting, researchers are often concerned with how the variables interact in a high-dimensional space. To that end, several researchers have proposed combining cluster analysis with data reduction techniques to obtain low-dimensional representations of the cluster structure while including information about all of the variables.

The current presentation proposes a new method for preserving the cluster structure when reducing the dimensionality of the original, observed data. In contrast to existing procedures developed explicitly for this purpose, the proposed procedure does not rely on any clustering algorithm to project the cluster structure into the desired lower dimensional space. The development of the proposed procedure, termed principal cluster axes projection pursuit (PCAPP), is based on projection pursuit techniques pioneered by Friedman and Tukey (1974). First, the structure and nature of projection pursuit is presented, followed by the underlying theory of PCAPP and an algorithmic description that outlines its implementation. Finally, after the technique for extracting the projections is outlined, a procedure for determining the number of principal cluster axes (i.e., the dimensionality of the reduced data) is introduced.

A detailed example of the procedure is given and followed by a comparison with current practice in the literature on the classic Fisher Iris data. Through a simulation study, it is demonstrated that PCAPP outperforms extant procedures, with the results being reinforced by the analysis of specific data sets commonly used to validate cluster analytic methods. Lastly, we analyze Supreme Court voting data using PCAPP, illustrating approaches to interpretation and considerations that result in implications that are different from data reduction techniques that aim to create more continuous latent spaces (e.g., principal component analysis, etc.). Finally, a conclusion is provided that discusses several reasons why existing procedures may have trouble finding clusters when data are projected into lower dimensional space.

Principal Cluster Axes Projection Pursuit

Notation

To provide a common framework for the methods to be discussed, the following notational scheme is adopted.

N := the number of objects, indexed i = 1, …, N;

V := the number of variables, indexed v = 1, …, V;

U := the number of variables in the reduced space, indexed u = 1, …, U;

X := an N × V data matrix whose elements, x_iv, represent the measurement of object i on variable v;

K := the number of clusters, indexed k = 1, …, K;

C_k := the set of objects in the k^th cluster;

N_k := the number of objects in C_k;

σ²(x_v) := the variance of the v^th variable;

r(x_v) := the range of the v^th variable;

c := a V × 1 vector of coefficients.

I(c) := the value of the index associated with the linear combination, Xc

Projection Pursuit

Prior to the presentation of PCAPP, a short review of projection pursuit is provided. The common use of projection techniques in psychology is for data reduction, for example, principal component analysis. For instance, the first principal component is the projection of the data onto the unidimensional space with maximum variance. In the format of the present discussion, this goal is represented as

$$I_{\mathit{\text{PCA}}}({\mathbf{c}}_v)=\underset{\mathbf{c}}{max}{\sigma }^2(\mathbf{X}\mathbf{c}),$$ (1)

where the length of c_v is unity (e.g., ${\mathbf{c}}_v^{\text{'}}{\mathbf{c}}_v=1$) and c_v is orthogonal to the remaining V – 1 principal components (e.g., c_v⊥c_k ∀k < v; v = 2, …, V). Projection pursuit is also concerned with data reduction; however, the nature of the space into which the data are projected varies based on the application. Projection pursuit originated with Friedman and Tukey (1974) as a procedure to find non-Gaussian projections of high-dimensional data (for excellent full-length reviews, see Friedman, 1987; Huber, 1985; Jones & Sibson, 1987). This initial conjecture is that non-Gaussian projections are the most “interesting” projections to investigate as they provide insight into the structure of high-dimensional data beyond the standard principal components extraction of directions of most variation. To quote Friedman (1987, p. 250), based on the arguments of Huber (1985) and Jones (1983), it is most useful to identify what constitutes the most “uninteresting” projection, which is in fact the normal distribution:

1. “The multivariate normal density is elliptically symmetric and is totally specified by its linear structure (location and covariances).

2. All projections of a multivariate normal distribution are normal. Therefore, evidence for nonnormality in any projection is evidence against multivariate joint normality. Conversely, if the least normal projection is – not significantly different from – normal, then there is evidence for joint normality of the measurement variables.

3. Even if several linear combinations of variables (possibly high) structured (nonnormal), most linear combinations (views) will be distributed approximately normally. Roughly, this is a consequence of the central limit theorem (sums tend to be normally distributed). This notion was made precise by Diaconis and Freedman (1984).

4. For fixed variance, the normal distribution has the least information (Fisher, negative entropy).” (p. 250)

In fact, the primary motivation behind projection pursuit is that directions of high variation are not guaranteed to be the same as directions of structured variation. Unfortunately, when moving away from principal component analysis, analytic solutions for projections of functions other than maximal variance are almost exclusively non-existant and the desired projections must be found numerically (see Jones & Sibson, 1987). Once the notion of what is “interesting” is defined by the researcher, an appropriate index is chosen to maximize/minimize in order to extract the appropriate projections. Naturally, since the solutions are driven by a numerical process and not an analytic solution, the possibility of finding locally optimal solutions (e.g., projections that do not find the global maximum or minimum value for the projection pursuit index). However, Jones and Sibson (1987) indicated that solutions that are “close” to the optimal solution will often suffice and too much concern should not be given to the lack of a guarantee of finding the globally optimal solution. Prior to presenting the algorithm developed for extracting the projections that result in the directions of most clusterability, we discuss past indices used in projection pursuit and propose the use of a measure developed by Steinley and Brusco (2008b).

Projection Pursuit Indices

Over the years, several different types of projection pursuit indices have been proposed to find various structures. For the task at hand, we are interested in indices that are designed to preserve clusters when the data space is reduced. Friedman and Tukey (1974) developed an index with the purpose of finding clusters within the data by using a measure of local density to find relatively dense regions of the high-dimensional space that would be preserved and projected into lower dimensional space; however, Jones and Sibson (1987) called into question its use and indicated that this original index often found structures that would not usually be thought of as clusters and proposed the alternative index

$$I_{\kappa }(\mathbf{c})=max({\kappa }_3^2(\mathbf{c})+{\kappa }_4^2(\mathbf{c})/4)/12,$$ (2)

where the first term is the square of the third cumulant (e.g., the square of the numerator of skewness) and the second term is the square of the fourth cumulant (e.g., the square of the numerator of kurtosis). Obviously, if one were to choose c to maximize (2), then the denominator can be eliminated from the computation; however, we leave it for fidelity to the original source. Additionally, this index is used as an approximation to an entropy index, which is minimized by the normal distribution; consequently, this index will search for maximal departures from normality. This follows Huber's (1985) suggestion that an index is suitable for projection pursuit as long as it measures some departure from normality, and, if one so desired, standard test statistics for normality could be used directly as the projection pursuit index. However, Friedman (1987) indicated that one must exercise caution if looking for clusters because using cumulants (or related statistics) can also highlight departures from normality that do not necessarily reflect cluster structure. Indeed, this was recently supported by Steinley and Brusco (2008a) when showing the comparatively poor performance of chi-square index designed by Montanari and Lizzani (2001) to select variables that exhibit cluster structure.

Proposed Index and Properties

We propose to use the “clusterability” index designed by Steinley and Brusco (2008b) as the projection pursuit index to maximize. The clusterability index is basically the ratio of a variable's variance to its range. The index is computed for each variable

$$CI(x_v)=\frac{12\times {\sigma }^2(x_v)}{{(r(x_v))}^2}.$$ (3)

The potential drawback of this procedure is the fact that each variable is evaluated independently and multivariate relationships are not pursued or considered. For the theoretical properties of the univariate index, we refer readers to Steinley and Brusco (2008b). Additionally, there is potential for the index, as presented, to be influenced by outlying observations. In the case where outliers are expected, we follow the recommendations of Steinley and Brusco (2008b) and trim the data before the calculation of univariate descriptive statistics ¹.

To account for the relationship between variables in a multivariate setting, the goal shifts from individually computing the clusterability index for each variable to finding the linear combination that results in the maximum clusterability for the data set. Like other data reduction techniques (i.e., principal component analysis), multiple linear combinations are extracted subject to the constraint that they are mutually orthogonal. Recalling that c_v represents a V × 1 vector of coefficients, the corresponding linear combination is given by

$${\mathbf{x}}_v^{\ast }=\mathbf{X}{\mathbf{c}}_v=c_{v1}{\mathbf{x}}_1+c_{v2}{\mathbf{x}}_2+\cdots +c_{vV}{\mathbf{x}}_V.$$ (4)

The goal then becomes finding c₁ such that

$$\begin{array}{ccc}{I}_{CI}(\mathbf{c})=\underset{\mathbf{c}}{max}\frac{12\times {\sigma }^2(\mathbf{X}{\mathbf{c}}_1)}{{(r(\mathbf{X}{\mathbf{c}}_1))}^2}& \text{subject to}& {\mathbf{c}}_1^{\text{'}}{\mathbf{c}}_1=1.\end{array}$$

The subsequent linear combinations, c₂, …, c_V are “extracted” under similar conditions:

$$\begin{array}{ccccc}\underset{\mathbf{c}}{max}\frac{12\times {\sigma }^2(\mathbf{X}{\mathbf{c}}_v)}{{(r(\mathbf{X}{\mathbf{c}}_v))}^2}& \text{subject to}& {\mathbf{c}}_v^{\text{'}}{\mathbf{c}}_v=1;& {\mathbf{c}}_v\perp {\mathbf{c}}_k\forall k<v;& v=2,\dots ,V,\end{array}$$

creating a system of V mutually orthogonal projections where each projection maximizes the clusterability of the data given it is orthogonal to the prior projection ². Before proceeding to the algorithmic implementation, we show that the proposed index is both affine invariant and robust to outliers.

Affine Invariance

To be appropriate for projection pursuit, Huber (1985) recommends that an index is affine invariant, where in general the index is affine invariant if

$$\begin{array}{cc}f(aZ+b)=f(Z),& a\ne 0.\end{array}$$ (5)

Theorem. CI(x_v) is affine invariant if CI(x_v) = CI(ax_v + b).

Proof. Let u = max(x_v) and l = min(x_v).

$$\begin{array}{c}CI(a{x}_v+b)=(12{\sigma }^2(a{x}_v+b))/({(r(a{x}_v+b))}^2)\\ =(12a^2{\sigma }^2(x_v))/({(au+b-al-b)}^2)\\ =(12a^2{\sigma }^2(x_v))/(a^2{u}^2-2a^{2}ul+a^2{l}^2)\\ =(12a^2{\sigma }^2(x_v))/(a^2{(u-l)}^2)\\ =12{\sigma }^2(x_v)/(r{(x_v)}^2)=CI(x_v)\end{array}$$ (6)

Robustness

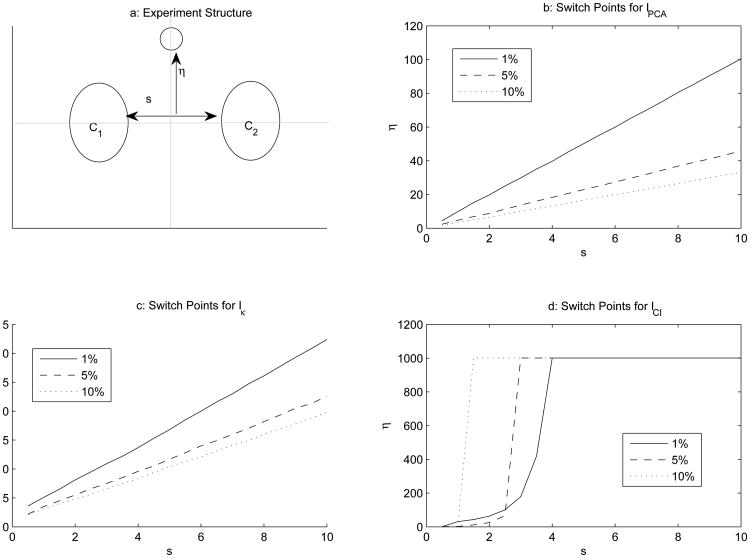
To illustrate the robustness of the index, we repeat the experiment designed by Nason (2001) and compare I_PCA, I_κ, and I_CI. The initial setup of the experiment is presented in Figure 1a, with results for each of the measures presented in the remaining three panels. In Figure 1a, there are two clusters (each cluster is bivariate standard normal) separated by distance s, each centered on the y-axis. Centered on the x-axis, there is a small group of outliers distance η from the zero value of the y-axis (also a bivariate standard normal). If the goal were to reduce the dimensionality from two dimensions to one dimension – which is essentially a choice between the horizontal and the vertical axis – the horizontal axis should be chosen to preserve the cluster structure; on the other hand, choosing the vertical axis would cause the clusters to overlap and obscure the inherent structure in the data.

Figure 1. Experiment Schematic and Results for Testing Robustness of Projection Pursuit Indices.

For an index I, the outliers are moved in increments until η reaches a value such that the projection onto the y-axis is preferred over the projection onto the x-axis. Nason (2001) deemed this the switch point, with larger values for the switch point indicating that the index is more resilient to a small number of points determining the direction of the preferred projection(s). In this investigation, values of s range from 1 to 10 in steps of .5, and η begins at the origin and is incremented at levels of .1 until the switch point is located (or until η = 1000 as a practical limit). Finally, the clusters each are bivariate standard normal with one thousand observations apiece. The number of outliers assumed three levels of 1%, 5%, and 10% of the total number of observations in the clusters (e.g., 20, 100, and 200 – see Milligan, 1980, and Steinley, 2003, for prior use of 10% of all observations being the threshold for what constitutes the smallest cluster).

I_PCA and I_κ both behave as predicted. As the small cloud of outliers increases in size and moves away from the origin, the switch points decrease. Thus, larger numbers of outliers that are more “outlying” are more likely to cause the indices to prefer the incorrect projection. However, I_CI behaves in somewhat of an opposite manner. First, at s = 1 for 1%, I_CI dominates all other solutions of I_κ across all conditions; likewise, at s = 5 for 1%, I_CI dominates all other solutions of I_PCA across all conditions. Second, as the outlier cloud grows in size, given sufficient s, I_CI favors the outliers as a small cluster, projecting them between the two larger clusters on the x-axis, dramatically favoring correct projection in almost all instances regardless of the value of η. Indeed, I_CI was more than 10 times as robust as I_PCA for the majority of conditions, and more than 25 times as robust than I_κ.

Algorithmic Implementation

This section outlines the procedure for finding c₁, …, c_V. The algorithmic implementation is akin to a procedure used by Posse (1995). At first, the process seems somewhat haphazard in that it is a random search optimization method; however, Posse (1995) showed that this approach outperforms many of the steepest-ascent techniques that have been implemented for projection pursuit (Martinez, Martinez, & Soka, 2011). We have augmented Posse's general algorithm in several subtle manners. Primarily, we have added a stochastic element that is akin to simulated annealing (Kirkpatrick, Gelatt, & Vecchi, 1983) and variable neighborhood search (Hansen & Mladenoviĉ, 2001).

To begin the extraction of linear combinations, special attention is given to c₁.

1. The user defines values for max_it (the maximum number of iterations without a change in the index being maximized), ∊ (the minimum size of the neighborhood around the current projection to search), S (the initial step size for searching for a new projection), and sets J = 0 (the current iteration).

2. Create the matrix of candidate projections, P_N+1×V, which contains the V eigenvectors of S (the covariance matrix of X), the rows of X after it has been centered at the origin and each row normalized to have length one, and if V ≤ 10, include all 2^V hyperoctants (e.g., all possible sign vectors). Compute I_i = CI(Xp_i) ∀i = 1, …, V and choose the initialization projection to be a = p_i such that I_i > I_j ∀i ≠ j.

3. Generate two random linear combination vectors, b₁ and b₂ (from the unit sphere), and augment a by ${\mathbf{a}}_1^{\ast }=(\mathbf{a}+S{\mathbf{b}}_1)/\Vert \mathbf{a}+S{\mathbf{b}}_1\Vert$ and ${\mathbf{a}}_2^{\ast }=(\mathbf{a}+S{\mathbf{b}}_2)/\Vert \mathbf{a}+S{\mathbf{b}}_2\Vert$ where ‖ · ‖ denotes the norm of a vector.

4. Compute ${\mathbf{X}}_1^{\ast }=\mathbf{X}{\mathbf{a}}_1^{\ast }$ and ${\mathbf{X}}_2^{\ast }=\mathbf{X}{\mathbf{a}}_2^{\ast }$. Compute $I_1^{\ast }=CI(\mathbf{X}{\mathbf{a}}_1^{\ast })$ and $I_2^{\ast }=CI(\mathbf{X}{\mathbf{a}}_2^{\ast })$. Choose $I^{\ast }=max(I_1^{\ast },I_2^{\ast })$.

5. If I^* > I then set I = I^*, a = a^*. GO TO step 3.

6. If I ≥ I^* then J = J + 1, S = S/2, and let t = 1 – J/max_it.

7. If t > Uniform(0,1), randomly generate a new vector, a′ from the unit sphere. If I′ > I, then a = a′, J = 0 and GO TO step 3. If I > I′ or t ≤ Uniform(0,1), then a is unchanged and GO TO step 8.

8. STOP if J > max_it or S < ∊, set c₁ = a, else GO TO step 3.

Step 1 requires the user to provide a set of parameters that govern the implementation of the algorithm, including the number of iterations, max_it, without a change that will result in termination of the algorithm, ∊ the minimum size of the neighborhood around the projection to search for a better projection, and S the initial step size to move away from the current projection to search for a better projection. Experimentation has shown that reasonable values for these parameters are max_it = 100, ∊ = 1 × 10⁻⁷, and S = 50, respectively.

Step 2 creates a candidate matrix of initial projections to begin the process. Daszykowski (2007) recommended using each observation as a potential projection as this is a manner in which to cover the directions in which the data are present, while an anonymous reviewer suggested using the first eigenvector as a starting point. We have included all V eigenvectors to protect against the instance of the cluster separation being embedded orthogonal to directions of large variance. Finally, for cases when V ≤ 10, all 2^V hyperoctants are included as recommended by Switzer (1985). The starting point, a, of the algorithm is the chosen to be the vector which maximizes I across all vectors.

Step 3 generates two candidate random vectors from the unit sphere. Each vector is then multiplied by the neighborhood size, S and adds it to the original vector a. The new vectors are normalized to unit length, resulting in two new projections within the neighborhood of a. Two candidates are chosen, rather than one, as it provides an additional potential direction of movement that seems to help avoid locally optimal solutions.

Step 4 calculates the new clusterability index for both projections and chooses the value which is largest.

Step 5 compares the maximum chosen in Step 4, I^*, to the incumbent value, I. If the new value is greater, the augmented projection, a^* replaces a and the search procedure continues by returning to Step 3.

Step 6 handles the situation where the incumbent solution is preferred to the randomly perturbed solutions. If this is the case, the number of iterations is increased by one, the neighborhood is reduced by half and the value t is set equal to 1 – J/max_it. The relevant property of t is that it decreases as the number of iterations increases.

Step 7 compares t to a random variable drawn from a Uniform(0,1) distribution. If t is greater than that value, the algorithm searches the quality of a random projection in a different part of the unit sphere. This step allows a probabilistic mechanism for potentially escaping locally optimal solutions. As the neighborhood around a particular projection is investigated more fully and it is determined to be more stable, the probability of abandoning the solution decreases.

Step 8 determines when the algorithm converges. If at any time, the number of random searches around the incumbent solution (i.e., J) exceeds the maximum allowed (i.e., max_it), convergence is assumed and the algorithm is terminated. Alternatively, if the neighborhood of the search around a particular vector (i.e., S) is smaller than the minimum neighborhood size (i.e., ∊), convergence is assumed and the algorithm is terminated. If one chooses the values of S and ∊ recommended in Step 1, convergence requires 25 iterations around the same projection without a change.

After c₁ has been determined, the subsequent V × 1 linear combinations are guaranteed to be orthogonal through the Gram-Schmidt orthogonalization procedure (see Golub & Van Loan, 1996, pp. 230-232). The process proceeds the same as for c₁ except in Step 3. For instance, when searching for c_V, the appropriate step is:

• 3. Generate a from the unit sphere. Compute $\mathbf{b}=(\mathbf{a}-\sum _{i=1}^{v-1}{\mathbf{c}}_i^{\text{'}}\mathbf{a}{\mathbf{c}}_i)/\Vert \mathbf{a}-\sum _{i=1}^{v-1}{\mathbf{c}}_i^{\text{'}}\mathbf{a}{\mathbf{c}}_i\Vert$.

The final set of linear combinations is collected in C_V×V = [c₁ c₂ … c_V]. Finally, given the nature of the algorithm, it is clear that the solution is only guaranteed to be a locally optimal solution rather than a globally optimal solution. However, Jones and Sibson (1987) indicate that the local optima do not require “very high accuracy” (p. 9) because the projected data do not change abruptly with projection direction.

Choosing the Projected Dimensionality

To choose the appropriate number of principal cluster axes, we adapted a procedure illustrated by Steinley (2008). Tibshirani, Walter, and Hastie (2001) indicated that a uniform distribution is the most likely to lead to “spurious” clusters in the data space. Thus, as recommended by Lattin, Carroll, and Green (2003) when estimating the number of components in prinicpal component analysis, we adopt the following strategy ³:

1. For each of the variables in X, compute the lower and upper bounds (i.e., the minimum and maximum values observed for each of the variables). For the v^th variable, the two values are represented by LB_v and UB_v, respectively.

2. Generate an N × V data set, X_fake, where the v^th variable of X_fake is generated from a uniform distribution, U(LB_v, UB_v).

3. Conduct the principal cluster axes analysis on X_fake, computing CI for each of these projections.

4. Repeat steps one, two, and three several times (we have chosen 100 repetitions), saving the values of CI at each repetition.

5. The average values of CI for C and C_fake are plotted on the same graph (akin to scree plots in principal component analysis). The number of principal cluster axes retained corresponds to the number prior to the intersection point on the graph (for a visual demonstration, see the example below).

Detailed Example: Iris Data

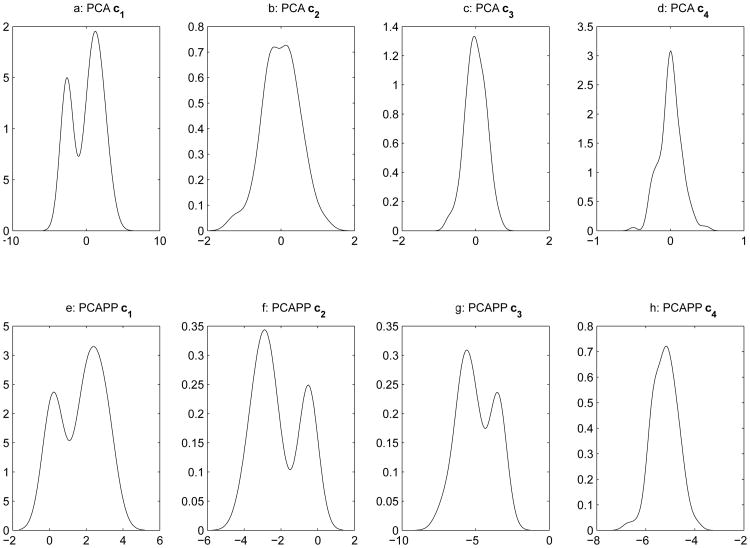
The initial example is provided on the ubiquitous Iris data (Fisher, 1936) containing measurements (in millimeters) on sepal length, sepal width, petal length, and petal width on fifty specimens from each of three species: Iris Setosa, Iris Versicolor, and, Iris Virginica. The data set provides a nice “real world” example where the cluster structure is generally assumed to be known in advance. Table 1 provides the coefficients determined for each variable across all 4 projections. Additionally, Table 1 provides the corresponding loadings extracted from a prinicpal component analysis (with the loadings from a varimax rotated PCA solution in parantheses). Figure 2 provides marginal kernel density plots of both the principal components solution (panels (a)-(d)) and the principal axes clusters solution (panels(e) - panels(h)). Upon inspection, one can see that the first component is the only component that provides a bimodal distribution and it is also the only component with a clusterability index above one. For principal axes clustering, two projections have a clusterability index above one, while three of the marginal projections exhibit bimodality in their projections.

Table 1. Principal Clusters Axes Projection Pursuit for Iris Data.

	Principal Cluster Axes				Principal Components
Variable	c1	c2	c3	c4	c1	c2	c3	c4
Sepal Length	-.0530	.2454	-.8784	-.4067	.3614	.6566	.5820	-.3155
Sepal Width	-.0428	-.1321	.3876	-.9113	-.0845	.7302	-.5979	.3197
Petal Length	.2629	-.9245	-.2761	.0043	.8587	-.1734	-.0762	.4798
Petal Width	.9624	.2602	.0443	-.0641	.3583	-.0755	-.5458	-.7534
CI	1.329	1.116	.799	.367	1.030	.4178	.4437	.2800

Figure 2. Kernel Density Plots for Comparing Marginal Projections of Both PCA and PPCAP.

When inspecting the coefficients of the principal cluster axes, it is seen that the first axis is comprised almost solely of information regarding the petal, with the most emphasis placed on width. On the other hand, the second principal cluster axis is defined mostly by petal length, with some minor contrasts with sepal length and petal width. The general interpretation attributed to the principal cluster axes should follow standard guidelines for interpreting any set of orthogonal linear combinations (i.e., principal component analysis and some variants of factor analysis).

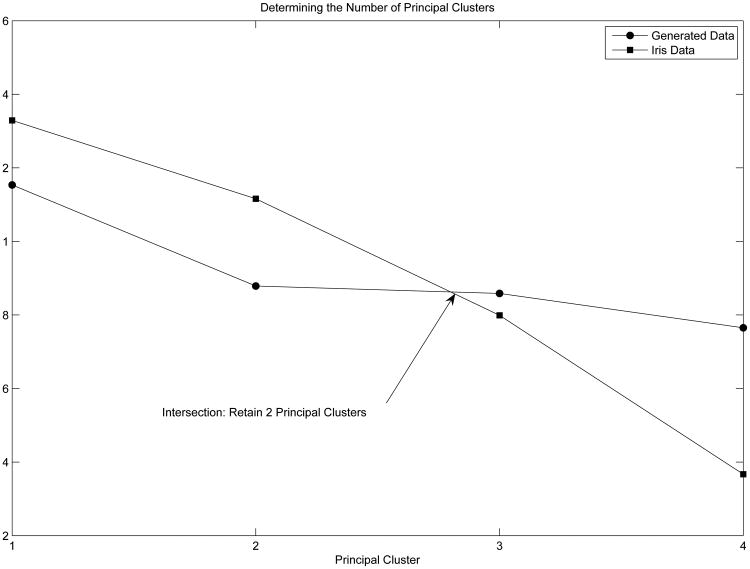
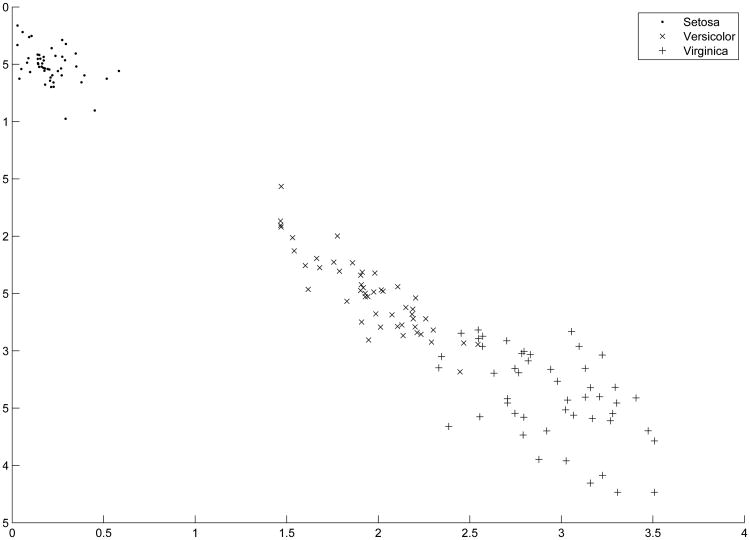
Figure 3 provides the plots to determine the dimensionality of the cluster structure. Figure 3 indicates that two principal cluster axes should be retained (note that the intersection occurs between the second and third principal cluster), while Figure 4 provides the two dimensional projection of the Iris data by PCAPP. After the appropriate projections are determined, the transformed data can be clustered using any standard procedure for finding the groups in data. The important aspect to note is that the data reduction process is independent from any clustering algorithm or other method for finding groups in data. However, the index itself is designed to highlight cluster structures that are usually sought when trying to minimize the sum-of-squares error (see Brusco & Steinley, 2007, for an extensive review). Thus, this projection pursuit procedure will be most effective when used in conjunction with techniques that optimize this criterion, some examples include: H-means (Forgy, 1965), K-means (MacQueen, 1967), HK-means (Hansen & Mladenovic, 2001), KI-means (Banfield & Bassil, 1977), J-means+ (Hansen & Mladenovic, 2001), tabu-search (Pacheco & Valencia, 2003), simulated annealing (Klein & Dubes, 1989), genetic algorithms (Maulik & Bandyopadhyay, 2000), variable neighborhood search (Hansen & Mladenovic, 2001), and Ward's method (Ward, 1963).

Figure 3. Determining the Number of principal cluster axes for the Iris Data.

Figure 4. Two Dimensional Projection of Iris Data by PCAPP.

In this example and throughout the remainder of the paper, we implement the popular K-means algorithm (Steinley 2003, 2006a, 2006b) on the reduced data sets. To evaluate the quality of the cluster analysis, we use the Hubert-Arabie adjusted Rand index (ARI; Hubert & Arabie, 1985; Steinley, 2004). For the ARI, values of unity indicate perfect cluster recovery while values of zero indicate recovery equal to chance. When clustering the direction of the first principal cluster axis, the ARI is .9030, and adding the second principal cluster axis raises the ARI to .9410–the equivalent result of conducting a discriminant analysis (see Figure 3 for a graphical depiction of the transformed data in the principal cluster axes space). Thus, using the PCAPP on the Iris data set results in a solution that is equivalent to knowing the original group structure.

Comparison to Existing Methods

K-means Clustering

In order to illustrate the utility of the proposed procedure, comparisons were made to a selected set of existing procedures in the literature. The methods chosen for comparison are recent methods that have been proposed to find clustering in low-dimensional space. Many of the methods rely on a combination of cluster analysis and dimensionality reduction. Thus, the following notation is adapted to introduce a clustering procedure into the process. All of the methods utilize the popular K-means clustering procedure (MacQueen, 1967). Recalling that X is the N × V data matrix, the goal of K-means clustering is to assign each object into one of K clusters to minimize

$$F(\mathbf{R},\mathbf{M})=\text{tr}[{(\mathbf{X}-\mathbf{M}R)}^{\prime }(\mathbf{X}-\mathbf{M}R)],$$ (7)

where R is a K × V matrix with each row being the centroid vector for the k^th clusters and an N × K membership matrix, M where m_ik = 1 if object i belongs to the k^th cluster. The general estimation procedure is to use an alternating least squares algorithm that alternates between minimizing (7) with respect to M given the current estimate of R and minimizing (7) with respect to R given the current cluster membership.

Principal Component Analysis

Principal component analysis has long been used to reduce the dimensionality of data sets. Some authors, as recently as Ben-Hur, Horn, Siegelmann, and Vapnik (2001) and De Backer and Scheunders (1999), advocate conducing a principal component analysis on the original data set X and then clustering the data that is projected into the space of the principal components, denoted as P = XA_U, where A_U is a U-dimensional matrix of orthonormal projections (i.e., the first U eigenvectors of X′X). This basically transforms the original objective function in (7) into

$$F({\mathbf{R}}^{(U)},\mathbf{M})=\text{tr}[{({\mathbf{P}}_{N\times U}-{\mathbf{M}}_{N\times K}{\mathbf{R}}_{K\times U}^{(U)})}^{\prime }({\mathbf{P}}_{N\times U}-{\mathbf{M}}_{N\times K}{\mathbf{R}}_{K\times U}^{(U)})],$$ (8)

where R^(U) is a K times; U matrix of cluster centroids in reduced space. However, this process-often referred to as tandem analysis-has long been cautioned against (see Chang, 1983; Arabie & Hubert, 1994). The primary caution is that while the first few principal components define the directions which account for the maximum amount of variance in the original data they do not necessarily result in a subspace that is most representative of the cluster structure present in the data.

Reduced K-means (De Soete & Carroll, 1994)

De Soete and Carroll (1994) attempted to incorporate clustering and data reduction into the same objective function. Their insight was to rewrite (7) as

$$F(\mathbf{R},\mathbf{M})=\sum _{i=1}^N\sum _{v=1}^V{(x_{iv}-\sum _{k=1}^K{m}_{ik}{r}_{kv})}^2$$ (9)

and then rewriting (7) as

$$F(\mathbf{R},\mathbf{M})=\sum _{i=1}^N\sum _{k=1}^K{m}_{ik}\sum _{v=1}^V{(x_{iv}-y_{kv})}^2+\sum _{k=1}^K{n}_k\sum _{v=1}^V{(y_{kv}-r_{kv})}^2$$ (10)

where $y_{kv}=n_k^{-1}{\sum }_{i=1}^N{m}_{ik}{x}_{iv}$ and n_k is the number of objects in the k^th cluster. The key to this problem is that De Soete and Carroll (1994) required the rank of R to be U (i.e., the K centroids are restricted to lie in a U-dimensional subspace). Like the standard K-means algorithm, (8) is minimized by an alternating least squares algorithm that alternates between minimizing with respect to R given M and minimizing with respect to M given R.

Given R, the estimate of M is determined by assigning each object to the cluster

$$\begin{array}{cc}{m}_{ik}=1\iff \sum _{v=1}^V{(x_{ij}-r_{kj})}^2<\sum _{v=1}^V{(x_{ij}-r_{k\ast j})}^2\forall k^{\ast }=1,\dots ,K& k\ne k^{\ast }\end{array}$$ (11)

and m_ik = 0 otherwise. Once M is determined the estimate of R is updated by

$$\mathbf{R}={\mathbf{N}}^{-1/2}{\mathbf{U}}_U{\mathbf{\Lambda }}_U{\mathbf{V}}_U^{\prime }$$ (12)

where ${\mathbf{U}}_U{\mathbf{\Lambda }}_U{\mathbf{V}}_U^{\prime }$ is the rank U truncated singular value decomposition of N^1/2Y and N ≡ diag(n₁, n₂, …, n_K). The algorithm proceeds by updating M via (9) and R via (10) until no change occurs in M. Like the standard K-means algorithm, either initial estimates of R or M is required. Following the recommendation in Steinley (2003) and Steinley and Brusco (2007), which includes estimating the best clustering from 5,000 random initializations of the K-means algorithm, we provide an initial estimate of M derived from conducting a K-means clustering of X in the full V-dimensional data space. To insure that these initial values for M were reasonable, we also initialized M with 1,000 random initializations.

Factorial K-means (Vichi & Kiers, 2001)

Vichi and Kiers (2001) postulated the model

$$\mathbf{X}\mathbf{B}{\mathbf{B}}^{\prime }=\mathbf{M}\mathbf{R}{\mathbf{B}}^{\prime }+\mathbf{E}$$ (13)

where E is a matrix of error components and B is a columnwise orthonormal matrix. The coordinates of the projections onto the orthonormal subspace are given by D = XB. Then, the minimized function is

$$F(\mathbf{B},\mathbf{M})=\text{tr}[{(\mathbf{X}B-\mathbf{M}{\mathbf{R}}^{\ast })}^{\prime }(\mathbf{X}B-\mathbf{M}{\mathbf{R}}^{\ast })],$$ (14)

where R^* = (M′M)⁻¹M′XB. The algorithm proceeds by

1. Choosing initial values for B and M. For initialization, we chose B = A (i.e., the eigendecomposition used in principal component analysis) and M was chosen from a K-means clustering on X in V-dimensional space. After the initial estimates of B and M were chosen, R^* was computed via (12). To insure that these initial values for M were reasonable, we also initialized M with 1,000 random initializations.

2. Given the current estimate of B and R^* update M by assigning d_ij to the cluster centroid in the lower dimensional space that it is closest (i.e., compute the Euclidean distance between each projected object and each projected cluster centroid).

3. Set B equal to the first U eigenvectors of X′(M(M′M)⁻¹M′ – I_N)X, then set R^* = (M′M)⁻¹M′XB.

4. Repeat Steps 2 and 3 until M remains unchanged between subsequent iterations. For a detailed discussion concerning the relationship between the Vichi and Kiers (2001) procedure and the DeSoete and Carroll (1994) procedure, the interested readers are referred to Timmerman, Ceulemans, Kiers, & Vichi (2010).

Simulation

Prior to analyzing real-world data sets, the procedures were compared across several factors. To our knowledge, this is the first systematic simulation involving varying factors while investigating a range of projection pursuit indices and data reduction techniques for their ability to recover an embedded cluster structure. The six procedures compared were: (i) K-means clustering (KM) on the non-reduced data set to provide a baseline of performance, (ii) tandem analysis (TA; principal component analysis followed by cluster analysis), (iii) reduced K-means (RKM), (iv) factorial K-means (FKM), (v) projection pursuit clustering using the measure based on kurtosis (PPCK; see Equation 2) and, (vi) principal cluster axes projection pursuit (PCAPP). To maintain focus on the index, the same projection pursuit algorithm is used for both the kurtosis index and the proposed method, with the only change being how I is computed within the algorithm. The “between-methods” factors that were manipulated were: (a) the number of true variables, defined as the subspace of variables that define the cluster structure and assuming four levels TV = 4, 6, 8, 12, (b) the number of masking variables, defined as variables exhibiting no cluster structure (i.e., merely noise) and assuming four levels MV = 4, 6, 8, 12, (c) the relative density of each cluster, assuming levels 10%, 60%, and equal, with the first level indicating there is one small cluster that has 10% of all observations while the other 90% of observations is divided between the remaining K – 1 clusters (a similar definition is given for 60%, while equal indicates all clusters are of equal size), and (d) the number of clusters, assuming three levels K = 4, 6, 8.

The true cluster structure was generated following the procedure outlined in Milligan (1985), which ensures that each cluster is well-separated (e.g., using Cormack's, 1971, definition, they are internally cohesive and externally isolated) on some subspace of the data. The masking variables were generated from spherical multivariate normal distributions with variance equal to the largest variance of the variables defining the cluster structure. This condition ensures that any discovered structure is not due to coincidence of a large variance, the primary reason that principal component analysis can seem to be successful in certain situations. Every data set was generated with 200 observations and all conditions were completely crossed (resulting in 144 separate conditions). Consistent with the prior literature on evaluating cluster analysis techniques, each condition was replicated three times (see Milligan, 1980; Milligan & Cooper, 1985; Steinley, 2003, 2006).

Each procedure projected the higher dimensional data into a lower dimensionality defined per the method described above. Thus, the proposed method, PCAPP, chose the dimensionality and then the remaining five methods also projected the full data set into the chosen dimensionality with the goal of determining if the competing methods can maintain the fidelity of the cluster structure to the same degree as the proposed technique. To determine how well the cluster structure was maintained in the lower dimensional representation, each of the projected data sets were cluster analyzed with K-means clustering per the guidelines outlined in Steinley and Brusco (2007). The resultant partitions were compared with the “true” cluster structure by computing the adjusted Rand index, recalling that values of one indicate perfect agreement and values of zero indicate chance agreement. Table 3 provides the mean adjusted Rand index by each factor level for all of the approaches.

Table 3. Mean Differences of Adjusted Rand Indices Between PCAPP and Other Methods.

Comparison	Difference in Means	SD	Effect Sizes†
PCAPP vs. KM	(.51-.26)=.25**	.29	1.28
PCAPP vs. TA	(.51-.18)=.33**	.28	1.69
PCAPP vs. RKM	(.51-.31)=.20**	.30	0.95
PCAPP vs. FKM	(.51-.17)=.34**	.30	1.65
PCAPP vs. PPK	(.51-.06)=.45**	.22	3.09

Note. df = 431 for each t-test.

^**p ≤ .0001, two-tailed.

^†the effect size was computed assuming independent groups to protect against over-inflating the estimate as recommended by Dunlop, Cortina, Vaslow, and Burke (1996).

KM = K-means clustering; TA = Tandem Analysis; RKM = Reduced K-means; FKM = Factorial K-means; PPK = Projection Pursuit Kurtosis; PCAPP = Principal Cluster Axes Projection Pursuit.

Within each row, an asterisk denotes the best-performing method, on average, for a particular factor level. Across all levels, PCAPP has the greatest cluster recovery. Conversely, the projection-pursuit method relying on the third and fourth cumulants has the worst cluster recovery across all levels. Unexpectedly, the multiple restarts for FKM and RKM performed worse than those same procedures initialized with a K-means clustering on the full data sets. The performance of K-means clustering on the full-dimensional data set mirrored results found in Milligan (1980), Steinley (2003 Steinley (2006) and Steinley and Brusco (2011a and Steinley and Brusco (2011b). Given the best performance across all conditions is observed for PCAPP, discussion of effects focuses on this technique. As it turns out, the effects of each of the factors are what we would expect.

First, as the number of clusters increases, the ability to reliably detect them in a reduced dimensionality decreases. To some degree, this is to be expected as projecting points from a higher dimensional space into a lower dimensional space increases the chances that the clusters will overlap. Second, for PCAPP there is a reduced cluster recovery as the number of cluster defining variables increases; whereas, for the other methods, recovery increases as the number of true variables increases. This is most likely due to the nature of the cluster generation algorithm pioneered by Milligan (1985). Specifically, for any pair of clusters, they are only guaranteed to not overlap on one of the V dimensions. Furthermore, each of the $(\begin{array}{c}K\\ 2\end{array})$ pairs of clusters may be separated on different dimensions. Thus, as the number of variables increase and the number of clusters increase, it is highly likely that there is not a unidimensional projection through the V-dimensional space that captures all of the cluster separation. The number of masking variables does not have as strong of an effect on PCAAP as the other methods, which is consistent with the results provided in Steinley and Brusco (2008b) concerning the robustness of the clusterability index with respect to irrelevant noise in the data. Finally, for cluster density, the best performance is when all clusters are of equal size — this is consistent with the expected properties of K-means clustering (see Steinley & Brusco, 2011a see Steinley & Brusco, 2011b) and may be a consequence of clustering the projected data with K-means clustering rather than an inherent property of the projection pursuit procedure.

Data Sets

The first comparison will be carried out using the Iris data set from the detailed example provided above. The second data set is the Crab data set discussed in Venables and Ripley (1999). The 200 crabs are either orange or blue and male or female, resulting in four real groups of crabs. Additionally, there are five measurements that serve as variables: carapace length (CL), carapace width (CW), frontal lobe (FL), rear width (RW), and body depth (BD). There is good separation between the colors but not between the sexes. The third data set is the forensic Glass data set (Ripley, 1996) containing 214 glass fragments with measurements of the proportions of eight elements and the refraction index, resulting in a total of nine variables.

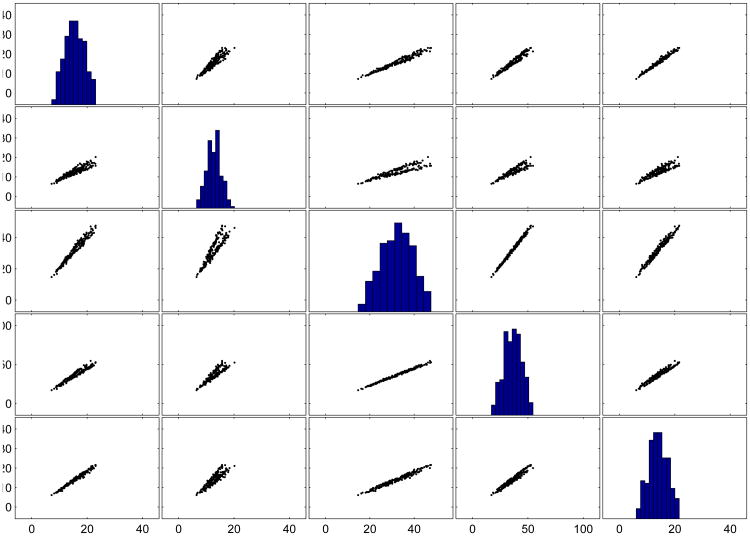
Table 4 provides the general cluster recovery for the proposed procedure, the four alternative procedures, and a K-means cluster analysis on the original data set. For the Iris data, the projection pursuit procedure using kurtosis performs the worst of all the procedures, while PCAPP technique performed 29% better than the next best method. The crab data set consists of highly correlated variables and is more difficult to cluster than the Iris data. Figure 5 depicts the bivariate scatterplot matrix of the crab data (where the univariate histograms are depicted on the diagonal). Inspection of the scatterplots reveals that it is difficult to detect any separation between the bivariate distributions and the histograms are all unimodal in nature. This trend is further reflected in the recovery of the cluster structure by the K-means clustering of the original data–a dismal .0157 ARI.

Table 4. Cluster Recovery (ARI) for Example Data Sets by Technique.

	Dataset
Technique	Iris	Crab	Glass
K-means	.7302	.0157	.2702
Principal Component Analysis (Tandem Analysis)	.7163	.0207	.2501
Reduced K-means	.7302	.0157	.2542
Factorial K-means	.7163	.0068	.0694
Projection Pursuit Kurtosis	.6743	.0176	.0548
Principal Cluster Axes Projection Pursuit	.9410	.7876	.2841

Figure 5. Bivariate Scatterplot Matrix of Crab Data.

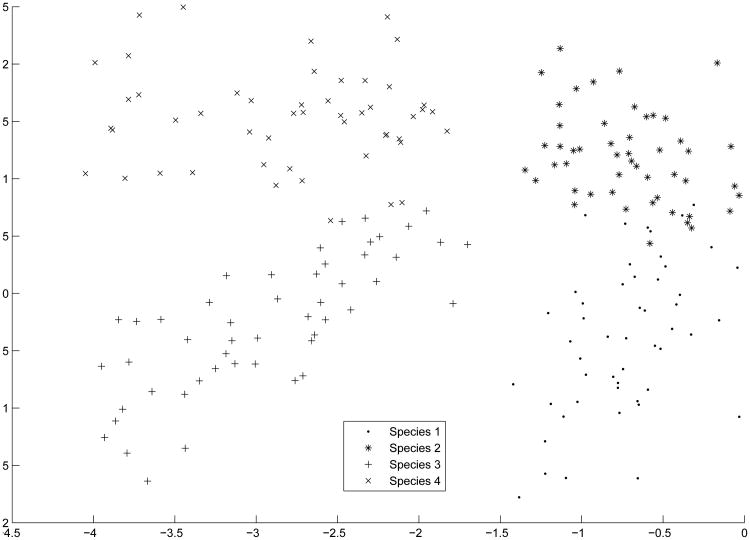
In fact, all of the competing methods had an ARI of near chance performance. Conversely, the principal clustering procedure exhibited an ARI = .7876, an average of 5,879.2% better than the other methods. The lower dimensional representation is depicted in Figure 6. As is seen in Figure 4, the clusters are not spherical in nature. Thus, if a different clustering procedure was chosen that was more appropriate for elliptical clusters (e.g., finite mixture model), cluster recovery would likely improve. We did not do so here because the competing methods use K-means clustering as an integral part of their dimensionality reduction process and we did not want to confound the results with the clustering algorithm chosen for the analysis.

Figure 6. Principal Cluster Axes of Crab Data.

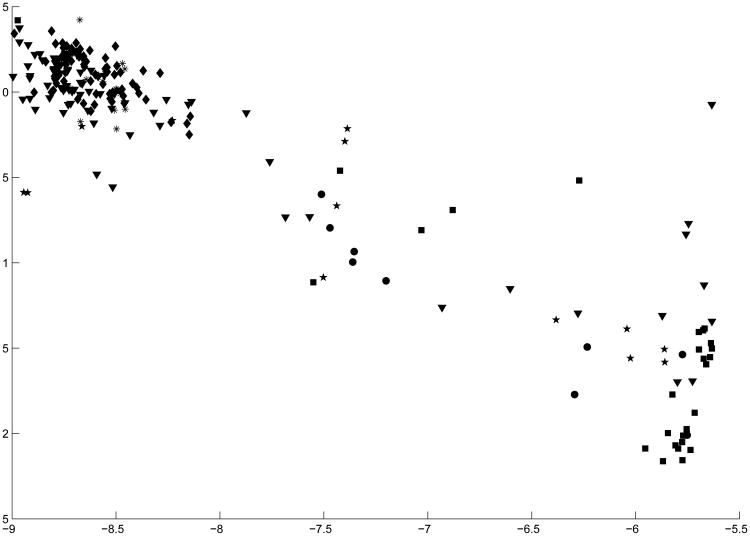
The performances of all methods for the Glass data were very poor. The projection pursuit and factorial K-means procedures performed near chance recovery levels, while the remaining methods exhibited ARI's between .25 and .30. PCAPP performed the best, but it was not an outstanding level of cluster recovery. Figure 7 displays the projected space of the six clusters in the GLASS data. As can be seen, most of the clusters do not appear to be well separated. In fact, the projected data appear to lie on a fairly continuous one-dimensional line through space. If the groups of glass that appear in the middle of the continuum were sampled more, this may provide an argument for some type of common factor model. More generally, if the projected space exhibits very little cluster structure, it is likely that a strong cluster structure does not exist in the high-dimensional data⁴. In fact, Steinley and McDonald (2007) extensively discuss the relationship between the factor model and the ability to detect cluster structure in a reduced (i.e., latent) space.

Figure 7. Principal Cluster Axes of Glass Data.

Analysis of Empirical Data: Supreme Court Justices

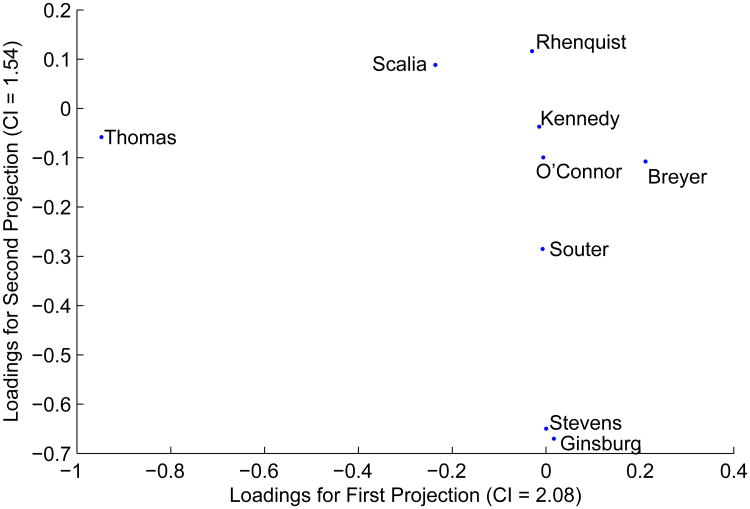
For this example, we analyze the voting records of the Supreme Court Justices on the so-called “Rhenquist Court” (e.g., the Supreme Court from 1994/95 – 2003/04)⁵. Hubert and Steinley (2005) analyzed a proximity matrix derived from these data in an attempt to determine whether a categorical or continuous model was more appropriate. For the present analysis, the data set consists of 971 court cases (e.g., the observations of the data set) and nine variables (e.g., the Supreme Court Justices). After removing cases where some of the justices did not vote and all cases where there was a unanimous decision, 507 cases remained. Subsequently, in this analysis, the specific cases are of less interest; rather, the interest is in how the projections are defined in relation to the original variables. The nine projections are given in Table 5. According to the method for determining the number of dimensions, two projections were adequate to represent the cluster structure in reduced space. Figure 8 plots the loadings for the first two projections. In general, there are broad agreements with these results and the unidimensional representation provided by Hubert and Steinley (2005), and it is quite natural to visualize the conservative faction of the Supreme Court (e.g., Thomas, Scalia, Rhenquist) as being on the opposite side of the two dimensional space as the more liberal faction (e.g., Ginsberg, Stevens, Souter), both of which are separated by the other three members (e.g., O'Connor, Kennedy, Breyer). However, there are some subtle differences in the interpretation than that provided by either the unidimensional scaling or the ultrametric representation (a form of hierarchical clustering) previously presented.

Table 5. Projections for Supreme Court Data.

				Projections
Rehnquist	-0.03	0.12	0.83	-0.26	-0.16	-0.21	0.08	0.37	0.12
Stevens	0.00	-0.65	-0.01	-0.13	-0.27	0.10	0.68	-0.11	0.08
O'Connor	-0.01	-0.10	0.09	0.91	-0.09	-0.20	0.12	0.29	-0.01
Scalia	-0.24	0.09	0.36	0.17	0.01	-0.24	0.05	-0.83	-0.16
Kennedy	-0.01	-0.04	0.35	0.16	0.28	0.81	0.03	0.01	-0.33
Souter	-0.01	-0.29	-0.03	-0.16	0.24	-0.38	-0.02	0.19	-0.81
Thomas	-0.95	-0.06	-0.10	-0.04	0.19	0.02	0.02	0.18	0.13
Ginsburg	0.02	-0.67	0.17	0.02	-0.02	0.01	-0.68	-0.08	0.21
Breyer	0.21	-0.11	0.08	0.01	0.85	-0.19	0.22	-0.03	0.36
CI	2.08	1.54	0.92	0.91	0.71	0.53	0.45	0.38	0.34

Figure 8. Loadings for Dimensions for Supreme Court Justice Data.

The primary interpretation derived from the current projections is what mostly determines the cluster structure in the reduced dimensionality are Justices Thomas, Scalia, and Breyer on the first dimension and Stevens and Ginsburg (with Souter, Rhenquist, and Scalia to a lesser degree) on the second dimension. To demonstrate why this analysis does not strictly follow the unidimensional representation in Hubert and Steinley (2005), a more in-depth analysis of voting patterns is required. For ease of presentation, we focus first on Justice Thomas and Justice Breyer as they anchor the two ends of the first dimension. Of the 507 cases, Justices Thomas and Breyer agreed 172 times, and of those agreements 168 of them placed them in the majority and four placed them in the minority vote. Additionally, the number of 5-4 decisions in which Thomas and Breyer were in the majority was only 12. Similarly, the number of agreements for 6-3, 7-2, and 8-1 decisions were 38, 40, and 78, respectively. Furthermore, when Thomas and Breyer are in agreement, Rhenquist and Stevens are only in agreement 23 (out of 121) times. Furthermore, Thomas, Breyer, Rhenquist, and Stevens are never in agreement in a 5-4 split (of which there are 188), whether it be in the majority or the minority. For 6-3 splits, they are in agreement 3 times (out of 118); for 7-2 splits, they are in agreement 8 times (out of 111); for 8-1 splits, they are in agreement 12 times (out of 90).

These four judges lack enough mutual overlap to provide a strong separation between the sets of cases. This is expected, as PCAPP focuses on the variables (in this case, judges) who provide the most discrimination – which would be the judges that are less likely to “bridge” the two ends of the political spectrum. Whereas specific case information was not included in the downloaded file, it is likely that substantive knowledge concerning the types of cases in which the Supreme Court Justices agreed/disagreed would provide a more nuanced view than purely conservative vs. liberal.

Discussion

A procedure has been proposed to preserve the cluster structure in a high-dimensional data set on a “few” lower dimensional projections. Termed principal cluster axes projection pursuit, the spirit of the procedure is similar to that of principal component analysis. Specifically, the relevant cluster information is preserved in a set of orthogonal projections. When analyzing several data sets previously used in the literature, we found that the proposed procedure was superior in terms of cluster recovery.

The main advantage of principal cluster analysis is that the data reduction is independent of the clustering algorithm employed by the analyst. This is the distinction that likely results in the observed performance difference. The likely Achilles' heels of the competing procedures examined here are:

1. If the full data set is clustered via K-means, it has been repeatedly shown that noisy dimensions, or merely ill-defined cluster structure, can have a detrimental effect on cluster recovery (see Milligan, 1980; Steinley, 2003, 2006b).

2. It has long been known that standard data reduction practices are poor precursors to a cluster analysis. Primarily, the objective functions that are maximized during procedures such as principal component analysis or factor analysis are not congruent with preserving cluster structure (see Chang, 1983; Arabie & Hubert, 1994). Additionally, it has long been argued that principal component analysis does a poor job of identifying heterogeneity in the data.

3. The Reduced K-means procedure suffers from the fact that it requires an initial estimate of the cluster membership. The procedure then uses the initial estimate of the cluster membership to obtain a lower-dimensional projection. Unfortunately, obtaining a rational estimate for the cluster membership could be compromised by extraneous information in the data space (see Point #1). All results are extremely dependent on this initial estimate.

4. Similar to Reduced K-means, Factorial K-means requires an initial estimate of the cluster structure and an initial estimate of the projection. Moreover, the final results can be severely impacted by initial choices. Vichi & Kiers (2001) recommend using prior analysis of the data to determine the initial values. However, as seen in Points #1 and #2, prior analyses of the data can be corrupted if there is a sufficient amount of noise or if the objective functions do not correspond with the goals of cluster analysis. Both the logical choices for determining the initial cluster analysis (e.g., conducting a cluster analysis on the full data) and principal component analysis (a standard eigendecomposition on the covariance matrix) suffer from this drawback.

5. Surprisingly, using multiple random restarts for both Reduced K-means and Factorial K-means did not improve the results over the rationally started procedures. We hypothesize that if the initialization is completely random in the higher dimension, then there is nothing to “tether” the cluster structure in the reduced dimensionality to the true cluster structure that is embedded in the full dimensional space. Prior research (Milligan, 1980; Steinley, 2003; 2006b, Steinley & Brusco, 2008a) has shown that while noisy dimensions degrade cluster performance, cluster recovery still remains above chance levels. Thus, conducting a K-means clustering on the full data set results in a starting point for the data reduction that still contains some information about the true cluster structure. Conversely, when using random initialization, the data reduction procedure starts from “no information” about the true cluster structure, resulting in degraded performance in the long run.

The proposed technique navigates around these weaknesses and provides the additional flexibility of accommodating many procedures that are geared at finding groups in data.

Potential Limitations and Future Directions

The orthogonality constraint introduced by the extraction process allows for a couple of desirable properties; namely, the independence of each of the projected dimensions. This independence allows both for an additive nature between the dimensions and the ability to demarcate how much “clusterability” is accounted for by each projection. One potential limitation is that the projection pursuit procedure designed here extracts one dimension at a time in a sequential fashion. It is entirely possible that interesting structure may be embedded completely in a joint lower dimensional space that cannot be realized by a series of unidimensional projections. Indeed, the clusters for the simulation were generated in such a fashion. However, Huber (1985) indicates that one dimension at a time is a reasonable place to start. Furthermore, the ordered set of projections provided here are easier to interpret as a multidimensional projection requires the interpretation of the full subspace. From a theoretical perspective, understanding the properties of the index for one-dimensional projections will aid in generalizing the current index to one that is appropriate for multivariate projections (e.g., planer projections and beyond), allowing for the inclusions of subspaces that are oblique and effectively eliminating the orthogonality constraint. One avenue of future research is to develop a multivariate index and augment the projection pursuit algorithm in such a manner that the optimization over U * V variables is not too computationally demanding for practical purposes.

Another property that deserves further investigation is the decrease in cluster recovery as the number of true variables increases and the eventual ability of masking variables to swamp the true variables (a similar result was observed in Steinley & Brusco, 2008b). What this suggests is that neither variable selection or data reduction should be used independently, but rather as complementary procedures with results that mutually reinforce the other. Currently, we are working on a hybrid procedure that combines variable selection with data reduction, with the goal being to conduct data reduction on the most “pure” cluster variables. The logic behind the hybrid procedure is that, if masking variables are in the system, they will be included — even if only to a minimal degree – in each projection because the projections include information about every one of the original variables. Eventually, if there are enough masking variables (e.g., too much noise) it will be highly unlikely for any data reduction technique to be successful.

Table 2. Mean ARI by Method and Factor Level.

Factor		KM	TA	RKM	FKM	PPK	PCAPP
# of Clusters	4	.30	.23	.39 (.23)	.21 (.12)	.06	.64*
	6	.24	.18	.31 (.19)	.15 (.14)	.07	.49*
	8	.23	.14	.24 (.16)	.15 (.12)	.06	.41*
# of True Variables	2	.14	.07	.16 (.16)	.11 (.10)	.04	.58*
	4	.19	.12	.27 (.19)	.15 (.12)	.06	.52*
	6	.22	.21	.33 (.23)	.18 (.16)	.07	.48*
	12	.46	.34	.46 (.34)	.24 (.21)	.08	.47*
# of Masking Variables	2	.36	.29	.45 (.27)	.29 (.20)	.11	.53*
	4	.29	.20	.36 (.24)	.18 (.14)	.18	.52*
	6	.22	.16	.28 (.19)	.13 (.12)	.13	.54*
	12	.15	.08	.16 (.08)	.08 (.06)	.02	.42*
Cluster Density	Equal	.26	.18	.32 (.17)	.11 (.12)	.04	.56*
	10%	.30	.19	.34 (.17)	.14 (.10)	.06	.51*
	60%	.20	.18	.28 (.25)	.26 (.17)	.09	.45*

Note: KM = K-means clustering; TA = Tandem Analysis; RKM = Reduced K-means; FKM = Factorial K-means; PPK = Projection Pursuit Kurtosis; PCAPP = Principal Cluster Axes Projection Pursuit. For FKM and RKM, the values in parantheses are the results from the multiple random restarts with 1,000 random restarts.